Power Law Fluid Film Lubrication of Journal Bearing with Squeezing and Temperature Effects

Abstract

This paper presents theoretical investigations of the rheological effects of lubricant on the performance of the Journal bearing system under steady state condition including squeezing. Runga Kutta Fehlberg method is employed to solve the Reynolds and the energy equations governing the flow of power law fluids simultaneously. Those equations are coupled due to the consistency which is a function of pressure and temperature both. The results show that this simple innovative model can reasonably calculate delta profile and hence the pressure and the temperature. The obtained results that the pressure and the temperature both increase with the power law flow index n and decrease with the increase of the squeezing parameter q. These results are found to be similar to the results available in the literature.

1 Introduction

The squeeze is an important issue from many tribological aspects. This feature significantly affects minimum film thickness, pressure and temperature distributions in concentrated contact film mechanism. During squeezing, the surfaces come closer to each other so it can also increase the risk of wear, scuffing and pitting if the surfaces are not enough smooth. Further, it is commonly observed in the bearings of automotive engines, aircraft engines, machine tools, turbo machinery, and skeletal joints. There are several investigations done on squeezing and some of them are Lin, Oliver and Scot [1–3].

Conventionally, the prediction of squeeze film motion assumes that the lubricant behaves as a Newtonian viscous fluid. However, experimental results show that the addition of small amounts of long-chained additives to a Newtonian fluid minimizes the sensitivity of the lubricant to change in shear rate and provides beneficial effects on the load-carrying and frictional characteristics [2, 3]. Moreover, a base oil blended with additives can stabilize the behavior of lubricants in elasto hydrodynamic contacts and reduce friction and surface damage, which describe the rheological behavior of non-Newtonian lubricants [4].

In addition, high pressure in concentrated contact can influence the temperature rise there, and hence it introduces the field of thermo hydrodynamic lubrication which measures the performance of journal bearings with thermal effects in the lubrication process. Since it can naturally yield the peak bearing temperature, then the bearing failure can be predicted at the design stage when the maximum temperature exceeds a certain limit. The research into THD lubrication has drawn research effort. For example, Ferron [5] solved Dowson’s [6] generalized Reynolds equation simultaneously with the energy equation and reported excellent results. Khonsari and Beaman [7] obtained THD solutions under severe boundary conditions considering the mixing of the recirculating fluid and the supply oil.

On the line of non-Newtonian fluid model, Power law lubricant model has got attention in the recent years because of its simplicity and potential to describe many lubricants such as silicon fluids, polymer solutions Chu et al. [8], Suneetha et al. [9]. In fact, this power law model characterizes two different types of non-Newtonian fluids i.e. Viscoelastic and dilatants plus Newtonian as well when index n of the power law model is unity [10]. Dein and Elrod [11] examined the analysis of lubrication of journal bearing with the same non-Newtonian fluid model and developed a new numerical technique based on perturbation expansion for velocity under Couette dominated flow condition.

Xiong and Wang [12] investigated a steady state problem of smooth surface hydrodynamic lubrication of a pocketed pad plain journal bearing based on Payvar—Salant mass conservation model leaving the importance of thermal effect. Balasoiu et al. [13] presented a 3D analysis of cylindrical porous journal bearing characterized by a self circulating lubricating system that eliminates the necessity of external pump. However, the thermal effect was also ignored. Further, in contrast to the heavy loaded system it has been believed that in conformal contact such as in journal bearings and thrust bearing elastic deformation can be ignored under low load because the fluid pressure is insufficient to cause large deformation of the surfaces Yagi and Sugimura [14].

Hence in this paper, hydrodynamic lubrication of rigid journal bearing with the power law is studied including thermal and squeezing effects. The consistency of the lubricant is assumed to vary with pressure and fluid film mean temperature. The last assumption and the condition of rigidity of the bearing surfaces in fact provide us the solution in almost closed form.

2 Mathematical Formulation

2.1 Fluid Flow Governing Equations

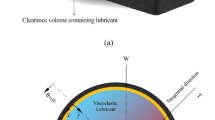
The fluid flow governing equations of the hydrodynamic lubrication with some usual assumptions are [15] (Fig. 1).

Fig. 1

Journal bearing

$$ \frac{\text{d}p}{\text{d}x}\,\, = \,\,\frac{\partial }{\partial y}\left[ {m\left| {\frac{\partial u}{\partial y}} \right|^{n - 1} \frac{\partial u}{\partial y}} \right] $$

(1)

$$ \frac{\partial u}{\partial x}\, + \,\frac{\partial v}{\partial y}\,\, = \,\,0 $$

(2)

where

$$ m = m_{0} e^{{\alpha p - \beta (T_{m} - T_{0} )}} $$

(3)

with

$$ T_{m} \,\, = \,\,\frac{1}{h}\,\,\int\limits_{0}^{h} {T\,\,dy} $$

(4)

and

$$ h = \,c\,(1 - \varepsilon \,\cos \,\theta) $$

(5)

Let y = h₁ be the height where the velocity gradient $\frac{\partial u}{\partial y}\, = \,0$

The boundary conditions for the above governing equations are:

$$ u = 0, \;at \;y =0;\; {\text{and}}\;u = 0\;at\;y = h $$

(6)

The velocity boundary conditions for the geometry under consideration are:

$$ \frac{{\partial u_{1} }}{\partial y}\,\, \ge \,\,0,\,\,\,0 \le y\,\, \le \,\,h_{1} $$

(7)

$$ \frac{{\partial u_{2} }}{dy}\,\, \le \,\,0\,\,,\,\,\,h_{1} \,\, \le \,\,y\,\, \le \,\,h, $$

(8)

Using the sign of the velocity gradient and integrating Eq. (1) twice for $0\, \le \,\,y\,\, \le \,\,h_{1}$; one may obtain

$$ u_{1} \,\, = \,\,\,\,\left( {\frac{n}{n + 1}} \right)\left( { -\frac{1}{m}\frac{dp}{dx}} \right)^{1/n}\left[ {(h_{1} )^{{\frac{n + 1}{n}}} \, - \,\left( {h_{1} - y} \right)^{{\frac{n + 1}{n}}} } \right], $$

(9)

And similarly for $h_{1} \, \le \,\,y\,\, \le \,\,h$

$$ u_{2} \, = \,\,\,\left( {\frac{n}{n + 1}} \right)\left( { -\frac{1}{{m_{1} }}\frac{dp}{dx}} \right)^{1/n}\left[ {(h - h_{1} )^{{\frac{n + 1}{n}}} \, - \,\left( {y - h_{1} } \right)^{{\frac{n + 1}{n}}} } \right], $$

(10)

At ${y} = {h}_{ 1}$ the velocities are continuous so from Eqs. (9) and (10) one can get $\left( {h\, - \,h_{1} } \right)^{{\frac{n + 1}{n}}} \, = \,\left( {h_{1} } \right)^{{\frac{n + 1}{n}}}$ which gives ${h}_{ 1} = {h}/ 2,$ Thus the flow is symmetrical about the middle point of the film thickness.

Hence we can write the equation (9) and (10) as

$$ u_{1} \,\, = \,\,\,\,\left( {\frac{n}{n + 1}} \right)\left( { -\frac{1}{m}\frac{dp}{dx}} \right)^{1/n}\,\left[ {\left( \frac{h}{2} \right)^{{\frac{n + 1}{n}}} \, - \,\left( {\frac{h}{2} - y} \right)^{{\frac{n + 1}{n}}} } \right], $$

(11)

$$ u_{2} \,\, = \,\,\,\,\left( {\frac{n}{n + 1}} \right)\left( { - \frac{1}{m}\frac{dp}{dx}} \right)^{1/n} \,\left[ {\left( \frac{h}{2} \right)^{{\frac{n + 1}{n}}} \, - \,\left( {y - \frac{h}{2}} \right)^{{\frac{n + 1}{n}}} } \right], $$

(12)

Now the volume flux Q of the fluid is defined as

$$ Q\, = \int\limits_{0}^{h} {u\,\,\,dy} $$

(13)

or

$$ Q\,\, = \,\,\int\limits_{0}^{h/2} {u_{1} } \,dy\,\, + \,\,\int\limits_{h/2}^{h} {u_{2} } \,dy $$

(14)

or

$$ Q\, = \,\,\left( {\frac{2n}{2n + 1}} \right)\left( { - \frac{1}{m}\frac{dp}{dx}} \right)^{1/n} \,\left( \frac{h}{2} \right)^{{\frac{2n + 1}{n}}} $$

(15)

Now the equation of continuity $\frac{\partial u}{\partial x}\, + \,\frac{\partial v}{\partial y}\,\, = \,\,0$ can be solved with respect to the boundary conditions for v which are ${v} = \, - {V}$ at ${{y }} = \, 0$ and ${v} = \, 0$ at ${y} = {h}$ we get

$$ \frac{\partial \,Q}{\partial \,x}\, = \, - \,V $$

(16)

Using Eqs. (15) into (16) it comes over to be

$$ \frac{\partial }{\partial x}\left[ {\,\,\left( {\frac{2n}{2n + 1}} \right)\left( { -\frac{1}{m}\frac{dp}{dx}} \right)^{1/n} \,\left( \frac{h}{2} \right)^{{\frac{2n + 1}{n}}} } \right]\, = \, - V $$

(17)

Assuming $x\, = \,R\,\theta \,\,\,\,\,\,\text{and}\,\,\,\,dx\, = R\,d\theta$ Eq. (17) can be written as

$$ \frac{1}{R}\,\frac{\partial }{\partial \theta }\,\left\{ {\frac{2n}{2n + 1}\,\left( {\frac{ - 1}{mR}\,\frac{dp}{d\theta }} \right)^{1/n} \,\left( \frac{h}{2} \right)^{{\frac{2n + 1}{n}}} } \right\}\, = \, - V $$

(18)

where $h = \,c\,\left( {1 - \,\varepsilon \,\cos \,\theta \,} \right)\,\,\,{\text{and}}\,\,\,V\, = \, - c\,\frac{d\varepsilon }{dt}\,\cos \theta$

Substituting for V in Eq. (18) we get

$$ \frac{1}{R}\,\frac{\partial }{\partial \theta }\,\left\{ {\frac{2n}{2n + 1}\,\left( {\frac{ - 1}{mR}\,\frac{dp}{d\theta }} \right)^{1/n} \,\left( \frac{h}{2} \right)^{{\frac{2n + 1}{n}}} } \right\}\, = \,\,c\,\frac{d\varepsilon }{dt}\,\cos \theta $$

(19)

Integrating Eq. (19) we get

$$ \frac{\text{d}p}{\text{d}\theta }\, = \, - mR\,\left( {\frac{2n + 1}{2n}\,Rc\,\frac{d\varepsilon }{dt}} \right)^{n} \left( \frac{2}{h} \right)^{2n + 1} \,\sin^{n} \theta $$

(20)

2.2 Heat Fluid Flow Equation

The heat energy equation with usual assumptions is taken as [15]

$$ \rho \,\,c_{p} \,\left( {u\frac{\partial T}{dx} + v\frac{\partial T}{dy}\,} \right) = k\frac{{\partial^{2} T}}{{\partial y^{2} }}\, + \,m\,\,\left| {\frac{\partial u}{\partial y}} \right|^{n - 1} \,\,\,\left( {\frac{\partial u}{\partial y}} \right)^{2} \,\, $$

This is modified for the problem under consideration is [19]:

$$ \rho \,\,c_{p} \,u\left( {\frac{{\text{d}T_{m} }}{\text{d}x}} \right)\, = k\frac{{\partial^{2} T}}{{\partial y^{2} }}\, + \,m\,\,\left| {\frac{\partial u}{\partial y}} \right|^{n - 1} \,\,\,\left( {\frac{\partial u}{\partial y}} \right)^{2} \,\, $$

(21)

The boundary conditions for the above equation are:

$$ {T} = {T}_{ 1 1}\; {\text{at}} \;y= \, 0 \, , {T} = {T}_{ 1 2}\; {\text{at }} \;y= h $$

(22)

Now the values of T₁ and T₂ are calculated in the region $0\, \le \,\,y\,\, \le \,\,h/2$ and $h/2\, \le \,\,y\,\, \le \,\,h$ respectively and are obtained as

$$ \begin{aligned} T_{1} & =A\left[ {\left( \frac{h}{2} \right)^{{\frac{n + 1}{n}}} \,\,\frac{{y^{2} }}{2}\, - \frac{{n^{2} }}{{\left( {2n + 1} \right)\,\left( {3n + 1} \right)}}\,\left( {\frac{h}{2} - y} \right)^{{\frac{3n + 1}{n}}} } \right]\, \hfill \\ & -B\,\,\frac{{n^{2} }}{{\left( {2n + 1} \right)\,\left( {3n + 1} \right)}}\left( {\frac{h}{2} - y} \right)^{{\frac{3n + 1}{n}}} \, + c_{1} y\, + d_{1} \hfill \\ \end{aligned} $$

(23)

$$ \begin{gathered} T_{2} \, = A\left[ {\left( \frac{h}{2} \right)^{{\frac{n + 1}{n}}} \,\,\frac{{y^{2} }}{2}\, - \frac{{n^{2} }}{{\left( {2n + 1} \right)\,\left( {3n + 1} \right)}}\,\left( {y - \frac{h}{2}} \right)^{{\frac{3n + 1}{n}}} } \right]\, \hfill \\ - B\,\,\frac{{n^{2} }}{{\left( {2n + 1} \right)\,\left( {3n + 1} \right)}}\left( {y - \frac{h}{2}} \right)^{{\frac{3n + 1}{n}}} + c_{2} y + d_{2} \hfill \\ \end{gathered} $$

(24)

Use of the temperature matching condition T₁ = T₂ at y = h/2 and the matching heat flux condition

$$ {\text{one may get} \,c}_{ 1} = {c}_{ 2} = {c}\left( {\text{say}} \right){\text{and}\; d}_{1} = {d}_{ 2} = {d}\left( {\text{say}} \right) $$

(25)

Using the last temperature boundary conditions (22) and (25), in (23) and (24) one can get

$$ c = \,\frac{1}{h}\,\left[ {T_{12\,} - 2A\left( \frac{h}{2} \right)^{{\frac{3n + 1}{n}}} \, + \,\left( {A + B} \right)\frac{{n^{2} }}{{\left( {2n + 1} \right)\,\left( {3n + 1} \right)}}\,\left( \frac{h}{2} \right)^{{\frac{3n + 1}{n}}} - d} \right] $$

(26)

and

$$ cd = \,T_{11\,} + \,\left( {A\, + B} \right)\frac{{n^{2} }}{{\left( {2n + 1} \right)\,\left( {3n + 1} \right)}}\,\left( \frac{h}{2} \right)^{{\frac{3n + 1}{n}}} $$

(27)

where

$$ A\, = \,\frac{{\rho \,c_{p} \,}}{k}\,\frac{{dT_{m} }}{dx}\left( { - \frac{1}{m}\frac{dp}{dx}} \right)^{\frac{1}{n}} \frac{n}{n + 1}\,\,\,\,{\text{and}}\,\,{\kern 1pt} \,B\, = \left( \frac{m}{k} \right)\,\left( { - \frac{1}{m}\,\frac{\text{d}p}{\text{d}x}} \right)^{{\frac{n + 1}{n}}} $$

(28)

Thus, T₁₁, T₁₂ are explicitly known functions of x and y analytically. Finally, the mean temperature T_m defined as in (4) is obtained as

$$ T_{m} \,\, = \,\,\frac{1}{h}\left[ {\int\limits_{0}^{h/2} {T_{1} \,dy\,\, + \,\int\limits_{h/2}^{h} {T_{2} \,dy\,} \,} } \right] $$

(29)

or

$$ T_{m} = \,\frac{{T_{11} + T_{12} }}{2}\,\, + \,\left( \frac{h}{2} \right)^{{\frac{3n + 1}{n}}} \left\{ {\frac{{\rho \,c_{p} \,D}}{k}\,\frac{{dT_{m} }}{dx}\,\left( { - \frac{1}{m}\frac{\text{d}p}{\text{d}x}} \right)^{\frac{1}{n}} \, + \,\left( {\frac{mE}{k}\,} \right)\left( { - \frac{1}{m}\frac{\text{d}p}{\text{d}x}} \right)^{{\frac{n + 1}{n}}} } \right\} $$

(30)

or

$$ \frac{{\text{d}T_{m} }}{\text{d}x}\, = \,\frac{{\left( {T_{m} - \,\frac{{T_{11} + T_{12} }}{2}} \right)\,\left( \frac{2}{h} \right)^{{\frac{3n + 1}{n}}} - \,\left( {\frac{mE}{k}\,} \right)\left( { - \frac{1}{m}\frac{dp}{dx}} \right)^{{\frac{n + 1}{n}}} }}{{\frac{{\rho \,c_{p} \,D}}{k}\,\,\left( { - \frac{1}{m}\frac{dp}{dx}} \right)^{\frac{1}{n}} }} $$

(31)

We can write Eq. (30) using x = Rθ as

$$ \frac{{dT_{m} }}{d\theta }\, = \,\frac{{\left( {T_{m} - \,\frac{{T_{11} + T_{12} }}{2}} \right)\,\left( \frac{2}{h} \right)^{{\frac{3n + 1}{n}}} - \,\left( {\frac{mE}{k}\,} \right)\,\left( \frac{2}{h} \right)^{{\left(\frac{(2n + 1)(n + 1)}{n}\right)}} \,\left( {\frac{2n + 1}{2n}\,RC\,\sin \theta } \right)^{n + 1} \,\left( {\frac{d\varepsilon }{dt}} \right)^{n + 1} }}{{\frac{{\rho \,c_{p} \,D}}{k}\left( \frac{2}{h} \right)^{{\frac{2n + 1}{n}}} \,\,\left( {\frac{2n + 1}{2n}\,RC\,\sin \theta \,\frac{d\varepsilon }{dt}} \right)}} $$

(32)

where $D\, = \,\frac{{n^{3} }}{{\left( {n + 1} \right)\left( {2n + 1} \right)\,\left( {4n + 1} \right)}} - \frac{n}{{3\left( {n + 1} \right)}}$ and $E\, = \,\frac{{n^{2} }}{{\left( {2n + 1} \right)\left( {4n + 1} \right)}}$

2.3 Dimensionless Schemes

$$ \begin{aligned} \overline{m} &= m\left( \frac{U}{c} \right)^{n} \alpha \;U = \,c\frac{d\varepsilon }{dt}\;p_{e} = \frac{{\rho \,C_{p} \,C\,U}}{k}\;\overline{D} = \,D\sin \theta \frac{2n + 1}{n}\\ \overline{E} &= \frac{E}{D}\left( {\frac{2n + 1}{n}} \right)^{n} \sin^{n} \theta \hfill \\ \overline{\gamma } &= \frac{\beta }{\rho Cp\,\alpha }\quad \overline{R} = \frac{R}{C}\;\overline{h} = \frac{h}{C}\quad B = \left( {\frac{2n + 1}{2n}} \right)^{n} \sin^{n} \theta \hfill \\ \end{aligned} $$

The dimension less equations

$$ \frac{{\text{d}\overline{{T_{m} }} }}{\text{d}\theta } = \frac{2}{{P_{e} \overline{h} \overline{D} }}\left( {\overline{T}_{m} - \frac{{\overline{T}_{11} + \overline{T}_{12} }}{2}} \right) - \overline{E} \,\overline{m} \,\,\left( {\overline{R} \,} \right)^{n + 1} \overline{\gamma } \,\left( {\frac{2}{{\overline{h} }}} \right)^{2n + 1} $$

(33)

$$ \frac{{\text{d}\overline{p} }}{\text{d}\theta } = -\overline{m} \,\,\left( {\overline{R} \,} \right)^{n + 1} \left( {\frac{2}{{\overline{h} }}} \right)^{2n + 1} B $$

(34)

2.4 Load

$$ \begin{aligned} {\text{W}} & = { 2}\int\limits_{0}^{\pi } {p\,\cos \theta \,R\,\text{d}\theta } = - 2R\int\limits_{0}^{\pi } {\sin \theta \,\frac{\text{d}p}{\text{d}\theta }\,\text{d}\theta } \, \\ & = \, - 2R\int\limits_{0}^{\pi } {\left( { - \overline{m} \,\,\left( {\overline{R} \,} \right)^{n + 1} \left( {\frac{2}{{\overline{h} }}} \right)^{2n + 1} \left( {\frac{2n + 1}{n}} \right)^{n} \sin^{n + 1} \theta } \right)\,\text{d}\theta } \\ \end{aligned} $$

(35)

2.5 Result and Discussion

Theoretical aspects of numerically computed results for various bearing characteristics are elaborated through figures and tables which follow. These characteristics are functions of the flow behavior index n. Results are calculated by the following behavior of n i.e., in between 0.4 and 1.15. For numerical calculation following sets of values are used:

$$ \begin{aligned} \bar{R} &= 14.96,\alpha = 1.6\, \times \,10^{ - 6} \,dyne^{ - 1} \,m^{2},\;\bar{\gamma } = 0.4, \hfill \\ \varepsilon &= 0.252,\;d\varepsilon /dt = 1.0, Pe = 2.0 \hfill \\ \end{aligned} $$

In order to study the qualitative behavior of consistency variations of the incompressible lubricant, pressure and temperature must be computed first. This is achieved by solving the simultaneous Eqs. (33) and (34) numerically for dimensionless pressure $\bar{P}\,\,$ and temperature $\bar{T}$ by Runge–Kutta fourth order method. The variation of $\bar{P}\,\,$ and $\bar{T}$ are shown in Figs. 2 and 3 respectively. All these cases have one feature in common that the variation in n does not change the general shape of the profile.

Fig. 2

Pressure profile

Fig. 3

Temperature profile

2.6 Pressure Distribution

The pressure distribution $\bar{P}\,\,$ versus θ for various values of n have been depicted in Fig. 2. $\bar{P}\,\,$ decreases continuously when θ from 0 to π increases. The pressure profile $\bar{P}\,\,$ against θ for each n is similar to that of Peng and Khonsari [16] and Singh et al. [17]. Xiong and Wang [12], Chen et al. [18]. The pressure imposition in this Fig. 2 i.e. instead of $0 \le \theta \le \pi$, if we take $- \pi \le \theta \le \pi$ profile becomes very similar to [13, 19, 20].

2.7 Temperature Distribution

The temperature distribution for various value of n is presented in Fig. 3. It is interesting to note that $\bar{T}$ decreases with respect to θ increase except in the vicinity of zero where the trend is reversed. The similar trend has been found by Liu et al. [21]. The difference is however not very significant both for Newtonian as well as non-Newtonian fluid.

2.8 Load Ratio

A ratio W _R  = W _π/W _π/2 of load capacities is used to study the variation in the load with n. Fig. 4 shows the load ratio W_R is a function of n for various values of ε. This indicates that for the low value of ε (epsilon) the load ratio is higher than the load capacity ratio at higher value of ε.; this indicates that for low values of ε the load in a full journal bearing is much greater than the load in a half journal bearing. Figure 4 shown that the load ratio decreases as n increases; this indicates that a decrease in actual load capacity of both the full and half journal bearing. The same has been reported by Singh and Sinha [22].

Fig. 4

Load ratio

3 Conclusion

As it is difficult to non dimensional zed pressure and temperature in case of power law lubricant Singh and Sinha [22], an attempt has been made to complete this assignment further it is concluded that the load ratio decreases with increase in n. It also shown that there is a significant change in pressure and temperature for non Newtonian lubricants.