A Response Threshold Sigmoid Function Model for Swarm Robot Collaboration

Abstract

We present a multi agent collaboration algorithm to recruit an approximate number of individually simple robots with controllable variance. We propose a sigmoid response threshold function motivated by task allocation in social insects, and describe macro-level models backed by micro-level simulations to predict the resulting team sizes and their variance. These results are further validated through physical experiments using the “Droplet” swarm robotics platform. We show that the slope of the response threshold function can be used to control the variance of group size, allowing agents to trade off deterministic team size with coordination speed, and making the proposed mechanism applicable to a variety of applications.

1 Introduction

We propose a probabilistic, threshold based multi agent collaboration algorithm and analysis to recruit an approximate number of robots for a collective task. Recruiting robots to collaboratively solve a task is a canonical problem in robotics [13]. Formally introduced in the stick-pulling experiment, as described by Martinoli et al. [19, 20], to recruit exactly two robots to collaboratively pull a stick out of the ground, Lerman et al. [18] have extended this model to larger teams of constant size. In each case the result of collaboration is binary, success or failure, based on whether an exact number of robots are present at the collaboration site or not.

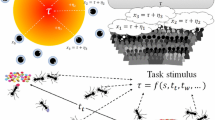
We wish to extend the stick pulling model of constant group sizes of robots to include a more general case of collaboration tasks that involve only approximate robot group sizes for successful collaboration. More specifically, we deal with tasks that have the property of “concurrent benefit” where single agents must wait for a group—with a range of permissible size—to form at their collaboration site before being able to collectively begin the task and complete it successfully. Examples of such tasks include fire containment, collective transport [22], pattern recognition [3], real-time mapping of oil spills [2], determining coverage area of forest fires [17], and many others that require a subset of a swarm to coalesce and tackle a task collaboratively.

A concrete example is fire containment (See Fig. 1). Dropping incremental amounts of water on a fire will be futile until a critical mass of robots drop their water at the same time. Waiting for an exact number of robots, however, is not necessary either, motivating a task allocation scheme that will result in an average number of robots with predictable variance.

It is important to note that we do not study any particular task in detail but rather, outline a general approach to modeling scenarios with the aforementioned properties. Here, tuning the permissible variance allows one to tune the likelihood with which collaborations happen. Formally understanding the dynamics of the underlying coordination mechanisms allows the designer not only to predict performance, but also to optimize a swarming system [8].

The proposed algorithm and model is inspired from task allocation in biological systems such as ant colonies [5, 16]. We employ the use of a response threshold sigmoid function that probabilistically triggers the beginning of a collaboration step between robots at the same collaboration site. We study this approach via macroscopic models and microscopic simulations. The sigmoid function used in our model is commonly referred to as the Logistic function and has control parameters that allow us to alter its offset and slope. We study the effects that changing these parameters has on the system-wide behavior of the robot swarm. We also draw comparisons between this collaboration model and similar models used by Lerman et al. for the n-robot stick pulling experiment [18] and discuss situations where it is beneficial to use one model over the other.

The rest of the paper is organized as follows. Section 2 introduces the task allocation algorithm that we will be studying throughout the course of the paper. Section 3 provides a mathematical basis for the threshold based collaboration model and attempts to explain how the voting strategy being employed affects group sizes and their variance. Section 4 provides an explanation of the agent level controller in the system. This section further outlines the experimental setup being used to run simulations and the important parameters of the system. We compare collaboration rates of our model with the constant group size model introduced by Lerman et al. [18] using micro-level Gillespie simulation in Sect. 4, showing that the dynamics are comparable for similar team sizes, yet allow us to tune the variance of the resulting group size. We also discuss results obtained from conducting real physical experiments and compare them to microscopic simulation results. Finally, Sects. 6 and 7 provide discussion of the drawbacks and limitations of the proposed model and scenarios where it could fail as well as discussing possible avenues for future work.

1.1 Related Work

Task allocation is a canonical problem in multi-robot systems [13]. Whereas capable robots might be able to approximate optimal task allocation, e.g., using market-based approaches [1, 23] or using leader-follower coalition algorithms [7], probabilistic algorithms are of particular interest for swarm robotics with individually simple controllers [10]. Recruitment of an exact number of robots to a particular task has been extensively studied using the “Stick Pulling” experiment [18, 19]. The problem of distributing a swarm of robots across a discrete number of sites/tasks with a specific desired distribution has been studied in [4, 8]. The proposed algorithm extends upon the first group of work, and we show how the proposed stochastic task allocation algorithm reduces to the ones described in [18, 19] when using appropriate parameters. Mather [21] instead presents a stochastic approach that is a hybrid between the work in [4] and [19], allowing allocation to tasks requiring a varying number of robots. While a response threshold function can also be applied to the swarm distribution problem, this problem is complementary to the problem of recruiting teams of varying sizes addressed in this paper.

2 Response Threshold-Based Task Allocation

We consider a generic collaboration task with m uniformly distributed collaboration sites within a flat arena with area A. A swarm of individually simple robots such as the Droplet platform [11, 15] is deployed within the arena, uniformly and at random. The number of robots being used per experiment varies, as we discuss results for a number of different scenarios. Collaboration sites in the arena can be of various sizes and configurations.

Fig. 1

A visual representation of the collaboration experiment firefighting scenario using the Droplet swarm robotic platform

Each individual agent is capable of locomotion [15] and local sensing [11]. The agents do not require global positioning and no centralized controller exists, but we assume each agent to be capable of local omnidirectional communication with other agents within its communication range. The agents are also capable of sensing the boundary of a collaboration site—we assume that sites have easily distinguishable boundary regions, as shown in Fig. 1, for the purposes of the model studied in this paper.

The objective of each agent in the robot swarm is to find a collaboration site in the arena and perform a collective task with other agents at that site. The precise details of the collective task are not important for the purpose of understanding the coordination mechanism. We assume the actual collective task takes each agent a probabilistic, finite amount of time to complete. Once collaboration is complete, the agent detaches itself from its current site and returns to searching for other sites in the arena.

It is perfectly reasonable to assume that agents arrive at the same collaboration site after having just completed a task there (possibly unsuccessfully) but will now be part of a new collaboration group. Each agent individually decides whether or not to collaborate at a given time step, while waiting at a collaboration site. If the majority of agents at that site decide to collaborate then the entire population is recruited for the task and thus a collective consensus is reached using a majority voting scheme. Here, we consider a “majority” to mean exactly half or more of a given population.

An individual agent-i’s willingness to collaborate is a stochastic term governed by a sigmoid based threshold function that takes as input, the number of agents $x_{\hat{m}}$ currently at the same collaboration site as agent-i and outputs a probability of collaboration using control parameters $\theta$ and $\tau$:

$$\begin{aligned} \mathscr {S}(x_{\hat{m}}) = \frac{1}{1+e^{\theta (\tau - x_{\hat{m}})}} \end{aligned}$$

(1)

The parameter $\theta$ controls the slope of the sigmoid function, while $\tau$ controls its offset along the x axis, as seen in Fig. 2. Each agent is independently responsible for estimating the group size $x_{\hat{m}}$ at a given time either by direct sensing or by communication. In practice, this involves building a list of unique identifiers of the agents sharing its collaboration site. The overall algorithm, followed by each individual agent in the system, is provided in Algorithm 1.

Fig. 2

Sigmoidal response threshold function and its parameters. a Changing $\tau$ offsets the curve along the x axis, allowing to set the desired mean team size. b Changing $\theta$ changes the slope at the point $x^{*}=\tau$, $\mathscr {S}(x^{*})=0.5$, allowing to control the team’s variance

Note that the proposed response threshold function is different from [5], who uses high-order polynomials. While these functions work well in regimes with moderate slope, they create numerical problems when approximating unit-step-like responses such as those (implicitly) used in [18]. We particularly chose the Logistic function from the large class of sigmoid functions due to the intuitive nature of the parameters $\tau$ and $\theta$.

3 Macroscopic Analysis

In this section we study how the local parameters $\tau$ and $\theta$ from an individual agent’s sigmoid threshold function affect formation of groups of different sizes at the macroscopic system level.

3.1 A General Model of Probabilistic Task Allocation

Equation (1) is a cumulative probability density function approaching 1.0 as the number of agents approaches infinity, that is $\lim _{x \rightarrow \infty }\mathscr {S}(x)=1$. For $\theta \rightarrow \infty$, Eq. (1) approximates the unit step:

$$\begin{aligned} \lim _{\theta \rightarrow \infty } \frac{1}{1+e^{\theta (\tau -x_{\hat{m}})}}\approx \left\{ \begin{array}{cc} 1 &{} \quad x_{\hat{m}}>\tau \\ 1/2 &{} \quad x_{\hat{m}}=\tau \\ 0 &{} \quad x_{\hat{m}}<\tau \end{array} \right. \end{aligned}$$

(2)

Although, unlike the unit step function, the limit on the left in (2) is always continuous, even at $x_{\hat{m}}= \tau$ where the value of the sigmoid is 1 / 2. The proposed model is therefore a generalization of the “stick-pulling” task allocation model with deterministic team size [18], allowing us to tune the variable resulting group sizes using the tuning parameters $\tau$ and $\theta$ in (1).

3.2 From Individual Choices to Team-Level Collaboration

Assuming the agents to be loosely synchronized, e.g., by considering decisions within a finite window of time, determining a majority vote corresponds to a Bernoulli trial with each agent flipping a biased coin—the bias being computed using the sigmoid function—to decide whether or not to collaborate in the next time step. The probability that exactly k agents collaborate from a population of n agents at a collaboration site is given by the probability mass function (PMF) of a Binomial distribution.

$$\begin{aligned} B(n, k) = \left( {\begin{array}{c}n\\ k\end{array}}\right) \mathscr {S}(n)^{k}\left( 1 - \mathscr {S}(n)\right) ^{n - k} \end{aligned}$$

(3)

Since we care about the case when half or more of the agents (n / 2) decide to collaborate, the probability P(n) that half or more agents in a group of n collaborate is the cumulative probability of the above PMF from $k = {n/2}$ to $k = n$.

$$\begin{aligned} P(n) = \sum \limits _{i={n/2}}^{n}\left( {\begin{array}{c}n\\ i\end{array}}\right) \mathscr {S}(n)^{i}\left( 1 - \mathscr {S}(n)\right) ^{n - i} \end{aligned}$$

(4)

This equation describes the probability with which a group of size n at a given collaboration site will decide to successfully collaborate. Note that (4) is only an approximation for odd n, which requires rounding $\lceil n/2\rceil$ to the next integer.

For large group sizes, the Binomial distribution approximates the Normal distribution and (4) reduces to

$$\begin{aligned} P(n)=\int _{n/2}^{n} \mathscr {N}(n\mathscr {S}(n),n\mathscr {S}(n)(1-\mathscr {S}(n))) \end{aligned}$$

(5)

Therefore, in a group of size n, and n reasonably high (see below), an average of $n\mathscr {S}(n)$ robots will collaborate with group sizes of variance $n\mathscr {S}(n)(1-\mathscr {S}(n))$. In the special case of $n=\tau$, i.e., the group size has the desired value of $\tau$, (5) evaluates to $P(\tau ) = \mathscr {S}(\tau )=0.5$. Therefore, the probability of a group of n agents to collaborate is identical to the probability of a individual agent to collaborate. In all other cases (5) allows us to calculate the micro-macro matching from $\mathscr {S}(n)$ to P(n).

A caveat of (5) is that the Normal approximation yields poor results for small n, usually smaller than 20, and is better when $\mathscr {S}(x)$ is neither close to 0 or 1 [6]. In these cases, exact solutions for P(n) require numerical solutions of (4) using what is known as continuity correction [12].

Fig. 3

Agent controller used to drive group collaboration. There is a search state and m wait and collaboration states, $W_i$ and $C_i$ respectively—one for each collaboration site

4 Microscopic Model

As the proposed collaboration mechanism are strongly non-linear, we chose microscopic stochastic simulations to explore the underlying dynamics of the system. The approach followed to build the stochastic Gillespie simulation of the system is as follows.

• Perform random walk till a collaboration site is found (search state).

• Perform algorithm, Task_Allocation (see Algorithm 1) (wait state).

• Complete collective task and disperse. (collaborate state).

• Return to search.

The probabilistic finite state machine that describes individual agent behavior for this swarm system is shown in Fig. 3. From the individual agent’s perspective only one state each exists for wait and collaborate. From a probabilistic modeling perspective, the wait and collaborate states are meta states, divided into m states each, one for each collaboration site in the arena. This is done to clarify that the probability of collaborating at a given site only depends on the number of agents at that specific site and collaborations only happen between agents at the same site.

The probability $p_{SW_i}$ in the PFSM model of the system shown in Fig. 3 is the probability that an agent encounters a collaboration site. This is geometrically computed as the ratio between the total area of the search space (arena) and the total area of collaboration sites, i.e. $p_{SW_i} = n_s(A_s)/A$ ($n_s =$ number of sites, $A_s =$ area per site). The probability, $P_{W_iC_i}$, of going from a wait state to a collaboration state is given by Eq. (4) with input $N_{W_i}$, the number of agents at collaboration site-i. $P_{C_iS}$ stochastically models the time it takes for an agent to complete a generic collaborative task and is equal to 1 / T, where T is the amount of time (on average) that it takes an agent to complete the collective task. Note that agents have a zero probability of transitioning from the wait state back to the search without collaborating, i.e. once an agent is at a collaboration site, it will not leave till a collaboration event happens at that site. We chose the following numerical values for all simulations, unless otherwise noted: $A=100$ and $A_s=10\,\mathrm{cm}^2$.

For the sake of simplicity, consensus between agents—i.e. going from $W_i$ to $C_i$—at the same collaboration site is assumed to happen instantly and therefore the extra state(s) is/are omitted from robot controller.

In order to compare the dynamics of the proposed probabilistic task allocation mechanism with the deterministic one by Lerman et. al [18], we implemented a variation of the above algorithm using a unit-step at $\tau$ instead of the sigmoid function and removing the consensus step, which is not necessary in this model.

We use Gillespie simulation [14] to explore the dynamics of the proposed collaboration model. For both experiments a single collaboration site is used and each run simulates 300 s of time. The desired group size ($\tau$, in Eq. 1) is set to 4, 8, 16 and 32 agents out of a total of 100 robots. The collaboration task is programmed to take 10 s, on average, per agent. Data points are gathered by averaging data from 100 identically set up runs in each case. The rate of collaboration for the threshold model is computed by summing the number of groups that successfully collaborate and dividing by the total experiment time (300 s). For the deterministic model, collaboration rate is computed by summing all successful collaborations, i.e. collaborations involving team sizes equal to $\tau$, and dividing the the experiment time (300 s).

5 Results

We will first compare the dynamics of the proposed approach with Lerman et al.’s k-collaboration model [18] and then validate the emergence of group sizes with similar means but varying variances.

Fig. 4

Comparison of the collaboration rate for task allocation with probabilistic and deterministic [18] for different values of $\theta$ and team sizes $\tau$ in an environment with one collaboration site and one hundred robots. a $\theta =2$. b $\theta =1$. c $\theta =0$

Figure 4a shows collaboration rates for both models when $\theta$ is set to 2 (for the probabilistic model) and the wait time is set to $\infty$ (for the deterministic model), in order to allow for a fair comparison. (All experiments are run in a regime where infinite wait times are optimal wait times, i.e., there are more agents than collaboration sites.) Figure 4a, b and c show collaboration rates for $\theta = 2$, $\theta = 1$ and $\theta =0$ with infinite wait time. With $\theta =0$, the Logistic function is uniformly 0.5, allowing any team size to form. With increasing $\theta$ the Logistic function approximates a unit step, minimizing the variance.

We observe the collaboration rate to be qualitatively and quantitatively very similar for high values of $\theta$ (steep slope), and to exceed that of the deterministic model for very low values of $\theta$ (flat slope). This is expected as flat slopes increase the variance of the observed group size and therefore allow much smaller teams than $\tau$ agents to collaborate.

Figure 5 shows histograms of the resulting group sizes for various values of $\tau =4, 8, 16, 32$ and $\theta =[0;0.1;1]$ (100 simulations per data point). It is clearly seen that when $\theta$ is set to 0, the sigmoid becomes constant ($\mathscr {S}(x) = 1/(1 + e^{0}) = 0.5$) so agents have an equal probability to want to collaborate or not, no matter what the desired group size is. We therefore see a large number of small groups forming, with most groups consisting of 2 agents. This is to be expected since the expected number of agents willing to collaborate in a group of size 2 is 1, given the probability of collaboration is constant at 0.5.

Figure 6a displays average group sizes as $\theta$ is varied from 0 to 1 and $\tau$ from 4 to 32 based on the data from Fig. 5. We observe that for large enough values of $\theta$ the mean of the group size distribution approaches the desired group size and is largely unaffected by increasing $\theta$. Thereafter, its magnitude depends only on $\tau$ except in the special case where $\theta = 0$ where it is constant. The relative error of the mean compared to the desired average decreases with increasing number of agents as the Binomial distribution (4) approximates the Normal distribution (5).

Fig. 5

Histograms of resulting team sizes for various values of $\tau$ and $\theta$ with one hundred robots and one collaboration site. a $\tau =4$. b $\tau =8$. c $\tau =16$. d $\tau =32$

Fig. 6

Showing the effects of varying $\theta$ on means and variances corresponding to the histograms seen in Fig. 5

Figure 6b shows how the variance of group size decreases with increasing $\theta$. This is because the sigmoid function approximates the unit step, making the team size more and more deterministic. On the other hand, low values of $\theta$ lead to large variances in the group size. For $\theta =0$, the variance is constant for all values of $\tau$ and depends exclusively on the total number of robots.

Finally, we use the Droplet swarm robot platform to perform real experiments to study the effects of using the proposed task allocation scheme on a physical system. The Droplets are small individually simple robots capable of omni-directional motion and communication (via IR) as well as sensing patterns projected from above. In our experiment we assume that all agents have already arrived at a collaboration site and measure the corresponding collaboration rates for a team of 6 robots while varying values of $\tau$ and $\theta$. Each agent is individually running the algorithm described in Algorithm 1. A collaboration event is recognized by having all the robots turn on their green LEDs for 5 s. After such a collaboration event, each agent resets its group size estimate and runs Algorithm 1 again.

Fig. 7

The solid lines show collaborations per min, over 15 min, for a group of 6 real robots as the desired group size is varied from 3 to 7 and the slope of $\mathscr {S}$ is varied between 0.1, 1 and 10. The dashed lines indicate simulation results with the same parameters

We ran 5 repeated experiments for all 15 combinations of $\tau = 3,4,5,6$ and 7, and $\theta = 0.1, 1$ and 10, totally 75 runs. Each experiment lasted 15 min and an overhead camera system was set up to detect collaboration events using the software RoboRealm. The collaboration rate was a value computed by counting the number of collaborations over the course of each 15 min experiment, normalizing to collaborations per minute, and averaging over the 5 repeated runs. To account for the vision software’s detection errors, the raw data gathered from each experiment was de-bounced and passed through a low-pass filter to expose real collaboration events while eliminating observation error. The results of these experiments are seen in Fig. 7. While results are in accordance with simulation for $\theta$ being low, the collaboration rate on the real robot platform is much lower than expected for larger $\theta$ as simulation assumes perfect communication and group size estimates.

6 Discussion

Results in Figs. 4, 5 and 6 show that the proposed threshold-based task allocation mechanism is a generalization of the deterministic Lerman model in that it allows to approach what is seen with deterministic group sizes while retaining the elasticity to vary group sizes along any desired range of values. Also, these plots show how altering microscopic control parameters within the agents, $\theta$ and $\tau$ of their sigmoid functions, directly affects macroscopic behavior of the swarm system by altering means and variances of formed group sizes, respectively. Although the matching between microscopic results and macroscopic prediction is not perfect due to the discrete approximation, the plots show that a wide range of means and variances are feasible. Finding appropriate parameters to reach these could be easily achieved using a suitable optimization framework such as presented in [4, 8], using the macroscopic predictions as initial estimate.

The proposed task allocation algorithm requires an estimate of the group size at each collaboration site as well as the ability to communicate with the group in order to reach a consensus. While these assumptions seem to be limiting at first sight, they can be rolled into the analysis process and possibly exploited to design the task allocation process. For example, an increasing variance for observing the group size $\tau$ or noise in the consensus process simply increase the variance of the task allocation process and could therefore be countered—to some extent—by altering the properties of the response threshold function.

This effect is clearly observed in the physical experiment results (see Fig. 7). Since the communication between real robots is not perfect, they almost always underestimate the size of their group resulting in lower collaborations for high $\theta$ and $\tau$ values. As we observe from comparing the micro simulation results—that are modeled with perfect communication—with real experiment data, we observe a large discrepancy when $\theta = 10$. This happens because although individual agents are set up to be in a group of size 6, their estimates for the group size never cross 4 due to imperfect and blocked communication. Coupled with the fact that the sigmoid threshold effectively acts as a step function when $\theta = 10$, this results in approx. 0 probability of collaboration between agents for a desired group size of 6 but a group size estimate of ${\le }4$. Lower values of $\theta$ result in better matching between real and simulation data since lower slopes effectively increase the variance in allowed group sizes and mitigate this effect.

We note that there is no optimal wait time as in stick pulling-like collaboration [18]. This optimum exists in swarms with less robots than sticks, which is shown analytically in [19]. Such an optimum does not exist in the proposed model as there is a non-zero probability team sizes with $n<\tau$ will eventually collaborate. Indeed, Algorithm 1 eventually completes as $\mathscr {S}(x) > 0\,\forall \,x$, i.e., even if only very few robots are at a collaboration site and $\tau$ is large, there is a non-zero probability that half or more of the agents at the site eventually collaborate (see also Eq. 4).

Although the algorithm does not deadlock—the probability to collaborate even if the team size is far off the desired value—the resulting behavior might be undesirable, resulting in potentially very long wait times and poor task performance. This could be mitigated by introducing preferential detachment from small groups and preferential attachment to larger groups as customary in swarm robotic aggregation [9].

In practice, effective collaboration rates will also be limited by the embodiment of the robots, which might make finding physical space at a site cumbersome. In the presented microscopic simulation, for both stochastic and deterministic team sizes, the number of robots per site were not limited, allowing scenarios in which multiple groups collaborate in quick succession at the same site. While comparing both models without embodiment is reasonable, we wish to study the effect of embodiment in future work.

7 Conclusion

This paper introduces a task allocation algorithm that allows to recruit an approximate number of agents with a desired variance to a task. This allows to trade-off task execution accuracy with speed, resulting in increasing collaboration rates for teams with larger variances. We demonstrate that task allocation of teams with deterministic size is a subset of the proposed stochastic task allocation mechanism. As such, the proposed framework provides a computationally simple, adaptive, and robust alternative for coordination.

We investigate the limitations of the proposed approach, which shows lesser fidelity in macroscopic predictions if team sizes are small. In future work, we wish to investigate the impact of variance in estimating the number of agents waiting at a collaboration site as well as the impact of unrel iable communication between agents, both of which we conjecture to impact the variance of resulting team sizes in a similar way as the slope of the response threshold function. We are also interested in studying preferential attachment/detachment techniques from swarm robotic aggregation in order to improve scenarios with insufficient numbers of robots for strong teams to emerge.