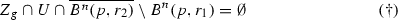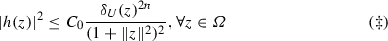Unbounded Pseudoconvex Domains in ${\mathbb {C}}^n$ and Their Invariant Metrics

Abstract

In this article, we introduce a method to study the positivity and the completeness of the Bergman metric for a broad collection of unbounded domains.

1 Some Problems

Whether a complex manifold admits a positive-definite and complete Bergman metric (as well as other invariant metrics) has attracted much attention for quite some time. While the Bergman metric of any bounded domain in ${\mathbb {C}}^n$ is positive-definite, the completeness was extensively studied and has satisfactory conclusion (cf. [Ohs, Diede] et al.). For manifolds, there are not many theorems in this direction; one of the well-known theorems is Theorem H of [GW]. In between, there are unbounded domains of ${\mathbb {C}}^n$. As pointed out in [HTS], even some of the most basic-looking features of bounded domains have turned out nontrivial when asked upon the general unbounded domains in ${\mathbb {C}}^n$.

Naturally, we wished to introduce a method for studying the positivity and the completeness of the Bergman metric for unbounded domains. But before focussing more narrowly, we feel that it may be appropriate to point out some more related problems whose answers are still in order.

Question 1.1

Which unbounded domains possess the property that their Bergman metric is positive-definite and complete?

One quick example is the domain

$$ \varOmega := \{(z,w) \in {\mathbb {C}}^2 :|w| < \exp (-|z|^2) \}. $$

This domain contains the complex line $\{(z,w) \in {\mathbb {C}}^2 :w=0\}$ and hence is not Kobayashi-hyperbolic and not biholomorphic to any bounded domain. But its volume is finite, as one can check by a direct computation. Therefore any constant function is square integrable. More generally, all holomorphic polynomial functions are of $L^2$. Thus the Bergman kernel exists. Moreover, in an unpublished note, the 3rd named author in a communication with S. Shimizu of Tohoku University (Japan) found explicit formulae of the Bergman kernel and metric; the result, showing the positivity and the completeness of the Bergman metric, is presented in [AGK].

Now, consider the famous examples (for $\varepsilon = 0, 1$)

$$ \varOmega _\mathrm {KN}^{\varepsilon } := \{ (z,w) \in {\mathbb {C}}^2 :{\mathrm {Re}}\,w + \varepsilon |zw|^2 + |z|^8 + \frac{15}{7} {\mathrm {Re}}\,|z|^2 z^6 < 0 \} $$

called the Kohn-Nirenberg domain. The case $\varepsilon =0$ was studied by Herbort [Herb]; its Bergman metric is positive and complete. The other case is not so much different, but requires some care. See [AGK] for details; the main theme of [AGK] is to set up a method that can be used in this direction of study, and we shall present a brief survey on this in the later part of this article.

A more general question is the following:

Question 1.2

Is the Kohn-Nirenberg domain biholomorphic to a bounded domain?

No progress has been made toward the solution of this problem as far as the authors are aware of, at least at the time of this writing. However, this may be interesting to see: according to Bedford and Fornaess [BF], the domain $\varOmega _\mathrm {KN}^{\varepsilon }$ has a holomorphic peak function at the origin, say h, that is continuous up to the boundary and enjoys exponential decay. Now if one considers the map $f:\varOmega _\mathrm {KN}^{\varepsilon } \rightarrow {\mathbb {C}}^3$ defined by

$$ f(z,w) = (h(z,w), z h(z,w), w h(z,w)), \forall (z,w) \in \varOmega _\mathrm {KN}^{\varepsilon } $$

then $f(\varOmega _\mathrm {KN}^{\varepsilon })$ is a bounded subset of ${\mathbb {C}}^3$. Notice that f is also 1-1 and holomorphic. This domain is, therefore, Caratheodory (and hence also Kobayashi) hyperbolic.

Question 1.3

Which unbounded convex domains are biholomorphic to a bounded convex domain?

For a complex manifold to be biholomorphic to a bounded domain, it must be Kobayashi hyperbolic. Then any Kobayashi hyperbolic convex domain is known to be biholomorphic to a bounded domain. However it is still unclear when the bounded realization of the unbounded convex hyperbolic domain should be convex.

This problem is more attractive when one recalls the theorem of Vinberg,Piatetskii-Shapiro and Gindikin which says that every bounded homogenous domain (hence in particular Kobayashi hyperbolic) is biholomorphic to a Siegel domain (of the second kind). Since every Siegel domain is an unbouned convex domain, the above question transforms into: “Which homogeneous domains are biholomorphic to a bounded convex domain?” It is an open conjecture that all homogeneous domains biholomorphic to a bounded convex domain is a bounded symmetric domain. [Known as Gindikin’s problem.]

The main focus of this article, however, is upon the Bergman metric, its positivity and completeness.

2 A Remark on Hahn-Lu Comparision Theorem

Toward Question 1.1, the following (slight) modification of the statement turns out to be useful:

Theorem 2.1

(Hahn-Lu Comparison Theorem, II) If the Bergman kernel $K_M$ of a complex manifold M satisfies the condition $K_M (p,p) \ne 0$ at $p \in M$ then, for the Caratheodory pseudometric $c_M$ and the Bergman (pseudo) metric $\beta _M$, it holds that

$$ ({\mathfrak {c}}_M (p, v))^2 \le \beta _M|_p (v,v), \forall v \in T_p M. $$

Here, the Caratheodory pseudometric is the classic concept defined upon the family ${{\mathscr {H}}}(M, D)$ of the holomorphic functions of M with image contained in the unit open disc D in ${\mathbb {C}}$:

$$ {\mathfrak {c}}_M (p,v) = \sup \{|d\psi _p (v)| :\psi \in {{\mathscr {H}}}(M,D), \psi (p)=0\}. $$

The Bergman (pseudo) metric at p is defined by the matrix representation (with respect to a holomorphic local coordinate system) with its jk-th entry

$$ \beta _{jk} (p) = \frac{\partial ^2}{\partial z_j \partial \bar{z}_k} \bigg |_p \log K_* (z,z), $$

where $K_*$ is the complex-valued function defined by

$$ K_M (z,w) = K_* (z,w) dz_1 \wedge \ldots \wedge dz_n \wedge d\bar{w}_1 \wedge \ldots \wedge d\bar{w}_n. $$

We recall that $K_M$ denotes the Bergman kernel of M. Notice that, if $K_M (p,p) \ne 0$, then the Bergman metric is nonnegative, but it may not in general be positive (or, positive-definite in this case). This is why we used the term “pseudo” in parentheses.

The theorem was proved in 1958 by Q.-K. Lu (the transliteration of his Chinese name then was written as K.-H. Look) for the bounded domains and was proved independently by K. T. Hahn around 1976 for complex manifolds with the assumption that both Caratheodory and Bergman metrics are positive [Lu, Hahn76]. Their proofs were essentially the same.

Then we observed that the “short” proof presented by Hahn in [Hahn78] actually demonstrated more than what was written in the statement of the theorem. Indeed, the above statement is just the result of the arguments there.

On the other hand, the significance of this observation is that this current version can be useful for showing the positivity of the Bergman metric; notice that the Bergman metric is positive whenever the kernel is nonzero and the Caratheodory metric is positive.

3 A Technique for Positivity and Completeness of Bergman Metric

From the preceding section, it became obvious that one should study the class of square integrable functions. The following theorem provides a technique which has turned out to be useful.

First we set the notation: we put $\delta _U (z) := \min \{1, \text { dist }(z, {\mathbb {C}}^n \setminus U)\}$, where U is an open subset in ${\mathbb {C}}^n$ and “dist” means the Euclidean distance. Moreover, with a holomorphic function g, define $Z(g) = \{ z :g(z)=1\}$.

Theorem 3.1

(Ahn et al. [AGK]) Let $\varOmega$ be a domain in ${\mathbb {C}}^n$. If $p \in \partial \varOmega$ satisfies the following two properties:

• 1. There exists an open neighborhood V of p and a function $g \in {{\mathscr {O}}}(V)$ supporting $V \cap \varOmega$ at p.

• 2. There are constants $r_1, r_2, r_3$ with $0<r_1<r_2<r_3<1$ and $B^n (p,r_3) \subset V$, and there exists a Stein neighborhood U of $\overline{\varOmega }$ and a function $h \in {{\mathscr {O}}}(\varOmega \cup V) \cap {{\mathscr {O}}}^*(V)$ satisfying

  

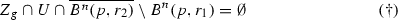
  and

  

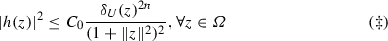
for some positive constant $C_0$, then $\varOmega$ admits a holomorphic peak function at p.

The reader would agree that construction of globally bounded holomorphic functions with peaking property at boundary points should be useful in the light of the exposition of this article, but would ask a question, incidentally, whether the conditions in the hypothesis of this theorem can be met in a broad collection of domains. We shall discuss this point in the next section with examples.

4 Examples

4.1 The Kohn-Nirenberg and Fornaess Domains

The first is the Kohn-Nirenberg domain mentioned earlier:

$$ \varOmega _\text {KN}^0 := \{ (z,w) \in {\mathbb {C}}^2 :\rho (z,w) = {\mathrm {Re}}\,w + |z|^8 + \frac{15}{7} {\mathrm {Re}}\,|z|^2 z^6 < 0 \} $$

For this domain we use the holomorphic peak-function, say f, constructed in [BF]. It enjoys the following properties:

• f vanishes nowhere,

• |f| decays exponentially at infinity. In particular it is square-integrable on $\varOmega _\varepsilon = \{\rho < \varepsilon (|z|^8 + |w|) \}$,

• f peaks at (0, 0), i.e., $|f(z)|<1$ for every $z \in \varOmega _\text {KN}$, and $f(z)\rightarrow 1$ as $z \in \varOmega _\text {KN}$ approaches (0, 0).

Thus one may let this f take the role of h. Then this constructs, via Theorem 3.1, global peak functions at every strongly pseudoconvex boundary point. Then the other properties (such as the facts that all weakly pseudoconvex boundary points are in the orbit of (0, 0) via the action by translation, and that the domain is weighted-homogeneous) combined shall imply that the domain is complete Caratheodory hyperbolic. Then the comparison theorem of Hahn-Lu applies here and one obtains that the Bergman metric is positive and complete.

The other domain

$$ \varOmega _\text {KN}^1 := \{ (z,w) \in {\mathbb {C}}^2 :\rho (z,w) = {\mathrm {Re}}\,w + |zw|^2 + |z|^8 + \frac{15}{7} {\mathrm {Re}}\,|z|^2 z^6 < 0 \} $$

as well as similar domains constructed by Fornaess [Fspso] can be shown, after some minor adjustments, to satisfy the same conclusion that their respective Bergman metric is positive and complete.

4.2 Other Domains

Herbort presented in [Herb] the concept of domains with diagonal type, and showed that their Bergman metrics are positive and complete. Our method is more general in its nature and shows that the same conclusion holds for all domains defined by a weighted-homogeneous pluri-subharmonic polynomial defining function regardless the dimension.

Notice that Theorem 3.1 concerns only the technique of finding a global peak function starting with a local holomorphic support function. This procedure is independent of the particular features of the defining function such as weighted-homogeneity. In fact this theorem works for the domain defined by $|w|<\exp (-|z|^2)$ for instance.

5 Remarks and More Questions

Earlier, the following theorem was discovered:

Theorem 5.1

(Chen et al. [CKO]) If $\rho :{\mathbb {C}}^n \rightarrow {\mathbb {R}}$ is a pluri-subharmonic function with $\lim _{\Vert z\Vert \rightarrow \infty } \rho (z) = + \infty$, then the Bergman metric of the domain $\varOmega = \{(z_0, \ldots , z_n) \in {\mathbb {C}}^{n+1} :{\mathrm {Re}}\,z_0 > \rho (z_1, \ldots , z_n) \}$ is positive and complete.

The proof-arguments appear quite different from ours. It is of interest to compare the two methods. For instance one can observe from the assumptions in Theorem 5.1 that $\varOmega$ admits a global holomorphic peak function at infinity. Indeed, $(z \in \varOmega ,\ ||z|| \rightarrow \infty ) \Leftrightarrow (z \in \varOmega ,\ |z_0| \rightarrow +\infty )$. Denote by $\varPhi$ that peak holomorphic function :

$$ \forall z \in \varOmega ,\ |{\varPhi }(z)| < 1\ \mathrm{and}\ \lim _{|z| \rightarrow \infty } {\varPhi }(z) = 1. $$

Since the Caratheodory (pseudo)metric decreases under the action of holomorphic maps, then $\lim _{z \in \varOmega ,\ |z| \rightarrow \infty }d^C_{\varOmega }(z,z^0) = +\infty$ for every $z^0 \in \varOmega$, where $d^C_{\varOmega }$ denotes the Caratheodory pseudodistance on $\varOmega$. The same condtion is satisfied for the Bergman metric according to the Hahn-Lu comparison Theorem. It seems particularly interesting to investigate the existence of holomorphic peak functions at boundary points of $\varOmega$.

Finally, we would like to suggest another problem. Fornaess constructed in [F04] a manifold exhausted by a sequence of biholomorphic images of the open unit ball, which admits a nonconstant bounded plurisubharmonic function, and yet its Kobayashi metric is identically zero. This is called a Short- ${\mathbb {C}}^k$ for every $k \ge 2$. Not much has been studied on this manifold. Although the problem seems to be beyond our techniques, we would like to close this article with the following question.

Question 5.1

Does a Short-${\mathbb {C}}^k$ admit Bergman metric?

For further details, the reader is invited to read [AGK].