Operadic Bridge Between Renormalization Theory and Vertex Algebras

Abstract

A construction is presented that provides a correspondence between renormalization groups in models of perturbative massless Quantum Field Theory and models of vertex algebras.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

The aim of this talk is to show how two different areas in Quantum Field Theory (QFT) are governed by one and the same algebraic structure. This opens perspectives of transferring constructions in both directions via this common structure. The two connected fields are the theory of Operator Product Expansion (OPE) algebras (called also vertex algebras) and the renormalization theory in perturbative QFT and more concretely, the renormalization group and its action. The bridge between these two structures is an operad, which we call the expansion operad $\mathcal{E}$, and whose algebras are the vertex (or OPE) algebras, while the group associated to this operand is the renormalization group. Thus, our plan in this lecture is to consider the following topics:

• A. What is a vertex algebra?

• B. What is an operad?

• C. What is the renormalization group and its action (i.e., a representation by formal diffeomorphisms on the physical parameters)?

• A. Starting with the firs topic, a vertex algebra is the structure that is closed by the OPE. The OPE in turn was introduced for the analysis of the short distance behavior in QFT [10]. According to the general principles of locality and causality in QFT one expects that the product of two local quantum fields posses an asymptotic expansion at short distances x − y → 0 of the form

  $$\displaystyle{\phi (\mathrm{x})\,\psi (\mathrm{y})\ \ \mathop{\mbox{ $ \sim $}}\limits _{\mathrm{x}\,\rightarrow \,\mathrm{y}}\ \ \mathop{ \sum }\limits _{A}\theta _{A}(\mathrm{y})\,C_{A}(\mathrm{x} -\mathrm{ y}),}$$

  for a suitable system of two-point numerical functions (distributions) C _A (x − y) that describes the local behavior of the product, and the coefficients θ _A (y) are again local fields (the sign $\mathop{\mbox{ $ \sim $}}\limits _{\mathrm{x}\,\rightarrow \,\mathrm{y}}$ stands for the asymptotic expansion at short distances). For instance, in perturbative massless QFT one can choose

  $$\displaystyle{C_{A}(\mathrm{x} -\mathrm{ y})\, =\,{\bigl ( (\mathrm{x} -\mathrm{ y})^{2}\bigr )}^{\nu }\,{\bigl ((\log (\mathrm{x} -\mathrm{ y}))\bigr )}^{\ell}\,h_{ m,\sigma }(\mathrm{x} -\mathrm{ y})\,,\quad A\, =\, (\nu,\ell,m,\sigma )\,,}$$

  where $\nu \in \mathbb{R}$, $\ell\in \{ 0,1,\ldots \}$ and $\{h_{m,\sigma }(\mathrm{x})\}_{\sigma }$ is a basis of harmonic homogeneous polynomials (spherical functions) of degree $m = 0,1,\ldots$. Thus, for every index A we obtain a binary operation

  $$\displaystyle{\theta _{A}\ =:\ \phi \,\mathop{ {\ast}}\limits _{A}\,\psi \qquad \Longrightarrow\quad {\bigl \{\,\mathop{ {\ast}}\limits _{A}\,\bigr \}}_{A}}$$

  in the vector space of all local quantum fields (this space is called “Borchers class”). A vertex algebra is determined as the algebraic structure defined by this infinite system of binary products ${\bigl \{\,\mathop{{\ast}}\limits _{A}\,\bigr \}}_{A}$. The main condition on the latter system of operations comes from the operator product associativity:

  $$\displaystyle{\phi _{1}(\mathrm{x}_{1})\,{\bigl (\phi _{2}(\mathrm{x}_{2})\,\phi _{3}(\mathrm{x}_{3})\bigr )}\, =\,{\bigl (\phi _{1}(\mathrm{x}_{1})\,\phi _{2}(\mathrm{x}_{2})\bigr )}\,\phi _{3}(\mathrm{x}_{3})\,.}$$

However, it is rather nontrivial to reformulate this associativity in a purely algebraic way for the system of binary products ${\bigl \{\,\mathop{{\ast}}\limits _{A}\,\bigr \}}_{A}$. This is completely understood only in the following cases:

• In space-time dimension D = 1 (chiral) Conformal Field Theory (“on a light ray”) the OPE takes the form

  $$\displaystyle{\phi (z)\,\psi (w)\, =\,\mathop{ \sum }\limits _{n\,\in \,\mathbb{Z}}{\bigl (\phi _{(n)}\psi \bigr )}(w)(z - x)^{-n-1}}$$

  and its associativity and further properties was first axiomatized by R. Borcherds [1].

• A generalization to higher D was introduced in [2] but in the context of QFT vertex algebras have been considered in [6]. It has been shown it the latter paper that these algebras are in one–to–one correspondence with models of Wightman axioms possessing the so called Global Conformal Invariance [8].

• B. We proceed by considering vertex algebras as algebras over an operad. So first, what is an operad? Besides one of the first references on this topic [5] we shall mention one recent book [4], from which we follow the definitions and conventions.

One can think of an operad as a generalized type of algebras. An algebra of a certain type is determined by introducing a set of multilinear operations subject to certain identities that use compositions of these operations, eventually combined with permutations of the input arguments. Instead of this one can consider the spaces of all possible multilinear operations obtained under compositions and the action of permutations (and all this quotient by the relations). This will be the operad corresponding to the considered type of algebras.

In more details, an operad includes

• a sequence of vector spaces $\{\mathcal{M}(n)\}_{n\,=\,1}^{\infty }$ ($\mathcal{M}(2)$ being the space of binary operations, …).

• The structure is endowed by various structure maps called operadic compositions,

  $$\displaystyle{\begin{array}{rclll} \mathcal{M}(k) \otimes \mathcal{M}(j_{1})& \otimes \cdots \otimes &\mathcal{M}(j_{k})&\,\longrightarrow \,&\mathcal{M}(n) \\ \mu ^{{\prime\prime}}\otimes \mu _{1}^{{\prime}}&\otimes \cdots \otimes &\mu _{k}^{{\prime}} &\,\longmapsto \,&\ \mu ^{{\prime\prime}}\circ (\mu _{1}^{{\prime}},\cdots \,,\mu _{k}^{{\prime}})\,,\end{array} }$$

  where $n = j_{1} + \cdots + j_{k}$, and permutation actions

  $$\displaystyle{\mathcal{M}(n) \times \mathcal{S}_{n}\, \ni \,\mu \times \sigma \,\mapsto \,\mu ^{\sigma }\,\in \,\mathcal{M}(n)\,,\quad (\mu ^{\sigma _{1}})^{\sigma _{2}}\, =\,\mu ^{\sigma _{1}\sigma _{2}}\,.}$$

The operadic composition $\mu ^{{\prime\prime}}\circ (\mu _{1}^{{\prime}},\cdots \,,\mu _{k}^{{\prime}})$ is pictorially drawn as:

One of the main examples of an operad is the endomorphism operad $\mathcal{E}\mathit{nd}_{V }$ for a vector space V:

$$\displaystyle{\mathcal{E}\mathit{nd}_{V }(n)\,:=\, \mathit{Hom}{\bigl (V ^{\otimes \,n},V \bigr )}\,,}$$

where $\mu ^{{\prime\prime}}\circ (\mu _{1}^{{\prime}},\cdots \,,\mu _{k}^{{\prime}})$ is the actual composition of multilinear maps and

$$\displaystyle{\mu ^{\sigma }(v_{1},\cdots \,,v_{n})\,:=\,\mu (v_{\sigma _{1}},\cdots \,,v_{\sigma _{n}})\,.}$$

Morphisms of operads are defined as follows:

$$\displaystyle{\{\mathcal{M}(n)\}_{n\,=\,1}^{\infty }\,\rightarrow \,\{\mathcal{N}(n)\}_{ n\,=\,1}^{\infty }\ \ \mbox{ $ \equiv $}\ \ {\bigl \{\mathcal{M}(n)\, \rightarrow \,\mathcal{N}(n)\bigr \}}_{ n\,=\,1}^{\infty }\,}$$

plus compatibility with all structure maps. In particular, morphisms from an operad to the endomorphisms operads have a meaning of “representations” but are called algebras over the corresponding operad:

$$\displaystyle\begin{array}{rcl} & & \qquad \text{Representation}\ \ \equiv \ \ \text{Algebra over an operad,} {}\\ & & \text{i.e.,}\ \ \{\mathcal{M}(n)\}_{n}\, \rightarrow \,\{\mathcal{E}\mathit{nd}_{V }(n)\}_{n}\ \ \text{\textendash }\ \ \text{morphism of operads,} {}\\ & & \qquad \qquad \text{i.e.,}\ \ \mathcal{M}(n)\, \rightarrow \,\mathit{Hom}{\bigl (V ^{\otimes \,n},V \bigr )}\, {}\\ \end{array}$$

(the abstract operations in $\mathcal{M}(n)$ become actual n–linear maps on V that is the underlined space of the algebra).

FormalPara Example.

The Lie operad $\mathcal{L}\mathit{ie}$ corresponds the class of Lie algebras and is defined as:

$$\displaystyle\begin{array}{rcl} & & \quad \mathcal{L}\mathit{ie}(1)\, =\, \mathit{Span}_{\mathbb{C}}\{1\}\,\mathop{\longrightarrow }\limits ^{\pi _{1}}\,\mathit{Hom}(V,V )\,, {}\\ & & \quad \mathcal{L}\mathit{ie}(2)\, =\, \mathit{Span}_{\mathbb{C}}\{\lambda \}\,\mathop{ \longrightarrow }\limits ^{\pi _{2} }\,\mathit{Hom}(V ^{\otimes 2},V )\,, {}\\ & & \qquad \qquad \qquad \pi _{2}(\lambda )(a,b)\, =\, [a,b]\,, {}\\ & & \begin{array}{rcccc} \mathcal{L}\mathit{ie}(3)\, =\, \mathit{Span}_{\mathbb{C}}\{ & \lambda \circ (1,\lambda ) &,\, & \lambda \circ (\lambda,1) &\} \\ & \downarrow & & \downarrow & \\ {\bigl (\lambda \circ (\lambda,1)\bigr )}^{(1,3,2)}\, \rightarrow \, [[a,c],b]\, =\,&[a,[b,c]]&-&[[a,b],c]\,,& \end{array} {}\\ & & \qquad {\bigl (\lambda \circ (\lambda,1)\bigr )}^{(1,3,2)}\, =\,\lambda \circ (\lambda,1) -\lambda \circ (1,\lambda )\,, {}\\ \end{array}$$

where μ ^σ for an element μ in the nth operadic space and a permutation $\sigma \in \mathcal{S}_{n}$ stands for the (right) actions of the permutation groups on the operad (that is one of the basic structures in the operad).

The main construction in this work is based on a particular example of an operad, which we call the expansion operad $\mathcal{E} ={\bigl \{ \mathcal{E}(n)\bigr \}}_{n}$. It is defined for a sequence of graded function spaces

$$\displaystyle{\mathcal{O}_{n}\, \subseteq \, C^{\infty }\bigr (\bigl (\mathbb{R}^{D}\bigr )^{\times n}\,\setminus \,\text{all diagonals}\bigr )}$$

for $n = 2,3,\ldots$ admitting expansions

$$\displaystyle{G(\mathrm{x}_{1},\ldots,\mathrm{x}_{n})\, =\,\mathop{ \sum }\limits _{\ell}G_{\ell}^{{\prime}}(\mathrm{x}_{ j},\ldots,\mathrm{x}_{j+k})\,G_{\ell}^{{\prime\prime}}(\mathrm{x}_{ 1},\ldots,\mathrm{x}_{j-1},\mathrm{x}_{j+k},\ldots,\mathrm{x}_{n})}$$

for $\vert \mathrm{x}_{a} -\mathrm{ x}_{j+k}\vert \ll \vert \mathrm{x}_{b} -\mathrm{ x}_{j+k}\vert$ when $a \in \{ j,\ldots,j + k\}\,\ni /b$. We set

$$\displaystyle{\mathcal{E}(n)\, =\, \mathcal{O}_{n}^{{\prime}}\,,}$$

which is the graded dual. In the applications to vertex algebras and renormalization theory of massless fields:

$$\displaystyle{\begin{array}{rl} \mathcal{O}_{n}\, =&\mbox{ The algebra of rational $n$\textendash point functions }\ \frac{P(\mathrm{x}_{1} -\mathrm{ x}_{2},\ldots,\mathrm{x}_{n-1} -\mathrm{ x}_{n})} {\mathop{\prod }\limits _{1\,\leqslant \,j\,<\,k\,\leqslant \,n}{\bigl ((\mathrm{x}_{j} -\mathrm{ x}_{k})^{2}\bigr )}^{\nu _{j,k}}} \\ & \mbox{ on $\mathbb{R}^{D} \ni \mathrm{ x}_{1},\ldots,x_{n}$ with light\textendash cone singularities, graded by the degree} \\ &\text{of homogeneity.}\end{array} }$$

The key relation between the operad $\mathcal{E}$ and the vertex algebras is that every vertex algebra induces a system of linear maps

where the down arrow is the dual of the correlation functions maps:

$$\displaystyle{\begin{array}{rcccl} V ^{\,\otimes n}&\otimes &V ^{{\prime}}&\longmapsto &\mathcal{O}_{n} \\ a_{1} \otimes \cdots \otimes a_{n}&\otimes & \lambda &\longmapsto &\lambda \bigl (a_{1}(\mathrm{x}_{1} -\mathrm{ x}_{n})\,\cdots \,a_{n-1}(\mathrm{x}_{n-1} -\mathrm{ x}_{n})\,a_{n}\bigr ) \\ & & && \equiv \,\bigl \langle\lambda \bigr | a_{1}(\mathrm{x}_{1} -\mathrm{ x}_{n})\,\cdots \,a_{n-1}(\mathrm{x}_{n-1} -\mathrm{ x}_{n})\,a_{n}\bigr \rangle\end{array}} $$

(here we assume that the graded pieces of V are finite dimensional). Thus, the operadic structure on $\mathcal{E}$ is such that the above system maps $\mathcal{E}(n)\longrightarrow \mathcal{E}\mathit{nd}_{V }(n)$ gives an operadic morphism. On the other hand, one can show that this operadic structure can be described entirely in terms of the expansions’ operations in $\mathcal{O}_{n}$.

• C. Passing to the renormalization let us mention first that the same rational functions belonging to $\mathcal{O}_{n}$ appear as “Feynman amplitudes” (= integrands in the Feynman integrals) in massless field theories. Here is an example of such a Feynman amplitude in the ϕ ⁴–theory:

  

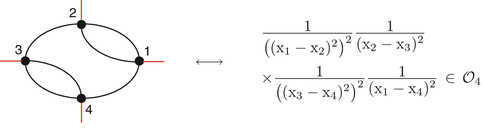
  It is important for the present construction that we consider the ultraviolet renormalization on configuration space. In terms of Feynman amplitudes the renormalization is given by a system of linear maps

  $$\displaystyle{\mathcal{O}_{n} \rightarrow \mathcal{D}^{{\prime}}{\bigl ((\mathbb{R}^{D})^{\times (n-1)}\bigr )}}$$

  subject to (recursive) conditions (cf. [7, 9] and references therein). In particular, the renormalization ambiguity at order n is described by a linear map: $\mathcal{O}_{n}\, \rightarrow \,\mathcal{D}^{{\prime}}[0_{n}]$, where $\mathcal{D}^{{\prime}}[0_{n}]$ stands for the space of distributions on $(\mathbb{R}^{D})^{\times (n-1)}$ supported at the origin. We obtain a sequence of vector spaces

  $$\displaystyle{\mathcal{R}(n)\,:=\,\bigl \{ Q: \mathcal{O}_{n}\, \rightarrow \,\mathcal{D}^{{\prime}}[0_{ n}]\,\bigl |\,\text{commuting with multiplication by polynomials}\bigr \}}$$

  where the condition comes from the requirements on the renormalization maps (as explained in [7] and [9]).

The bridge between the theory of the vertex algebras and renormalization is based on an existence of a natural isomorphism [7]

$$\displaystyle{\mathcal{E}(n)\,\mathop{\cong}\,\mathcal{R}(n)\,.}$$

Furthermore, the operadic compositions in $\mathcal{E}(n)$ have an interpretation on $\mathcal{R}(n)$ that corresponds to basic operations used in the renormalization group composition. The later has a very natural pictorial illustration

and its combinatorial version was described in [3].

The role of the operad $\mathcal{R}$ in renormalization theory is that it describes the Stückelberg–Bogoliubov renormalization group. The latter group is formed by all possible changes in the renormalization:

where $\{Q_{n}^{{\prime}}\}$ and $\{Q_{n}^{{\prime\prime}}\}$ are arbitrary sequences of changes of the renormalization $Q_{n}^{{\prime}},Q_{n}^{{\prime\prime}}\in \mathcal{R}(n)$.

In the paper [3] a functor was constructed

$$\displaystyle{{\Bigl \{\text{Operads}\Bigr \}}\,\longrightarrow \,{\Bigl \{\text{Groups}\Bigr \}}\,,}$$

which produces:

• the Renormalization group when applied to $\mathcal{E}$;

• the group of formal diffeomorphisms when applied on $\mathcal{E}\mathit{nd}_{V }$;

• the renormalization group action via an operadic morphism $\mathcal{E}\rightarrow \mathcal{E}\mathit{nd}_{V }$.

Our conclusion is summarized in the following scheme:

$$\displaystyle{\begin{array}{c} \mbox{ The $\mathcal{E}$-algebras are vertex algebras} \\ \uparrow \ \\ \mbox{ Expansion operad $\mathcal{E}$}\ \ \mathop{\cong}\ \ \mbox{ Renormalization operad $\mathcal{R}$} \\ \downarrow \\ \mbox{ The group associated to $\mathcal{R}$ is the renormalization group}\end{array} }$$