Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Bosonic String in the Weakly Curved Background

Let us consider the closed string moving in the coordinate dependent background, described by the action [1]

$$\displaystyle{ S[x] =\kappa \int _{\varSigma }d^{2}\xi \ \partial _{ +}x^{\mu }\varPi _{ +\mu \nu }[x]\partial _{-}x^{\nu }. }$$
(1)

The background is defined by the space-time metric G μ ν and the antisymmetric Kalb-Ramond field B μ ν

$$\displaystyle{ \varPi _{\pm \mu \nu }[x] = B_{\mu \nu }[x] \pm \frac{1} {2}G_{\mu \nu }[x]. }$$
(2)

The light-cone coordinates are

$$\displaystyle{ \xi ^{\pm } = \frac{1} {2}(\tau \pm \sigma ),\qquad \partial _{\pm } = \partial _{\tau } \pm \partial _{\sigma }, }$$
(3)

and the action is given in the conformal gauge (the world-sheet metric is taken to be \(g_{\alpha \beta } = e^{2F}\eta _{\alpha \beta }\)).

The world-sheet conformal invariance is required, as a condition of having a consistent theory on a quantum level. This leads to the space-time equations for the background fields, which equal

$$\displaystyle{ R_{\mu \nu } -\frac{1} {4}B_{\mu \rho \sigma }B_{\nu }^{\ \rho \sigma } = 0,\quad D_{\rho }B_{\ \mu \nu }^{\rho } = 0, }$$
(4)

in the lowest order in slope parameter α ′ and for the constant dilaton field Φ = const. Here \(B_{\mu \nu \rho } = \partial _{\mu }B_{\nu \rho } + \partial _{\nu }B_{\rho \mu } + \partial _{\rho }B_{\mu \nu }\) is the field strength of the field B μ ν , and R μ ν and D μ are Ricci tensor and covariant derivative with respect to the space-time metric.

We will consider a weakly curved background [2, 3], defined by

$$\displaystyle\begin{array}{rcl} G_{\mu \nu }[x]& =& const, \\ B_{\mu \nu }[x]& =& b_{\mu \nu } + h_{\mu \nu }[x] = b_{\mu \nu } + \frac{1} {3}B_{\mu \nu \rho }x^{\rho },\qquad b_{\mu \nu },B_{\mu \nu \rho } = const.{}\end{array}$$
(5)

Here, the constant B μ ν ρ is infinitesimal. The background (5) is the solution of the field equations (4) in the first order in B μ ν ρ .

2 Partial T-Dualization

In the paper [3], we generalized the Buscher prescription for a construction of a T-dual theory. This prescription, unlike the standard one [4], is applicable to the string backgrounds depending on all the space-time coordinates, such as the weakly curved background. We performed the procedure along all the coordinates and obtained T-dual theory. The noncommutativity of the T-dual coordinates we investigated in [5]. In the present paper we consider the partial T-dualization, i.e. the application of the procedure to some without subset of the coordinates. We construct the partially T-dualized theory. The noncommutativity of the coordinates in similar theories was considered in [6].

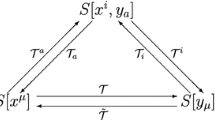
Let us mark the T-dualization along the coordinate x μ by T μ , and separate the coordinates into two subsets (x i, x a) with \(i = 0,\ldots,d - 1\) and \(a = d,\ldots,D - 1\) and mark the T-dualizations along these subsets of coordinates by

$$\displaystyle{ T^{i} \equiv T_{ 0} \circ \ldots \circ T_{d-1},\quad T^{a} \equiv T_{ d} \circ \ldots \circ T_{D-1}. }$$
(6)

In this section we will find the partially T-dualized action performing T-dualization along coordinates x a, \(\mathcal{T}^{a}: S\).

The closed string action in the weakly curved background has a global symmetry

$$\displaystyle{ \delta x^{\mu } =\lambda ^{\mu }. }$$
(7)

Let us localize this symmetry for the coordinates x a

$$\displaystyle{ \delta x^{a} =\lambda ^{a}(\tau,\sigma ),\quad a = d,\ldots,D - 1, }$$
(8)

by introducing the gauge fields v α a and substituting the ordinary derivatives with the covariant ones

$$\displaystyle{ \partial _{\alpha }x^{a} \rightarrow D_{\alpha }x^{a} = \partial _{\alpha }x^{a} + v_{\alpha }^{a}. }$$
(9)

The gauge invariance of the covariant derivatives is obtained by imposing the following transformation law for the gauge fields

$$\displaystyle{ \delta v_{\alpha }^{a} = -\partial _{\alpha }\lambda ^{a}. }$$
(10)

Also, substitute x a in the argument of the background fields with its invariant extension, defined by

$$\displaystyle\begin{array}{rcl} \varDelta x_{inv}^{a}& \equiv & \int _{ P}d\xi ^{\alpha }\,D_{\alpha }x^{a} =\int _{ P}(d\xi ^{+}D_{ +}x^{a} + d\xi ^{-}D_{ -}x^{a}) \\ & =& x^{a} - x^{a}(\xi _{ 0}) +\varDelta V ^{a}, {}\end{array}$$
(11)

where

$$\displaystyle{ \varDelta V ^{a} \equiv \int _{ P}d\xi ^{\alpha }v_{\alpha }^{a} =\int _{ P}(d\xi ^{+}v_{ +}^{a} + d\xi ^{-}v_{ -}^{a}). }$$
(12)

The line integral is taken along the path P, from the initial point \(\xi _{0}^{\alpha }(\tau _{0},\sigma _{0})\) to the final one \(\xi ^{\alpha }(\tau,\sigma )\). To preserve the physical equivalence between the gauged and the original theory, one introduces the Lagrange multiplier y a and adds the term \(\frac{1} {2}y_{a}F_{+-}^{a}\) to the Lagrangian, which will force the field strength \(F_{+-}^{a} \equiv \partial _{+}v_{-}^{a} - \partial _{-}v_{+}^{a} = -2F_{01}^{a}\) to vanish. In this way, we obtain the gauge invariant action

$$\displaystyle\begin{array}{rcl} S_{inv}& =& \kappa \int d^{2}\xi \Big[\partial _{ +}x^{i}\varPi _{ +ij}[x^{i},\varDelta x_{ inv}^{a}]\partial _{ -}x^{j} + \partial _{ +}x^{i}\varPi _{ +ia}[x^{i},\varDelta x_{ inv}^{a}]D_{ -}x^{a} \\ & & +D_{+}x^{a}\varPi _{ +ai}[x^{i},\varDelta x_{ inv}^{a}]\partial _{ -}x^{i} + D_{ +}x^{a}\varPi _{ +ab}[x^{i},\varDelta x_{ inv}^{a}]D_{ -}x^{b} \\ & & +\frac{1} {2}(v_{+}^{a}\partial _{ -}y_{a} - v_{-}^{a}\partial _{ +}y_{a})\Big], {}\end{array}$$
(13)

where the last term is equal to \(\frac{1} {2}y_{a}F_{+-}^{a}\) up to the total divergence. Now, we can use the gauge freedom to fix the gauge x a(ξ) = x a(ξ 0). The gauge fixed action equals

$$\displaystyle\begin{array}{rcl} S_{fix}& =& \kappa \int d^{2}\xi \Big[\partial _{ +}x^{i}\varPi _{ +ij}[x^{i},\varDelta V ^{a}]\partial _{ -}x^{j} + \partial _{ +}x^{i}\varPi _{ +ia}[x^{i},\varDelta V ^{a}]v_{ -}^{a}\ \\ & & +\ v_{+}^{a}\varPi _{ +ai}[x^{i},\varDelta V ^{a}]\partial _{ -}x^{i} + v_{ +}^{a}\varPi _{ +ab}[x^{i},\varDelta V ^{a}]v_{ -}^{b}\ \\ & & +\ \frac{1} {2}(v_{+}^{a}\partial _{ -}y_{a} - v_{-}^{a}\partial _{ +}y_{a})\Big]. {}\end{array}$$
(14)

The equations of motion for the Lagrange multiplier y a , \(\partial _{+}v_{-}^{a} - \partial _{-}v_{+}^{a} = 0\), have a solution v ± a = ∂ ± x a, which turns the gauge fixed action to the initial one.

2.1 The Partially T-Dualized Action

The partially T-dualized action will be obtained after elimination of the gauge fields from the gauge fixed action (14), using their equations of motion. Varying over the gauge fields v ± a one obtains

$$\displaystyle{ \varPi _{\pm ai}[x^{i},\varDelta V ^{a}]\partial _{ \mp }x^{i} +\varPi _{ \pm ab}[x^{i},\varDelta V ^{a}]v_{ \mp }^{b} + \frac{1} {2}\partial _{\mp }y_{a} = \pm \beta _{a}^{\pm }[x^{i},V ^{a}], }$$
(15)

where \(\beta _{a}^{\pm }[x^{i},V ^{a}]\) is the infinitesimal contribution from the background fields argument. Using the inverse of the background fields composition 2κ Π ±ab , defined by \(\tilde{\varTheta }_{\pm }^{ab} \equiv -\frac{2} {\kappa } (\tilde{G}_{E}^{-1})^{ac}\varPi _{ \pm cd}(\tilde{G}^{-1})^{db}\!,\) where \(\tilde{G}_{ab} \equiv G_{ab}\) and \(\tilde{G}_{Eab} \equiv G_{ab} - 4B_{ac}(\tilde{G}^{-1})^{cd}B_{db}\), we can extract the gauge fields v ± a from Eq. (15)

$$\displaystyle{ v_{\mp }^{a} = -2\kappa \tilde{\varTheta }_{ \mp }^{ab}[x^{i},\varDelta V ^{a}]\Big[\varPi _{ \pm bi}[x^{i},\varDelta V ^{a}]\partial _{ \mp }x^{i} + \frac{1} {2}\partial _{\mp }y_{b} \mp \beta _{b}^{\pm }[x^{i},V ^{a}]\Big]. }$$
(16)

Substituting (16) into the action (14), we obtain the partially T-dualized action

$$\displaystyle\begin{array}{rcl} S_{\pi }[x^{i},y_{ a}]& =& \kappa \int d^{2}\xi \bigg[\partial _{ +}x^{i}\bar{\varPi }_{ +ij}[x^{i},\varDelta V ^{a}(x^{i},y^{a})]\partial _{ -}x^{j} \\ & & + \frac{\kappa } {2}\,\partial _{+}y_{a}\tilde{\varTheta }_{-}^{ab}[x^{i},\varDelta V ^{a}(x^{i},y^{a})]\partial _{ -}y_{b} \\ & & -\kappa \,\partial _{+}x^{i}\varPi _{ +ia}[x^{i},\varDelta V ^{a}(x^{i},y^{a})]\tilde{\varTheta }_{ -}^{ab}[x^{i},\varDelta V ^{a}(x^{i},y^{a})]\partial _{ -}y_{b} \\ & & +\kappa \,\partial _{+}y_{a}\tilde{\varTheta }_{-}^{ab}[x^{i},\varDelta V ^{a}(x^{i},y^{a})]\varPi _{ +bi}[x^{i},\varDelta V ^{a}(x^{i},y^{a})]\partial _{ -}x^{i}\bigg],\qquad {}\end{array}$$
(17)

where

$$\displaystyle{ \bar{\varPi }_{+ij} \equiv \varPi _{+ij} - 2\kappa \varPi _{+ia}\tilde{\varTheta }_{-}^{ab}\varPi _{ +bj}. }$$
(18)

In order to find the explicit value of the background fields argument Δ V a(x i, y a), one substitutes the zeroth order of the equations of motion (16) into (12) and obtains

$$\displaystyle\begin{array}{rcl} \varDelta V ^{(0)a}& =& -\kappa \Big[\tilde{\varTheta }_{ 0+}^{ab}\varPi _{ 0-bi} +\tilde{\varTheta }_{ 0-}^{ab}\varPi _{ 0+bi}\Big]\varDelta x^{(0)i}\ \\ & & -\ \kappa \Big[\tilde{\varTheta }_{0+}^{ab}\varPi _{ 0-bi} -\tilde{\varTheta }_{0-}^{ab}\varPi _{ 0+bi}\Big]\varDelta \tilde{x}^{(0)i}\ \\ & & -\ \frac{\kappa } {2}\Big[\tilde{\varTheta }_{0+}^{ab} +\tilde{\varTheta }_{ 0-}^{ab}\Big]\varDelta y_{ b}^{(0)} - \frac{\kappa } {2}\Big[\tilde{\varTheta }_{0+}^{ab} -\tilde{\varTheta }_{ 0-}^{ab}\Big]\varDelta \tilde{y}_{ b}^{(0)},{}\end{array}$$
(19)

where \(\tilde{\varTheta }_{0\pm }^{ab}\) stands for the zeroth order value of \(\tilde{\varTheta }_{\pm }^{ab}\), which can be written as

$$\displaystyle{ \tilde{\varTheta }_{0\pm }^{ab} \equiv -\frac{2} {\kappa } (\tilde{g}^{-1})^{ac}\,\varPi _{ 0\pm cd}(\tilde{G}^{-1})^{db} =\tilde{\theta }_{ 0}^{ab} \mp \frac{1} {\kappa } (\tilde{g}^{-1})^{ab}, }$$
(20)

where \(\tilde{g}_{ab} = G_{ab} - 4b_{ac}(\tilde{G}^{-1})^{cd}b_{db}\); \(\tilde{\theta }_{0}^{ab} \equiv -\frac{2} {\kappa } (\tilde{g}^{-1})^{ac}\,b_{ cd}(\tilde{G}^{-1})^{db}\) and

$$\displaystyle{ \varDelta \tilde{y}_{a}^{(0)} =\int (d\tau y_{ a}^{(0){\prime}} + d\sigma \dot{y}_{ a}^{(0)}),\quad \varDelta \tilde{x}^{(0)i} =\int (d\tau x^{(0){\prime}i} + d\sigma \dot{x}^{(0)i}). }$$
(21)

Initial theory, the partially T-dualized theory and the totally T-dualized theory obtained in [3] are physically equivalent theories. In the next section we will partially T-dualize the partially T-dualized theory.

3 The Total T-Dualization of the Initial Action

The T-dual theory, derived in [3], a result of T-dualization of the initial action along all the coordinates, is given by

$$\displaystyle{ ^{\star }S[y] =\kappa \int d^{2}\xi \ \partial _{ +}y_{\mu }\,^{\star }\varPi _{ +}^{\mu \nu }[\varDelta V (y)]\,\partial _{ -}y_{\nu } =\, \frac{\kappa ^{2}} {2}\int d^{2}\xi \ \partial _{ +}y_{\mu }\varTheta _{-}^{\mu \nu }[\varDelta V (y)]\partial _{ -}y_{\nu }, }$$
(22)

with

$$\displaystyle\begin{array}{rcl} \varTheta _{\pm }^{\mu \nu }& \equiv & -\frac{2} {\kappa } (G_{E}^{-1}\varPi _{ \pm }G^{-1})^{\mu \nu } = \theta ^{\mu \nu } \mp \frac{1} {\kappa } (G_{E}^{-1})^{\mu \nu },{}\end{array}$$
(23)

where

$$\displaystyle{ G_{E\mu \nu } \equiv G_{\mu \nu } - 4(BG^{-1}B)_{\mu \nu },\quad \theta ^{\mu \nu } \equiv -\frac{2} {\kappa } (G_{E}^{-1}BG^{-1})^{\mu \nu }. }$$
(24)

The T-dual background fields are equal to

$$\displaystyle{ ^{\star }G^{\mu \nu }[\varDelta V (y)] = (G_{ E}^{-1})^{\mu \nu }[\varDelta V (y)],\quad ^{\star }B^{\mu \nu }[\varDelta V (y)] = \frac{\kappa } {2}\theta ^{\mu \nu }[\varDelta V (y)]. }$$
(25)

The argument of the background fields is given by

$$\displaystyle{ \varDelta V ^{\mu }(y) = -\kappa \theta _{0}^{\mu \nu }\varDelta y_{\nu } + (g^{-1})^{\mu \nu }\varDelta \tilde{y}_{\nu }, }$$
(26)

where \(\varDelta y_{\mu } = y_{\mu }(\xi ) - y_{\mu }(\xi _{0})\) and \(\tilde{y}_{\mu } =\int (d\tau y_{\mu }^{{\prime}} + d\sigma \dot{y}_{\mu })\), while \(g_{\mu \nu } = G_{\mu \nu } - 4b_{\mu \nu }^{2}\) and \(\theta _{0}^{\mu \nu } = -\frac{2} {\kappa } (g^{-1}bG^{-1})^{\mu \nu }\).

Let us now show that the same result will be obtained applying the T-dualization procedure to the coordinates x i of the partially T-dualized theory (17), \(\mathcal{T}^{i}: S_{\pi }[x^{i},y_{a}]\). Substituting the ordinary derivatives ∂ ± x i with the covariant derivatives

$$\displaystyle{ D_{\pm }x^{i} = \partial _{ \pm }x^{i} + v_{ \pm }^{i}, }$$
(27)

where the gauge fields \(v_{\pm }^{i}\) transform as \(\delta v_{\pm }^{i} = -\partial _{\pm }\lambda ^{i}\), and substituting the coordinates x i in the background field arguments by

$$\displaystyle{ \varDelta x_{inv}^{i} =\int _{ P}(d\xi ^{+}D_{ +}x^{i} + d\xi ^{-}D_{ -}x^{i}), }$$
(28)

we obtain the gauge invariant action, which after fixing the gauge by \(x^{i}(\xi ) = x^{i}(\xi _{0})\) becomes

$$\displaystyle\begin{array}{rcl} S_{\pi }^{fix}& =& \kappa \int d^{2}\xi \bigg[v_{ +}^{i}\bar{\varPi }_{ +ij}[\varDelta V ^{\mu }]v_{ -}^{j} + \frac{\kappa } {2}\,\partial _{+}y_{a}\tilde{\varTheta }_{-}^{ab}[\varDelta V ^{\mu }]\partial _{ -}y_{b} \\ & & -\kappa \,v_{+}^{i}\varPi _{ +ia}[\varDelta V ^{\mu }]\tilde{\varTheta }_{ -}^{ab}[\varDelta V ^{\mu }]\partial _{ -}y_{b} +\kappa \, \partial _{+}y_{a}\tilde{\varTheta }_{-}^{ab}[\varDelta V ^{\mu }]\varPi _{ +bi}[\varDelta V ^{\mu }]v_{ -}^{i} \\ & & +\frac{1} {2}(v_{+}^{i}\partial _{ -}y_{i} - v_{-}^{i}\partial _{ +}y_{i})\bigg]. {}\end{array}$$
(29)

Here Δ V i is defined by

$$\displaystyle{ \varDelta V ^{i} \equiv \int _{ P}(d\xi ^{+}v_{ +}^{i} + d\xi ^{-}v_{ -}^{i}), }$$
(30)

and Δ V a is defined in (19), whose arguments are in this case Δ V i and y a.

The totally T-dualized action will be obtained by eliminating the gauge fields from the gauge fixed action, using their equations of motion. Varying the action (29) over the gauge fields \(v_{\pm }^{i}\) one obtains

$$\displaystyle{ \bar{\varPi }_{\pm ij}v_{\mp }^{j} -\kappa \varPi _{ \pm ia}\tilde{\varTheta }_{\mp }^{ab}\partial _{ \mp }y_{b} + \frac{1} {2}\partial _{\mp }y_{i} = \pm \beta _{i}^{\pm }. }$$
(31)

Using the fact that the background field composition \(\bar{\varPi }_{\pm ij}\) is inverse to \(2\kappa \varTheta _{\mp }^{ij}\), we can rewrite the equation of motion (31) expressing the gauge fields as

$$\displaystyle\begin{array}{rcl} v_{\mp }^{i}& =& 2\kappa \varTheta _{ \mp }^{ij}\Big[\kappa \varPi _{ \pm ja}\tilde{\varTheta }_{\mp }^{ab}\partial _{ \mp }y_{b} -\frac{1} {2}\partial _{\mp }y_{j} \pm \beta _{j}^{\pm }\Big].{}\end{array}$$
(32)

Using \(\varPi _{\pm ab}\varTheta _{\mp }^{bi} = -\varPi _{\pm aj}\varTheta _{\mp }^{ji},\) we note that

$$\displaystyle{ \varTheta _{\mp }^{ij}\varPi _{ \pm ja}\tilde{\varTheta }_{\mp }^{ab} = -\varTheta _{ \mp }^{ic}\varPi _{ \pm ca}\tilde{\varTheta }_{\mp }^{ab} = -\frac{1} {2\kappa }\varTheta _{\mp }^{ib}, }$$
(33)

and obtain

$$\displaystyle\begin{array}{rcl} v_{\mp }^{i}& =& -\kappa \varTheta _{ \mp }^{i\mu }\partial _{ \mp }y_{\mu } \pm 2\kappa \varTheta _{\mp }^{ij}\beta _{ j}^{\pm }.{}\end{array}$$
(34)

Substituting (34) into (29), the action becomes

$$\displaystyle\begin{array}{rcl} S& =& \kappa \int d^{2}\xi \Big[\partial _{ +}y_{i}\Big(\kappa \varTheta _{-}^{ij} -\kappa ^{2}\varTheta _{ -}^{ik}\bar{\varPi }_{ +kl}\varTheta _{-}^{lj}\Big)\partial _{ -}y_{j}\ {} \\ & & +\,\partial _{+}y_{a}\Big(-\kappa ^{2}\varTheta _{ -}^{aj}\bar{\varPi }_{ +jk}\varTheta _{-}^{ki} + \frac{\kappa } {2}\varTheta _{-}^{ai} -\kappa ^{2}\tilde{\varTheta }_{ -}^{ab}\varPi _{ +bj}\varTheta _{-}^{ji}\Big)\partial _{ -}y_{i}\ \\ & & +\,\partial _{+}y_{i}\Big(-\kappa ^{2}\varTheta _{ -}^{ij}\bar{\varPi }_{ +jk}\varTheta _{-}^{ka} + \frac{\kappa } {2}\varTheta _{-}^{ia} -\kappa ^{2}\varTheta _{ -}^{ij}\varPi _{ +jb}\tilde{\varTheta }_{-}^{ba}\Big)\partial _{ -}y_{a}\ \\ & & +\,\partial _{+}y_{a}\Big( \frac{\kappa } {2}\tilde{\varTheta }_{-}^{ab} -\kappa ^{2}\varTheta _{ -}^{ai}\bar{\varPi }_{ +ij}\varTheta _{-}^{jb} -\kappa ^{2}\varTheta _{ -}^{ai}\varPi _{ +ic}\tilde{\varTheta }_{-}^{cb} -\kappa ^{2}\tilde{\varTheta }_{ -}^{ac}\varPi _{ +ci}\varTheta _{-}^{ib}\Big)\partial _{ -}y_{b}\Big]. \\ \end{array}$$
(35)

Using \(\bar{\varPi }_{\pm ij}\varTheta _{\mp }^{jk} =\varTheta _{ \mp }^{kj}\bar{\varPi }_{\pm ji} = \frac{1} {2\kappa }\delta _{i}^{k}\); \(\tilde{\varPi }_{\pm ab}\varTheta _{\mp }^{bc} =\varTheta _{ \mp }^{cb}\tilde{\varPi }_{\pm ba} = \frac{1} {2\kappa }\delta _{a}^{c}\); \(\varPi _{\pm ab}\varTheta _{\mp }^{bi} = -\varPi _{\pm aj}\varTheta _{\mp }^{ji}\); \(\varPi _{\pm ij}\varTheta _{\mp }^{ja} = -\varPi _{\pm ib}\varTheta _{\mp }^{ba}\) and \(\varTheta _{\mp }^{ci}\bar{\varPi }_{\pm ik} = -\tilde{\varTheta }_{\mp }^{ca}\varPi _{\pm ak}\), one can rewrite this action as

$$\displaystyle{ S = \frac{\kappa ^{2}} {2}\int d^{2}\xi \,\partial _{ +}y_{\mu }\varTheta _{-}^{\mu \nu }\partial _{ -}y_{\nu }. }$$
(36)

In order to find the background fields argument Δ V i, we consider the zeroth order of Eq. (34)

$$\displaystyle{ v_{0\mp }^{i} = -\kappa \varTheta _{ 0\mp }^{i\mu }\partial _{ \mp }y_{\mu }, }$$
(37)

and conclude that

$$\displaystyle{ \varDelta V ^{i} = -\kappa \theta _{ 0}^{i\mu }\varDelta y_{\mu } + (g^{-1})^{i\mu }\varDelta \tilde{y}_{\mu }. }$$
(38)

Using the integral form of the variables and the relations \(\varPi _{\pm ac}\varTheta _{\mp }^{cb} +\varPi _{\pm ai}\varTheta _{\mp }^{ib} = \frac{1} {2\kappa }\delta _{a}^{b}\); \(\varTheta _{\mp }^{ib} = -2\kappa \bar{\varTheta }_{\mp }^{ij}\varPi _{\pm ja}\varTheta _{\mp }^{ab}\); \(\varTheta _{\mp }^{aj} = -2\kappa \tilde{\varTheta }_{\mp }^{ab}\varPi _{\pm bi}\varTheta _{\mp }^{ij}\), we obtain that \(\varDelta V ^{a}(\varDelta V ^{i},y^{a})\) defined in (19) equals

$$\displaystyle{ \varDelta V ^{a}(\varDelta V ^{i},y_{ a}) = -\kappa \theta _{0}^{a\mu }\varDelta y_{\mu } + (g^{-1})^{a\mu }\varDelta \tilde{y}_{\mu }. }$$
(39)

Therefore, we conclude that action (36) is the totally T-dualized action (22).

In this paper we performed the partial T-dualizations and obtained the T-duality chain

$$\displaystyle{ S[x^{\mu }]\mathop{\longrightarrow}\limits_{}^{\mathcal{T}^{a}}S_{\pi }[x^{i},y_{ a}]\mathop{\longrightarrow}\limits_{}^{\mathcal{T}^{i}}{}^{\star }S[y_{\mu }]. }$$
(40)

The first action describes the geometrical background, while the second and the third describe the non-geometrical backgrounds with nontrivial fluxes. From this chain one can find the relations between the arbitrary two coordinates in the chain. These general T-duality coordinate transformation laws are used in the investigation of the relations between the Poisson structures of the original, the partially T-dualized and the totally T-dualized theory [5]. Their canonical form will be used in deriving the complete closed string non-commutativity relations, which are the important features of the non-geometrical backgrounds.