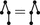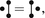Abstract
We study renormalization in a kinetic scheme (realized by subtraction at fixed external parameters as implemented in the BPHZ and MOM schemes) using the Hopf algebraic framework, first summarizing and recovering known results in this setting. Then we give a direct combinatorial description of renormalized amplitudes in terms of Mellin transform coefficients, featuring the universal property of rooted trees H R . In particular, a special class of automorphisms of H R emerges from the action of changing Mellin transforms on the Hochschild cohomology of perturbation series. Furthermore, we show how the Hopf algebra of polynomials carries a refined renormalization group property, implying its coarser form on the level of correlation functions. Application to scalar quantum field theory reveals the scaling behaviour of individual Feynman graphs.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
As was shown in [6, 16, 24], we may decompose Feynman integrals into functions of a single scale parameter s only (further forking into logarithmic divergent parts multiplied by suitable powers of s) and scale-independent functions of the other kinematic variables, called angles. Furthermore, the Hopf algebra H R of rooted trees suffices to encode the full structure of subdivergences in quantum field theory by [8, 9, 16].
We can therefore study such generic Feynman rules in a purely algebraic framework as pioneered in [9, 18]. Renormalizing short-distance singularities by subtraction at a reference scale μ (which we refer to as kinetic scheme) leads to amplitudes of a distinguished algebraic kind: Theorem 4 proves them to implement the universal property of H R , delivering an explicit combinatorial evaluation in terms of Mellin transform coefficients.
Further investigating the role of Hochschild cohomology, in Sect. 6 we define a class of automorphisms of H R which transform the perturbation series in a way equivalent to changing the Feynman rules. This clarifies how exact one-cocycles describe variations.
In Sects. 4 and 5 we advertise to think about the renormalization group property as a Hopf algebra morphism to polynomials, determining higher logarithms in (28). We show how it implies the renormalization group on correlation functions and extend the propagator-coupling-duality of [5] which yields the functional equation (34).
After analysing the differences to the minimal subtraction scheme in Sect. 7, we show explicitly how our general results manifest themselves in scalar field theory.
2 Connected Hopf Algebras
The fundamental mathematical structure behind perturbative renormalization is the Hopf algebra as discovered in [16]. We briefly summarize the results on Hopf algebras we need and recommend [21, 22] for detailed introductions with a focus on renormalization.
All vector spaces live over a field \(\mathbb{K}\) of zero characteristic (in examples \(\mathbb{K} = \mathbb{R}\)), Hom(⋅ , ⋅ ) denotes \(\mathbb{K}\)-linear maps and linM the linear span. Every algebra \((\mathcal{A},m,u)\) shall be unital, associative and commutative, any bialgebras \((H,m,u,\varDelta,\varepsilon )\) in addition also counital and coassociative. They split into the scalars and the augmentation ideal \(\ker \varepsilon\) as \(H = \mathbb{K}\! \cdot 1\!\!1\oplus \ker \varepsilon = \mathrm{im}u\oplus \ker \varepsilon\), inducing the projection \(P:=\mathrm{ id} - u\circ \varepsilon \!:\ H \twoheadrightarrow \ker \varepsilon\). We use Sweedler’s notation \(\varDelta (x) =\sum _{x}x_{1} \otimes x_{2}\) and \(\tilde{\varDelta }(x) =\sum _{x}x^{\prime} \otimes x^{\prime\prime}\) to abbreviate the reduced coproduct \(\tilde{\varDelta }\mathop{:}=\varDelta -1\!\!1 \otimes \mathop{\mathrm{id}}-\mathop{\mathrm{id}}\otimes 1\!\!1.\)
We assume a connected grading \(H =\bigoplus _{n\geq 0}H_{n}\) (\(H_{0} = \mathbb{K} \cdot 1\!\!1\)) and write \(\left \vert x\right \vert \mathop{:}= n\) for homogeneous 0 ≠ x ∈ H n , defining the grading operator Y ∈End(H) by \(Y x = \left \vert x\right \vert \cdot x\). Exponentiation yields a one-parameter group \(\mathbb{K} \ni t\mapsto \theta _{t}\) of Hopf algebra automorphisms
An algebra \((\mathcal{A},m_{\mathcal{A}},u_{\mathcal{A}})\) induces the associative convolution product on \(\mathrm{Hom}(H,\mathcal{A})\) by
with unit given by \(e \mathop{:}= u_{\mathcal{A}}\circ \varepsilon\). As outcome of the connectedness of H we stress
-
1.
The characters \(G_{\mathcal{A}}^{H} \mathop{:}= \left \{\phi \in \mathrm{Hom}(H,\mathcal{A})\!:\ \phi \circ u = u_{\mathcal{A}}\ \text{and}\ \phi \circ m = m_{\mathcal{A}}\circ \right.\) \(\left.(\phi \otimes \phi )\right \}\) (morphisms of unital algebras) form a group under ⋆.
-
2.
Hence \(\mathop{\mathrm{id}} \in G_{H}^{H}\) has a unique inverse S: = id⋆−1, called antipode, turning H into a Hopf algebra. For all \(\phi \in G_{\mathcal{A}}^{H}\) we have ϕ ⋆−1 =ϕ ∘ S.
-
3.
The bijection \(\exp _{\star }\!:\ \mathfrak{g}_{\mathcal{A}}^{H} \rightarrow G_{\mathcal{A}}^{H}\) with inverse \(\log _{\star }\!:\ G_{\mathcal{A}}^{H} \rightarrow \mathfrak{g}_{\mathcal{A}}^{H}\) between \(G_{\mathcal{A}}^{H}\) and the infinitesimal characters \(\mathfrak{g}_{\mathcal{A}}^{H} \mathop{:}= \left \{\phi \in \mathrm{Hom}(H,\mathcal{A})\!:\ \phi \circ m\,=\,\phi \otimes e\,+\,e\otimes \phi \right \}\) is given by the pointwise finite series
$$\displaystyle{ \exp _{\star }(\phi ) \mathop{:}=\sum _{n\in \mathbb{N}_{0}} \frac{{\phi }^{\star n}} {n!}\quad \text{and}\quad \log _{\star }(\phi ) \mathop{:}=\sum _{n\in \mathbb{N}} \frac{{(-1)}^{n+1}} {n} {(\phi -e)}^{\star n}. }$$(2)
2.1 Hochschild Cohomology
The Hochschild cochain complex [1, 8, 22] we associate to H contains the functionals \(H^{\prime} = \mathrm{Hom}(H, \mathbb{K})\) as zero-cochains. One-cocycles \(L \in \text{HZ}_{\varepsilon }^{1}(H) \subset \mathrm{End}(H)\) are linear maps such that \(\varDelta \circ L = (\mathop{\mathrm{id}}\otimes L) \circ \varDelta +L \otimes 1\!\!1\) and the differential
determines the first cohomology group by \(\text{HH}_{\varepsilon }^{1}(H) \mathop{:}= \text{HZ}_{\varepsilon }^{1}(H)/\text{HB}_{\varepsilon }^{1}(H)\).
Lemma 1.
Cocycles \(L \in \text{HZ}_{\varepsilon }^{1}(H)\) fulfil \(\mathrm{im}L \subseteq \ker \varepsilon\) and \(L(1\!\!1) \in \mathrm{ Prim}(H) \mathop{:}=\ker \tilde{\varDelta }\) is primitive. The map \(\text{HH}_{\varepsilon }^{1}(H) \rightarrow \mathrm{ Prim}(H)\) , [L]↦L( 1 ) is well-defined since δα( 1 ) = 0 for all α ∈ H′.
2.2 Rooted Trees
The Hopf algebra HR of he domain of Feynman rules. As an algebra, \(H_{R} = S(\mathrm{lin}\mathcal{T} ) = \mathbb{K}[\mathcal{T} ]\) is free commutativeFootnote 1 generated by the rooted trees \(\mathcal{T}\) and spanned by their disjoint unions (products) called rooted forests \(\mathcal{F}\):

Every \(w \in \mathcal{F}\) is just the monomial \(w =\prod _{t\in \pi _{0}(w)}t\) of its multiset of tree components π 0(w), while 1 denotes the empty forest. The number \(\left \vert w\right \vert \mathop{:}= \left \vert V (w)\right \vert\) of nodes V (w) induces the grading \(H_{R,n} = \mathrm{lin}\mathcal{F}_{n}\) where \(\mathcal{F}_{n} \mathop{:}= \left \{w \in \mathcal{F}\!:\ \left \vert w\right \vert = n\right \}\).
Definition 1.
The (linear) grafting operator \(B_{+} \in \mathrm{End}(H_{R})\) attaches all trees of a forest to a new root, so for example

.
Clearly, B+ is homogenous of degree one with respect to the grading and restricts to a bijection \(B_{+}\!:\ \mathcal{F}\rightarrow \mathcal{T}\). The coproduct Δ is defined to make B+ a cocycle by requiring
Lemma 2.
In cohomology \(0\neq [B_{+}] \in \text{HH}_{\varepsilon }^{1}(H_{R})\) is non-trivial by B + ( 1 )= • ≠ 0.
It characterizes HR through the well-known (Theorem 2 of [8]) universal property of
Theorem 1.
To an algebra \(\mathcal{A}\) and \(L \in \mathrm{End}(\mathcal{A})\) there exists a unique morphism \({}^{L}\!\rho \!: H_{R} \rightarrow \mathcal{A}\) of unital algebras such that

This morphismL ρ simply replaces B+, \(m_{H_{R}}\) and 1 by L, \(m_{\mathcal{A}}\) and \(1\!\!1_{\mathcal{A}}\) as in

Example 1.
The cocycle \(\int _{0} \in \text{HZ}_{\varepsilon }^{1}(\mathbb{K}[x])\) of Sect. 4 induces the character
Definition 2.
The tree factorial \((\cdot )! \in G_{\mathbb{K}}^{H_{R}}\) is equivalently determined by requesting
3 The Generic Model
As explained in the introduction we consider Feynman rules as characters \(\phi \in G_{\mathcal{A}}^{H_{R}}\), mapping a rooted tree to a function of the parameter s (by Proposition 1 it lies in the algebra \(\mathcal{A} = \mathbb{K}[{z}^{-1},z]][{s}^{-z}]\)). Since B+ mimics the insertion of a subdivergence into a fixed graph γ (restricting to a single insertion place by a result from [24]), applying ϕ yields a subintegral and therefore
Definition 3.
The generic Feynman rulesz ϕ are given through Theorem 1 by
The integration kernel f is specified by γ after Wick rotation to Euclidean space, with the asymptotic behaviour f(ζ) ∼ζ −1 for ζ →∞ generating the (logarithmic) divergences of these integrals (we do not address infrared problems and exclude any poles in f). The regulator ζ −z ensures convergence when 0 < ℜ(z) < 1, with results depending analytically on z. We can perform all the integrals using this Mellin transform
Proposition 1.
For any forest \(w \in \mathcal{F}\) we have (called BPHZ model in[4])
Proof.
As both sides of (10) are clearly multiplicative, it is enough to prove the claim inductively for trees. Let it be valid for some forest \(w \in \mathcal{F}\), then for t = B+(w) observe
Example 2.
Using (10), we can directly write down the Feynman rules like

Many examples (choices of F) are discussed in [4], the particular case of the one-loop propagator graph γ of Yukawa theory is in [5] and for scalar Yukawa theory in six dimensions one has \(F(z) = \frac{1} {z(1-z)(2-z)(3-z)}\) as in [22]. Already noted in [17], the highest order pole of \(_{z}\phi _{s}(w)\) is independent of s and just the tree factorial
3.1 Renormalization
Algebraically, renormalization of a character \(\phi \in G_{\mathcal{A}}^{H}\) equals a Birkhoff decomposition [9, 21, 22] into the renormalized character \(\phi _{R} \mathop{:}=\phi _{+} \in G_{\mathcal{A}}^{H}\) and the counterterms \(Z \mathop{:}=\phi _{-}\in G_{\mathcal{A}}^{H}\) defined by the conditions
with respect to a splitting \(\mathcal{A} = \mathcal{A}_{+} \oplus \mathcal{A}_{-}\) determined by the renormalization scheme (the projection \(R\!: \mathcal{A}\twoheadrightarrow \mathcal{A}_{-}\)). Turning to minimal subtraction in Sect. 7 we now focus on
Definition 4.
On the target algebra \(\mathcal{A}\) of regularized Feynman rules depending on a single external variable s, define the kinetic scheme by evaluation at s =μ:
This scheme exploits that subtraction improves the decay at infinity: Let \(f(\zeta ) \sim \frac{1} {\zeta }\), meaning \(f(\zeta ) = \frac{1} {\zeta } +\tilde{ f}(\zeta )\) for some \(\tilde{f}(\zeta ) \in \mathcal{O}\left ({\zeta }^{-1-\varepsilon }\right )\) with \(\varepsilon > 0\). Then \(_{z}\phi _{s}\)

is logarithmically divergent (would it not be for the regulator ζ −z), but subtraction
yields a convergent integral even for z = 0. As R μ is a character of \(\mathcal{A}\), the Birkhoff recursion simplifies to \(Z = R_{\mu } \circ _{z}\phi \circ S = _{z}\phi _{\mu } \circ S\) and \(_{z}\phi _{R} = _{z}\phi _{\mu }^{\star -1} \star _{z}\phi _{s}\).
Example 3.
We find \(_{z}\phi _{R,s}\ (\bullet ) = \left ({s}^{-z} {-\mu }^{-z}\right )F(z)\) and S


results in

The goal of renormalization is to assure the finiteness of the physical limit
and indeed we find the finite \(_{0}\phi _{R,s}\ (\bullet ) = -c_{-1}^{}\ln \tfrac{s} {\mu }\). In the case of (15) check

where all poles in z perfectly cancel. Note that \(_{0}\phi _{R,s}\) maps a forest w to a polynomial in \(\mathbb{K}[\ln \tfrac{s} {\mu } ]\) of degree \(\leq \!\left \vert w\right \vert\) without constant term (except for \(_{0}^{}\phi _{}^{}(1\!\!1) = 1\)), due to the subtraction at s =μ. We now prove these properties in general, extending work in [18].
3.2 Subdivergences
Inductively, the Birkhoff decomposition is constructed as \(\phi _{+}(x) = (\mathop{\mathrm{id}}-R_{\mu })\bar{\phi }(x)\) where the Bogoliubov character \(\bar{\phi }(x)\) (\(\bar{R}\) -operation) serves to renormalize the subdivergences. It is defined by
Theorem 2.
For an endomorphism \(L \in \mathrm{End}(\mathcal{A})\) consider the Feynman rules ϕ:= L ρ induced by (5). Given a renormalization scheme \(R \in \mathrm{End}(\mathcal{A})\) such that
that is to say, L is linear over the counterterms, we have
Proof.
This is a straightforward consequence of the cocycle property of B+:
As the counterterms Z of our model are independent of s, they can be moved out of the integrals in (8) and (18) is fulfilled indeed. This is a general feature of quantum field theories: The counterterms to not depend on any external variables.Footnote 3
The significance of (19) lies in the expression of the renormalized ϕ R,0(t) for a tree t = B+(w) only in terms of the renormalized value \(_{z}\phi _{R}(w)\). This allows for inductive proofs of properties of \(_{z}\phi _{R}\) and also \(_{0}\phi _{R}\), without having to consider the unrenormalized Feynman rules or their counterterms at all.
3.3 Finiteness
Proposition 2.
The physical limit \(_{0}\phi _{R,s}\) exists and maps H R into polynomials \(\mathbb{K}[\ln \tfrac{s} {\mu } ]\) .
Proof.
We proceed inductively from \(_{0}\phi _{R,s}(1\!\!1) = 1\) and, as \(_{0}\phi _{R}\) is a character, only need to consider trees t = B+(w) in the induction step. Hence for this \(w \in \mathcal{F}\) we already know that \(_{0}\phi _{R,\zeta }(w) \in \mathcal{O}\left ({\ln }^{N}\zeta \right )\) for some \(N \in \mathbb{N}_{0}\) such that dominated convergence yields
recalling the term in square brackets to be from \(\mathcal{O}\left ({\zeta }^{-1-\varepsilon }\right )\) as in (14). This proves the cancellation of all z-poles in \(_{z}\phi _{R,s}(t)\) and we identify \(_{0}\phi _{R,s}(t)\) with the ∝ z0 term, which is a polynomial in lns and lnμ of degree \(\left \vert t\right \vert\) by inspection of (10): Each such logarithm comes with a factor z (expanding s−z) which needs to cancel with a pole \(\tfrac{c_{-1}} {z\left \vert t_{v}\right \vert }\) from some \(F(z\left \vert t_{v}\right \vert )\) in order to contribute to the ∝ z0 term. Finally the substitution ζ↦ζ μ gives
hence by induction \(_{0}\phi _{R,\zeta \mu }\) only depends on ζ and \(_{0}\phi _{R,s}\) is a function of \(\frac{s} {\mu }\) only.
Using (20), the physical limit of the renormalized Feynman rules can be obtained inductively by convergent integrations after performing the subtraction at s =μ on the integrand, in particular without the need of any regulator. Therefore \(_{0}\phi _{R}\) is independent of the choice of regularization prescription, so employing a cutoff regulator or dimensional regularization yields the same renormalized result in the physical limit.
4 The Hopf Algebra of Polynomials
We summarize relevant properties of the polynomials, focusing on their Hochschild cohomology (the relevance of ∫0 was already mentioned in [8]). First observe
Lemma 3.
Requiring Δ(x) = x ⊗ 1 + 1 ⊗ x induces a unique Hopf algebra structure on the polynomials \(\mathbb{K}[x]\) . It is graded by degree, connected, commutative and cocommutative with \(\varDelta \left ({x}^{n}\right ) =\sum _{ i=0}^{n}\binom{n}{i}{x}^{i} \otimes {x}^{n-i}\) and the primitive elements are \(\mathrm{Prim}\left (\mathbb{K}[x]\right ) = \mathbb{K} \cdot x\) .
The integration operator \(\int _{0}\!: {x}^{n}\mapsto \frac{1} {n+1}{x}^{n+1}\) furnishes a cocycle \(\int _{0} \in \text{HZ}_{\varepsilon }^{1}(\mathbb{K}[x])\) as
and is not a coboundary since ∫01 = x ≠ 0. In fact it generates the cohomology by
Theorem 3.
\(\text{HH}_{\varepsilon }^{1}(\mathbb{K}[x]) = \mathbb{K} \cdot [\int _{0}]\) is one-dimensional as the 1-cocycles of \(\mathbb{K}[x]\) are
Proof.
For an arbitrary cocycle \(L \in \text{HZ}_{\varepsilon }^{1}(\mathbb{K}[x])\), Lemma 1 ensures L(1) = xa−1 where \(a_{-1} \mathop{:}= \partial _{0}L(1)\). Hence \(\tilde{L} \mathop{:}= L - a_{-1}\int _{0} \in \text{HZ}_{\varepsilon }^{1}\) fulfils \(\tilde{L}(1) = 0\), so \(L_{0} \mathop{:}=\tilde{ L} \circ \int _{0} \in \text{HZ}_{\varepsilon }^{1}\) by
Repeating the argument inductively yields \(a_{n} \mathop{:}= \partial _{0}L_{n}(1) = \partial _{0} \circ L \circ \int _{0}^{n+1}(1) \in \mathbb{K}\) and \(L_{n+1} \mathop{:}= (L_{n} - a_{n}\int _{0}) \circ \int _{0} \in \text{HZ}_{\varepsilon }^{1}\), so for any \(n \in \mathbb{N}_{0}\) we may read off from
that indeed \(L = a_{-1}\int _{0}+\delta \alpha\) for the functional \(\alpha \mathop{:}= \partial _{0} \circ L \circ \int _{0}\) with \(\alpha (\frac{{x}^{n}} {n!} ) = a_{n}\).
Lemma 4.
Up to subtraction \(P =\delta \varepsilon =\mathop{ \mathrm{id}}-\mathrm{ev}_{0}\!: \mathbb{K}[x] \twoheadrightarrow \ker \varepsilon = x\mathbb{K}[x]\) of the constant part, direct computation exhibits δα for any \(\alpha \in \mathbb{K}[x]^{\prime}\) as the differential operator
Lemma 5.
As characters \(\phi \in G_{\mathbb{K}}^{\mathbb{K}[x]}\) of \(\mathbb{K}[x]\) are fixed by λ:= ϕ(x), they form the group \(G_{\mathbb{K}}^{\mathbb{K}[x]} = \left \{\mathrm{ev}_{\lambda }\!:\ \lambda \in \mathbb{K}\right \}\) of evaluations (the counit \(\varepsilon =\mathrm{ ev}_{0}\) equals the neutral element)
Proof.
Note \(\left [\mathrm{ev}_{a} \star \mathrm{ ev}_{b}\right ]\left ({x}^{n}\right ) ={ \left [\mathrm{ev}_{a}(1) \cdot \mathrm{ ev}_{b}(x) +\mathrm{ ev}_{a}(x) \cdot \mathrm{ ev}_{b}(1)\right ]}^{n} ={ (b + a)}^{n}\).
Lemma 6.
The isomorphism \((\mathbb{K},+) \ni a\mapsto \mathrm{ev}_{a} \in G_{\mathbb{K}}^{\mathbb{K}[x]}\) of groups is generated by the functional \(\partial _{0} =\mathrm{ ev}_{0} \circ \partial \in \mathfrak{g}_{\mathbb{K}}^{\mathbb{K}[x]}\) , meaning \(\log _{\star }\mathrm{ev}_{a} = a\partial _{0}\) and \(\mathrm{ev}_{a} =\exp _{\star }(a\partial _{0})\) .
Proof.
Expanding the exponential series reveals \(\exp _{\star }(a\partial _{0})({x}^{n}) = {a}^{n}\) as a direct consequence of \(\partial _{0}^{\star k} =\varepsilon \circ {\partial }^{\star k} =\varepsilon \circ {\partial }^{k}\):
4.1 Feynman Rules Induced by Cocycles
Let \(_{0}^{}\phi _{}^{}\!: H_{R} \rightarrow \mathbb{K}[x]\) denote the polynomials that evaluate to the renormalized Feynman rules \(_{0}\phi _{R,s} =\mathrm{ ev}_{\ell} \circ _{0}^{}\phi _{}^{}\) at \(\ell=\ln \frac{s} {\mu }\). We state
Theorem 4.
The renormalized Feynman rules \(_{0}^{}\phi _{}^{} {= }^{L}\!\rho\) arise out of the universal property of Theorem 1 , where the coefficients \(c_{n}^{}\) of (9) determine the cocycle
Proof.
We may set μ = 1 and produce logarithms of subdivergences by differentiation, exploiting analyticity of zF(z) and \(\frac{{s}^{-z}-1} {z}\) at z = 0 we obtain
By linearity we can replace lnn(sζ) in the integrand by any polynomial to prove Theorem 4 inductively: As \(_{0}^{}\phi _{}^{}\) andL ρ are algebra morphisms, it suffices to consider a tree t = B+(w) for a forest \(w \in \mathcal{F}\) already fulfilling \(_{0}^{}\phi _{}^{}(w) {= }^{L}\!\rho (w)\) in the induction step
where the convergence of (20) allows to reintroduce ζ −z into the integrand.
Corollary 1.
As L is a cocycle, by Theorem 1 the physical limit \(_{0}^{}\phi _{}^{}\!: H_{R} \rightarrow \mathbb{K}[x]\) of the renormalized Feynman rules (8) is a morphism of Hopf algebras.
This key property naturally yields the renormalization group as we shall see in the sequel. For now observe the simple and explicit combinatorial recursion Example 4, expressing \(_{0}^{}\phi _{}^{}\) in terms of the Mellin transform coefficients without any need for series expansions in z, as shown in
Example 4.
Using (24) we rederive \(_{0}^{}\phi _{}^{}\ (\bullet ) {= }^{L}\!\rho \circ B_{+}(1\!\!1) = L(1) = -c_{-1}^{}\,x\) and also

Defining \(\tilde{F}(z) \mathop{:}= F(z) -\frac{c_{-1}^{}} {z} =\sum _{n\in \mathbb{N}_{0}}c_{n}^{}{z}^{n}\), (22) uncovers \(\delta \eta = P \circ \tilde{ F}(-\partial _{x})\) and under the convention \(\partial _{x}^{-1} \mathop{:}=\int _{0}\) we may thus write L = P ∘ F(−∂x).
Corollary 2.
As in η only \(-c_{-1}^{}\int _{0}\) increases the degree in x, the highest order (called leading log) of \(_{0}^{}\phi _{}^{}\) is the tree factorial (note the analogy to (11) ): For any forest \(w \in \mathcal{F}\)
4.2 Feynman Rules as Hopf Algebra Morphisms
As \(_{0}^{}\phi _{}^{}\!: H_{R} \rightarrow \mathbb{K}[x]\) is a morphism of Hopf algebras, the induced map \(G_{\mathbb{K}}^{\mathbb{K}[x]} \rightarrow G_{\mathbb{K}}^{H_{R}}\) given by \(\mathrm{ev}_{a}\mapsto _{0}^{}\phi _{a}^{} \mathop{:}=\mathrm{ ev}_{a} \circ _{0}^{}\phi\) becomes a morphism of groups. In particular note
Corollary 3.
Using (23) we obtain the renormalization group equation (as in[17])
Before we obtain the generator of this one-parameter group in Corollary 4, note how this result gives non-trivial relations between individual trees (graphs) like

Proposition 3.
Let H be any connected bialgebra and \(\phi \!: H \rightarrow \mathbb{K}[x]\) a morphism of bialgebras. Footnote 4 Then log⋆ ϕ is given by the linear term in x through
Proof.
Letting ϕ: C → H and \(\psi \!: H \rightarrow \mathcal{A}\) denote morphisms of coalgebras and algebras, exploiting \({\left (\psi \circ \phi - u_{\mathcal{A}}\circ \varepsilon _{C}\right )}^{\star n} =\psi \circ {\left (\phi -u_{H} \circ \varepsilon _{H}\right )}^{\star n} ={ \left (\psi -u_{\mathcal{A}}\circ \varepsilon _{H}\right )}^{\star n}\circ \phi\) in (2) proves \((\log _{\star }\psi )\circ \phi =\log _{\star }(\psi \circ \phi ) =\psi \circ \log _{\star }\phi\). Now set ψ = eva and use Lemma 6.
Example 5.
In the leading-log case (6) we read off \(\partial _{0} {\circ }^{}\varphi =\ Z_{\bullet } \in \mathfrak{g}_{\mathbb{K}}^{H_{R}}\) where \(Z_{\bullet }(w) \mathop{:}=\delta _{w,\bullet }\). Comparing \({}^{}\varphi =\exp _{\star }(xZ_{\bullet })\) with (6) shows \(\left \vert w\right \vert ! = w! \cdot Z_{\bullet }^{\star \left \vert w\right \vert }(w)\), henceFootnote 5
Corollary 4.
The character \(_{0}^{}\phi _{}^{}\) is fully determined by the anomalous dimension
An analogous phenomenon happens with the counterterms in the minimal subtraction scheme: The first order poles ∝ z−1 alone already determine the full counterterm via the scattering formula proved in [10]. However, (28) is much simpler as illustrated in
Example 6.
Reading off \(\gamma \ \bullet = c_{-1}^{}\),

and

from the Example 4 above, Corollary 4 determines the higher powers of x through

Note how the fragment •• ⊗• of

does not contribute to the quadratic terms \(\frac{{x}^{2}} {2} \gamma \star \gamma\), as γ vanishes on products. We will exploit this in (33) of Sect. 5.1 and close with a method of calculating γ emerging from
Lemma 7.
From \(\gamma \circ B_{+} = -\partial _{0} \circ L \circ _{0}^{}\phi _{}^{} =\mathrm{ ev}_{0} \circ [zF(z)]_{-\partial _{x}} \circ \exp _{\star }(-x\gamma )\) we obtain the inductive formula \(\gamma \circ B_{+} =\sum _{n\in \mathbb{N}_{0}}c_{n-1}^{}{\gamma }^{\star n}.\)
Example 7.
We can recursively calculate \(\gamma \ \bullet = c_{-1}^{}\varepsilon (1\!\!1) = c_{-1}^{}\), similarly also

5 Dyson-Schwinger Equations and Correlation Functions
We now study the implications for the correlation functions (31) as formal power series in the coupling constant g. For simplicity we restrict to a single equation and refer to [24] for systems. With detailed treatments in [1, 11], for our purposes suffices
Definition 5.
To a parameter \(\kappa \in \mathbb{K}\) and a family of cocycles \(B_{\cdot }\!: \mathbb{N} \rightarrow \text{HZ}_{\varepsilon }^{1}(H_{R})\) we associate the combinatorial Dyson-Schwinger equation Footnote 6
Lemma 8.
As perturbation series \(X(g) =\sum _{n\in \mathbb{N}_{0}}x_{n}{g}^{n} \in H_{R}[[g]]\) , Eq. (29) has a unique solution. It begins with x 0 = 1 while x n+1 is determined recursively from \(x_{0},\ldots,x_{n}\) . These coefficients generate a Hopf subalgebra, explicitly we find Footnote 7
Example 8.
In [5, 22], \(X(g) = 1\!\!1 - gB_{+}\left ( \frac{1} {X(g)}\right )\) features κ = −2, summing all trees

with a combinatorial factor.Footnote 8 Physically these correspond to (Yukawa) propagators

, arising from insertions of the one-loop graph

into itself.
Definition 6.
The correlation function G(g) evaluates the renormalized Feynman rules \(_{0}^{}\phi _{}^{}\!: H_{R} \rightarrow \mathbb{K}[\ell]\) on the perturbation series X(g), yielding the formal power series
We call \(\tilde{\gamma }(g) \mathop{:}=\gamma \circ X(g) = \left.-\partial _{\ell}\right \vert _{0}G(g) \in \mathbb{K}[[g]]\) the physical anomalous dimension.
Example 9.
The Feynman rules \({}^{}\varphi\) from (6) result in the convergent series \(G(g) = \sqrt{1 - 2g\ell}\) and \(\tilde{\gamma }(g) \mathop{=}\limits _{5 }-Z_{ \bullet} \circ X(g) = g\) for the propagator of Example 8. Perturbatively,

.
5.1 Propagator Coupling Duality
The Hopf subalgebra of the perturbation series allows to calculate convolutions in
Lemma 9.
Let \(\psi \in \mathfrak{g}_{\mathcal{A}}^{H_{R}}\) denote an infinitesimal character \(\varPsi \in G_{\mathcal{A}}^{H_{R}}\) a character and \(\lambda \in \mathrm{Hom}(H_{R},\mathcal{A})\) a linear map. Then (in suggestive notation)
Proof.
These are immediate consequences of Lemma 8, for (33) consider
Example 10.
Continuing 8 we deduce

and

proving \({}^{}\varphi (x_{n+1}) = -{2}^{-n}C{_{n}\ell}^{n+1}\) with the Catalan numbers Cn already noted in [20]. From Example 9 we find their generating function \(2g\sum _{n\in \mathbb{N}_{0}}{g}^{n}C_{n} = 1 -\sqrt{1 - 4g}\).
Corollary 5.
As \(_{0}^{}\phi _{}^{}\) is a morphism of Hopf algebras, for any \(a,b \in \mathbb{K}\) we can factor
These functional equations of formal power series make sense for the non-perturbative correlation functions as well. Relating the scale- with the coupling-dependence, this integrated form of the renormalization group equation becomes infinite- simally
Corollary 6.
From \(-\frac{\mathrm{{d}}^{}} {\mathrm{{d}}^{x}}\ _{0}^{}\phi _{}^{} =\gamma \star _{0}^{}\phi _{}^{} = _{0}^{}\phi _{}^{}\star \gamma\) or differentiating(34) by b at zero note
The first of these equations generalizes the propagator coupling duality in [5, 20]. For any fixed coupling g, it expresses the correlation function as the solution of the o.d.e.
determining Gℓ(g) completely from \(\tilde{\gamma }(g)\) in a non-perturbative manner as in (39).
Example 11.
The leading-log expansion takes only the highest power of ℓ in each g-order. Equally, \(\tilde{\gamma }(g) = c{g}^{n}\) for constants \(c \in \mathbb{K}\), \(n \in \mathbb{N}\) and (36) integrates to
As a special case we recover Example 9 for n = c = 1 and κ = −2.
Example 12.
In the linear case κ = 0, (34) states \(G_{a+b}(g) = G_{a}(g) \cdot G_{b}(g)\) in accordance with the scaling solution \(G_{\ell}(g) = {e}^{-\ell\tilde{\gamma }(g)}\) of (36), well-known from [19].
Example 13.
For vertex insertions as in [2] we have κ = 1, so \(G_{a+b}(g) = G_{b}(g) \cdot G_{a}\big[\tilde{G}_{b}(g)\big]\) expresses the running of the coupling constant \(\tilde{G} \mathop{:}= g \cdot G\): A change in scale by b is (up to a multiplicative constant) equivalent to replacing the coupling g by \(\tilde{G}_{b}(g)\).
5.2 The Physicist’s Renormalization Group
To cast (34) and (35) into the common forms of (7.3.15) and (7.3.21) in [7], we introduce the β-function \(\beta (g) \mathop{:}= -\kappa g\tilde{\gamma }(g)\) and the running coupling g(μ) as the solution of
Integration relates the correlation functions for different renormalization points μ in
Setting μ 1 = s we may thus write Gℓ(g) explicitly in terms of \(\tilde{\gamma }(g)\) as
5.3 Relation to Mellin Transforms
We finally exploit the analytic input from Theorem 4 to the perturbation series in
with Mellin transforms \(F_{n}(z) = \frac{1} {z}c_{-1}^{(n)} +\tilde{ F}_{ n}(z)\) corresponding to the insertionsFootnote 9 Bn.
Corollary 7.
The power series \(G_{\ell}(g) \in \mathbb{K}[\ell][[g]]\) is fully determined by
Restricting to a single cocycle \(F_{k}(z) = F(z)\delta _{k,n}\), choosing \(F(z) = \frac{c_{-1}^{}} {z}\) reproduces (37) from \(\partial _{-\ell}G_{\ell}(g) = {g}^{n}c_{-1}^{}G_{\ell}{(g)}^{1+n\kappa }.\) More generally, for any rational \(F(z) = \frac{p(z)} {q(z)} \in \mathbb{K}(z)\) with q(0) = 0, (40) collapses to a finite order ode \(q(-\partial _{\ell})G_{\ell}(g) = {g}^{n}p(-\partial _{\ell})G_{\ell}{(g)}^{1+n\kappa }\) that makes perfect sense non-perturbatively (extending the algebraic \(\partial _{\ell} \in \mathrm{End}(\mathbb{K}[\ell])\) to the analytic differential operator).
Example 14.
For \(F(z) = \frac{1} {z(1-z)}\), the propagator (κ = −2 as in Example 8) fulfils
At ℓ = 0 this evaluates to \(\tilde{\gamma }(g) -\tilde{\gamma } (g)(1 - 2g\partial _{g})\tilde{\gamma }(g) = g\), which is studied in [5, 24].
6 Automorphisms of HR
Applying the universal property to HR itself, adding coboundaries to B+ leads to
Definition 7.
For any α ∈ HR′, Theorem 1 defines the Hopf algebra morphism
Example 15.
The action on the simplest trees yields

These morphisms capture the change ofL ρ under a variation of L by a coboundary:
Theorem 5.
Let H denote a bialgebra \(L \in HZ_{\varepsilon }^{1}(H)\) a 1-cocycle and further α ∈ H′ a functional. Then for \({}^{L}\!\rho {,}^{L+\delta \alpha }\!\rho \!:\ H_{R} \rightarrow H\) given through Theorem 1 and \({}^{\alpha {\circ }^{L}\!\rho }\chi \!:\ H_{R} \rightarrow H_{R}\) from Definition 7 , we have

Proof.
As both sides of (42) are algebra morphisms, it suffices to prove it inductively for trees: Let it be true for a forest \(w \in \mathcal{F}\), then it holds as well for the tree B+(w) by
We used \((\delta \alpha ) {\circ }^{L}\!\rho {= }^{L}\!\rho \circ \delta \left (\alpha {\circ }^{L}\!\rho \right )\), following fromL ρ being a morphism of bialgebras.
Hence the action of a coboundary δ α on the universal morphisms induced by L is given by \({}^{\alpha {\circ }^{L}\!\rho }\chi\). This turns out to be an automorphism of HR as shown in
Theorem 6.
The map \({}^{\cdot }\chi \!:\ H_{R}^{\prime} \rightarrow \mathrm{End}_{\text{Hopf}}(H_{R})\) , taking values in the space of Hopf algebra endomorphisms of H R , fulfils the following properties:
-
1.
For any \(w \in \mathcal{F}\) and α ∈ H R ′ α χ(w) differs from w only by lower order forests:
$$\displaystyle{{ }^{\alpha }\chi (w) \in w + H_{R}^{\left \vert w\right \vert -1} = w +\bigoplus _{ n=0}^{\left \vert w\right \vert -1}H_{ R,n}. }$$(43) -
2.
⋅ χ maps H R ′ into the Hopf algebra automorphisms \(\mathrm{Aut}_{\text{Hopf}}(H_{R})\) . Its image is closed under composition, as for any α,β ∈ H R ′ we have \({}^{\alpha }\chi {\circ }^{\beta }\chi {= }^{\gamma }\chi\) taking
$$\displaystyle{ \gamma =\alpha +\beta {\circ {}^{\alpha }\chi }^{-1}. }$$(44) -
3.
The maps \(\delta \!: H_{R}^{\prime} \rightarrow HZ_{\varepsilon }^{1}(H_{R})\) and \({}^{\cdot }\chi \!: H_{R}^{\prime} \rightarrow \mathrm{Aut}_{\text{Hopf}}(H_{R})\) are injective, thus the subgroup \({\mathrm{im}}^{\cdot }\chi = \left\{{}^{\alpha }\chi \!:\ \alpha \in H_{R}^{\prime}\right \} \subset \mathrm{Aut}_{\text{Hopf}}(H_{R})\) induces a group structure on H R ′ with neutral element 0 and group law ⊳ given by
$$\displaystyle{ \alpha \vartriangleright \beta \mathop{:}{={ }^{\cdot }\chi }^{-1}\left ({}^{\alpha }\chi {\circ }^{\beta }\chi \right ) \mathop{=}\limits _{ (44)}\alpha +\beta {\circ {}^{\alpha }\chi }^{-1}\quad \text{and}{\quad \alpha }^{\vartriangleright -1} = -\alpha {\circ }^{\alpha }\chi. }$$(45)
Proof.
Statement (43) is an immediate consequence of \(\delta \alpha (H_{R}^{n}) \subseteq H_{R}^{n}\): Starting fromα χ (•) = (•), suppose inductively (43) to hold for forests \(w,w^{\prime} \in \mathcal{F}\). Then it obviously also holds for w ⋅ w′ as well and even so for B+(w) through
This already implies bijectivity ofα χ, but applying (42) to L = B+ +δ α and \({}^{\tilde{\alpha }}\chi\) for \(\tilde{\alpha }\mathop{:}= -\alpha {\circ }^{\alpha }\chi\) shows \(\mathop{\mathrm{id}} {= }^{\alpha }\chi {\circ }^{\tilde{\alpha }}\chi\) directly. We deduce bijectivity of allα χ and thus \({}^{\alpha }\chi \in \mathrm{Aut}_{\text{Hopf}}(H_{R})\) with the inverse \({}^{\alpha }{\chi }^{-1} {= }^{\tilde{\alpha }}\chi\). Now (44) follows from
Finally consider α,β ∈ HR′ with \({}^{\alpha }\chi {= }^{\beta }\chi\), then \(0 = {(}^{\alpha }\chi {-}^{\beta }\chi ) \circ B_{+} =\delta \circ (\alpha -\beta ) {\circ }^{\alpha }\chi\) reduces the injectivity of⋅ χ to that of δ. But if δ α = 0, for all \(n \in \mathbb{N}_{0}\)
Given an arbitrary forest \(w \in \mathcal{F}\) and \(n \in \mathbb{N}\), the expression

simplifies upon projection onto \(\mathbb{K}\)

to

. Iterating this formula exhibits α(w) as a scalar multiple of α

= 0 and proves α = 0.
6.1 Decorated Rooted Trees
Our observations generalize straight forwardly to the Hopf algebra \(H_{R}(\mathcal{D})\) of rooted trees with decorations drawn from a set \(\mathcal{D}\). In this case, the universal property assigns to each \(\mathcal{D}\)-indexed family \(L_{\cdot }\!:\ \mathcal{D}\rightarrow \mathrm{End}(\mathcal{A})\) the unique algebra morphism
For cocycles \(\mathrm{im}L_{\cdot }\subseteq HZ_{\varepsilon }^{1}(\mathcal{A})\) this is a morphism of bialgebras and even of Hopf algebras (should \(\mathcal{A}\) be Hopf). For a family \(\alpha _{\cdot }\!\!:\ \mathcal{D}\rightarrow H_{R}^{\prime}(\mathcal{D})\) of functionals, setting \(L_{d}^{\alpha _{\cdot }} \mathop{:}= B_{+}^{d} +\delta \alpha _{d}\) yields an automorphism \({}^{\alpha _{\cdot }}\chi \mathop{:}{= }^{L_{\cdot }^{\alpha _{\cdot }} }\!\rho\) of the Hopf algebra \(H_{R}(\mathcal{D})\). Theorems 5 and 6 generalize in the obvious way.
In view of the Feynman rules, decorations d denote different graphs into which \(B_{+}^{d}\) inserts a subdivergence. Hence we gain a family of Mellin transforms F⋅ and Theorem 4 generalizes straightforwardly as \(_{0}^{}\phi _{}^{} \circ B_{+}^{d} = P \circ F_{d}(-\partial _{\ell}) \circ _{0}^{}\phi _{}^{}\).
6.2 Subleading Corrections Under Variations of Mellin Transforms
As an application of (42) consider a change of the Mellin transform F to a different F′ that keeps c−1 fixed but alters the other coefficients \(c_{n}^{}\). With α:=η′ −η,
translates the new renormalized Feynman rules \(_{0}^{}\phi _{}^{}{^{\prime}}\) into the original \(_{0}^{}\phi _{}^{}\).
Fixing \(c_{-1}^{} = -1\), this in particular relates \(_{0}^{}\phi _{}^{}\) to \({}^{}\varphi {= }^{\int _{0}}\!\rho\) using Example 15 together with \(\eta {\circ }^{}\varphi (w) = {(-1)}^{\left \vert w\right \vert }\frac{\left \vert w\right \vert !} {w!}c_{\left \vert w\right \vert }\) as

Corollary 8.
The new correlation function \(_{0}^{}\phi _{}^{} \circ X {= }^{}\varphi \circ \tilde{ X}\) equals the original \({}^{}\varphi\) applied to a modified perturbation series \(\tilde{X}(g)\) , fulfilling a Dyson-Schwinger equation differing by coboundaries. By(43) the leading logs coincide and explicitly
7 Locality, Finiteness and Minimal Subtraction
Consider the regularized but unrenormalized Feynman rulesz ϕ. Now setting \(\mathcal{A}\mathop{:}= \mathbb{K}[{z}^{-1},z]]\) and \(\phi \mathop{:}= _{z}\phi _{1} \in G_{\mathcal{A}}^{H_{R}}\), (10) fixes the scale dependence \(_{z}\phi _{s} =\phi \circ \theta _{-\ln sz}\).
Proposition 4.
For any character \(\phi \in G_{\mathcal{A}}^{H_{R}}\) , the following are equivalent:
-
1.
ϕ ⋆−1 ⋆ (ϕ ∘ Y ) = ϕ ∘ (S ⋆ Y ) maps into \(\frac{1} {z}\mathbb{K}[[z]]\) , so \(\lim \limits {_{z\rightarrow 0}\phi }^{\star -1} \star (z\phi \circ Y )\) exists.
-
2.
For every \(n \in \mathbb{N}_{0}\) \({\phi }^{\star -1} \star (\phi \circ {Y }^{n}) =\phi \circ (S \star {Y }^{n})\) maps into \({z}^{-n}\mathbb{K}[[z]]\) .
-
3.
For any \(\ell\in \mathbb{K}\) \({\phi }^{\star -1} \star (\phi \circ \theta _{\ell z}) =\phi \circ (S \star \theta _{\ell z})\) maps into \(\mathbb{K}[[z]]\) .
Proof.
We refer to the accounts in [5, 10, 21], however only 1. ⇒ 2. is non-trivial and
yields an inductive proof. It exploits \((S \circ Y ) \star \mathop{ \mathrm{id}} = -S \star Y\) in the formula (α arbitrary)
Note that condition 3. is equivalent to the finiteness Proposition 2 of the physical limit \(_{0}^{}\phi _{}^{}\) as
Corollary 9.
The anomalous dimension can be obtained from the \(\frac{1} {z}\) -pole coefficients
The minimal subtraction scheme RMS projects onto the pole parts such that \(\mathcal{A} = \mathcal{A}_{-}\oplus \mathcal{A}_{+}\) where \(\mathcal{A}_{-}\mathop{:}= {z}^{-1}\mathbb{K}[{z}^{-1}]\) and \(\mathcal{A}_{+} \mathop{:}= \mathbb{K}[[z]]\). Though it renders finiteness trivial, its counterterms might depend on the scale s and violate locality. So from [10] we need
Definition 8.
A Feynman rule \(\phi \in G_{\mathcal{A}}^{H_{R}}\) is called local iff in the minimal subtraction scheme, the counterterm \((\phi \circ \theta _{\ell z})_{-}\) is independent of \(\ell\in \mathbb{K}\).
Proposition 5.
Locality of \(\phi \in G_{\mathcal{A}}^{H_{R}}\) is equivalent to the conditions of Proposition 4 .
Proof.
In case of Proposition 4, \(\phi \circ \theta _{\ell z} = {(\phi _{-})}^{\star -1} \star \big\{\phi _{+} \star {[\phi }^{\star -1} \star \left (\phi \circ \theta _{\ell z}\right )]\big\}\) is a Birkhoff decomposition by condition 3. such that \(\left (\phi \circ \theta _{\ell z}\right )_{-} =\phi _{-}\) from uniqueness. Conversely, for local ϕ,
implies \(\mathbb{K}[[z]] =\ker R_{\text{ MS}} \supseteq \mathrm{im}\phi _{-} \star \left (\phi \circ \theta _{\ell z}\right )\) and convolution with \(\phi _{+}^{\star -1} {=\phi }^{\star -1} \star \phi _{ -}^{\star -1}:\! H_{R} \rightarrow \mathbb{K}[[z]]\) yields condition 3. of Proposition 4.
So we showed algebraically that the problems of finiteness in the kinetic scheme and locality in minimal subtraction are precisely the same. These schemes are related by
Lemma 10.
If \(_{z}^{}\phi _{\text{ MS},s}^{}\) denotes the R MS -renormalized Feynman rule, then its scale dependence is given by \(_{0}^{}\phi _{}^{}\) through \(_{z}^{}\phi _{\text{ MS}}^{} = \left (R_{\mu } \circ _{z}^{}\phi _{\text{ MS}}^{}\right ) \star _{z}\phi _{R}\) (as already exploited in[4]).
Proof.
Locality of the minimal subtraction counterterms ϕ − implies \(R_{\mu } \circ \phi _{-} =\phi _{-}\), hence
The physical limit \(\mathrm{ev}_{\ln s} \circ _{0}^{}\phi _{\text{ MS}}^{} =\lim \limits _{z\rightarrow 0}{_{z}}^{}\phi _{\text{ MS},s}^{}\) yields polynomials \(_{0}^{}\phi _{\text{ MS}}^{}\) and Lemma 10 becomes
Corollary 10.
The characters \(_{0}^{}\phi _{\text{ MS}}^{},_{0}^{}\phi _{}^{}:\ H_{R} \rightarrow \mathbb{K}[x]\) fulfil the relations
In particular, the constant parts \(\varepsilon \circ _{0}^{}\phi _{\text{ MS}}^{} =\mathrm{ ev}_{0} \circ _{0}^{}\phi _{\text{ MS}}^{} \in G_{\mathbb{K}}^{H_{R}}\) determine \(_{0}^{}\phi _{\text{ MS}}^{}\) completely as the scale dependence is governed by \(_{0}^{}\phi _{}^{}\). Using \(_{0}^{}\phi _{}^{} =\exp _{\star }(-x\gamma )\), the β-functional \(_{0}^{}\phi _{ \text{ MS}}^{} =\exp _{\star }\left (x\beta \right ) \star \left (\varepsilon \circ _{0}^{}\phi _{\text{ MS}}^{}\right )\) from [10] relates to γ by conjugation:
Corollary 11.
Applying(32) to (47) expresses the correlation function of the RMS -scheme to the kinetic scheme by a redefinition of the coupling constant:
8 Feynman Graphs and Logarithmic Divergences
In a typical renormalizable scalar quantum field theory, the vertex function is logarithmically divergent and may be renormalized by a simple subtraction as studied above. Referring to [6] for quadratic divergences, we now restrict to logarithmically divergent graphs with only logarithmic subdivergences, in D dimensions of space-time.
Following the notation established in [3], the renormalized amplitude of a graph Γ in the Hopf algebra H of Feynman graphs is given by the forest formula Footnote 10
The forests \(\mathcal{F}(\varGamma )\) account for subdivergences, the first and second Symanzik polynomials \(\psi _{\varGamma },\varphi _{\varGamma }\) depend on the edge variables α e (Schwinger parameters) and we integrate over \(\mathbb{R}\mathbb{P}_{>0}^{\left \vert E(\varGamma )\right \vert -1}\) in projective space with canonical volume form Ω Γ .
Apart from a scale s, \(\varphi _{\varGamma }\) depends on dimensionless angle variables \(\varTheta = \left \{\frac{{m}^{2}} {s} \right \} \cup \left \{\frac{p_{i}\cdot p_{j}} {s} \right \}\) built from the mass m and external momenta pi. We abbreviate \(\frac{\varphi }{\psi }_{\varGamma } \mathop{:}= \frac{\varphi _{\varGamma }} {\psi _{\varGamma }}\) and denote evaluation at the renormalization point \((\tilde{s},\tilde{\varTheta })\) of the kinetic scheme by a tilde or \(\left.\cdot \right \vert _{R} \mathop{:}= \left.\cdot \right \vert _{(s,\varTheta )\mapsto (\tilde{s},\tilde{\varTheta })}\).
Definition 9.
Holding the angles Θ fixed, the period functional \(\mathcal{P}\in H^{\prime}\) is given by
Corollary 12.
For any graph Γ ∈ H, the value \(\mathcal{P}(\varGamma )\) is a period in the sense of[15] (provided that \(\tilde{s}\) and all \(\theta \in \tilde{\varTheta }\) are rational) by the formula
For primitive (subdivergence free) graphs, [23] gives equivalent definitions of this period in momentum and position space. The product rule, (49) and \(\left.\varPhi _{+}\right \vert _{R} =\varepsilon\) show
Corollary 13.
The period is an infinitesimal character \(\mathcal{P}\in \mathfrak{g}_{\mathbb{K}}^{H}\) (it vanishes on any graph that is not connected).
8.1 Renormalization Group
Proposition 6.
Holding the angles Θ fixed, differentiation by the scale results in Footnote 11
Proof.
Adding \(0 = \mathcal{P}(\varGamma ) -\mathcal{P}(\varGamma )\) and collecting the contributions of \(\tilde{\frac{\varphi }{\psi }}_{\gamma /F}\) in (∗) we find
With γ ≺Γ denoting a subdivergence γ ≠ Γ, the forests \(F \in \mathcal{F}(\varGamma )\) containing γ correspond bijectively to the forests of γ and Γ∕γ by
This is an immediate consequence of the definition of a forest, as for \(F \in \mathcal{F}_{\gamma }(\varGamma )\), each δ ∈ F is either disjoint to γ or strictly containing γ (in both cases it is mapped to δ∕γ ∈ F∕γ) or itself a subdivergence of γ. Thus integrating \(\int _{0}^{\infty } \frac{A-\tilde{A}} {(A+tB)(\tilde{A}+tB)}\mathrm{{d}}^{}t = {B}^{-1}\ln \frac{A} {\tilde{A}}\) in
reduces to the projective ∫Ω γ in the edge variables of the subgraph γ, making use of
The apparent factorization into \(\mathcal{P}(\gamma )\) and Φ +(Γ∕γ) shows that we obtain convergent integrals for each γ ≺Γ individually and may therefore separate into
Note that the terms γ ⊗Γ∕γ of Δ(Γ) with \(\left \vert \pi _{0}(\gamma )\right \vert > 1\) do not contribute here by Corollary 13.
Together with Corollary 13 and the connected graduation of H, this shows
where we set \(\ell\mathop{:}=\ln \frac{s} {\tilde{s}}\) and the series is pointwise finite. Hence note
Corollary 14.
The renormalized Feynman rules \(\varPhi _{+} = \left.\varPhi _{+}\right \vert _{\varTheta =\tilde{\varTheta }} \star \left.\varPhi _{+}\right \vert _{s=\tilde{s}}\) factorize ([6] gives a different decomposition) into the angle-dependent part \(\left.\varPhi _{+}\right \vert _{s=\tilde{s}}\) and the scale-dependence \(\left.\varPhi _{+}\right \vert _{\varTheta =\tilde{\varTheta }}\) given as the Hopf algebra morphism
Example 16.
For primitive Γ ∈ Prim(H), \(\varPhi _{+}(\varGamma ) = -\ell\cdot \mathcal{P}(\varGamma ) + \left.\varPhi _{+}\right \vert _{s=\tilde{s}}(\varGamma )\) disentangles the scale- and angle-dependence. Subdivergences evoke higher powers of ℓ with angle-dependent factors. Dunce’s cap of ϕ 4-theory gives

= 1 such that

.
8.2 Dimensional Regularization
The dimensional regularization of [7] assigns a Laurent seriesz Φ(Γ) in \(z \in \mathbb{C}\) to each Feynman graph Γ ∈ H, which for large ℜz is given by the convergent parametric integral
As \(\frac{\varphi }{\psi }_{\varGamma }\) is linear in the scale s and homogeneous of degree one in the edge variables, simultaneously rescaling of all α e yields (for logarithmically divergent graphs)
Corollary 15.
The scale dependence \(_{z}\varPhi = \left._{z}\varPhi \right \vert _{s=\tilde{s}} \circ \theta _{-z\ell}\) of (53) is induced from the grading Y of H given by the loop number.
Thus the finiteness of the physical limit \(\left.\varPhi _{+}\right \vert _{\varTheta =\tilde{\varTheta }} =\lim _{z\rightarrow 0}\left._{z}\varPhi \right \vert _{R} \circ (S \star \theta _{-z\ell})\) results by Proposition 4 in the local character \(\left._{z}\varPhi \right \vert _{R} \in G_{\mathcal{A}}^{H}\), evaluated at the renormalization point \((\tilde{s},\tilde{\varTheta })\).
Corollary 16.
In dimensional regularization, the period (50) is the \(\frac{1} {z}\) -pole coefficient
8.3 Dilatations
For λ > 0, consider the dilatation operator Λ λ scaling masses m↦λ ⋅ m and momenta \(p_{i}\mapsto \lambda \cdot p_{i}\). It fixes all angles Θ, multiplies the scale s with λ 2 and therefore acts as
In other words, the dilatations \(\mathbb{R}_{>0} \ni \lambda \mapsto \varLambda _{\lambda }\mapsto \exp _{\star }\left (-2\mathcal{P}\ln \lambda \right ) \star \cdot \) are represented on the group \(G_{\mathcal{A}}^{H}\) of characters by a left convolution. As the unrenormalized logarithmically divergent graphs are dimensionless and naively invariant under Λ λ , \(\mathcal{P}\) precisely measures how renormalization breaks this symmetry, giving rise to anomalous dimensions.
9 Conclusion
We stress that the physical limit of the renormalized Feynman rules results in a morphism \(_{0}^{}\phi _{}^{}\!: H_{R} \rightarrow \mathbb{K}[x]\) of Hopf algebras in case of the kinetic scheme. This compatibility with the coproduct allows to obtain \(_{0}^{}\phi _{}^{}\) from the linear terms γ only. As we just exemplified, these relations are statements about individual Feynman graphs unraveling scale- and angle-dependence in a simple way. Again we recommend [6] for further reading.
Secondly we revealed how Hochschild cohomology governs not only the perturbation series through Dyson-Schwinger equations, but also determines the Feynman rules. Addition of exact one-cocycles captures variations of Feynman rules and the anomalous dimension γ can efficiently be calculated in terms of Mellin transform coefficients.
Note how this feature is lost upon substitution of the kinetic scheme by minimal subtraction: We do not obtain a Hopf algebra morphism anymore due to the constant terms, which are also more difficult to obtain in terms of the Mellin transforms F.
Finally we want to emphasize the remarks in Sect. 5 towards a non-perturbative framework. Though this relation between F(z) and the anomalous dimension \(\tilde{\gamma }(g)\) is still under investigation and so far only fully understood in special cases, these already give interesting results [5, 24].
Notes
- 1.
We consider unordered trees
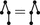
and forests
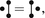
sometimes called non-planar.
- 2.
By wv we denote the subtree of w rooted at the node v ∈ V (w).
- 3.
Even if the divergence of a Feynman graph does depend on external momenta as happens for higher degrees of divergence, the Hopf algebra is defined such that the counterterms are evaluations on certain external structures, given by distributions in [9]. So in any case, ϕ − maps to scalars.
- 4.
This already implies ϕ to be a morphism of Hopf algebras.
- 5.
This combinatorial relation among tree factorials, noted in [17], thus drops out of \({\varDelta }^{}\varphi = {(}^{}\varphi {\otimes }^{}\varphi )\circ \varDelta\).
- 6.
As x0 =1, for arbitrary p the series \({\left [X(g)\right ]}^{p} \mathop{:}=\sum _{n\in \mathbb{N}_{0}}\binom{p}{n}{\left [X(g) -1\!\!1\right ]}^{n} \in H_{R}[[g]]\) is well defined.
- 7.
- 8.
Counting the number of corresponding ordered trees.
- 9.
For this generality we need decorated rooted trees as commented on in Sect. 6.1
- 10.
We prefer to work in the parametric representation as introduced in [14, Sect. 6-2-3].
- 11.
This simple form circumvents the decomposition into one-scale graphs utilized in [6] and therefore holds in the original renormalization Hopf algebra H.
References
Bergbauer, C., Kreimer, D.: Hopf algebras in renormalization theory: locality and Dyson-Schwinger equations from Hochschild cohomology. IRMA Lect. Math. Theor. Phys. 10, 133–164 (2006)
Bierenbaum, I., Kreimer, D., Weinzierl, S.: The next-to-ladder approximation for Dyson-Schwinger equations. Phys. Lett. B646, 129–133 (2007). doi:10.1016/j.physletb.2007.01.018
Bloch, S., Kreimer, D.: Mixed Hodge structures and renormalization in physics. Commun. Number Theory Phys. 2, 637–718 (2008)
Broadhurst, D.J., Kreimer, D.: Renormalization automated by Hopf algebra. J. Symb. Comput. 27, 581 (1999). doi:10.1006/jsco.1999.0283
Broadhurst, D.J., Kreimer, D.: Exact solutions of Dyson-Schwinger equations for iterated one-loop integrals and propagator-coupling duality. Nucl. Phys. B600, 403–422 (2001). doi:10.1016/S0550-3213(01)00071-2
Brown, F., Kreimer, D.: Angles, scales and parametric renormalization. Lett. Math. Phys. 103(9), 933–1007 (2013)
Collins, J.C.: Renormalization. Cambridge Monographs on Mathematical Physics. Cambridge University Press, Cambridge/New York (1984)
Connes, A., Kreimer, D.: Hopf algebras, renormalization and noncommutative geometry. Commun. Math. Phys. 199, 203–242 (1998). doi:10.1007/s002200050499
Connes, A., Kreimer, D.: Renormalization in quantum field theory and the Riemann-Hilbert problem I: the Hopf algebra structure of graphs and the main theorem. Commun. Math. Phys. 210, 249–273 (2000). doi:10.1007/s002200050779
Connes, A., Kreimer, D.: Renormalization in quantum field theory and the Riemann-Hilbert problem II: the β-function, diffeomorphisms and the renormalization group. Commun. Math. Phys. 216, 215–241 (2001). doi:10.1007/PL00005547
Foissy, L.: Faà di Bruno subalgebras of the Hopf algebra of planar trees from combinatorial Dyson-Schwinger equations. Adv. Math. 218(1), 136–162 (2008). doi:10.1016/j.aim.2007.12.003. http://www.sciencedirect.com/science/article/pii/S0001870807003301
Foissy, L.: Classification of systems of Dyson-Schwinger equations in the Hopf algebra of decorated rooted trees. Adv. Math. 224(5), 2094–2150 (2010). doi:10.1016/j.aim.2010.01.024. http://www.sciencedirect.com/science/article/pii/S0001870810000435
Foissy, L.: General Dyson-Schwinger equations and systems. ArXiv e-prints (2011)
Itzykson, C., Zuber, J.B.: Quantum Field Theory. Dover, New York (2005)
Kontsevich, M., Zagier, D.: Periods. In: Mathematics Unlimited – 2001 and Beyond. Springer, Berlin (2001)
Kreimer, D.: On the Hopf algebra structure of perturbative quantum field theories. Adv. Theor. Math. Phys. 2, 303–334 (1997)
Kreimer, D.: Chen’s iterated integral represents the operator product expansion. Adv. Theor. Math. Phys. 3, 3 (2000)
Kreimer, D.: Factorization in quantum field theory: an exercise in hopf algebras and local singularities. In: Cartier, P., Moussa, P., Julia, B., Vanhove, P. (eds.) On Conformal Field Theories, Discrete Groups and Renormalization, Frontiers in Number Theory, Physics, and Geometry, vol. 2, pp. 715–736. Springer, Berlin/Heidelberg (2007). http://dx.doi.org/10.1007/978-3-540-30308-4_14
Kreimer, D.: Étude for linear Dyson-Schwinger equations. In: Albeverio, S., Marcolli, M., Paycha, S., Plazas, J. (eds.) Traces in Number Theory, Geometry and Quantum Fields. Aspects of Mathematics E, vol. 38, pp. 155–160. Vieweg, Wiesbaden (2008). http://preprints.ihes.fr/2006/P/P-06-23.pdf
Kreimer, D., Yeats, K.: An étude in non-linear Dyson-Schwinger equations. Nucl. Phys. Proc. Suppl. 160, 116–121 (2006). doi:10.1016/ j.nuclphysbps.2006.09.036. Proceedings of the 8th DESY workshop on elementary particle theory
Manchon, D.: Hopf Algebras in Renormalisation. pp. 365–427. Elsevier/North-Holland (2008). doi:10.1016/S1570-7954(07)05007-3. http://www.sciencedirect.com/science/article/pii/S1570795407050073
Panzer, E.: Hopf-algebraic renormalization of kreimer’s toy model. Master’s thesis, Humboldt-Universität zu Berlin (2011)
Schnetz, O.: Quantum periods: a census of ϕ 4-transcendentals. Commun. Number Theory Phys. 4, 1–48 (2010)
Yeats, K.A.: Rearranging Dyson-Schwinger equations. Mem. Am. Math. Soc. 211(995), 1–82 (2011)
Acknowledgements
Alexander von Humboldt Chair in Mathematical Physics, supported by the Alexander von Humboldt Foundation and the BMBF.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer-Verlag Wien
About this chapter
Cite this chapter
Kreimer, D., Panzer, E. (2013). Renormalization and Mellin Transforms. In: Schneider, C., Blümlein, J. (eds) Computer Algebra in Quantum Field Theory. Texts & Monographs in Symbolic Computation. Springer, Vienna. https://doi.org/10.1007/978-3-7091-1616-6_8
Download citation
DOI: https://doi.org/10.1007/978-3-7091-1616-6_8
Published:
Publisher Name: Springer, Vienna
Print ISBN: 978-3-7091-1615-9
Online ISBN: 978-3-7091-1616-6
eBook Packages: Computer ScienceComputer Science (R0)