A Guide to the Tucker Tensor Decomposition for Data Mining: Exploratory Analysis, Clustering and Classification

Abstract

Tensors are powerful multi-dimensional mathematical objects, that easily embed various data models such as relational, graph or time series. Furthermore, tensor decomposition operators are of great utility to reveal hidden patterns and complex relationships in data. Among these decompositions, the Tucker decomposition allows to factorize a tensor into a smaller core tensor and a set of factor matrices. In this article, we propose to study the capabilities of the Tucker decomposition when it is used in data mining techniques such as exploratory analysis, clustering and classification of data. We apply these different techniques on practical examples using several datasets having a ground truth. It is a preliminary work to add the Tucker decomposition to the Tensor Data Model, a model aiming at making tensors data-centric, and at optimizing operators in order to enable the manipulation of large tensors.

1 Introduction

When facing the volume and the variety of data, data mining techniques are often used to extract value. These techniques are rather diverse, and can consist in, for example, finding patterns in data, clustering similar elements, or training a model in order to classify new data [32]. However, depending on the technique used, data often have to be transformed in order to fit the data model required by the algorithm. When doing so, if the data model used is too restrictive to fully represent the data, the result obtained can be of a lesser quality than one obtained with a data model that allows to fully represent the characteristics of data.

In this context, tensors are a valuable solution [7]. Indeed, their multi-dimensional nature allows to easily embed different data models. For example, a tensor can naturally contains the adjacency matrix of a graph, but also more complex representation of graphs such as the labelled one [3]. Time series can also be represented along with their context, thus allowing to give more insights regarding data. Furthermore, tensors have powerful analytical operators, the tensor decompositions, that are used for various purposes such as dimensionality reduction, noise elimination, identification of latent factors, pattern discovery, ranking, recommendation or data completion. They are applied in a wide range of applications, including genomics [18], analysis of health records [46], graph mining [44] and identification and evolution of communities in social networks [3, 34]. Papalexakis et al. in [35] review major usages of tensor decompositions in data mining applications.

One of the decompositions is the Tucker decomposition, that factorizes a tensor with N dimensions into a smaller core tensor and a set of N factor matrices, i.e., one for each dimension. The columns of the factor matrices can be seen as the features for the concerned dimension, and the lines as the signature of a specific element of the dimension over the features. The core tensor is also of major importance, as it represents the relationships of the features among dimensions. However, these different elements make the results of the Tucker decompositon tricky to interpret, especially compared to more straightforward decompositions, such as the CANDECOMP/PARAFAC [41] that does not produce a core tensor.

In this article, we study how different data mining techniques can be applied with the Tucker decomposition. These techniques include the exploratory analysis, that aims at finding patterns in data without having particular knowledge regarding the specificities of the data, the clustering, that gathers similar elements without supervision, and the classification, that gives a class to a new element depending on a model trained on known data. Several datasets covering different domains have been used to illustrate these techniques. It is a preliminary work aiming at integrating the Tucker decomposition into the Tensor Data Model [15, 28]. TDM adds the notion of schema and data manipulation operators to tensors, in order to make them data-centric and to avoid technical and functional errors brought by the manipulation of dimensions and elements of dimensions solely through integer indexes [39]. It also uses optimization techniques to allow the execution of operators, including the decompositions, on large-scale data [13].

The remaining of this article is organized as follows: Sect. 2 gives an overview of tensors and of some main operators, Sect. 3 details how main data models can be embedded into tensors, Sect. 4 presents the Tucker decomposition and two major algorithms to compute it, Sect. 5 relates of data mining techniques available with the Tucker decomposition that have been experimented on datasets, Sect. 6 evaluates the robustness of the Tucker decomposition regarding missing values, and finally Sect. 7 concludes the article and presents perspectives of future works.

2 Background of Tensors

Tensors are general abstract mathematical objects which can be considered according to various points of view, such as a multi-linear application or as the generalization of matrices to multiple dimensions. We will use the definition of a tensor as an element of the set of the functions from the product of N sets $I_j, j=1,\dots ,N$ to , where N is the number of dimensions of the tensor or its order or its mode (see Fig. 1). Table 1 summarizes the notations used in this article. We adopt the same notation as Cichocki in [7].

Fig. 1.

Tensors of different orders

Tensor operators, by analogy with operations on matrices and vectors, are multiplications, transpositions, matricizations (or unfolding) and decompositions (also named factorizations). We only highlight the most significant operators on tensors and matrices which are used in Tucker decomposition algorithms. The reader can consult [7, 27] for an overview of the major operators.

Table 1. Symbols and operators used

A fiber noted consists in extracting a vector $\textbf{v} \in \mathbb {R}^{I_n}$ from the dimension n of a tensor . To do so, all the dimensions except the one to extract are fixed on a specific index, and the values of the vector are obtained with:

$$v_{i_n} = y_{i_1, i_2 \dots ,i_{n-1}, i_n, i_{n+1}, \dots , i_N}$$

Slices are close to fibers, and aim at extracting a matrix ${\textbf {M}} \in \mathbb {R}^{I_{n_1} \times I_{n_2}}$ from the dimensions $n_1$ and $n_2$ of a tensor . All the dimensions except two are fixed on a specific index, and the values are obtained with:

$$m_{i_{n_1},i_{n_2}} = y_{i_1, i_2, \dots , i_{n_1 - 1}, i_{n_1}, i_{n_1 + 1}, \dots , i_{n_2 - 1}, i_{n_2}, i_{n_2 + 1}, \dots , i_N} $$

The concept of fibers and slices can be extended to extract a n-order sub-tensor from a N-order tensor with $n < N$, by fixing all the dimensions on a specific index except for n dimensions.

The outer product between a tensor and another tensor noted produces a tensor in which the elements are equal to:

$$z_{i_1, i_2, \dots , i_N, j_1, j_2, \dots , j_M} = y_{i_1, i_2, \dots , i_N} x_{j_1, j_2, \dots , j_M}$$

It allows to combine all the values from both tensors, by having as many dimensions as the sum of the order of the input tensors. For example, when applying the outer product on two vectors (1-order tensors), it will produce a matrix (2-order tensor), in which an element $e_{i,j}$ corresponds to the $i^{th}$ element of the first vector multiplied by the $j^{th}$ element of the second vector.

The mode-n product allows to multiply a tensor by a matrix or a vector. For a tensor and a matrix ${\textbf {M}} \in \mathbb {R}^{I_n \times J_n}$, the result of the mode-n product noted is a new tensor where:

$$y_{j_1, \dots , j_{n-1}, i_n, j_{n+1}, \dots , j_N} = \sum _{j_n=1}^{J_n}{x_{j_1, \dots , j_{n-1}, j_n, j_{n+1}, \dots , j_N} m_{i_n,j_n}}$$

It modifies the size of the dimension n from $J_n$ to $I_n$. It can be compared to a standard matrix multiplication: for all the indexes of the dimension n, a fiber $\mathbf {v_1} \in \mathbb {R}^{J_n}$ is obtained, and the multiplication ${\textbf {M}} \times \mathbf {v_1}$ is performed, resulting in a vector $\mathbf {v_2} \in \mathbb {R}^{I_n}$ that replaces the fiber extracted from the tensor.

The mode-n product between a N-order tensor and a vector $\textbf{v} \in \mathbb {R}^{I_n}$ noted produces a $(N-1)$-order tensor where:

$$y_{i_1, \dots , i_{n-1}, i_{n+1}, \dots , i_N} = \sum _{i_n=1}^{I_n}{x_{i_1, \dots , i_{n-1}, i_n, i_{n+1}, \dots , i_N} v_{i_n}}$$

The behavior of the mode-n product between a tensor and a vector is the same as the one between a tensor and a matrix, except that the product is a dot product between $\textbf{v}$ and $\mathbf {v_1} \in \mathbb {R}^{I_n}$, that yields a scalar. Thus, the resulting size of the dimension n is 1, and it can be removed from the tensor.

The mode-n matricization of a tensor noted produces a matrix ${\textbf {M}} \in \mathbb {R}^{I_n\times \Pi _{j\ne n}I_j}$, where:

$$m_{i_n,j} = x_{i_1, \dots , i_n, \dots , i_N} \text { with } j = 1 + \sum _{\begin{array}{c} k=1\\ k \ne n \end{array}}^{N}(i_k - 1)\prod _{\begin{array}{c} m=1 \\ m \ne n \end{array}}^{k-1}I_m$$

The matricization is a useful operator, that allows to convert a tensor into a matrix without losing information, in order to apply matrix operators such as the Hadammard product, the Kronecker product or the Khatri-Rao product [7].

The Kronecker product between two matrices ${\textbf {A}} \in \mathbb {R}^{I \times J}$ and ${\textbf {B}} \in \mathbb {R}^{K \times L}$ noted ${\textbf {A}} \otimes {\textbf {B}}$ produces a matrix ${\textbf {C}} \in \mathbb {R}^{(I K) \times (J L)}$, in which every elements of ${\textbf {A}}$ are multiplied by the matrix ${\textbf {B}}$:

$$c_{m,n} = a_{i,j} b_{k,l} \text { where } m = k + (i - 1)K \text { and } n = l + (j - 1)L$$

The Frobenius norm of a tensor noted is computed with:

It is often used on the difference between two tensors in order to estimate their similarity.

3 From Data Models to Tensors

By means of their multi-dimensional nature, tensors can represent various data models. This section highlights how common data models can be embedded into a tensor.

3.1 Key-Value Model

The key-value model stores data as (key, value) pairs [4]. Thus, 1-order tensors can be used to represent this model, with the dimension storing the keys, and the values of the tensor being the value of the pairs. With tensors, the key-value model can be extended to a multi-keys model, in which a value is indexed by several keys. To do so, the tensor must have as many dimensions as the number of keys in a pair, i.e., for K keys the tensor will have K dimensions .

3.2 Relational and Column Models

A relation R (or table) [24] is a set of tuples $(v_1, v_2,\dots , v_N)$, where each element $v_i$ is a member of a domain $Dom_i$, so the set-theoretic relation R is a subset of the cartesian product of the domain $Dom_1 \times \dots \times Dom_N$. With this definition, any relation can be represented with a N-order tensor in which the values are the number of occurrences of this combination of elements.

OLAP data cubes [16], that are obtained from GROUP BY queries, are naturally embedded into tensors because they already represent a multi-dimensional array (see Fig. 2). By formally defining a data cube with $f: (A_1, \dots , A_N) \rightarrow v$, we can use a N-order tensor populated with the v values.

Fig. 2.

Building a tensor from a GROUP BY query

This representation can also model a relation in which the association of $N-1$ elements guarantees a unique combination (e.g., a primary key), and a last element that carries a specific value. For example, for tuples that represent a user, its city and its age, the users and the cities can each be embedded into a dimension, and the age can be the value of the tensor.

The column model, which we consider as a semi-structured model with a fixed schema (i.e., that has a fixed number of columns), includes CSV files and dataframes [36]. This type of model is close to the relational one, thus the same mechanisms of modelling can be used.

3.3 Graph Models

A simple graph $G=(V,E)$, where V is the set of the vertices (or nodes) and $E\subseteq V\times V$ the set of the edges (or links), can be represented by its adjacency matrix, and thus by a 2-order tensor that can take into consideration the direction and the weight of the edges.

However, this is a basic representation, and embedding a graph into a tensor can be even more useful. In a lot of real world graphs, the edges are labelled. An edge labelled graph has its edges defined by $E\subseteq V \times Lab \times V$, where Lab is a set of labels [2]. For example, in a social network the interactions among users are represented by edges that can carry more information, such as the time of the interaction or important words (or hashtags) used in the message. Tensors, as opposed to classical graph representations, can naturally put each type of label into a dimension and have a more complete representation of the data, i.e., for a graph with L different labels and $|Lab_i|$ the number of distinct values taken by the label $Lab_i$, we have (see Fig. 3). The previous example can be modeled as a 4-order tensor, with one dimension for the source user, one for the destination user, one for the hashtag and one for the time.

Fig. 3.

Building a tensor from a labelled graph

Multi-layer networks [26] are also of high interest. A multi-layer network $M = (V_M, E_M, V, \textbf{L})$ with D layers has a set of vertices V and a set of layers $\textbf{L} = \{L_1, \dots , L_D\}$. A vertex can be present in multiple layers, so $V_M \subseteq V \times L_1 \times \dots \times L_D$. Thus, the edges link a vertex within a layer to another vertex within a layer, that is $E_M \subseteq V_M \times V_M$. Each layer represents a category of vertices. This type of graph can be embedded into a 4-order tensor, i.e., , with one dimension for the source vertex, one for the destination vertex, one for the source layer and one for the destination layer. On top of that, by adding dimensions to this representation, tensors can represent easily labelled multi-layer networks.

3.4 Time Series

A time series $Y = (Y_t: t \in T)$ follows the evolution of a metrics for a given element during time [17]. A 1-order tensor can represent a standard time series by storing the time in the dimension. However, tensors can shine as model for time series, as they allow to integrate much more parameters of the creation of the time series (e.g., the sensor, the location), each parameter being represented as a dimension (see Fig. 4). By doing so, time series are viewed in their global context, and therefore it adds more precision and information to the analyses performed on them.

Fig. 4.

Building a tensor from time series

3.5 Images and Videos

A gray scale image of size $x \times y$ is a matrix ${\textbf {GI}} \in \mathbb {R}^{x \times y}$, thus a 2-order tensor . More complex images that use multiple color channels (e.g., RGB, YUV, CYMK) can be embedded in a 3-order tensor , where c is the number of channels. Videos can be considered as a succession of images, called frames. In this configuration, a video is a 4-order tensor where f is the number of frames.

4 Tucker Decomposition

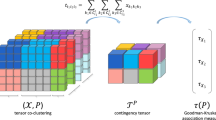
The Tucker decomposition [45] factorizes a N-order tensor into a core tensor and N factor matrices ${\textbf {A}}^{(n)} \in \mathbb {R}^{I_n \times R_n}$. The Fig. 5 shows a representation of the Tucker decomposition applied on a 3-order tensor. The ranks $R_1, \dots , R_N$ are input parameters that determine the number of column vectors (that can be seen as the different features) for each factor matrix. For each rank $R_i$, we have $R_i \le I_i$, and most of the time $R_i \ll I_i$. The input tensor can be approximated from the result of the decomposition with:

Fig. 5.

The Tucker decomposition, with the input tensor, the core tensor, and ${\textbf {A}}^{(1)} \in \mathbb {R}^{I_1 \times R_1}$, ${\textbf {A}}^{(2)} \in \mathbb {R}^{I_2 \times R_2}$ and ${\textbf {A}}^{(3)} \in \mathbb {R}^{I_3 \times R_3}$ the factor matrices

The order of the elements of the dimensions of the input tensor does not impact the result of the decomposition. Indeed, changing it would only reorder the line vectors of the factor matrices, as each line vector stores the result of the decomposition for a given element on the dimension corresponding to the factor matrix.

To compute the Tucker decomposition, several algorithms have been proposed. Each has some advantages, as for example imposing more easily the orthogonality constraint (that allows a good clustering of elements) or the non-negativity constraint (that provides more interpretable results). Two major algorithms are presented in this section: the Higher-Order Orthogonal Iteration (HOOI) and the Hierarchical Alternating Least Squares Non-negative Tucker Decomposition (HALS-NTD).

4.1 Higher-Order Orthogonal Iteration Algorithm

The HOOI algorithm [8] is the most famous one to compute the Tucker decomposition (Algorithm 1). It depends primarily on the Singular Value Decomposition (SVD), that it extends to cope with multiple dimensions.

The HOOI starts by initializing the factor matrices, by matricizing the original tensor on each dimension in order to apply the SVD and to use the $R_n$ left singular vectors (matrix ${\textbf {U}}$ of the result of the SVD truncated at the ${R_n}^{th}$ column) as factor matrices. During the iterative phase (lines 2 to 7), each factor matrix is improved. To do so, a partial core tensor is computed by performing the mode-n product on the original tensor and all the factor matrices except the one being improved. This partial core tensor is then matricized on the mode corresponding to the concerned dimension, and the SVD is executed on it. As for the initialization step, the $R_n$ left singular vectors are used as the new factor matrix. The iterative phase allows to refine the result, as the partial core tensor takes into consideration the other factor matrices. So, each factor matrix is improved depending on the other factor matrices, thus reinforcing the discovering of relationships among elements of dimensions. When a convergence criteria is met, the final core tensor is computed from the original core tensor and all the factor matrices (line 8).

A simpler version of the HOOI algorithm exists, the Higher-Order Singular Value Decomposition (HOSVD), that removes the iterative part of the HOOI algorithm (lines 2 to 7). It is less precise, as the iterative part of the HOOI allows to refine the result until a convergence criterion is met.

The HOOI algorithm inherits from the orthogonality constraint of the SVD for the computation of the factor matrices. Thus, it works pretty well to cluster elements of a dimension depending on their behavior on the other dimensions. However, as the SVD produces matrices with positive and negative values, the HOOI is not well suited to impose the non-negativity constraint on factor matrices, as some negative values will be found (and must be removed) at each iteration.

An advantage of this algorithm is that it can easily be implemented on large tensors. The most costly operation is the computation of the SVD, that is found at the initialization (line 1) and during the iterative phase (line 5). During the iterations, as the SVD is executed on the mode-n matricized partial core tensor, that is relatively small compared to the matricized original tensor, the time and space complexity is reduced. At the initialization of the algorithm, it can be replaced with a random initialization to avoid the computation of the SVD on a too large matrix.

4.2 Hierarchical Alternating Least Squares Algorithm

The HALS-NTD algorithm [7] uses a different approach than the HOOI algorithm (Algorithm 2), even if the initialization step (line 1) can be done by using the HOSVD. An alternative version of the HALS-NTD was later proposed [37].

The HALS-NTD starts also by initializing the factor matrices (line 1), but adds a non-negativity constraint to manipulate only positive values in the remaining of the algorithm. An error tensor (noted ${\textbf {E}}_{(n)}$ when it is matricized on dimension n), that stores the difference between the original tensor and the reconstructed tensor from the core tensor and the factor matrices, is computed (line 2). The iterative phase (lines 3 to 16) is more complex than the one of the HOOI algorithm. Rather than improving a whole factor matrix at a time, it improves a vector of a factor matrix at a time. To do so, at the line 6, the current vector (the one being improved) is put in relation with all the other factor matrices associated with the part of the core tensor representing the strength of the relationships of the current vector regarding the vectors of the other factor matrices. This result is added to the error tensor, and stored in ${\textbf {X}}^{(r)}_{(n)}$, that can be seen as a matricized tensor representing the contribution of the current vector to the global result combined to the error tensor. At line 7, the current vector is improved by multiplying ${\textbf {X}}^{(r)}_{(n)}$ with the part of the reconstructed tensor corresponding to the current vector. The current vector is then normalized with a $L_2$ norm (line 8), and the error tensor is updated (line 9). Once all the vectors of the factor matrices have been improved, the core tensor is updated from the previous core tensor, the error tensor and the new vectors of the factor matrices (line 13), and finally the error tensor is updated to integrate the changes in the core tensor (line 14).

The major advantage of the HALS-NTD is that it enforces the non-negativity constraint by imposing it during the initialization step, and then by improving the result without obtaining (and without having to eliminate) negative values during the iterative part (line 3 to 12). Thus, it eases the direct interpretation of the factor matrices as well as the core tensor.

However, as this algorithm computes the decomposition column vector by column vector for each factor matrices, it is computationally demanding, and harder to optimize than the HOOI one. Furthermore, there is almost no implementation of the HALS-NTD alogrithm. To the best of our knowledge, only Cichocki and Phan have provided a Matlab implementation in [7].

4.3 Related Work

The Tucker decomposition has been used in several kind of applications on specific data such as in social and collaboration network analysis, in web mining, in topic modelling, in recommendation systems, in urban computing, in vision, image or speech processing. While the number of works on the CANDECOMP/PARAFAC decomposition algorithm is significant, much less work has been done to study the Tucker decomposition algorithms. Some of these works focus on specific issues of algorithms to compute the Tucker decomposition.

In [22] the authors proposed the D-Tucker decomposition, as a fast and memory-efficient method for Tucker decomposition on large dense tensors using 3 phases: the approximation, the initialization, and the iterative phases. The main ideas is to compress an input tensor by computing randomized SVD of matrices sliced from the input tensor, and to obtain orthogonal factor matrices and a core tensor by using SVD results.

In [23] the authors proposed Tucker decomposition methods for large dense static tensors and online streaming data. They decomposed large dense tensors by using the randomized SVD, avoiding the reconstruction from SVD results, and carefully determining the order of operations.

Chachlakis et al. in [6] explored the use of $L_1$-norm for reformulation of the Tucker decomposition to overcome the effect of outliers. They also adapted two algorithms: the $L_1$-norm Higher-Order Singular Value Decomposition ($L_1$-HOSVD) and the $L_1$-norm Higher-Order Orthogonal Iterations ($L_1$-HOOI).

In [29], the authors defined a scalable GPU-based Tucker decomposition, which partitions large-scale tensors into subtensors to process them. They showed that their decomposition reduced the overhead on a single machine.

Most of the Tucker decomposition implementations make use of explicit matricizations and could introduce extra costs in terms of data conversion and memory usage. In [10] the authors proposed A-Tucker, a framework for input-adaptive and matricization-free Tucker decomposition of dense tensors. Their decomposition algorithm enables the switch of different solvers for the factor matrices and core tensor, and a machine-learning adaptive algorithm is applied to automatically cope with the variations of both the input data and the hardware. They showed that A-Tucker improves existing algorithm on GPUs.

Several applications of the Tucker decomposition can be found in the literature.

Fernandes et al. [12] presented an overview of tensor decompositions for analyzing time-evolving social networks and showed that while most of the approaches use the CANDECOMP/PARAFAC decomposition, Tucker is most appropriate for studying time evolving networks. Sun et al. [43] used Tucker on social network data in order to find clusters. They applied it on the Enron dataset. They also proposed visualization techniques based on graphs to display the result of the decomposition. Al-Sharoa et al. in [1] proposed an approach to determine sub-spaces across time which relies on Tucker decomposition.

Shao et al. in [40] developed a model for temporal knowledge graphs completion based on a specific tensor decomposition model for temporal knowledge graphs completion inspired by the Tucker decomposition, but only for 4-order tensors. For handling missing data, [30] introduced a Tucker decomposition with $L_2$ regularization and applied it on urban IoT data.

Romeo et al. [38] used the Tucker decomposition to cluster documents. Thanks to this decomposition, they were able to process documents in several languages in the same tensor, in order to find similarities in the whole dataset.

Huang et al. [20] compared the Tucker decomposition to the PCA and SVD associated to k-means. They ran experiments on three datasets of images to show the similarities among these algorithms. Zhou et al. [47] took a different approach and used the Tucker decomposition as a supervised learning algorithm. They obtained promising results to cluster images.

Cichocki in his book [7] showed several applications of various decompositions on small tensors, mainly for image and brain data signal analysis. In [19], the authors approximated both spectral and spatial information, and proposed a novel 3-order Tucker decomposition and a reconstruction detector for hyperspectral change detection. They designed a singular value energy accumulation method to determine the number of principal components in different factor matrices.

Brandoni et al. in [5] defined a method which can handle three or more order tensors in the Tensor-Train model and they proposed to tackle the memory consumption with a truncation strategy. For 3-order tensors, the Tensor-Train decomposition corresponds to the classical Tucker decomposition. They applied their method for image classification.

In [33] the authors used Tucker decomposition as the core of a deep neural network method for speech emotion recognition. 2D, 3D Spectrogram and Temporal Modulation Spectrogram are explored to investigate tensor factorization based architectures to capture salient information corresponding to emotion. Hidden layers are extracted from Tucker decomposition. The core tensor produced in each hidden layer is the feature associated with that factorization layer.

Due to the lack of implementation for the HALS-NTD algorithm, articles are mainly related to the HOOI algorithm. Thus, they only benefit from a part of the Tucker decomposition capabilities. They aim at clustering data, and do not rely on the direct interpretability of the factor matrices and the core tensor even if it brings valuable insights.

5 Data Mining Techniques

This section presents the datasets used for the experiments, as well as the different data mining techniques that can be applied with the Tucker decomposition. In [14], we observed that the HALS-NTD algorithm with its non-negativity constraint is best suited for producing interpretable results, while the HOOI algorithm with its orthogonality constraint is best suited for clustering tasks. So, in this article we focus only on the different data mining techniques without analyzing the impact of each algorithm on the techniques. The code of the experiments is available online¹ as well as the links to datasets in order to make the experiments reproducible.

5.1 Datasets Overview

To illustrate the different data mining techniques, we rely on several well-known datasets. They are rather diverse and concern different domain applications, such as image recognition, temporal graph or machine learning reference dataset.

Iris ²

The Iris dataset contains characteristics of 150 flowers, namely the sepal width, the sepal length, the petal width and the petal length. There are 3 species of Iris flowers in this dataset, each being represented by 50 samples. This dataset is known for having one species that are linearly separable from the two others, and two species that are not linearly separable.

COIL-20 [31]

Fig. 6.

The 20 objects of the COIL-20 dataset

The COIL-20 dataset gathers 20 different objects (see Fig. 6). For each object, there are 72 pictures that represent the object in a specific position (a difference of 5$^{\circ }$ in the orientation of the object). The pictures have $128 \times 128$ pixels.

MNIST [9].

Fig. 7.

An extract of the MNIST dataset

The MNIST dataset is composed of 70 000 images representing a hand-written digit, of $28 \times 28$ pixels (see Fig. 7). It is often used to evaluate algorithms of image classification, as the hand-written nature of the images induces a different complexity to deal with than a static object.

Primary School [42]

Fig. 8.

Network overview of the primary school dataset

The primary school dataset represents the interactions among 232 students and 10 teachers in a French primary school, that contains 10 classes (see Fig. 8). The participants wore RFID devices, that recorded an interaction if it had lasted at least 20 seconds. The experiment was carried on during 2 days. The records are of the form (person1, person2, timestamp), and the class of each student is the ground truth of this dataset.

5.2 Exploratory Analysis

The Tucker decomposition can be used to highlight patterns of multi-dimensional data. Indeed, as each factor matrix gives information regarding elements of a dimension depending on their behavior on other dimensions, it helps to find structures or patterns in data. Furthermore, the core tensor allows to link this kind of information among all the dimensions, and thus to contextualise each insight.

To illustrate this use of the Tucker decomposition, we rely on the primary school dataset. We build a 3-order tensor of size $242 \times 242 \times 208$, with two symmetric dimensions used to represent the persons, and the third dimension to represent the time with a granularity of 5 min. If a person has been in contact with another person at a time t, then the value in the tensor indexed by the corresponding dimension values is 1.

This kind of use of the Tucker decomposition is best interpreted when the non-negativity constraint is enforced during the decomposition algorithm execution. So, in the experiment of this section, we use the HALS-NTD algorithm. We run the Tucker decomposition with ranks 13 (for the first person dimension), 13 (for the second person dimension) and 4 (for the time dimension). To choose these ranks, we ran the SVD for each dimension on the tensor matricized on the corresponding dimension, and we select as rank the number of significant singular values.

Fig. 9.

Factor matrix for the dimension representing the persons in the primary school experiment

The factor matrix for the first dimension is shown in Fig. 9. Each line represents a rank, and the columns are the persons. The students are ordered by their class: the first columns are the students of the class 1A, then 1B, and so on until 5B, and the 10 teachers are the last 10 columns. We can distinguish 10 ranks in which each class appears distinctly, and three heterogeneous ranks.

Fig. 10.

Factor matrix for the dimension representing the time in the primary school experiment. The morning and afternoon breaks are approximate, as all the classes do not have the breaks at the same time

Figure 10 shows the factor matrix for the time dimension. There are four distinct periods. The first period indicates an activity during class hours and the morning and afternoon breaks, the second period concerns the breaks, including the lunch one, the third period also covers the class hours with more activity at the end of the days, and the last one shows activity during morning and afternoon breaks and just before and after the lunch time.

For exploratory analysis, the role of the core tensor is also important: it gives insights regarding the strength of the relationships of the ranks among dimensions. For example, the $g_{1,1,1}$ value indicates if the vectors $\textbf{a}^{(1)}_{1}$, $\textbf{a}^{(2)}_{1}$ and $\textbf{a}^{(3)}_{1}$ are strongly related or not.

To illustrate the usefulness of the core tensor, we can focus on a particular rank of the first dimension and see how it is related to the ranks of the other dimensions. The Fig. 11 represents this mechanism when fixing the rank of the first dimension to the one corresponding to the class 1A.

Fig. 11.

Ranks from each factor matrix that are strongly related to each other when fixing the rank of the first dimension to the one representing the class 1A

This figure shows some interesting results. The first strongest value of the core tensor indicates that the class 1A has strong ties with itself, mainly at the break times and before and after the lunch break (Fig. 11a). It makes sense because at the breaks the students move from their classroom and go outside, so it creates more interactions among students. The second strongest value of the core tensor shows again a relationship of the class 1A with itself, but this time during the class hours (Fig. 11b). The third strongest value indicates a relationship between the class 1A and 1B during the breaks, including the lunch one (Fig. 11c). As the students of these two classes are of the same age, it is logical that they have more ties. Finally, the fourth value of the core tensor shows a relationship between the class 1A and a heterogeneous cluster that gathers students from grades 1, 2 and 3, during the breaks (Fig. 11d).

Fig. 12.

(from [42])

Number of contacts among classes

The Fig. 12 indicates the number of contacts that have occurred among classes, and it confirms the observations made from the result of the Tucker decomposition. In each class, most of the contacts are made with students of the same class, or with students with a close age.

To summarize, the advantages of using the Tucker decomposition for exploratory analysis are twofold: 1) the vectors of the factor matrices give insights regarding the elements that contribute to the rank; and 2) the core tensor allows to link the ranks of one factor matrix to the ranks of the other factor matrices, and thus it gives more context to the result, as for example in Fig. 11 where we have the temporal activity of the different communities.

5.3 Clustering

The Tucker decomposition produces factor matrices that represent the proximity of the elements of a dimension depending on their behavior on all the other dimensions. Therefore, classic clustering techniques can be applied on a selected factor matrix to cluster its elements.

To apply this technique, the tensor must be built with a dimension representing the samples to cluster. Enforcing the orthogonality constraint on factor matrices is of great help to separate more clearly the different clusters, so it is better to use the HOOI algorithm. The number of ranks can be chosen identically to the exploratory analysis technique.

From the result of the Tucker decomposition, it is possible to execute clustering algorithms on the factor matrix of the dimension of the elements to cluster, in order to gather similar elements. To illustrate this technique, we apply it on all the datasets presented in Sect. 5.1.

Table 2. Modeling of the tensors for the clustering experiment (the dimension on which we apply the clustering algorithm is in bold)

The Table 2 summarizes the tensors built for the experiment for each dataset. The Iris dataset is embedded into a 2-order tensor, in which each sample has a vector of characteristics, namely the sepal length, the sepal width, the petal length and the petal width. For the MNIST dataset, a 3-order tensor stores the image corresponding to each sample. To reduce the size of the tensor, only 10 000 samples are kept, with 1 000 samples for each digit. For the COIL-20 dataset, we have tried two different modeling: one that includes the position of the object in a dimension, and another that uses the same representation as for the MNIST dataset, without modeling the position. Finally for the primary school dataset, we use the same modelling as for the exploratory analysis experiment.

Table 3. Result of the clustering experiment on each dataset

From these tensors, we run the Tucker decomposition with the HOOI algorithm, and we apply the k-medoids algorithm [25] on the factor matrix corresponding to the dimension to cluster, with k being the number of classes of the dataset. The Table 3 shows the ranks used for each dataset, the precision of the clustering and the Adjusted Rand Index [21] (ARI). In this experiment, the precision is computed as follows:

$$ \text {precision} = \frac{\text {number of elements correctly clustered}}{\text {total number of elements}}$$

The cluster gathering the most elements of a given class is considered as the cluster for this class. The ARI is computed as follows:

$$ \text {ARI} = \frac{\sum _{i=1}^{N_c}{\sum _{j=1}^{N_c}{{n_{i,j} \atopwithdelims ()2}}} - \frac{\sum _{i=1}^{N_c}{{n_{i,.} \atopwithdelims ()2}}\sum _{j=1}^{N_c}{{n_{.,j} \atopwithdelims ()2}}}{{N \atopwithdelims ()2}}}{\frac{1}{2}(\sum _{i=1}^{N_c}{{n_{i,.} \atopwithdelims ()2}} + \sum _{j=1}^{N_c}{{n_{.,j} \atopwithdelims ()2}}) - \frac{\sum _{i=1}^{N_c}{{n_{i,.} \atopwithdelims ()2}}\sum _{j=1}^{N_c}{{n_{.,j} \atopwithdelims ()2}}}{{N \atopwithdelims ()2}}} $$

with N the number of elements to cluster, $N_c$ the number of classes and $n_{i,j}$ the value at line i and column j of the confusion matrix. $n_{.,j}$ is the sum of the column j and $n_{i,.}$ is the sum of the line i.

The clustering provides good results for the Iris (80% precision and 0.5623 ARI) and the primary school (91.38% precision and 0.8189 ARI) datasets. The confusion matrix for the Iris dataset is given in Fig. 13. As expected, the species that are not linearly separable concentrate most of the clustering errors. For the primary school dataset, we cluster only students and not the teachers, as we do not know which teacher is affected to which class.

Fig. 13.

Confusion matrix for the clustering of the Iris dataset

The results for the MNIST and the COIL-20 datasets are less satisfying. Indeed, for the MNIST dataset, the decomposition does not seems to be able to naturally find a pattern for each digit, and a precision of only 12.83% is obtained with an ARI of 0.015. For the COIL-20 dataset, when modeling the position into the tensor, the result is far worse (5.63% precision and -0.0046 ARI) than when the position is not represented in the tensor (42.43% precision and 0.337 ARI). Our hypothesis for this result is that the position is not a characteristics of the objects, thus the same object is never found twice with the same value on the position dimension, and the decomposition has more difficulties to find patterns in these conditions. Similarly, when the position is not represented as a dimension of the tensor, the clusters are not well defined because each sample concerns an object and a position, and the decomposition finds patterns for both at the same time.

To conclude on this technique, the experiments showed that the modeling of the tensor impacts the result, but also that the quality of the result is better if the elements of the dimension to cluster share a similar behavior on the other dimensions.

5.4 Classification

With the Tucker decomposition, it is possible to classify new elements by first building a model from elements with known class, and then by sending the new element into the same space as the model to be able to compare it with existing classes and to choose the most fitting one.

In this use case, the Tucker decomposition is used to build a model from training data. To do so, the modeling of the data into a tensor must have a dimension to represent the existing classes, that is used to indicate at which class each sub-tensor belongs. For example, for the MNIST dataset, a 4-order training tensor can be built, with two dimensions to represent the pixels (p1 and p2), one dimension to represent the samples (s), and a last one for the digits written on images (c). The values of the tensor are the values of the corresponding pixels.

Once the training tensor is built, the Tucker decomposition can be applied to produce the model. In this use case, it is better to use an algorithm enforcing the orthogonality constraint such as the HOOI one. With our MNIST example, we obtain the following model:

with the core tensor, ${\textbf {P1}} \in \mathbb {R}^{p1 \times R_{p1}}$ and ${\textbf {P2}} \in \mathbb {R}^{p2 \times R_{p2}}$ the factor matrices for the two pixel dimensions, ${\textbf {S}} \in \mathbb {R}^{s \times R_{s}}$ the factor matrix for the sample dimension, and ${\textbf {C}} \in \mathbb {R}^{c \times R_{c}}$ the factor matrix for the class dimension.

The goal of a classification task is to deduce the class of a new element. To continue with the MNIST example, it consists in deducing the digit written on a new image. We consider a new image as a matrix ${\textbf {I}} \in \mathbb {R}^{p1 \times p2}$. To classify this image according to the model, both must be in a comparable space. To do so, we rely on the relation among the input tensor, the core tensor and the factor matrices, that implies that the core tensor can be obtained from the input tensor by applying successive mode-n products on the input tensor and each factor matrix transposed. More formally, this relation can be summarized as follows:

By exploiting this relation, the matrix ${\textbf {I}}$ can be partially sent into the same space as the model, by applying the mode-n product on known dimensions, namely the first and the second that represent the pixels. To be closer to the model, the matrix ${\textbf {I}}$ can be considered as a 4-order tensor , by adding two dimensions of size 1:

With this representation, it is not possible to fully send the element to classify in the same space as the model. Indeed, the size of the dimensions s and c does not match the size of the dimensions 3 and 4 of . In order to solve this problem on the third dimension, rather than only simulating a dimension of size 1, we duplicate the matrix ${\textbf {I}}$ s times to obtain the 4-order tensor and to be able to use one more factor matrix to send the element in the same space as the model³:

To finally classify the element, we compare with by keeping only one class at a time in . To do so, for each class i we use the product mode-4 on the core tensor and the column vector i of factor matrix ${\textbf {C}}$ to produce a class specific core tensor :

As and are now of the same size and in the same space, they can be compared with the Frobenius norm applied on the difference of the two tensors. The class for which the Frobenius norm is the lowest (i.e., for which the two tensors are the closest) can be considered as the class of the element. The classification process is summarized in Algorithm 3 for a N-order training tensor and a M-order element to classify.

Table 4. Modeling of the tensors for the classification experiment (the dimension that holds information about classes is in bold)

To apply the classification technique on the dataset of Sect. 5.1, we build tensors as specified in Table 4. The MNIST tensor has 8 000 samples rather than 7 000 because the digits are not evenly distributed and some digits are represented in more than 7 000 images. The classes of the primary school dataset concern the students of the first dimension. To experiment the technique, we use the cross validation method and perform the training and the classification task 5 times. The data used for the training step are modified at each iteration to avoid overfitting bias.

Table 5. Result of the classification experiment on each dataset. For the COIL-20 dataset, “without position” indicates that images were classified only regarding objects and “with position” indicates that the images were classified regarding positions and objects

Table 6. Detailed metrics for each class of each dataset for the classification technique

The results obtained are summarized in Table 5, and the detailed metrics for each class are given in Table 6. Most of the samples are correctly classified for all the datasets. For the MNIST dataset, there is a great improvement compared to the clustering technique: the global precision is almost 8 times better. It indicates that, when integrating more contextual information into the tensor (in this case, the digit written), the Tucker decomposition can find patterns more easily.

With the COIL-20 dataset, it is possible to illustrate a useful mechanism of the classification performed from a model obtained with the Tucker decomposition. Indeed, it can be used to classify an element according to several different class dimensions rather than just one. In the COIL-20 dataset, each image represents an object, but also a specific position. To illustrate this behavior, we classify the test images according to the object that they represent but also to their position. The Fig. 14 shows the confusion matrices obtained for this experiment. The objects are better recognized, and the position is found for 94.81% of the test images with a precision of ± 5$^{\circ }$.

Fig. 14.

The confusion matrices obtained when classifying elements of the COIL-20 dataset according to the object that they represent and their position

The Tucker decomposition shows promising results when using it in classification tasks. It can be used to classify a new element depending on one or several parameters, only by using the model produced by the decomposition algorithm.

6 Robustness of the Tucker Decomposition

It is important to evaluate the robustness of an algorithm, as it gives information about the perturbations that can occur in data without significantly impacting the result. We study the robustness of the Tucker decomposition when it is used for clustering or for classifying tasks with missing values, and show that it has a fairly good robustness.

6.1 Clustering

For testing the robustness of the Tucker decomposition when performing clustering tasks with missing data, the primary school dataset is used as it presents the best results for the clustering task with all the data. 5 students are selected from each class, and 10% of data are randomly removed at each iteration only for those students, for 9 iterations. Thus, the clustering is performed with 90% of the students’ data for the first execution and with 10% of the data for the last execution. Table 7 gives the precision and the ARI for the whole data and for the selected students, and Fig. 15 shows the confusion matrices of the result of the experiment. Confusion matrices on the left are for the whole dataset and confusion matrices on the right are for the selected students only.

Table 7. Result of the clustering experiment on the primary school dataset with missing data for selected students

Fig. 15.

Confusion matrices for the clustering of the primary school dataset with missing data for selected students

This experiment shows that the clustering is almost not affected when removing up to 40% of the data of the selected students. However, the quality of the clustering drops significantly when removing 50% and 60% of the data. For 70% or more missing data, all the selected students are gathered into a single cluster: the algorithm is unable to differentiate them due to the strong degradation of the data.

6.2 Classification

The robustness of the Tucker decomposition for performing classification tasks have been experimented on the primary school and the COIL-20 datasets. Compared to Sect. 5.4, the step for building the model is identical and is performed with the whole data. The data are removed in the test set evenly for all elements to classify. As for the clustering experiment, data are randomly removed 10% by 10% until reaching 90% of missing data. Table 8 shows the precision results for this experiment.

Table 8. Global precision of the classification experiment on the primary school and the COIL-20 datasets with missing data

For the primary school and the COIL-20 datasets, the quality of the classification with 10% to 30% missing data is close to the classification with no missing data. Starting from 50% of missing data, the precision of the classification of the primary school dataset declines steadily at each 10% removal of data. However, for the COIL-20 dataset, the decline is more abrupt: the precision is cut in half with 40% of missing data and is inferior to 10% when removing 50% of data or more.

6.3 Summary

The study of the robustness of the Tucker decomposition shows that it is fairly resistant to missing data. Indeed, the quality of the result is not significantly reduced when removing up to 30% of data. Furthermore, when comparing results obtained from the primary school dataset and from the COIL-20 dataset, the lowering of quality is less abrupt with the primary school dataset, thus indicating that it is a well suited data mining technique when working with sparse data that present imperfections of the real world (e.g., students of a same class do not act identically).

7 Conclusion

To conclude, the Tucker decomposition is a useful data mining algorithm, robust to missing data. Indeed, it can be used to perform exploratory analysis on data, in order to retrieve patterns that give insights regarding elements of a given dimension, and regarding relationship of elements among dimensions. It can also be used to cluster elements of a dimension when they behave similarly on all the other dimensions, or to produce a model allowing to classify new data according to one or several characteristics.

Both the HOOI and the HALS-NTD algorithms are useful for these techniques, as the non-negativity constraint of the HALS-NTD greatly helps when interpreting results of exploratory analysis, while the orthogonality constraint of the HOOI algorithm is efficient to cluster or classify data. However, the HALS-NTD algorithm is less known than the HOOI one, and in consequence it has almost never been implemented. We plan to integrate these Tucker algorithms to the Tensor Data Model, and to optimize them in order to allow their execution on large tensors, as we did for the CANDECOMP/PARAFAC decomposition [13]. Indeed, real data can create such tensors, that emphasis the need for optimized algorithms regarding the space and the execution time.

We also plan to improve data mining techniques based on the experiments made on this article, for example to consider a proximity among elements of a dimension (e.g., two consecutive time slices on a temporal dimension are closer than non-consecutive time slices), or to perform a coupled decomposition, i.e., a decomposition with two tensors that share at least one dimension.