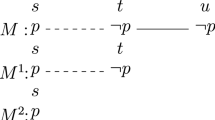Group Announcement Logic with Distributed Knowledge

Abstract

Public announcement logic (PAL) is an extension of epistemic logic with dynamic operators that model the effects of all agents simultaneously and publicly acquiring the same piece of information. One of the extensions of PAL, group announcement logic (GAL), allows quantification over (possibly joint) announcements made by agents. In GAL, it is possible to reason about what groups can achieve by making such announcements. It seems intuitive that this notion of coalitional ability should be closely related to the notion of distributed knowledge, the implicit knowledge of a group. Thus, we study the extension of GAL with distributed knowledge, and in particular possible interaction properties between GAL operators and distributed knowledge. The perhaps surprising result is that there in fact are no interaction properties, contrary to intuition. We make this claim precise by providing a sound and complete axiomatisation of GAL with distributed knowledge.

1 Introduction

The main contribution of this paper is extending Group Announcement Logic (GAL) [1] with distributed knowledge [11], and a sound and complete axiom system for the resulting logic GALD.

Our motivation for studying this combination of modalities is twofold. First, extending epistemic logics with quantifiers over information-changing actions [2, 7, 8, 16], of which GAL is a representative, with group knowledge modalities is an open problem. Second, the quest for a better understanding of both types of logical operators and their interaction is interesting in its own right. Distributed knowledge is often intuitively understood as closely related to the knowledge the agents would arrive at if they could communicate their individual knowledge to each other. Deep analyses of this intuition [4, 17, 20] shows that it is not always accurate, but when we started investigating GAL with distributed knowledge operator D we nevertheless expected to find non-trivial interaction axioms. We consider several plausible candidates for such interaction axioms, and show that none of them are actually valid. Then we show that in fact there are no interaction axioms at all: the axiom system obtained by the independent combination of axioms for epistemic logic with distributed knowledge and GAL is complete. This is contrary to intuition, and therefore an interesting result.

We also consider the relationship between resolved distributed knowledge [4] and distributed knowledge in the context of announcement logics, and give some preliminary results on their relative expressive power.

The paper is organised as follows. In the next section we briefly review the technical background. In Sect. 3 we look at some potential interaction axioms relating group announcements and group knowledge. In Sect. 4 we present a Hilbert-style axiomatic system for group announcement logic with distributed knowledge, and show that it is sound and complete. Resolved distributed knowledge is discussed in Sect. 5, before we conclude in Sect. 6.

2 Background

In this section, we introduce the necessary background information on epistemic and group announcement logic.

2.1 Languages

The language of GALD is defined relative to a finite set of agents A and a countable set of propositional variables P. Below we also define a positive fragment of this language.

Definition 1

The language of group announcement logic with distributed knowledge and its positive fragment are defined by the following BNFs:

where $p \in P$, $a \in A$ and $G \subseteq A$.

The sublanguage only containing $K_a$ modalities in addition to the propositional operators and variables is referred to as $\mathcal {L}_{EL}$ (epistemic logic) [11], with addition of $D_G$ it becomes $\mathcal {L}_{ELD}$, $\mathcal {L}_{EL}$ with announcements $[\varphi ]$ is referred to as $\mathcal {L}_{PAL}$ [19], with $D_G$ as $\mathcal {L}_{PALD}$, and $\mathcal {L}_{GALD}$ without $D_G$ is $\mathcal {L}_{GAL}$. The intuitive meaning of formulas is as follows: $K_a \varphi$ means that agent a knows that $\varphi$; $D_G \varphi$ means that G has distributed knowledge of $\varphi$ ($\varphi$ is true in the set of states that all agents in G consider possible); $[\varphi ] \psi$ means that if $\varphi$ is true, then after it is announced (and everyone’s knowledge updated by removing states not satisfying $\varphi$), $\psi$ is true; $[G] \varphi$ means that after any joint announcement by agents in G of formulas they know, $\varphi$ is true. The quantification in the latter modality is over conjunctions of formulas of $\mathcal {L}_{ELD}$ prefixed by $K_a$ for $a \in G$.

Duals are defined as $\widehat{K}_a \varphi := \lnot K_a \lnot \varphi$, $\langle \varphi \rangle \psi := \lnot [\varphi ] \lnot \psi$, and $\langle G \rangle \varphi := \lnot [G] \lnot \varphi$.

2.2 Models and Bisimulation

Definition 2

An epistemic model M is a triple $(S, \sim , V)$, where S is a non-empty set of states, $\sim : A \rightarrow 2^{S \times S}$ assigns to each agent an equivalence relation, and $V:P \rightarrow 2^S$ is a valuation. If necessary, we refer to the elements of the tuple as $S^M$, $\sim ^M$, and $V^M$.

A model M with a designated state $s \in S$ is called a pointed model and denoted by $M_s$.

Model M is called finite if S is finite. Also, we write $M \subseteq N$ if $S^M \subseteq S^N$, $\sim ^M$ and $V^M$ are results of restricting $\sim ^N$ and $V^N$ to $S^M$, and call M a submodel of N.

An updated model $M^\varphi$ is $(S^\varphi , \sim ^\varphi , V^\varphi )$, where $S^\varphi = \{s \in S \mid M_s \models \varphi \}$, $\sim ^\varphi _a\, =\, \sim _a \cap$ $(S^\varphi \times S^\varphi )$ for all $a \in A$, and $V^\varphi (p) = V(p) \cap S^\varphi$ ($\models$ is given in Definition 5).

For a group $G \subseteq A$, $\sim _G$ denotes $\bigcap _{a \in G} \sim _a$.

Definition 3

(Bisimulation). Let $M = (S^M, \sim ^M, V^M)$ and $N = (S^N,$ $\sim ^N,$ $V^N)$ be two models. A non-empty binary relation $Z \subseteq S^M \times S^N$ is called a bisimulation if and only if for all $s \in S^M$ and $u \in S^N$ with $(s,u) \in Z$:

• for all $p \in P$, $s \in V^M(p)$ if and only if $u \in V^N(p)$;

• for all $a \in A$ and all $t \in S^M$: if $s \sim _a^M t$, then there is a $v \in S^N$ such that $u \sim _a^N v$ and $(t,v) \in Z$;

• for all $a \in A$ and all $v \in S^N$: if $u \sim _a^N v$, then there is a $t \in S^M$ such that $s \sim _a^M t$ and $(t,v) \in Z$.

If there is a bisimulation between models M and N linking states s and u, we say that $M_s$ and $N_u$ are bisimilar, and write $M_s \rightleftarrows N_u$.

Definition 4

(Bisimulation contraction). Let $M = (S, \sim , V)$ be an epistemic model. The bisimulation contraction of M is the model $\Vert M\Vert = (\Vert S\Vert , \Vert \! \! \sim \! \! \Vert , \Vert V\Vert )$, where $\Vert S\Vert = \{[ s ] \mid s \in S\}$ and $[ s ] = \{t \in S \mid M_s \leftrightarrows N_t\}$, $[ s ] \Vert \! \! \sim \! \! \Vert _a [ t ]$ if and only if $\exists s^\prime \in [s]$, $\exists t^\prime \in [t]$ such that $s^\prime \sim _a t^\prime$ in M, and $[s] \in \Vert V\Vert (p)$ if and only if $\exists s' \in [s]$ such that $s' \in V(p)$.

It is a known result that $M_s \leftrightarrows \Vert M\Vert _{[s]}$ [15].

2.3 Semantics of GALD

Let us denote by $\psi _G$ a formula of the form $\bigwedge _{a \in G} K_a \psi _a$ where $\psi _a \in \mathcal {L}_{EL}$. We refer to this fragment as $\mathcal {L}_{EL}^G$. We will also write $\top _{G}$ to denote $\bigwedge _{a \in G} K_a (p \vee \lnot p)$.

Definition 5

(Semantics of GALD). Let $M_s$ be a pointed epistemic model. The semantics of GALD is defined as follows (boolean cases are as usual and we omit them):

$$\begin{aligned} \begin{array} {lcl} M_s \models K_a\varphi &{}\text {iff} &{}\forall t \in S: s \sim _a t \text { implies } M_t \models \varphi \\ M_s \models D_G\varphi &{}\text {iff} &{}\forall t \in S: s \sim _G t \text { implies } M_t \models \varphi \\ M_s \models [\psi ] \varphi &{}\text {iff} &{} M_s \models \psi \text { implies } M_s^\psi \models \varphi \\ M_s \models [G] \varphi &{}\text {iff} &{} \forall \psi _G: M_s \models [\psi _G] \varphi \\ \end{array} \end{aligned}$$

Definition 6

(Validity and satisfiability). $\varphi$ is valid ($\models \varphi$) if and only if for any pointed model $M_s$ it holds that $M_s \models \varphi$. $\varphi$ is satisfiable if and only if there is some $M_s$ such that $M_s \models \varphi$.

2.4 The Positive Fragment

Positive formulas can be considered as a particularly well behaved fragment of public announcement logic [9]. In particular, they remain true after an announcement.

Definition 7

A formula $\varphi$ is said to be preserved under submodels if and only if $M_s \models \varphi$ implies $N_s \models \varphi$ for any pointed models $M_s$ and $N_s$ such that $N_s \subseteq M_s$.

Proposition 1

Formulas of $\mathcal {L}_{{GALD}^+}$ are preserved under submodels.

Proof

Let $M = (S^M, \sim ^M, V^M)$ and $N = (S^N, \sim ^N, V^N)$ be models such that $s \in S^M$, $s \in S^N$, and $N_s \subseteq M_s$. Boolean cases, case $K_a \varphi ^+$, and case $[\lnot \psi ^+] \varphi ^+$ are proved in [9, Proposition 8]. We show the remaining two cases $D_G \varphi ^+$ and $[G]\varphi ^+$.

Induction hypothesis. If $M_s \models \varphi ^+$, then $N_s \models \varphi ^+$.

Case $D_G \varphi ^+$. Let $M_s \models D_G \varphi ^+$. By the definition of semantics, this is equivalent to the fact that $\forall t \in S^M$: $s \sim _G t$ implies $M_t \models \varphi ^+$. The latter implies that $\forall t \in S^N$: $s \sim _G t$ implies $M_t \models \varphi ^+$. By the induction hypothesis, we have that $\forall t \in S^N$: $s \sim _G t$ implies $N_t \models \varphi ^+$, which is equivalent to $N_s \models D_G \varphi ^+$.

Case $[G] \varphi ^+$. Assume towards a contradiction that $M_s \models [G] \varphi ^+$ and $N_s \not \models [G] \varphi ^+$. By the duality of group announcements, this is equivalent to $N_s \models \langle G \rangle \lnot \varphi ^+$, and by the definition of semantics, the latter is equivalent to $\exists \psi _G:$ $N_s \models \langle \psi _G \rangle \lnot \varphi ^+$, which equals to $N_s \models \psi _G$ and $N_s^{\psi _G} \not \models \varphi ^+$. Now observe that $N_s^{\psi _G} \subseteq N_s \subseteq M_s$. From that and the contraposition of the induction hypothesis, it follows that $M_s \not \models \varphi ^+$. However, $M_s \models [G] \varphi ^+$ implies that $M_s \models [\top _G] \varphi ^+$. Finally, $M_s \models [\top _G] \varphi ^+$ is equivalent to $M_s \models \varphi ^+$, which contradicts $M_s \not \models \varphi ^+$.

3 Ability, Announcements, and Group Knowledge

Distributed knowledge is often described as potential individual (or even common) knowledge, that the individual members of the group can establish “through communication” or by “pooling their knowledge together”. However, this intuition is in fact not correct [4]. For example, a group can have distributed knowledge of a formula of the form $p \wedge \lnot K_a p$ (sometimes called a Moore sentence [18]), which can never become individual knowledge in a group that contains agent a [4]. Nevertheless, that doesn’t mean that there are no interaction properties between group announcements and group knowledge. Indeed, the natural intuition is that there is. In this section, we consider possible interaction axioms relating group announcements and group knowledge.

It is known that the following potential axioms are not valid [1]:

• $\langle G \rangle \varphi \rightarrow D_G \langle G \rangle \varphi$

• $D_G \langle G \rangle \varphi \rightarrow \langle G \rangle D_G \varphi$

It is also known that the following are valid:

• $\langle G \rangle D_G \varphi \rightarrow D_G \langle G \rangle \varphi$ (implied by Proposition 28 of [1] and the fact that knowledge de re implies knowledge de dicto)

• $D_G \langle G \rangle \varphi \rightarrow \langle G \rangle \varphi$ (distributed knowledge is veridical)

Consider weaker properties which involve ‘everybody knows’ operator $E_G$ where $E_G \varphi := \bigwedge _{a \in G} K_a \varphi$. These properties encapsulate the intuition that distributed knowledge can be made explicit through public communication. It is known that the following is not valid:

• $D_G \varphi \rightarrow \langle G \rangle E_G \varphi$ (take $\varphi : = p \wedge \lnot K_a p$ where $a \in G$ [4])

The other direction also does not hold:

Fact 1

$\langle G \rangle E_G \varphi \rightarrow D_G \varphi$ is not valid.

Fig. 1.

Models M and $M^{\psi _{\{a,b\}}}$

Proof

Consider Fig. 1.

Let $\varphi := K_b p \vee K_b \lnot p$ and $\psi _{\{a,b\}}:= K_a (p \rightarrow K_b p) \wedge K_b (p \vee \lnot p)$. We have that $M_s \models \langle \psi _{\{a,b\}} \rangle E_{\{a,b\}} \varphi$, which is equivalent to $M_s \models \psi _{\{a,b\}}$ and $M_s^{\psi _{\{a,b\}}} \models E_{\{a,b\}} \varphi$. On the other hand, it is easy to verify that $M_s \not \models D_{\{a,b\}} \varphi$ as the only $\sim _{\{a,b\}}$-accessible state is s itself, and $M_s \not \models \varphi$.

In general, implicit knowledge in a group cannot be made explicit via public communication. However, there is an exception. Positive formulas can be made known on bisimulation contracted models (this restriction is not surprising given analysis in [17]).

Fact 2

$D_G \varphi ^+ \rightarrow \langle G \rangle E_G \varphi ^+$ is valid on finite bisimulation contracted models.

Proof

Let $M_s \models D_G \varphi ^+$ for an arbitrary finite bisimulation contracted $M_s$. Since distributed knowledge is veridical, the latter implies $M_s \models \varphi ^+$. Now let us a consider the maximally informative announcement by agents from G. Since $M_s$ is finite and bisimulation contracted, each state in the model can be uniquely described by a characteristic formula. Moreover, disjunctions of these formulas correspond to sets of states. Agents from G can announce characteristic formulas that describe their equivalence classes and include s, i.e. for (see [3, 13] for details). In the resulting model $M_s^{\psi _G}$, relation $\sim _{G}$ on set of states $S^{\psi _G}$ is universal. Moreover, since $\varphi ^+$ is preserved under submodels, we have that $M_s^{\psi _G} \models E_G \varphi ^+$, and, consequently, $M_s \models \langle G \rangle E_G \varphi ^+$.

The restriction to finite bisimulation contracted models is essential in the previous proposition.

Fact 3

$D_G \varphi ^+ \rightarrow \langle G \rangle E_G \varphi ^+$ is not valid.

Fig. 2.

Models M

Proof

Consider the model in Fig. 2. It is easy to check that $M_s \models D_{\{a,b\}} p$ and $M_s \not \models \langle \{a,b\} \rangle E_{\{a,b\}} p$. Indeed, any announcement by a that preserves $\{s,t\}$ also preserves $\{u,v\}$. The same holds for agent b and sets $\{s,u\}$ and $\{t,v\}$.

4 Proof System for GALD

In this section, we provide a sound and complete axiomatisation for GALD. Our proofs follow general strategies of proofs from [1, 5, 22].

4.1 Axiomatisation of GALD

In order to provide the proof system, we first define necessity forms [14].

Definition 8

Necessity forms are defined by the following grammar:

$$\eta (\sharp ) :\,\!:= \sharp \mid \varphi \rightarrow \eta (\sharp ) \mid K_a \eta (\sharp ) \mid D_G \eta (\sharp ) \mid [\varphi ] \eta (\sharp )$$

where $\varphi \in \mathcal {L}_{GALD}$, and $\sharp$ has a unique occurrence in $\eta (\sharp )$. The result of substituting $\varphi$ for $\sharp$ in $\eta$ is denoted by $\eta (\varphi )$.

Definition 9

The axiomatisation of GALD is comprised of axiom systems for EL [11], PAL [10], GAL [1], and PALD [22].

We denote by GALD the smallest set that contains all instances of A0–A17 and is closed under R0–R3. Elements of GALD are called theorems.

Lemma 1

Rule R3 is truth-preserving.

Proof

The proof is by induction on the construction of $\eta$. Let $M_s$ be a pointed epistemic model. We show only the case $D_H \eta (\sharp )$, and other cases are similar.

Case $D_H \eta (\sharp )$. Let $\forall \psi _G:$ $M_s \models D_H \eta ([\psi _G] \varphi )$. By the semantics this means that $\forall \psi _G,\forall t:$ $s \sim _H t$ implies $M_t \models \eta ([\psi _G] \varphi )$. Pick any t such that $s \sim _H t$. By the induction hypothesis we have $M_t \models \eta ([G] \varphi )$. Since t was arbitrary, $\forall t:$ $s \sim _H t$ implies $M_t \models \eta ([G] \varphi )$, which is equivalent to $M_s \models D_H \eta ([G] \varphi )$.

Theorem 1

GALD is sound.

Proof

Soundness of R2 is easy to show. The rest follows from the soundness of PALD [22], GAL [1], and Lemma 1.

4.2 Completeness

Following the technique from [22, 23], we prove the completeness of GALD by making a detour through pre- and pseudo models, where distributed knowledge operators are treated as classic knowledge modalities.

Definition 10

An epistemic pre-model is a tuple $\mathcal {M} = (S, \sim , V)$, where $\sim$ maps every agent a and every subset $G \subseteq A$ to an element of $2^{2^S}$. A pre-model is called a pseudo-model (and is written $\mathfrak {M}$) if for all a it holds that $\sim _{\{a\}} = \sim _a$, and for all $G, H \subseteq A$: if $G \subseteq H$, then $\sim _H \subseteq \sim _G$.

Next, we define theories that will be used for the construction of the canonical model.

Definition 11

A set x of formulas of $\mathcal {L}_{GALD}$ is called a theory, if it contains all theorems and is closed under R0 and R3. A theory is consistent if for all $\varphi$, either $\varphi \not \in x$ or $\lnot \varphi \not \in x$. A theory is called maximal if for all $\varphi$, either $\varphi \in x$ or $\lnot \varphi \in x$.

Theories are not required to be closed under R1 and R2 since this rules of inference, unlike R0 and R3, preserve only validity and not truth.

Lemma 2

Let x be a theory, and $\varphi , \psi \in \mathcal {L}_{GALD}$. The following are theories: $x+\varphi = \{\psi \mid \varphi \rightarrow \psi \in x\}$, $K_a x = \{\varphi \mid K_a \varphi \in x\}$, $D_G x = \{\varphi \mid D_G \varphi \in x\}$, and $[\varphi ] x = \{\psi \mid [\varphi ] \psi \in x\}$.

Proof

Cases for $x+\varphi$, $K_a x$, $[\varphi ]x$ are proved in [5, Lemma 4.11]. Here we argue that $D_G x$ is a theory.

We need to show that $D_G x$ contains GALD and is closed under R0 and R3. Let $\varphi \in$ GALD. Then we also have that $D_G \varphi \in$ GALD by the necessitation of $D_G$, which is derivable in PALD [22]. Since x is a theory, and hence GALD $\subseteq x$, we have that $D_G \varphi \in x$, and $\varphi \in D_G x$. This establishes that GALD $\subseteq D_G x$.

Assume that $\varphi \rightarrow \psi , \varphi \in D_G x$. By A5 and R0 this implies that $D_G \psi \in x$, or, equivalently, $\psi \in D_G x$.

Suppose that $\forall \psi _G$: $\eta ([\psi _G] \varphi ) \in D_G x$. This means that $\forall \psi _G$: $D_G \eta ([\psi _G] \varphi ) \in x$, and from the fact that $D_G \eta (\sharp )$ is a necessity form, we conclude by R3 that $D_G \eta ([G] \varphi ) \in x$. Finally, by the definition of $D_G x$ we yield $\eta ([G] \varphi ) \in D_G x$.

Lemma 3

For all consistent theories x, $\lnot \varphi \not \in x$ if and only if $x + \varphi$ is consistent.

Lemma 4

(Theorem 2.5.2 of [14]). Every consistent theory can be extended to a maximal consistent theory.

Definition 12

The canonical pseudo model is $\mathfrak {M}^C = (S^C, \sim ^C, V^C)$, where $S^C = \{x \mid x \text { is maximal consistent theory}\}$, $x \sim _a^C y$ if and only if $K_a x \subseteq y$, $x \sim _G^C y$ if and only if $D_H x \subseteq y$ and $H \subseteq G$, and $V^C(p) = \{x \in S^C \mid p \in x\}$.

For the rest of the section, we employ the following strategy. First, we prove the truth lemma for the canonical pseudo model. Next, we unravel $\mathfrak {M}^C$ into the tree-like pre-model $\mathcal {M}^C$, which satisfies the same GALD formulas as $\mathfrak {M}^C$. After that, we fold $\mathcal {M}^C$ into the model $M^C$. Folding preserves trans-bisimulation, and hence we will be able to conclude the completeness of GALD.

Definition 13

The size and $[]$-depth of $\varphi \in \mathcal {L}_{GALD}$ are defined as follows:

$\begin{array}{ll} Size (p) = 1 &{}d_{[]} (p) = 0\\ Size (\lnot \varphi ) = Size (K_a \varphi ) = &{}d_{[]} (\lnot \varphi ) = d_{[]} (K_a \varphi ) = \\ \quad =Size (D_G \varphi ) = Size ([G] \varphi ) = &{}\quad = d_{[]} (D_G \varphi ) = d_{[]} (\varphi )\\ \quad =Size (\varphi ) + 1 &{}d_{[]} (\varphi \wedge \psi ) = \mathrm {max} \{d_{[]} (\varphi ), d_{[]} (\psi )\}\\ Size (\varphi \wedge \psi ) = \mathrm {max} \{Size (\varphi ), Size (\psi )\} + 1 &{}d_{[]} ([\psi ] \varphi ) = d_{[]} (\psi ) + d_{[]} (\varphi ) \\ Size ([\psi ] \varphi ) = Size (\psi ) + 3 \cdot Size (\varphi ) &{}d_{[]} ([G]\varphi ) = d_{[]} (\varphi ) + 1 \end{array}$

Definition 14

(Size Relation). The binary relation $<^{Size}_{[]}$ between $\varphi , \psi \in \mathcal {L}_{GALD}$ is defined as follows:

$\varphi <^{Size}_{[]} \psi$ iff $d_{[]} (\varphi ) < d_{[]} (\psi )$, or $d_{[]} (\varphi ) = d_{[]} (\psi )$ and $Size (\varphi ) < Size (\psi )$. The relation is a well-founded strict partial order between formulas. Note that for all epistemic formulas $\psi$ we have that $d_{[]} (\psi ) = 0$.

Lemma 5

Let $\varphi , \chi \in \mathcal {L}_{GALD}$.

Lemma 6

Let x be a theory. If $D_G \varphi \not \in x$, then there is a maximal consistent theory y such that $D_G x \subseteq y$ and $\varphi \not \in y$.

Proof

Assume that $D_G \varphi \not \in x$. This means that $\varphi \not \in D_G x$, and hence $D_G x + \lnot \varphi$ is a consistent theory by Lemma 3. By Lemma 4, $D_G x + \lnot \varphi$ can be extended to a maximal consistent theory y. Since $\lnot \varphi \in y$, by consistency we have that $\varphi \not \in y$.

Lemma 7

Let x be a theory. If $K_a \varphi \not \in x$, then there is a maximal consistent theory y such that $K_a x \subseteq y$ and $\varphi \not \in y$.

Proof

Similar to the proof of Lemma 6.

Lemma 8

For all formulas $\varphi$ and maximal consistent theories x it holds that $\mathfrak {M}^C_x \models \varphi$ if and only if $\varphi \in x$.

Proof

The proof is by induction on the size of $\varphi$. Boolean cases are straightforward, and cases with public announcements are dealt with using A11–A16. Here we show only cases with distributed knowledge and group announcements.

Case $D_G \varphi$. $(\Rightarrow )$: Let $\mathfrak {M}^C_x \models D_G \varphi$. By the semantics we have that for all $y \in S^C$: $x \sim _G y$ implies $\mathfrak {M}^C_y \models \varphi$. By the definition of the canonical pseudo model, Lemma 5, and the induction hypothesis, the latter is equivalent to the fact that for all $y \in S^C$ and all $H \subseteq G$: $D_H x \subseteq y$ implies $\varphi \in y$. In particular, for all $y \in S^C$: $D_G x \subseteq y$ implies $\varphi \in y$. By the contraposition of Lemma 6 this implies that $D_G \varphi \in x$.

$(\Leftarrow )$: Assume that $D_G \varphi \in x$ and $x \sim ^C_G y$ for some maximal consistent theory y. By A7 and R0 it holds that $D_G D_G \varphi \in x$. By the definition of the canonical model, we have that $D_G \varphi \in y$. Since y is a maximal consistent theory and thus contains $D_G \varphi \rightarrow \varphi$, it holds that $\varphi \in y$. Next, by the induction hypothesis we have that $\mathfrak {M}^C_y \models \varphi$. Since y was arbitrary, we have that $\mathfrak {M}^C_y \models \varphi$ for all y such that $x \sim _G^C y$. The latter is equivalent to $\mathfrak {M}^C_x \models D_G \varphi$ by the semantics.

Case $[\varphi ] D_G \psi$. $\mathfrak {M}^C_x \models [\varphi ] D_G \psi$ if and only if $\mathfrak {M}^C_x \models \varphi \rightarrow D_G [\varphi ] \psi$ by A15. By Lemma 5 and the induction hypothesis, $\mathfrak {M}^C_x \models \varphi \rightarrow D_G [\varphi ] \psi$ if and only if $\varphi \rightarrow D_G [\varphi ] \psi \in x$ if and only if $[\varphi ] D_G \psi \in x$ by A15.

Case $[\varphi ] [G] \psi$. $(\Rightarrow )$: Let $\mathfrak {M}^C_x \models [\varphi ] [G] \psi$. By the semantics, $\forall \psi _G$: $\mathfrak {M}^C_x \models [\varphi ] [\psi _G] \psi$. By Lemma 5 and the induction hypothesis, $[\varphi ] [\psi _G] \psi \in x$ for all $\psi _G$. Note that $[\varphi ](\sharp )$ is a necessity form, hence, by R3, we have that $[\varphi ] [G] \psi \in x$.

$(\Leftarrow )$: Let $[\varphi ] [G] \psi \in x$. The distributivity rule for public announcements is derivable in PAL [10, Proposition 4.46]. Hence, by A17 and R0 it holds that $[\varphi ] [\psi _G] \psi \in x$. By Lemma 5 and the induction hypothesis, $\forall \psi _G$: $\mathfrak {M}^C_x \models [\varphi ] [\psi _G] \psi$. By the semantics, $\forall \psi _G$: $\mathfrak {M}^C_x \models \varphi$ implies $(\mathfrak {M}^C_x)^\varphi \models [\psi _G] \psi$. The latter is equivalent to $\mathfrak {M}^C_x \models \varphi$ implies $(\mathfrak {M}^C_x)^\varphi \models [G] \psi$, and thus $\mathfrak {M}^C_x \models [\varphi ][G] \psi$.

Case $[G] \varphi$. $(\Rightarrow )$: Let $\mathfrak {M}^C_x \models [G] \varphi$. By the semantics, $\forall \psi _G$: $\mathfrak {M}^C_x \models [\psi _G] \varphi$. By Lemma 5 and the induction hypothesis, $\forall \psi _G$: $[\psi _G] \varphi \in x$, and by R3, $[G] \varphi \in x$.

$(\Leftarrow )$: Let $[G] \varphi \in x$. By A17, $[\psi _G] \varphi \in x$ for all $\psi _G$. By Lemma 5 and the induction hypothesis, $\forall \psi _G$: $\mathfrak {M}^C_x \models [\psi _G] \varphi$, which is equivalent to $\mathfrak {M}^C_x \models [G] \varphi$ by the semantics.

Due to the lack of space, we briefly sketch the second part of the proof. It follows closely [22] and details can be found there.

Canonical pseudo model $\mathfrak {M}^C$ can be unravelled into the treelike canonical pre-model $\mathcal {M}^C$. Such an operation preserves bisimulation. After that, the pre-model can be folded into the canonical model. Folding preserves trans-bisimulation (denoted $\leftrightarrows ^T$), which can be considered as a generalisation of standard bisimulation with a separate case for groups of agents. In such a way we can relate pre-models and models. The corresponding notion of equivalence between pre-models and models is trans-equivalence (denoted $\equiv ^T$).

Before stating the completeness, we need one more result.

Lemma 9

Given $M_s$, $\mathcal {M}_t$, and $\mathfrak {M}_u$, if $M_s \leftrightarrows ^T \mathcal {M}_t \leftrightarrows \mathfrak {M}_u$, then $M_s \equiv ^T \mathcal {M}_t$.

Proof

The proof is by induction on $\varphi$. Boolean cases, cases for knowledge and distributed knowledge, and the case for public announcements are proved in [22, Lemma 26]. We show the case of $[G]\psi$.

Assume that $M_s \models [G] \psi$. By the semantics this is equivalent to $\forall \psi _G$: $M_s \models [\psi _G] \psi$. By the induction hypothesis we have that $\forall \psi _G$: $\mathcal {M}_t \models [\psi _G] \psi$, which is equivalent to $\mathcal {M}_t \models [G] \psi$ by the semantics.

Finally, we have everything we need to prove the completeness of GALD.

Theorem 2

For all $\varphi \in \mathcal {L}_{GALD}$, if $\varphi$ is valid, then $\varphi \in$ GALD.

Proof

Suppose towards a contradiction that $\varphi$ is valid and $\varphi \not \in$ GALD. Since GALD is a consistent theory, by Lemma 3 GALD $+ \lnot \varphi$ is a consistent theory. By Lemma 4, GALD $+ \lnot \varphi$ can be extended to a maximal consistent theory x such that GALD $+ \lnot \varphi \subseteq x$, and $\lnot \varphi \in x$. By Lemma 8, the latter is equivalent to $\mathfrak {M}^C_x \not \models \varphi$. Next, the canonical pseudo model $\mathfrak {M}^C_x$ can be unravelled into bisimilar canonical pre-model $\mathcal {M}^C_y$, and the latter can be folded into the trans-bisimilar canonical model $M^C_z$. So, we have that $\mathfrak {M}^C_x \leftrightarrows \mathcal {M}^C_y$ and $\mathcal {M}^C_y \leftrightarrows ^T M_z^C$. From $\mathfrak {M}^C_x \not \models \varphi$ by bisimilarity we have $\mathcal {M}^C_y \not \models \varphi$. Finally, by Lemma 9, $\mathfrak {M}^C_x \leftrightarrows \mathcal {M}^C_y$ and $\mathcal {M}^C_y \leftrightarrows ^T M_z^C$ imply $M_z^C \equiv ^T \mathcal {M}^C_y$, and from $\mathcal {M}^C_y \not \models \varphi$ we can infer that $M_z^C \not \models \varphi$, which contradicts $\varphi$ being a validity.

5 Resolved Distributed Knowledge

Resolved distributed knowledge models private publicly observable communication within a group [4]. Distributed knowledge deals with agents’ knowledge before any communication has taken place, and resolved distributed knowledge models the situation after all agents within a group have shared their knowledge. In a way, resolved distributed knowledge is a kind of a dynamic operator in disguise. In this section, we consider the relationship between group announcements, distributed, and resolved distributed knowledge.

Definition 15

Let $M = (S, \sim , V)$ be an epistemic model. A global G-resolved update of M is the model $M^G = (S^G, \sim ^G, V^G)$, where $S^G=S$, $V^G=V$, and

$$ \sim ^G_a = {\left\{ \begin{array}{ll} \bigcap _{b \in G} \sim _b &{} \text {if }a \in G, \\ \sim _a &{} \text {otherwise.} \end{array}\right. } $$

The semantics for $R_G \varphi$ is

$$\begin{aligned} \begin{array} {lcl} M_s \models R_G \varphi&\text {iff}&M_s^G \models \varphi \end{array} \end{aligned}$$

The immediate result is that resolution and distributed knowledge are indeed different.

Fact 4

$D_{G} \varphi \rightarrow R_{G} \varphi$ and $R_{G} \varphi \rightarrow D_{G} \varphi$ are not valid.

Proof

For the first formula, consider a model $M_s$ such that $M_s \models D_{\{a,b\}} (p \wedge \lnot K_a p) \wedge K_b p$. Then obviously $M_s \not \models R_{\{a,b\}} (p \wedge \lnot K_a p)$.

And for the second formula, $R_{\{a\}} p$ does not necessarily imply $D_{\{a\}} p$. For example, there is an $M_s$ such that $M_s \models p \wedge \lnot K_a p$, and hence $M_s \models R_{\{a\}} p$ (the model remains the same and $R_G p \leftrightarrow p$) and $M_s \not \models D_{\{a\}} p$ (since $D_{a} \varphi \leftrightarrow K_a \varphi$).

An interesting thing to note is that in our counterexample to $R_G \varphi \rightarrow D_G \varphi$, the target $\varphi$ was a positive formula $K_a p$. Thus, $R_G \varphi ^+ \rightarrow D_G \varphi ^+$ is not valid as well.

Since resolved distributed knowledge models private communication, it does not coincide with group announcements.

Fact 5

$\langle G \rangle \varphi \rightarrow R_G \varphi$ and $R_G \varphi \rightarrow \langle G \rangle \varphi$ are not valid.

Proof

For the first formula, consider a two-state model $M_s$ such that $M_s \models \langle \{b\} \rangle (K_a p \wedge K_b p) \wedge \lnot K_a p$. The b-resolved update of the model, leaves the model intact. Hence, $M_s \not \models R_{\{b\}} K_a p$.

For the second formula, consider a two-state model $M_s$ such that $M_s \models R_{\{a,c\}} (K_a p \wedge \lnot K_b p) \wedge K_c p \wedge \lnot K_a p \wedge \lnot K_b p$. In such a model, no announcement by $\{a,c\}$ can both inform a that p is true, and leave b unaware of this fact. Hence, $M_s \not \models \langle \{a,c\} \rangle (K_a p \wedge \lnot K_b p)$.

Even if we require the target formula to be positive, neither resolution implies ability, nor ability implies resolution. In the previous proposition, the counterexample for $\langle G \rangle \varphi \rightarrow R_G \varphi$ used positive formula $K_a p$.

Fact 6

$R_G \varphi ^+ \rightarrow \langle G \rangle \varphi ^+$ is not valid.

Proof

Consider model M from Fig. 2. We have that $M_s \models R_{\{a,b\}} K_a p$ if and only if $M_s^{\{a,b\}} \models K_a p$, and at the same time $M_s \not \models \langle \{a,b\} \rangle K_a p$. The rest of the argument is similar to the one in the proof of Fact 3.

The surprising corollary of this proposition is that semi-private communication between all agents does not imply the possibility of equivalent public communication between all agents. Formally, $R_A \varphi \rightarrow \langle A \rangle \varphi$ is not valid even for positive $\varphi$.

The special case when private communication between all agents implies the ability of equivalent public communication is considered in the next proposition.

Fact 7

$R_A \varphi ^+ \rightarrow \langle A \rangle \varphi ^+$ is valid on finite bisimulation contracted models.

Proof

On a finite bisimulation contracted model $M_s$, resolution for all agents results in a model with the universal relation for all agents. This corresponds to the maximal informative announcement by all agents (see Fact 2).

5.1 First Step Towards the Relative Expressivity of GALR and GALD

In the future, we would like to study the language of GAL extended with resolved distributed knowledge. Let us denote such a language GALR. In this section we make a first step towards comparing it to GALD.

Definition 16

Let $L_1$ and $L_2$ be two languages. We say that $L_1$ is at least as expressive as $L_2$ ($L_2 \leqslant L_1$) if and only if for all $\varphi \in L_2$ there is an equivalent $\psi \in L_1$. If $L_1$ is not at least as expressive as $L_2$, we write $L_2 \not \leqslant L_1$.

Some results on the expressivity of logics with distributed knowledge and resolution are presented in [4]. Relative expressivity of GALR and GALD is an open question. Here we present a partial result which establishes that a fragment GALD without distributed knowledge operators within public announcements (we call such a fragment GALD$^{-}$) is not at least as expressive as GALR.

Proposition 2

GALR $\not \leqslant$ GALD$^{-}$.

Fig. 3.

Model M

Fig. 4.

Model N

Proof

Consider a GALR formula $R_{\{b,c\}} \langle \{a,b,c\} \rangle (\lnot p \wedge \widehat{K}_a (K_b p \wedge K_c p) \wedge \widehat{K}_a (\widehat{K}_b (\lnot p \wedge K_a \lnot p) \wedge (\widehat{K}_c (\lnot p \wedge K_a \lnot p)))$. Assume towards a contradiction that there is an equivalent GALD$^{-}$ formula $\psi$, and $|\psi | = n$.

Consider models M and N (Figs. 3 and 4), where p holds in white states.

These models are bisimilar, and hence they agree on formulas of GAL. Structurally, every model is almost symmetric, and the only difference are bits on the right.

For M it holds that $M_s \models R_{\{b,c\}} \langle \{a,b,c\} \rangle (\lnot p \wedge \widehat{K}_a (K_b p \wedge K_c p) \wedge \widehat{K}_a (\widehat{K}_b (\lnot p \wedge K_a \lnot p) \wedge (\widehat{K}_c (\lnot p \wedge K_a \lnot p)))$. Indeed, resolution $R_{\{b,c\}}$ has no effect on the model, and the agents can make $\lnot p \wedge \widehat{K}_a (K_b p \wedge K_c p) \wedge \widehat{K}_a (\widehat{K}_b (\lnot p \wedge K_a \lnot p) \wedge (\widehat{K}_c (\lnot p \wedge K_a \lnot p))$ true (note that intersection of agents’ relations is the identity). This formula describes the configuration depicted in Fig. 5.

On the other hand, we have that $N_t \not \models R_{\{b,c\}} \langle \{a,b,c\} \rangle (\lnot p \wedge \widehat{K}_a (K_b p \wedge K_c p) \wedge \widehat{K}_a (\widehat{K}_b (\lnot p \wedge K_a \lnot p) \wedge (\widehat{K}_c (\lnot p \wedge K_a \lnot p)))$. Update of $N_t$ with $R_{\{b,c\}}$ results in model $N^{\{b,c\}}$, which is fully symmetric and bisimilar in both directions from state t ($R_{\{b,c\}}$ removes b and c relations in the upper right part). Thus, whatever the agents announce, if they preserve the $\{b,c\}$-equivalence class (on the right in Fig. 5), then they preserve the same equivalence class on the left. Hence, the configuration depicted in Fig. 5 is unattainable.

That no GALD$^-$ formula can distinguish $M_s$ and $N_t$ can be shown using a modification of formula games for GAL [12]. For brevity, we present an intuitive explanation here. For all cases, apart from distributed knowledge, evaluation on the models coincide. The models differ only in the upper rightmost parts, and this difference can only be expressed using a formula with D due to the fact that the models are bisimilar. However, since $\psi$ has a finite length n, and the models are $2^n+1$ bisimilar (in fact, they are isomorphic up to this depth), $\psi$ cannot ‘reach’ the states with different valuations of D.

Fig. 5.

An $\{a,b,c\}$-definable submodel of M

6 Conclusions and Future Work

In this paper, we have shown that GALD has a complete and sound axiomatisation that is obtained by putting together the axiomatisations of GAL and ELD. This shows that surprisingly there are no non-trivial interaction axioms required for the proof system. However, in special cases (positive fragment, bisimulation contracted models) the operators interact more in agreement with the intuition. Same holds for the interactions between group announcements and resolved distributed knowledge.

GALD is the first step towards enriching the logics of quantified announcements with group knowledge modalities. In future work, we plan to consider GAL with common knowledge [21] and relativised common knowledge [6, 23]. Another avenue of further research is to consider coalition announcement logic (CAL) [2] with group knowledge. In CAL, as opposed to GAL, agents outside of a group make a simultaneous announcement as well, and thus they may preclude the group from reaching its epistemic goals. Finally, we would like to investigate GALR. In particular, we are interested in its axiomatisation and expressivity relative to GALD.