Proton Transfer in Biomolecules

Abstract

Intra-protein proton transfer is perhaps the most fundamental flux in the biosphere. It is essential for such important processes as photosynthesis, respiration and ATP synthesis. Within a protein, protons appear only in covalently bound states. Here proton transfer is essentially the motion along a hydrogen bond, for instance peptide or DNA H-bonds or the more complicated pathways in proton-pumping proteins. The energy barrier for this reaction depends strongly on the conformation of the reaction complex, concerning as well its geometry as its protonation state. Due to the small mass of the proton the description of the proton transfer process has to be discussed on the basis of quantum mechanics. This chapter begins with a discussion of the photocycle of the proton pump bacteriorhodopsin. We introduce the double Born-Oppenheimer separation for the different time scales of electrons, protons and the heavier nuclei and discuss nonadiabatic proton transfer in analogy to Marcus’ electron transfer theory. We present the model by Borgis and Hynes which includes non-Condon effects. Finally, we comment on adiabatic proton transfer.

Intra-protein proton transfer is perhaps the most fundamental flux in the biosphere [153]. It is essential for such important processes as photosynthesis, respiration, and ATP synthesis [154]. Within a protein, protons appear only in covalently bound states. Here proton transfer is essentially the motion along a hydrogen bond, for instance, peptide or DNA H-bonds (Fig. 27.1) or the more complicated pathways in proton-pumping proteins.

Fig. 27.1

Proton transfer in peptide H-bonds (a) and in DNA H-bonds (b)

The energy barrier for this reaction depends strongly on the conformation of the reaction complex, concerning as well its geometry as its protonation state. Due to the small mass of the proton, the description of the proton transfer process has to be discussed on the basis of quantum mechanics. This chapter begins with a discussion of the photocycle of the proton pump bacteriorhodopsin. We introduce the double Born–Oppenheimer separation for the different time scales of electrons, protons, and the heavier nuclei and discuss nonadiabatic proton transfer in analogy to Marcus’ electron transfer theory. We present the model by Borgis and Hynes which includes non-Condon effects. Finally, we comment on adiabatic proton transfer.

1 The Proton Pump Bacteriorhodopsin

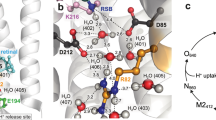
Rhodopsin proteins collect the photon energy in the process of vision. Since the end of the 1950s, it has been recognized that the photoreceptor molecule retinal undergoes a structural change, the so-called cis-trans isomerization (Fig. 27.4) upon photo-excitation (G. Wald, R. Granit, H.K. Hartline, Nobel prize for medicine 1961). Rhodopsin is not photostable and its spectroscopy remains difficult. Therefore, much more experimental work has been done on its bacterial analogue bacteriorhodopsin [155], which performs a closed photocycle (Figs. 27.2 and 27.3).

Fig. 27.2

X-ray structure of bR. The most important residues and structural waters are shown, together with possible pathways for proton transfer. Coordinates are from the structure 1kzu [133–137] in the protein data bank [138, 139]. Molekel graphics [65]

Fig. 27.3

The photocycle of bacteriorhodopsin [156]. Different states are labeled by the corresponding absorption maximum (nm)

Fig. 27.4

Photoisomerization of bR

Bacteriorhodopsin is the simplest known natural photosynthetic system. Retinal is covalently bound to a lysine residue forming the so-called protonated Schiff base. This form of the protein absorbs sun light very efficiently over a large spectral range (480–360 nm).

After photoinduced isomerization a proton is transferred from the Schiff base to the negatively charged ASP85 ($L\rightarrow M)$. This induces a large blue shift. In wild type bR, under physiological conditions, a proton is released into the extracellular medium on the same timescale of $10\,\upmu$s. The proton release group is believed to consist of GLU194, GLU204, and some structural waters. During the M state, a large rearrangement on the cytoplasmatic side appears, which is not seen spectroscopically and which induces the possibility to reprotonate the Schiff base from ASP96 subsequently ($M\rightarrow N)$. ASP96 is then reprotonated from the cytoplasmatic side and the retinal reisomerizes thermally to the all trans configuration $(N\rightarrow O)$. Finally, a proton is transferred from ASP85 via ARG82 to the release group and the ground state BR is recovered.

2 Born–Oppenheimer Separation

Protons move on a faster time scale than the heavy nuclei but are slower than the electrons. Therefore, we use a double BO approximation for the wavefunction¹

$$\begin{aligned} \psi (r,R_{P},Q)\chi (R_{p}, Q)\varPhi (Q). \end{aligned}$$

(27.1)

The protonic wavefunction $\chi$ depends parametrically on the coordinates Q of the heavy atoms and the electronic wavefunction $\psi$ depends parametrically on all nuclear coordinates. The Hamiltonian consists of the kinetic energy contributions and a potential energy term

$$\begin{aligned} H=T_{el}+T_{p}+T_{N}+V. \end{aligned}$$

(27.2)

The Born–Oppenheimer approximation leads to the following hierarchy of equations. First all nuclear coordinates ($R_{p}, Q)$ are fixed and the electronic wavefunction of the state s is obtained from

$$\begin{aligned} (T_{el}+V(r,R_{p},Q))\psi _{s}(r,R_{p},Q)=E_{el,s}(R_{p},Q)\psi _{s}(r,R_{p}, Q). \end{aligned}$$

(27.3)

In the second step, only the heavy atoms (Q) are fixed but the action of the kinetic energy of the proton on the electronic wavefunction is neglected. Then the wavefunction of proton state n obeys

$$\begin{aligned} (T_{p}+E_{el,s}(R_{p},Q))\chi _{s,n}(R_{p},Q)=\varepsilon _{s,n}(Q)\chi _{s,n}(R_{p}, Q). \end{aligned}$$

(27.4)

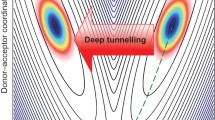
The electronic energy $E_{el}(R_{p}, Q)$ plays the role of a potential energy surface for the nuclear motion. It is shown schematically in Fig. 27.5 for one proton coordinate (for instance the O-H bond length) and one promoting mode of the heavy atoms which modulates the energy gap between the two minima.

Fig. 27.5

Proton transfer potential. The figure shows schematically the potential which, as a function of the proton coordinate x, has two local minima corresponding to the structures$\cdots N-H\cdots O\cdots$ and $\cdots N\cdots H-O\cdots$ and which is modulated by a coordinate y representing the heavy atoms

For fixed positions Q of the heavy nuclei $E_{el}(R_{p}, Q)$ has a double well structure as shown in Fig. 27.6. The rate of proton tunneling depends on the configuration and is most efficient if the two localized states are in resonance.

Fig. 27.6

Proton tunneling. The double well of the proton along the H-bond is shown schematically for different configurations of the reaction complex

Finally, the wavefunction of the heavy nuclei in state $\alpha$ is the approximate solution of

$$\begin{aligned} (T_{N}+\varepsilon _{s,n}(Q))\varPhi _{s,n,\alpha }(Q)=E_{s,n,\alpha }\varPhi _{s, n,\alpha }(Q). \end{aligned}$$

(27.5)

3 Nonadiabatic Proton Transfer (Small Coupling)

Initial and final states (s, n) and $(s', m)$ are stabilized by the reorganization of the heavy nuclei. The transfer occurs whenever fluctuations bring the two states in resonance.

Fig. 27.7

Harmonic model for proton transfer

We use the harmonic approximation (Fig. 27.7)

$$\begin{aligned} \varepsilon _{s,n}(Q)=\varepsilon _{s, n}^{(0)}+\frac{a}{2}(Q-Q_{s}^{(0)})^{2}+\cdots =\varepsilon _{s, 0}(Q)+(\varepsilon _{s,n}-\varepsilon _{s, 0}) \end{aligned}$$

(27.6)

similar to nonadiabatic electron transfer theory (Chap. 16). The activation free energy for the $(s, 0)\rightarrow (s', 0)$ transition is given by

$$\begin{aligned} \varDelta G_{00}^{\ddagger }=\frac{(\varDelta G_{0}+E_{R})^{2}}{4E_{R}} \end{aligned}$$

(27.7)

and for the transition $(s,n)\rightarrow (s', m)$ we have approximately

$$\begin{aligned}&\varDelta G_{nm}^{\ddagger }=\varDelta G_{0}^{\ddagger }+(\varepsilon _{sm}-\varepsilon _{s0})-(\varepsilon _{s'n}-\varepsilon _{s'0}) \nonumber \\&=\frac{(\varDelta G_{0}+E_{R}+\varepsilon _{sm}-\varepsilon _{s'n}-\varepsilon _{s0}+\varepsilon _{s'0})^{2}}{4E_{R}}. \end{aligned}$$

(27.8)

The partial rate $k_{nm}$ is given in analogy to the ET rate (16.23) as

$$\begin{aligned} k_{nm}=\frac{\omega }{2\pi }\kappa _{nm}^{P}\exp \left\{ -\frac{\varDelta G_{nm}^{\ddagger }}{kT}\right\} . \end{aligned}$$

(27.9)

The interaction matrix element will be calculated using the BO approximation and treating the heavy nuclei classically

$$\begin{aligned}&V_{sns'm}=\int dr\, dR_{p}\,\psi _{s}(r,R_{P},Q)\chi _{sn}(R_{p},Q)\quad V\quad \chi _{s'm}(R_{p},Q)\psi _{s'}(r,R_{P},Q) \\&=\int dR_{p}\,\left( \int dr\,\psi _{s}(r,R_{P},Q)V\psi _{s'}(r,R_{P},Q)\right) \chi _{sn}(R_{p},Q)\chi _{s'm}(R_{p},Q) \\&=\int dR_{p}V_{ss'}^{el}(R_{p},Q)\,\chi _{sn}(R_{p},Q)\chi _{s'm}(R_{p}, Q). \end{aligned}$$

The electronic matrix element

$$\begin{aligned} V_{ss'}^{el}=\int \psi _{s}(r,R_{p},Q)V\psi _{s'}(r,R_{p}, Q)dr \end{aligned}$$

(27.10)

is expanded around the equilibrium position of the proton $R_{p}^{*}$

$$\begin{aligned} V_{ss'}^{el}(R_{p},Q)\approx V_{ss'}^{el}(R_{P}^{*}, Q)+\cdots \end{aligned}$$

(27.11)

and we have approximately

$$\begin{aligned} V_{sns'm}\approx V_{ss'}^{el}(R_{P}^{*}, Q)S_{ss'}^{nm}(Q) \end{aligned}$$

(27.12)

with the overlap integral of the protonic wavefunctions (Franck–Condon factor)

$$\begin{aligned} S_{ss'}^{nm}(Q)=\int \chi _{sn}\chi _{s'm}dR_{p}. \end{aligned}$$

(27.13)

4 Strongly Bound Protons

The frequencies of O-H or N-H bond vibrations are typically in the range of $3000\,\mathrm{cm}^{-1}$ which is much larger, than thermal energy. If on the other hand, the barrier for proton transfer is on the same order, only the transition between the vibrational ground states is involved. For small electronic matrix element $V^{el}$, the situation is very similar to electron transfer described by Marcus theory (Chap. 16) and the reaction rate is given by [157] for symmetrical proton transfer ($E_{R}\gg \varDelta G_{0},\varDelta G_{00}^{\ddagger }=E_{R}/4)$

$$\begin{aligned} k=\frac{2\pi V_{0}^{2}}{\hbar }\sqrt{\frac{1}{4\pi kTE_{R}}}\exp \left( -\frac{E_{R}}{4kT}\right) . \end{aligned}$$

(27.14)

In the derivation of (27.14), the Condon approximation has been used which corresponds to application of (27.11) and approximation of the overlap integral (27.13) by a constant value. However, for certain modes (which influence the distance of the two potential minima), the modulation of the coupling matrix element can be much stronger than in the case of electron transfer processes due to the larger mass of the proton. The dependence on the transfer distance $\delta Q=Q_{s'}^{(0)}-Q_{s}^{(0)}$ is approximately exponential

$$\begin{aligned} V_{s0s'0}\sim \mathrm{e}^{-\alpha \delta Q} \end{aligned}$$

(27.15)

where typically $\alpha \approx 25\cdots 35A^{-1}$ whereas for electron transfer processes typical values are around $\alpha \approx 0.5\cdots 1A^{-1}$. Borgis and Hynes [157] found the following result for the rate when the low-frequency substrate mode with frequency $\varOmega$ and reduced mass M is thermally excited

$$\begin{aligned} k=\frac{2\pi <V^{2}>}{\hbar }\sqrt{\frac{1}{4\pi kT4\varDelta G_{tot}}}\exp \left( -\frac{\varDelta G_{tot}}{kT}\right) \chi _{SC} \end{aligned}$$

(27.16)

where the average coupling square can be expanded as

$$\begin{aligned} <V^{2}>=V_{0}^{2}\exp \left( \frac{\hbar \alpha ^{2}}{2M\varOmega }\left\{ \frac{4kT}{\hbar \varOmega }+\frac{\hbar \varOmega }{3kT}+O\left( \left( \frac{\hbar \varOmega }{kT}\right) ^{2}\right) \right\} \right) \end{aligned}$$

(27.17)

the activation energy is

$$\begin{aligned} \varDelta G_{tot}=\varDelta G^{\ddagger }+\frac{\hbar ^{2}\alpha ^{2}}{8M} \end{aligned}$$

(27.18)

and the additional factor $\chi _{SC}$ is given by

$$\begin{aligned} \chi _{SC}=\exp \left( \gamma _{SC}\left( 1-\frac{\gamma _{SC}kT}{4\varDelta G_{tot}}\right) \right) \end{aligned}$$

(27.19)

$$\begin{aligned} \gamma _{SC}=\frac{\alpha <D>}{M\varOmega ^{2}} \end{aligned}$$

(27.20)

where

$$\begin{aligned} D=\frac{\partial \varDelta H}{\partial Q}(Q_{0}) \end{aligned}$$

(27.21)

measures the modulation of the energy difference by the promoting mode $\varOmega$.

5 Adiabatic Proton Transfer

If $V^{el}$ is large and the tunnel factor approaches unity (for s=s’), then the application of the low friction result (8.28) gives

$$ k_{nm}=\frac{\omega }{2\pi }\exp \left\{ -\frac{\varDelta G_{nm}^{\ddagger \, ad}}{kT}\right\} $$

where the activation energy has to be corrected by the tunnel splitting

$$ \varDelta G_{nm}^{\ddagger \, ad}=\varDelta G_{nm}^{\ddagger }-\frac{1}{2}\varDelta \varepsilon _{nm}^{p} $$