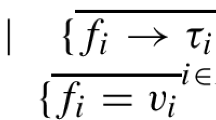APLicative Programming with Naperian Functors

Abstract

Much of the expressive power of array-oriented languages such as Iverson’s APL and J comes from their implicit lifting of scalar operations to act on higher-ranked data, for example to add a value to each element of a vector, or to add two compatible matrices pointwise. It is considered a shape error to attempt to combine arguments of incompatible shape, such as a 3-vector with a 4-vector. APL and J are dynamically typed, so such shape errors are caught only at run-time. Recent work by Slepak et al. develops a custom type system for an array-oriented language, statically ruling out such errors. We show here that such a custom language design is unnecessary: the requisite compatibility checks can already be captured in modern expressive type systems, as found for example in Haskell; moreover, generative type-driven programming can exploit that static type information constructively to automatically induce the appropriate liftings. We show also that the structure of multi-dimensional data is inherently a matter of Naperian applicative functors—lax monoidal functors, with strength, commutative up to isomorphism under composition—that also support traversal.

1 Introduction

Array-oriented programming languages such as APL [21] and J [23] pay special attention, not surprisingly, to manipulating array structures. These encompass not just rank-one vectors (sequences of values), but also rank-two matrices (which can be seen as rectangular sequences of sequences), rank-three cuboids (sequences of sequences of sequences), rank-zero scalars, and so on.

One appealing consequence of this unification is the prospect of rank polymorphism [34]—that a scalar function may be automatically lifted to act element-by-element on a higher-ranked array, a scalar binary operator to act pointwise on pairs of arrays, and so on. For example, numeric function $square$ acts not only on scalars:

but also pointwise on vectors:

and on matrices and cuboids:

Similarly, binary operators act not only on scalars, but also on vectors:

and on matrices:

The same lifting can be applied to operations that do not simply act pointwise. For example, the $sum$ and prefix $sums$ functions on vectors can also be applied to matrices:

In the right-hand examples above, $sum$ and $sums$ have been lifted to act on the rows of the matrix. J also provides a reranking operator , which will make them act instead on the columns—essentially a matter of matrix transposition:

Furthermore, the arguments of binary operators need not have the same rank; the lower-ranked argument is implicitly lifted to align with the higher-ranked one. For example, one can add a scalar and a vector:

or a vector and a matrix:

1.1 Static Types for Multi-dimensional Arrays

In recent work [34], Slepak et al. present static and dynamic semantics for a typed core language Remora. Their semantics clarifies the axes of variability illustrated above; in particular, it makes explicit the implicit control structures and data manipulations required for lifting operators to higher-ranked arguments and aligning arguments of different ranks. Moreover, Remora’s type system makes it a static error if the shapes in a given dimension do not match—for example, when attempting to add a 2-vector to a 3-vector, or a $\mathrm {2}\mathord {\times }\mathrm {2}$-matrix to a $\mathrm {2}\mathord {\times }\mathrm {3}$-matrix. (Incidentally, we adopt Slepak et al.’s terminology: the shape of a multi-dimensional array is a sequence of numbers, specifying the extent in each dimension; the rank of the array is the length of that list, and hence the number of dimensions; and the size of the array is the product of that list, and hence the number of elements.)

Slepak et al. model the type and evaluation rules of Remora in PLT Redex [11], and use this model to prove important properties such as type safety. PLT Redex provides complete freedom to model whatever semantics the language designer chooses; but the quid pro quo for this freedom is that it does not directly lead to a full language implementation—with type inference, a compiler, libraries, efficient code generation, and so on. They write that “our hope [for future work] is that we can exploit this type information to compile programs written in the rank-polymorphic array computation model efficiently” and that “Remora is not intended as a language comfortable for human programmers to write array computations. It is, rather, an explicitly typed, ‘essential’ core language on which such a language could be based” [34, p. 29]. Moreover, “the transition from a core semantics modeled in PLT Redex to a complete programming system requires a more flexible surface language and a compiler [...] the added code is mostly type and index applications. Type inference would be necessary in order to make a surface language based on Remora practical” [34, p. 45].

1.2 Embedding Static Typing

This is the usual trade-off between standalone and embedded domain-specific languages. If the type rules of Remora had been embedded instead in a sufficiently expressive typed host language, then the surrounding ecosystem of that host language—type inference, the compiler, libraries, code generation—could be leveraged immediately to provide a practical programming vehicle. The challenge then becomes to find the right host language, and to work out how best to represent the rules of the DSL within the features available in that host language. Sometimes the representation comes entirely naturally; sometimes it takes some degree of encoding.

In this paper, we explore the embedded-DSL approach to capturing the type constraints and implicit lifting and alignment manipulations of rank-polymorphic array computation. We show how to capture these neatly in Haskell, a pure and strongly-typed functional programming language with growing abilities to express and exploit dependent types. To be more precise, we make use of a number of recent extensions to standard Haskell, which are supported in the primary implementation GHC [13]. We do not assume familiarity with fancy Haskell features, but explain them as we go along.

The point is not particularly to promote such fancy features; although the expressive power of modern type systems is quite impressive. Nor is the point to explain to aficionados of dependent types in Haskell how to perform rank-polymorphic array computation; most of our constructions are already folklore. Rather, the point is to demonstrate to a wider programming language audience that it is often not necessary to invent a new special-purpose language in order to capture a sophisticated feature: we have sufficiently expressive general-purpose languages already.

1.3 The Main Idea

The main idea is that a rank-n array is essentially a data structure of type $D_1(D_2(\ldots (D_n\,a)))$, where each $D_i$ is a dimension: a container type, categorically a functor; one might think in the first instance of lists. However, in order to be able to transpose arrays without losing information, each dimension should be represented by a functor of fixed shape; so perhaps vectors, of a fixed length in each dimension, but allowing different lengths in different dimensions.

The vector structure is sufficient to support all the necessary operations discussed above: mapping (for pointwise operations), zipping (for lifting binary operations), replicating (for alignment), transposing (for reranking), folding (for example, for $sum$), and traversing (for $sums$). Moreover, these can also be handled crisply, with static types that both prevent incoherent combinations and explain the implicit lifting required for compatible ones. However, although sufficient, the vector structure is not necessary, and other functors (such as pairs, triples, block vectors, and even perfect binary trees) suffice; we show that the necessary structure is that of a traversable, Naperian, applicative functor (and we explain what that means). The richer type structure that this makes available allows us to go beyond Remora, and in particular to explain the relationship between nested and flat representations of multi-dimensional data, leading the way towards higher-performance implementations of bulk operations, for example on multicore chips [24] and on GPUs [5].

Specifically, our novel contributions are as follows:

• formalizing the lifting required for rank polymorphism;

• doing so within an existing type system, rather than creating a new one;

• identifying necessary and sufficient structure for dimensions;

• implementing it all (in Haskell), and providing executable code;

• showing how to connect to flat and sparse representations.

Although our definitions are asymptotically efficient, or can easily be made so using standard techniques such as accumulating parameters, we do not make performance claims in comparison with serious array libraries such as Repa and Accelerate [5, 24]. Rather, we see this work as providing a flexible but safe front-end, delegating performance-critical computations to such libraries.

1.4 Structure of This Paper

The remainder of this paper is structured as follows. Section 2 uses type-level natural numbers for bounds checking of vectors; Sect. 3 explains the requirements on vectors to support maps, zips, and transposition; and Sect. 4 similarly for reductions and scans; these are all fairly standard material, and together show how to generalize the dimensions of an array from concrete vectors to other suitable types. Our contribution starts in Sect. 5, where we show how to accommodate arrays of arbitrary rank. Section 6 shows how to automatically lift unary and binary operators to higher ranks. Section 7 shows how to avoid manifesting replication and transposition operations by representing them symbolically instead, and Sect. 8 shows a more efficient representation using flat built-in arrays, while still preserving the shape information in the type. Section 9 concludes.

This paper is a literate Haskell script, and the code in it is all type-checked and executable, albeit with tidier formatting in the PDF for publication purposes. The extracted code is available for experimentation [14]. We exploit a number of advanced type features, explained as we proceed; but we make no use of laziness or undefinedness, treating Haskell as a total programming language.

2 Vectors with Bounds Checking

Our approach makes essential use of lightweight dependent typing, which is now becoming standard practice in modern functional programming languages such as Haskell. We introduce these ideas gradually, starting with traditional algebraic datatypes, such as lists:

This declaration defines a new datatype constructor $List$ of kind $\mathbin {*}\rightarrow \mathbin {*}$. Which is to say, kind $\mathbin {*}$ includes all those types with actual values, such as $Int$ and $List \; Int$ and $Int \rightarrow Int$; and $List$ is an operation on types, such that for any type $A$ of kind $\mathbin {*}$, there is another type $List \; A$ (also of kind $\mathbin {*}$) of lists whose elements are drawn from $A$. The declaration also introduces two constructors $Nil$ and $Cons$ of the declared types for the new datatype, polymorphic in the element type.

All lists with elements of a given type have the same type; for example, there is one type $List \; Int$ of lists of integers. This is convenient for operations that combine lists of different lengths; but it does not allow us to guarantee bounds safety by type checking. For example, the tail function

and the list indexing operator

are partial functions, and there is no way statically to distinguish their safe from their unsafe uses through the types. The way to achieve that end is to partition the type $List \; A$ into chunks, so that each chunk contains only the lists of a given length, and to index these chunks by their common lengths. The index should be another type parameter, just like the element type is; so we need a type-level way of representing natural numbers. One recent Haskell extension [39] has made this very convenient, by implicitly promoting all suitable datatype constructors from the value to the type level, and the datatypes themselves from the type level to the kind level. For example, from the familiar datatype of Peano naturals

we get not only a new type $Nat$ with value inhabitants $Z , S \; Z ,\mathbin {...}$, but in addition a new kind, also called $Nat$, with type inhabitants $\mathord {'\! Z },\mathord {'\! S }\;\mathord {'\! Z },\mathbin {...}$. In Haskell, the inhabitants can be distinguished by the initial quote character (which is in fact almost always optional, but for clarity we will make explicit use of it throughout this paper). For convenience, we define synonyms for some small numbers at the type level:

We can now define a datatype of length-indexed vectors:

The length is encoded in the type: $VNil$ yields a vector of length zero, and $VCons$ prefixes an element onto an $n$-vector to yield an $( n \mathbin {+}\mathrm {1})$-vector. For example, $Vector \; Three \; Int$ is the type of 3-vectors of integers, one of whose inhabitants is the vector $\langle \mathrm {1},\mathrm {2},\mathrm {3}\rangle$:

The first type parameter of $Vector$ is called a ‘phantom type’ [19] or ‘type index’ [38], because it is not related to the type of any elements: a value of type $Vector \; Three \; Int$ has elements of type $Int$, but does not in any sense ‘have elements of type $Three$’. The type index does not interfere with ordinary recursive definitions, such as the mapping operation that applies a given function to every element, witnessing to $Vector \; n$ being a functor:

For example,

More interestingly, we can now capture the fact that the ‘tail’ function should be applied only to non-empty vectors, and that it yields a result one element shorter than its argument:

Similarly, we can write a ‘zip’ function that combines two vectors element-by-element using a binary operator, and use the additional type information to restrict it to take vectors of a common length $n$ and to produce a result of the same length:

Because of the type constraints, the patterns on the left-hand side in both examples are exhaustive: it would be ill-typed to take the tail of an empty vector, or to zip two vectors of different lengths.

The functions $vtail$ and $vzipWith$ consume vectors; the length indices constrain the behaviour, but they are not needed at run-time because the value constructors provide sufficient information to drive the computation. The situation is different when producing vectors from scratch. Consider a function $vreplicate$ to construct a vector of a certain length by replicating a given value. The type $a \rightarrow Vector \; n \; a$ uniquely determines the implementation of such a function; however, it is the type of the result that contains the length information, and that isn’t available for use at run-time. Nevertheless, for each $n$, there is an obvious implementation of $vreplicate$ on $Vector \; n$; it would be nice to be able to state that obvious fact formally. In Haskell, this sort of ‘type-driven code inference’ is modelled by type classes—it is the same mechanism that determines the appropriate definition of equality or printing for a given type. Similarly, there is an obvious implementation of $vlength \mathbin {::} Vector \; n \; a \rightarrow Int$, which in fact does not even need to inspect its vector argument—the length is statically determined. We introduce the class $Count$ of those types $n$ (of kind $Nat$) that support these two ‘obvious implementations’:

Indeed, every type $n$ of kind $Nat$ is in the class $Count$, as we demonstrate by providing those two obvious implementations at each type $n$:

(One might see class $Count$ as representing ‘natural numbers specifically for vector purposes’; it is possible with some pain to represent ‘natural numbers’ in Haskell more generally [25].)

The operations $vmap$, $vzipWith$, and $vreplicate$ are the essential ingredients for lifting and aligning operations to higher-ranked arguments (albeit not yet sufficient for the other operations). For example, to lift $square$ to act on vectors, we can use $vmap \; square$; to lift $(\mathbin {+})$ to act on two vectors of the same length, we can use $vzipWith \;(\mathbin {+})$; and to align a scalar with a vector, we can use $vreplicate$:

(Note that the types of $vzipWith$ and its second argument $v123$ together determine which instance of $vreplicate$ is required; so no explicit type annotation is needed.) But in order fully to achieve rank polymorphism, we want operators such as squaring and addition to implicitly determine the appropriate lifting and alignment, rather than having explicitly to specify the appropriate amount of replication. We see next how that can be done, without sacrificing static typing and type safety.

3 Applicative and Naperian Functors

We have seen that vectors show promise for representing the dimensions of an array, because they support at least three of the essential operations, namely mapping, zipping, and replicating. But vectors are not the only datatype to support such operations; if we can identify the actual requirements on dimensions, then there are other types that would serve just as well. In particular, one of the dimensions of an array might be ‘pairs’:

since these too support the three operations discussed above:

Generalizing in this way would allow us to handle vectors of pairs, pairs of triples, and so on.

The first requirement for a type constructor $f$ to be suitable as a dimension is to be a container type, that is, an instance of the type class $Functor$ and so providing an $fmap$ operator:

The other two operators arise from $f$ being a fortiori an applicative functor [26]:

Informally, $pure$ should yield an $f$-structure of copies of its argument; this serves as the ‘replicate’ operation:

(Here, the context “$Applicative \; f \Rightarrow$” denotes that $areplicate$ has type $a \rightarrow f \; a$ for any $f$ in type class $Applicative$; in contrast, the type variable $a$ is unconstrained.) The method should combine an $f$-structure of functions with an $f$-structure of arguments to yield an $f$-structure of results. The two methods together give rise to the ‘zip’ operation:

Vectors, of course, are applicative functors:

Note that we make the assumption that the length index type $n$ is in type class $Count$, so that we can infer the appropriate definition of $vreplicate$. This assumption is benign, because the length indices are of kind $Nat$, and we have provided a $Count$ instance for every type of that kind.

Pairs too are applicative functors:

However, being an applicative functor is not sufficient for serving as a dimension: that interface is not expressive enough to define transposition, which is needed in order to implement reranking. For that, we need to be able to commute the functors that represent dimensions: that is, to transform an $f \;( g \; a )$ into a $g \;( f \; a )$. The necessary additional structure is given by what Hancock [17] calls a Naperian functor, also known as a representable functor; that is, a container of fixed shape. Functor $f$ is Naperian if there is a type $p$ of ‘positions’ such that $f \; a \simeq p \rightarrow a$; then $p$ behaves a little like a logarithm of $f$—in particular, if $f$ and $g$ are both Naperian, then $Log \;( f \mathbin {\times } g )\simeq Log \; f \mathbin {+} Log \; g$ and .

Informally, $Log \; f$ is the type of positions for $f$; $lookup \; xs \; i$ looks up the element of $xs$ at position $i$; $tabulate \; h$ yields an $f$-structure where for each position $i$ the element at that position is $h \; i$; and $positions$ yields an $f$-structure where the element at each position $i$ is $i$ itself. The first two operations should be each other’s inverses; they are witnesses to the isomorphism between $f \; a$ and $Log \; f \rightarrow a$. The latter two operations are interdefinable, so an instance need only provide one of them; it is often convenient to implement $positions$, but to use $tabulate$. For simplicity, we rule out empty data structures, insisting that the type $Log \; f$ should always be inhabited. Naperian functors are necessarily applicative too:

Transposition in general consumes an $f$-structure of $g$-structures in which all the $g$-structures have the same shape, and produces a $g$-structure of $f$-structures in which all the $f$-structures have the same shape, namely the outer shape of the input. For general functors $f$ and $g$, this is a partial function, or at best a lossy one. However, the essential point about Naperian functors is that all inhabitants of a datatype have a common shape. In particular, in an $f$-structure of $g$-structures where both $f$ and $g$ are Naperian, all the inner $g$-structures necessarily have the same (namely, the only possible) shape. Then transposition is total and invertible:

Here, $flip \mathbin {::}( a \rightarrow b \rightarrow c )\rightarrow ( b \rightarrow a \rightarrow c )$ is a standard function that swaps the argument order of a binary function. We use the $lookup$ function for the outer and the inner structures of the input of type $f \;( g \; a )$, yielding a binary function of type $Log \; f \rightarrow Log \; g \rightarrow a$; we flip the arguments of this function, yielding one of type $Log \; g \rightarrow Log \; f \rightarrow a$; then we tabulate both structures again, yielding the result of type $g \;( f \; a )$ as required. For example, we have

As a consequence, composition of Naperian functors is commutative, up to isomorphism; we will insist on our dimensions being at least Naperian functors.

Of course, pairs are Naperian, with two positions—the usual ordering on booleans in Haskell has $False \le True$, so we use this ordering on the positions too:

And vectors are Naperian. An $n$-vector has $n$ positions, so to represent the logarithm we need a type with precisely $n$ inhabitants—the bounded naturals:

Thus, $Fin \; n$ has $n$ inhabitants $FZ , FS \; FZ ,\mathbin {...}, FS ^{ n \mathbin {-}\mathrm {1}}\; FZ$. Extracting an element from a vector is defined by structural induction simultaneously over the vector and the position—like with zipping, the type constraints make bounds violations a type error:

A vector of positions is obtained by what in APL is called the ‘iota’ function. As with replication, we need to provide the length as a run-time argument; but we can represent this argument as a vector of units, and then infer the appropriate value from the type:

With these three components, we are justified in calling vectors Naperian:

4 Folding and Traversing

Another requirement on the dimensions of an array is to be able to reduce along one of them; for example, to sum. In recent versions of Haskell, that requirement is captured in the $Foldable$ type class, the essence of which is as follows:

Informally, $foldr$ aggregates the elements of a collection one by one, from right to left, using the binary operator and initial value provided. Vectors are foldable in the same way that lists are:

and pairs are foldable by combining their two elements:

A foldable functor imposes a left-to-right ordering on its positions; so we can extract the elements as a list, in that order:

Similarly, we can sum those elements, provided that they are of a numeric type:

An additional requirement for array dimensions is to be able to transform values along a dimension, for example to compute prefix sums. This is captured by the $Traversable$ type class:

One way of thinking of $traverse$ is as an effectful ‘map’ function [3], visiting each element in order, precisely once each, and collecting effects in some applicative functor $f$. For example, stateful computations can be modelled by state-transforming functions:

(This construction declares $State \; s \; a$ to be a record type, with a data constructor also called $State$, and a single field called $runState$; in this way, the function $runState$ extracts the state-transformer from the record.) This datatype forms an applicative functor, in a standard way. Here is a little function to increase and return a numeric state—whatever the current state $n$, when applied to $m$, this yields the final state $m \mathbin {+} n$, and returns as result the same value $m \mathbin {+} n$:

Using this, one can compute prefix sums by traversing a data structure, starting with an initial state of $\mathrm {0}$, increasing the state by each element in turn, preserving the running totals and discarding the final state:

so in particular

Vectors and pairs are both traversable, with instances following a common pattern:

We take these various constraints as our definition of ‘dimension’:

We have added a $size$ method for convenience and with no loss of generality—it is in fact statically determined, so may admit better type-specific definitions:

But other less obvious datatypes, such as perfect binary trees of a given height, are suitable dimensions too:

For example, a $Perfect \; Three \; a$ is essentially a $Pair \;( Pair \;( Pair \; a ))$. Perhaps more usefully, rather than indexing vectors by a unary representation of the natural numbers, we can use a more compact binary representation:

under the obvious interpretation

Then we can define a datatype of (non-empty) vectors built up via balanced join rather than imbalanced cons:

When used as the dimensions of a matrix, this will allow a quad tree decomposition [12] for recursive functions. We leave the instance definitions as an exercise for the energetic reader.

In fact, one may start from any numeric representation and manufacture a corresponding datatype [18, 29]. Sandberg Eriksson and Jansson [31] use a redundant binary representation of the positive natural numbers (with constructors 1 and $+$) as the type index in a formalization of block matrices. Each of these dimension types—pairs, triples, perfect binary trees of a given height, block vectors of a given structure—is equivalent to some vector type, so no additional expressivity is gained; but the alternatives may be more natural in given contexts.

As an example of a generic function, inner product involves summing pairwise products, and so works for any dimension type:

Multiplying an $f \mathord {\times } g$-matrix by a $g \mathord {\times } h$-matrix entails lifting both to $f \mathord {\times } h \mathord {\times } g$-matrices then performing pairwise inner product on the $g$-vectors:

Again, this works for any dimension types $f , g , h$; the same definition works for vectors, pairs, block vectors, and any mixture of these.

5 Multidimensionality

Now that we can represent vectors with elements of an arbitrary type, we can of course represent matrices too, as vectors of vectors:

However, with this representation, integer vectors and integer matrices are of quite different types, and there is no immediate prospect of supporting rank polymorphism over them—for example, a single operation that can both add two matrices and add a vector to a matrix. In order to do that, we need one datatype that encompasses both vectors and matrices (and scalars, and arrays of higher rank).

One way to achieve this goal is with a nested [4] or polymorphically recursive [28] datatype:

(we make a convention of subscripting definitions that will be refined later). This datatype corresponds to APL’s multi-dimensional arrays. We use the name $Hyper _{0}$, for ‘hypercuboid’, so as not to clash with Haskell’s $Array$ type that we will use later. Thus, $Scalar _{0}$ constructs a scalar hypercuboid from its sole element; and $Prism _{0}$ yields a hypercuboid of rank $r \mathbin {+}\mathrm {1}$ from a hypercuboid of rank $r$ whose elements are all $n$-vectors (for some $n$, but crucially, the same $n$ for all elements at this rank). This definition makes essential use of polymorphic recursion, because a composite hypercuboid of $a$s is constructed inductively not from smaller hypercuboids of $a$s, but from a (single) hypercuboid of vectors of $a$s.

This datatype satisfies the requirement of encompassing hypercuboids of arbitrary rank. However, it is somewhat unsatisfactory, precisely because it lumps together all hypercuboids of a given element type into a single type; for example, a vector and a matrix of integers both have the same type, namely $Hyper _{0}\; Int$. We have sacrificed any ability to catch rank errors through type checking. Perhaps worse, we have also sacrificed any chance to use the rank statically in order to automatically lift operators. We can solve this problem in much the same way as we did for bounds checking of vectors, by specifying the rank as a type index:

Now a vector of integers has type $Hyper _{1}\; One \; Int$, and a matrix of integers has type $Hyper _{1}\; Two \; Int$; it is a type error simply to try to add them pointwise, and the rank index can be used (we will see how in due course) to lift addition to act appropriately.

That is all well and good for rank, but we have a similar problem with size too: a 3-vector and a 4-vector of integers both have the same type when viewed as hypercuboids, namely $Hyper _{1}\; One \; Int$; so we can no longer catch size mismatches by type checking. Apparently indexing by the rank alone is not enough; we should index by the size in each dimension—a list of natural numbers. Then the rank is the length of this list. Just as in Sect. 2 we promoted the datatype $Nat$ to a kind and its inhabitants $Z , S \; Z ,\mathbin {...}$ to types $\mathord {'\! Z },\mathord {'\! S }\;\mathord {'\! Z },\mathbin {...}$, we can also promote the datatype $[\,]$ of lists to the kind level, and its constructors $[\,]$ and $(\mathbin {:})$ to operators $\mathord {'[\,]}$ and $(\mathbin {'\mathord {:}})$ at the type level:

Now a 3-vector of integers has type $Hyper _{2}\;\mathord {'[ Three ]}\; Int$, a 4-vector has type $Hyper _{2}\;\mathord {'[ Four ]}\; Int$, a $\mathrm {2}\mathord {\times }\mathrm {3}$-matrix has type $Hyper _{2}\;\mathord {'[ Three , Two ]}\; Int$, and so on. (Note that the latter is essentially a 2-vector of 3-vectors, rather than the other way round; it turns out to be most convenient for the first element of the list to represent the extent of the innermost dimension.) There is enough information at the type level to catch mismatches both of rank and of size; but still, the indexed types are all members of a common datatype, so can be made to support common operations.

That deals with multi-dimensional vectors. But as we discussed in Sect. 3, there is no a priori reason to restrict each dimension to be a vector; other datatypes work too, provided that they are instances of the type class $Dimension$. Then it is not enough for the datatype of hypercuboids to be indexed by a type-level list of lengths, because the lengths are no longer sufficient to characterize the dimensions—instead, we should use a type-level list of the dimension types themselves.

We call these type-level lists of dimension types shapely [22]. Following the example of vectors in Sect. 2, we introduce a type class of shapely types, which support replication and size:

We ensure that every possible type-level list of dimensions is an instance:

Here, $first$ returns the first element of a hypercuboid, so $first \; x$ is the first ‘row’ of $Prism \; x$:

and the size of a hypercuboid is of course the product of the lengths of its dimensions.

Now, a hypercuboid of type $Hyper \; fs \; a$ has shape $fs$ (a list of dimensions) and elements of type $a$. The rank zero hypercuboids are scalars; at higher ranks, one can think of them as geometrical ‘right prisms’—congruent stacks of lower-rank hypercuboids.

For example, we can wrap up a vector of vectors as a rank-2 hypercuboid:

Hypercuboids are of course functorial:

Furthermore, they are applicative; the type class $Shapely$ handles replication, and zipping is simply a matter of matching structures:

With these two, we can install shapely hypercuboids as an applicative functor:

(In fact, hypercuboids are also Naperian, foldable, and traversable too, so they can themselves serve as dimensions; but we do not need that power in the rest of this paper.)

Now we can fold along the ‘major’ (that is, the innermost) axis of a hypercuboid, given a suitable binary operator and initial value:

Moreover, we can transpose the hypercuboid in order to be able to fold along the ‘minor’ (that is, the next-to-innermost) axis:

Thus, given a hypercuboid of type $Hyper \;( f \mathbin {'\mathord {:}}( g \mathbin {'\mathord {:}} fs ))\; a$, which by construction must be of the form $Prism \;( Prism \; x )$ with $x$ of type $Hyper \; fs \;( g \;( f \; a ))$, we $transpose$ each of the inner hypercuboids from $g \;( f \; a )$ to $f \;( g \; a )$, then put the two $Prism$ constructors back on to yield the result of type $Hyper \;( g \mathbin {'\mathord {:}}( f \mathbin {'\mathord {:}} fs ))\; a$ as required. And with multiple transpositions, we can rearrange a hypercuboid to bring any axis into the ‘major’ position.

6 Alignment

We can easily lift a unary operator to act on a hypercuboid of elements:

We can similarly lift a binary operator to act on hypercuboids of matching shapes, using $azipWith$. But what about when the shapes do not match? A shape $fs$ is alignable with another shape $gs$ if the type-level list of dimensions $fs$ is a prefix of $gs$, so that they have innermost dimensions in common; in that case, we can replicate the $fs$-hypercuboid to yield a $gs$-hypercuboid.

Scalar shapes are alignable with each other; alignment is the identity function:

Alignments can be extended along a common inner dimension:

Finally, and most importantly, a scalar can be aligned with an arbitrary hypercuboid, via replication:

(Note that, ignoring the accompanying definitions of the $align$ function, the heads of the three $Alignable$ instance declarations can be read together as a logic program for when one sequence is a prefix of another.)

The $Alignable$ relation on shapes is an ordering, and in particular asymmetric. In order to be able to lift a binary operator to act on two compatible hypercuboids, we should treat the two arguments symmetrically: we will align the two shapes with their least common extension, provided that this exists. We express that in terms of the $Max$ of two shapes, a type-level function:

For example, a $\mathrm {2}\mathord {\times }\mathrm {3}$-matrix can be aligned with a $\mathrm {3}$-vector:

Here, $\mathbin {\sim }$ denotes type compatibility in Haskell. Provided that shapes $fs$ and $gs$ are compatible, we can align two hypercuboids of those shapes with their least common extension $hs$, and then apply a binary operator to them pointwise:

For example,

Note that as a function on types, $Max$ is partial: two shapes $f \mathbin {'\mathord {:}} fs$ and $g \mathbin {'\mathord {:}} gs$ are incompatible when $f \not \equiv g$, and then have no common extension. In that case, it is a type error to attempt to align two hypercuboids of those shapes. However, the type error can be a bit inscrutable. For example, when trying to align a 3-vector with a 4-vector, the compiler cannot simplify $Max \;\mathord {'[ Vector \; Three ]}\;\mathord {'[ Vector \; Four ]}$, and GHC (version 7.10.3) gives the following error:

We can use type-level functions to provide more helpful error messages too [33]. We define an additional type function as a predicate on types, to test whether the shapes are compatible:

Here, $Symbol$ is the kind of type-level strings, and $IsDefined$ is a type-level version of the booleans, but extended to incorporate also an explanation in the case that the predicate fails to hold:

If we now add this test as a constraint to the type of a lifted binary operator:

(note that the code is precisely the same, only the type has become more informative) then we get a slightly more helpful error message when things go wrong:

7 Symbolic Transformations

Although alignment of arrays of compatible but different shapes morally entails replication, this is an inefficient way actually to implement it; instead, it is better simply to use each element of the smaller structure multiple times. One way to achieve this is perform the replication symbolically—that is, to indicate via the type index that an array is replicated along a given dimension, without manifestly performing the replication. This can be achieved by extending the datatype of hypercuboids to incorporate an additional constructor:

The idea is that $ReplR \; x$ denotes the same array as $Prism \;( fmap \; areplicate \; x )$, but takes constant time and space to record the replication. It allows us to implement replication to multiple ranks in time and space proportional to the rank, rather than to the size. This would be of no benefit were it just to postpone the actual replication work until later. Fortunately, the work can often be avoided altogether. Mapping is straightforward, since it simply distributes through $ReplR$:

Similarly for zipping two replicated dimensions. When zipping a replicated dimension ($ReplR$) with a manifest one ($PrismR$), we end up essentially with a map—that, after all, was the whole point of the exercise. The other cases are as before.

Here, $azipWithL$ and $azipWithR$ are variants of $azipWith$ with one argument constant:

(note that they only need a $Functor$ constraint rather than $Applicative$, since they only use $fmap$ and not $pure$ and ).

Similarly for transposition; if either of the innermost two dimensions is symbolically replicated, it is just a matter of rearranging constructors, and only when they are both manifest do we have to resort to actual data movement:

It is only when it comes to folding or traversing a hypercuboid that a symbolic replication really has to be forced. This can be achieved by means of a function that expands a top-level $ReplR$ constructor, if one is present, while leaving the hypercuboid abstractly the same:

A similar technique can be used to represent transposition itself symbolically, via its own constructor:

The idea is that $TransT \; x$ represents the transposition of $x$, without actually doing any work. We can maintain the invariant that there are never two adjacent $TransT$ constructors, by using the following ‘smart constructor’ in place of the real one, to remove a transposition if one is present and to add one otherwise:

Of course, with the help of this additional constructor, transposition is trivial, and replication is no more difficult than it was with plain $Hyper$; zipping is the only operation that requires any thought. Where the two structures match, zipping simply commutes with them—and in particular, symbolic transpositions may be preserved, as in the third equation for $tzipWith$ below. Only when zipping a $TransT$ with a $PrismT$ does the symbolic transposition need to be forced, for which we provide a function that expands a top-most $TransT$ constructor if one is present, while leaving the hypercuboid abstractly the same:

(Here, the ‘as-pattern’ $x \mathord {@} p$ binds $x$ to the whole of an argument whilst simultaneously matching against the pattern $p$, and is a wild card. On account of the type constraints, together with the invariant that there are no two adjacent $TransT$ constructors, these three clauses are sufficient to guarantee that the outermost constructor is not a $TransT$.) Then we have:

Again, folding and traversing seem to require manifesting any symbolic transpositions.

We can even combine symbolic replication and transposition in the same datatype, providing trivial implementations of both operations. The only tricky part then is in zipping, while preserving as much of the symbolic representation as possible. We have all the cases of $rzipWith$ for prisms interacting with replication, plus those of $tzipWith$ for prisms interacting with transposition, plus some new cases for replication interacting with transposition. The details are not particularly surprising, so are left again to the energetic reader.

8 Flat Representation

The various nested representations above precisely capture the shape of a hypercuboid. This prevents dimension and size mismatches, by making them type errors; more constructively, it drives the mechanism for automatically aligning the arguments of heterogeneous binary operators. However, the nested representation is inefficient in time and space; high performance array libraries targetting GPUs arrange the data as a simple, flat, contiguous sequence of values, mediated via coordinate transformations between the nested index space and the flat one. In this section, we explore such flat representations.

Since each dimension of a hypercuboid is Naperian, with a fixed collection of positions, the total size of a hypercuboid is statically determined; so one can rather straightforwardly flatten the whole structure to an immutable linear array. To get the full benefits of the flat representation, that really should be an array of unboxed values [30]; for simplicity, we elide the unboxing here, but it should not be difficult to provide that too.

In order to flatten a hypercuboid into a linear array, we need the total size and a list of the elements. The former is provided as the $hsize$ method of the type class $Shapely$; for the latter, we define

As a representation of flattened hypercuboids, we introduce an indexed version of arrays, preserving the shape $fs$ as a type index:

to which we can transform a hypercuboid:

Here, $listArray$ is a standard Haskell function that constructs an array from a pair of bounds and an ordered list of elements. This representation is essentially the same as is used for high-performance array libraries such as Repa [24] for multicore architectures and Accelerate [5] for GPUs; so it should be straightforward to use the abstractions defined here as a front end to guarantee safety, with such a library as a back end for high performance.

The flat contiguous $Array$ is one possible representation of the sequence of elements in a hypercuboid, but it is not the only possibility. In particular, we can accommodate sparse array representations too, recording the shape as a type index, and explicitly storing only the non-null elements together with their positions. When the elements are numeric, we could make the convention that the absent ones are zero; more generally, we could provide a single copy of the ‘default’ element:

so that $Sparse \; e \; xs$ denotes a sparse array with default element $e$ and list $xs$ of proper elements paired with their positions. This can be expanded back to a traditional flat array as follows:

Here, $elems$ yields the list of elements of an $Array$, which for us will be a list of pairs; and $accumArray \; f \; e \;( i , j )\; xs$ constructs a $B$-array with bounds $( i , j )$ from a list $xs$ of $A$-elements paired with positions, accumulating the subsequence of elements labelled with the same position using the initial value $e \mathbin {::} B$ and the binary operator $f \mathbin {::} B \rightarrow A \rightarrow B$. For us, the types $A , B$ coincide, and $second$ keeps the second of its two arguments. For simplicity, we compute the size $l$ from a regular $Hyper$ of the same shape; more sophisticated approaches are of course possible.

One could similarly provide a run-length-encoded representation, for arrays expected to have long constant sections of different values, and space-efficient representations of diagonal and triangular matrices.

Note that neither the $Flat$ nor the $Sparse$ representation as shown enforce the bounds constraints. The underlying array in both cases is merely assumed to have the appropriate length for the shape index $fs$. Moreover, for the sparse representation, the positions are additionally assumed to be within range; a more sophisticated representation using bounded naturals $Fin$ could be used to enforce the constraints, should that be deemed important. One might also want to maintain the invariant that the elements in the sparse representation are listed in order of position, so that two arrays can easily be zipped via merging without first expanding out to a dense representation; it is straightforward to impose that ordering invariant on the position using dependent typing [27].

In order to provide efficient element access and manipulation, one could combine the array representation with an explicit index transformation [16]. Replication and transposition can then be represented by modifying the index transformation, without touching the array elements. We leave the pursuit of this possibility for future work.

9 Conclusions

We have shown how to express the rank and size constraints on multidimensional APL array operations statically, by embedding into a modern strongly typed functional programming language. This means that we benefit for free from all the infrastructure of the host language, such as the type checking, compilation, code optimizations, libraries, and development tools—all of which would have to be built from scratch for a standalone type system such as that of Remora [34].

The embedding makes use of lightweight dependently typed programming features, as exhibited in Haskell. What is quite remarkable is that there is no need for any sophisticated solver for size constraints; the existing traditional unification algorithm suffices (with admittedly many extensions since the days of Hindley and Milner, for example to encompass generalized algebraic datatypes, polymorphic recursion, type families, and so on). This is perhaps not surprising when all one does with sizes is to compare them, but it still applies for certain amounts of size arithmetic. For example, there is no difficulty at all in defining addition and multiplication of type-level numbers,

and then writing functions to append and split vectors, and to concatenate and group vectors of vectors:

We have shown how the approach supports various important optimizations, such as avoiding unnecessary replication of data, and flat storage of multidimensional data. In future work, we plan to integrate this approach with existing libraries for high-performance GPU execution, notably Repa [24] and Accelerate [5].

9.1 Related Work

We are, of course, not the first to use a type system to guarantee size constraints on dimensions of array operations. The length-indexed vector example is the ‘hello, world’ of lightweight approaches to dependently typed programming, dating back at least to Xi’s Dependent ML [38]. The particular case in which the shape is data-independent, as we address here, can also be traced back to Jay’s work [22] on shapely types, in which data structures may be factored into ‘shape’ and ‘contents’, the latter a simple sequence of elements; then shapely operations are those for which the shape of the output depends only on the shape of the input, and not on its contents.

Jay already considered the example of two-dimensional matrices; many others have also used size information at the type level to statically constrain multi-dimensional array operations. Eaton [7] presented a demonstration of statically typed linear algebra, by which he meant “any tool which makes [static guarantees about matching dimensions] possible”. Scholz’s Single-Assignment C [32] represents the extents of multi-dimensional arrays in their types, and Trojahner and Grelck [36] discuss shape-generic functional array programming in SaC/Qube. Abe and Sumii [1] present an array interface that enforces shape consistency through what they call generative phantom types, and conclude that “practical size checking for a linear algebra library can be constructed on the simple idea of verifying mostly the equality of sizes without significantly restructuring application programs”.

Elsman and Dybdal’s subset of APL [10] and Veldhuizen’s Blitz++ [37] have array types indexed by rank but not size. Chakravarty et al.’s Haskell libraries Repa [24] and Accelerate [5] similarly express the rank of a multi-dimensional array in its type, but represent its shape only as part of the value, so that can only be checked at run-time (note that they use both “rank” and “shape” in their papers to refer to what we call rank). Thiemann and Chakravarty [35] explore the trade-offs in developing a front-end to Accelerate in the true dependently typed language Agda in order (among other things) to statically capture shape information; we have shown that it is not necessary to leave the more familiar world of Haskell to achieve that particular end.

None of these works cover full rank polymorphism as in APL and Remora and as in our work: although operations such as map may be applied at arbitrary shape, binary operations such as zip require both arguments to have the same shape—there is no lifting and alignment.

The representation of an array in terms of its $lookup$ function, as in our $Naperian$ class and our basis for transposition, also has quite a long history. The representation is known as pull arrays in the Chalmers work on the digital signal processing language Feldspar [2] and the GPU language Obsidian [6], and delayed arrays in Repa [24]. But it is also the essence of functional reactive animation, for example in Elliott’s Pan [8] and his and Hudak’s Fran [9], and in Hudak and Jones’s earlier experiment on geometric region servers [20].