Logarithmic Query Complexity for Approximate Nash Computation in Large Games

Abstract

We investigate the problem of equilibrium computation for “large” n-player games where each player has two pure strategies. Large games have a Lipschitz-type property that no single player’s utility is greatly affected by any other individual player’s actions. In this paper, we assume that a player can change another player’s payoff by at most $\frac{1}{n}$ by changing her strategy. We study algorithms having query access to the game’s payoff function, aiming to find $\varepsilon$-Nash equilibria. We seek algorithms that obtain $\varepsilon$ as small as possible, in time polynomial in n.

Our main result is a randomised algorithm that achieves $\varepsilon$ approaching $\frac{1}{8}$ in a completely uncoupled setting, where each player observes her own payoff to a query, and adjusts her behaviour independently of other players’ payoffs/actions. $O(\log n)$ rounds/queries are required. We also show how to obtain a slight improvement over $\frac{1}{8}$, by introducing a small amount of communication between the players.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In studying the computation of solutions of multi-player games, we have the well-known problem that a game’s payoff function has description length exponential in the number of players. One approach is to assume that the game comes from a concisely-represented class (for example, graphical games, anonymous games, or congestion games), and another one is to consider algorithms that have query access to the game’s payoff function.

In this paper, we study the computation of approximate Nash equilibria of multi-player games having the feature that if a player changes her behaviour, she only has a small effect on the payoffs that result to any other player. These games, sometimes called large games, or Lipschitz games, have recently been studied in the literature, since they model various real-world economic interactions; for example, an individual’s choice of what items to buy may have a small effect on prices, where other individuals are not strongly affected. Note that these games do not have concisely-represented payoff functions, which makes them a natural class of games to consider from the query-complexity perspective. It is already known how to compute approximate correlated equilibria for unrestricted n-player games. Here we study the more demanding solution concept of approximate Nash equilibrium.

Large games (equivalently, small-influence games) are studied in Kalai [16] and Azrieli and Shmaya [1]. In both of these the existence of pure $\varepsilon$-Nash equilibria for $\varepsilon = \gamma \sqrt{8n\log (2mn)}$ is established, where $\gamma$ is the largeness/Lipschitz parameter of the game. In particular, since we assume that $\gamma = \frac{1}{n}$ and $m =2$ we notice that $\varepsilon = O(n^{-1/2})$ so that there exist arbitrarily accurate pure Nash equilibria in large games as the number of players increases. Kearns et al. [17] study this class of games from the mechanism design perspective of mediators who aim to achieve a good outcome to such a game via recommending actions to players. Babichenko [2] studies large binary-action anonymous games. Anonymity is exploited to create a randomised dynamic on pure strategy profiles that with high probability converges to a pure approximate equilibrium in $O(n \log n)$ steps.

Payoff query complexity has been recently studied as a measure of the difficulty of computing game-theoretic solutions, for various classes of games. Upper and lower bounds on query complexity have been obtained for bimatrix games [6, 7], congestion games [7], and anonymous games [11]. For general n-player games (where the payoff function is exponential in n), the query complexity is exponential in n for exact Nash, also exact correlated equilibria [15]; likewise for approximate equilibria with deterministic algorithms (see also [4]). For randomised algorithms, query complexity is exponential for well-supported approximate equilibria [3], which has since been strengthened to any $\varepsilon$-Nash equilibria [5]. With randomised algorithms, the query complexity of approximate correlated equilibrium is $\varTheta (\log n)$ for any positive $\varepsilon$ [10].

Our main result applies in the setting of completely uncoupled dynamics in equilibria computation. These dynamics have been studied extensively: Hart and Mas-Colell [13] show that there exist finite-memory uncoupled strategies that lead to pure Nash equilibria in every game where they exist. Also, there exist finite memory uncoupled strategies that lead to $\varepsilon$-NE in every game. Young’s interactive trial and error [18] outlines completely uncoupled strategies that lead to pure Nash equilibria with high probability when they exist. Regret testing from Foster and Young [8] and its n-player extension by Germano and Lugosi in [9] show that there exist completely uncoupled strategies that lead to an $\varepsilon$-Nash equilibrium with high probability. Randomisation is essential in all of these approaches, as Hart and Mas-Colell [14] show that it is impossible to achieve convergence to Nash equilibria for all games if one is restricted to deterministic uncoupled strategies. This prior work is not concerned with rate of convergence; by contrast here we obtain efficient bounds on runtime. Convergence in adaptive dynamics for exact Nash equilibria is also studied by Hart and Mansour in [12] where they provide exponential lower bounds via communication complexity results. Babichenko [3] also proves an exponential lower bound on the rate of convergence of adaptive dynamics to an approximate Nash equilibrium for general binary games. Specifically, he proves that there is no k-queries dynamic that converges to an $\varepsilon$-WSNE in $\frac{2^{\varOmega (n)}}{k}$ steps with probability of at least $2^{-\varOmega (n)}$ in all n-player binary games. Both of these results motivate the study of specific subclasses of these games, such as “large” games.

2 Preliminaries

We consider games with n players where each player has two actions $\mathcal {A}= \{0,1\}$. Let $a = (a_i, a_{-i})$ denote an action profile in which player i plays action $a_i$ and the remaining players play action profile $a_{-i}$. We also consider mixed strategies, which are defined by the probability distributions over the action set $\mathcal {A}$. We write $p = (p_i, p_{-i})$ to denote a mixed-strategy profile where player i plays action 1 with probability $p_i$ and the remaining players play the profile $p_{-i}$. We will sometimes abuse notation to use $p_i$ to denote i’s mixed strategy, and write $p_{i0}$ and $p_{i1}$ to denote the probabilities that player i plays the action 0 and 1 respectively.

Each player i has a payoff function $u_i:\mathcal {A}^n \rightarrow [0, 1]$ mapping an action profile to some value in [0, 1]. We will sometimes write $u_i(p) = {{\mathrm{\mathbb {E}}}}_{a\sim p}\left[ u_i(a)\right]$ to denote the expected payoff of player i under mixed strategy p. An action a is player i’s best response to mixed strategy profile p if $a \in {{\mathrm{\mathrm {argmax}}}}_{j\in \{0, 1\}} u_i(j , p_{-i})$.

We assume our algorithms or the players have no other prior knowledge of the game but can access payoff information through querying a payoff oracle $\mathcal {Q}$. For each payoff query specified by an action profile $a\in \mathcal {A}^n$, the query oracle will return $(u_i(a))_{i=1}^n$ the n-dimensional vector of payoffs to each player. Our goal is to compute an approximate Nash equilibrium with a small number of queries. In the completely uncoupled setting, a query works as follows: each player i chooses her own action $a_i$ independently of the other players, and learns her own payoff $u_i(a)$ but no other payoffs.

Definition 1

(Regret; (approximate) Nash equilibrium). Let p be a mixed strategy profile, the regret for player i at p is

$$ reg(p, i) = \max \limits _{k\in \{0, 1\}} \mathop {{\mathbb {E}}}\limits _{a_{-i}\sim p_{-i}}{[u_i(k, a_{-i})]} - \mathop {{\mathbb {E}}}\limits _{a \sim p}{[u_i(a)]} $$

A mixed strategy profile p is an $\varepsilon$-approximate Nash equilibrium if for each player i, the regret satisfies $reg(p, i) \le \varepsilon$.

Observation. To find an exact Nash (or even, correlated) equilibrium of a large game, in the worst case it is necessary to query the game exhaustively, even with randomised algorithms. This uses a similar negative result for general games due to [15], and noting that we can obtain a strategically equivalent large game, by scaling down the payoffs into the interval $[0,\frac{1}{n}]$.

We will also use the following useful notion of discrepancy.

Definition 2

(Discrepancy). Letting p be a mixed strategy profile, the discrepancy for player i at p is

$$ disc(p, i) = \left| \mathop {{\mathbb {E}}}\limits _{a_{-i}\sim p_{-i}}{[u_i(0, a_{-i})]} - \mathop {{\mathbb {E}}}\limits _{a_{-i}\sim p_{-i}}{[u_i(1, a_{-i})]} \right| $$

We will assume the following largeness condition in our games. Informally, such largeness condition implies that no single player has a large influence on any other player’s utility function.

Definition 3

(Large Games). A game is large if for any two distinct players $i\ne j$, any two distinct actions $a_j$ and $a_j'$ for player j, and any tuple of actions $a_{-j}$ for everyone else:

$$ |u_i(a_j, a_{-j}) - u_i(a_j', a_{-j})| \le \frac{1}{n}. $$

One immediate implication of the largeness assumption is the following Lipschitz property of the utility functions.

Lemma 1

For any player $i\in [n]$, and any action $j\in \{0,1\}$, the utility $u_i(j, p_{-i})$ is a $(\frac{1}{n})$-Lipschitz function in the second coordinate $p_{-i}$ w.r.t. the $\ell _1$ norm, and the mixed strategy profile of all other players.

Estimating payoffs for mixed profiles. We can approximate the expected payoffs for any mixed strategy profile by repeated calls to the oracle $\mathcal {Q}$. In particular, for any target accuracy parameter $\beta$ and confidence parameter $\delta$, consider the following procedure to implement an oracle $\mathcal {Q}_{\beta , \delta }$:

• For any input mixed strategy profile p, compute a new mixed strategy profile $p' = (1 - \frac{\beta }{2})p + (\frac{\beta }{2})\mathbf {1}$ such that each player i is playing uniform distribution with probability $\frac{\beta }{2}$ and playing distribution $p_i$ with probability $1 - \frac{\beta }{2}$.

• Let $N = \frac{64}{\beta ^3} \log \left( 8n /\delta \right)$, and sample N payoff queries randomly from p, and call the oracle $\mathcal {Q}$ with each query as input to obtain a payoff vector.

• Let $\widehat{u}_{i,j}$ be the average sampled payoff to player i for playing action j.¹ Output the payoff vector $(\widehat{u}_{ij})_{i\in [n], j\in \{0, 1\}}$.

Lemma 2

For any $\beta , \delta \in (0, 1)$ and any mixed strategy profile p, the oracle $\mathcal {Q}_{\beta , \delta }$ with probability at least $1 - \delta$ outputs a payoff vector $(\widehat{u}_i)_{i\in [n], j\in \{0, 1\}}$ that has an additive error of at most $\beta$, that is for each player i, and each action $j\in \{0, 1\}$,

$$ |u_i(j, p_{-i}) - \widehat{u}_{i, j}| \le \beta . $$

The lemma follows from Proposition 1 of [10] and the largeness property.

Extension to Stochastic Utilities. We consider a generalisation where the utility to player i of any pure profile a may consist of a probability distribution $D_{a,i}$ over [0, 1], and if a is played, i receives a sample from $D_{a,i}$. The player wants to maximise her expected utility with respect to sampling from a (possibly mixed) profile, together with sampling from any $D_{a,i}$ that results from a being chosen. If we extend the definition of $\mathcal {Q}$ to output samples of the $D_{a,i}$ for any queried profile a, then $\mathcal {Q}_{\beta ,\delta }$ can be defined in a similar way as before, and simulated as above using samples from $\mathcal {Q}$. Our algorithmic results extend to this setting.

3 Warm-Up: 0.25-Approximate Equilibrium

As a starting point, we will show that without any payoff queries, we could easily give a $\frac{1}{2}$-approximate Nash equilibrium.

Observation. Consider the following “uniform” mixed strategy profile. Each player puts $\frac{1}{2}$ probability mass on each action: for all i, $p_{i} = \frac{1}{2}$. Such a mixed strategy profile is a $\frac{1}{2}$ -approximate Nash equilibrium.

In this section, we will present two simple and query-efficient algorithms that allows us to get a better approximation than $\frac{1}{2}$. Both algorithms could be regarded as a simple refinement of the above “uniform” mixed strategy. For simplicity of presentation, we will assume that we have access to a mixed strategy query oracle $\mathcal {Q}_M$ that returns exact expected payoff values for any input mixed strategy p. Our results continue to hold if we replace $\mathcal {Q}_M$ by $\mathcal {Q}_{\beta , \delta }$.²

Obtaining $\varepsilon = 0.272$. First, we show that having each player making small adjustment from the “uniform” strategy can improve $\varepsilon$ from $\frac{1}{2}$ to around 0.27. We simply let players with large regret shift more probability weight towards their best responses. More formally, consider the following algorithm OneStep with two parameters $\alpha , \varDelta \in [0, 1]$:

• Let the players play the “uniform” mixed strategy. Call the oracle $\mathcal {Q}_{M}$ to obtain the payoff values of $u_i(0, p_{-i})$ and $u_i(1, p_{-i})$ for each player i.

• For each player i, if $u_i(0, p_{-i}) - u_i(1, p_{-i}) > \alpha$, then set $p_{i0} = \frac{1}{2} + \varDelta$ and $p_{i1} = \frac{1}{2} - \varDelta$; if $u_i(1, p_{-i}) - u_i(0, p_{-i}) > \alpha$, set $p_{i1} = \frac{1}{2} + \varDelta$ and $p_{i0} = \frac{1}{2} - \varDelta$; otherwise keep playing $p_{i} = \frac{1}{2}$.

Lemma 3

If we set the parameters $\alpha = 2 - \sqrt{11/3}$ and $\varDelta = \sqrt{11/48} - 1/4$ in the instantiation of the algorithm OneStep, then the resulting mixed strategy profile is an $\varepsilon$-approximate Nash equilibrium with $\varepsilon \le 0.272$.

Obtaining $\varepsilon = 0.25$. We now give a slightly more sophisticated algorithm than the previous one. We will again have the players starting with the “uniform” mixed strategy, then let players shift more weights toward their best responses, and finally let some of the players switch back to the uniform strategy if their best responses change in the adjustment. Formally, the algorithm TwoStep proceeds as:

• Start with the “uniform” mixed strategy profile, and query the oracle $\mathcal {Q}_M$ for the payoff values. Let $b_i$ be player i’s best response.

• For each player i, set the probability of playing their best response $b_i$ to be $\frac{3}{4}$. Call $\mathcal {Q}_M$ to obtain payoff values for this mixed strategy profile, and let $b'_i$ be each player i’s best response in the new profile.

• For each player i, if $b_i\ne b'_i$, then resume playing $p_{i0} = p_{i1} = \frac{1}{2}$. Otherwise maintain the same mixed strategy from the previous step.

Lemma 4

The mixed strategy profile output by TwoStep is an $\varepsilon$-approximate Nash equilibrium with $\varepsilon \le 0.25$.

4 $\frac{1}{8}$-Approximate Equilibrium via Uncoupled Dynamics

In this section, we present our main algorithm that achieves approximate equilibria with $\varepsilon \approx \frac{1}{8}$ in a completely uncoupled setting. In order to arrive at this we first model game dynamics as an uncoupled continuous-time dynamical system where a player’s strategy profile updates depend only on her own mixed strategy and payoffs. Afterwards we present a discrete-time approximation to these continuous dynamics to arrive at a query-based algorithm for computing $(\frac{1}{8} + \alpha )$-Nash equilibrium with logarithmic query complexity in the number of players. Finally, as mentioned in Sect. 2, we recall that these algorithms carry over to games with stochastic utilities, where we can show that our algorithm uses an essentially optimal number of queries.

Throughout the section, we will rely on the following notion of a strategy-payoff state, capturing the information available to a player at any moment of time.

Definition 4

(Strategy-payoff state). For any player i, the strategy-payoff state for player i is defined as the ordered triple $s_i = (v_{i1}, v_{i0}, p_i)\in [0, 1]^3$, where $v_{i1}$ and $v_{i0}$ are the player’s utilities for playing pure actions 1 and 0 respectively, and $p_i$ denotes the player’s probability of playing action 1. Furthermore, we denote the player’s discrepancy by $D_i = |v_{i1} - v_{i0}|$ and we let $p_i^*$ denote the probability mass on the best response, that is if $v_{i1} \ge v_{i0}$, $p_i^* = p_i$, otherwise $p_i^* = 1-p_i$.

4.1 Continuous-Time Dynamics

First, we will model game dynamics in continuous time, and assume that a player’s strategy-payoff state (and thus all variables it contains) is a differentiable time-valued function. When we specify these values at a specific time t, we will write $s_i(t) = (v_{i1}(t), v_{i0}(t), p_i(t))$. Furthermore, for any time-differentiable function g, we denote its time derivative by $\dot{g} = \frac{d}{dt} g$. We will consider continuous game dynamics formally defined as follows.

Definition 5

(Continuous game dynamic). A continuous game dynamic consists of an update function f that specifies a player’s strategy update at time t. Furthermore, f depends only on $s_i(t)$ and $\dot{s}_i(t)$. In other words, $\dot{p}_i(t) = f(s_i(t), \dot{s}_i(t))$ for all t.

Observation. We note that in this framework, a specific player’s updates do not depend on other players’ strategy-payoff states nor their history of play. This will eventually lead us to uncoupled Nash equilibria computation in Sect. 4.2.

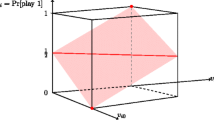
A central object of interest in our continuous dynamic is a linear sub-space $\mathcal {P} \subset [0,1]^3$ such that all strategy-payoff states in it incur a bounded regret. Formally, we will define $\mathcal {P}$ via its normal vector $\varvec{n} = (-\frac{1}{2},\frac{1}{2},1)$ so that $\mathcal {P} = \{ s_i | \ s_i \cdot \varvec{n} = \frac{1}{2} \}$. Equivalently, we could also write $\mathcal {P} = \{s_i \ | \ p_i^* = \frac{1}{2}(1+D_i)\}$. (See Fig. 1 for a visualisation.) With this observation, it is straightforward to see that any player with strategy-payoff state in $\mathcal {P}$ has regret at most $\frac{1}{8}$.

Fig. 1.

Visualisation of $\mathcal {P}$; on the red line, $v_{i0}=v_{i1}$ so the player is indifferent and mixes with equal probabilities; at the red points the player has payoffs of 0 and 1, and makes a pure best response. (Color figure online)

Lemma 5

Suppose that the player’s strategy-payoff state satisfies $s_i\in \mathcal {P}$, then her regret is at most $\frac{1}{8}$.

Proof

This follows from the fact that a player’s regret can be expressed as $D_i(1-p_i^*)$ and the fact that all points on $\mathcal {P}$ also satisfy $p_i^* = \frac{1}{2}(1+D_i)$. In particular, the maximal regret of $\frac{1}{8}$ is achieved when $D_i = \frac{1}{2}$ and $p_i^* = \frac{3}{4}$.

Next, we want to show there exists a dynamic that allows all players to eventually reach $\mathcal {P}$ and remain on it over time. We notice that for a specific player, $\dot{v}_{i1}$, $\dot{v}_{i0}$ and subsequently $\dot{D}_i$ measure the cumulative effect of other players shifting their strategies. However, if we limit how much any individual player can change their mixed strategy over time by imposing $|\dot{p}_i| \le 1$ for all i, Lemma 1 guarantees $|\dot{v}_{ij}| \le 1$ for $j = 0,1$ and consequently $|\dot{D}_i| \le 2$. With these quantities bounded, we can consider an adversarial framework where we construct game dynamics by solely assuming that $|\dot{p}_i(t)| \le 1$, $|\dot{v}_{ij}(t)| \le 1$ for $j = 0,1$ and $|\dot{D}_i(t)| \le 2$ for all times $t\ge 0$.

Now assume an adversary controls $\dot{v}_{i0}$, $\dot{v}_{i1}$ and hence $\dot{D}_i$, one can show that if a player sets $\dot{p}_i(t) = \frac{1}{2}(\dot{v}_{i1}(t) - \dot{v}_{i0}(t))$, then she could stay on $\mathcal {P}$ whenever she reaches the subspace.

Lemma 6

If $s_i(0) \in \mathcal {P}$, and $\dot{p}_i(t) = \frac{1}{2}(\dot{v}_{i1}(t) - \dot{v}_{i0}(t))$, then $s_i(t) \in \mathcal {P} \ \forall \ t \ge 0$.

Theorem 1

Under the initial conditions $p_i(0) = \frac{1}{2}$ for all i, the following continuous dynamic, Uncoupled Continuous Nash (UCN), has all players reach $\mathcal {P}$ in at most $\frac{1}{2}$ time units. Furthermore, upon reaching $\mathcal {P}$ a player never leaves.

$$ \dot{p}_i(t) = f(s_i(t), \dot{s}_i(t)) = {\left\{ \begin{array}{ll} \ \ 1 &{} \text { if } s_i \notin \mathcal {P} \text { and } v_{i1} \ge v_{i0} \\ -1 &{} \text { if } s_i \notin \mathcal {P} \text { and } v_{i1} < v_{i0} \\ \frac{1}{2}(\dot{v}_{i1}(t) - \dot{v}_{i0}(t)) &{} \text { if } s_i \in \mathcal {P} \end{array}\right. } $$

Proof

From Lemma 6 it is clear that once a player reaches $\mathcal {P}$ they never leave the plane. It remains to show that it takes at most 1/2 time steps to reach $\mathcal {P}$.

Since $p_i(0) = p_i^*(0) = \frac{1}{2}$, it follows that if $s_i(0) \notin \mathcal {P}$ then $p_i^*(0) < \frac{1}{2}(1 + D_i(0))$. On the other hand, if we assume that $\dot{p}_i^*(t) = 1$ for $t \in [0,\frac{1}{2}]$, and that player preferences do not change, then it follows that $p_i^*(\frac{1}{2}) = 1$ and $p_i^*(\frac{1}{2}) \ge \frac{1}{2}(1 + D_i(\frac{1}{2}))$, where equality holds only if $D_i(\frac{1}{2}) = 1$. By continuity of $p_i^*(t)$ and $D_i(t)$ it follows that for some $k \le \frac{1}{2}$, $s_i(k) \in \mathcal {P}$. It is simple to see that the same holds in the case where preferences change.

4.2 Discrete Time-Step Approximation

The continuous-time dynamics of the previous section hinge on obtaining expected payoffs in mixed strategy profiles, thus we will approximate expected payoffs via $\mathcal {Q}_{\beta ,\delta }$. Our algorithm will have each player adjusting their mixed strategy over rounds, and each round query $\mathcal {Q}_{\beta , \delta }$ to obtain the payoff values.

Since we are considering discrete approximations to UCN, the dynamics will no longer guarantee that strategy-payoff states stay on the plane $\mathcal {P}$. For this reason we define the following region around $\mathcal {P}$:

Definition 6

Let $\mathcal {P}^\lambda = \{ s_i \ | \ s_i \cdot \varvec{n} \in [\frac{1}{2} - \lambda , \frac{1}{2} + \lambda ]\}$, with normal vector $\varvec{n} = (-\frac{1}{2},\frac{1}{2},1)$. Equivalently, $\mathcal {P} = \{s_i \ | \ p_i^* = \frac{1}{2}(1+D_i) + c, \ c \in [-\lambda ,\lambda ]\}$.

Just as in the proof of Lemma 5, we can use the fact that a player’s regret is $D_i(1-p_i^*)$ to bound regret on $\mathcal {P}^\lambda$.

Lemma 7

The worst case regret of any strategy-payoff state in $\mathcal {P}^\lambda$ is $\frac{1}{8}(1+2\lambda )^2$. This is attained on the boundary: $\partial \mathcal {P}^\lambda = \{ s_i \ | \ s_i \cdot \varvec{n} = \frac{1}{2} \pm \lambda \}$

Corollary 1

For a fixed $\alpha > 0$, if $\lambda = \frac{\sqrt{1+ 8\alpha } - 1}{2}$, then $\mathcal {P}^\lambda$ attains a maximal regret of $\frac{1}{8} +\alpha$.

We present an algorithm in the completely uncoupled setting, UN($\alpha ,\eta$), that for any parameters $\alpha , \eta \in (0, 1]$ computes a $(\frac{1}{8} + \alpha )$-Nash equilibrium with probability at least $1 - \eta$.

Since $p_i(t) \in [0,1]$ is the mixed strategy of the i-th player at round t we let $p(t) = (p_i(t))_{i=1}^n$ be the resulting mixed strategy profile of all players at round t. Furthermore, we use the mixed strategy oracle $\mathcal {Q}_{\beta ,\delta }$ from Lemma 2 that for a given mixed strategy profile p returns the vector of expected payoffs for all players with an additive error of $\beta$ and a correctness probability of $1-\delta$.

The following lemma is used to prove the correctness of UN($\alpha ,\eta$):

Lemma 8

Suppose that $w \in \mathbb {R}^3$ with $\Vert w \Vert _\infty \le \lambda$ and let function $h(x) = x \cdot \varvec{n}$, where $\varvec{n}$ is the normal vector of $\mathcal {P}$. Then $h(x + w) - h(x) \in [-2\lambda , 2\lambda ]$. Furthermore, if $w_3 = 0$, then $h(x + w) - h(x) \in [-\lambda , \lambda ]$.

Proof

The statement follows from the following expression:

$$ h(x + w) - h(x) = w \cdot \varvec{n} = \frac{1}{2} (w_2 - w_1) + w_3 $$

We now give a formal description for UN($\alpha ,\eta$):

• 1. Set $\lambda = \frac{\sqrt{1+8\alpha }-1}{2}$, $\varDelta = \frac{\lambda }{4}$, and $N = \lceil \frac{2}{\varDelta } \rceil$

• 2. For each player i, let $p_i(0) = \frac{1}{2}$ and $\widehat{v}_{ij}(-1) = \left( \mathcal {Q}_{(\varDelta ,\frac{\eta }{N})}(p(0)) \right) _{i,j}$ for $j = 0,1$

• 3. During $t \le N$ rounds, for each player i, calculate $\widehat{v}_{ij}(t) = \left( \mathcal {Q}_{(\varDelta ,\frac{\eta }{N})}(p(t)) \right) _{i,j}$ and let $\varDelta \widehat{v}_{ij}(t) = \widehat{v}_{ij}(t) - \widehat{v}_{ij}(t-1)$ for $j = 0,1$.

• 4. if $\widehat{s}_i(t) = \left( \widehat{v}_{i1}(t),\widehat{v}_{i0}(t),p_i(t) \right) \notin \mathcal {P}^{\lambda /4}$, then $p_i^*(t+1) = p_i^*(t) + \varDelta$, otherwise $p_i^*(t+1) = p_i^*(t) + \frac{1}{2}(\varDelta \widehat{v}_{i1}(t) - \varDelta \widehat{v}_{i0}(t))$

• 5. return p(t)

Theorem 2

With probability $1 - \eta$, UN($\alpha ,\eta$) correctly returns a $(\frac{1}{8} + \alpha )$ approximate Nash equilibrium by using $O(\frac{1}{\alpha ^4} \log \left( \frac{n}{\alpha \eta } \right) )$ queries.

Proof

By Lemma 2 and union bound, we can guarantee that with probability at least $1-\eta$ all sample approximations to mixed payoff queries have an additive error of at most $\varDelta = \frac{\lambda }{4}$. We will condition on this accuracy guarantee in the remainder of our argument. Now we can show that for each player there will be some round $k \le N$, such that at the beginning of the round their strategy-payoff state lies in $\mathcal {P}^{\lambda /2}$. Furthermore, at the beginning of all subsequent rounds $t \ge k$, it will also be the case that their strategy-payoff state lies in $\mathcal {P}^{\lambda /2}$.

The reason any player generally reaches $\mathcal {P}^{\lambda /2}$ follows from the fact that in the worst case, after increasing $p^*$ by $\varDelta$ for N rounds, $p^*=1$, in which case a player is certainly in $\mathcal {P}^{\lambda /2}$. Furthermore, Lemma 8 guarantees that each time $p^*$ is increased by $\varDelta$, the value of $\widehat{s}_i \cdot \varvec{n}$ changes by at most $\frac{\lambda }{2}$ which is why $\widehat{s}_i$ are always steered towards $\mathcal {P}^{\lambda /4}$. Due to inherent noise in sampling, players may at times find that $\widehat{s}_i$ slightly exit $\mathcal {P}^{\lambda /4}$ but since additive errors are at most $\frac{\lambda }{4}$. We are still guaranteed that true $s_i$ lie in $\mathcal {P}^{\lambda /2}$.

The second half of step 4 forces a player to remain in $\mathcal {P}^{\lambda /2}$ at the beginning of any subsequent round $t \ge k$. The argumentation for this is identical to that of Lemma 6 in the continuous case.

Finally, the reason that individual probability movements are restricted to $\varDelta = \frac{\lambda }{4}$ is that at the end of the final round, players will move their probabilities and will not be able to respond to subsequent changes in their strategy-payoff states. From the second part of Lemma 8, we can see that in the worst case this can cause a strategy-payoff state to move from the boundary of $\mathcal {P}^{\lambda /2}$ to the boundary of $\mathcal {P}^{\frac{3\lambda }{4}} \subset \mathcal {P}^\lambda$. However, $\lambda$ is chosen in such a way so that the worst-case regret within $\mathcal {P}^{\lambda }$ is at most $\frac{1}{8}+\alpha$, therefore it follows that UN($\alpha ,\eta$) returns a $\frac{1}{8} + \alpha$ approximate Nash equilibrium. Furthermore, the number of queries is

$$ (N+1) \left( \frac{1024}{\lambda ^3} \log \left( \frac{8nN}{\eta } \right) \right) = \left( \frac{1}{\lambda } + 1 \right) \left( \frac{1024}{\lambda ^3} \log \left( \frac{8n}{\lambda \eta } \right) \right) . $$

It is not difficult to see that $\frac{1}{\lambda } = O(\frac{1}{\alpha })$ which implies that the number of queries made is $O \left( \frac{1}{\alpha ^4} \log \left( \frac{n}{ \alpha \eta } \right) \right)$ in the limit.

4.3 Logarithmic Lower Bound

As mentioned in the preliminaries section, all of our previous results extend to stochastic utilities. In particular, if we assume that G is a game with stochastic utilities where expected payoffs are large with parameter $\frac{1}{n}$, then we can apply UN($\alpha ,\eta$) with $O( \log (n))$ queries to obtain a mixed strategy profile where no player has more than $\frac{1}{8} + \alpha$ incentive to deviate. Most importantly, for $k>2$, we can use the same methods as [10] to lower bound the query complexity of computing a mixed strategy profile where no player has more than $(\frac{1}{2} - \frac{1}{k})$ incentive to deviate.

Theorem 3

If $k>2$, the query complexity of computing a mixed strategy profile where no player has more than $(\frac{1}{2} - \frac{1}{k})$ incentive to deviate for stochastic utility games is $\varOmega (\log _{k(k-1)} (n))$. Alongside Theorem 2 this implies the query complexity of computing mixed strategy profiles where no player has more than $\frac{1}{8}$ incentive to deviate in stochastic utility games is $\varTheta (\mathrm{log}(n))$.

5 Achieving $\varepsilon < \frac{1}{8}$ with Communication

We return to continuous dynamics to show that we can obtain a worst-case regret of slightly less than $\frac{1}{8}$ by using limited communication between players, thus breaking the uncoupled setting we have been studying until now.

First of all, let us suppose that initially $p_i(0) = \frac{1}{2}$ for each player i and that UCN is run for $\frac{1}{2}$ time units so that strategy-payoff states for each player lie on $\mathcal {P} = \{ s_i \ | \ p_i^* = \frac{1}{2}(1 + D_i) \}$. We recall from Lemma 5 that the worst case regret of $\frac{1}{8}$ on this plane is achieved when $p_i^* = \frac{3}{4}$ and $D_i = \frac{1}{2}$. We say a player is bad if they achieve a regret of at least 0.12, which on $\mathcal {P}$ corresponds to having $p_i^* \in [0.7,0.8]$. Similarly, all other players are good. We denote $\theta \in [0,1]$ as the proportion of players that are bad. Furthermore, as the following lemma shows, we can in a certain sense assume that $\theta \le \frac{1}{2}$.

Lemma 9

If $\theta > \frac{1}{2}$, then for a period of 0.15 time units, we can allow each bad player to shift to their best response with unit speed, and have all good players update according to UCN to stay on $\mathcal {P}$. After this movement, at most $1-\theta$ players are bad.

Proof

If i is a bad player, in the worst case scenario, $\dot{D}_i = 2$, which keeps their strategy-payoff state, $s_i$, on $\mathcal {P}$. At the end of 0.15 time units however, $p_i^* > 0.85$, hence they will no longer be bad. On the other hand, good players stay on $\mathcal {P}$, so at worst, all of them become bad.

Observation. After this movement, players who were bad are the only players possibly away from $\mathcal {P}$ and they have a discrepancy that is greater than 0.1. Furthermore, all players who become bad lie on $\mathcal {P}$.

We can now outline a continuous-time dynamic that utilises Lemma 9 to obtain a $(\frac{1}{8} - \frac{1}{220})$ maximal regret.

• 1. Have all players begin with $p_i(0) = \frac{1}{2}$

• 2. Run UCN for $\frac{1}{2}$ time units.

• 3. Measure, $\theta$, the proportion of bad players. If $\theta > \frac{1}{2}$ apply the dynamics of Lemma 9.

• 4. Let all bad players use $\dot{p}_i^* = 1$ for $\varDelta = \frac{1}{220}$ time units.

Theorem 4

If all players follow the aforementioned dynamic, no single player will have a regret greater than $\frac{1}{8} - \frac{1}{220}$.

Proof

Technical details of this proof can be found in the full paper, but in essence one shows that if $\varDelta$ is a small enough time interval (less than 0.1 to be exact), then all bad players will unilaterally decrease their regret by at least $0.1\varDelta$ and good players won’t increase their regret by more than $\varDelta$. The time step $\varDelta = \frac{1}{220}$ is thus chosen optimally.

As a final note, we see that this process requires one round of communication in being able to perform the operations in Lemma 9, that is we need to know if $\theta > \frac{1}{2}$ or not to balance player profiles so that there are at most the same number of bad players to good players. Furthermore, in exactly the same fashion as UN($\alpha ,\eta$), we can discretise the above process to obtain a query-based algorithm that obtains a regret of $\frac{1}{8} - \frac{1}{220} + \alpha < \frac{1}{8}$ for arbitrary $\alpha$.

6 Conclusion and Further Research

We have assumed a largeness parameter of $\gamma = \frac{1}{n}$, but in the full paper we extend our techniques to $\gamma = \frac{c}{n}$ for constant c. We can obtain approximate equilibria approaching $\varepsilon = \frac{c}{8}$ for $c \le 2$ and $\varepsilon = \frac{1}{2} - \frac{1}{2c}$ for $c >2$. In the full paper, we also extend our techniques to games where players have k strategies.

An obvious question raised by our results is the possible improvement in the additive approximation obtainable since pure approximate equilibria are known to exist for these games. A slightly weaker objective than this would be the search for well-supported approximate equilibria. It would also be interesting to investigate lower bounds in the completely uncoupled setting. Finally, since our algorithms are randomised, it would be interesting to see what can be achieved using deterministic algorithms.