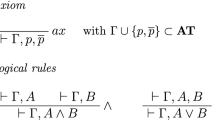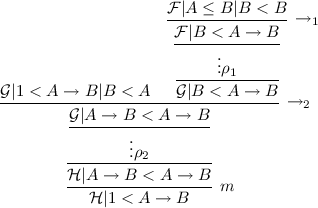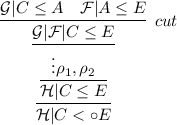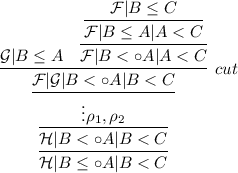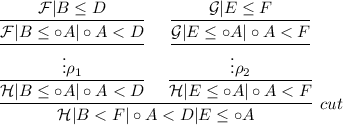Cut Elimination for Gödel Logic with an Operator Adding a Constant

Abstract

We consider an extension of propositional Gödel logic by an unary operator that enables the addition of a positive real to truth values. We provide a suitable calculus of relations and show completeness and cut elimination.

Partially supported by FWF grants P-26976-N25, I-1897-N25, I-2671-N35, and W1255-N23.

1 Introduction

Propositional Gödel logic is an extension of intuitionistic logic that takes truth values in the set [0, 1]. We consider an extension of Gödel logic by a unary operator $\circ$ that adds a positive constant to truth values. This logic can be considered as a logic extending Gödel logic by properties of Łukasiewicz logic that themselves imply the non-recursive-enumerability of the first-order analog. The propositional fragment of this extension can be axiomatized by adding to an axiomatization of Gödel logic the following two simple formulae [2]:

• 1. $A \prec \circ A$, and

• 2. $\circ (A \rightarrow B) \leftrightarrow (\circ A \rightarrow \circ B)$.

We construct an analytic sequents-of-relations calculus based on the relations < and $\le$, where $\le$ corresponds to implication ($A \rightarrow B$) and < corresponds to the connective $\prec$, where $A \prec B$ is defined as $(B \rightarrow A) \rightarrow B$. In Sect. 4, we prove cut elimination of the calculus using a Gentzen-style argument based on inductive decomposition of formulae. This calculus is surprisingly more closely related to usual sequent calculi than to the only known analytic calculus for Łukasiewicz propositional logic (see [3, 4]). Although it is very simple, its cut elimination is not that straightforward due to the asymmetry of the new operator $\circ$. Indeed, we make use of two technical tools that are not otherwise required: the first one is Avron’s communication rule; the second one is the following artificial-looking cut:

$$\begin{aligned} {\frac{A< A}{1 < A}} \end{aligned}$$

This rule is eliminated together with the other cuts.

2 Preliminaries

Definition 1

We consider the language $\mathcal {L}$ of propositional logic, augmented with a unary operator $\circ$. A propositional Gödel $\circ$ -valuation ${\mathfrak I}$ is a function from the set of propositional variables into [0, 1] with ${\mathfrak I}(\bot ) = 0$ and ${\mathfrak I}(\top ) = 1$, together with a real number $c \in (0, 1]$. This valuation can be extended to a function mapping formulas from $\mathcal {L}$ into [0, 1] as follows:

$$\begin{aligned} {\mathfrak I}(A\wedge B)&= \min \{{\mathfrak I}(A),{\mathfrak I}(B)\},\\ {\mathfrak I}(A\vee B)&= \max \{{\mathfrak I}(A),{\mathfrak I}(B)\},\\ {\mathfrak I}(A\rightarrow B)&= {\left\{ \begin{array}{ll}{\mathfrak I}(B) &{} if \ {\mathfrak I}(A) > {\mathfrak I}(B), \\ 1 &{} if\ {\mathfrak I}(A) \le {\mathfrak I}(B),\end{array}\right. } \\ {\mathfrak I}(\circ A )&= \min \{{\mathfrak I}(A) + c, 1\}.\\ \end{aligned}$$

We define $\lnot A$ by $A \rightarrow \bot$ and $A \prec B$ by $(B \rightarrow A) \rightarrow B$. Thus, we get

$$\begin{aligned} {\mathfrak I}(\lnot A)&= {\left\{ \begin{array}{ll} 0 &{} \text {if}\ {\mathfrak I}(A)>0,\\ 1 &{} \text {otherwise,}\end{array}\right. }\\ {\mathfrak I}(A\prec B)&= {\left\{ \begin{array}{ll} 1 &{} \text {if } {\mathfrak I}(A) < {\mathfrak I}(B),\\ {\mathfrak I}(B) &{} \text {if }{\mathfrak I}(A) \ge {\mathfrak I}(B). \end{array}\right. } \end{aligned}$$

Note, in particular, that ${\mathfrak I}(A \prec B) = 1$ if ${\mathfrak I}(A) = {\mathfrak I}(B) = 1$. A formula is called valid if it is mapped to 1 for all valuations. The set of all formulas which are valid is called the $\circ$ -propositional Gödel logic and will be denoted by ${ G_\circ }$.

Proposition 2

A Hilbert-type axiom system for ${ G_\circ }$ is given by the following axioms and rules:

$$\begin{aligned} \mathrm {I1}&\quad \bot \rightarrow A&\mathrm {I8}&\quad (A \rightarrow B) \rightarrow [(C \rightarrow A) \rightarrow (C \rightarrow B)]\\ \mathrm {I2}&\quad A \rightarrow (B \rightarrow A)&\mathrm {I9}&\quad [A \rightarrow (C \rightarrow B)] \rightarrow [C \rightarrow (A \rightarrow B)]\\ \mathrm {I3}&\quad (A \wedge B) \rightarrow A&\mathrm {I10}&\quad (A \rightarrow C)\wedge (B \rightarrow C) \rightarrow ((A \vee B) \rightarrow C)\\ \mathrm {I4}&\quad (A \wedge B) \rightarrow B&\mathrm {I11}&\quad (C \rightarrow A) \wedge (C \rightarrow B) \rightarrow (C \rightarrow (A \wedge B))\\ \mathrm {I5}&\quad A \rightarrow (B \rightarrow (A \wedge B))&\mathrm {I12}&\quad (A \rightarrow (B \rightarrow C)) \rightarrow (A \wedge B \rightarrow C)\\ \mathrm {I6}&\quad A \rightarrow (A \vee B)&\mathrm {I13}&\quad [A \rightarrow (A \rightarrow B)] \rightarrow (A \rightarrow B) \\ \mathrm {I7}&\quad B \rightarrow (A \vee B)&\mathrm {I14}&\quad A \prec \top \\ \mathrm {R1}&\quad A \prec \circ A&\mathrm {R2}&\quad \circ (A \rightarrow B) \leftrightarrow (\circ A \rightarrow \circ B)&\\ \mathrm {G1}&\quad (A \rightarrow B) \vee (B \rightarrow A)&\mathrm {MP}&\quad {\frac{A\quad A \rightarrow B}{B}} \end{aligned}$$

Proof

(Soundness). The axioms ($\mathrm {I1}$)–($\mathrm {I14}$), as well as $\mathrm {G1}$ and $\mathrm {MP}$, are well known to be sound for any extension of Gödel Logic. If ${\mathfrak I}(\circ A) = 1$, then $A \prec \circ A$ holds. If ${\mathfrak I}(\circ A) < 1$, then ${\mathfrak I}(A) < {\mathfrak I}(\circ A)$, whence $A \prec \circ A$ holds as well. Hence, $\mathrm {R1}$ is valid.

To show validity of $\mathrm {R2}$, we distinguish two cases: (i) if ${\mathfrak I}(A) \le {\mathfrak I}(B)$, then ${\mathfrak I}(\circ A) \le {\mathfrak I}(\circ B)$, whereby $1 = {\mathfrak I}(\circ (A \rightarrow B)) = {\mathfrak I}(\circ B)$. Hence, $\mathrm {R2}$ holds. (ii) If ${\mathfrak I}(A) > {\mathfrak I}(B)$, then ${\mathfrak I}(A \rightarrow B) = {\mathfrak I}(B)$, and so ${\mathfrak I}(\circ (A \rightarrow B)) = {\mathfrak I}(\circ B)$. Thus, $\circ (A\rightarrow B) \rightarrow (\circ A \rightarrow \circ B)$. Now, either ${\mathfrak I}(\circ A) \le {\mathfrak I}(\circ B)$ holds, whence $1 = {\mathfrak I}(\circ B) = {\mathfrak I}(\circ A)$ follows, or ${\mathfrak I}(\circ A) > {\mathfrak I}(\circ B)$ holds, whence ${\mathfrak I}(\circ A \rightarrow \circ B) = {\mathfrak I}(\circ B)$. In any case, $\mathrm {R2}$ holds.

(Completeness). In [2, Theorem 3, (c)], it was shown that the axiom system obtained by replacing $\mathrm {R1}$ by the two axioms

• 1. $(\bot \prec \circ \bot ) \rightarrow (A \prec \circ A)$,

• 2. $(\bot \leftrightarrow \circ \bot ) \rightarrow (A \leftrightarrow \circ A)$,

is complete for ${ G_\circ }^+$, a variation of ${ G_\circ }$ where c could be taken to be zero. $(\bot \prec \circ \bot )$ is an instance of $\mathrm {R1}$ and therefore $\mathrm {R1}$ and $\mathrm {R2}$ are sufficient to derive 1 and 2 above if c is not zero. $\quad \square$

We remark that the deduction theorem holds for the axiom system given by Proposition 2 because it holds for its restriction without the operator $\circ$.

3 The Calculi ${ \mathsf {RG}_\circ ^- }$ and ${ \mathsf {RG}_\circ }$

We will define a sequents-of-relations calculus ${ \mathsf {RG}_\circ }$, as well as a fragment thereof, called ${ \mathsf {RG}_\circ ^- }$. As we show, the calculus ${ \mathsf {RG}_\circ ^- }$ is already sound and complete (Proposition 4). Moreover, ${ \mathsf {RG}_\circ }$ admits cut elimination. This is proved in Sect. 4.

Herein a sequent is a finite set of components of the form $A < B$ or $A \le B$ for formulae A, B. We denote sequents by expressions of the form

$$A_1 \lhd _1 B_1 | \ldots | A_n \lhd _n B_n ,$$

where the sign $\lhd _i$ is either < or $\le$ and plays a role similar to the sequent arrow in traditional sequent calculi. By ‘component,’ we always mean ‘an occurrence of the component,’ e.g., the sequent $A< B | A < B$ has two components.

We say a component $A < B$ is satisfied by an interpretation ${\mathfrak I}$ if ${\mathfrak I}(A \prec B) = 1$ and a component $A \le B$ is satisfied by an interpretation ${\mathfrak I}$ if ${\mathfrak I}(A \rightarrow B) = 1$. A sequent $\varSigma$ is satisfied by ${\mathfrak I}$ if ${\mathfrak I}$ satisfies at least one of its components. Thus, the separation sign “|” is interpreted as disjunction at the meta-level. A sequent $\varSigma$ is valid if it is satisfied by all interpretations.

The axioms of ${ \mathsf {RG}_\circ ^- }$ are:

$$\begin{aligned} \mathrm {A1.}&\quad A \le A&\mathrm {A2.}&\quad 0 \le A&\mathrm {A3.}&\quad A < 1.&\end{aligned}$$

The external structural rules are¹:

$$\begin{aligned} \frac{{ \mathcal {H} }| A< B | A< B}{{ \mathcal {H} }| A < B}c_1 \,\,\,\, \frac{{ \mathcal {H} }| A \le B | A \le B }{{ \mathcal {H} }| A \le B}c_2 \end{aligned}$$

$$\begin{aligned} \frac{{ \mathcal {H} }}{{ \mathcal {H} }| A < B }\,w_1 \,\,\,\, \frac{{ \mathcal {H} }| A \lhd _1 B \qquad { \mathcal {H} }| C \lhd _3 D }{{ \mathcal {H} }| A \lhd _3 D | C \lhd _4 B }\,com \end{aligned}$$

where either $\lhd _1\,=\,\lhd _2\,=\,\le$ and $\{\lhd _3, \lhd _4\} = \{<, \le \}$, or $< \ \in \{\lhd _1, \lhd _2\}$ and $\lhd _{3}\,=\,\lhd _{4}\,=\,<$. The internal structural rules are

$$\begin{aligned} \frac{{ \mathcal {H} }| A< B}{ { \mathcal {H} }| A \le B}\,w_2 \,\,\,\, \frac{{ \mathcal {H} }|A \le B}{{ \mathcal {H} }| A < C | C \le B}\,w_3 \end{aligned}$$

$$\begin{aligned} \frac{ { \mathcal {H} }| A \le B}{{ \mathcal {H} }| A \le C | C< B}\,w_4 \,\,\,\, \frac{ { \mathcal {H} }| A< B}{{ \mathcal {H} }| A< C | C < B}\,w_5 \end{aligned}$$

$$\begin{aligned} \frac{ { \mathcal {H} }| A< B \qquad { \mathcal {H} }| B< C }{{ \mathcal {H} }| A< C}\,cut_1 \,\,\,\, \frac{ { \mathcal {H} }| A< B \qquad { \mathcal {H} }| B \le C }{{ \mathcal {H} }| A < C}\,cut_2 \end{aligned}$$

$$\begin{aligned} \frac{ { \mathcal {H} }| A \le B \qquad { \mathcal {H} }| B< C }{{ \mathcal {H} }| A < C}\,cut_3 \,\,\,\, \frac{{ \mathcal {H} }| A \le B \qquad { \mathcal {H} }| B \le C }{{ \mathcal {H} }| A \le C}\,cut_4 \end{aligned}$$

We proceed to logical inferences. The rules for conjunction and disjunction are obtained by replacing $\lhd$ by < or $\le$ in the following rules:

$$\begin{aligned} \frac{{ \mathcal {H} }| C \lhd A \quad { \mathcal {H} }| C \lhd B}{{ \mathcal {H} }| C \lhd (A \wedge B)}\wedge ^{\lhd }_1 \,\,\,\, \frac{ { \mathcal {H} }| A \lhd C | B \lhd C }{{ \mathcal {H} }| (A \wedge B) \lhd C}\wedge ^{\lhd }_2 \end{aligned}$$

$$\begin{aligned} \frac{ { \mathcal {H} }| C \lhd A | C \lhd B}{{ \mathcal {H} }|C \lhd (A \vee B) }\vee ^{\lhd }_1 \,\,\,\, \frac{ { \mathcal {H} }| A \lhd C \qquad { \mathcal {H} }| B \lhd C }{{ \mathcal {H} }| (A \vee B) \lhd C}\vee ^{\lhd }_2 \end{aligned}$$

The rules for implication are:

$$\begin{aligned} \frac{{ \mathcal {H} }| A \le B \mid C< B }{{ \mathcal {H} }| C< (A \rightarrow B)}\rightarrow _1 \,\,\,\,\, \frac{ { \mathcal {H} }| 1< C | B< A \qquad { \mathcal {H} }| B< C }{{ \mathcal {H} }| (A \rightarrow B) < C}\rightarrow _2 \end{aligned}$$

$$\begin{aligned} \frac{ { \mathcal {H} }| A \le B \mid C \le B}{{ \mathcal {H} }| C \le (A \rightarrow B) }\rightarrow _3 \,\,\,\, \frac{{ \mathcal {H} }| 1 \le C \mid B < A \qquad { \mathcal {H} }| B \le C }{{ \mathcal {H} }|(A \rightarrow B) \le C }\rightarrow _4 \end{aligned}$$

Finally, the rules for the operator $\circ$ are as follows:

$$\begin{aligned} \frac{{ \mathcal {H} }| A \le B}{{ \mathcal {H} }| A < \circ B}\circ _1 \,\,\,\, \frac{ { \mathcal {H} }| A \le B}{{ \mathcal {H} }| \circ A \le \circ B}\circ _2 \end{aligned}$$

The rule $w_1$ is an internal weakening. By external weakening we mean one of $w_2$–$w_5$. The critical components of an inference are those displayed above, i.e., all components not in ${ \mathcal {H} }$. We say a component is introduced by an inference if it appears in its conclusion but is not among its premises. The concept of a formula being introduced by an inference is defined analogously. An end-segment of a proof $\pi$ is a downwards-closed subset of $\pi$ taken as a tree.

Lemma 3

• 1. Modus ponens, i.e., the sequent $A \le B | A \rightarrow B \le B$, is derivable in ${ \mathsf {RG}_\circ ^- }$.

• 2. ${ \mathsf {RG}_\circ ^- }$ derives $1 \le A \rightarrow B$ if, and only if, it derives $A \le B$.

• 3. ${ \mathsf {RG}_\circ ^- }$ derives $1 < A \prec B$ if, and only if, it derives $A < B$.

• 4. ${ \mathsf {RG}_\circ ^- }$ derives $1 \le A \vee B$ if, and only if, it derives $1 \le A | 1 \le B$. ${ \mathsf {RG}_\circ ^- }$ derives $1 < A \vee B$ if, and only if, it derives $1< A | 1 < B$.

Proof

1. Modus ponens is derived as follows:

2. From $A \le B$, we derive $1 \le A \rightarrow B$ by $w_1$ and $\rightarrow _3$. Assume $1 \le A \rightarrow B$ is derivable. The following computation, starting from modus ponens, shows $A \le B$ is derivable:

3. Proceed as follows, where (*) as is obtained from $1 \le (B \rightarrow A) \rightarrow B$ as in 2:

4. We deal only with $\le$. The other case is analogous. One implication is obtained immediately by applying $\vee _1^\lhd$. For the converse:

$\quad \square$

Proposition 4

The calculus ${ \mathsf {RG}_\circ ^- }$ is sound and complete for the intended interpretation.

Proof

(Soundness). The proof relies on a sequents-of-relations calculus for Gödel Logic formulated in [1]. Therein < is interpreted in such a way that $A < B$ is satisfied if and only if ${\mathfrak I}(A) < {\mathfrak I}(B)$. All axioms and rules coincide under both interpretations of < except for rule $(\rightarrow _2)$ and axiom A3. Axiom A3 is clearly sound. To verify that rule $(\rightarrow _2)$ is valid, note that $A \rightarrow B < C$ is equivalent to $(A \le B \wedge 1< C) \vee (B< A \wedge B < C)$. By distributing, we see that it is also equivalent to the formula

$$\begin{aligned} (A \le B \vee B< A) \wedge (A \le B \vee B< C) \wedge (1< C \vee B< A) \wedge (1< C \vee B < C). \end{aligned}$$

The first conjunct is a tautology. As $1 < C$ implies $B < C$, the fourth conjunct reduces to $B < C$, which subsumes the second one. This gives the validity of the rule. Finally, axioms $\circ _1$ and $\circ _2$ are clearly sound.

(Completeness). It suffices to note that any cut-free proof in the complete calculus in [1] can be simulated by the axioms and rules of ${ \mathsf {RG}_\circ ^- }$ using axioms and weakening rules to obtain the axioms of the former. Any proof of $1 \le A$, where A is a formula already valid in Gödel Logic can be simulated in ${ \mathsf {RG}_\circ ^- }$. The only rule in [1] which is different to the corresponding rule in ${ \mathsf {RG}_\circ ^- }$ has premises which are weakenings of the premises of the original rule. Thus, it suffices to verify that the axioms involving $\circ$ are derivable in ${ \mathsf {RG}_\circ ^- }$. Axiom $(\mathrm {R1})$ can be derived directly by rule $\circ _1$. Axiom $(\mathrm {R2})$ can be derived from modus ponens by the following two inferences:

Since we can derive $1 \le A$ for all instances of any axiom, as well as modus ponens, we can use rule $cut_4$ to obtain $1 \le A$ for any formula derivable in the Hilbert-style calculus given by Proposition 2. $\quad \square$

Corollary 5

All true sequents are derivable in ${ \mathsf {RG}_\circ ^- }$.

Proof

Assume $A_1 \lhd B_1 | ... | A_n \lhd B_n$ is a true sequent, where each occurrence of $\lhd$ is either < or $\le$. By Proposition 4, the sequent $1 \le \bigvee _i A_i \gg B_i$ is derivable, where each occurrence of $\gg$ is either $\rightarrow$ or $\prec$, as appropriate. By Lemma 3.4, the sequent $1 \lhd A_1 \gg B_1 | ... | 1 \lhd A_n \gg B_n$ is derivable. Finally, by Lemmas 3.2 and 3.3, $A_1 \lhd B_1 | ... | A_n \lhd B_n$ is derivable, as desired. $\quad \square$

Proposition 6

Compound axioms are derivable in ${ \mathsf {RG}_\circ ^- }$ from atomic axioms.

Proof

We consider only the axiom $F \le F$ for simplicity. The others are similar. Proceed by induction:

• 1. $F = A \wedge B$:

  

• 2. $F = A \vee B$:

  

• 3. $F = A \rightarrow B$:

  

• 4. $F = \circ A$:

  $$\begin{aligned} \frac{A \le A}{\circ A \le \circ A}\circ _2 \end{aligned}$$

$\quad \square$

3.1 An Extension

We consider an auxiliary extension of ${ \mathsf {RG}_\circ ^- }$ by the following self-cut rule:

$$\begin{aligned} \frac{{ \mathcal {H} }| A< A }{{ \mathcal {H} }| 1 < A}m \end{aligned}$$

It is easy to see that this rule is valid.

Definition 7

The calculus ${ \mathsf {RG}_\circ }$ is the extension of ${ \mathsf {RG}_\circ ^- }$ resulting by the addition of the self-cut rule.

In the following section, we show that ${ \mathsf {RG}_\circ }$ admits cut elimination. By a cut, we mean either any instance of $cut_1$–$cut_4$, or an instance of m. This addition corresponds operationally to the extension of ${ \mathsf {LK} }$ or ${ \mathsf {LJ} }$ by the mix rule.

4 Cut Elimination

The following is the main theorem:

Theorem 8

${ \mathsf {RG}_\circ }$ admits cut elimination; hence, so too does ${ \mathsf {RG}_\circ ^- }$.

To prove Theorem 8, we need a few auxiliary lemmata. We state and prove them now. As the reader will notice, we will sometimes omit cases and/or labeling of rules if we deem it harmless.

Lemma 9

If there exists a cut-free proof of a sequent ${ \mathcal {H} }$, then there exists a cut-free proof of ${ \mathcal {H} }$ where all instances of $w_3$–$w_5$ are such that the formula introduced in the critical components is either atomic or of the form $\circ C$.

Proof

This can be checked by induction on the size of the introduced formula. We consider the inference $w_5$. The others are taken care of analogously. For example, a weakening introducing $A \wedge B$, can be replaced as follows:

If the introduced formula is of the form $A \rightarrow B$, then consider the following derivation:

The other cases are treated similarly. $\quad \square$

Lemma 10

For any proof $\pi$ ending with an instance of m cutting an atomic A and otherwise cut-free, there exists a proof agreeing with $\pi$ up to that inference, with no instances of m, and such that all cuts have A as cut formula.

Proof

We proceed by going upwards through $\pi$ up to the point where $A < A$ was introduced and modifying $\pi$ as follows:

• 1. If the inference is some weakening, say $w_3$, of the form

  $$\begin{aligned} \frac{{ \mathcal {H} }| A \le B}{{ \mathcal {H} }| A < A | A \le B}w_3 \end{aligned}$$

  then modify $\pi$ by omitting this inference. At the end of the proof, add an instance of $w_1$ as follows:

  $$\begin{aligned} \frac{{ \mathcal {H} }}{{ \mathcal {H} }| 1 < A}w_1 \end{aligned}$$

• 2. If the inference is an instance of com, say

  $$\begin{aligned} \frac{{ \mathcal {H} }| A< B \qquad { \mathcal {H} }| C< A }{{ \mathcal {H} }| A< A | C < B}com \end{aligned}$$

  Replace this inference with appropriate instances of $cut_1$ and $w_1$.

• 3. If the inference is a contraction, apply these three steps to each of the two occurrences of $A < A$.

The resulting proof is as required.

$\quad \square$

Lemma 11

If $\pi$ is an otherwise-cut-free proof of ${ \mathcal {H} }$ whose last inference is an atomic instance of one of $cut_1$–$cut_4$, then there is a cut-free proof of ${ \mathcal {H} }$.

Proof

Suppose for definiteness that the last inference is an atomic instance of $cut_4$. Consider the end-segment of the proof of the form

where $\mathcal {G}| C < A$ is the sequent that introduces the indicated instance of $C<A$. We proceed by cases according to how $C < A$ was inferred. Repeatedly apply any of the following steps until the proof is as desired:

• 1. If the inference is an instance of $w_5$ of the form

  $$\begin{aligned} \frac{\mathcal {G}'| C< B}{\mathcal {G}' | C< A | A < B}w_5 \end{aligned}$$

  we apply an instance of communication as follows:

  $$\begin{aligned} \frac{\mathcal {G}' | C< B \qquad { \mathcal {H} }| A< D }{\mathcal {G}' | { \mathcal {H} }| C< D | A < B}com \end{aligned}$$

  but then the lower hypersequent is simply $\mathcal {G} | { \mathcal {H} }| C < D$. Repeat the proof $\rho$ below this hypersequent to obtain ${ \mathcal {H} }| C < D$.

• 2. If the inference is an instance of $w_1$, instead, weaken to introduce the sequent $C < D$ and apply $\rho$ to arrive at ${ \mathcal {H} }| C < D$.

• 3. If the inference is an instance of com, say,

  $$\begin{aligned} \frac{\mathcal {G}' | B< A \quad \mathcal {G}' | C< E }{\mathcal {G}' | C< A | B < E}com \end{aligned}$$

  we apply the cut rule before this instance of communication as follows:

  

• 4. If the inference is a contraction, then apply the four steps at the inference where each of the two instances of $C < A$ is introduced.

• 5. A remaining possibility is that the cut formula A is the constant 1 introduced via an axiom in the left-hand side. In this case, the component $1 < D$ on the right-hand side can only be introduced either via an external weakening, in which case we proceed as in case 1, or via an internal weakening, in which case we replace the inference by an instance of com.

$\quad \square$

Lemma 12

Suppose $\pi$ is a cut-free proof of ${ \mathcal {H} }| \circ A \le B$. Then there is a cut-free proof of ${ \mathcal {H} }| A < B$.

Proof

We proceed according as how the sequent $\circ A \le B$ is inferred. There are three cases. (i) If $\circ A \le B$ is inferred by an instance of $w_1$, then simply apply $w_1$ to infer $A < B$. Else, either (ii) $\circ A \le B$ is the critical sequent of an inference

$$\begin{aligned} \frac{{ \mathcal {H} }| A \le C }{{ \mathcal {H} }| \circ A \le \circ C}\circ _2 \end{aligned}$$

(1)

in which case we replace (1) by

$$\begin{aligned} \frac{{ \mathcal {H} }| A \le C }{{ \mathcal {H} }| A < \circ C}\circ _1 \end{aligned}$$

or (iii) the sequent is obtained through a weakening:

$$\begin{aligned} \frac{{ \mathcal {H} }| C \le D }{{ \mathcal {H} }| C < \circ A | \circ A \le D} \end{aligned}$$

If so, we replace this inference as follows:

   $\square$

Lemma 13

For any proof $\pi$ ending with an instance of m cutting a formula $\circ A$ and otherwise cut-free, there exists a proof agreeing with $\pi$ up to that inference, with no instances of m, and such that all cuts have A as cut formula.

Proof

As before, let $\mathcal {G} | \circ A < \circ A$ be the hypersequent where $\circ A < \circ A$ is inferred. If $\mathcal {G} | \circ A < \circ A$ is the lower sequent of an inference $\circ _1$, then apply Lemma 12 to obtain a cut-free proof of $\mathcal {G} | A < A$ and infer $\mathcal {G} | 1 < A$ by m. Apply Lemma 10 to obtain a proof agreeing with $\pi$ up to this point and where all cuts have A as cut formula and infer $\mathcal {G} | 1 < \circ A$ using $\circ _1$. Finally, adjoin to the resulting proof the second half of $\pi$.

If $\mathcal {G} | \circ A < \circ A$ is the lower sequent of an inference

$$\begin{aligned} \frac{\mathcal {G}' | C< \circ A \quad \mathcal {G}' | \circ A< D }{\mathcal {G}' | \circ A< \circ A | C < D}com \end{aligned}$$

then replace this inference with an instance of $cut_1$ and $w_1$ to obtain $\mathcal {G}' | C< D | 1 < \circ A$.

Finally, if $\mathcal {G} | \circ A < \circ A$ is the lower sequent of an instance of an internal weakening, say,

$$\begin{aligned} \frac{\mathcal {G}' | \circ A \le D }{\mathcal {G}' | \circ A < \circ A | \circ A\le D} \end{aligned}$$

then simply replace this weakening with an external weakening $w_1$ with critical formula $1 < \circ A$. $\quad \square$

Lemma 14

If $\pi$ is an otherwise cut-free proof of ${ \mathcal {H} }$ whose last inference is an instance of $cut_1$–$cut_4$ with cut formula $\circ A$, then there is a proof of ${ \mathcal {H} }$ whose only cuts have A as cut formula.

The proof of Lemma 14 may be found in the Appendix. With this, we can proceed to:

Proof of Theorem 8. We proceed by going downwards through the proof. By induction, assume we are given a proof whose only cut is the last inference I. We proceed by a simultaneous induction on the complexity of the cut formula and the type of cut. Specifically, we successively transform the proof to obtain one of the following:

• 1. a proof whose only cuts have as cut formula a proper subformula of the initial cut formula, provided I is an instance of one of $cut_1$–$cut_4$;

• 2. if I is an instance of m, then we obtain either a proof whose only cuts are instances of $cut_1$–$cut_4$ with the same cut formula as I, or a proof whose only cut is an instance of m and with a proper subformula of the initial cut formula as cut formula.

If the cut formula is atomic (including the case where it is the constant1), proceed by applying Lemma 10 or Lemma 11, as appropriate. If it is of the form $\circ A$, apply Lemma 13 or Lemma 14. We consider only one more case—implication. For example, suppose there is an end-segment of the proof of the form

Replace the end-segment of the proof with

Suppose the last inference is an instance of m with cut formula $A \rightarrow B$. Since both the left-hand and right-hand sides of the component must be introduced, we can assume by Lemma 9 that they are introduced by a logical inference. Hence, the proof must have an end-segment with one of the following forms:

• 1.
  
• 2.
  

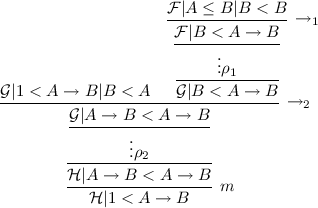
In this case, replace the end-segment with the following:

$\quad \square$

As a consequence of the cut-elimination theorem, we obtain the following result. Say a rule A / B is strongly sound if under every interpretation $\mathfrak I$, $\mathfrak I(A) = 1$ implies $\mathfrak I(B) = 1$.

Corollary 15

Every strongly sound rule can be eliminated.

Proof

As the deduction theorem holds for the Hilbert-style calculus, every strongly sound rule can be eliminated by the addition of a valid formula and cuts. The valid formula can be proved and the cuts eliminated. $\quad \square$

5 Conclusion

It is not clear whether the communication rule is actually essential for the proof. It remains open whether it can be eliminated from the cut-free calculus. If this were the case, then one could arrive at a Maehara-style proof of interpolation, i.e., construct interpolants by induction on the depth of cut-free proofs (see [5] for the classical and intuitionistic formulation of the lemma).

Appendix

Proof of Lemma 14. The end-segment of the proof will be of the form

where $C < \circ A$ and $\circ A < D$ are inferred, respectively, at the hypersequents $\mathcal {G}| C < \circ A$ and $\mathcal {F}| \circ A < D$. We proceed according to which inferences were used above $\mathcal {G}| C < \circ A$ and $\mathcal {F}| \circ A < D$.

• 1. If the inferences were respectively $\circ _1$ or $\circ _2$, so that the proof is

  

  then replace it with

  

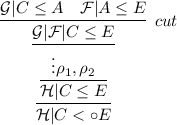
• 2. If the inferences were both $\circ _2$, so that the proof is

  

  then replace it with

  

• 3. If the inference on the left-hand side is $\circ _1$ and the inference on the right-hand side is an internal weakening, the proof will be of the form

  

  Replace it with

  

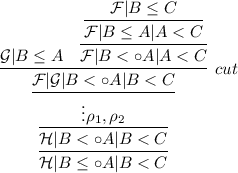
• 4. If the inference on the left-hand side is $\circ _2$ and the inference on the right-hand side is an internal weakening, the proof will be of the form

  

  Replace it with

  

• 5. If the inference on the right-hand side is $\circ _2$ and the inference on the left-hand side is an internal weakening, the proof will be of the form

  

  Replace it with

  

• 6. The final case is that both inferences are internal weakenings:

  

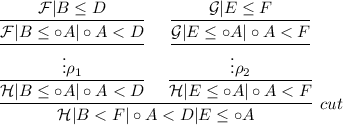
  Replace it with

  

$\quad \square$