Abstract
We study the polynomial time approximation of the max k-vertex cover problem in bipartite graphs and propose a purely combinatorial algorithm that beats the only such known algorithm, namely the greedy approach. We present a computer-assisted analysis of our algorithm, establishing that the worst case approximation guarantee is bounded below by 0.821.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
- Approximation Guarantee
- Computer-assisted Analysis
- Semiregular Bipartite Graph
- Generalized Reduced Gradient (GRG)
- Approximation Ratio
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
In max k-vertex cover, a graph \(G=(V,E)\) with \(|V| = n\) and \(|E| = m\) is given together with an integer \(k \leqslant n\). The goal is to find a subset \(K \subseteq V\) with k vertices such that the total number of edges covered by K is maximized. We say that an edge \(e = \{u,v\}\) is covered by a subset of vertices K if \(K \cap e \ne \emptyset \). max k-vertex cover is NP-hard in general graphs (as a generalization of min vertex cover) and it remains so in bipartite graphs [1, 2].
The approximation of max
k-vertex cover has been originally studied in [3], where ratio  (\(\approx 0.632\)) is achieved by the natural greedy algorithm. This ratio is tight even in bipartite graphs [4]. Using a sophisticated linear programming method, the approximation ratio for max
k-vertex cover was improved to
(\(\approx 0.632\)) is achieved by the natural greedy algorithm. This ratio is tight even in bipartite graphs [4]. Using a sophisticated linear programming method, the approximation ratio for max
k-vertex cover was improved to  [5], which, until very recently, was the best known ratio even in bipartite graphs. The best approximation ratio in bipartite graphs is now
[5], which, until very recently, was the best known ratio even in bipartite graphs. The best approximation ratio in bipartite graphs is now  and is still based on linear programming [2]. A direct reduction from min vertex cover shows that max
k-vertex cover can not admit a polynomial time approximation schema (PTAS), unless \(\mathbf {P} = \mathbf {NP}\) [6].
and is still based on linear programming [2]. A direct reduction from min vertex cover shows that max
k-vertex cover can not admit a polynomial time approximation schema (PTAS), unless \(\mathbf {P} = \mathbf {NP}\) [6].
Finally, we may observe that max k-vertex cover is easy in semiregular bipartite graphs (where all the vertices of each color class have the same degree). Indeed, any k vertices in the color class of maximum degree yield an optimal solution. Obviously, if this color class contains less than k vertices, then one can cover all the edges.
Our Contribution. The principal motivation of this paper is to determine to what extent combinatorial methods compete with linear programming for max
k-vertex cover. In other words, what ratio can a purely combinatorial algorithm guarantee? To this purpose, we first devise a very simple algorithm that guarantees approximation ratio  , improving so the ratio of the greedy algorithm in bipartite graphs. The proof is given in [7]. Our main contribution consists of an approximation algorithm which computes six distinct solutions and returns the best among them.
, improving so the ratio of the greedy algorithm in bipartite graphs. The proof is given in [7]. Our main contribution consists of an approximation algorithm which computes six distinct solutions and returns the best among them.
Analyzing the performance guarantee of such an algorithm is a challenging task. Indeed, there is no obvious way to compare the different solutions and argue globally over a lower bound on the maximum value taken by the six solutions. The large number of variables (in all, 48) used to express the many solution values participates in the difficulty of the analysis.
Similar situation was faced, for example, in [8] where the authors gave a 0.921 approximation guarantee for max cut in graphs of maximum degree 3 (and an improved 0.924 for 3-regular graphs) by a computer-assisted analysis of the quantities generated by theoretically analyzing a particular semi-definite relaxation of the problem at hand. Similarly, by setting up a suitable non-linear program and solving it, we give a computer-assisted analysis of a 0.821-approximation guarantee for max k-vertex cover in bipartite graphs. We give all the details of the implementation in [7].
2 Preliminaries
Consider a bipartite graph \(B=(V_1,V_2,E)\), instance of max k-vertex cover and fix an optimal solution O (i.e., a set of k vertices covering a maximum number of edges in E) as well as its parts \(O_1\) and \(O_2\) lying in color classes \(V_1\) and \(V_2\), respectively.
The algorithm (called \(k\text {-}{} \mathtt{VC\_ALGORITHM}\)) proposed for solving max k-vertex cover can be sketched as follows:
1. guess the cardinality \(k_1\) and therefore \(k_2=k-k_1\) of its subsets \(O_1\) and \(O_2\) lying in the color classes \(V_1\) and \(V_2\), respectively;
2. compute the sets \(S_i\) of \(k_i\) vertices in \(V_i\), \(i = 1,2\) that cover the most of edges; obviously \(S_i\) is a set of the \(k_i\) largest degree vertices in \(V_i\) (breaking ties arbitrarily);
3. guess the cardinalities \(k'_i\) of the intersections \(S_i \cap O_i\), \(i = 1, 2\);
4. compute the sets \(X_i\) of the \(k_i - k'_i\) vertices from \(V_i\), \(i = 1, 2\), that cover the most of edges in graphs \(B[(V\setminus S_1) \cup V_2]\) and \(B[V_1 \cup (V_2\setminus S_2)]\), respectively;
5. choose the best among six solutions built as described in Sect. 3.
Let us note that our  -approximation algorithm in [7] guarantees ratio
-approximation algorithm in [7] guarantees ratio  , when both \(k'_i = 0\), \(i = 1,2\).
, when both \(k'_i = 0\), \(i = 1,2\).
Sets \(S_i\), \(X_i\) and \( O_i\) separate each color class in 6 regions, namely, \(S_i \cap O_i\), \(S_i \setminus O_i\), \(X_i \cap O_i\), \(X_i \setminus O_i\), \(O_i \setminus (S_i \cup X_i)\) (denoted by \(\bar{O}_i\), in what follows) and \(V_i \setminus (S_i \cup X_i \cup O_i)\). In total, there exist 36 groups of edges (cuts) among them, the group \((V_1 \setminus (S_1 \cup X_1 \cup O_1), V_2 \setminus (S_2 \cup X_2 \cup O_2))\) being irrelevant as it will become clear in the sequel. We will use the following notations to refer to the values of the 35 relevant cuts (illustrated in Fig. 1.):
-
B: the number of edges in the cut \((S_1 \setminus O_1, S_2 \cap O_2)\);
-
C: the number of edges in the cut \((S_2 \setminus O_2, S_1 \cap O_1)\);
-
\(F_1,F_2,F_3\): the number of edges in the cuts \((S_1 \setminus O_1, X_2 \setminus O_2)\), \((S_1 \setminus O_1, O_2 \setminus (X_2 \cup S_2))\) and \((S_1 \setminus O_1, O_2 \cap X_2)\), respectively;
-
\(H_1, H_2\): the number of edges in the cuts \((S_1 \cap O_1, X_2 \setminus O_2)\) and \((S_1 \cap O_1, V_2 \setminus (S_2 \cup X_2 \cup O_2))\), respectively;
-
\(\{I_i\}_{i \in [6]}\): the number of edges in the cuts \((X_1 \setminus O_1, X_2 \setminus O_2)\), \((X_1 \setminus O_1, V_2 \setminus (S_2 \cup X_2 \cup O_2))\), \((O_1 \setminus (S_1 \cup X_1), X_2 \setminus O_2)\), \((O_1 \setminus (S_1 \cup X_1), V_2 \setminus (S_2 \cup X_2 \cup O_2))\), \((X_1 \cap O_1, X_2 \setminus O_2)\) and \((X_1 \cap O_1, V_2 \setminus (S_2 \cup X_2 \cup O_2))\), respectively;
-
\(J_1,J_2,J_3\): the number of edges in the cuts \(({S_2} \setminus O_2, X_1 \setminus O_1)\), \(({S_2} \setminus O_2, O_1 \setminus (S_1 \cup X_1))\) and \(({S_2} \setminus O_2, O_1 \cap X_1)\), respectively;
-
\(\{L_i\}_{i \in [9]}\): the number of edges in the cuts \((S_1 \cap O_1, S_2 \cap O_2)\), \((S_1 \cap O_1, X_2 \cap O_2)\), \((S_1 \cap O_1, O_2 \setminus (S_2 \cup X_2))\), \((X_1 \cap O_1, S_2 \cap O_2)\), \((X_1 \cap O_1, X_2 \cap O_2)\), \((X_1 \cap O_1, O_2 \setminus (S_2 \cup X_2))\), \((O_1 \setminus (S_1 \cup X_1), S_2 \cap O_2)\), \((O_1 \setminus (S_1 \cup X_1), X_2 \cap O_2)\), and \((O_1 \setminus (S_1 \cup X_1), O_2 \setminus (S_2 \cup X_2))\), respectively;
-
\(N_1,N_2\): the number of edges in the cuts \((S_2 \cap O_2, X_1 \setminus O_1)\) and \((S_2 \cap O_2, V_1 \setminus (S_1 \cup X_1 \cup O_1))\), respectively;
-
\(\{P_i\}_{i \in [5]}\): the number of edges in the cuts \(({X_2} \setminus O_2, V_1 \setminus (S_1 \cup X_1 \cup O_1))\), \(({O_2} \setminus (S_2 \cup X_2), X_1 \setminus O_1)\), \(({O_2} \setminus (S_2 \cup X_2), V_1 \setminus (S_1 \cup X_1 \cup O_1))\), \((X_2 \cap O_2, X_1 \setminus O_1)\), and \((X_2 \cap O_2, V_1 \setminus (S_1 \cup X_1 \cup O_1))\), respectively;
-
\(U_1, U_2, U_3\): the number of edges is the cuts, \((S_1 \setminus O_1, S_2 \setminus O_2)\), \((S_1 \setminus O_1, V_2 \setminus (S_2 \cup X_2 \cup O_2))\) and \((S_2 \setminus O_2, V_1 \setminus (S_1 \cup X_1 \cup O_1))\), respectively.
Denoting by \(\delta (V')\), \(V' \subseteq V\), the number of edges covered by \(V'\) and by \(\mathrm {opt}(B)\) the value of an optimal solution (i.e., the number edges covered) for max k-vertex cover in the input graph B, the following holds (see also Fig. 1):
Without loss of generality, we assume \(k_1 \leqslant k_2\) and we set: \(k_1 = \mu k_2\) (\(\mu \leqslant 1\)), \(k_1' = |S_1\cap O_1| = \nu k_1\) (\(0 \leqslant \nu \leqslant 1\)) and \(k_2' = |S_2\cap O_2| = \xi k_2\) (\(0 \leqslant \xi \leqslant 1\)). Let us note that, since \(k_i'\) vertices lie in the intersections \(S_i \cap O_i\), the following hold for \(\bar{O}_i = O_i \setminus (S_i \cup X_i)\), \(i = 1,2\): \(|\bar{O}_1| = |O_1 \setminus (S_1 \cup X_1)| \leqslant (1-\nu )k_1 = \mu (1-\nu )k_2\) and \(|\bar{O}_2| = |O_2 \setminus (S_2 \cup X_2)| \leqslant (1-\xi )k_2\). From the definitions of the cuts and using (1) to (6) and the expressions for \(|\bar{O}_1|\) and \(|\bar{O}_2|\), simple average arguments and the assumptions for \(k_1\), \(k_2\), \(k_1'\) and \(k_2'\) just above, the following holds:

For \(i= 1,2\), the two first inequalities in (8) hold because \(S_i\) is the set of \(k_i\) highest-degree vertices in \(V_i\); the third and fourth ones because the lefthand side quantities are the number of edges covered by \(X_i \cup (S_i\cap O_i)\); each of these sets has cardinality \(k_i\) and obviously covers more edges than \(O_i\); the fifth and sixth inequalities because the average degree of \(S_i\) is at least the average degree of \(X_i\) and \(|X_1| = (1-\nu )k_1\) and \(|X_2| = (1-\xi )k_2\); seventh and eighth ones because the average degree of vertices in \(S_i \cup X_i\) is at least the average degree of vertices in \(O_i \setminus (S_i \cup X_i)\); finally, for the last two inequalities the sum of degrees of the \(k_i - k_i'\) vertices in \(S_i \setminus O_i\) is at least the sum of degrees of the \(k_i - k_i'\) vertices of \(X_i\).
In Sect. 3, we specify the approximation algorithm sketched above. In [7] a computer assisted analysis of its approximation-performance is presented. The non-linear program that we set up, not only computes the approximation ratio of our algorithm but it also provides an experimental study over families of graphs. Indeed, a particular configuration on the variables (i.e., a feasible value assignments on the variables that represent the set of edges \(B,C,\dots \)) corresponds to a particular family of bipartite graphs with similar structural properties (characterized by the number of edges belonging to the several cut considered). Given such a configuration, it is immediate to find the ratio of the algorithm, because we can simply substitute the values of the variables in the corresponding ratios and output the largest one. We can view our program as an experimental analysis over all families of bipartite graphs, trying to find the particular family that implements the worst case for the approximation ratio of the algorithm. Our program not only finds such a configuration, but also provides data about the range of approximation factor on other families of bipartite graphs. Experimental results show that the approximation factor for the absolute majority of the instances is very close to 1, i.e., \(\ge 0.95\). Moreover, our program is independent on the size of the instance. We just need a particular configuration on the relative value of the variables \(B,C, \dots \), thus providing a compact way of representing families of bipartite graphs sharing common structural properties.
For the rest of the paper, we call “best” vertices a set of vertices that cover the most of uncovered edgesFootnote 1 in B. Given a solution \(\mathrm {SOL}_k(B)\), we denote by \(\mathrm {sol}_k(B)\) its value. For the quantities implied in the ratios corresponding to these solutions, one can be referred to Fig. 1 and to expressions (1) to (7).
Let us note that the algorithm above, since it runs for any value of \(k_1\) and \(k_2\), it will run for \((k_1,k_2) = (k,0)\) and (0, k). So, it will compute the optimum for the instances of [4], where the greedy algorithm attains the ratio  . Observe finally that, when \(k \geqslant \min \{|V_1|,|V_2|\}\), then \(\min \{|V_1|,|V_2|\}\) is an optimal solution since it covers the whole of E. This remark will be useful for some solutions in the sequel, for example in the completion of solution \(\mathrm {SOL}_5(B)\).
. Observe finally that, when \(k \geqslant \min \{|V_1|,|V_2|\}\), then \(\min \{|V_1|,|V_2|\}\) is an optimal solution since it covers the whole of E. This remark will be useful for some solutions in the sequel, for example in the completion of solution \(\mathrm {SOL}_5(B)\).
3 A 0.821-Approximation for the Bipartite Max k-vertex Cover
Algorithm \(k\text {-}{} \mathtt{VC\_ALGORITHM}\) builds the following max k-vertex cover -solutions:
\(\mathbf {SOL_1(B)}\) and \(\mathbf {SOL_2(B)}\), take, respectively, \(S_1\) plus the \(k_2\) remaining best vertices from \(V_2\), and \(S_2\) plus the \(k_1\) remaining best vertices from \(V_1\);
\(\mathbf {SOL_3(B)}\) takes first \(S_1 \cup X_1\) in the solution and completes it with the \((1-\mu (1-\nu ))k_2\) best vertices from \(V_2\);
\(\mathbf {SOL_4(B)}\) takes \(S_2\) and completes it either with vertices from \(V_2\), or with vertices from both \(V_2\) and \(V_1\) (as specified in the next page);
\(\mathbf {SOL_5(B)}\) takes a \(\pi \)-fraction of the best vertices in \(S_1\) and \(X_1\),  ; then, solution is completed with the \(k_1 + k_2 - \pi (2k_1 - k_1')\) best vertices in \(V_2\);
; then, solution is completed with the \(k_1 + k_2 - \pi (2k_1 - k_1')\) best vertices in \(V_2\);
\(\mathbf {SOL_6(B)}\) takes a \(\lambda \)-fraction of the best vertices in \(S_2\) and \(X_2\),  ; then solution is completed with the \(k_1 + k_2 - \lambda (2k_2 - k_2')\) best vertices in \(V_1\).
; then solution is completed with the \(k_1 + k_2 - \lambda (2k_2 - k_2')\) best vertices in \(V_1\).
Let us note that the values of \(\lambda \) and \(\pi \) are parameters that we can fix. In what follows, we analyze solutions \(\mathrm {SOL}_1(B) \ldots \mathrm {SOL}_6(B)\) computed by \(k\text {-}{} \mathtt{VC\_ALGORITHM}\) and give analytical expressions for their ratios. A fully detailed analysis of all these solutions is given in [7].
Solution \(\mathbf{SOL_1(B)}\) . The best \(k_2\) vertices in \(V_2\), provided that \(S_1\) has already been chosen, cover at least the maximum of the following quantities:
So, the approximation ratio for \(\mathrm {SOL}_1(B)\) satisfies:
Solution \(\mathbf{SOL_2(B)}\). The best \(k_1\) vertices in \(V_1\), provided that \(S_2\) has already been chosen, cover at least the maximum of the following quantities:
So, the approximation ratio for \(\mathrm {SOL}_2(B)\) satisfies:
Solution \(\mathbf{SOL_3(B)}\) . Taking first \(S_1 \cup X_1\) in the solution, \(k - (k_1 + k_1 - k_1') = k_1 + k_2 - 2k_1 + k_1' = k_2 - (k_1 - k_1') = (1-\mu (1-\nu ))k_2\) vertices remain to be taken in \(V_2\). The best such vertices will cover at least the maximum of the following quantities:
where (9) corresponds to a completion by the \((1-\mu (1-\nu ))k_2\) best vertices of \(S_2\), (10) corresponds to a completion by the \((1-\mu (1-\nu ))k_2\) best vertices of \(S_2 \cup X_2\), while (11) corresponds to a completion by the \((1-\mu (1-\nu ))k_2\) best vertices of \(S_2 \cup X_2 \cup \bar{O}_2\). The denominator \(3-2\xi \) in (11) is due to the fact that, using the expression for \(\bar{O}_2\), \(|S_2 \cup X_2 \cup (O_2 \setminus (S_2 \cup X_2))| \leqslant (3-2\xi )k_2\). So, the approximation ratio for \(\mathrm {SOL}_3(B)\) is:
Solution \(\mathbf{SOL_4(B).}\) Once \(S_2\) is taken in the solution, \(k_1 = \mu k_2\) are still to be taken. Completion can be done in the following ways:
-
1.
if \(k_1 \leqslant k_2 - k_2'\), i.e., \(\mu \leqslant 1 - \xi \), completion can be done by vertices taken either from \(X_2\), or from \(X_2 \cup \bar{O}_2\); in the first case, the best vertices taken for completion will cover at least either a
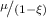 fraction of edges incident to \(X_2\); in the second case, they will cover at least a
fraction of edges incident to \(X_2\); in the second case, they will cover at least a  fraction of edges incident to \(X_2 \cup \bar{O}_2\), i.e., at least \(\mathcal {M}_1\) edges, where \(\mathcal {M}_1\) is given by: $$\begin{aligned} \max \left\{ \frac{\mu }{1-\xi }\delta \left( X_2\right) , \frac{\mu }{2(1-\xi )}\left( \delta \left( X_2\right) + F_2+L_3+L_6+L_9+P_2+P_3\right) \right\} \end{aligned}$$(13)
fraction of edges incident to \(X_2 \cup \bar{O}_2\), i.e., at least \(\mathcal {M}_1\) edges, where \(\mathcal {M}_1\) is given by: $$\begin{aligned} \max \left\{ \frac{\mu }{1-\xi }\delta \left( X_2\right) , \frac{\mu }{2(1-\xi )}\left( \delta \left( X_2\right) + F_2+L_3+L_6+L_9+P_2+P_3\right) \right\} \end{aligned}$$(13) -
2.
else, completion can be done by taking the whole set \(X_2\) and then the additional vertices taken:
-
(a)
either within the rest of \(V_2\) covering, in particular, a
 fraction of edges incident to \(\bar{O}_2\) (quantity \(\mathcal {M}_2\) in (14)),
fraction of edges incident to \(\bar{O}_2\) (quantity \(\mathcal {M}_2\) in (14)), -
(b)
or in \(S_1\) covering, in particular, a
 fraction of uncovered edges incident to \(S_1\) (quantity \(\mathcal {M}_3\) in (14)),
fraction of uncovered edges incident to \(S_1\) (quantity \(\mathcal {M}_3\) in (14)), -
(c)
or in \(S_1 \cup X_1\) covering, in particular, a
 fraction of uncovered edges incident to \(S_1\cup X_1\) (quantity \(\mathcal {M}_4\) in (14)),
fraction of uncovered edges incident to \(S_1\cup X_1\) (quantity \(\mathcal {M}_4\) in (14)), -
(d)
or, finally, in \(S_1 \cup X_1 \cup \bar{O}_1\) covering, in particular, a
 fraction of uncovered edges incident to this vertex-set (quantity \(\mathcal {M}_5\) in (14));
fraction of uncovered edges incident to this vertex-set (quantity \(\mathcal {M}_5\) in (14));
in any case such a completion will cover a number of edges that is at least the maximum of the following quantities:
$$\begin{aligned} \begin{array}{rcl} \mathcal {M}_2 &{} = &{} \min \left\{ 1, \frac{\mu -1+\xi }{1-\xi }\right\} \left( F_2 +L_3+L_6+L_9+ P_2 + P_3\right) \\ \mathcal {M}_3 &{} = &{} \frac{\mu -1+\xi }{\mu }\left( F_2 + H_2+L_3+U_2\right) \\ \mathcal {M}_4 &{} = &{} \frac{\mu -1+\xi }{\mu (2-\nu )}\left( F_2+H_2+I_2+I_6+L_3+L_6+P_2+U_2\right) \\ \mathcal {M}_5 &{} = &{} \frac{\mu -1+\xi }{\mu (3-2\nu )}\left( F_2+H_2+I_2+I_4+I_6+L_3+L_6+L_9+P_2+U_2\right) \end{array} \end{aligned}$$(14) -
(a)
Using (13) and (14), the following holds for the approximation ratio of \(\mathrm {SOL}_4(B)\):
Vertical Separations – Solutions
\(\mathbf{SOL_5(B)}\)
and
\(\mathbf{SOL_6(B)}\)
. For \(i = 1,2\), given a vertex subset \(V' \subseteq V_i\), we call vertical separation of
\(V'\)
with parameter
 , a partition of \(V'\) into two subsets such that one of them contains a c-fraction of the best (highest degree) vertices of \(V'\) (i.e., contains the \(c|V'|\) best vertices of \(V'\)). Then, the following easy claim holds for a vertical separation of \(V' \cup V''\) with parameter c.
, a partition of \(V'\) into two subsets such that one of them contains a c-fraction of the best (highest degree) vertices of \(V'\) (i.e., contains the \(c|V'|\) best vertices of \(V'\)). Then, the following easy claim holds for a vertical separation of \(V' \cup V''\) with parameter c.
Claim
Let \(A(V')\) be a c-fraction of the best vertices in \(V'\) and \(A(V'')\) the same in \(V''\). Then \(\delta (A(V')) + \delta (A(V'')) \ge c \delta (V'\cup V'')\).
Proof
Assume that in \(V'\) we have \(n'\) vertices. To form \(A(V')\) we take the \(cn'\) vertices of \(V'\) with highest degree. The average degree of \(V'\) is  . The average degree of \(A(V')\) is
. The average degree of \(A(V')\) is  . But, from the selection of \(A(V')\) as the \(cn'\) vertices with highest degree, we have that
. But, from the selection of \(A(V')\) as the \(cn'\) vertices with highest degree, we have that  . Similarly for \(V''\), i.e., \(\delta (A(V'')) \ge c \delta (V'')\).
. Similarly for \(V''\), i.e., \(\delta (A(V'')) \ge c \delta (V'')\).
Solutions \(\mathrm {SOL}_5(B)\) and \(\mathrm {SOL}_6(B)\) are based upon vertical separations of \(S_i \cup X_i\), \(i= 1,2\), with parameters \(\pi \) and \(\lambda \), called \(\pi \)- and \(\lambda \)-vertical separations, respectively.
The idea behind vertical separation, is to handle the scenario when there is a “tiny” part of the solution (i.e. few in comparison to, let’s say, \(k_1\) vertices) that covers a large part of the solution and the “completion” of the solution done by the previous cases does not contribute more than a small fraction to the final solution. The vertical separation indeed tries to identify such a small part, and then continues the completion on the other side of the bipartition.
Solution
\(\mathbf{SOL_5(B)}\)
. It consists of separating
\(S_1 \cup X_1\)
with parameter
 , of taking a
\(\pi \)
-fraction of the best vertices of
\(S_1\)
and a
\(\pi \)
-fraction of the best vertices of
\(X_1\)
in the solution and of completing it with the adequate vertices from
\(V_2\). A \(\pi \)-vertical separation of \(S_1 \cup X_1\) introduces in the solution \(\pi \left( 2k_1 - k_1'\right) = \pi (2-\nu )\mu k_2\) vertices of \(V_1\), which are to be completed with \(k - \pi (2-\nu )\mu k_2 = (1+\mu )k_2 - \pi (2-\nu )\mu k_2 = (1-\mu (2\pi -1) + \mu \nu \pi )k_2\) vertices from \(V_2\). Observe that such a separation implies the cuts with corresponding cardinalities B, C, \(F_i\), \(i = 1, 2, 3\), \(H_1\), \(H_2\), \(I_1\), \(I_2\), \(I_5\), \(I_6\), \(J_1\), \(J_3\), \(L_j\), \(j = 1, \ldots ,6\), \(N_1\), \(P_2\), \(P_4\), \(U_1\) and \(U_2\). Let us group these cuts in the following way:
, of taking a
\(\pi \)
-fraction of the best vertices of
\(S_1\)
and a
\(\pi \)
-fraction of the best vertices of
\(X_1\)
in the solution and of completing it with the adequate vertices from
\(V_2\). A \(\pi \)-vertical separation of \(S_1 \cup X_1\) introduces in the solution \(\pi \left( 2k_1 - k_1'\right) = \pi (2-\nu )\mu k_2\) vertices of \(V_1\), which are to be completed with \(k - \pi (2-\nu )\mu k_2 = (1+\mu )k_2 - \pi (2-\nu )\mu k_2 = (1-\mu (2\pi -1) + \mu \nu \pi )k_2\) vertices from \(V_2\). Observe that such a separation implies the cuts with corresponding cardinalities B, C, \(F_i\), \(i = 1, 2, 3\), \(H_1\), \(H_2\), \(I_1\), \(I_2\), \(I_5\), \(I_6\), \(J_1\), \(J_3\), \(L_j\), \(j = 1, \ldots ,6\), \(N_1\), \(P_2\), \(P_4\), \(U_1\) and \(U_2\). Let us group these cuts in the following way:
We may also notice that group \(\varPi _1\) refers to \(S_2 \setminus O_2\), \(\varPi _2\) refers to \(S_2 \cap O_2\), \(\varPi _3\) to \(X_2 \cap O_2\), \(\varPi _5\) to \(\bar{O}_2\) and \(\varPi _4\) to \(X_2 \setminus O_2\). Assume that a \(\pi _i < 1\) fraction of each group \(\varPi _i\), \(i= 1, \dots 6\) contributes in the \(\pi \) vertical separation of \(S_1 \cup X_1\). Then, a \(\pi \)-vertical separation of \(S_1 \cup X_1\) will contribute with a value:
to \(\mathrm {sol}_5(B)\). We now distinguish two cases.
Case 1: \((1-\mu (2\pi -1) + \mu \nu \pi )k_2 \geqslant k_2\), i.e., \(1-\mu (2\pi -1) + \mu \nu \pi \geqslant 1\). Then we further distinguish the following two subcases 1. and 2.:
1. \(\mu (1- 2\pi ) + \mu \nu \pi \le 1-\xi \); then, the partial solution induced by the \(\pi \)-vertical separation will be completed in such a way that the contribution of the completion is at least equal to \(\max \{Z_i, i = 1, \ldots , 5\}\), where:
\(Z_1\) refers to \(S_2\) plus the best \((1-\mu (2\pi -1) + \mu \nu \pi )k_2 - k_2 = (\mu (1- 2\pi ) + \mu \nu \pi )k_2\) vertices of \(O_2\) having a contribution of:
\(Z_2\) refers to \(S_2\) plus the best \((\mu (1- 2\pi ) + \mu \nu \pi )k_2\) vertices of \(X_2\) having a contribution of:
\(Z_3\) and \(Z_4\) refer to the best \((1-\mu (2\pi -1) + \mu \nu \pi )k_2\) vertices of \(S_2 \cup X_2\) and of \(S_2 \cup O_2\) having, respectively, contributions:
\(Z_5\) refers to the best \((1-\mu (2\pi -1) + \mu \nu \pi )k_2\) vertices of \(S_2 \cup X_2 \cup \bar{O}_2\) having a contribution of:
2. \(\mu (1- 2\pi ) + \mu \nu \pi \ge 1-\xi \); in this case, the partial solution induced by the \(\pi \)-vertical separation will be completed in such a way that the contribution of the completion is at least \(\max \{\varTheta _i, i = 1, \ldots , 3\}\), where:
\(\varTheta _1\) refers to \(S_2 \cup X_2\) plus the best \((\mu (1- 2\pi ) + \mu \nu \pi -(1-\xi ))k_2\) vertices of \(\bar{O}_2\), all this having a contribution of:
\(\varTheta _2\) refers to \(S_2 \cup O_2\) plus the best \((\mu (1- 2\pi ) + \mu \nu \pi -(1-\xi ))k_2\) vertices of \(X_2 \setminus O_2\), all this having a contribution of:
\(\varTheta _3\) refers to the best \((1-\mu (2\pi -1) + \mu \nu \pi )k_2\) vertices of \(S_2 \cup X_2 \cup \bar{O}_2\) having a contribution of:
Case 2: \(1-\mu (2\pi -1) + \mu \nu \pi < 1\). The partial solution induced by the \(\pi \)-vertical separation will be completed in such a way that the contribution of the completion is at least equal to \(\max \{\varPhi _i, i = 1, \ldots , 5\}\), where:
\(\varPhi _1\) refers to the best \((1-\mu (2\pi -1) + \mu \nu \pi )k_2\) vertices in \(S_2\) with a contribution:
\(\varPhi _2\) refers to the best \((1-\mu (2\pi -1) + \mu \nu \pi )k_2\) vertices in \(X_2\) with a contribution:
\(\varPhi _3\) refers to the best \((1-\mu (2\pi -1) + \mu \nu \pi )k_2\) vertices in \(O_2\) with a contribution:
\(\varPhi _4\) refers to the best \((1-\mu (2\pi -1) + \mu \nu \pi )k_2\) vertices in \(S_2 \cup X_2\) with a contribution:
\(\varPhi _5\) refers to the best \((1-\mu (2\pi -1) + \mu \nu \pi )k_2\) vertices in \(S_2 \cup X_2 \cup \bar{O}_2\) with a contribution:
Setting \(Z^* = \max \{Z_i: i= 1, \ldots 5\}\), \(\varTheta ^* = \max \{\varTheta _i: i = 1,2,3\}\) and \(\varPhi ^* = \max \{\varPhi _i: i= 1, \ldots 5\}\), and putting (16) and (17) together with expressions (18) to (19), we get the following lower bound for ratio \(r_5\):
Solution
\(\mathbf{SOL_6(B)}\)
. In a complete analogy with \(\mathrm {SOL}_5\), solution \(\mathrm {SOL}_6(B)\) consists of separating
\(S_2 \cup X_2\)
with parameter
 . It consists of separating
\(S_2 \cup X_2\)
with parameter
\(\lambda \), of taking a
\(\lambda \)
fraction of the best vertices of
\(S_2\)
and
\(X_2\)
in the solution and of completing it with the adequate vertices from
\(V_1\). Here, we need that
. It consists of separating
\(S_2 \cup X_2\)
with parameter
\(\lambda \), of taking a
\(\lambda \)
fraction of the best vertices of
\(S_2\)
and
\(X_2\)
in the solution and of completing it with the adequate vertices from
\(V_1\). Here, we need that  .
.
A \(\lambda \)-vertical separation of \(S_2 \cup X_2\) introduces in the solution \(\lambda (2-\xi )k_2\) vertices of \(V_2\), which are to be completed with \(k - \lambda (2-\xi )k_2 = (1+\mu )k_2 - \lambda (2-\xi )k_2 = (1+\mu - \lambda (2-\xi ))k_2\) vertices from \(V_1\).
Observe that such a separation implies the cuts with corresponding cardinalities B, C, \(F_1\), \(F_3\), \(H_1\), \(I_1\), \(I_3\), \(I_5\), \(J_i\), \(i = 1, 2, 3\), \(L_1\), \(L_2\), \(L_4\), \(L_5\), \(L_7\), \(L_8\), \(N_1\), \(N_2\), \(P_1\), \(P_4\), \(P_5\), \(U_1\) and \(U_3\). We group these cuts in the following way:
Group \(\varLambda _1\) refers to \(S_1 \setminus O_1\), \(\varLambda _2\) to \(S_1 \cap O_1\), \(\varLambda _3\) to \(X_1 \cap O_1\), \(\varLambda _5\) to \(\bar{O}_1\) and \(\varLambda _4\) to \(X_1 \setminus O_1\). Assume, as previously, that a \(\lambda _i < 1\) fraction of each group \(\varLambda _i\), \(i= 1, \dots 6\) contributes in the \(\lambda \) vertical separation of \(S_2 \cup X_2\). Then, a \(\lambda \)-vertical separation of \(S_2 \cup X_2\) will contribute with a value:
to \(\mathrm {sol}_6(B)\). We again distinguish two cases.
Case 1. \((1+\mu - \lambda (2-\xi ))k_2 \geqslant \mu k_2\), i.e., \(1+\mu - \lambda (2-\xi ) \geqslant \mu \). Here we have the two following subcases.
(a) \(1-\lambda (2-\xi ) \le (1-\nu )\mu \); then, the partial solution induced by the \(\lambda \)-vertical separation will be completed in such a way that the contribution of the completion is at least equal to \(\varUpsilon ^* = \max \{\varUpsilon _i, i = 1, \ldots , 5\}\), where: \(\varUpsilon _1\) refers to \(S_1\) plus the best \((1-\lambda (2-\xi ))k_2\) vertices of \(X_1\);
\(\varUpsilon _2\) refers to \(S_1\) plus the best \((1-\lambda (2-\xi ))k_2\) vertices of \(O_1\);
\(\varUpsilon _3\) and \(\varUpsilon _4\) refer to the best \((1+\mu - \lambda (2-\xi ))k_2\) vertices of \(S_1 \cup X_1\) and \(S_1 \cup O_1\);
\(\varUpsilon _5\) refers to the best \((1+\mu - \lambda (2-\xi ))k_2\) vertices of \(S_1 \cup X_1 \cup \bar{O}_1\). (b) \(1-\lambda (2-\xi ) \ge (1-\nu )\mu \); in this case, the partial solution induced by the \(\lambda \)-vertical separation will be completed in such a way that the contribution of the completion is at least \(\varPsi ^* = \max \{\varPsi _i, i = 1, \ldots , 3\}\), where:
\(\varPsi _1\) refers to \(S_1 \cup X_1\) plus the best \((1 - \lambda (2-\xi ) - (1-\nu ))k_2\) vertices of \(\bar{O}_1\);
\(\varPsi _2\) refers to \(S_1 \cup O_1\) plus the best \((1 - \lambda (2-\xi ) - (1-\nu ))k_2\) vertices of \(X_1 \setminus O_1\);
\(\varPsi _3\) refers to the best \((\mu +1 - \lambda (2-\xi ))k_2\) vertices of \(S_1 \cup X_1 \cup \bar{O}_1\).
Case 2. \(1+\mu - \lambda (2-\xi ) \leqslant \mu \). The partial solution induced by the \(\lambda \)-vertical separation will be completed in such a way that the contribution of the completion is at least equal to \(\varOmega ^* = \max \{\varOmega _i, i = 1, \ldots , 5\}\), where:
\(\varOmega _1\) refers to the best \((1+\mu - \lambda (2-\xi ))k_2\) vertices in \(S_1\);
\(\varOmega _2\) refers to the best \((1+\mu - \lambda (2-\xi ))k_2\) vertices in \(X_1\);
\(\varOmega _3\) refers to the best \((1+\mu - \lambda (2-\xi ))k_2\) vertices in \(O_1\);
\(\varOmega _4\) refers to the best \((1+\mu - \lambda (2-\xi ))k_2\) vertices in \(S_1 \cup X_1\);
\(\varOmega _5\) refers to the best \((1+\mu - \lambda (2-\xi ))k_2\) vertices in \(S_1 \cup X_1 \cup \bar{O}_1\).
Putting all this together we get:
The complete study of solution \(\mathrm {SOL}_6(B)\) is deferred to [7].
4 Results and Discussion
To analyze the performance guarantee of \(k\text {-}{} \mathtt{VC\_ALGORITHM}\), we set up a non-linear program and solved it to optimality. Here, we interpret the cardinalities of the edge-sets \(B,C, F_i, \dots \), as variables, the expressions in (8) as constraints and the objective function is \(\min Z (\equiv \max _{j=1}^{6} r_j)\). In other words, we try to find a value assignments to the set of variables such that the maximum among all the six ratios defined is minimized. This value would give us the desired approximation guarantee of \(k\text {-}{} \mathtt{VC\_ALGORITHM}\).
Towards this goal, we set up a GRG (Generalized Reduced Gradient [9]) program. The reasons this method is selected are presented in [7], as well as a more detailed description of the implementation. GRG is a generalization of the classical Reduced Gradient method [10] for solving (concave) quadratic problems so that it can handle higher degree polynomials and incorporate non-linear constraints.
As the values of parameters \(\pi \) and \(\lambda \) decrease, the approximation guarantee increases. The maximum of these ratios is attained for \(\pi = \lambda = 10^{-5}\). For these values, the corresponding values of ratios \(r_1 \div r_6\) computed for them are the following:

These results correspond to the cycle that outputs the minimum value for the approximation factor and this is 0.821, given by solution \(\mathrm {SOL}_5\).
To conclude, let us note that the formulation of the non-linear program we developed for bounding the ratio below, could provide useful insights for problem’s understanding and could be applied for solving the problem on other graph-classes. Finally, since the overall algorithm chooses the best among a certain number of solutions it is easily parallelizable.
Remark. As we note in [7], the GRG solver does not guarantee the global optimal solution. The 0.821 guarantee is the minimum value that the solver returns after several runs from different initial starting points. However, successive re-executions of the algorithm, starting from this minimum value, were unable to find another point with smaller value. In each one of these successive re-runs, we tested the algorithm on 1000 random different starting points (which is greater than the estimation of the number of local minima) and the solver did not find value worse that the reported one.
Notes
- 1.
For instance, “we take \(S_1\) plus the \(k_2\) best vertices in \(V_2\)” means that we take \(S_1\) and then \(k_2\) vertices of highest degree in \(B[(V_1 \setminus S_1),V_2]\).
References
Apollonio, N., Simeone, B.: The maximum vertex coverage problem on bipartite graphs. Discrete Appl. Math. 165, 37–48 (2014)
Caskurlu, B., Mkrtchyan, V., Parekh, O., Subramani, K.: On partial vertex cover and budgeted maximum coverage problems in bipartite graphs. In: Diaz, J., Lanese, I., Sangiorgi, D. (eds.) TCS 2014. LNCS, vol. 8705, pp. 13–26. Springer, Heidelberg (2014)
Hochbaum, D.S., Pathria, A.: Analysis of the greedy approach in problems of maximum \(k\)-coverage. Naval Res. Logistics 45, 615–627 (1998)
Badanidiyuru, A., Kleinberg, R., Lee, H.: Approximating low-dimensional coverage problems. In: Dey, T.K., Whitesides, S. (eds.) SoCG 2012, pp. 161–170. ACM, Chapel Hill (2012)
Ageev, A.A., Sviridenko, M.I.: Approximation algorithms for maximum coverage and max cut with given sizes of parts. In: Cornuéjols, G., Burkard, R.E., Woeginger, G.J. (eds.) IPCO 1999. LNCS, vol. 1610, p. 17. Springer, Heidelberg (1999)
Petrank, E.: The hardness of approximation: gap location. Comput. Complex. 4, 133–157 (1994)
Bonnet, E., Escoffier, B., Paschos, V.T., Stamoulis, G.: A 0.821-ratio purely combinatorial algorithm for maximum \(k\)-vertex cover in bipartite graphs. CoRR arXiv:1409.6952v2 (2015)
Feige, U., Karpinski, M., Langberg, M.: Improved approximation of max-cut on graphs of bounded degree. J. Algorithms 43, 201–219 (2002)
Abadie, J., Carpentier, J.: Generalization of the wolfe reduced gradient method to the case of non-linear constraints. In: Abadie, J., Carpentier, J. (eds.) Optimization. Academic Publishers (1969)
Frank, M., Wolfe, P.: An algorithm for quadratic programming. Naval Res. Logistics Q. 3, 95–110 (1956)
Acknowledgement
The work of the last author was supported by the Swiss National Research Foundation Early Post-Doc mobility grant P1TIP2_152282.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Bonnet, É., Escoffier, B., Paschos, V.T., Stamoulis, G. (2016). A 0.821-Ratio Purely Combinatorial Algorithm for Maximum k-vertex Cover in Bipartite Graphs. In: Kranakis, E., Navarro, G., Chávez, E. (eds) LATIN 2016: Theoretical Informatics. LATIN 2016. Lecture Notes in Computer Science(), vol 9644. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-49529-2_18
Download citation
DOI: https://doi.org/10.1007/978-3-662-49529-2_18
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-49528-5
Online ISBN: 978-3-662-49529-2
eBook Packages: Computer ScienceComputer Science (R0)






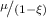 fraction of edges incident to
fraction of edges incident to  fraction of edges incident to
fraction of edges incident to  fraction of edges incident to
fraction of edges incident to  fraction of uncovered edges incident to
fraction of uncovered edges incident to  fraction of uncovered edges incident to
fraction of uncovered edges incident to  fraction of uncovered edges incident to this vertex-set (quantity
fraction of uncovered edges incident to this vertex-set (quantity