Train Rolling Bearing Degradation Condition Assessment Based on Local Mean Decomposition and Support Vector Data Description

Abstract

For effective utilization of a large amount of vibration data which are collected during the normal operation of train rolling bearing, this paper puts forward a new method for rolling bearing degradation condition assessment which combines the local mean decomposition (LMD) and support vector data description (SVDD). LMD is used to decompose the vibration signal, after the decomposition, we extract feature vector from three points of view: time–frequency, energy and entropy, statistical characteristic value. Principal component analysis can help to reduce dimension. Therefore, we just need to collect the data when rolling bearing normally operates to establish the evaluation model, and then realize the rolling bearing degradation status quantitative evaluation.

18.1 Introduction

Rolling bearing is the key component of urban rail train, whose performance directly affects the safety operation of train. In recent years, most research focus on status identification based on failure data. However, under normal working conditions, failure data is difficult to obtain. So how to use the bearing data during normal operation to assess the state of rolling bearing degradation performance has become a popular method for research these years.

In the 1970s, Jay Lee put forward the concept of equipment performance degradation. It aims to forecast the fault of product and manage its health. This study attracted much attention since it appeared both at home and abroad. In 2001, the University of Wisconsin and Michigan joined with nearly 40 companies to build an intelligent maintenance system research center; some performance degradation assessment methods are put forward in succession, such as the cerebellum model of neural network [1], the self-organizing neural network [2], logistic regression [3], hidden markov models [4], etc.

In order to extract more comprehensive signal features, in this paper, we extract feature vector from three aspects separately after local mean decomposition (LMD): time–frequency, energy and entropy, statistical characteristic value. Principal component analysis can be used to reduce the dimension and save most of the effective information at the same time. Then we build a hypersphere to measure the degradation degree by support vector data description (SVDD).

18.2 Basic Principle of the Research

18.2.1 Local Mean Decomposition

In recent years, Jonathan S. Smith put forward a new adaptive nonstationary signal processing method called LMD, which was used to analyze the computer signal and achieved a good result. After that, some scholars applied this method to the field of mechanical vibration and obtained good effect too [5]. In this paper, we use the LMD based on cubic spline function to process the vibration data. Here are the steps for LMD [6].

• Step 1: x(t) is the original signal, find all local extreme values and connect them with cubic spline curve, get the up envelope E _max(t) and low envelope E _min(t);

• Step 2: m ₁₁(t) is the local mean function and the envelope estimation function c ₁₁(t);

  $$ m_{11} (t) = \frac{{E_{\hbox{max} } (t) + E_{\hbox{min} } (t)}}{2} $$

  (18.2.1)
  $$ c_{11} (t) = \frac{{\left| {E_{\hbox{max} } (t) - E_{\hbox{min} } (t)} \right|}}{2} $$

  (18.2.2)

• Step 3: m ₁₁(t) is subtracted from the original data x(t);

  $$ h_{11} \left( t \right) = x\left( t \right) - m_{11} (t) $$

  (18.2.3)

• Step 4: h ₁₁(t) is shown as amplitude demodulated by dividing it by c ₁₁(t);

  $$ s_{11} (t) = \frac{{h_{11} \left( t \right)}}{{c_{11} (t)}} $$

  (18.2.4)

• Step 5: A smoothed local mean $m_{12} (t)$ is calculated for $s_{11} ( t )$, subtracted from demodulated using $s_{11} ( t )$, and the resulting function is amplitude demodulated using $c_{12} ( t )$. This iteration process continues n times until a purely frequency modulated signal $s_{1n} ( t )$ is obtained. So

  $$ \left\{ {\begin{array}{*{20}l} {h_{11} \left( t \right) = x\left( t \right) - m_{11} (t)} \hfill \\ {h_{12} \left( t \right) = s_{11} \left( t \right) - m_{12} (t)} \hfill \\ \vdots \hfill \\ {h_{1n} \left( t \right) = s_{1(n - 1)} \left( t \right) - m_{1n} (t)} \hfill \\ \end{array} } \right. $$

  (18.2.5)

  where

  $$ \left\{ {\begin{array}{*{20}l} {s_{11} (t) = \frac{{h_{11} \left( t \right)}}{{c_{11} (t)}}} \hfill \\ {s_{12} (t) = \frac{{h_{12} \left( t \right)}}{{c_{12} (t)}}} \hfill \\ \vdots \hfill \\ {s_{1n} (t) = \frac{{h_{1n} \left( t \right)}}{{c_{1n} (t)}}} \hfill \\ \end{array} } \right. $$

  (18.2.6)

  where the objective is that $\mathop {\lim }\limits_{n \to \infty } c_{1n} (t) = 1$.

• Step 6: $c_{1} ( t )$ is the envelope;

  $$ c_{1} (t) = c_{11} (t) \cdot c_{12} (t) \cdots c_{1n} (t) = \prod\limits_{i = 1}^{n} {c_{1i} (t)} $$

  (18.2.7)

• Step 7: $PF_{1} \left( {\text{t}} \right)$ is the component of the decomposition;

  $$ PF_{1} (t) = c_{1} (t) \cdot s_{1n} (t) $$

  (18.2.8)

• Step 8: $r_{1} ( t )$ now becomes the new data and the whole process is repeated k times until $r_{k} ( t )$ is a constant or contains no more oscillations;

  $$ \left\{ {\begin{array}{*{20}l} {r_{1} \left( t \right) = x\left( t \right) - PF_{1} (t)} \hfill \\ {r_{2} \left( t \right) = r_{1} \left( t \right) - PF_{2} (t)} \hfill \\ \vdots \hfill \\ {r_{k} \left( t \right) = r_{k - 1} \left( t \right) - PF_{k} (t)} \hfill \\ \end{array} } \right. $$

  (18.2.9)

The scheme is complete in the sense that the original signal can be reconstructed according to

$$ x(t) = \sum\limits_{v = 1}^{k} {PF_{v} (t) + r_{k} (t)} $$

(18.2.10)

18.2.2 Support Vector Data Description

SVDD, proposed by Tax and Duin [7] in the year 2004, is a model which aims at finding spherically shaped boundary around a dataset. Given a set of training data $x\left( i \right) \in R^{n} ,i = 1,2, \ldots ,l,$ Tax and Duin solved the following optimization problem:

$$ \mathop {\hbox{min} }\limits_{R,a,\xi } \left( {R^{2} + C\sum\limits_{i = 1}^{l} {\xi^{2} } } \right) $$

(18.2.11)

$$ {\text{subject}}\,{\text{to}}\quad \begin{array}{*{20}l} {\left\| {\Phi (x_{i} ) - a} \right\|^{2} \le R^{2} + \xi_{i} ,\quad i = 1, \ldots ,l,} \hfill \\ {\xi_{i} \ge 0,\quad i = 1, \ldots ,l} \hfill \\ \end{array} $$

where $\Phi$ is a function mapping the data to a higher dimensional space, and C > 0 is a user-specified parameter. After (18.2.11) is solved, a hyperspherical model is characterized by the center a and the radius R. A testing instance x is detected as an outlier if

$$ \left\| {\Phi \left( x \right) - a} \right\|^{2} \ge R^{2} $$

(18.2.12)

As can been seen from the formula, what we need to do is to find a smallest super ball to obtain all of the normal data. During this process, there must be some point far away form the center of the sphere, controlling the value of ξ could help adjust the size of the sphere. Figure 18.8 shows a sphere of SVDD in two-dimensional space, the data come from a banana dataset, the red points are the support vector.

18.3 Train Rolling Bearing Degradation Condition Assessment

18.3.1 Data Sources and the Technology Roadmap

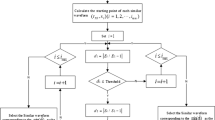
The data which this paper used was generated by the NSF I/UCR Center for Intelligent Maintenance Systems with support from Rexnord Corp. in Milwaukee, WI. The rotation speed was kept constant at 2000 RPM by an AC motor coupled to the shaft via rub belts. A radial load of 6000 lbs is applied onto the shaft and bearing by a spring mechanism. Each dataset consists of individual files that are 1-s vibration signal snapshots recorded at specific intervals. Each file consists of 20,480 points with the sampling rate set at 20 kHz. Figure 18.1 is the technology roadmap.

Fig. 18.1

The technology roadmap of this research

18.3.2 Example of Train Rolling Bearing Degradation Condition Assessment

Based on the technology roadmap mentioned, decomposing signal is the first step to processing the data. 1-s vibration signal can be divided into 34 pieces (600 points/piece, one revolution), every piece of data is decomposed by LMD. From the result of the decomposition, amount of the PF is not constant, some pieces are five, but the others are six. To solve this problem, we pick the minimum number of the PF, and cancel the other PF.

Figure 18.2 provides a process of decomposition which comes from one piece of data. As we can see from it, LMD could obtain less PF, it is convenient for extracting feature vectors. And for strengthening the difference, we add the 34 pieces feature together.

Fig. 18.2

A vibration signal and its PFs

• 1. Time–frequency domain: root mean square (RMS), peak, kurtosis, Xr, mean, crest factor, kurtosis factor, shape factor;

• 2. Energy and entropy: energy, Shanon entropy, energy moment;

• 3. Statistical characteristic value: Weibull shape parameter, Weibull scale parameters.

Figures 18.3, 18.4, and 18.6 are the features from three domains which obtain the whole life signal of the first PF.

Fig. 18.3

Time–frequency feature

Fig. 18.4

Energy and entropy feature

Fig. 18.5

Weibull distribution fitting check

Fig. 18.6

Statistical characteristic feature

Before fitting statistical distribution type, the original PF signal should be processed. Here the original vibration data is transferred by Hilbert to easily to detect an early failure, and then get the spectral envelope [8]. Figure 18.5 is checking for fitting, if the relationship is linear, the processed data is supposed to fit the statistical distribution, as we can see in the picture, it fits the distribution well (Fig. 18.6).

PCA is a method to reduce the dimension at the same time without losing important information. The principle to choose the main component is the cumulative variance contribution rate, according to it, we pick the component that occupies most of the information to be a feature vector and put it into the SVDD (Fig. 18.7).

Fig. 18.7

The whole life signal of the principal components

In this paper, the first 200 pieces (here every 34 groups become one piece, which represent the status of one second) of signal data (test data) are put into the SVDD to build a hypersphere, Gauss is chosen to be the kernel function. And the last 515 pieces of the whole life data are the test data. Here the problem is, the points and hypersphere of two-dimensional feature can be seen, but if the amount of feature dimension is above two, we cannot see any feature points and boundary, so how to adjust the parameter is the key point. Figure 18.8 is an example to show different parameters C and kernel and makes different borders, and the differences between them are obviously (the remarked points are the support vectors). From the figure, we can see that the parameter of kernel affects the shape most, to choose an appropriate parameter, this paper uses the test data to check if these points in the hypersphere we build, and change the parameter of kernel to check the error rate and then find 12.4 is the appropriate parameter kernel, as can be seen from the Fig. 18.9.

Fig. 18.8

A sphere of SVDD in two-dimensional space

Fig. 18.9

Relationship between parameter of kernel and error rate

Degradation condition assessment can be measured by the distance between the spot of the test data in the space and the center of the super ball. Figure 18.10 is the SVDD distance for the whole rolling bearing life. As we can see from Fig. 18.10, the bearing begins to degenerate at the point 700, and from the point 1600, the bearing degenerates deeply.

Fig. 18.10

Distance of SVDD

18.4 Conclusion

In this paper, the method of assessing train rolling bearing degradation status is investigated. The result show that the way we extract feature vector could better save the most of the key information, and it is also convenient for computing. What is more, SVDD can help to realize the rolling bearing degradation status quantitative evaluation using the normal operation data before the bearing completely runs out, then it is important to ensure the safety of passengers’ life and property.