PPP-Codes for Large-Scale Similarity Searching

Abstract

Many current applications need to organize data with respect to mutual similarity between data objects. A typical general strategy to retrieve objects similar to a given sample is to access and then refine a candidate set of objects. We propose an indexing and search technique that can significantly reduce the candidate set size by combination of several space partitionings. Specifically, we propose a mapping of objects from a generic metric space onto main memory codes using several pivot spaces; our search algorithm first ranks objects within each pivot space and then aggregates these rankings producing a candidate set reduced by two orders of magnitude while keeping the same answer quality. Our approach is designed to well exploit contemporary HW: (1) larger main memories allow us to use rich and fast index, (2) multi-core CPUs well suit our parallel search algorithm, and (3) SSD disks without mechanical seeks enable efficient selective retrieval of candidate objects. The gain of the significant candidate set reduction is paid by the overhead of the candidate ranking algorithm and thus our approach is more advantageous for datasets with expensive candidate set refinement, i.e. large data objects or expensive similarity function. On real-life datasets, the search time speedup achieved by our approach is by factor of two to five.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The complexity and diversity of digital data is permanently increasing, which naturally generates new requirements for data retrieval. For many contemporary data types, it is convenient or even essential that the access methods be based on mutual similarity of the data objects because it corresponds to the human perception of the data or because exact matching would be too restrictive (various multimedia, biomedical or sensor data, etc.). We adopt a generic approach to this problem, where the data space is modeled by a data domain and a general metric function $\delta$ to assess dissimilarity between pairs of objects from .

The field of metric-based similarity search has been studied for almost two decades [29]. The general objective of metric accesses methods (MAMs) is to preprocess the indexed dataset in such a way that, given a query object , the MAM can effectively identify objects x from with the shortest distances $\delta (q,x)$. A good motivating example for our work is an image search based on visual similarity of the image content. Recent advances in the area of deep neural networks allow to “extract” a semantically rich visual feature from a digital image [9, 17]; these features are 4096-dimensional float vectors (16 KB each vector). The search domain is then the feature space and the similarity function $\delta$ is Euclidean distance or other vector-based distance. For instance, if the data collection contains 10 million objects, the goal of the MAM is to organize 160 GB of the feature data and answer queries like “find me a dozen images from the collection that are the most similar to this query image”.

Current MAMs designed for large data collections are typically approximate [25, 29] and adopt the following high-level approach: Dataset  is split into Partitions; given a query, partitions with the highest “likeliness” to contain query-relevant data are read from the disk and this data form the candidate set of objects x to be refined by explicit evaluation of $\delta (q,x)$. The search costs of this schema consist mainly of (1) the I/O costs of reading the candidate partitions from the disk (they can be accessed as continuous data chunks) and (2) CPU costs of refinement; thus, the overall costs of the search typically strongly correlate with the candidate set size.

In this work, we propose a technique that can significantly reduce the candidate set size. In complex data spaces, the data partitions often span relatively large areas of the space and thus the candidate set is either large or imprecise. The key idea of our approach is to use several independent space partitionings; given a query, each of these partitionings generates a ranked set of candidate objects and we propose a way to aggregate these rankings so that the resulting candidate set is small and precise. Only objects identified in this way are actually retrieved from the disk and refined. Specifically, our approach works as follows:

• The data space is partitioned using a set of pivots (reference objects, anchors) where position of each data object is determined by its closest pivots and their order; this defines a mapping of the data into a pivot space. We use such pivot spaces to partition the dataset independently multiple times. In this way, each object is mapped onto a code denoted as PPP-Code; its size can be adjusted so that codes of the whole dataset fit into the main memory.

• Given a query, we first rank the object codes within each pivot spaces with respect to the query. Further and more importantly, we propose a way to aggregate these several rankings, which provably increases the probability that the query-relevant objects appear high in the final ranking.

• The PPP-Codes are organized by an indexing structure, which can lower their memory occupation. This index is also used by the proposed PPPRank algorithm that efficiently calculates individual candidate rankings and their aggregation; the algorithm exploits principles introduced by Fagin et al. [13].

This approach was designed with the idea of making the best use of contemporary trends in hardware development: (1) Larger main memories allow to maintain a rich memory index, (2) multi-core CPU architectures well support our demanding but accurate candidate set identification, and (3) SSD disks without mechanical seeks allow efficient retrieval of the candidate objects from the disk one-by-one (not as continuous data chunks).

Combination of independent partitionings was proposed before by LSH approaches [15] and it was also recognized by a few MAMs as a way to increase answer quality [11, 23]; these works propose to simply replicate the data in multiple indexes and to widen the query candidate set by union of multiple independent candidate sets. On the contrary, our aggregation mechanism shrinks the candidate set significantly while maintaining the same answer quality.

The experiments conducted on three diverse datasets show that this approach can reduce the candidate set size by two orders of magnitude. The response times depend on the time spared by this candidate set reduction (reduced I/O costs and $\delta$-refinement time) versus the overhead of the PPPRank algorithm. To analyze this tradeoff, we have run experiments on an artificial dataset with adjustable object sizes and tunable time of $\delta$ evaluation; the results show that our approach is not worthwhile only for the smallest data objects with the fastest $\delta$ function. Most of the evaluations were realized on two real-life datasets (100M CoPhIR [6] and 1M complex visual signatures [5]); for these, our approach was two- to five-times faster than competitors on the same HW platform.

The paper is further organized as follows. In Sect. 2, we define fundamental terms and analyze current approaches; in Sect. 3, we propose the PPP-Encoding (Sect. 3.1), ranking within individual pivot spaces (Sect. 3.2) and rank aggregation (Sects. 3.3 and 3.4); Sect. 4 describes our index and search algorithm. Our approach is evaluated and compared with others in Sect. 5 and the paper is concluded in Sect. 6 with a reference to an online demonstration application built with the aid of the proposed technique. This work is an extension of a paper presented at DEXA 2014 [24].

2 Preliminaries and Related Work

We focus on indexing and searching based on mutual object distances and we primarily assume that the data is modeled as a metric space [29]:

Definition 1

Metric space is an ordered pair , where is a domain of objects and $\delta$ is a total distance function satisfying postulates of non-negativity, identity, symmetry, and triangle inequality.

Our technique does not explicitly demand triangle inequality. In general, the metric-based techniques manage the dataset and search it by the nearest neighbors query $K$-NN($q$), which returns K objects from with the smallest distances to given (ties broken arbitrarily). We assume that the search answer A may be an approximation of the precise $K$-NN answer $A^P$ and the result quality is measured by $recall (A)= precision (A)=\frac{|A\cap A^P|}{K} \cdot 100\,\%.$

During two decades of research, many approximate metric access methods (MAMs) have been proposed [25, 29]. Further in this section, we focus especially on (1) techniques based on the concept of pivot permutations, (2) approaches that use several independent space partitionings, and (3) techniques that propose memory encoding of data objects. Having a set of k pivots , $\varPi _x$ is a pivot permutation defined with respect to object iff $\varPi _x(i)$ is the index of the i-th closest pivot to x; accordingly, sequence $p_{\varPi _x(1)},\ldots ,p_{\varPi _x(k)}$ is ordered with respect to distances between the pivots and x (ties broken by order of the increasing pivot index). Formally:

Definition 2

Having a set of k pivots (reference objects) and an object , let $\varPi _x$ be permutation on $\{1,\ldots ,k\}$ such that $\forall i: 1\le i<k$:

$\varPi _x$ will be referred to as pivot permutation (PP) with respect to x.

Several techniques based on this principle [7, 10, 11, 20] use the PPs to group data objects together (data partitioning); given a query, relevant partitions are read from the disk and refined; the relevancy is assessed based on the PPs. Unlike these methods, the MI-File [1] builds inverted file index according to object PPs; these inverted files are used to rank the data according to a query and the candidate set is then refined by accessing the objects one-by-one [1]. In this respect, our approach adopts similar principle and we compare our results with the MI-File (see Sect. 5.3).

In this work, we propose to use several independent pivot spaces (sets of pivots) to define several PPs for each data object and to identify candidate objects. The idea of multiple indexes is known from the Locality-sensitive Hashing (LSH) [15] and it was also applied by a few metric-based approaches [11, 23]; some metric indexes actually define families of metric LSH functions [22]. All these works benefit from enlarging the candidate set by a simple union of the top results from individual indexes; on the contrary, we propose such rank aggregation that can significantly reduce the size of the candidate set in comparison with a single index while preserving the same answer quality. Recently, the C2LSH technique [14] proposed a way to combine LSH functions resulting in a partially ranked candidate set; this work aims mainly at vector spaces with known families of LSH functions and it does not assume any pre-ranking of candidate sets from individual indexes.

Several recent works focused on reducing the size of data by source coding (or quantization) of Euclidean vector spaces so that the codes fit into memory; the authors use approaches like unsupervised machine learning [27], spectral hashing [28], or product quantization [16] to define data objects codes together with new ranking methods on these codes. A purely distance-based approach was also proposed [18]; it uses k pairs of pivots, that divide the space by k generalized hyperplanes, and each i-th bit of the k-bit code of reflects on which side of the i-th hyperplane object x lies. From a high perspective, this approach is similar to ours, but we propose techniques for indexing and ranking and corresponding non-exhaustive search algorithm.

3 PPP-Encoding and Ranking

In this section, we introduce the principal ideas of our approach: (1) the PPP-Encoding of the data (Sect. 3.1), (2) ranking within individual pivot spaces (Sect. 3.2), and (3) aggregation of these rankings which defines the overall ranking of the PPP-Codes (Sect. 3.3). Section 3.4 contains basic effectiveness evaluation of the proposed ranking.

3.1 Encoding by Pivot Permutation Prefixes

For a data domain with distance function $\delta$, object and a set of k pivots $P=\{p_1,\ldots ,p_k\}$, the pivot permutation (PP) $\varPi _x$ is defined as in Definition 2. In our technique, we do not use the full PP but only its prefix, i.e. the ordered list of a given number of nearest pivots:

Notation:

Having pivots $\{p_1,\ldots ,p_{k}\}$ and PP $\varPi _x$, , we denote $\varPi _x(1..l)$ the pivot permutation prefix (PPP) of length l: $1\le l\le k$, specifically

$$\begin{aligned} \varPi _x(1..l) = \langle \varPi _x(1),\varPi _x(2),\ldots ,\varPi _x(l)\rangle . \end{aligned}$$

(1)

The pivot permutation prefixes have a geometrical interpretation important for the similarity search – the PPPs actually define recursive Voronoi partitioning of the metric space [26]. Let us explain this principle on an example in Euclidean plane with four pivots $p_1,\ldots ,p_4$ in Fig. 1; the thick solid lines depict borders between standard Voronoi cells – sets of points for which specific pivot $p_i$ is the closest one: $\varPi _x(1)=i$. The dashed lines further partition these cells using other pivots; these sub-areas are labeled $C_{\langle i,j\rangle }$ and they cover all objects for which ${\varPi _x(1)} = i$ and ${\varPi _x(2)} = j$, thus $\varPi _x(1..2)=\langle i,j\rangle$.

Notation:

For an l-tuple $\langle i_1,\ldots ,i_l\rangle$, we denote $C_{\langle i_1,\ldots ,i_l\rangle }$ the Voronoi cell of level l that contains all objects for which $\varPi _x(1..l) = \langle i_1,\ldots ,i_l\rangle$.

Fig. 1.

Recursive Voronoi partitioning ($k=4$, $l = 2$) and query-pivot distances.

The pivot permutation prefixes (PPPs) $\varPi _x(1..l)$ form the base of the proposed PPP-Encoding, which is composed of several PPPs for each object. Thus, let us further assume having $\lambda$ independent sets of k pivots $P^1,P^2,\ldots ,P^\lambda$, $P^j=\{p_1^j,\ldots ,p_k^j\}$. For any , each of these sets generates a PP $\varPi _x^j$ , $j\in \{1,\ldots ,\lambda \}$ and we can define the PPP-Encoding as follows.

Table 1. Notation used throughout this paper.

Definition 3:

Having $\lambda$ sets of k pivots and parameter l :  $1\le l\le k$, we define PPP-Code of object as a $\lambda$-tuple

$$\begin{aligned} PPP _l^{1..\lambda }(x) = \langle \varPi _x^1(1..l),\ldots ,\varPi _x^\lambda (1..l)\rangle . \end{aligned}$$

(2)

Individual components (PPPs) of the PPP-Code will be also denoted as $PPP ^j_l(x) = \varPi _x^j(1..l)$, $j\in \{1,\ldots ,\lambda \}$; to shorten the notation, we set $\varLambda = \{1,\ldots ,\lambda \}$. These and other symbols used throughout this paper are summarized in Table 1.

The PPP-Encoding is exemplified in Fig. 2 where each of the $\lambda =2$ pivot sets defines an independent Voronoi partitioning of the data space. Every object is encoded by $PPP ^j_l(x)=\varPi ^j_x(1..l)$, $j\in \varLambda$. Object $x_5$ is depicted in both diagrams and, for instance, within the first partitioning, the closest pivots from $x_5$ are $p_7^1, p_4^1, p_8^1, p_5^1$, which corresponds to $PPP ^1_4(x_5)=\varPi _{x_5}^1(1..4)=\langle 7,4,8,5\rangle$.

Fig. 2.

Principles of encoding data objects as PPP-Codes $PPP _l^{1..\lambda }(x)$ with two pivot sets ($\lambda =2$) each with eight pivots ($k=8$) and using pivot permutation prefixes of length four ($l=4$). Each object x is encoded by $PPP _4^{1..2}(x) = \langle \varPi _x^1(1..4),\varPi _x^2(1..4)\rangle$; the figure shows example of object $x_5$: $PPP _4^{1..2}(x_5) = \langle \langle 7,4,8,5\rangle ,\langle 7,8,4,6\rangle \rangle$.

3.2 Ranking of Pivot Permutation Prefixes

Having objects from encoded as described above, we want to find ranking mechanism of $PPP _l^{1..\lambda }(x)$, with respect to query , which would be an approximation of the ranking generated by distances $\delta (q,x)$. To achieve this, we first define rankings on components of $PPP _l^{1..\lambda }(x)$, prefixes $\varPi _x(1..l)$. In the following, we define and compare two such ranking measures $d_{K}$ and $d_{\varDelta }$.

Measures Based Purely on Permutations. A natural approach is to project the query object q to the same space as the data objects by encoding q into its PP $\varPi _q$ (or prefix $\varPi _q(1..l)$) and to calculate “distance” between $\varPi _q$ and $\varPi _x(1..l)$. There are several standard ways to measure difference between full permutations that were also used in similarity search: Spearman Footrule, Spearman Rho or Kendall Tau measure [2, 7]; the last mentioned seems to slightly outperform the others [7]. The Kendall Tau between permutations $\varPi _x$ and $\varPi _y$ defines for every pair $\{i,j\}$, $0\le i,j\le k$: $K_{i,j}(\varPi _x,\varPi _y) = 0$ if indexes i, j are in $\varPi _x$ in the same order as in $\varPi _y$; otherwise, we set $K_{i,j}(\varPi _x,\varPi _y)=1$. The Kendall Tau is then defined as [12]:

$$ K(\varPi _x,\varPi _y) = \sum _{1\le i,j\le k} K_{i,j}(\varPi _x,\varPi _y). $$

This measure can be generalized in several ways to work with permutation prefixes, where not all $K_{i,j}$ are known [12]. We propose a measure $d_{K}$ which calculates a distance between the query object and $\varPi (1..l)$ as minimum of Kendall Tau distances between the full permutation $\varPi _q$ and all permutations $\varPi '$ on $\{1,\ldots ,k\}$ that have $\varPi (1..l)$ as prefix [12]:

$$\begin{aligned} d_{K}(q,\varPi (1..l)) = \min _{\varPi ': \varPi '(1..l)=\varPi (1..l)} K(\varPi _q, \varPi '). \end{aligned}$$

(3)

The accuracy of this measure with respect to the original distance $\delta$ is evaluated later in this section. There exists an algorithm for computation of the full Kendall Tau with $O(k\cdot \log k)$ complexity [8]. The same idea can be used to design an $O(l\cdot \log l)$ algorithm for $d_{K}$ on permutation prefixes.

Measures that Use Query-Pivot Distances. The query object in the ranking function can be represented more richly than by permutation $\varPi _q$, specifically, we can use directly the query-pivot distances $\delta (q,p_1),$ $\ldots ,\delta (q,p_k)$; see Fig. 1, which depicts such distances.

If we consider only the first-level Voronoi cells ($l=1$), thus only the closest pivots $\varPi _x(1)$, we can approximate the distance between a query and objects in cell $C_{\varPi (1)}$ by distance $\delta (q,p_{\varPi (1)})$ (this idea was described in [16]); for instance in Fig. 1, distance between q and cell $C_{\langle 4\rangle }$ (delimited by the thick solid lines around pivot $p_4$) would be $\delta (q,p_4)$. Having the cells further partitioned according to other pivots, we propose to shift the distance estimation towards the next pivots that define cell $C_{\varPi (1..l)}$; influence of these next pivots should be smaller than of the first one. For instance, distances between q and cells $C_{\langle 4,1\rangle }$, $C_{\langle 4,3\rangle }$ would be (weighted) averages between $d(q,p_4)$ and $d(q,p_1)$, $d(q,p_3)$, respectively, which should make the estimations more precise.

Formally, we propose to measure the distance between q and $\varPi (1..l)$ as a weighted arithmetic mean of distances between q and the l pivots from $\varPi (1..l)$:

$$\begin{aligned} d_{\varDelta }(q,\varPi (1..l)) = \left( \sum \nolimits _{i=1}^l c^{i-1} \delta (q,p_{\varPi (i)}) \right) / \sum \nolimits _{i=1}^l c^{i-1} , \end{aligned}$$

(4)

where c is parameter $0<c\le 1$ to control the influence of the next pivots; for now, we set $c=0.75$ and its influence is properly evaluated in Sect. 5.1. Naturally, this heuristic does not improve the distance estimation in all cases, but we consider the average influence. We measure the precision of the distance estimator as mean squared error [16] defined as

$$ \mathrm {MSDE}(d_{\varDelta })\! =\! \iint \! (\delta (q,x) - d_{\varDelta }(q,\varPi _x(1..l)))^2 p(x) \mathrm{d}x \, p(q) \mathrm{d}q $$

where $p(\cdot )$ is the probability distribution function of the data domain , . Figure 3 depicts the values of $\mathrm {MSDE}(d_{\varDelta })$ measured by Monte-Carlo sampling (averages over a large set of samples) on the CoPhIR dataset (see Sect. 5 for description of the dataset). The graph shows development of MSDE as the space partitioning is refined by growing number of pivots k and by increasing PPP length l used by $d_{\varDelta }$. We can see that levels $l>1$ can improve MSDE so that k would have to be multiplied to achieve such MSDE values for $l=1$. The same trends were observed for all other datasets (Sect. 5).

Fig. 3.

Mean squared error of $d_{\varDelta }$ (4) with $c=0.75$ on 1M CoPhIR dataset.

Comparison of the PPP Ranking Measures. Let us briefly compare effectiveness of the measures $d_{K}$ (3) and $d_{\varDelta }$ (4) proposed in the previous two subsections. In the following, d will stand for any dissimilarity measure between and $\varPi (1..l)$ such as $d_{K}$ or $d_{\varDelta }$. Such measures d together with naturally induce ranking $\psi _q$ of the indexed set according to growing distance from q. Formally, ranking is the smallest numbering of set that fulfills the following condition for all :

$$\begin{aligned} d(q,\varPi _x(1..l)) \le d(q,\varPi _y(1..l))\Rightarrow \psi _q(x) \le \psi _q(y) . \end{aligned}$$

(5)

We define the effectiveness of measure d as average recall of $K$-NN if the dataset is accessed in the order $\psi _q$ generated by d. We have compared this effectiveness on several datasets and with various settings; Fig. 4 shows graphs of the $10$-NN recall on a 1M subset of the CoPhIR dataset (see Sect. 5) as up to 1 % of this set is accessed according to $d_{K}$ and $d_{\varDelta }$ with several selected parameters of k and l.

Fig. 4.

Recall of $10$-NN on 1M CoPhIR dataset as accessing up to 1 % of the data ordered according to $d_{K}$ and $d_{\varDelta }$; $k=64$, 128, 256, $l=4$, 6, 8.

These graphs well illustrate the generally observed trend: $d_{\varDelta }$ is slightly better for smaller values of k and l (and also for very small numbers of accessed objects) while for extremely fine-grained space partitioning, both measures have practically the same effectiveness. These results are in compliance with previous works [20]. Regarding the lower complexity of $d_{\varDelta }$ ($\varTheta (l)$) in comparison to $d_{K}$ ($O(l\cdot \log l)$), we choose $d_{\varDelta }$ as the measure used in the rest of this paper.

3.3 Aggregation of Multiple Rankings

At this point, we know how to rank objects with respect to within one pivot space. As above, we assume that this ranking $\psi _q(x)$ (5) is induced by measure d such as $d_{K}$ (3) or $d_{\varDelta }$ (4) applied on q and PPPs $\varPi _x(1..l)$. Let us now assume that x is encoded by $PPP _l^{1..\lambda }(x)$ codes composed of $\lambda$ such PPPs and that we have a mechanism able to provide $\lambda$ sorted lists of objects generated by measure d between q and $\varPi _x^j(1..l)$, $j\in \varLambda$. Then, $\psi _q^j(x)$ denotes the position of x in the j-th ranking, $j\in \varLambda$. Figure 5 (top part) shows an example of five rankings $\psi _q^j$, $j\in \{1,\ldots ,5\}$.

These rankings are partial – objects with the same PPP $\varPi (1..l)$ have the same rank (objects from the same recursive Voronoi cell). This is the main source of inaccuracy of these rankings because, in complex data spaces, the Voronoi cells typically span relatively large areas and thus the top positions of $\psi _q$ contain both objects close to q and more distant ones. Having several independent partitionings, the query-relevant objects should be at top positions of most of the rankings while the “noise objects” should vary because the Voronoi cells are of different shapes. The objective of our rank aggregation is to filter out these noise objects. Namely, we propose to assign each object the $\mathbf {p}$-percentile of its ranks, $0\le \mathbf {p}\le 1$:

$$\begin{aligned} \varPsi _\mathbf {p}(q,x) = percentile _{\mathbf {p}}(\psi _q^1(x),\psi _q^2(x),\ldots ,\psi _q^\lambda (x)). \end{aligned}$$

(6)

For instance, $\varPsi _{0.5}$ assigns median of the ranks; see Fig. 5 for an example – positions of object x in individual rankings are: 1, 3, 1, unknown, 4 and median of these ranks is $\varPsi _{0.5}(q,x) = 3$. This principle was used by Fagin et al. [13] for a different purpose and they propose MedRank algorithm for efficient calculation of $\varPsi _\mathbf {p}$. This algorithm does not require to explicitly find out all ranks of a specific object, but only $\lceil \mathbf {p}\lambda \rceil$ first (best) ranks (this is explicit in Fig. 5). Details and properties of the MedRank algorithm [13] are provided in Sect. 4.

Fig. 5.

Rank aggregation by $\varPsi _{\mathbf {p}}$ of object , $\lambda =5$, $\mathbf {p}=0.5$.

Now, we would like to show that the $\varPsi _\mathbf {p}$ aggregation actually improves the ranking in comparison with a single $\psi _q$ ranking by increasing the probability that objects close to q will be assigned top positions (and vice versa). Also, we would like to find theoretically suitable values of $\mathbf {p}$.

Let x be an object from the dataset and $p_z$ be the probability such that $p_z=Pr[\psi _q(x)\le z]$, where $z\ge 1$ is a position in $\psi _q$ ranking. Having $\lambda$ independent rankings $\psi _q^j(x)$, $j\in \varLambda$, we want to determine probability $Pr[\varPsi _{\mathbf {p}}(q,x)\le z]$ with respect to $p_z$. Let X be a random variable representing the number of $\psi _q^j$ ranks of x that are smaller than z: $|\{\psi ^j_q(x)\le z, j\in \varLambda \}|$. Assuming that the probability distribution of $p_z$ is the same for each of $\psi _q^j(x)$, we get

$$ Pr[X = j] = {{\lambda }\atopwithdelims (){j}}\cdot (p_z)^{j}\cdot (1-p_z)^{\lambda -j} . $$

In order to have $\varPsi _{\mathbf {p}}(q,x)\le z$, at least $\lceil \mathbf {p}\lambda \rceil$ positions of x must be $\le z$ and thus

$$ Pr[\varPsi _{\mathbf {p}}(q,x)\le z] = \sum _{j=\lceil \mathbf {p}\lambda \rceil }^\lambda Pr[X = j] . $$

for the variable $\mathbf {p}$ and selected values of $p_z$ ($\lambda =8$). We can see that the aggregation increases the differences between individual levels of $p_z$ (for non-extreme $\mathbf {p}$ values); e.g. for $\mathbf {p}=0.5$, probabilities $p_z=0.1$ and $p_z=0.3$ are transformed to lower probability values whereas $p_z=0.5$ and $p_z=0.7$ are pushed to higher probabilities. The probability $p_z=Pr[\psi _q(x)\le z]$ naturally grows with z but, more importantly, we assume that $p_z$ is higher for objects close to q then for distant ones. Because $\psi _q^j$ are generated by distance between q and Voronoi cells (5) and these cells may be large, there may be many distant objects that appear at top positions of individual $\psi _q$ although having low probability $p_z$. The rank aggregation $\varPsi _{\mathbf {p}}(q,x)$ for non-extreme $\mathbf {p}$ values can push away such objects and increase the probability that top ranks are assigned only to objects close to q (Fig. 6).

Fig. 6.

Development of $Pr[\varPsi _\mathbf {p}(q,x)\le z]$ for $\lambda =8$, selected $p_z$ and variable $\mathbf {p}$.

Table 2. Sequential scan experiment parameters.

3.4 Accuracy of the PPP-Encoding and Ranking

Let us evaluate the basic accuracy of the $K$-NN search if the objects are encoded by PPP-Codes and ranked by $\varPsi _\mathbf {p}(q,x)$. Results in this section are independent of any indexing and searching algorithms, namely, we use the sequential scan and focus entirely on the trends and mutual influence of several parameters summarized in Table 2; all results are on the 1M CoPhIR dataset (see Sect. 5). We measure the accuracy as $K$-NN recall within the top R candidate objects identified by $\varPsi _\mathbf {p}(q,x)$. In this section, we present results of $1$-NN recall, which has the same trend as other values of K. All results are averaged over 1,000 randomly selected queries outside the dataset and all pivot sets $P^j$ were selected independently at random from the dataset.

Graphs in Fig. 7 focus on the influence of percentile $\mathbf {p}$. The left graph shows average $1$-NN recall within the top $R=100$ objects for variable $\mathbf {p}$ and selected k. We can see that, as expected, the higher k the better and, more importantly, the peak of the results is at $\mathbf {p}=0.75$ (just for clarification, for $\lambda =4$, $\varPsi _{0.75}(q,x)$ is equal to the third $\psi _q^j(x)$ rank of x out of four). These measurements are in compliance with the expectations discussed in the previous section.

The right graph in Fig. 7 shows the probe depth [13] – the average number of objects that had to be accessed in each ranking $\psi _q^j(x)$, $j\in \varLambda$ in order to discover $R=100$ objects in at least $\lceil \mathbf {p}\lambda \rceil$ rankings (and thus determine their $\varPsi _\mathbf {p}(q,x)$). Naturally, the probe depth grows with $\mathbf {p}$, especially for $\mathbf {p}\ge 0.75$. We can also see that finer space partitioning (higher k) results in a lower probe depth because the Voronoi cells are smaller and thus objects close to q appear in $\lceil \mathbf {p}\lambda \rceil$ rankings sooner. The general lessons learned are: the more pivots the better (for both recall and efficiency), ideal percentile seems to be around 0.5–0.75, which is in compliance with results of Fagin et al. [13].

Fig. 7.

1NN recall within the top $R=100$ objects (left) and average probe depth of each $\psi _q^j$, $j\in \varLambda$ (right) using rank aggregation $\varPsi _\mathbf {p}$ for $l=8$, $\lambda =4$ and various number of pivots k and percentile $\mathbf {p}$.

In general, we can assume that accuracy of the ranking will grow with increasing values of k, l, and $\lambda$, but these parameters influence the size of the PPP-code representation of an object:

$$\begin{aligned} \mathrm{size\,\,of}\,\, PPP ^{1..\lambda }_l(x) = \lambda \cdot l\cdot \lceil \log _2k\rceil \,\,\mathrm{bits.} \end{aligned}$$

(7)

Figure 8 shows recall for the variable bit size of $PPP _l^{1..\lambda }$ codes for selected values of $\lambda$. In the left graph, the prefix length is fixed at $l=8$ and the code size is influenced by increasing number of pivots k; we can see that higher values of recall can be achieved only with larger $\lambda$ but, on the other hand, considering the PPP-Code lengths, it is more convenient to increase k than $\lambda$. The right graph presents a similar experiment, only here $k=128$ and parameter l is increased; we can see that it pays off to increase l than to increase $\lambda$. The recall improvement achieved by increasing k and l is practically the same (with respect to PPP-Code size); higher k means more query-pivot distance computations.

Fig. 8.

1NN recall within the top $R=100$ objects ranked by $\varPsi _{0.75}$ for selected $\lambda$ and various bit length of $PPP ^{1..\lambda }_l(x)$ influenced either by number of pivots k (left, $l=8$) or by prefix length l (right, $k=128$).

The graph in Fig. 9 adopts an inverse point of view – it answers the question how the aggregation approach reduces the candidate set size R necessary to achieve given recall (80 %, in this case); please, notice the logarithmic scales. The small numbers in the graph show the reduction factor with respect to $\lambda =1$; we can see that R is reduced down to about 5 % using $\lambda =8$.

4 Indexing of PPP-Codes and Search Algorithm

So far, we have proposed a way to encode metric objects by PPP-Codes and to rank these codes according to given query object. In this section, we propose (1) an index to be built on a PPP-encoded dataset that can decrease the memory footprint of the PPP-Codes, and (2) an efficient non-exhaustive search algorithm.

Fig. 9.

Cand. set size R necessary for 80 % $1$-NN recall.

4.1 Dynamic PPP-Tree Index

The $PPP _l^{1..\lambda }(x)$ code is composed of $\lambda$ PPPs $\varPi _x(1..l)$. Given a set of these l-tuples, some of them would share common prefixes of variable lengths. In order to spare memory, we propose a PPP-Tree index – a dynamic trie structure that would keep the $l'$-prefixes of the PPP-Codes only once for all objects sharing the same $l'$-prefix, $l'\le l$. This PPP-Tree index is to be built for each of the $\lambda$ pivot spaces. Similar indexes were used in PP-Index [11] and in M-Index [20], but without the objective of memory representation reduction.

Schema of the PPP-Tree index is sketched in Fig. 10. Intuitively, let $i_1,\ldots ,i_{l'}$ be indexes on a path from the root of the tree to a certain node at level $l'$. This node and its subtree contains all objects for which $\varPi _x(1..l') = \langle i_1,\ldots ,i_{l'}\rangle$. This node also corresponds to Voronoi cell $C_{\langle i_1,\ldots ,i_{l'}\rangle }$ (see Sect. 3.1). An internal node at level $l'< l$ is composed of these entries:

$$ \langle i_{l'+1}, ptr \rangle ,\quad \text{ where } i_{l'+1}\in \{1,\ldots ,k\}\setminus \{i_1,\ldots ,i_{l'}\} ; $$

pointer $ptr$ points at subtree containing objects with PPP $\langle i_1,\ldots ,i_{l'},i_{l'+1}\rangle$; possible values of index $i_{l'+1}$ are limited because the indexes must be unique within a permutation. Let us recall that $\varPi _x(l'\!+\!1..l)$ denotes the part of the pivot permutation of object x between positions $l'\!+\!1$ and l; further, let $\oplus$ denote concatenation of two tuples. A leaf node at level $l'$ is composed of entries

$$ \langle \varPi _x(l'\!+\!1..l),\mathrm {ID}_x\rangle , $$

where $\mathrm {ID}_x$ is the unique identifier of object for which $\varPi _x(1..l)=\langle i_1,\ldots ,i_{l'}\rangle \oplus \varPi _x(l'\!+\!1..l)$. Entries in leaves at level $l'=l$ degenerate to $\langle \langle \rangle ,\mathrm {ID}_x\rangle$ where $\varPi _x(1..l)=\langle i_1,\ldots ,i_l\rangle$.

Fig. 10.

Schema of a single dynamic PPP-Tree.

The key to memory efficiency of such a structure is its dynamic leveling. Splitting a leaf node with $n'$ objects at level $l'$, $1\le l' <l$ spares $n'\cdot \lceil \log _2 k\rceil$ bits because the memory representation of $\varPi _x(l'\!+\!1..l)$ would be shorter by one index if these $n'$ objects are moved to level $l'+1$. On the other hand, the split creates new leaves with certain overhead; thus we propose to split the leaf iff

$$ n'\cdot \lceil \log _2k\rceil > b\cdot \textsc {NodeOverhead}$$

where b is potential branching of the leaf, $b \le n'$ and $b\le k-l'+1$. The actual value of b can be either precisely measured for each leaf or estimated based on the statistics of average branching at level $l'$. Value of $\textsc {NodeOverhead}$ depends on implementation details.

So far, we have described a single PPP-Tree (as if $\lambda = 1$). Having $\lambda > 1$, we propose to build a separate PPP-Tree for each $j\in \varLambda$. In this case, an object x in all $\lambda$ trees is “connected” by its $\mathrm {ID}_x$ stored in the leaf cells of the trees. This generates additional memory overhead per data object in comparison with sequential scan, because $\lambda - 1$ additional $\mathrm {ID}$s need to be stored. We consider that an identifier $\mathrm {ID}$ has $\lceil \log _2 n\rceil$ bits for dataset .

4.2 Non-Exhaustive Search Algorithm

In Sect. 3.3, we have proposed a way to aggregate $\lambda$ rankings of indexed objects and we have briefly mentioned the MedRank algorithm [13]. Having the PPP-Tree indexes as described above, we can now propose the PPPRank algorithm that does this aggregation effectively. The main procedure (Algorithm 1) follows the idea of MedRank; the PPP-Tree structures are used for effective generation of individual $\lambda$ rankings (subroutine GetNextIDs).

Given a query object , percentile $0\le \mathbf {p}\le 1$ and number R, PPPRank returns $\mathrm {ID}$s of R indexed objects with the lowest value of $\varPsi _\mathbf {p}(q,x)$; please, recall that this aggregated rank is defined as the $\lceil \mathbf {p}\lambda \rceil$-th best position from $\psi _q^j(x)$ ranks, $j\in \varLambda$ (6). In every iteration (lines 4–9), the algorithm accesses next objects of all rankings (routine GetNextIDs(q, j), $j\in \varLambda$); set S carries the already seen objects x together with the number of their occurrences in the rankings (frequencies $f_x$). GetNextIDs(q, j) always returns next object(s) with the best $\psi _q^j$ rank and thus, when an object x achieves frequency $f_x\ge \lceil \mathbf {p}\lambda \rceil$, it is guaranteed that any object y achieving $f_y\ge \lceil \mathbf {p}\lambda \rceil$ in a subsequent iteration of PPPRank must have higher rank $\varPsi _\mathbf {p}(q,y)>\varPsi _\mathbf {p}(q,x)$ [13].

Idea of the GetNextIDs(q, j) subroutine is to traverse the j-th PPP-Tree using a priority queue Q. As we know, each PPP-Tree node corresponds to Voronoi cell $C_{\langle i_1,\ldots ,i_{l'}\rangle }$, $l'\le l$; the queue Q is always ordered by $d(q,\langle i_1,\ldots ,i_{l'}\rangle )$ (where d is the measure that generates ranking $\psi _q^j$ (5)). In every iteration, the head of Q is processed; if head is a leaf node, its objects identifiers $\mathrm {ID}_x$ are inserted into Q ranked by $d(q,\varPi ^j_x(1..l))$. When object identifiers appear at the head of Q, they are returned as “next objects in the j-th ranking”. Algorithm 2 formalizes this routine: Q is composed of triples $\langle dist, \langle i_1,\ldots ,i_{l'}\rangle , \_\rangle$ where the third component is either a node N or an object ID. Initially, Q contains the root of the j-th PPP-Tree (line 2) and, in every step, the tree node at the head of Q (line 4) is decomposed and either its successors are inserted into Q (if N is internal, line 8) or the object $\mathrm {ID}$s are put into Q (if N is a leaf, line 12). In both cases, the PP prefix of the successor node (or object) is reconstructed from the PP prefix of node N and information from the node entry. If object $\mathrm {ID}$s appear at the head of Q, the top $\mathrm {ID}$s with the same distance $d(q,\varPi _x^j(1..l))$ are returned (lines 13–18); these are $\mathrm {ID}$s of objects with the same j-th rank (see Fig. 5).

Symbol d stands for a measure between and $\varPi (1..l)$ such as $d_{K}$ (3) or $d_{\varDelta }$ (4). The following property is key to correctness of Algorithm 2: For any PP $\varPi$ and $l',$ $1\le l'< l$:

$$\begin{aligned} d(q,\varPi (1..l'))\le d(q,\varPi (1..l'\!+\!1)). \end{aligned}$$

(8)

This property is fulfilled by $d_{K}$ (3) but not by $d_{\varDelta }$ (4); thus, we slightly modify Eq. (4) to calculate weighted sum of the query-pivot distances (instead of weighted average):

See Appendix I for correctness of Algorithm 2.

Complexity of GetNextIDs. This routine strongly influences efficiency of the whole PPPRank algorithm. The amortized complexity of the nested loops in Algorithm 2 depends on the number of items inserted to the queue Q; the queue can be implemented as a binary heap and thus the whole complexity would be $O(|Q|\cdot \log |Q|)$. In an ideal case, Q would contain only the data $\mathrm {ID}$s to be returned and the tree nodes on the path from the root to these data $\mathrm {ID}$s. As Q is ordered by the d-distance to individual nodes, this case would require that all other tree nodes have distances larger than the d-distances to the returned $\mathrm {ID}$s. Consequently, the length of Q depends on “tightness” of Eq. (8) – difference between the d-distance of an internal cell and the d-distance of its successors. See Appendix II for three algorithm optimizations that help to shorten the Q.

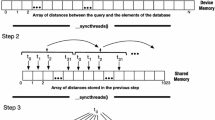
Search Process Review. Schema in Fig. 11 reviews the whole search process. Given a $K$-NN($q$) query, the first step is calculating distances between q and all pivots: $\delta (q,p_i^j)$, $i\in \{1,\ldots ,k\}$, $j\in \varLambda$. This is a necessary initialization of the GetNextIDs(q, j) procedures (steps 3), which generate the continual rankings $\psi _q^j$ that are consumed by the main PPPRank $(q,\mathbf {p},R)$ algorithm (step 2). The candidate set of R objects x is retrieved from the disk (step 4) and refined by calculating $\delta (q,x)$ (step 5). The whole process can be parallelized in the following way: The $\lambda$ steps 3 run fully in parallel and step 2 continuously reads their results; in this way, the full ranking $\varPsi _\mathbf {p}(q,x)$ is generated item-by-item and is immediately consumed by steps 4 and then 5.

Fig. 11.

Search pipeline using the PPP-Encoding and PPPRank algorithm.

5 Efficiency Evaluation

We evaluate efficiency of our approach on three datasets; two of them are real-life, and the third one is artificially created to have fully controlled test conditions:

• CoPhIR 100 million objects each consisting of five MPEG-7 global visual descriptors extracted from an image [6]. The distance function $\delta$ is a weighted sum of partial descriptor distances [3]; each object consumes 590 B on the disk (59 GB for 100M objects) and the computation of $\delta$ takes around 0.01 ms;

• SQFD 1 million visual feature signatures each consisting of, on average, 60 cluster centroids in a 7-dimensional space; each cluster has a weight and such signatures are compared by Signature Quadratic Form Distance (SQFD) [5] which is a cheaper alternative to Earth Movers Distance. Each object occupies around 1.8 kB on disk and the SQFD distance takes around 0.5 ms;

• ADJUSTABLE 10 million float vectors uniformly generated from $[0,1]^{32}$ compared by Euclidean distance; the disk size of each object can be artificially set from 512 B to 4096 B (5 GB to 40 GB for 10M objects) and time of $\delta$ computation can be tuned between 0.001 ms and 1 ms.

As a result of the analysis reported in Sect. 3.4, the indexes use these parameters: $l=8$, $\lambda =5$, $\mathbf {p}=0.5$ (3 out of 5); the CoPhIR index uses $k=256$, 384 and 512, SQFD index has $k=64$, and the ADJUSTABLE index $k=128$. The pivot sets $P^j$ were selected independently at random from the datasets. As in Sect. 3.4, we use $d_{\varDelta }$ $(4^{\prime })$ to generate individual $\psi _q^j$. The presented results are an average over 1,000 random $K$-NN($q$) queries. The efficiency is gauged by standard measures from similarity search field [23, 29]:

• I/O costs number of 4 kB block reads; in our approach, it is practically equal to the candidate set size R (step 4);

• distance computations (DC) number of evaluations of distance $\delta$; equal to $\lambda \cdot k + R$ (steps 1 and 5);

• search time the wall-clock time of the search process running parallel as described above.

All experiments were conducted on a machine with 8-core Intel Xeon @ 2.0 GHz, 12 GB of RAM and a SATA SSD disk (CrystalDiskMark benchmark speed: sequential read 440 MB/s, random 4K QD32 read 270 MB/s); for comparison, we also present some results on the following HDD configuration: two 10,000 rpm magnetic disks in RAID 1 array (CrystalDiskMark sequential read 150 MB/s). All techniques used the full memory for their index and for disk caching; caches were cleared before every batch of 1,000 queries. The implementation is in Java using the MESSIF framework [4].

5.1 PPP-Tree and PPPRank Overhead

Our approach encodes each object by a PPP-Code and a PPP-Tree index is built on these codes. Table 3 shows the sizes of this representation for individual datasets. The third column shows the size of the PPP-Code representation (7) plus the object $\mathrm {ID}$ size (unique within given dataset); the fourth column is the overall size of the sequential scan built on these PPP-Codes for given dataset. The next column shows PPP-Code sizes as reduced by PPP-Tree – in this case, the object $\mathrm {ID}$s are stored $\lambda$-times (see Sect. 4.1); the last column shows the overall sizes of the PPP-Tree indexes. We can see that the memory reduction by PPP-Trees and increase by multiple ID storage are practically equal.

Table 3. Size of PPP-Code representation without index (sequential scan) and with the dynamic PPP-Tree Index.

From now on, let us focus on the search efficiency. As mentioned above, the I/O costs and the number of $\delta$ computations (DC) are generated in steps 1, 4 and 5 of the search and can be directly derived from the algorithm parameters k, $\lambda$ and R. Let us have a closer look at the costs of the PPPRank algorithm itself – steps 2 and 3. Complexity of the aggregation step 2 depends directly on the probe depth, which was already mentioned in Sect. 3.4.

Figure 12 shows statistics of the PPPRank algorithm on the full 100M CoPhIR dataset. The left graph shows the development of the probe depth (left axis) and the $10$-NN recall (right axis) with respect to the weight c from the weighted sum $d_{\varDelta }$ $(4^{\prime })$. As we know, this weight influences individual $\psi _q^j(x)$, $j\in \varLambda$ and thus the result quality – we can see that the optimal recall is achieved around $c=0.8$. It is interesting that the recall is in a perfect inverse correlation with the probe depth – if the PPPRank needs to read fewer objects from individual $\psi _q^j(x)$ rankings, then the output objects are closer to q. This confirms the idea behind our aggregation approach.

Fig. 12.

PPPRank on 100M CoPhIR varying coefficient c from $d_{\varDelta }$ $(4^{\prime })$; the candidate set size $R=1000$. Left: probe depth and $10$-NN recall; right: length of priority queue Q, response time (without steps 4 and 5).

The right graph in Fig. 12 shows length of the queue Q (left axis) that determines complexity of GetNextIDs. As analyzed in Sect. 4.2, the Q length depends on tightness of Eq. (8), which is directly influenced by parameter c; the response time (right axis) depends on the probe depth and on Q length. Considering these results, we further fixate $c=0.75$ as a compromise between answer quality and efficiency.

5.2 The Overall Efficiency

Naturally, the quality of the search result comes at the expense of higher search costs. In Sect. 3.4, we have studied influence of the code size (fineness of the partitioning adjusted at the building phase) to the answer recall, but the main parameter to increase the recall at query time is R (the size of the candidate set). Figure 13 shows development of recall (left axis) and search time (right axis) with respect to R on the CoPhIR dataset ($k=512$). We can see that our approach can achieve very high recall while accessing thousands of objects out of 100M. The recall grows very steeply in the beginning, achieving about 90 % for $1$-NN and $10$-NN around $R=5000$; the time grows practically linearly.

Fig. 13.

Recall and search time on 100M CoPhIR as the candidate set grows; $k=512$.

Table 4 presents more measurements on the CoPhIR dataset. We have selected two values of $R=1000$ and $R=5000$ ($10$-NN recall 64 % and 84 %, respectively) and we present the I/O costs, computational costs, and the overall search times on both SSD and HDD disks. All these results should be put in context – comparison with other approaches. At this point, let us mention metric structure M-Index [20], which is based on similar fundamentals as our approach: it computes a PPP for each object, maintains an index structure similar to our single PPP-Tree (Fig. 10), and it accesses the leaf nodes based on a scoring function similar to $d_{\varDelta }$; our M-Index implementation shares the core with the PPP-Codes and it stores the data in continuous disk chunks for efficient reading. Comparison of M-Index and PPP-Codes shows precisely the gain and the overhead of PPPRank algorithm, which aggregates $\lambda$ partitionings.

Table 4. Results on 100M CoPhIR ($k=512$) and SQFD ($k=64$) with PPP-Codes and M-Index (512 and 64 pivots).

Looking at Table 4, we can see that M-Index with 512 pivots needs to access and refine $R=110000$ or $R=400000$ objects to achieve 65 % or 85 % $10$-NN recall, respectively; the I/O costs and number of distance computations correspond with R. According to these measures, the PPP-Codes are one or two orders of magnitude more efficient than M-Index; looking at the search times, the dominance is not that significant because of the PPPRank algorithm overhead. Please, note that the M-Index search algorithm is also parallel – both reading of the data and refinement are parallelized [20].

Table 5. Search times [ms] of PPP-Codes / M-Index on ADJUSTABLE with $10$-NN recall 85 %. PPP-Codes: $k=128$, $R=1000$, M-Index: 128 pivots, $R=400000$.

In order to clearly uncover the conditions under which the PPP-Codes overhead is worth the gain of reduced I/O and DC costs, we have introduced the ADJUSTABLE dataset. Table 5 shows the search times of PPP-Codes/M-Index while the object disk size and the DC time are adjusted. The results are measured on $10$-NN recall level of 85 %, which is achieved at $R=1000$ and $R=400000$ for the PPP-Codes and M-Index, respectively; please, note that these values of R mean even more dramatic candidate set reduction observed for this uniformly distributed dataset than in case of CoPhIR. Looking at the search times at Table 5, we can see that for the smallest objects and fastest distance, the M-Index beats PPP-Codes but as values of these two variables grow, the PPP-Codes show their strength. We believe that this table well summarizes the overall strength and costs of our approach.

The SQFD dataset is an example of data type belonging to the lower middle part of Table 5 – the signature objects occupy almost 2 kB and the SQFD distance function takes 0.5 ms on average. A graph in Fig. 14 presents the PPP-Codes $K$-NN recall and search times while increasing R (note that size of the dataset is 1M and $k=64$). We can see that the index achieves excellent results between $R=500$ and $R=1000$ with search time under 300 ms. Again, let us compare these results with M-Index with 64 pivots – the lower part of Table 4 shows that the PPP-Code aggregation can decrease the candidate set size R down under 1/10 of the M-Index results (for comparable recall values). For this dataset, we let the M-Index store precomputed object-pivot distances together with the objects and use them at query time for distance computation filtering [20, 29]; this significantly decreases its DC costs and search times, nevertheless, the times of PPP-Codes are about 1/5 of the M-Index.

Fig. 14.

Recall and search time on 1M SQFD dataset as candidate set grows; $k=64$.

These results can be summarized as follows: The proposed approach is worthwhile for data types with larger objects (over 512 B) or with the time-consuming $\delta$ function (over 0.001 ms). For the two real-life datasets, our aggregation schema cuts the I/O and $\delta$ computation costs down by one or two orders of magnitude. The overall speed-up factor is about 1.5 for CoPhIR and 5 for the SQFD dataset.

5.3 Comparison with Other Approaches

Finally, let us compare our approach with selected relevant techniques for approximate metric-based similarity search. We focus especially on those works that present results on the full 100M CoPhIR dataset; the results on this dataset are summarized in Table 6 and analyzed below.

M-Index. We have described the M-Index [20] and compared it with our approach in the previous section, because it shares the core idea with PPP-Codes which makes these approaches well comparable. We have chosen the M-Index also because its scoring function seems to be at least as good [20] as of other PP-based approaches [7, 11]. The first two lines in Table 6 summarize the results of PPP-Codes and M-Index on 100M CoPhIR. The third line shows variant when four M-Indexes are combined by a standard union of the candidate sets [23]; we can see that this approach can reduce the candidate set size R but the PPP-Codes still outperform it significantly.

PP-Index. The PP-Index [11] also uses prefixes of pivot permutations to partition the data space; it builds a slightly different tree structure on the PPPs, identifies query-relevant partitions using a different heuristic, and reads these candidate objects in a disk-efficient way. In order to achieve high recall values, the PP-Index also combines several independent indexes by merging their results [11]; Table 6 shows selected results – we can see that the values are slightly better than those of M-Index, especially when a high number of pivots is used (8,000) but the PPP-Codes access less than 1/10 of the PP-Index candidate set.

Table 6. Comparison with other approaches on 100M CoPhIR dataset.

MI-File. The MI-File [1] creates inverted files according to pivot-permutations; at query time, it determines the candidate set, reads it from the disk one-by-one and refines it. Table 6 shows selected results on 100M CoPhIR; we can see that extremely high number of pivots (20,000) resulted in even smaller candidate set then in case of PPP-Codes. The I/O costs are higher due to the disk size of the MI-File index and the computational costs are higher due to a high number of query-pivot $\delta$ distance evaluations.

As mentioned above, structures like PP-Index [11] or M-Index [20, 23] use multiple independent partitionings and they union candidate sets (or answers) from them; this is also well known from the LSH approach [15]. Let us compare the rank aggregation proposed in this work with the simple union of ranked candidate sets from multiple partitionings. Figure 15 shows candidate set size R necessary to achieve 80 % 1-NN recall when $\lambda$ ranks generated by $d_{\varDelta }$ are merged either by $\varPsi _{0.75}$ or by union (results are on 1M CoPhIR with the same settings as in Sect. 3.4). We can see that the $\varPsi$ aggregation results in less than half R.

Fig. 15.

Comparison of R using candidate set union vs. PPP-Codes rank aggregation; 1M CoPhIR, $k=128$, $l=8$, $\mathbf {p}=0.75$, 80 % 1-NN recall.

6 Conclusions

Efficient generic similarity search on a very large scale would have applications in many areas dealing with various complex data types. This task is difficult especially because identification of query-relevant data in complex data spaces typically requires accessing and refining relatively large candidate sets. If the data objects are large or if the refining similarity function is time-consuming then the search process may be unacceptably demanding. Since contemporary data types are often large and use complex similarity functions, we have designed a technique that would pay much more attention to identifying an accurate candidate set at the expense of higher algorithm complexity.

We have proposed a rich index by encoding each object using multiple pivot spaces; this PPP-Code index can be adjusted to fit into the main memory. Further, we have proposed a two-tier search algorithm – the first part of the algorithm generates several independent data object rankings according to distance between a query and the data codes, and the second part aggregates these rankings into one that provably increases the probability that query-relevant objects are accessed sooner.

We have conducted experiments on three datasets and in all cases our aggregation approach reduced the candidate set size by one or two orders of magnitude while preserving the answer quality. Because our search algorithm is relatively demanding, the overall search time gain depends on specific dataset. First, an artificial dataset with adjustable properties has helped us to show that our approach is not profitable only for data types with small objects and cheap similarity function. The second dataset was the 100M content-based image retrieval collection CoPhIR [6]; our approach speeded up the search on this set twice. Finally, we have used a dataset of 1M signature descriptors with a demanding SQFD distance function [5] where the candidate set reduction speeded up the search process more than five times.

Our approach differs from others in three aspects. First, it transfers a large part of the search computational burden from the similarity function evaluation towards the search process itself and thus the search times are very stable across different data types. Second, our index explicitly exploits a larger chunk of main memory in comparison with an implicit use for disk caching. And third, our approach reduces the I/O costs and it fully exploits the strength of the SSD disks without mechanical seeks or, possibly, of a fast distributed key-value store [19].

The PPP-Codes index forms the heart of an application that demonstrates a large-scale visual image search [21]. A collection of 20 million images has been processed by a deep convolutional neural network to obtain powerful visual features [9]. Compared by Euclidean distance, these 4096-dimensional vector features well express semantic similarity of digital images; uncompressed, 20M features occupy over 320 GB on the disk. The PPP-Codes index can reach a very good answer quality accessing only 5,000 out of these 20M features, which results in search times around 500 ms. The demonstration application is available online at http://disa.fi.muni.cz/demos/profiset-decaf/.

Appendices

Appendix I: Correctness of Algorithm 2

Lemma 1

If d maintains Eq. (8) then Algorithm 2 GetNextIDs(q, j) returns $\mathrm {ID}$s of objects with the lowest j-th ranking $\psi _q^j(x)$, $j\in \varLambda$ that were not returned so far.

Proof

The algorithm returns $\mathrm {ID}$s from Q containing nodes and $\mathrm {ID}$s from the j-th PPP-Tree. Because every node and $\mathrm {ID}$ is inserted into Q maximally once, the algorithm always returns something, unless all $\mathrm {ID}$s were returned. Q is ordered by $d(q,\langle i_1,\ldots ,i_{l'}\rangle )$ where $\langle i_1,\ldots ,i_{l'}\rangle$ is either path to a node or it is equal to $\varPi _x^j(1..l)$ for $\mathrm {ID}_x$ (recall that $d(q,\varPi _x^j(1..l))$ generate $\psi _q^j(x)$). Let $\mathrm {ID}_x$ be returned by the algorithm; we prove the lemma by contradiction. Let us assume that there exists : $d(q,\varPi _y^j(1..l))<d(q,\varPi _x^j(1..l))$ and $\mathrm {ID}_y$ was not returned by the algorithm. If $\mathrm {ID}_y$ is in Q then it must be ahead of $\mathrm {ID}_x$ (contradiction). Thus, $\mathrm {ID}_y$ is not in Q, but Q must contain a node with path $\langle i_1,\ldots ,i_{l'}\rangle$, $l'\le l$ such that $\langle i_1,\ldots ,i_{l'}\rangle =\varPi _y^j(1..l')$, because Q initially contains root of j-th PPP-Tree and then recursively all child nodes are inserted into Q (line 8). Because of (8), $d(q,\langle i_1,\ldots ,i_{l'}\rangle )\le d(q,\varPi _y^j(1..l))<d(q,\varPi _x^j(1..l))$ which is in contradiction with the fact that $\mathrm {ID}_x$ was on top of Q.

Appendix II: Optimizations of Algorithm 2

Complexity of the GetNextIDs routine is $O(|Q|\cdot \log |Q|)$ and the length of Q depends on “tightness” of Eq. (8). We propose the following optimizations for the $d_{\varDelta }$ distance.

Optimization 1. Distance $d_{\varDelta }(q,\varPi (1..l'))$ between and PP prefix on level $l'<l$ is corrected so that it returns the minimum theoretical distance to PPP-Codes on level l with prefix $\varPi (1..l')$:

$$\begin{aligned} d_{\varDelta }'(q,\varPi (1..l')) = d_{\varDelta }(q,\varPi (1..l') \oplus \varPi _q(1..l\!-\!l')). \end{aligned}$$

Notation $\oplus \, \varPi _q(1..l\!-\!l'))$ is concatenation of the pivot indexes closest to the query. This addition does not break the condition (8) but, in our test cases, it resulted to reduction of the queue length by factor of 0.4–0.7.

Optimization 2. This optimization is relatively trivial: A leaf of the PPP-Tree at level $l'<l$ can keep $\mathrm {ID}$s with the same PP suffix together as $\langle \varPi (l'\!+\!1..l);\mathrm {ID}_{x_1},\ldots ,\mathrm {ID}_{x_m}\rangle$ (see Sect. 4.1 for the original proposal); the list of $\mathrm {ID}$s can be further optimized e.g. using delta encoding . This results in index memory reduction and, especially, in a slight reduction of the Q size, because such entry is inserted to Q only once.

Optimization 3. Another important cost component of the GetNextIDs algorithm are distances $d(q,\langle i_1,\ldots ,i_{l'},i_{l'+1}\rangle )$ evaluated for each item added into Q (lines 8 and 12). If the formula of distance d is a sum of independent values for each level from 1 to $l'\!+\!1$ (as the $d_{\varDelta }$ distance $(4^{\prime })$) then value of $d(q,\langle i_1,\ldots ,i_{l'},i_{l'+1}\rangle )$ can be calculated as a sum of distance of its parent node $dist =d(q, \langle i_1,\ldots ,i_{l'}\rangle )$ plus the addend for level $l'+1$. In this case, the distances are calculated stepwise and no calculations are repeated.