New Complexity Results and Algorithms for the Minimum Tollbooth Problem

Abstract

The inefficiency of the Wardrop equilibrium of nonatomic routing games can be eliminated by placing tolls on the edges of a network so that the socially optimal flow is induced as an equilibrium flow. A solution where the minimum number of edges are tolled may be preferable over others due to its ease of implementation in real networks. In this paper we consider the minimum tollbooth (${MINTB}$) problem, which seeks social optimum inducing tolls with minimum support. We prove for single commodity networks with linear latencies that the problem is NP-hard to approximate within a factor of 1.1377 through a reduction from the minimum vertex cover problem. Insights from network design motivate us to formulate a new variation of the problem where, in addition to placing tolls, it is allowed to remove unused edges by the social optimum. We prove that this new problem remains NP-hard even for single commodity networks with linear latencies, using a reduction from the partition problem. On the positive side, we give the first exact polynomial solution to the ${MINTB}$ problem in an important class of graphs—series-parallel graphs. Our algorithm solves ${MINTB}$ by first tabulating the candidate solutions for subgraphs of the series-parallel network and then combining them optimally.

1 Introduction

Traffic congestion levies a heavy burden on millions of commuters across the globe. The congestion cost to the U.S. economy was measured to be $126 billion in the year 2013 with an estimated increase to $186 billion by year 2030 [16]. Currently the most widely used method of mitigating congestion is through congestion pricing, and one of the most common pricing schemes is through placing tolls on congested roads that users have to pay, which makes these roads less appealing and diverts demand, thereby reducing congestion.

Mathematically, an elegant theory of traffic congestion was developed starting with the work of Wardrop [18] and Beckman et al. [6]. This theory considered a network with travel time functions that are increasing in the network flow, or the number of users, on the corresponding edges. Wardrop differentiated between two main goals: (1) user travel time is minimized, and (2) the total travel time of all users is minimized. This led to the investigation of two different resulting traffic assignments, or flows, called a Wardrop equilibrium and a social or system optimum, respectively. It was understood that these two flows are unfortunately often not the same, leading to tension between the two different objectives. Remarkably, the social optimum could be interpreted as an equilibrium with respect to modified travel time functions, that could in turn be interpreted as the original travel time functions plus tolls.

Consequently, the theory of congestion games developed a mechanism design approach to help users routing along minimum cost paths reach a social optimum through a set of optimal tolls that would be added to (all) network edges. Later, through the works of Bergendorff et al. [7] and Hearn & Ramana [12], it was understood that the set of optimal tolls is not unique and there has been work in diverse branches of literature such as algorithmic game theory, operations research and transportation on trying to limit the toll cost paid by users by limiting the number of tolls placed on edges.

Related Work. The natural question of what is the minimum number of edges that one needs to place tolls on so as to lead selfish users to a social optimum, was first raised by Hearn and Ramana [12]. The problem was introduced as the minimum tollbooth (${MINTB}$) problem and was formulated as a mixed integer linear program. This initiated a series of works which led to new heuristics for the problem. One heuristic approach is based on genetic algorithms [3, 8]. In 2009, a combinatorial benders cut based heuristic was proposed by Bai and Rubin [2]. The following year, Bai et al. proposed another heuristic algorithm based on LP relaxation using a dynamic slope scaling method [1]. More recently, Stefanello et al. [15] have approached the problem with a modified genetic algorithm technique.

The first step in understanding the computational complexity of the problem was by Bai et al. [1] who proved that ${MINTB}$ in multi commodity networks is NP-hard via a reduction from the minimum cardinality multiway cut problem [10]. In a related direction, Harks et al. [11] addressed the problem of inducing a predetermined flow, not necessarily the social optimum, as the Wardrop equilibrium, and showed that this problem is APX-hard, via a reduction from length bounded edge cuts [4]. Clearly, ${MINTB}$ is a special case of that problem and it can be deduced that the hardness results of Harks et al. [11] do not carry forward to the ${MINTB}$ problem. A related problem is imposing tolls on a constrained set of edges to minimize the social cost under equilibrium [13].

The latest work stalls at this point leaving open both the question of whether approximations for multi commodity networks are possible, and what the hardness of the problem is for single commodity networks or for any meaningful subclass of such networks.

Our Contribution. In this work, we make progress on this difficult problem by deepening our understanding on what can and cannot be computed in polynomial time. In particular, we make progress in both the negative and positive directions by providing NP-hardness and hardness of approximation results for the single commodity network, and a polynomial-time exact algorithm for computing the minimum cardinality tolls on series-parallel graphs.

Specifically, we show in Theorem 1 that the minimum tollbooth problem for single commodity networks and linear latencies is hard to approximate to within a factor of 1.1377, presenting the first hardness of approximation result for the ${MINTB}$ problem.

Further, motivated by the observation that removing or blocking an edge in the network bears much less cost compared to the overhead of toll placement, we ask: if all unused edges under the social optimum are removed, can we solve ${MINTB}$ efficiently? The NP-hardness result presented in Theorem 2 for ${MINTB}$ in single commodity networks with only used edges, settles it negatively, yet the absence of a hardness of approximation result creates the possibility of a polynomial time approximation scheme upon future investigation.

Observing that the Braess structure is an integral part of both NP-hardness proofs, we seek whether positive progress is possible for the problem in series-parallel graphs. We propose an exact algorithm for series-parallel graphs with $\mathcal {O}(m^3)$ runtime, m being the number of edges. Our algorithm provably (see Theorem 4) solves the ${MINTB}$ problem in series-parallel graphs, giving the first exact algorithm for ${MINTB}$ on an important class of graphs.

2 Preliminaries and Problem Definition

We are given a directed graph G(V, E) with edge delay or latency functions $(\ell _e)_{e \in E}$ and demand r that needs to be routed between a source s and a sink t. We will abbreviate an instance of the problem by the tuple $\mathcal {G}=(G(V, E), (\ell _e)_{e \in E}, r)$. For simplicity, we usually omit the latency functions, and refer to the instance as (G, r). The function $\ell _e : \mathbb {R}_{\ge 0} \rightarrow \mathbb {R}_{\ge 0}$ is a non-decreasing cost function associated with each edge e. Denote the (non-empty) set of simple $s-t$ paths in G by $\mathcal {P}$.

Flows. Given an instance (G, r), a (feasible) flow f is a non-negative vector indexed by the set of feasible $s-t$ paths $\mathcal {P}$ such that $\sum _{p \in \mathcal {P}} f_p = r$. For a flow f, let $f_e = \sum _{p: e \in p} f_p$ be the amount of flow that f routes on each edge e. An edge e is used by flow f if $f_e > 0$, and a path p is used by flow f if it has strictly positive flow on all of its edges, namely $\min _{e \in p} \{ f_e \} > 0$. Given a flow f, the cost of each edge e is $\ell _e(f_e)$ and the cost of path p is $\ell _p(f) = \sum _{e \in p} \ell _e(f_e)$.

Nash Flow. A flow f is a Nash (equilibrium) flow, if it routes all traffic on minimum latency paths. Formally, f is a Nash flow if for every path $p \in \mathcal {P}$ with $f_p > 0$, and every path $p' \in \mathcal {P}$, $\ell _p(f) \le \ell _{p'}(f)$. Every instance (G, r) admits at least one Nash flow, and the players’ latency is the same for all Nash flows (see e.g., [14]).

Social Cost and Optimal Flow. The Social Cost of a flow f, denoted C(f), is the total latency $C(f) = \sum _{p \in \mathcal {P}} f_p \ell _p(f) = \sum _{e \in E} f_e \ell _e(f_e)$ . The optimal flow of an instance (G, r), denoted o, minimizes the total latency among all feasible flows.

In general, the Nash flow may not minimize the social cost. As discussed in the introduction, one can improve the social cost at equilibrium by assigning tolls to the edges.

Tolls and Tolled Instances. A set of tolls is a vector ${\varTheta }=\{\theta _e\}_{e\in E}$ such that the toll for each edge is nonnegative: $\theta _e\ge 0$. We call size of ${\varTheta }$ the size of the support of ${\varTheta }$, i.e., the number of edges with strictly positive tolls, $|\{e:\theta _e>0\}|$. Given an instance $\mathcal {G}= (G(V, E), (\ell _e)_{e \in E}, r)$ and a set of tolls ${\varTheta }$, we denote the tolled instance by $\mathcal {G}^{\theta }= (G(V, E), (\ell _e+\theta _e)_{e \in E}, r)$. For succinctness, we may also denote the tolled instance by $(G^{\theta },r)$. We call a set of tolls, ${\varTheta }$, opt-inducing for an instance $\mathcal {G}$ if the optimal flow in $\mathcal {G}$ and the Nash flow in $\mathcal {G}^{\theta }$ coincide.

Opt-inducing tolls need not be unique. Consequently, a natural problem is to find a set of optimal tolls of minimum size, which is the problem we consider here.

Definition 1

(Minimum Tollbooth problem (${MINTB}$)). Given instance $\mathcal {G}$ and an optimal flow o, find an opt-inducing toll vector ${\varTheta }$ such that the support of ${\varTheta }$ is less than or equal to the support of any other opt-inducing toll vector.

The following definitions are needed for Sect. 4.

Series-Parallel Graphs. A directed $s-t$ multi-graph is series-parallel if it consists of a single edge (s, t) or of two series-parallel graphs with terminals $(s_1, t_1)$ and $(s_2, t_2)$ composed either in series or in parallel. In a series composition, $t_1$ is identified with $s_2$, $s_1$ becomes s, and $t_2$ becomes t. In a parallel composition, $s_1$ is identified with $s_2$ and becomes s, and $t_1$ is identified with $t_2$ and becomes t.

A series-parallel (${SP}$) graph G with n nodes and m edges can be efficiently represented using a parse tree decomposition of size $\mathcal {O}(m)$, which can be constructed in time $\mathcal {O}(m)$ due to Valdes et al. [17].

Series-Parallel Parse Tree. A series-parallel parse tree T is a rooted binary tree representation of a given ${SP}$ graph G that is defined using the following properties:

• 1. Each node in the tree T represents a ${SP}$ subgraph H of G, with the root node representing the graph G.

• 2. There are three type of nodes: ‘series’ nodes, ‘parallel’ nodes, which have two children each, and the ‘leaf’ nodes which are childless.

• 3. A ‘series’ (‘parallel’) node represents the SP graph H formed by the ‘series combination’ (‘parallel combination’) of its two children $H_1$ and $H_2$.

• 4. The ‘leaf’ node represents a parallel arc network, namely one with two terminals s and t and multiple edges from s to t.

For convenience, when presenting the algorithm, we allow ‘leaf’ nodes to be multi-edge/parallel-arc networks. This will not change the upper bounds on the time complexity or the size of the parse tree.

3 Hardness Results for ${MINTB}$

In this section we provide hardness results for ${MINTB}$. We study two versions of the problem. The first one considers arbitrary instances while the second considers arbitrary instances where the optimal solution uses all edges, i.e. $\forall e\in E:o_e>0$. Recall that the motivation for separately investigating the second version comes as a result of the ability of the network manager to make some links unavailable.

3.1 Single-Commodity Network with Linear Latencies

We give hardness results on finding and approximating the solution of ${MINTB}$ in general instances with linear latencies. In Theorem 1 we give an inapproximability result by a reduction from a Vertex Cover related NP-hard problem and as a corollary (Corollary 1) we get the NP-hardness of ${MINTB}$ on single commodity networks with linear latencies. The construction of the network for the reduction is inspired by the NP-hardness proof of the length bounded cuts problem in [4].

Theorem 1

For instances with linear latencies, it is NP-hard to approximate the solution of ${MINTB}$ by a factor of less than 1.1377.

Proof

The proof is by a reduction from an NP-hard variant of Vertex Cover (${VC}$) due to Dinur and Safra [9]. Reminder: a Vertex Cover of an undirected graph G(V, E) is a set $S\subseteq V$ such that $\forall \{u,v\}\in E:S\cap \{u,v\} \ne \emptyset$.

Given an instance $\mathcal {V}$ of ${VC}$ we are going to construct an instance $\mathcal {G}$ of ${MINTB}$ which will give a one-to-one correspondence (Lemma 1) between Vertex Covers in $\mathcal {V}$ and opt-inducing tolls in $\mathcal {G}$. The inapproximability result will follow from that correspondence and an inapproximability result concerning Vertex Cover by [9]. We note that we will not directly construct the instance of ${MINTB}$. First, we will construct a graph with edge costs that are assumed to be the costs of the edges (used or unused) under the optimal solution and then we are going to assign linear cost functions and demand that makes the edges under the optimal solution to have costs equal to the predefined costs.

We proceed with the construction. Given an instance $G_{vc}(V_{vc},E_{vc})$ of ${VC}$, with $n_{vc}$ vertices and $m_{vc}$ edges, we construct a directed single commodity network G(V, E) with source s and sink t as follows:

• 1. For every vertex $v_i\in V_{vc}$ create gadget graph $G_i(V_i,E_i)$, with $V_i=\{a_i, b_i, c_i,$ $d_i\}$ and $E_i=\{(a_i,b_i), (b_i,c_i),$ $(c_i,d_i), (a_i,d_i)\}$, and assign costs equal to 1 for edges $e_{1,i}=(a_i,b_i)$ and $e_{3,i}=(c_i,d_i)$, 0 for edge $e_{2,i}=(b_i,c_i)$, and 3 for edge $e_{4,i}=(a_i,d_i)$. All edges $e_{1,i}$ ,$e_{2,i}$,$e_{3,i}$ and $e_{4,i}$ are assumed to be used.

• 2. For each edge $e_k=\{v_i,v_j\}\in E_{vc}$ add edges $g_{1,k}=(b_i,c_j)$ and $g_{2,k}=(b_j,c_i)$ with cost 0.5 each. Edges $g_{1,k}$ and $g_{2,k}$ are assumed to be unused.

• 3. Add source vertex s and sink vertex t and for all $v_i\in V_{vc}$ add edges $s_{1,i}=(s,a_i)$ and $t_{1,i}=(d_i,t)$ with 0 cost, and edges $s_{2,i}=(s,b_i)$ and $t_{2,i}=(c_i,t)$ with cost equal to 1.5. Edges $s_{1,i}$ and $t_{1,i}$ are assumed to be used and edges $s_{2,i}$ and $t_{2,i}$ are assumed to be unused.

The construction is shown in Fig. 1 where the solid lines represent used edges and dotted lines represent unused edges. The whole network consists of $(2+4n_{vc})$ nodes and $(8n_{vc}+2m_{vc})$ edges, therefore, it can be constructed in polynomial time, given $G_{vc}$.

Fig. 1.

Gadgets for the reduction from ${VC}$ to ${MINTB}$. The pair of symbols on each edge corresponds to the name and the cost of the edge respectively. Solid lines represent used edges and dotted lines represent unused edges.

We go on to prove the one-to-one correspondence lemma.

Lemma 1

(I) If there is a Vertex Cover in $G_{vc}$ with cardinality x, then there are opt-inducing tolls for G of size $n_{vc}+x$.

(II) If there are opt-inducing tolls for G of size $n_{vc}+x$, then there is a Vertex Cover in $G_{vc}$ with cardinality x.

Proof

Readers are referred to the proof of Lemma 1 in [5].

Statement (I) in the above lemma directly implies that if the minimum Vertex Cover of $G_{vc}$ has cardinality x then the optimal solution of the ${MINTB}$ instance has size at most $n_{vc}+x$.

From the proof of Theorem 1.1 in [9] we know that there exist instances $G_{vc}$ where it is NP-hard to distinguish between the case where we can find a Vertex Cover of size $n_{vc}\cdot (1 - p + \epsilon )$, and the case where any vertex cover has size at least $n_{vc}\cdot (1 - 4p^3+3p^4 - \epsilon )$, for any positive $\epsilon$ and $p = (3 - \sqrt{5})/2$. We additionally know that the existence of a Vertex Cover with cardinality in between the gap implies the existence of a Vertex Cover of cardinality $n_{vc}\cdot (1 - p + \epsilon )$.¹

Assuming that we reduce from such an instance of ${VC}$, the above result implies that it is NP-hard to approximate ${MINTB}$ within a factor of $1.1377<\frac{2 - 4p^3+3p^4 - \epsilon }{2 - p + \epsilon }$ (we chose an $\epsilon$ for inequality to hold). To reach a contradiction assume the contrary, i.e. there exists a $\beta$-approximation algorithm $Algo$ for ${MINTB}$, where $\beta \mathbf {\le } 1.1377<\frac{2 - 4p^3+3p^4 - \epsilon }{2 - p + \epsilon }$. By Lemma 1 statement (I), if there exists a Vertex Cover of cardinality $\hat{x}=n_{vc}\cdot (1 - p + \epsilon )$ in $G_{vc}$, then the cardinality in an optimal solution to ${MINTB}$ on the corresponding instance is $OPT \le n_{vc}+\hat{x}$. Further, Algo produces opt-inducing tolls with size $n_{vc}+y$, from which we can get a Vertex Cover of cardinality y in the same way as we did inside the proof of statement (II) of Lemma 1. Then by the approximation bounds and using $\hat{x}=n_{vc}\cdot (1 - p + \epsilon )$ we get

$$\frac{n_{vc}+y}{n_{vc}+\hat{x}} \le \frac{n_{vc}+y}{OPT}\le \beta < \frac{2 - 4p^3+3p^4 - \epsilon }{2 - p + \epsilon }\Rightarrow y< (1 - 4p^3+3p^4 - \epsilon )n_{vc}$$

The last inequality would answer the question whether there exists a Vertex Cover with size $n_{vc}\cdot (1 - p + \epsilon )$, as we started from an instance for which we additionally know that the existence of a Vertex Cover with cardinality $y< (1 - 4p^3+3p^4 - \epsilon )n_{vc}$ implies the existence of a Vertex Cover of cardinality $n_{vc}\cdot (1 - p + \epsilon )$.

What is left for concluding the proof is to define the linear cost functions and the demand so that at an optimal solution all edges have costs equal to the ones defined above.

Define the demand to be $r=2n_{vc}$ and assign: for every i the cost functions $\ell _0(x)=0$ to edges $s_{1,i}$, $t_{1,i}$ and $e_{2,i}$, the cost function $\ell _1(x)=\frac{1}{2}x+\frac{1}{2}$ to edges $e_{1,i}$ and $e_{3,i}$, the cost function $\ell _2(x)=1.5$ to edges $s_{2,i}$ and $t_{2,i}$, and the cost function $\ell _3(x)=3$ to edge $e_{4,i}$, and for each k, the cost function $\ell _4(x)=0.5$ to edges $g_{1,k}$ and $g_{2,k}$. The optimal solution will assign for each $G_i$ one unit of flow to path $s-a_i-b_i-c_i-d_i-t$ and one unit of flow to $s-a_i-d_i-t$. This makes the costs of the edges to be as needed, as the only non constant cost is $\ell _1$ and $\ell _1(1)=1$.

To verify that this is indeed an optimal flow, one can assign to each edge e instead of its cost function, say $\ell _e(x)$, the cost function $\ell _e(x)+x\ell _e'(x)$. The optimal solution in the initial instance should be an equilibrium for the instance with the pre-described change in the cost functions (see e.g. [14]). This will hold here as under the optimal flow and with respect to the new cost functions the only edges changing cost will be $e_{1,i}$ and $e_{3,i}$, for each i, and that new cost will be 1.5 ($\ell _1(1)+1\ell '_1(1)=1.5$).    $\square$

Consequently, we obtain the following corollary.

Corollary 1

For single commodity networks with linear latencies, ${MINTB}$ is NP-hard.

Proof

By following the same reduction, by Lemma 1 we get that solving MINTB in G gives the solution to ${VC}$ in $G_{vc}$ and vice versa. Thus, ${MINTB}$ is NP-hard.    $\square$

3.2 Single-Commodity Network with Linear Latencies and All Edges Under Use

In this section we turn to study ${MINTB}$ for instances where all edges are used by the optimal solution. Note that this case is not captured by Theorem 1, as in the reduction given for proving the theorem, the existence of unused paths in network G was crucially exploited. Nevertheless, ${MINTB}$ remains NP hard for this case.

Theorem 2

For instances with linear latencies, it is NP-hard to solve ${MINTB}$ even if all edges are used by the optimal solution.

Proof

The proof comes by a reduction from the partition problem (PARTITION) which is well known to be NP-complete (see e.g. [10]). ${PARTITION}$ is: Given a multiset $S=\{\alpha _1,\alpha _2,\dots ,\alpha _n\}$ of positive integers, decide (YES or NO) whether there exists a partition of S into sets $S_1$ and $S_2$ such that $S_1\cap S_2=\emptyset$ and $\sum _{\alpha _i\in S_1} \alpha _i =\sum _{\alpha _j \in S_2} \alpha _j=\frac{\sum _{i=1}^{n}\alpha _i}{2}$.

Given an instance of ${PARTITION}$ we will construct an instance of ${MINTB}$ with used edges only and show that getting the optimal solution for ${MINTB}$ solves ${PARTITION}$. Though, we will not directly construct the instance. First we will construct a graph with edge costs that are assumed to be the costs of the edges under the optimal solution and then we are going to assign linear cost functions and demand that makes the edges under the optimal solution to have costs equal to the predefined costs. For these costs we will prove that if the answer to ${PARTITION}$ is YES, then the solution to ${MINTB}$ puts tolls to 2n edges and if the answer to ${PARTITION}$ is NO then the solution to ${MINTB}$ puts tolls to more than 2n edges. Note that the tolls that will be put on the edges should make all s-t paths of the ${MINTB}$ instance having equal costs, as all of them are assumed to be used.

Next, we construct the graph of the reduction together with the costs of the edges. Given the multi-set $S=\{\alpha _1,\alpha _2,\dots ,\alpha _n\}$ of ${PARTITION}$, with $\sum _{i=1}^n \alpha _i=2B$, construct the ${MINTB}$ instance graph G(V, E), with source s and sink t, in the following way:

• 1. For each i, construct graph $G_i=(V_i,E_i)$, with $V_i=\{u_i, w_i,x_i,v_i\}$ and $E_i=\{(u_i,w_i), (w_i,v_i), (u_i,x_i), (x_i,v_i),$ $(w_i,x_i), (w_i,x_i)\}$. Edges $a_i=(u_i,w_i)$ and $b_i=(x_i,v_i)$ have cost equal to $\alpha _i$, edges $c_{1,i}=(w_i,x_i)$ and $c_{2,i}=(w_i,x_i)$ have cost equal to $2\alpha _i$ and edges $q_i=(w_i,v_i)$ and $g_i=(u_i,x_i)$ have cost equal to $4 \alpha _i$.

• 2. For $i=1$ to $n-1$ identify $v_i$ with $u_{i+1}$. Let the source vertex be $s=u_1$ and the sink vertex be $t=v_n$.

• 3. Add edge $h=(s,t)$ to connect s and t directly with cost equal to 11B.

The constructed graph is presented in Fig. 2. It consists of $(3n+1)$ vertices and $6n+1$ edges and thus can be created in polynomial time, given S.

Fig. 2.

The graph for ${MINTB}$, as it arises from ${PARTITION}$. The pair of symbols on each of $G_i$’s edges correspond to the name and the cost of the edge respectively.

We establish the one-to-one correspondence between the two problems in the following lemma.

Lemma 2

(I) If the answer to ${PARTITION}$ on S is YES then the size of opt-inducing tolls for G is equal to 2n.

(II) If the answer to ${PARTITION}$ on S is NO then the size of opt-inducing tolls for G is strictly greater than 2n.

Proof

The proof is identical to the proof of Lemma 2 in [5].

What is left for concluding the proof is to define the linear cost functions and the demand so that at the optimal solution all edges have costs equal to the ones defined above.

Define the demand to be $r=4$ and assign the cost function $\ell _h=11B$ to edge h and for each i, the cost function $\ell _i^1(x)=\frac{1}{4}\alpha _i x+\frac{1}{2}\alpha _i$ to edges $a_i$, $b_i$, the cost function $\ell _i^2(x)=\alpha _i x+\frac{3}{2}\alpha _i$ to edges $c_{1,i}$ and $c_{2,i}$, and the constant cost function $\ell _i^3(x)=4\alpha _i$ to edges $q_i$ and $g_i$. The optimal flow then assigns 1 unit of flow to edge h which has cost 11B, and the remaining 3 units to the paths through $G_i$. In each $G_i$, 1 unit will pass through $a_i-q_i$, 1 unit will pass through $g_i-b_i$, 1 / 2 units will pass through $a_i-c_{1,i}-b_i$, and 1 / 2 unit will pass through $a_i-c_{2,i}-b_i$. This result to $a_i$ and $b_i$ costing $\alpha _i$, to $c_{1,i}$ and $c_{2,i}$ costing $2\alpha _i$, and to $q_i$ and $g_i$ costing $4\alpha _i$, as needed. We can easily verify that it is indeed an optimal flow using a technique similar to the one used in Theorem 1.

4 Algorithm for MINTB on Series-Parallel Graphs

In this section we propose an exact algorithm for ${MINTB}$ in series-parallel graphs. We do so by reducing it to a solution of an equivalent problem defined below.

Consider an instance $\mathcal {G}=\{G(V,E),(\ell _e)_{e\in E},r\}$ of ${MINTB}$, where G(V, E) is a ${SP}$ graph with terminals s and t. Since the flow we want to induce is fixed, i.e. the optimal flow o, by abusing notation, let length $\ell _e$ denote $\ell _e(o_e)$, for each $e\in E$, and let used edge-set, $E_u=\{e\in E:o_e>0\}$, denote the set of used edges under o. For $\mathcal {G}$, we define the corresponding $\ell$-instance (length-instance) to be $\mathcal {S}(\mathcal {G})=\{G(V,E),\{\ell _e\}_{e\in E}, E_u\}$. We may write simply $\mathcal {S}$, if $\mathcal {G}$ is clear form the context. By the definition below and the equilibrium definition, Lemma 3 easily follows.

Definition 2

Given an $\ell$-instance $\mathcal {S}=\{G(V,E),\{\ell _e\}_{e\in E}, E_u\}$, inducing a length L in G is defined as the process of finding $\ell '_e \ge \ell _e$, for all $e\in E$, such that when replacing $\ell _e$ with $\ell _e'$: (i) all used $s-t$ paths have length L and (ii) all unused $s-t$ paths have length greater or equal to L, where a path is used when all of its edges are used, i.e. they belong to $E_u$.

Lemma 3

Consider an instance $\mathcal {G}$ on a ${SP}$ graph G(V, E) with corresponding $\ell$-instance $\mathcal {S}$. L is induced in G with modified lengths $\ell _e'$ if and only if $\{\ell '_e-\ell _e\}_{e\in E}$ is an opt-inducing toll vector for $\mathcal {G}$.

We call edges with $\ell _e'>\ell _e$ tolled edges as well. Under these characterizations, observe that finding a toll vector ${\varTheta }$ that solves ${MINTB}$ for instance $\mathcal {G}$ with graph G, is equivalent to inducing length L in G with minimum number of tolled edges, where L is the common equilibrium cost of the used paths in $G^\theta$. In general, this L is not known in advance and it might be greater than $\ell _{max}$, i.e. the cost of the most costly used path in G, see e.g. Fig. 4. Though, for ${SP}$ graphs we prove (Lemma 4) a monotonicity property that ensures that inducing length $\ell _{max}$ results in less or equal number of tolled edges than inducing any $\ell '>\ell _{max}$. Our algorithm relies on the above equivalence and induces $\ell _{max}$ with minimum number of tolled edges.

Fig. 3.

Example of list

Algorithm for Parallel Link Networks: Before introducing the algorithm for ${MINTB}$ on ${SP}$ graphs, we consider the problem of inducing a length L in a parallel link network P using minimum number of edges. It is easy to see that all edges with length less than the maximum among used edges, say $\ell _{max}$, should get a toll. Similarly, to induce any length $\ell >\ell _{max}$, all edges with cost less than $\ell$ are required to be tolled.

Define an ‘edge-length’ pair as the pair $(\eta ,\ell )$ such that by using at most $\eta$ edges a length $\ell$ can be induced in a given graph. Based on the above observations we create the ‘edge-length’ pair list, $lst_P$, in Algorithm 1. By reordering the edges in increasing length order, let edge k have length $\ell _k$ for $k=1$ to m. Also let there be $i_0$ number of edges with length less than $\ell _{max}$. The list gets the first entry $(i_0,\ell _{max})$ and subsequently for each $i=i_0+1$ to m, gets the entry $(i,\ell _{i+1})$, where $\ell _{m+1}=\infty$.

To induce any length $\ell$, starting from the first ‘edge-length’ pair in list $lst_P$ we linearly scan the list until for the first time we encounter the ‘edge-length’ pair with $\eta$ edges and length strictly greater than $\ell$. Clearly $(\eta -1)$ is the minimum number of edges required to induce $\ell$ as illustrated in Fig. 3.

Algorithm Structure: The proposed algorithm for ${MINTB}$ proceeds in a recursive manner on a given parse tree T of the ${SP}$ graph G of an $\ell$-instance $\mathcal {S}$, where we create $\mathcal {S}$ given instance $\mathcal {G}$ and optimal flow o. Recall that for each node v of the parse tree we have an associated ${SP}$ subgraph $G_v$ with the terminals $s_v$ and $t_v$. The two children of node v, whenever present, represent two subgraphs of $G_v$, namely $G_1$ and $G_2$. Similar to the parallel link graph our algorithm creates an ‘edge-length’ pair list for each node v. Due to lack of space the algorithms are presented in the full version of this paper [5]. From hereon Algorithm i in this paper will refer to Algorithm i in [5], for all $i\ge 2$.

Central Idea. Beginning with the creation of a list for each leaf node of the parse tree using Algorithm 1 we keep on moving up from the leaf level to the root level. At every node the list of its two children, $lst_1$ and $lst_2$, are optimally combined to get the current list $lst_v$. For each ‘edge-length’ pair $(\eta ,\ell )$ in a current list we maintain two pointers (p1, p2) to point to the two specific pairs, one each from its descendants, whose combination generates the pair $(\eta ,\ell )$. Hence each element in the list of a ‘series’ or ‘parallel’ node v is given by a tuple, $(\eta ,\ell ,p1,p2)$.

The key idea in our approach is that the size of the list $lst_v$ for every node v, is upper bounded by the number of edges in the subgraph $G_v$. Furthermore, for each series or parallel node, we devise polynomial time algorithms, Algorithm 5 and Algorithm 6 respectively, which carry out the above combinations optimally.

Optimal List Creation. Specifically, we first compute the number of edges necessary to induce the length of maximum used path between $s_v$ and $t_v$, which corresponds to the first ‘edge-length’ pair in $lst_v$. Moreover, the size of the list is limited by the number of edges necessary for inducing the length $\infty$, as computed next. Denoting the first value by s and the latter by f, for any ‘edge-length’ pair $(\eta ,\ell )$ in $lst_v$, $\eta \in \{s,s+1,\dots ,f\}$.

Considering an $\eta$ in that range we may use $\eta '$ edges in subgraph $G_1$ and $\eta -\eta '$ edges in subgraph $G_2$ to induce some length, which gives a feasible division of $\eta$. Let $\eta '$ induce $\ell _1$ in $G_1$ and $\eta -\eta '$ induce $\ell _2$ in $G_2$. In a ‘series’ node the partition induces $\ell =\ell _1+\ell _2$ whereas in a ‘parallel’ node it induces $\ell =\min \{\ell _1,\ell _2\}$.

Next we fix the number of edges to be $\eta$ and find the feasible division that maximizes the induced length in G and subsequently a new ‘edge-length’ pair is inserted in $lst_v$. We repeat for all $\eta$, starting from s and ending at f. This gives a common outline for both Algorithms 5 and 6. A detailed description is provided in Theorem 3.

Placing Tolls on the Network. Once all the lists have been created, Algorithm 4 traverses the parse tree starting from its root node and optimally induces the necessary lengths at every node. At the root node the length of the maximum used path in G is induced. At any stage, due to the optimality of the current list, given a length $\ell$ that can be induced there exists a unique ‘edge-length’ pair that gives the optimal solution. In the recursive routine after finding this specific pair, we forward the length required to be induced on its two children. For a ‘parallel’ node the length $\ell$ is forwarded to both of its children, whereas in a ‘series’ node the length is appropriately split between the two. Following the tree traversal the algorithm eventually reaches the leaf nodes, i.e. the parallel link graphs, where given a length $\ell$ the optimal solution is to make each edge e with length $\ell _e < \ell$ equal to length $\ell$ by placing toll $\ell -\ell _e$. A comprehensive explanation is presented under Lemma 5 in [5].

4.1 Optimality and Time Complexity of Algorithm SolMINTB

Proof Outline: The proof of Theorem 4 which states that the proposed algorithm solves the ${MINTB}$ problem in ${SP}$ graphs in polynomial time, is split into Lemmas 4 and 5 and Theorem 3. The common theme in the proofs is the use of an inductive reasoning starting from the base case of parallel link networks, which is natural given the parse tree decomposition. Lemma 4 gives a monotonicity property of the number of edges required to induce length $\ell$ in a ${SP}$ graph guiding us to induce the length of maximum used path to obtain an optimal solution.

The key Theorem 3 is essentially the generalization of the ideas used in the parallel link network to ${SP}$ graphs. It proves that the lists created by Algorithm 2 follow three desired properties. (1) The maximality of the ‘edge-length’ pairs in a list, i.e. for any ‘edge-length’ pair $(\eta ,\ell )$ in $lst_v$ it is not possible to induce a length greater than $\ell$ in $G_v$ using at most $\eta$ edges. (2) The ‘edge-length’ pairs in a list follows an increasing length order which makes it possible to locate the optimal solution efficiently. (3) Finally the local optimality of a list at any level of the parse tree ensures that the ‘series’ or ‘parallel’ combination preserves the same property in the new list.

In Lemma 5 we prove that the appropriate tolls on the edges can be placed provided the correctness of Theorem 3. The basic idea is while traversing down the parse tree at each node we induce the required length in a locally optimal manner. Finally, in the leaf nodes the tolls are placed on the edges and the process inducing a given length is complete. Exploiting the linkage between the list in a specific node and the lists in its children we can argue that these local optimal solutions lead to a global optimal solution.

Finally, in our main theorem, Theorem 4, combining all the elements we prove that the proposed algorithm solves ${MINTB}$ optimally. In the second part of the proof of Theorem 4, the analysis of running time of the algorithm is carried out. The creation of the list in each node of the parse tree takes $\mathcal {O}(m^2)$ time, whereas the number of nodes is bounded by $\mathcal {O}(m)$, implying that Algorithm 2 terminates in $\mathcal {O}(m^3)$ time. Here m is the number of edges in the ${SP}$ graph G.

Proof of Correctness: In what follows we state the key theorems and lemmas, while interested readers are referred to [5] for the complete proofs.

Lemma 4

In an $\ell$-instance $\mathcal {S}$, with ${SP}$ graph G and maximum used (s, t) path length $\ell _{max}$, any length L can be induced in G if and only if $L\ge \ell _{max}$. Moreover if length L is induced optimally with T edges then length $\ell _{max}\le \ell \le L$ can be induced optimally with $t \le T$ edges.

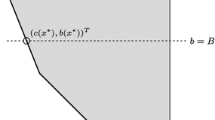
Note: The above lemma breaks in general graphs. As an example, in the graph in Fig. 4 to induce a length of 3 we require 3 edges, whereas to induce a length of 4 only 2 edges are sufficient.

Fig. 4.

Counter Example

Theorem 3

Let $\mathcal {S}$ be an $\ell$-instance and G be the associated ${SP}$ graph with parse tree representation T. For every node v in T, let the corresponding ${SP}$ network be $G_v$ and $\ell _{max,v}$ be the length of the maximum used path from $s_v$ to $t_v$. Algorithm 3 creates the list, $lst_v$, with the following properties.

• 1. For each ‘edge-length’ pair $(\eta _i,\ell _i)$, $i=1$ to $m_v$, in $lst_v$, $\ell _i$ is the maximum length that can be induced in the network $G_v$ using at most $\eta _i$ edges.

• 2. For each ‘edge-length’ pair $(\eta _i,\ell _i)$ in the list $lst_v$, we have the total ordering, i.e. $\eta _{i+1}=\eta _{i}+1$ for all $i=1$ to $m_v-1$, and $\ell _{max,v}=\ell _1 \le \ell _2 \le \dots \le \ell _{m_v}=\infty$.

• 3. In $G_v$, length $\ell$ is induced by minimum $\eta _{\hat{i}}$ edges if and only if $\ell \ge \ell _1$ and $\hat{i}= {{\mathrm{arg\,min}}}\{\eta _j:(\eta _j,\ell _j)\in lst_v \wedge \ell _j\ge \ell \}$.

Lemma 5

In an $\ell$-instance $\mathcal {S}$ with ${SP}$ graph G, suppose we are given lists $lst_{v}$, for all nodes v in the parse tree T of G, all of which satisfy properties 1, 2 and 3 in Theorem 3. Algorithm 4 induces any length $\ell _{in}\ge \ell _1$ optimally in G, where $\ell _1$ is the length of the first ‘edge-length’ pair in $lst_r$, r being the root node of T. Moreover, it specifies the appropriate tolls necessary for every edge.

Theorem 4

Algorithm 2 solves the ${MINTB}$ problem optimally in time $\mathcal {O}\left( m^3\right)$ for the instance $\mathcal {G}=\{G(V,E),(\ell _e)_{e\in E},r\}$, where G(V, E) is a ${SP}$ graph with $|V|=n$ and $|E|=m$.

5 Conclusion

In this paper we consider the problem of inducing the optimal flow as network equilibrium and show that the problem of finding the minimum cardinality toll, i.e. the ${MINTB}$ problem, is NP-hard to approximate within a factor of 1.1377. Furthermore we define the minimum cardinality toll with only used edges left in the network and show in this restricted setting the problem remains NP-hard even for single commodity instances with linear latencies. We leave the hardness of approximation results of the problem open. Finally, we propose a polynomial time algorithm that solves ${MINTB}$ in series-parallel graphs, which exploits the parse tree decomposition of the graphs. The approach in the algorithm fails to generalize to a broader class of graphs. Specifically, the monotonicity property proved in Lemma 4 holds in series-parallel graphs but breaks down in general graphs revealing an important structural difficulty inherent to ${MINTB}$ in general graphs. Future work involves finding approximation algorithms for ${MINTB}$. The improvement of the inapproximability results presented in this paper provides another arena to this problem, e.g. finding stronger hardness of approximation results for ${MINTB}$ in multi-commodity networks.