Linear-Time Algorithms for the Farthest-Segment Voronoi Diagram and Related Tree Structures

Abstract

We present linear-time algorithms to construct tree-like Voronoi diagrams with disconnected regions after the sequence of their faces along an enclosing boundary (or at infinity) is known. We focus on the farthest-segment Voronoi diagram, however, our techniques are also applicable to constructing the order-$(k{+}1)$ subdivision within an order-k Voronoi region of segments and updating a nearest-neighbor Voronoi diagram of segments after deletion of one site. Although tree-structured, these diagrams illustrate properties surprisingly different from their counterparts for points. The sequence of their faces along the relevant boundary forms a Davenport-Schinzel sequence of order $\ge 2$. Once this sequence is known, we show how to compute the corresponding Voronoi diagram in linear time, expected or deterministic, augmenting the existing linear-time frameworks for points in convex position with the ability to handle non-point sites and multiple Voronoi faces.

Research supported in part by the Swiss National Science Foundation, project 20GG21-134355, under the ESF EUROCORES program EuroGIGA/VORONOI.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

It is well known that the Voronoi diagram of points in convex position can be computed in linear time, given the order of their convex hull [1]. Linear-time constructions also exist for a class of related diagrams such as the farthest-point Voronoi diagram, computing the medial axis of a convex polygon, and deleting a point from the nearest-neighbor Voronoi diagram. In an abstract setting, a Hamiltonian abstract Voronoi diagram can be computed in linear time [9], given the order of Voronoi regions along an unbounded simple curve, which visits each region exactly once and can intersect each bisector only once. This construction has been extended recently to include forest structures [5] under similar conditions where no region can have multiple faces within the domain enclosed by the curve. The medial axis of a simple polygon can also be computed in linear time [8]. It is therefore natural to ask what other types of Voronoi diagrams can be constructed in linear time.

Classical variants of Voronoi diagrams such as higher-order Voronoi diagrams for sites other than points, had surprisingly been ignored in the literature of computational geometry until recently [4, 13]. Given a set S of n simple geometric objects in the plane, called sites, the order- k Voronoi diagram of S is a partitioning of the plane into regions such that every point within a region has the same k nearest sites. For $k=1$, this is the nearest-neighbor Voronoi diagram and for $k=n-1$ it is the farthest-site Voronoi diagram of S. Despite similarities, these diagrams for non-point sites, e.g., line segments, illustrate fundamental structural differences from their counterparts for points, such as the presence of disconnected regions (see also [2, 6, 10]). This had been a gap in the computational geometry literature, until recently, as segment Voronoi diagrams are fundamental to problems involving proximity among polygonal objects. This paper contributes further in closing this gap. For more information on Voronoi diagrams see the book of Aurenhammer et al. [3]. For application examples of higher order segment Voronoi diagrams see, e.g., [11] and references therein.

In this paper we give linear-time algorithms (expected and deterministic) for constructing tree-like Voronoi diagrams with disconnected regions, after the sequence of their faces within an enclosing boundary (or at infinity) is known. We focus on the farthest-segment Voronoi diagram, however, the same techniques are applicable to constructing the order-$(k{+}1)$ subdivision within a given order-k segment Voronoi region, and updating in linear time the nearest-neighbor segment Voronoi diagram after the deletion of one site. Interestingly, the latter two problems require computing initially two different tree-like diagrams. A major difference from the respective problems for points is that the sequence of faces along the relevant enclosing boundary forms a Davenport-Schinzel sequence of order at least two,¹ in contrast to the case of points, where no repetition can exist. Repetition introduces several complications, including the fact that the sequence of Voronoi faces along the relevant boundary for a subset of the original segments, $S'\subset S$, is not a subsequence of the respective sequence for S. In addition, such a subsequence may not even correspond to a Voronoi diagram. Thus, the intermediate diagrams computed by our algorithms are interesting on their own right. They have the structural properties of the relevant segment Voronoi diagram, however, they do not correspond to such a diagram nor are they instances of abstract Voronoi diagrams.

The purpose of this paper is to extend the paradigm of the existing linear constructions for tree-structured diagrams beyond the case of points in convex position [1]. Our goal is to generalize fundamental techniques known for points to more general objects so that the computation of their basic diagrams can be unified, despite their structural differences. As a byproduct we also improve the time complexity of the basic iterative approach to construct the order-k segment Voronoi diagram to $O(k^2n+ n\log n)$ from the standard $O(k^2n\log n)$ [13], and also updating a nearest neighbor diagram after deletion of one site in time proportional to the number of updates performed in the diagram.

2 Preliminaries and Definitions

Let S be a set of arbitrary line segments in $\mathbb {R}^2$; segments in S may intersect or touch at a single point. The distance between a point q and a line segment $s_i$ is $d(q,s_i)=\min \{d(q,y) \mid y\in s_i\}$, where d(q, y) denotes the ordinary distance between two points q, y in the $L_2$ (or the $L_p$) metric. The bisector of two segments $s_i,s_j\in S$ is $b(s_i,s_j) = \{x \in \mathbb {R}^{2} \mid d(x, s_{i}) = d(x,s_{j})\}.$ For disjoint segments, $b(s_i,s_j)$ is an unbounded curve that consists of a constant number of pieces, where each piece is a portion of an elementary bisector between the endpoints and open portions of $s_i, s_j$. If two segments intersect at point p, their bisector consists of two such curves intersecting at p.

The farthest Voronoi region of a segment $s_{i}$ is $\textit{freg}(s_{i}) = \{x \in \mathbb {R}^{2} \mid d(x, s_{i}) > d(x,s_{j}), 1 \le j \le n, j\ne i \}$. For disjoint line segments or line segments that intersect but do not touch at endpoints, the order-k Voronoi region of a set H, where $H \subset S$, $|H|=k$, and $1\le k\le n-1$, is $\textit{k-reg}(H)= \{x~|~\forall s\in H, \forall t\in S\setminus H~d(x,s)<d(x,t)\}$. For an extension of this definition to line segments forming a planar straight-line graph, see [13]. Note, for $k=n-1$, $\textit{freg}(s_{i}) = \textit{k-reg}(S\setminus \{s_i\})$. The (non-empty) farthest (resp., order-k) Voronoi regions of the segments in S, together with their bounding edges and vertices, define a partition of the plane, called the farthest-segment Voronoi diagram, denoted $\mathrm {FVD}(S)$, see Fig. 1(a) (resp., order- k Voronoi diagram). Any maximally connected subset of a Voronoi region is called a face.

Fig. 1.

[12] (a) $\mathrm {FVD}(S)$, $S = \{s_1,\dots ,s_5\}$; (b) its farthest hull; (c) $\mathrm {Gmap}(S)$

A farthest Voronoi region $\textit{freg}(s_i)$ is non-empty and unbounded in direction $\phi$ if and only if there exists an open halfplane, normal to $\phi$, which intersects all segments in S but $s_i$ [2]. The line $\ell$, normal to $\phi$, bounding such a halfplane, is called a supporting line. The direction $\phi$ (normal to $\ell$) is referred to as the hull direction of $\ell$ and it is denoted by $\nu (\ell )$. An unbounded Voronoi edge separating $\textit{freg}(s_i)$ and $\textit{freg}(s_j)$ is a portion of b(p, q), where p, q are endpoints of $s_i$ and $s_j$, such that the line through $\overline{pq}$ induces an open halfplane that intersects all segments in S, except $s_i,s_j$ (and possibly except additional segments incident to p, q). Segment $\overline{pq}$ is called a supporting segment; the direction normal to it pointing to the inside of this halfplane is denoted by $\nu (\overline{pq})$ and is called the hull direction of $\overline{pq}$. A segment $s_i\in S$ such that the line $\ell$ through $s_i$ is supporting, is called a hull segment; its hull direction is $\nu (s_i)=\nu (\ell )$, normal to $\ell$. The closed polygonal line obtained by following the supporting and hull segments in the angular order of their hull directions is called the farthest hull. Figures 1(a) and (b) illustrate a farthest-segment Voronoi diagram and its hull respectively. In Fig. 1(b), supporting segments are shown in dashed lines, and hull segments are shown in bold. Arrows indicate the hull directions of all supporting and hull segments. For more information see [12].

The Gaussian map of $\mathrm {FVD}(S)$, denoted $\mathrm {Gmap}(S)$, (see Fig. 1(c)) provides a correspondence between the faces of $\mathrm {FVD}(S)$ and a circle of directions K [12]. K can be assumed to be a unit circle, where each point x on K corresponds to a direction as indicated by the radius of K at x. Each Voronoi face is mapped to an arc on K, which represents the set of directions along which the face is unbounded. An arc is delimited by two consecutive hull directions of supporting segments. The $\mathrm {Gmap}(S)$ can be viewed as a cyclic sequence of consecutive arcs on K, where each arc corresponds to one face of $\mathrm {FVD}(S)$. Two neighboring arcs $\alpha , \gamma$ are separated by the hull direction $\nu (\alpha , \gamma )$ of a supporting segment $\overline{pq}$ ($\nu (\alpha , \gamma ) = \nu (\overline{pq})$); $\nu (\alpha , \gamma )$ is the direction towards infinity of the relevant portion of bisector b(p, q). The arc of a hull segment is called a segment arc and consists of two sub-arcs separated by the hull direction $\nu$ of the segment, where each sub-arc corresponds to an endpoint of the hull segment. An arc that corresponds to a single endpoint of a segment is called a single-vertex arc. The $\mathrm {Gmap}(S)$ can be computed in $O(n\log n)$ time (or output-sensitive $O(n\log h)$ time, where $h=|\mathrm {Gmap}(S)|$) [12].

The standard point-line duality transformation T offers a correspondence between the faces of $\mathrm {FVD}(S)$ and envelopes of wedges [2]. A segment $s_i=uv$ corresponds to a lower wedge, defined by the lower envelope of T(u) and T(v) (see, e.g., Fig. 5), and to an upper wedge defined as the area above the upper envelope of T(u), T(v). Let E (resp., $E'$) be the boundary of the union of the lower (resp., upper) wedges. The faces of $\mathrm {FVD}(S)$ correspond exactly to the edges of E and $E'$ [2]. Let the upper and lower Gmap be the portion of $\mathrm {Gmap}(S)$ above and below the horizontal diameter of K respectively.

There is a clear correspondence between E (resp., $E'$) and the upper (resp., lower) Gmap: the vertices of E are exactly the hull directions of supporting segments on the upper Gmap and the apexes of wedges in E are exactly the hull directions of hull segments [12]. In fact, any x-monotone path $\pi$ in the arrangement of upper (resp., lower) wedges can be transformed into a sequence of arcs in the portion of K above (resp., below) its horizontal diameter. Each edge of $\pi$, portion of T(u), corresponds to an arc on K for u, and each vertex of $\pi$, which is an intersection point $T(u)\cap T(v)$, corresponds to the hull direction $\nu (\overline{uv})$ of the supporting segment $\overline{uv}$.

Throughout this paper, given an arc $\alpha$, let $s_\alpha$ denote the segment in S that induces $\alpha$.

3 The Farthest Voronoi Diagram of a Sequence

Let G be a sequence of arcs on the circle of directions K, corresponding to a pair of x-monotone paths in the dual space, one in the arrangement of upper (resp. lower) wedges. No arcs in the sequence can overlap and no gaps are allowed. We call G an arc sequence. Consecutive arcs of the same segment in G are assumed unified into a single maximal arc.

In the following we define the farthest Voronoi diagram of such an arc sequence G, $\mathrm {FVD}(G)$. For $G=\mathrm {Gmap}(S)$, $\mathrm {FVD}(G)=\mathrm {FVD}(S)$. The diagrams of such sequences appear as intermediate diagrams in the process of computing $\mathrm {FVD}(S)$, however, they do not correspond to any type of segment Voronoi diagram. We first define such a diagram and then present an arc deletion and arc insertion operation, which constitute the basis for our algorithms.

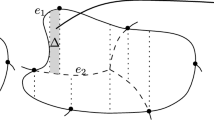
Given an arc $\alpha \in G$ and a point $x\in \mathbb {R}^2$, $x \not \in s_\alpha$, let $r(x,s_\alpha )$ denote the ray emanating from x in the direction $\overrightarrow{px}$, where p is the point in $s_\alpha$ closest to x (see Fig. 2). We say that x is attainable from $\alpha$ if the direction of $r(x,s_\alpha )$ is contained in $\alpha$. A point x in the interior of $s_\alpha$ is attainable from $\alpha$ if $\nu (s_\alpha )$ is in $\alpha$ (i.e., if $\alpha$ is a segment arc). An endpoint of $s_\alpha$ is attainable from all its corresponding arcs (see Sect. 2).

Let $d(x, \alpha ) = d(x, s_{\alpha })$, if x is attainable from $\alpha$, and let $d(x, \alpha ) = -\infty$, otherwise. The locus of points attainable from arc $\alpha$ is called the attainable region of $\alpha$, $R(\alpha )$. Figure 2 illustrates the attainable regions of arcs $\alpha _1, \alpha _2$, and $\beta$, shaded. Intuitively, an arc $\alpha$ exists only for points within its attainable region (i.e., $\alpha$ is relevant exclusively within $R(\alpha )$ and it should not be considered outside).

Remark 1

For arcs $\alpha _1, \alpha _2 \in G$ of the same segment $s_\alpha$, $R(\alpha _1)\cap R(\alpha _2) \setminus \{s_\alpha \}=\emptyset$.

Given two arcs $\alpha ,\beta$ ($s_\alpha \ne s_\beta$) we define their arc bisector by $b(\alpha ,\beta ) = b(s_\alpha ,s_\beta ) \cap R(\alpha )\cap R(\beta )$. If $s_\alpha =s_\beta$ and $\alpha ,\beta$ are consecutive, then $b(\alpha ,\beta )= R(\alpha )\cap R(\beta )$ is called the artificial bisector of $\alpha ,\beta$. The farthest Voronoi region of an arc $\alpha$ is now defined in the ordinary way

$$ \textit{freg}(\alpha ) = \{x \in \mathbb {R}^{2} \mid d(x, \alpha ) > d(x, \gamma ), \forall \text { arc } \gamma \in G, \gamma \ne \alpha \}. $$

The subdivision of the plane derived by the farthest regions of all arcs in G and their boundaries, is called the farthest Voronoi diagram of G, denoted $\mathrm {FVD}(G)$. The closure of $\textit{freg}(\alpha )$ is denoted by $\overline{\textit{freg}}(\alpha )$.

Definition 1

Let $\mathcal {T}(G)=\mathbb {R}^{2} \setminus \displaystyle {\cup _{\alpha \in G}}\textit{freg}(\alpha )$. If all edges of $\mathcal {T}(G)$ are portions of arc bisectors, then G, $\mathcal {T}(G)$, and $\mathrm {FVD}(G)$ are all called proper.

For a proper sequence, $\mathcal {T}(G)$ is simply the graph structure of $\mathrm {FVD}(G)$. The diagrams and sequences produced by our algorithms are always proper. Note, however, that for an arbitrary arc sequence, $\mathcal {T}(G)$ may contain boundaries of attainable regions and even two-dimensional regions. Figure 3(a) illustrates $\mathrm {FVD}(G)$ for a proper arc sequence G, which consists of three maximal arcs of segments $s_1, s_4,$ and $s_5$ and is derived from $\mathrm {Gmap}(S)$ of Fig. 1. Ray r indicates an artificial bisector between two consecutive arcs of $s_5$ (which have been unified into a single maximal arc for $s_5$). Figure 3(b) illustrates $\mathrm {FVD}(G'')$, where $G''$ contains an additional arc $\beta$ of segment $s_3$ ($G''= G\oplus \beta$).

Fig. 2.

Attainable regions $R(\alpha _1), R(\alpha _2), R(\beta )$

Fig. 3.

$\mathrm {FVD}(G)$ for an arc sequence of Fig. 1; (a) $\mathrm {FVD}(G)$; (b) $\mathrm {FVD}(G''), G''=G\oplus \beta$.

Lemma 1

For a proper arc sequence G, $\mathcal {T}(G)$ is a tree.

Proof

(Sketch). Since G is proper, all the edges of $\mathcal {T}(G)$ are portions of arc bisectors. Let x be a point on $\mathcal {T}(G)$ along arc bisector $b(\alpha ,\beta )$. We first prove that the entire ray $r(x,s_\alpha )$ must be enclosed in $\overline{\textit{freg}}(\alpha )$, i.e., regions are unbounded. This is because no arc bisector involving $\alpha$ can bound $r(x,s_\alpha )$ as we walk on it starting at x, unless an arc $\delta$ suddenly becomes attainable because $r(x,s_\alpha )$ intersects $R(\delta )$ at point z and $d(z,\delta )> d(z,\alpha )$; but then $z\in \mathcal {T}(G)$ without being on an arc bisector, a contradiction. It remains to show that $\mathcal {T}(G)$ is connected. If $\mathcal {T}(G)$ contained two different components, there would be a face of a segment $s_\alpha$ inducing two non consecutive arcs in G, $\alpha _1$ and $\alpha _2$. But then $\textit{freg}(\alpha _1)$ and $\textit{freg}(\alpha _2)$ would be neighboring, contradicting Remark 1.    $\square$

An arc sequence G is called a subsequence of $\mathrm {Gmap}(S)$ if every arc of G entirely contains a corresponding arc of $\mathrm {Gmap}(S)$ induced by the same segment. The arcs in G are simply expanded versions of the arcs in $\mathrm {Gmap}(S)$. The arcs in $\mathrm {Gmap}(S)$ as well as their expanded versions in G are called original arcs. A sequence $G'$ is called an augmented subsequence of $\mathrm {Gmap}(S)$ if $G'$ contains at least one arc of $\mathrm {Gmap}(S)$ for every segment with an arc in $G'$. An augmented subsequence consists of original arcs, which are expanded versions of the arcs in $\mathrm {Gmap}(S)$, and new arcs, which do not correspond to arcs of $\mathrm {Gmap}(S)$. An augmented subsequence $G'$, which has the same original arcs as G, is said to be corresponding to G. Note that in the dual space, G and $G'$ no longer correspond to envelopes of wedges, but to x-monotone paths that contain portions of these envelopes. The intermediate sequences of diagrams produced by our algorithms are always augmented subsequences of $\mathrm {Gmap}(S)$.

3.1 Deletion and Insertion of Arcs

Throughout our algorithms we use a deletion and a re-insertion operation for original arcs in sequences derived from $\mathrm {Gmap}(S)$. The deletion operation produces subsequences of $\mathrm {Gmap}(S)$ that are not necessarily proper. As a result, the insertion operation introduces new arcs, creating augmented subsequences, which are always proper. Let $G \ominus \beta$ (resp., $G\oplus \beta$) denote the arc sequence derived from G after deleting from it (resp., inserting to it) arc $\beta$.

Fig. 4.

Sequence $\alpha \beta \gamma$, $s_{\alpha }=s_\gamma$. (a) The dual wedges; (b) G; (c) $G\ominus \{\beta \}$; (d) The artificial bisector $b(\alpha , \gamma )=r$; the dashed curve indicates $b(s_\alpha ,s_\beta )$.

Arc Deletion. A subsequence G is derived from $\mathrm {Gmap}(S)$ by deleting arcs. When an arc $\beta$ is deleted from G, the neighboring arcs $\alpha$ and $\gamma$ expand over $\beta$ (see Fig. 4(a)–(c)). Either both $\alpha$ and $\gamma$ expand (see Figs. 4 and 5(a) illustrating segments in the dual space) or one expands while the other shrinks (see Fig. 5(b)). During the expansion, $\alpha$ and $\gamma$ may change from being a single-vertex arc to a segment arc. Since $\alpha$ and $\gamma$ are original, they both remain present in $G\ominus \{\beta \}$, and their common endpoint becomes $\nu (\alpha ,\gamma )$. Assuming $s_\alpha \ne s_\gamma$, $\nu (\alpha ,\gamma )$ corresponds to bisector $b(\alpha , \gamma )$ as obtained from $b(s_\alpha ,s_\gamma )$. If $s_\alpha =s_\gamma$, we let $\alpha$ and $\gamma$ expand until they reach $\nu (s_\beta )$, i.e., $\nu (\alpha ,\gamma ) = \nu (s_\beta )$. If $s_\alpha =s_\beta$ then $\alpha$ expands to cover the entire $\beta$ and $\nu (\alpha ,\gamma )=\nu (\beta ,\gamma )$.

Remark 2

The artificial bisector $b(\alpha ,\gamma )$ (for $s_\alpha =s_\gamma$) is (or contains) a ray perpendicular to $s_\beta$, emanating from the relevant endpoint of $s_\alpha$ and extending away from $s_\beta$ (see Fig. 4(d)).

Fig. 5.

Deleting and re-inserting $\beta$ in sequence $\alpha \beta \gamma$. (a) $\alpha$ and $\gamma$ enlarge; (b) $\gamma$ enlarges, $\alpha$ shrinks. From left to right: the initial sequence; after deleting $\beta$; after re-inserting $\beta$.

Arc Insertion. Let $G'$ be a proper augmented subsequence of $\mathrm {Gmap}(S)$ and let $\beta$ be an original arc, $\beta \not \in G'$. Let $\alpha ,\gamma$ be two consecutive original arcs in $G'$, such that $\beta$ is between $\alpha ,\gamma$ in $\mathrm {Gmap}(S)$. A number of new arcs may lie between $\alpha ,\gamma$ in $G'$. To insert $\beta$ in $G'$ there are several cases to consider. The insertion of arc $\beta$ in $G'$ corresponds to inserting $\textit{freg}(\beta )$ in $\mathrm {FVD}(G')$. Figure 5 illustrates in dual space the deletion and re-insertion of an arc $\beta$ in a sequence $\alpha \beta \gamma$.

Basic cases are as follows (assuming for simplicity that $\alpha ,\gamma$ are consecutive in $G'$): (1) $s_\alpha , s_\beta ,$ and $s_\gamma$ are all distinct, and $\nu (\alpha ,\gamma )$ is in $\beta$. This is the standard case, resulting in $\alpha \beta \gamma$, see Fig. 5(a). (2) $s_\alpha =s_\gamma$. Then $\beta$ is inserted over $\nu (s_\beta )=\nu (\alpha ,\gamma )$, resulting in $\alpha \beta \gamma$, and $\textit{freg}(\beta )$ is inserted over the artificial bisector $b(\alpha ,\gamma )$ in $\mathrm {FVD}(G')$, see Fig. 3. (3) Arc $\gamma$ (equiv. $\alpha$), as it appears expanded in $G'$, entirely contains $\beta$, see Fig. 5(b) (note that $\alpha$ had shrunk during the deletion of $\beta$). Then the insertion of $\beta$ splits $\gamma$ in two arcs resulting in $\alpha \gamma '\beta \gamma$, where $\gamma '$ is a new arc. In $\mathrm {FVD}(G')$, $\textit{freg}(\beta )$ splits $\textit{freg}(\gamma )$ into $\textit{freg}(\gamma )$ and $\textit{freg}(\gamma ')$. (4) $s_\alpha =s_\beta$ (equiv. $s_\beta =s_\gamma$). Then $\alpha$ is split by $\nu (\alpha ,\beta )$ and one part becomes $\beta$. Note that $\nu (\alpha ,\beta )$ is determined when $\alpha$ and $\beta$ became consecutive in a deletion operation, and that $\alpha ,\beta$ cannot be neighbors in $\mathrm {Gmap}(S)$.

If $\alpha$ and $\gamma$ are not consecutive in $G'$, a number of new arcs may be traced to find the actual entry point for $\beta$ between $\alpha$ and $\gamma$. The insertion of $\beta$ may delete a series of such consecutive new arcs. Assuming that $G'$ is proper, it is not hard to show that $G''= G'\oplus \beta$ is also a proper augmented subsequence of $\mathrm {Gmap}(S)$.

Fig. 6.

$\mathrm {FVD}(G)$ and G. (a) $G = \mathrm {Gmap}(S)$ for $S = \{s_\alpha ,s_\beta \}$; (b) $G = \mathrm {Gmap}(S)$ for $S = \{s_\alpha ,s_\delta \}$; (c) $G = \alpha \gamma \delta = \mathrm {Gmap}(S)\ominus \beta$ where $S = \{s_\alpha ,s_\delta \}$

Note that arc sequences defined by two segments are always proper. Figure 6 illustrates such sequences and their Voronoi diagrams. Figures 6(a) and (b) show $\mathrm {FVD}(S)$ and $\mathrm {Gmap}(S)$ for two disjoint and intersecting segments respectively. Figure 6(c) illustrates $\mathrm {FVD}(G)$ for $G=\mathrm {Gmap}(S)\ominus \beta$, where S is the same as in Fig. 6(b). In the latter figure, arcs $\alpha$ and $\gamma$ ($s_\alpha =s_\gamma$) become neighbors inducing one maximal arc $\alpha \gamma$; region $\textit{freg}(\alpha \gamma )$ is shown shaded; it is split into $\textit{freg}(\alpha )$ and $\textit{freg}(\gamma )$ by the artificial bisector $b(\alpha ,\gamma )=r_\beta \cup s_\alpha$.

4 A Randomized Linear Construction

We sketch an expected linear-time algorithm to compute $\mathrm {FVD}(S)$, given $\mathrm {Gmap}(S)$. It is inspired by the simple two-phase randomized approach of [7] for points in convex position and uses the concepts of Sect. 3. Let $\alpha _1,\alpha _2,\ldots , \alpha _h$ be a random permutation of arcs in $\mathrm {Gmap}(S)$, and let $A_i=\{\alpha _1,\alpha _2,\ldots , \alpha _i\}$, $1\le i\le h$, be the set of the first i arcs in this order. Let t be the largest index such that $\alpha _1,\ldots ,\alpha _t$ consists of arcs of only two segments that form exactly two maximal arcs.

The algorithm proceeds in two phases. Phase 1 computes the subsequence $G_i$, $t \le i < h$, where $G_h = \mathrm {Gmap}(S)$, and $G_i$ is obtained from $G_{i+1}$ by deleting arc $\alpha _{i+1}$ as described in Sect. 3. The two neighbors of $\alpha _{i+1}$ in $G_{i+1}$ are recorded as a tentative re-entry point for $\alpha _{i+1}$ during phase 2. Note that both neighbors may correspond to the same segment or the segment of one neighbor may coincide with $s_{\alpha _{i+1}}$. In phase 2, the algorithm computes incrementally $G'_i$ and $\mathrm {FVD}(G_i')$, for $t < i \le h$, starting with $\mathrm {FVD}(G_{t}')$, $G_{t}' = G_{t}$. $G_t'$ is proper as it consists of exactly two maximal arcs. $G'_{i+1}$ is obtained from $G'_{i}$ by inserting back $\alpha _{i+1}$ ($G'_{i+1}=G'_i\oplus \alpha _{i+1}$). During the re-entry of $\alpha _{i+1}$ a new arc may be created, thus, $G_{i+1}'\ne G_{i+1}$. The entry point for $\alpha _{i+1}$ is either an unbounded bisector (regular or artificial) or an arc $\sigma$ that entirely contains $\alpha _{i+1}$. In the latter case, a new arc is created. At the end of phase 2 we obtain $\mathrm {FVD}(G_h')=\mathrm {FVD}(S)$ ($G_h'=G_h$).

In the full paper we prove: (1) the complexity of $G_i'$ is O(i) despite the new arcs; (2) the expected number of new arcs traced in a step of phase 2 is constant. Then using backwards analysis we can derive the following theorem.

Theorem 1

Given $\mathrm {Gmap}(S)$, the $\mathrm {FVD}(S)$ can be computed in expected O(h) time, where h is the complexity of $\mathrm {FVD}(S)$.

5 A Deterministic Linear Divide-and-Conquer Algorithm

We now augment the framework of Aggarwal et al. [1] for points in convex position with techniques from Sects. 3, 4, and derive a linear-time algorithm to compute $\mathrm {FVD}(S)$, given $\mathrm {Gmap}(S)$. Let G be a subsequence of $\mathrm {Gmap}(S)$, and let $G'$ be a corresponding proper augmented subsequence such that the complexity of $G'$ is O(|G|), where |G| denotes the number of arcs of the sequence G. Our algorithm follows the flow of [9], which in turn follows [1].

• 1. Unite consecutive arcs of the same segment in G into single maximal arcs.

• 2. Color each arc of G red or blue by applying the following two rules:

  • (a) For each 5-tuple F of consecutive arcs $\alpha \beta \gamma \delta \epsilon$ in G, compute $\mathrm {FVD}(F')$ as follows: start with the sequence $\gamma \delta$, and consecutively insert the arcs $\beta , \epsilon , \alpha$ (in this order) resulting in $\mathrm {FVD}(F')$. ($F'$ is a possibly augmented version of F.) In $\mathrm {FVD}(F')$, if $\textit{freg}(\gamma )$ does not neighbor any region of segments $s_{\alpha }$ and $s_{\epsilon }$, color $\gamma$ red; else color $\gamma$ blue.

  • (b) For each series of consecutive blue arcs, color red every other arc, except the last one.

• 3. Let B (blue) be the sequence obtained from G by deleting all the red arcs. Recursively compute $\mathrm {FVD}(B')$. ($B'$ is a possibly augmented version of B.)

• 4. Partition the red arcs into crimson and garnet: Re-color as crimson at least a constant fraction of the red arcs, such that for any two crimson arcs, if they were inserted in $\mathrm {FVD}(B')$, their Voronoi regions would not touch.

• 5. Insert the crimson arcs one by one in $\mathrm {FVD}(B')$ resulting in $\mathrm {FVD}(V')$.

• 6. Let Gr (garnet) be the sequence obtained from G by deleting all blue and crimson arcs. Recursively compute $\mathrm {FVD}(Gr')$.

• 7. Merge $\mathrm {FVD}(V')$ and $\mathrm {FVD}(Gr')$ into $\mathrm {FVD}(G')$ so that $|G'|$ is O(|G|).

• 8. For any arcs united in Step 1, subdivide their regions in $\mathrm {FVD}(G')$ into finer parts by inserting the corresponding artificial bisectors.

The recursion ends when the number of maximal arcs in G is at most five. Then $\mathrm {FVD}(G')$ can be directly computed in O(1) time and also enhanced as indicated in Step 8. If all arcs in G are of the same segment, no diagram is generated but instead G is returned as a list of arcs. In this case, in Step 7, we obtain $\mathrm {FVD}(G')$ by inserting this list of arcs in $\mathrm {FVD}(V')$ one by one.

Step 2. Rules 2a and 2b guarantee that no two consecutive arcs in G are red and no three consecutive arcs in G are blue. The insertion order in Rule 2a guarantees that $\gamma$ neighbors at most one new arc.

Step 4. To choose the crimson arcs we apply the combinatorial lemma of [1] on (a modified) $\mathcal {T}(B')$. The lemma states that for a binary tree T with n leaves embedded in $\mathbb {R}^2$, if each leaf of T is associated with a subtree of T and if for any two successive leaves these subtrees are disjoint, then in O(n) time we can choose a set of leaves, whose number is at least a constant fraction of n and whose subtrees are pairwise disjoint. We associate each red arc $\beta$ in G with a unique leaf of $\mathcal {T}(B')$, which would be the entry point for $\beta$ in $\mathrm {FVD}(B')$. If the insertion of $\beta$ splits an arc of $B'$ in two, then we also add an artificial bisector to $\mathcal {T}(B')$ to serve as an entry point for $\beta$. The leaf in $\mathcal {T}(B')$ associated with $\beta$ is in turn associated with the incident subtree of $\mathcal {T}(B')$, which would be intersected by $\textit{freg}(\beta )$, if $\beta$ were inserted in $\mathrm {FVD}(B')$. The modified $\mathcal {T}(B')$ satisfies the requirements of the combinatorial lemma, and has complexity proportional to $|B'|$ plus the number of red arcs |R|.

Step 7. We obtain $G'$ and $\mathrm {FVD}(G')$ by merging $\mathrm {FVD}(V')$ and $\mathrm {FVD}(Gr')$. To keep the complexity of $G'$ within O(|G|), we merge the two diagrams while discarding parts that are guaranteed to contain no original arcs. Merging is done in two steps: (1) identify starting points for the merge curves between the two diagrams, and (2) trace the merge curves. Here, we identify starting points only for the merge curves that are related to original arcs. Skipping a merge curve has the effect of discarding the portion of one diagram that is bounded by it. This can be safely done because any portions of the diagram that are associated with only new arcs can not appear in $\mathrm {FVD}(S)$. $G'$ contains all the original arcs of $V'$ and $Gr'$; furthermore, $|G'|$ is $O(|V'|+|Gr'|)$. Since $G'$ contains all the original arcs of G, it is an augmented subsequence of $\mathrm {Gmap}(S)$ corresponding to G. It is not hard to prove that $G'$ is proper.

$G'$ is an augmented subsequence of $\mathrm {Gmap}(S)$ corresponding to G, and the recursive algorithm starts with $G=\mathrm {Gmap}(S)$. Thus, at the end of the algorithm, the resulting arc sequence must be $G'=\mathrm {Gmap}(S)$ (easy to see in dual space).

Lemma 2

$|G'|$ is O(|G|).

Proof

Let $m=|G|$ and $S(m)=|G'|$. Since Step 4 is performed by applying the combinatorial lemma of [1], $|Gr|\le q|R|$, where $0<q<1$ and |R| is the number of red arcs ($|R|= |G|-|B|$). Thus, (following [1, 9]) there exist positive constants $q_1$ and $q_2$, $q_1+q_2 < 1$, such that $|B| \le q_1|G|$ and $|Gr| \le q_2|G|$. At Step 4, at most one new arc is generated for every crimson arc inserted in $B'$, thus, $|V'| = S(q_1m) + O(m)$. At Step 7, $|G'| \le |V'| + |Gr'| + O(m)$. Thus, $|G'| \le S(q_1m) + S(q_2m) + O(m)$. Hense, $S(m) = O(m)$.    $\square$

Since the size of the augmented subsequences is always kept bounded, the time complexity can be analyzed similarly to [1]. We conclude:

Theorem 2

Given $\mathrm {Gmap}(S)$, the $\mathrm {FVD}(S)$ can be computed in O(h) time, where h is the combinatorial complexity of $\mathrm {FVD}(S)$.

Concluding Remarks

Theorems 1 and 2 apply also to computing the order-$(k{+}1)$ subdivision within an order-k Voronoi region in time proportional to the complexity of the region’s boundary. It also applies to updating a nearest-neighbor segment Voronoi diagram after the deletion of one segment in time proportional to the number of updates in the diagram. In this paper we considered line segments, however, the presented techniques are not specific to them. For example, the constructions can be easily adapted for the respective farthest abstract Voronoi diagram (to be described in the full paper). Note that the farthest abstract Voronoi diagram can be constructed in expected $O(n\log n)$ time by a randomized incremental construction [10], which is not related to the randomized linear-time approach in this paper.