Stability of a Cantilevered Flexible Plate with Non-uniform Thickness in Viscous Channel Flow

Abstract

Most studies analysing the instability of a cantilevered flexible plate in an axial flow are based on models assuming an inviscid flow and uniform properties for the plate. However, for some applications, such as biomechanical fluid-structure interaction (FSI) systems, these simplifications may not be valid due the scale of the problems and the non-uniform geometric and mechanical properties of the soft tissue. In this study, a parametric investigation is conducted to determine the conditions leading to flutter instability of a cantilevered flexible plate with a non-uniform thickness immersed in a two-dimensional viscous channel flow. It is shown that, depending on the mass ratio, the thinning and thickening of the plate free-end can stabilise or destabilise the FSI system and change the critical mode at instability onset.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The stability of a cantilevered flexible plate in an axial flow is a fundamental fluid-structure interaction (FSI) problem with applications in many fields of engineering, both long-established and emerging, such as energy harvesting (Tang et al. 2009) and biomechanics. When immersed in a two-dimensional channel flow, a cantilevered flexible plate can constitute a model analogue of the soft-palate in the upper airway, of which the flutter instability represents the occurrence of snoring (Elliott et al. 2011; Cisonni et al. 2014). While the mechanisms and the conditions leading to flutter remain unclear, recent investigations have shown that the critical velocity at which a single-mode instability is triggered is mainly determined by the fluid-to-plate mass and time-scale ratios (Eloy et al. 2008). Further, investigations taking into account the fluid viscosity in the FSI model have provided a better understanding of the energy exchange between the fluid and the flexible structure, particularly for a cantilevered plate in a confined flow (Balint and Lucey 2005). Hitherto, in the vast majority of studies, the properties of the plate have been assumed to be uniform. However, anatomical structures, such as soft tissue, in biomechanical systems can have non-uniform geometric and mechanical properties. Therefore, in this study, a parametric investigation is conducted to determine the conditions leading to flutter instability of a cantilevered flexible plate with a non-uniform thickness immersed in a two-dimensional viscous channel flow.

Fig. 1

Description of the FSI system modelling a cantilevered flexible plate immersed in a viscous channel flow, and the physical quantities of the problem

2 Method

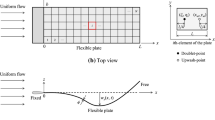
The FSI system is composed of a cantilevered flexible plate immersed in a viscous channel flow, as depicted in Fig. 1. The flow with mean inlet velocity $U^*$ in a two-dimensional channel of height $H^*$ and length $L^*$ is governed by the non-dimensional Navier–Stokes and continuity equations. Using the principle of virtual displacements, the deformation of the flexible plate of length $L^*_{P}$ and thickness $h^*$ is governed by the one-dimensional Kirchhoff–Love beam equation allowing for geometric non-linearity. The problem is formulated using the open-source finite-element library oomph-lib (Heil and Hazel 2006). The flexible plate is spatially discretised using two-node Hermite beam elements and the fluid domain using nine-node quadrilateral Taylor-Hood elements with adaptive mesh refinement capabilities. Time stepping is done with a Newmark scheme for the solid and a BDF2 scheme for the fluid. The FSI problem is discretised monolithically and the Newton-Raphson method is used to solve the non-linear system of equations, employing the SuperLU direct linear solver within the Newton iteration.

The numerical experiments are carried out at constant Reynolds number $\text {Re}=\rho ^*_f \, U^* \, H^* / \mu ^*=100$ and plate-to-channel aspect ratio $L_P/H=L_P^*/H^*=2$. The analysis of the stability/instability of the FSI system is conducted for variations of mass ratio $M=(\rho ^*_f L^*_P)/(\rho ^*_s h^*)$ and reduced flow velocity $U=U^*/(L^*_P f^*_P)$, where $\rho ^*_f$ is the fluid density, $\mu ^*$ the fluid dynamic viscosity, $\rho ^*_s$ the plate density, $f^*_P=\sqrt{B^*/(\rho ^*_s h^*)}/L_P^{*2}$ the plate characteristic frequency, and $B^*$ the plate flexural rigidity. The non-uniform flexural rigidity and mass are varied locally through a plate thickness function (see Fig. 2) dividing the plate into two sections (1 and 2 denoting the fixed-end and the free-end, respectively) of equal length ($L^*_1=L^*_2=L^*_P/2$) and keeping the total plate mass, and hence the mass ratio M, constant. Three cases are considered is this study, namely: (i) the reference system including a flexible plate of uniform thickness ($h_2/h_1=1$), (ii) a system including a flexible plate with a thinner free-end ($h_2/h_1=0.5$) and (iii) a system including a flexible plate with a thicker free-end ($h_2/h_1=2$).

Fig. 2

Flexible plate thickness profiles showing the two distinct sections for the three cases considered: uniform thickness (black solid line), thinner free-end (dark gray dotted line) and thicker free-end (light gray dashed line)

3 Results and Discussion

The amplitude decay/amplification of the plate motion for the three cases is determined through the analysis of the exponential growth rate in time of the span-wise deflection $\eta ^*$ of the oscillating plate tip. Figure 3 shows the exponential growth rate normalized by the oscillation frequency as a function of the mass ratio M and reduced flow velocity U for the uniform thickness plate ($h_2/h_1=1$). This growth rate “map” illustrates the complex influence of the interactions of the flow with the different structural modes on the stability of the system. The neutral stability curve corresponding to a zero growth rate, as shown in Fig. 3, is characterized by different branches corresponding to different flutter modes. For low mass ratios ($M<1$), Mode 2 dominates the FSI system behaviour and the growth rate consistently increases as the reduced flow velocity increases. For higher mass ratios ($M>1$), higher mode ($n>2$) instabilities start to predominate successively the FSI system behaviour as the mass ratio increases. Moreover, it can be observed that the variation of the pre-critical growth rate as a function of the reduced flow velocity becomes non-monotonic, denoting the changes between predominant flutter modes.

Fig. 3

Exponential growth rate of the tip displacement amplitude during the flexible cantilevered plate oscillation as a function of the mass ratio M and reduced flow velocity U for the uniform thickness plate ($h_2/h_1=1$). A higher growth rate (normalized by the oscillation frequency) indicates a more unstable system and a negative growth rate indicates a stabilisation of the FSI system. Neutral stability of the system is indicated with the black solid line

Fig. 4

Critical reduced flow velocity as a function of the mass ratio for the three cases considered: uniform thickness (black solid line), thinner free-end (dark gray dotted line) and thicker free-end (light gray dashed line)

The introduction of a non-uniform thickness produces a shift of the neutral stability curve along both the mass ratio and the reduced flow velocity axes, as can be seen in Fig. 4. For the flexible plate with a thinner free-end, the predominance of the higher mode instabilities is triggered for lower mass ratios, in comparison to the uniform thickness plate. In addition, all the different modal branches of the neutral stability curve are characterized by lower critical reduced flow velocities, in comparison to the uniform thickness plate. Conversely, for the flexible plate with a thicker free-end, the predominance of the higher mode instabilities is triggered for higher mass ratios and all the different modal branches of the neutral stability curve are characterized by higher critical reduced flow velocities. Despite the similar shapes of the neutral stability curves corresponding to the three cases, the thinning and thickening of the plate free-end greatly influence the motion of the cantilevered flexible plate. The altered plate dynamics result in drastically contrasting effects on the flutter instability thresholds and induce non-linear modifications of the pre- and post-critical behaviours. Thus, depending on the mass ratio, the thinning and thickening of the plate free-end can stabilise or destabilise the FSI system and change the critical mode in which the system first becomes unstable.