Keywords

1 Introduction

The floating zone method has been developed and widely used on the ground, which is considered as one of the most promising methods in space material product [1]. In this method, thermocapillary convection is the vital factor of controlling the quality of crystal growth under microgravity which is driven by surface tension gradient. Experiments have proven that the striations in crystals grown in space may be caused by oscillatory thermocapillary flow in floating zone configurations [2]. Temperature gradient plays a vital role in thermocapillary convection and thus influences the crystal growth. With the development of space technique, the crystal growth technique has been an important research subject.

In 1978, C.H. Chun and Wuest carried out an experiment of the thermocapillary oscillatory convection at reduced gravity effect for the first time [3]. Studies of Ruquan Liang, Shuo Yang and Jizhao Li showed that the axial magnetic fields which generate the Lorentz force affect the velocity level both inside the liquid bridge and on the free surface and hindered the fluid motion [4]. Silicon floating zone experiments under static axial magnetic fields, employing P- and Sb-doped crystals of 8 mm diameter and zones of 10–12 mm length, showed that the magnetic field has an effect on the formation of dopant striations [5]. Herrmann et al. (1992) and Cröll et al. (1994) have experimentally proven that steady magnetic fields can suppress the unsteady thermocapillary convection and enhance the character of floating zone [6]. Many studies have focused the attention on the effects of temperature difference and aspect ratios on the stability of liquid bridge. But the effect of these factors under magnetic field on stability of low Prandtl number (Pr = 0.09) liquid bridge is rarely reported in the literature. Therefore, it is studied in the present paper.

2 Physical and Mathematical Models

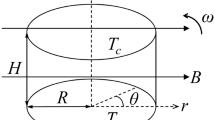
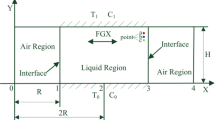
The liquid bridge is taken as the study model to simulate the industrial floating zone technique [7]. The liquid region is defined between two flat coaxial disks which are horizontal and differently heated. The radius of liquid bridge with height H and coaxial cylindrical tube used to control gas stream are R and 2R, respectively. Correspondingly, the aspect ratio is signed by H/R. The diameter of the model considered is d = 2R = 5.0 mm and the aspect ratio is 1. The temperatures of upper and lower rods are T u and T l, respectively. Hereafter, the temperature difference is ∆T = T u − T l. In this investigation, when dealing with the effect of aspect ratio on thermocapillary, we define T u = 730 K and T l = 705 K as the default value. The liquid bridge is surrounded by a concentric annular gas channel under axial magnetic field with strength B = 0.01 T, see Fig. 1.

Fig. 1
figure 1

Model of the half-floating zone liquid bridge under axial magnetic fields

Full size image

Let be the velocity field, ρ the density and the dynamic viscosity. Besides, g and p are denoted as the gravity vector and the pressure, respectively. Then, is taken as the characteristic velocity, as the dimensionless temperature and \( L = 2R \) as the characteristic length. Therefore, through a series of simplifying calculations, the dimensionless governing equations for this model are expressed as follows:

$$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0 $$
(1)
$$ \begin{aligned} \frac{{\partial \varvec{u}}}{\partial t} + \nabla \cdot \left( {\varvec{uu}} \right) & = - \frac{\nabla P}{\rho } + \frac{1}{\rho Re}\nabla \cdot \left( {2\mu \varvec{D}} \right) + \left( {\frac{{1 - Ca\Theta }}{We}} \right)\frac{{\kappa \delta \left( d \right)\varvec{n}}}{\rho } \\ & \quad + \frac{{Ha^{2} }}{\rho Re}(\varvec{u} \times B_{0} \varvec{e}_{y} \times B_{0} \varvec{e}_{y} ) \\ \end{aligned} $$
(2)
$$ \frac{{\partial\Theta }}{\partial t} + u\frac{{\partial\Theta }}{\partial x} + v\frac{{\partial\Theta }}{\partial y} = \frac{1}{RePr}{\Delta \varTheta } $$
(3)
$$ \frac{{\partial\Phi }}{\partial t} + u\frac{{\partial\Phi }}{\partial x} + v\frac{{\partial\Phi }}{\partial y} = 0 $$
(4)

where κ is the curvature, δ is the Dirac delta function, is the level set function, n is the unit normal vector directing to the air region and is the viscous stress tensor. The surface tension varies linearly with the liquid temperature which is measured by the temperature coefficient. Therefore, the surface tension can be formulated by, where is the surface tension value which is set at reference temperature T l. The kinematic viscosity is denoted as where is the dynamic viscosity. The related dimensionless parameters are expressed as follows: is the capillary number; is the Weber number; is the Reynolds number; is the Prandtl number is the Marangoni number; and is the Hartman number. Under the static magnetic field, the Lorentz force is formulated by where is the current density vector and is the induced electric potential. Considering no electric potential, the Lorentz force is simplified as [8]. Apart from that, this paper supposes that the liquid motion is laminar and buoyancy effects are not considered.

In this paper, a uniform mesh is adopted to discretize the axisymmetric liquid bridge, and the determination of time step not only meets the CFL condition but also ensure the convergence of calculation. Moreover, the SIMPLE algorithm is used to solve the governing equation and a staggered grid is adopted for the velocity and distance function. The parts of the boundary conditions are implemented by using the user-defined functions (user-defined function, UDF). The continuum surface force (CSF) model is taken to solve the difficulties in modeling topologically complex interfaces which have surface tension [9]. Finally, the numerical simulation under the axial uniform magnetic fields is completed.

3 Results and Discussion

Figure 2 characterizes the deformation on the free surface at different temperature differences. It is found that the maximum value of surface deformation is reached when the distance from cold disk is around 0.43. The magnitude of surface deformation increases with the larger temperature difference. Besides, the effect of temperature difference on the middle part is larger than that on both sides to some extent.

Fig. 2
figure 2

Deformation on the free surface at different temperature difference

Full size image

Figure 3 shows the axial velocity distribution at different temperature differences and radius, where x = 0 and x = 0.5 represent the central axis and the free surface, respectively. By comparing Fig. 3a, b, it is found that with the temperature difference increasing, the axial velocity from x = 0 to x = 0.4 becomes a bit smaller, but larger for free surface, see Fig. 3. In Fig. 3a, the maximum value of axial velocity on the free surface is 3.5 × 10−3 or so, while in Fig. 3b is 4.5 × 10−3 or so. The starting point of oscillation on the free surface moves about 0.1 unit distance toward the hot disk. The increase of temperature difference has an enhancing effect on the instability on the free surface.

Fig. 3
figure 3

Axial velocity distribution under different temperature difference. a ΔT = 20 K, b ΔT = 25 K, c ΔT = 30 K

Full size image

Figure 4 shows the axial velocity distribution at different radial places at different aspect ratios. The velocity distribution is almost the same when the aspect ratios are H/R = 0.8 and H/R = 1.2, see Fig. 4a, c. For H/R = 1, oscillation and variation ranges on the free surface is a bit smaller comparing with the value when the aspect ratios are H/R = 0.8 and H/R = 1.2, see Fig. 4b, which means that the axial uniform magnetic field can have a better suppressing effect on the thermocapillary convection of the liquid bridge when the aspect ratio is H/R = 1.

Fig. 4
figure 4

Axial velocity distribution by different radial places. a H/R = 0.8, b H/R = 1, c H/R = 1.2

Full size image

4 Conclusions

In this paper, it is found that under a certain axial magnetic field, the increasing of temperature difference increases the magnitude of surface deformation and enhances the oscillation on the free surface but has little effect on inside motion. On the other hand, the oscillatory onset of thermocapillary flow is also slightly delayed. The aspect ratio H/R = 1 has a suppressing influence on the fluid motion of the liquid bridge, but this effect is only shown on the free surface rather than the inside.