Some Transportation Problems Under Uncertain Environments

Abstract

Transportation problem (TP) is a very important area in operations research and management science. TPs not only involve with cost minimization, but also involve with many other goals such as profit maximization, time minimization, minimization of total deterioration of goods, etc. Also the available data of a transportation system such as transportation costs, resources, demands, conveyance capacities are not always crisp or precise but are uncertain. In this dissertation some transportation problems have been formulated and solved in different uncertain environments, e.g., fuzzy, type-2 fuzzy, rough and linguistic.

Section 1 is introductory. Some basic concepts and definitions of fuzzy set, type-2 fuzzy set, rough set and variable are introduced in Sect. 2. In Sect. 3, we have formulated and solved two solid transportation problems (STPs) with fuzzy parameters namely a multi-objective STP with budget constraints and a multi-objective multi-item STP. Section 4 presents some theoretical developments related to type-2 fuzzy variables (T2 FVs) - a defuzzification method of T2 FVs and an interval approximation method of continuous T2 FVs. In this section, three transportation models with type-2 fuzzy parameters have been formulated and solved. In Sect. 5, we have presented two transportation mode selection problems with linguistic evaluations represented by fuzzy variables and interval type-2 fuzzy variables respectively. Here we have developed two fuzzy multi-criteria group decision making methods and these methods are applied to solve the respective mode selection problems. Section 6 presents a practical solid transportation model considering per trip capacity for each type of conveyances. Also in this problem fluctuating cost parameters are represented by rough variables. Rough chance constrained programming model, rough expected value model and rough dependent-chance programming model are used to solve the problem with rough cost parameters.

This article is an extract from the Author’s Doctoral Dissertation.

1 Introduction

1.1 Transportation Problem (TP)

Transportation problem is one of the most important and practical application based area of operations research. The classical transportation problem (TP) is a distribution problem in which some goods/products are to be transported from some sources (factories, warehouses, etc.) to some destinations (demand points). The objective is to determine which routes to be considered for shipment and the amount of the shipment so that total transportation cost become minimum. Mathematically classical TP can be defined as a special type of linear programming problem.

Basic Terminologies in TP. The transportation systems depend on several parameters such as origin or source, destination, availability or resource, demand, unit transportation cost, conveyance, constraint, etc. Detailed descriptions on these parameters are available in the literature on transportation problems.

Origin or source: The places where the goods/products originate from, i.e. the goods are available (e.g., the plant, production center or warehouse etc.) are called the origins or the sources.

Destination: The places where the goods are to be transported are called destinations.

Availability or resource: The amount of goods available at some source that can be transported from the source is refereed as availability or resource of that source.

Demand: The amount of goods that is required at some destination is refereed as the demand of that destination.

Unit transportation cost: The cost of transportation of unit product from some source to some destination is called unit transportation cost of the product for that source-destination route.

Constraint: The availabilities as well as demands are limited to certain amount. Limitations on resource availability and fulfilment of demand of each destination form what are known as constraints.

Conveyance: Modes of transportation (e.g., trucks, goods trains, cargo flights, ships, etc.) are called conveyances.

Different Types of Transportation Models:

Basic Transportation Problem (TP): The classical transportation problem (TP) deals with transportation of goods from some sources (supply points) to some destinations (demand points) so that total transportation cost becomes minimum. Suppose there are m origins (or sources) $O_{i},~(i=1,2,...,m)$ and n destinations (or demand points) $D_{j},~(j=1,2,...,n)$ and $a_{i}$ be the amount of a homogeneous product available at i-th origin and $b_{j}$ be the demand at j-th destination. Let $c_{ij}$ is the cost for transportation of unit of product from source i to destination j and $x_{ij}$ be decision variable which represents the unknown quantity to be transported from i-th origin to j-th destination. Then the mathematical form of TP is

$$\begin{aligned} Min~ Z=\sum _{i=1}^m\sum _{j=1}^n~c_{ij}~x_{ij}, \end{aligned}$$

(1)

$$\begin{aligned} s.t.~ \sum _{j=1}^n x_{ij}~(=,\le & {} )~ a_{i},~~i=1,2,...,m, \end{aligned}$$

(2)

$$\begin{aligned} \sum _{i=1}^m x_{ij}~(=,\ge & {} )~ b_{j},~~j=1,2,...,n, \end{aligned}$$

(3)

$$\begin{aligned} x_{ij}\ge 0,~\forall ~ i,j,~\sum _{i=1}^m~a_{i}~(=,\ge )\sum _{j=1}^n~b_{j}. \end{aligned}$$

(4)

The constraint (2) ensures that total transported amount to the destinations from some source must be equal or less than the availability of that source. The constraint (3) indicates that total transported amount from the sources should at least satisfy the demand of each destination. If the constraints (2) and (3) are of equality types and total available resources are equal to the total demands, then the problem is called balanced TP. However in some real systems, the balance condition does not always holds, i.e., it may happen that total available resources are greater or equal to the total demands. Then the constraints become inequality types and the problem is called unbalanced TP.

Fixed Charge Transportation Problem (FCTP): A transportation problem is often associated with additional costs (termed as fixed costs) besides transportation cost. This fixed costs may be due to permit fees, property taxes, toll charges etc. Suppose $d_{ij}$ be the fixed cost associated with route (i, j). Mathematical formulation of FCTP is

$$\begin{aligned} Min Z=\sum _{i=1}^m\sum _{j=1}^n~(c_{ij}~x_{ij}+d_{ij}~y_{ij}), \end{aligned}$$

(5)

$$\begin{aligned} s.t.~ \sum _{j=1}^n x_{ij}~(=,\le & {} )~ a_{i},~~i=1,2,...,m \end{aligned}$$

(6)

$$\begin{aligned} \sum _{i=1}^m x_{ij}~(=,\ge & {} )~ b_{j},~~j=1,2,...,n, \end{aligned}$$

(7)

$$\begin{aligned} \sum _{i=1}^m~a_{i}~(=,\ge )\sum _{j=1}^n~b_{j}, \end{aligned}$$

(8)

$$\begin{aligned} x_{ij}\ge 0,~;~y_{ij}= \left\{ \begin{array}{ll} 1, &{} \hbox {if}\, x_{ij}>0; \\ 0, &{} \hbox {otherwise.} \end{array}\right. ~\forall ~ i,j \end{aligned}$$

(9)

The notations $c_{ij}$, $a_{i}$, $b_{j}$ and $x_{ij}$ have the same meaning as in the above model. It is obvious that the fixed charge $d_{ij}$ will be costed for a route (i, j) only if any transportation activity is assigned to that route. So $y_{ij}$ is defined such that if $x_{ij}>0$ then $y_{ij}=1$, otherwise it will be 0.

Multi-objective Transportation Problem (MOTP): If more than one objectives is to be optimized in an TP, then the problem is called multi-objective transportation problem (MOTP). The several objectives may be minimization of total transportation costs, maximization of profit, minimization of breakability, total delivery time, etc. If P objectives are to be optimized and $c_{ij}^p$ represents the unit transportation penalty (transportation cost, profit, breakability rate, distance, time etc.) for p-th objective $(p=1,2,...,P)$, then mathematical formulation is

$$\begin{aligned} Min/Max~Z_{p}=\sum _{i=1}^m\sum _{j=1}^n~~c_{ij}^p~x_{ij}~p=1,2,...,P, \end{aligned}$$

(10)

$$\begin{aligned} s.t.~ \sum _{j=1}^n x_{ij}~(=,&\le )&a_{i},~~i=1,2,...,m, \end{aligned}$$

(11)

$$\begin{aligned} \sum _{i=1}^m x_{ij}~(=,\ge & {} ) b_{j},~~j=1,2,...,n, \end{aligned}$$

(12)

$$\begin{aligned} x_{ij}\ge 0,~\forall ~ i,j,~\sum _{i=1}^m~a_{i}~(=,\ge )\sum _{j=1}^n~b_{j}. \end{aligned}$$

(13)

Multi-item Transportation Problem (MITP): In multi-item TP, several types of items/goods are transported instead of one type of good. If l items are to be transported and $c_{ij}^p$ be the unit transportation cost from i-th source to j-th destination for p-th $(p=1,2,...,l)$ item, then the mathematical formulation of MITP becomes

$$\begin{aligned} Min~Z=\sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n~~c_{ij}^p~x_{ij}^p \end{aligned}$$

(14)

$$\begin{aligned} s.t.~ \sum _{j=1}^n x_{ij}^p~(=,\le & {} ) a_{i}^p,~~i=1,2,...,m;~p=1,2,..,l \end{aligned}$$

(15)

$$\begin{aligned} \sum _{i=1}^m x_{ij}^p~(=,\ge & {} ) b_{j}^p,~~j=1,2,...,n;~p=1,2,..,l \end{aligned}$$

(16)

$$\begin{aligned} x_{ij}^p\ge 0, \forall ~ i,j,p;~\sum _{i=1}^m~a_{i}^p~(=,\ge ) \sum _{j=1}^n~b_{j}^p~,~p=1,2,...,l, \end{aligned}$$

(17)

where, $a_{i}^p$ be the availability of p-th item at i-th origin, $b_{j}^p$ be the demand of p-th item at j-th destination and $x_{ij}^p$ be the decision variable represents the amount of p-th item to be transported from i-th origin to j-th destination.

Solid Transportation Problem (STP): Solid transportation problem (STP) is an extension of the basic TP. In a transportation system, there may be different types of mode of transport available, such as trucks, goods trains, cargo flights, ships, etc. In STP, modes of transportation are considered. STP deals with three type of constraints instead of two (source and destination) in a TP. This extra constraint is due to modes of transportation (conveyance). Mathematical formulation of STP is

$$\begin{aligned} Min~Z=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~~c_{ijk}~x_{ijk} \end{aligned}$$

(18)

$$\begin{aligned} s.t.~ \sum _{j=1}^n\sum _{k=1}^K x_{ijk}~(=,\le & {} ) a_{i},~~i=1,2,...,m \end{aligned}$$

(19)

$$\begin{aligned} \sum _{i=1}^m\sum _{k=1}^K x_{ijk}~(=,\ge & {} ) b_{j},~~j=1,2,...,n\end{aligned}$$

(20)

$$\begin{aligned} \sum _{i=1}^m\sum _{j=1}^n~x_{ijk}~(=,\le & {} ) e_{k},~~k=1,2,...,K \end{aligned}$$

(21)

$$\begin{aligned} x_{ijk}\ge 0, \forall ~ i,j,k, \end{aligned}$$

(22)

$$\begin{aligned} \sum _{i=1}^m~a_{i}~(=,\ge ) \sum _{j=1}^n~b_{j}~ and ~\sum _{k=1}^K~e_{k}~(=,\ge )\sum _{j=1}^n~b_{j} \end{aligned}$$

(23)

where, $c_{ijk}$ be the unit transportation cost from i-th origin to j-th destination through k-th conveyance, $x_{ijk}$ is the decision variable represents the amount of goods to be transported from i-th origin to j-th destination through k-th conveyance and $a_{i}$, $b_{j}$ have the same meaning as mentioned before. $e_{k}$ be the transportation capacity of conveyance k, so that the constraint (21) indicates that the total amount transported by conveyance k is no more than its transportation capacity.

1.2 Uncertain Environment

In many real world problems the available data are not always exact or precise. Various types of uncertainties appear in those data due to various reason such as insufficient information, lack of evidence, fluctuating financial market, linguistic information, imperfect statistical analysis, etc. In order to describe and extract the useful information hidden in uncertain data and to use this data properly in practical problems, many researchers have proposed a number of improved theories such as fuzzy set, type-2 fuzzy set, random set, rough set etc. When some of or all the system parameters associated with a decision making problem are not exact or precisely defined, moreover those are represented by fuzzy, type-2 fuzzy, random or rough sets(/variables), etc., then it is called that the problem is defined in those uncertain environment respectively. Methodologies or Techniques to deal with such imprecision, uncertainty, partial truth, and approximation to achieve practicability, robustness and low solution cost is called Soft Computing.

1.3 Historical Review of Transportation Problems

Historical Review of Transportation Problem in Crisp Environment: The basic transportation problem (TP) was originally developed by Hitchcock [58] and later discussed in detail by Koopmans [69]. There are several methods introduced by many researchers for solving the basic transportation problems, such as the Vogel approximation method (VAM), the north-west corner method, the shortcut method, Russel’s approximation method (Greig, [50]). Dantzig [34] formulated the transportation problem as a special case of linear programming problems and then developed a special case form of Simplex technique (Dantzig, [33]) taking advantage of the special nature of the coefficient matrix. Kirca and Satir [67] presented a heuristic algorithm for obtaining an initial solution for TP. Gass [47] described various aspects of TP methodologies and computational results. Ramakrishnan [128] improved Goyals modified VAM for finding an initial feasible solution for unbalanced transportation problem.

Balinski [11], Hirch and Dantzig [57] introduced fixed charge transportation problem (FCTP). Palekar et al. [119] introduced a branch-and-bound method for solving the FCTP. Adlakha and Kowalski [3] reviewed briefly the FCTP. Adlakha et al. [4] provided a more-for-less algorithm for solving FCTP. Kowalski and Lev [70] developed the fixed charge transportation problem as a nonlinear programming problem. Lee and Moore [79] studied the optimization of transportation problems with multiple objectives. To solve multi-objective transportation problem, Zimmerman [159, 160] introduced and developed fuzzy linear programming. The solid transportation problem (STP) was first stated by Schell [130]. Haley [53] described a solution procedure of a solid transportation problem, which is an extension of the Modi method. Gen et al. [48] solved a bicriteria STP by genetic algorithm. Pandian and Anuradha [120] introduced a new method using the principle of zero point method for finding an optimal solution of STPs.

Historical Review of Transportation Problem in Fuzzy Environment: Several researchers studied various types of TPs with the parameters such as transportation costs, supplies, demands, conveyance capacities as fuzzy numbers(/variables). Chanas et al. [17] presented an FLP model for solving transportation problems with fuzzy supply and demand values. Chanas and Kuchta [18] studied transportation problem with fuzzy cost coefficients. Jiménez and Verdegay [60] considered two types of uncertain STP, one with interval numbers and other with fuzzy numbers. Jiménez and Verdegay [61] applied an evolutionary algorithm based parametric approach to solve fuzzy solid transportation problem. Bit et al. [13] applied fuzzy programming technique to multi-objective STP. Li and Lai [80], Waiel [135] applied fuzzy programming approach to multi-objective transportation problem. Saad and Abass [129] provided parametric study on the transportation problems in fuzzy environment. Liu and Kao [98] solved fuzzy transportation problems based on extension principle. Gao and Liu [46] developed the two-phase fuzzy algorithms for multi-objective transportation problem. Ammar and Youness [6] studied multi-objective transportation problem with unit transportation costs, supplies and demands as fuzzy numbers. Li et al. [81] presented a genetic algorithm for solving the multi-objective STP with coefficients of the objective function as fuzzy numbers. Pramanik and Roy [126] introduced a intuitionistic fuzzy goal programming approach for solving multi-objective transportation problems. Yang and Liu [153] presented expected value model, chance-constrained programming model and dependent chance programming for fixed charge STP with unit transportation costs, supplies, demands and conveyance capacities as fuzzy variables. Liu and Lin [93] solved a fuzzy fixed charge STP with chance constrained programming. Ojha et al. [118] studied entropy based STP with general fuzzy cost and time. Chakraborty and Chakraborty [15] considered a transportation problem having fuzzy parameters with minimization of transportation cost as well as time of transportation. Fegad et al. [42] found optimal solution of TP using interval and triangular membership functions. Kaur and Kumar [64] provided a new approach for solving TP with transportation costs as generalized trapezoidal fuzzy numbers. Kundu et al. [72] modeled a multi-objective multi-item STP with fuzzy parameters and solved it by using two different methods.

Historical Review of Transportation Problem in Type-2 Fuzzy Environment: Though type-2 fuzzy sets/varibles are used in various fields such as group decision making system (Chen et al. [21]; Chen et al. [26]), Portfolio selection problem (Hasuike and Ishi [54]), Pattern recognition (Mitchell, [112]), data envelopment analysis (Qin et al., [127]), neural network (Aliev et al. [5]), Ad hoc networks (Yuste et al. [155]) etc., Figueroa-Garca and Hernndez [43] first considered a transportation problem with interval type-2 fuzzy demands and supplies and we (Kundu et al. [75]) are the first to model and solve transportation problem with parameters as general type-2 fuzzy variables.

Historical Review of Transportation Problem with Rough Sets/Variables: Tao and Xu [132] developed rough multi-objective programming for rough multi-objective solid transportation problem considering a appropriately large feasible region as a universe and equivalent relationship is induced to generate an approximate space. Kundu et al. [73] first developed some practical solid transportation models with transportation cost as rough variables.

Historical Review of Transportation Mode Selection Problem: Kiesmüller et al. [65] discussed transportation mode decision problem taken into account both distribution of goods and the manufacturing of products. Kumru and Kumru [71] considered a problem of selecting the most suitable way of transportation between two given locations for a logistic company and applied multi-criteria decision-making method to solve the problem. Tuzkaya and Önüt [134] applied fuzzy analytic network process to evaluate the most suitable transportation mode between Turkey and Germany. The evaluation ratings and the weights of the criteria in that problem are expressed in linguistic terms generated by triangular fuzzy numbers. There are also other several articles available related to transportation mode selection problem (Monahan and Berger [113]; Eskigun et al. [41]; Wang and Lee [138]).

1.4 Motivation and Objective of the Article

Motivation: Transportation problem (TP) is one of the most important and practical application based area of operations research. TP has vast economic importance because price of every commodity includes transportation cost. Transportation problems not only involve with economic optimization such as cost minimization, profit maximization but also involve with many other goals such as minimization of total deterioration of goods during transportation, time minimization, risk minimization etc.

The available data of a transportation system, such as unit transportation cost, supplies, demands, conveyance capacities are not always exact or precise but are uncertain or imprecise due to uncertainty in judgment, insufficient information, fluctuating financial market, linguistic information, uncertainty of availability of transportation vehicles etc. This motivated us to consider some innovative transportation problems (TPs) under uncertain environments like fuzzy, type-2 fuzzy, rough etc.

Many researchers developed TPs in stochastic and fuzzy (type-1) environments. However at the beginning of this research work, we observed that no TP with type-2 fuzzy, rough parameters was available the in literature though these improved uncertainty theories are applied in many other decision making fields. This motivated us to develop and solve some TPs with type-2 fuzzy, rough parameters.

Also appropriate transportation mode selection is a very important issue in a transportation system and human judgments are generally expressed in linguistic terms. These linguistic terms are generally of uncertain nature as a word does not have the same meaning to different people. This motivated us to consider some transportation mode selection problems with linguistic evaluations.

Objective of the Article: The main objectives of the presented thesis are:

• To formulate different types of transportation models: Some innovative and useful transportation models could have been formulated to deal with the rapidly growing financial competition, technological development, real-life situations, etc. Here we have formulated some different types of transportation models such as multi-objective multi-item solid transportation model, multi-item solid transportation model with restriction on conveyances and items, solid transportation models with limited vehicle capacity, etc.

• To consider transportation problems with type-1 fuzzy parameters: Though some research works have been done about transportation problem in fuzzy environment, however there are some scopes of research work in this field. This includes new improved methodologies/techniques to solve different types of TPs with fuzzy parameters. In this thesis, we have formulated and solved two different solid transportation models with type-1 fuzzy parameters using improved defuzzification and solution techniques.

• To consider transportation problems with type-2 fuzzy parameters: Decision making with type-2 fuzzy parameters is an emerging area. Type-2 fuzzy sets (/variables) give additional degrees of freedom to represent uncertainty. However computational complexity is very high to deal with type-2 fuzzy sets. Here we have contributed some theoretical development of type-2 fuzzy variables, formulated and solved two transportation models with parameters as type-2 fuzzy variables. To the best of our knowledge, very few TPs with type-2 fuzzy variables were developed.

• To consider transportation problems with rough parameters: Rough set theory is moderately new and growing field of uncertainty. For the first time we have formulated and solved a solid transportation model with unit transportation costs as rough variables.

• To consider transportation mode selection problem with linguistic evaluations: Linguistic judgments are always uncertain. Many researchers represented linguistic terms using type-1 fuzzy sets (/variables). Recently from literature it is known that modeling word by interval type-2 fuzzy set is more scientific and reasonable than by type-1 fuzzy set. Here we have developed two fuzzy multi-criteria group decision making methods and successfully applied to solve two transportation mode selection problems with linguistic evaluations represented by type-1 and interval type-2 fuzzy variables respectively.

1.5 Organization of the Article

This article is based on my Ph.D. thesis [77]. In this article, some transportation problems have been formulated and solved in different uncertain environments, e.g., fuzzy, type-2 fuzzy, rough and linguistic. We classified our thesis into the following sections:-

Section 1 is introductory. It contains brief discussion about different types of transportation problems, uncertain environments and historical review of transportation problems.

In Sect. 2, some basic concepts and definitions of fuzzy set and variable, type-2 fuzzy set and variable, rough set and variable and representation of linguistic terms are introduced. Some methodologies to solve single/multi-objective linear/nonlinear programming problems in crisp and various uncertain environments have been discussed.

Section 3 presents transportation problems with fuzzy (type-1) parameters. In this section, we have formulated and solved two solid transportation models with type-1 fuzzy parameters. The first model is a multi-objective solid transportation problem (MOSTP) with unit transportation penalties/costs, supplies, demands and conveyance capacities as fuzzy variables. Also, apart from source, demand and capacity constraints, an extra constraint on the total budget at each destination is imposed. The second model is a multi-objective multi-item solid transportation problem with fuzzy coefficients for the objectives and constraints. A defuzzifcation method based on fuzzy linear programming is applied for fuzzy supplies, demands and conveyance capacities, including the condition that both total supply and conveyance capacity must not fall below the total demand.

In Sect. 4, we have first provided some theoretical developments related to type-2 fuzzy variables. We have proposed a defuzzification method of type-2 fuzzy variables. An interval approximation method of continuous type-2 fuzzy variables is also introduced. We have formulated and solved three transportation problems with type-2 fuzzy parameters namely, fixed charge transportation problem with type-2 fuzzy cost parameters, fixed charge transportation problem with type-2 fuzzy costs, supplies and demands and multi-item solid transportation problem having restriction on conveyances with type-2 fuzzy parameters.

Section 5 contains problems related to transportation mode selection with respect to several criteria for a particular transportation system. Here we have developed two fuzzy multi-criteria (/attribute) group decision making (FMCGDM/FMAGDM) methods, the first one based on ranking fuzzy numbers and the second one based on ranking interval type-2 fuzzy variables. These proposed methods are applied to solve two transportation mode selection problems with the evaluation ratings of the alternative modes and weights of the selection criteria are presented in linguistic terms generated by fuzzy numbers and interval type-2 fuzzy variables respectively.

In Sect. 6 we have represented fluctuating cost parameters by rough variables and formulated solid transportation model with rough cost parameters. The formulated transportation model is applicable for the system in which full vehicles, e.g. trucks, rail coaches are to be booked for transportation of products so that transportation cost is determined on the basis of full conveyances. The presented model is extended including different constraints with respect to various situations like restriction on number of vehicles, utilization of vehicles, etc.

In Sect. 7, overall contribution of the article and possible future extensions of the models and methods are discussed.

2 Basic Concepts and Methods/Techniques

2.1 Classical Set Theory

Classical (crisp) set is defined as a well defined collection of elements or objects which can be finite, countable or infinite. Here ‘well defined’ means an element either definitely belongs to or not belongs to the set. In other words, for a given element, whether it belongs to the set or not should be clear. The word crisp means dichotomous, that is, yes-or-no type rather than more-or-less type. In set theory, an element can either belongs to a set or not; and in optimization, a solution is either feasible or not.

Subset: If every element of a set A is also an element of a set B, then A is called a subset of B and this is written as $A\subseteq B$. If $A\subseteq B$ and $B\subseteq A$, then we say that A and B are equal, written as A = B. A is called a proper subset of B, denoted by $A\subset B$ if A is a subset of B with $A\ne B$ and $A\ne \emptyset$, where $\emptyset$ denotes the empty set.

Characteristic function: Let A be a subset of X. The characteristic function of A is defined by

$$\chi (x)=\left\{ \begin{array}{ll} 1, &{} \hbox {if}\,x\in A; \\ 0, &{} \hbox {otherwise.} \end{array}\right. $$

Convex set: A subset $S\subset \mathfrak {R}^n$ is said to be convex, if for any two points $x_{1}$, $x_{2}$ in S, the line segment joining the points $x_{1}$ and $x_{2}$ is also contained in S. In other words, a subset $S\subset \mathfrak {R}^n$ is convex, if and only if $x_{1}$, $x_{2}\in S$ $\Rightarrow$ $\lambda x_{1} + (1 - \lambda )x_{2} \in S;~0\le \lambda \le 1$.

Interval arithmetic: Here we discussed for given two closed intervals in $\mathfrak {R}$, how to add, subtract, multiply and divide these intervals. Suppose $*$ be a binary operation such as +, -, $\cdot$, /etc. defined over $\mathfrak {R}$. If A and B are closed intervals, then $A*B = \{a*b : a\in A, b\in B\}$ defines a binary operation on the set of closed intervals (Moore [115]). Let $A = [a_{1}, a_{2}]$ and $B = [b_{1}, b_{2}]$ be two closed intervals in $\mathfrak {R}$. Then operations on the closed intervals A and B are defined as follows:

Addition: $A+B=[a_{1}, a_{2}]+[b_{1}, b_{2}]=[a_{1}+b_{1},a_{2}+b_{2}]$

Subtraction: $A-B=[a_{1}, a_{2}]-[b_{1}, b_{2}]=[a_{1}-b_{1},a_{2}-b_{2}]$

Multiplication: $A\cdot B=[a_{1}, a_{2}]\cdot [b_{1}, b_{2}]=[\min (a_{1}b_{1},a_{1}b_{2},a_{2}b_{1},a_{2}b_{2}),\max (a_{1}b_{1},a_{1}b_{2},a_{2}b_{1},a_{2}b_{2})]$

In particular if these intervals are in $\mathfrak {R}^+$, the set of positive real numbers, then the multiplication formula gets simplified to

$A\cdot B=[a_{1}, a_{2}]\cdot [b_{1}, b_{2}]=[a_{1}b_{1},a_{2}b_{2}]$

Division: $\frac{A}{B}=\frac{[a_{1}, a_{2}]}{[b_{1}, b_{2}]}=[a_{1}, a_{2}]\cdot [\frac{1}{b_{2}}, \frac{1}{b_{1}}]=[\min (\frac{a_{1}}{b_{2}},\frac{a_{1}}{b_{1}},\frac{a_{2}}{b_{2}},\frac{a_{2}}{b_{1}}),\max (\frac{a_{1}}{b_{2}},\frac{a_{1}}{b_{1}},\frac{a_{2}}{b_{2}},\frac{a_{2}}{b_{1}}]$, provided 0 not belongs to $[b_{1}, b_{2}]$.

In particular if these intervals are in $\mathfrak {R}^+$, the set of positive real numbers, then the division formula gets simplified to

$\frac{A}{B}=[\frac{a_{1}}{b_{2}},\frac{a_{2}}{b_{1}}]$.

Scalar multiplication: For $k\in \mathfrak {R}^+$ the scalar multiplication $k\cdot A$ is defined as

$k\cdot A=k\cdot [a_{1}, a_{2}]=[k a_{1}, k a_{2}]$.

2.2 Fuzzy Set Theory

In the real world, various situations, concepts, value systems, human thinking, judgments are not always crisp and deterministic and cannot be described or represented precisely. Very often they are uncertain or vague. In real systems, there exist collection of objects so that those can not be certainly classified as a member of certain set. Zadeh [156] introduced the concept of fuzzy set in order to represent class of objects for which there is no sharp boundary between objects that belong to the class and those that do not. For example consider collection of real numbers close to 5. Then the number 4.5 can be taken as close to 5. The number 4.4 can also be taken as close to 5. Then how about the number 4.3 that smaller than 4.4 by only 0.1. Continuing in this way, it is difficult to determine an exact number beyond which a number is not close to 5. In fact there is no sharp boundary between close and not close to 5. Fuzzy sets describe such types of sets by assigning a number to every element in the universe, which indicates the degree (grade) to which the element belongs to the sets. This degree or grade is called membership degree or grade of the element in the fuzzy set. Mathematically a fuzzy set is defined as follows.

Definition 2.1

(Fuzzy Set). Let X be a collection of objects and x be an element of X, then a fuzzy set $\tilde{A}$ in X is a set of ordered pairs

$$\tilde{A}=\{(x,\mu _{\tilde{A}}(x))|~x\in X\},$$

where $\mu _{\tilde{A}}(x)$ is called the membership function or grade of membership of x in $\tilde{A}$ which maps X into the membership space M which is a subset of nonnegative real numbers having finite supremum.

Generally the range of the membership function $\mu _{\tilde{A}}(x)$ is constructed as the close interval [0, u], $0<u\le 1$ and the representation of fuzzy set becomes (Mendel [101])

$$\tilde{A}=\{(x,\mu _{\tilde{A}}(x))|\mu _{\tilde{A}}(x)\in [0,1], \forall x\in X\}.$$

A classical set A can be described in this way by defining membership function $\mu _{A}(x)$ that takes only two values 0 and 1 such that $\mu _{A}(x)=1$ or 0 indicates x belongs to or does not belongs to A.

Some Basic Definitions Related to Fuzzy Set: The following definitions and properties are based on Zadeh [156], Klir and Yuan [68], Zimmermann [160], Kaufmann [62], Bector and Chandra [12] and Wang et al. [144].

Support: The support of a fuzzy set $\tilde{A}$ in X is a crisp set $S(\tilde{A})$ defined as $S(\tilde{A})=\{x\in X|~\mu _{\tilde{A}}(x)> 0\}$.

Core: The core of a fuzzy set $\tilde{A}$ is a set of all points having unit membership degree in $\tilde{A}$ denoted by $Core(\tilde{A})$, and defined as $Core(\tilde{A})=\{x\in X|~\mu _{\tilde{A}}(x)=1\}$

Centroid: The centroid $C(\tilde{A})$ of a fuzzy set $\tilde{A}$ is defined by $C(\tilde{A})=\frac{\sum _{x} x \mu _{\tilde{A}}(x)}{\sum _{x} \mu _{\tilde{A}}(x)}$ for discrete case (discrete set of points) and $C(\tilde{A})=\frac{\int _{-\infty }^{\infty } x \mu _{\tilde{A}}(x) dx}{\int _{-\infty }^{\infty } \mu _{\tilde{A}}(x) dx}$ for continuous case.

Height: The height of a fuzzy set $\tilde{A}$, denoted by $h(\tilde{A})$ is defined as $h(\tilde{A})=\sup _{x\in X}\mu _{\tilde{A}}(x)$.

If $h(\tilde{A})=1$ for a fuzzy set $\tilde{A}$ then the fuzzy set $\tilde{A}$ is called a normal fuzzy set.

Complement: The complement of a fuzzy set $\tilde{A}$ is a fuzzy set denoted by $\tilde{A^c}$ is defined by the membership function $\mu _{\tilde{A^c}}(x)$, where $\mu _{\tilde{A^c}}(x)=h(\tilde{A})-\mu _{\tilde{A}}(x),~\forall x\in X$. If $\tilde{A}$ is normal then obviously $\mu _{\tilde{A^c}}(x)=1-\mu _{\tilde{A}}(x),~\forall x\in X$.

$\alpha$ -cut: $\alpha$-cut of a fuzzy set $\tilde{A}$ in X where $\alpha \in (0,1]$ is the crisp set $A_{\alpha }$ given by $A_{\alpha }=\{x\in X~|~\mu _{\tilde{A}}(x)\ge \alpha \}$.

Some Properties of Fuzzy Set: Union: The union of two fuzzy sets $\tilde{A}$ and $\tilde{B}$ is a fuzzy set $\tilde{C}$ whose membership function is given by $\mu _{\tilde{C}}(x)=\max (\mu _{\tilde{A}}(x),\mu _{\tilde{B}}(x)),$ $\forall ~x\in X$. This is expressed as $\tilde{C}=\tilde{A}\cup \tilde{B}$.

Intersection: The intersection of two fuzzy sets $\tilde{A}$ and $\tilde{B}$ is a fuzzy set $\tilde{D}$ whose membership function is given by $\mu _{\tilde{D}}(x)=\min (\mu _{\tilde{A}}(x),\mu _{\tilde{B}}(x)),~\forall ~x\in X$. This is expressed as $\tilde{D}=\tilde{A}\cap \tilde{B}$.

Convexity: A fuzzy set $\tilde{A}$ in X is said to be convex if and only if for any $x_{1}$, $x_{2}\in X$, $\mu _{\tilde{A}}(\lambda x_{1}+(1-\lambda )x_{2})\ge \min (\mu _{\tilde{A}}(x_{1}),\mu _{\tilde{A}}(x_{2}))$ for $0\le \lambda \le 1$. In terms of $\alpha$-cut, a fuzzy set is said to be convex if its $\alpha$-cuts $A_{\alpha }$ are convex for all $\alpha \in (0,1]$.

Containment: A fuzzy set $\tilde{A}$ is contained in $\tilde{B}$ or a subset of $\tilde{B}$ if $\mu _{\tilde{A}}(x)\le \mu _{\tilde{B}}(x),~\forall ~x\in X$. This is written as $\tilde{A}\subseteq \tilde{B}$.

Equality: Two fuzzy sets $\tilde{A}$ and $\tilde{B}$ in X is said to be equal if $\tilde{A}\subseteq \tilde{B}$ and $\tilde{B}\subseteq \tilde{A}$, i.e. if $\mu _{\tilde{A}}(x)=\mu _{\tilde{B}}(x),~\forall ~x\in X$.

Fuzzy Number: Fuzzy number can be taken as a generalization of interval of real numbers where rather than considering each point of an interval has the same importance or belongings, a membership grade in [0,1] is imposed to each element as in fuzzy set. This is done to handle a situation where one has to deal with approximate numbers or numbers that are close to a real number or around a interval of real numbers, etc. Let us consider set of numbers that are close to a real number r and try to represent this set by a fuzzy set, say by $\tilde{A}$. That is $\tilde{A}$ would be defined as an interval around r with each element having a membership grade that provided according to closeness of that point to r. Since the real number r is certainly close to r itself, so membership grade of r in $\tilde{A}$ should be defined as $\mu _{\tilde{A}}(r)=1$, i.e., $\tilde{A}$ should be a normal fuzzy set. Also the interval must be of finite length, i.e. support of $\tilde{A}$ need to be bounded. It is known that the only convex sets in $\mathfrak {R}$ are intervals. The fuzzy number is defined as follows:

Definition 2.2

(Fuzzy Number). A fuzzy subset $\tilde{A}$ of real number $\mathfrak {R}$ with membership function $\mu _{\tilde{A}}:\mathfrak {R}\rightarrow [0,1]$ is said to be a fuzzy number (Grzegorzewski [52]) if

• (i) $\tilde{A}$ is normal, i.e. $\exists$ an element $x_{0}$ s.t. $\mu _{\tilde{A}}(x_{0})=1$,

• (ii) $\mu _{\tilde{A}}(x)$ is upper semi-continuous membership function,

• (iii) $\tilde{A}$ is fuzzy convex, i.e. $\mu _{\tilde{A}}(\lambda x_{1}+(1-\lambda )x_{2})\ge \mu _{\tilde{A}}(x_{1})\wedge \mu _{\tilde{A}}(x_{2})~\forall x_{1},x_{2}\in \mathfrak {R}$ and $\lambda \in [0,1]$,

• (iv) Support of $\tilde{A}=\{x\in \mathfrak {R}:\mu _{\tilde{A}}(x)>0\}$ is bounded.

Klir and Yuan [68] proved the following theorem which gives characterization of a fuzzy number.

Theorem 2.1

Let $\tilde{A}$ be a fuzzy set in $\mathfrak {R}$. Then $\tilde{A}$ is a fuzzy number if and only if there exists a closed interval (which may be singleton) $[a, b]\ne \phi$ such that

$$\begin{aligned} \mu _{\tilde{A}}(x)=\left\{ \begin{array}{ll} l(x), &{} \hbox {if}\,x\in (-\infty ,a); \\ 1, &{} \hbox {if}\, x\in [a,b]; \\ r(x), &{} \hbox {if}\,x\in (b,\infty ), \end{array}\right. \end{aligned}$$

(24)

where (i) $l: (-\infty ,a)\rightarrow [0,1]$ is increasing, continuous from the right and $l(x)=0$ for $x\in (-\infty ,u)$, for some $u<a$ and (ii) $r: (b,\infty )\rightarrow [0,1]$ is decreasing, continuous from the left and $r(x)=0$ for $x\in (v,\infty )$, for some $v>b$.

In most of the practical applications the function l(x) and r(x) are continuous which give the continuity of the membership function.

$\alpha$ -cut of Fuzzy Number: the $\alpha$-cut/$\alpha$ - level set of a fuzzy number $\tilde{A}$, i.e. $A_{\alpha }=\{x\in \mathfrak {R}~|~\mu _{\tilde{A}}(x)\ge \alpha \}$ is a nonempty bounded closed interval (Wu [145]) denoted by $[A_{\alpha }^L,A_{\alpha }^R]$ or $[A_{\alpha }^-,A_{\alpha }^+]$, where, $A_{\alpha }^L$ and $A_{\alpha }^R$ are the lower and upper bounds of the closed interval and

$$A_{\alpha }^L=\inf \{x\in \mathfrak {R}~|~\mu _{\tilde{A}}(x)\ge \alpha \},~A_{\alpha }^R=\sup \{x\in \mathfrak {R}~|~\mu _{\tilde{A}}(x)\ge \alpha \}$$

Now some particular type of fuzzy numbers with continuous l(x) and r(x) defined over the set of real numbers are given below.

General Fuzzy Number (GFN): A GFN $\tilde{A}$ is specified by four numbers $a_{1}$, $a_{2}$, $a_{3}$, $a_{4}$ $\in \mathfrak {R}$ and two functions l(x) and r(x) (as defined in Theorem 2.1) with the following membership function

$$\begin{aligned} \mu _{\tilde{A}}(x)= \left\{ \begin{array}{ll} 0, &{} \hbox {if}\, x<a_{1};\\ l(x), &{} \hbox {if}\, a_{1}\le x< a_{2}; \\ 1, &{} \hbox {if}\, a_{2}\le x\le a_{3}; \\ r(x), &{} \hbox {if}\, a_{3}< x\le a_{4}; \\ 0, &{} \hbox {if}\, x>a_{4}. \end{array}\right. \end{aligned}$$

(25)

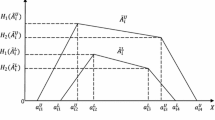
Triangular Fuzzy Number (TFN): A TFN $\tilde{A}$ is a fuzzy number fully determined by triplet $(a_{1},a_{2},a_{3})$ of crisp numbers with $a_{1}<a_{2}<a_{3}$, whose membership function is given by

$$\begin{aligned} \mu _{\tilde{A}}(x)= \left\{ \begin{array}{ll} \frac{x-a_{1}}{a_{2}-a_{1}}, &{} \hbox {if}\, a_{1}\le x\le a_{2}; \\ 1, &{} \hbox {if}\, x= a_{2}; \\ \frac{a_{3}-x}{a_{3}-a_{2}}, &{} \hbox {if}\, a_{2}\le x\le a_{3}; \\ 0, &{} \hbox {otherwise.} \end{array}\right. \end{aligned}$$

(26)

Fig. 1.

TFN $\tilde{A}$

The TFN $\tilde{A}$ is depicted in Fig. 1.

Trapezoidal Fuzzy Number (TrFN): A TrFN $\tilde{A}$ is a fuzzy number fully determined by quadruplet $(a_{1},a_{2},a_{3},a_{4})$ of crisp numbers with $a_{1}<a_{2}\le a_{3}<a_{4}$, whose membership function is given by

$$\begin{aligned} \mu _{\tilde{A}}(x)= \left\{ \begin{array}{ll} \frac{x-a_{1}}{a_{2}-a_{1}}, &{} \hbox {if}\, a_{1}\le x\le a_{2}; \\ 1, &{} \hbox {if}\, a_{2}\le x\le a_{3}; \\ \frac{a_{4}-x}{a_{4}-a_{3}}, &{} \hbox {if}\, a_{3}\le x\le a_{4}; \\ 0, &{} \hbox {otherwise.} \end{array}\right. \end{aligned}$$

(27)

where $\frac{x-a_{1}}{a_{2}-a_{1}}=\mu _{\tilde{A}}^l(x)$ and $\frac{a_{4}-x}{a_{4}-a_{3}}=\mu _{\tilde{A}}^r(x)$ are called the left and right hand side of the membership function $\mu _{\tilde{A}}(x)$. The TrFN $\tilde{A}$ is depicted in Fig. 2. Obviously if $a_{2}=a_{3}$ then TrFN becomes a TFN.

Fig. 2.

TrFN $\tilde{A}$

Arithmetic of Fuzzy Numbers: Operation Based on the Zadeh’s Extension Principle: Arithmetical operations of fuzzy numbers can be performed by applying the Zadehs extension principle (Zadeh [158]). If $\tilde{A}$ and $\tilde{B}$ be two fuzzy numbers and $*$ be any operation then the fuzzy number $\tilde{A}*\tilde{B}$ is defined as

$$\mu _{\tilde{A}*\tilde{B}}(z)=\sup _{z=x*y}\min (\mu _{\tilde{A}}(x),\mu _{\tilde{B}}(y)),~\forall z\in \mathfrak {R}.$$

So in particular we have

$$\mu _{\tilde{A}\oplus \tilde{B}}(z)=\sup _{z=x+ y}\min (\mu _{\tilde{A}}(x),\mu _{\tilde{B}}(y)),$$

$$\mu _{\tilde{A}\ominus \tilde{B}}(z)=\sup _{z=x- y}\min (\mu _{\tilde{A}}(x),\mu _{\tilde{B}}(y)),$$

$$\mu _{\tilde{A}\otimes \tilde{B}}(z)=\sup _{z=x\times y}\min (\mu _{\tilde{A}}(x),\mu _{\tilde{B}}(y)),$$

$$\mu _{\tilde{A}\oslash \tilde{B}}(z)=\sup _{z=x/ y}\min (\mu _{\tilde{A}}(x),\mu _{\tilde{B}}(y)),$$

where $\oplus$, $\ominus$, $\otimes$ and $\oslash$ denote the addition, substraction, multiplication and division operations on fuzzy numbers.

Operation Based on the $\alpha$ -cuts: Let $\tilde{A}$ and $\tilde{B}$ be two fuzzy numbers and $A_{\alpha }=[A_{\alpha }^L,A_{\alpha }^R]$, $B_{\alpha }=[B_{\alpha }^L,B_{\alpha }^R]$ be $\alpha$-cuts, $\alpha \in (0,1]$, of $\tilde{A}$ and $\tilde{B}$ respectively. Let $*$ denote any of the arithmetic operations $\oplus$, $\ominus$, $\otimes$, $\oslash$ of fuzzy numbers. Then the $*$ operation on fuzzy numbers $\tilde{A}$ and $\tilde{B}$, denoted by $\tilde{A}*\tilde{B}$, gives a fuzzy number in $\mathfrak {R}$ where

$$(\tilde{A}*\tilde{B})_{\alpha }=A_{\alpha }*B_{\alpha },~\alpha \in (0,1].$$

For particular operations we have

$$(\tilde{A}\oplus \tilde{B})_{\alpha }=A_{\alpha }\oplus B_{\alpha }=[A_{\alpha }^L+B_{\alpha }^L,A_{\alpha }^R+B_{\alpha }^R],$$

$$(\tilde{A}\ominus \tilde{B})_{\alpha }=A_{\alpha }\ominus B_{\alpha }=[A_{\alpha }^L-B_{\alpha }^R,A_{\alpha }^R-B_{\alpha }^L],$$

$$(\tilde{A}\otimes \tilde{B})_{\alpha }=A_{\alpha }\otimes B_{\alpha }=$$

$$=[\min \{A_{\alpha }^L B_{\alpha }^L,A_{\alpha }^L B_{\alpha }^R,A_{\alpha }^R B_{\alpha }^L,A_{\alpha }^R B_{\alpha }^R\},\max \{A_{\alpha }^L B_{\alpha }^L,A_{\alpha }^L B_{\alpha }^R,A_{\alpha }^R B_{\alpha }^L,A_{\alpha }^R B_{\alpha }^R\}].$$

If the fuzzy numbers $\tilde{A}$ and $\tilde{B}$ in $\mathfrak {R}^+$, the set of positive real numbers, then the multiplication formula becomes

$$(\tilde{A}\otimes \tilde{B})_{\alpha }=A_{\alpha }\otimes B_{\alpha }=[A_{\alpha }^L B_{\alpha }^L,A_{\alpha }^R B_{\alpha }^R].$$

Operations Under Function Principle: Hsieh [59] presented Function Principle in fuzzy theory for computational model avoiding the complications which are caused by the operations using Extension Principle. The fuzzy arithmetical operations under Function Principle of two trapezoidal fuzzy numbers $\tilde{A} =(a_{1},a_{2},a_{3},a_{4})$ and $\tilde{B} =(b_{1},b_{2},b_{3},b_{4})$ are

• (i) Addition: $\tilde{A}\oplus \tilde{B}=(a_{1}+b_{1}, a_{2}+b_{2}, a_{3}+b_{3}, a_{4}+b_{4})$,

• (ii) Substraction: $-\tilde{B}=(-b_{4},-b_{3},-b_{2},-b_{1})$ and $\tilde{A}\ominus \tilde{B}=(a_{1}-b_{4}, a_{2}-b_{3}, a_{3}-b_{2}, a_{4}-b_{1})$,

• (iii) Multiplication: $\tilde{A}\otimes \tilde{B}=(a_{1}b_{1}, a_{2}b_{2}, a_{3}b_{3}, a_{4}b_{4})$, where $a_{i}$, $b_{i}$, for $i=1,2,3,4$ are positive real numbers.

• (iv) Division: $\tilde{A}\oslash \tilde{B}=(a_{1}/b_{4}, a_{2}/b_{3}, a_{3}/b_{2}, a_{4}/b_{1})$, where $a_{i}$, $b_{i}$, for $i=1,2,3,4$ are positive real numbers.

• (v) $\lambda \otimes \tilde{A}=\left\{ \begin{array}{ll} (\lambda a_{1},\lambda a_{2},\lambda a_{3},\lambda a_{4}), &{} \hbox {if}\,\lambda \ge 0; \\ (\lambda a_{4},\lambda a_{3},\lambda a_{2},\lambda a_{1}), &{} \hbox {if}\,\lambda < 0. \end{array}\right.$

Here it should be mentioned that all the above operations can be defined using operations based on the $\alpha$-cuts of the fuzzy numbers that produce the same result.

Defuzzification of Fuzzy Numbers: Defuzzification methods/techniques of fuzzy numbers convert a fuzzy number or fuzzy quantity approximately to a crisp or deterministic value so that this can be used efficiently in practical applications. Some important defuzzification methods are presented below.

Graded Mean and Modified Graded Mean: Graded Mean (Chen and Hasieh [22]) Integration Representation method is based on the integral value of graded mean $\alpha$-level(cut) of generalized fuzzy number. For a fuzzy number $\tilde{A}$ the graded mean integration representation of $\tilde{A}$ is defined as

$$P(\tilde{A})=\int _{0}^1~\alpha \big [\frac{A_{\alpha }^L+A_{\alpha }^R}{2}\big ]d\alpha /\int _{0}^1~\alpha ~d\alpha ,$$

where $[A_{\alpha }^L,A_{\alpha }^R]$ is the $\alpha$-cut of $\tilde{A}$.

For example graded mean of a TrFN $\tilde{A}=(a_{1},a_{2},a_{3},a_{4})$ is $\frac{1}{6}[a_{1}+2a_{2}+2a_{3}+a_{4}]$.

Here, equal weightage has been given to the lower and upper bounds of the $\alpha$-level of the fuzzy number. But the weightage may depends on the decision maker’s preference or attitude. So, the modified graded mean $\alpha$-level value of the fuzzy number $\tilde{A}$ is $\alpha \big [k A_{\alpha }^L+(1-k) A_{\alpha }^R\big ]$, where $k\in [0,1]$ is called the decision makers attitude or optimism parameter. The value of k closer to 0 implies that the decision maker is more pessimistic while the value of k closer to 1 means that the decision maker is more optimistic. Therefore, the modified form of the above graded mean integration representation is

$$P(\tilde{A})=\int _{0}^1~\alpha \big [\frac{k A_{\alpha }^L+(1-k) A_{\alpha }^R}{2}\big ]d\alpha /\int _{0}^1~\alpha ~d\alpha .$$

For example modified graded mean of a TrFN $\tilde{A}=(a_{1},a_{2},a_{3},a_{4})$ is $\frac{1}{3}[k(a_{1}+2a_{2})+(1-k)(2a_{3}+a_{4})]$.

Centroid Method: The centroid $C(\tilde{A})$ of a fuzzy set $\tilde{A}$ is defined by

$$C(\tilde{A})=\frac{\sum _{x} x \mu _{\tilde{A}}(x)}{\sum _{x} \mu _{\tilde{A}}(x)}$$

for discrete case and

$$C(\tilde{A})=\frac{\int _{-\infty }^{\infty } x \mu _{\tilde{A}}(x) dx}{\int _{-\infty }^{\infty } \mu _{\tilde{A}}(x) dx}$$

for continuous case.

For example if $\tilde{A}=(a_{1},a_{2},a_{3})$ is triangular fuzzy number then its centroid value is $C(\tilde{A})=(a_{1}+a_{2}+a_{3})/3$.

Nearest Interval Approximation: Grzegorzewski [52], presented a method to approximate a fuzzy number by a crisp interval. Suppose $\tilde{A}$ is a fuzzy number with $\alpha$-cut $[A_{L}(\alpha ),A_{R}(\alpha )]$. Let $C_{d}(\tilde{A})=[C_{L},C_{R}]$ be the nearest interval approximation of the fuzzy number $\tilde{A}$ with distance metric d, where distance metric d to measure distance of $\tilde{A}$ from $C_{d}(\tilde{A})$ is given by

$$d(\tilde{A},C_{d}(\tilde{A}))=\sqrt{\int _{0}^1\{A_{L}(\alpha )-C_{L}\}^2d\alpha +\int _{0}^1\{A_{R}(\alpha )-C_{R}\}^2d\alpha }.$$

Now $C_{d}(\tilde{A})$ is optimum when $d(\tilde{A},C_{d}(\tilde{A})$ is minimum with respect to $C_{L}$ and $C_{R}$ and in this prospect the value of $C_{L}$ and $C_{R}$ are given by

$$\begin{aligned} C_{L}=\int _{0}^1A_{L}(\alpha )d\alpha ~ and~ C_{R}=\int _{0}^1A_{R}(\alpha )d\alpha . \end{aligned}$$

(28)

For example, $\alpha -$cut of a trapezoidal fuzzy number $(r_{1},r_{2},r_{3},r_{4})$ is $[r_{1}+\alpha (r_{2}-r_{1}),r_{4}-\alpha (r_{4}-r_{3})]$ and its interval approximation is obtained as $[(r_{1}+r_{2})/2,(r_{3}+r_{4})/2]$.

Fuzzy Variable: Zadeh [158] introduced the possibility theory to interpret degree of uncertainty of members of a fuzzy set. The membership $\mu _{\tilde{A}}(x)$ of an element x in a fuzzy set $\tilde{A}$ is then termed as degree of possibility that the element belongs to the set.

Possibility Measure: Suppose $\tilde{A}$ and $\tilde{B}$ be two fuzzy sets (/numbers) with memberships $\mu _{\tilde{A}}$ and $\mu _{\tilde{B}}$ respectively. Then possibility (Zadeh [158], Dubois and Prade [38], Liu and Iwamura [92]) of the fuzzy event $\tilde{A}\star \tilde{B}$ is defined as

$$\begin{aligned} Pos(\tilde{A}\star \tilde{B})=\sup _{x\star y}\min (\mu _{\tilde{A}}(x),\mu _{\tilde{B}}(y)),~x,y\in \mathfrak {R}, \end{aligned}$$

(29)

where $\star$ is any operations like $<$, $>$, $=$, $\le$, $\ge$, etc. Now for any real number b,

$$\begin{aligned} Pos(\tilde{A}\star b)=\sup _{x\star b}\{\mu _{\tilde{A}}(x),~x\in \mathfrak {R}\}. \end{aligned}$$

(30)

Definition 2.3

(Possibility Space). A triplet $(\varTheta ,p ,Pos)$ is called a possibility space, where $\varTheta$ is non-empty set of points, p is power set of $\varTheta$ and $Pos:\varTheta \mapsto [0,1]$ is a mapping, called possibility measure (Wang [136]) defined as

• (i) $Pos(\emptyset )=0$ and $Pos(\varTheta )=1$.

• (ii) For any $\{A_{i}|i\in I\}\subset \varTheta$, $Pos(\cup A_{i})=\sup _{i} ~Pos(A_{i})$.

Definition 2.4

(Fuzzy Variable). A fuzzy variable (Nahmias [117]) is defined as a function from the possibility space $(\varTheta ,p ,Pos)$ to the set of real numbers $\mathfrak {R}$ to describe fuzzy phenomena, where possibility measure (Pos) of a fuzzy event $\{\tilde{\xi }\in B\}$, $B\subset \mathfrak {R}$ is defined as $Pos\{\tilde{\xi }\in B\}=\sup _{x\in B}~\mu _{\tilde{\xi }}(x),$ $\mu _{\tilde{\xi }}(x)$ is referred to as possibility distribution of $\tilde{\xi }$.

Necessity measure is dual of the possibility measure, the grade of necessity of an event is the grade of impossibility of the opposite event. Necessity measure (Nes) of a fuzzy event $\{\tilde{\xi }\in B\}$, $B\subset \mathfrak {R}$ and $\sup _{x\in \mathfrak {R}}~\mu _{\tilde{\xi }}(x)=1$, is defined as $Nec\{\tilde{\xi }\in B\}=1-Pos\{\tilde{\xi }\in B^c\}=1-\sup _{x\in B^c}~\mu _{\tilde{\xi }}(x)$.

Credibility Theory: Liu and Liu [94] introduced the concept of credibility measure. Liu [88] [90] presented credibility theory as a branch of mathematics for studying the behavior of fuzzy phenomena. Let $\varTheta$ be a nonempty set, and $p$ the power set of $\varTheta$. Each element in $p$ is called an event. For an event A, a number $Cr\{A\}$ which indicates the credibility that A will occur has the following four axioms (Liu [90]):

• 1. Normality: $Cr\{\varTheta \} =1.$

• 2. Monotonicity: $Cr\{A\}\le Cr\{B\}$ whenever $A\le B$.

• 3. Self-Duality: $Cr\{A\} + Cr\{A^c\} = 1$ for any event A.

• 4. Maximality: $Cr\{\cup _{i}A_{i}\} = sup_{i} Cr\{A_{i}\}$ for any events $\{A_{i}\}$ with $sup_{i} Cr\{A_{i}\} < 0.5$.

Definition 2.5

(Credibility Measure, Liu, [90]). The set function Cr is called a credibility measure if it satisfies the normality, monotonicity, self-duality, and maximality axioms.

For example let $\mu$ be a nonnegative function on $\varTheta$ (for example, the set of real numbers) such that $\sup _{x\in \varTheta }~\mu (x)=1$, then the set function defined by

$$\begin{aligned} Cr\{A\}=\frac{1}{2}(\sup _{x\in A}~\mu (x)+1-\sup _{x\in A^c}~\mu (x)) \end{aligned}$$

(31)

is a credibility measure on $\varTheta$.

From it is clear that in case of a fuzzy variable $\tilde{\xi }$ with membership function (possibility distribution) $\mu _{\tilde{\xi }}$ and $B\subset \mathfrak {R}$, $\sup _{x\in \mathfrak {R}}~\mu _{\tilde{\xi }}(x)=1$, credibility measure is actually the average of possibility and necessity measure, i.e.

$$\begin{aligned} Cr\{\tilde{\xi }\in B\}= & {} \frac{1}{2}(\sup _{x\in B}~\mu _{\tilde{\xi }}(x)+1-\sup _{x\in B^c}~\mu _{\tilde{\xi }}(x))\nonumber \\= & {} \frac{1}{2}(Pos\{\tilde{\xi }\in B\}+Nec\{\tilde{\xi }\in B\}). \end{aligned}$$

(32)

Example of Some Important Fuzzy Variables:

Equipossible Fuzzy Variable: An equipossible fuzzy variable on [a, b] is a fuzzy variable whose membership function (possibility distribution) is given by

$$\mu _{x}= \left\{ \begin{array}{ll} 1, &{} \hbox {if}\,a\le x \le b; \\ 0, &{} \hbox {otherwise.} \end{array}\right. $$

Trapezoidal and Triangular Fuzzy Variable: Triangular fuzzy number and trapezoidal fuzzy number are two kinds of special fuzzy variables. As both trapezoidal and triangular fuzzy numbers are normal and defined over the set of real numbers $\mathfrak {R}$ so possibility, necessity as well as credibility measures are defined on them. So a trapezoidal fuzzy variable (TrFV) $\tilde{A}$ is a fuzzy variable fully determined by quadruplet $(a_{1},a_{2},a_{3},a_{4})$ of crisp numbers with $a_{1}<a_{2}\le a_{3}<a_{4}$, whose membership function is given by

$$\begin{aligned} \mu _{\tilde{A}}(x)= \left\{ \begin{array}{ll} \frac{x-a_{1}}{a_{2}-a_{1}}, &{} \hbox {if}\, a_{1}\le x\le a_{2}; \\ 1, &{} \hbox {if}\, a_{2}\le x\le a_{3}; \\ \frac{a_{4}-x}{a_{4}-a_{3}}, &{} \hbox {if}\, a_{3}\le x\le a_{4}; \\ 0, &{} \hbox {otherwise.} \end{array}\right. \end{aligned}$$

When $a_{2}=a_{3}$, the trapezoidal fuzzy variable becomes a triangular fuzzy variable (TFV).

Some Methodologies to Deal with Fuzzy Variables: Expected Value (Liu and Liu [94]): Let $\tilde{\xi }$ be a fuzzy variable. Then the expected value of $\xi$ is defined as

$$\begin{aligned} E[\tilde{\xi }]=\int _{0}^\infty cr\{\tilde{\xi }\ge r\}dr-\int _{-\infty }^0 cr\{\tilde{\xi }\le r\}dr \end{aligned}$$

(33)

provided that at least one of the two integrals is finite.

Example 2.1

Expected value of a triangular fuzzy variable $\tilde{\xi }=(r_{1},r_{2},r_{3})$ is $E[\tilde{\xi }]=\frac{r_{1}+2r_{2}+r_{3}}{4}.$

Optimistic and Pessimistic Value (Liu [86, 89]): Let $\tilde{\xi }$ be a fuzzy variable and $\alpha \in [0,1]$. Then

$$\begin{aligned} \xi _{sup}(\alpha )=\sup \{r:cr\{\tilde{\xi }\ge r\}\ge \alpha \} \end{aligned}$$

(34)

is called $\alpha$-optimistic value to $\tilde{\xi }$; and

$$\begin{aligned} \xi _{inf}(\alpha )=\inf \{r:cr\{\tilde{\xi }\le r\}\ge \alpha \} \end{aligned}$$

(35)

is called $\alpha$-pessimistic value to $\tilde{\xi }$.

Example 2.2

Let $\tilde{\xi }=(r_{1},r_{2},r_{3},r_{4})$ be a trapezoidal fuzzy variable. Then its $\alpha$-optimistic and $\alpha$-pessimistic values are

$$\begin{aligned} \tilde{\xi }_{sup}(\alpha )= \left\{ \begin{array}{ll} 2\alpha r_{3}+(1-2\alpha )r_{4}, &{} \hbox {if}\, \alpha \le 0.5; \\ (2\alpha -1)r_{1}+2(1-\alpha )r_{2}, &{} \hbox {if}\, \alpha >0.5. \end{array}\right. \end{aligned}$$

(36)

$$\begin{aligned} \tilde{\xi }_{inf}(\alpha )= \left\{ \begin{array}{ll} (1-2\alpha ) r_{1}+2\alpha r_{2}, &{} \hbox {if}\, \alpha \le 0.5; \\ 2(1-\alpha ) r_{3}+(2\alpha -1)r_{4}, &{} \hbox {if}\, \alpha >0.5. \end{array}\right. \end{aligned}$$

(37)

2.3 Type-2 Fuzzy Set

So far in the Subsect. 2.2, we have discussed fuzzy sets with crisply defined membership functions, i.e., membership degree (/grade) of each of the points is an precise real number in [0,1]. However it is not always possible to represents uncertainty by a fuzzy set with crisp membership function, i.e., points having crisp membership grades. For instance, in rule-based fuzzy logic systems, the words that are used in the antecedents and consequents of rules can be uncertain as human judgements are not always precise and also a word does not have the same meaning or value to different people. Zadeh [157] introduced an extension of the concept of usual fuzzy set into a fuzzy set whose membership function itself is a fuzzy set. Then the usual fuzzy set with crisp membership function is termed as type-1 fuzzy set and the fuzzy set with fuzzy membership function is termed type-2 fuzzy set. So membership grade of each element of a type-2 fuzzy set is no longer a crisp value but a fuzzy set with a support bounded by the interval [0,1] which provides additional degrees of freedom for handling uncertainties. So because of fuzzy membership function a type-2 fuzzy set has three-dimensional nature. This membership function is called type-2 membership function.

Definition 2.6

(Type-2 Fuzzy Set). A type-2 fuzzy set (T2 FS) $\tilde{A}$ in X is defined (Mendel and John [105, 106]) as

$$\tilde{A}=\{((x,u),\mu _{\tilde{A}}(x,u)):~\forall x\in X,~\forall u\in J_{x}\subseteq [0,1]\},$$

where $0\le \mu _{\tilde{A}}(x,u)\le 1$ is called the type-2 membership function, $J_{x}$ is the primary membership of $x\in X$ which is the domain of the secondary membership function $\tilde{\mu }_{\tilde{A}}(x)$ (defined below). The values $u\in J_{x}$ for $x\in X$ are called primary membership grades of x.

$\tilde{A}$ is also be expressed as

$$\begin{aligned} \tilde{A}=\int _{x\in X} \int _{u\in J_{x}} \mu _{\tilde{A}}(x,u)/(x,u)~,~J_{x}\subseteq [0,1], \end{aligned}$$

(38)

where $\int \int$ denotes union over all admissible x and u. For discrete universes of discourse $\int$ is replaced by $\sum$.

Secondary Membership Function: For each values of x, say $x=x'$, the secondary membership function (Mendel and John [105]), denoted by $\mu _{\tilde{A}}(x=x',u)$, $u\in J_{x'}\subseteq [0,1]$ is defined as

$$\begin{aligned} \mu _{\tilde{A}}(x',u)\equiv \tilde{\mu }_{\tilde{A}}(x')=\int _{u\in J_{x'}} f_{x'}(u)/u, \end{aligned}$$

(39)

where $0\le f_{x'}(u)\le 1$. The amplitude of a secondary membership function is called a secondary grade. So for a particular $x=x'$ and $u=u'\in J_{x'}$, $f_{x'}(u')=\mu _{\tilde{A}}(x',u')$ is the secondary membership grade.

Now using (39), $\tilde{A}$ can be written an another way as $\tilde{A}=\{(x,\tilde{\mu }_{\tilde{A}}(x)):x\in X\}$, i.e.

$$\begin{aligned} \tilde{A}=\int _{x\in X}\tilde{\mu }_{\tilde{A}}(x)/x=\int _{x\in X}\bigg [ \int _{u\in J_{x}} f_{x}(u)/u\bigg ]\bigg /x. \end{aligned}$$

(40)

Example 2.3

$X=\{4,5,6\}$ and the primary memberships of the points of X are $J_{4}=\{0.3,0.4,0.6\}$, $J_{5}=\{0.6,0.8,0.9\}$, $J_{6}=\{0.5,0.6,0.7,0.8\}$ respectively and the secondary membership functions of the points are

$\tilde{\mu }_{\tilde{A}}(4)=\mu _{\tilde{A}}(4,u)=(0.6/0.3)+(1/0.4)+(0.7/0.6)$

i.e., $\mu _{\tilde{A}}(4,0.3)=0.6$, $\mu _{\tilde{A}}(4,0.4)=1$ and $\mu _{\tilde{A}}(4,0.6)=0.7$. Here $\mu _{\tilde{A}}(4,0.3)=0.6$ means membership (secondary) grade that the point 4 has the membership (primary) 0.3 is 0.6.

$\tilde{\mu }_{\tilde{A}}(5)=\mu _{\tilde{A}}(5,u)=(0.7/0.6)+(1/0.8)+(0.8/0.9)$,

$\tilde{\mu }_{\tilde{A}}(6)=\mu _{\tilde{A}}(6,u)=(0.3/0.5)+(0.4/0.6)+(1/0.7)+(0.8/0.5)$.

So discrete type-2 fuzzy set $\tilde{A}$ is given by

$\tilde{A}=(0.6/0.3)/4+(1/0.4)/4+(0.7/0.6)/4+(0.7/0.6)/5+(1/0.8)/5+(0.8/0.9)/5+(0.3/0.5)/6+(0.4/0.6)/6+(1/0.7)/6+(0.8/0.5)/6$.

$\tilde{A}$ is also written as

$$\tilde{A}\sim \left\{ \begin{array}{ll} 4, &{} \hbox {with membership}\, \tilde{\mu }_{\tilde{A}}(4); \\ 5, &{} \hbox {with membership}\, \tilde{\mu }_{\tilde{A}}(5); \\ 6, &{} \hbox {with membership}\, \tilde{\mu }_{\tilde{A}}(6). \end{array}\right. $$

The T2 FS $\tilde{A}$ is depicted in Fig. 3.

Definition 2.7 (Interval Type-2 Fuzzy Set). If all the secondary membership grades are 1 (i.e. $f_{x}(u)=\mu _{\tilde{A}}(x,u)=1$, $\forall ~x,u$) then this T2 FS is called interval type-2 fuzzy set (IT2 FS) (Mendel et al. [107], Wu and Mendel [146]). The third dimension of the general T2 FS is not needed in this case and the IT2 FS can be expressed as a special case of the general T2 FS:

$$\begin{aligned} \tilde{A}=\int _{x\in X} \int _{u\in J_{x}} 1/(x,u)~,~J_{x}\subseteq [0,1] \end{aligned}$$

(41)

or, alternatively it can be represented as

$$\begin{aligned} \tilde{A}=\int _{x\in X}\tilde{\mu }_{\tilde{A}}(x)/x=\int _{x\in X}\bigg [ \int _{u\in J_{x}} 1/u\bigg ]\bigg /x. \end{aligned}$$

(42)

Footprint of Uncertainty: A IT2 FS is characterized by the footprint of uncertainty (FOU) which is the union of all of the primary memberships $J_{x}$, i.e. FOU of a IT2 FS $\tilde{A}$ is defined as

$$ FOU(\tilde{A}) = \bigcup _{x\in X}~J_{x}.$$

The FOU is bounded by an upper membership function $\bar{\mu }_{\tilde{A}}(x)$ (UMF) and a lower membership function $\underline{\mu }_{\tilde{A}}(x)$ (LMF), both are type-1 membership functions so that $J_{x}=[\underline{\mu }_{\tilde{A}}(x),\bar{\mu }_{\tilde{A}}(x)],~\forall ~x\in X$. So the IT2 FS can be represented by $(\tilde{A^U},\tilde{A^L})$, where $\tilde{A^U}$ and $\tilde{A^L}$ are TIFSs.

For example consider a IT2 FS $\tilde{A}$ whose upper and lower membership functions are type-1 triangular membership functions and it is depicted in Fig. 4.

Fig. 3.

Type-2 fuzzy set $\tilde{A}$

Fig. 4.

Interval type-2 fuzzy set $\tilde{A}$

Type Reduction: We already knows that a type-2 fuzzy set (T2 FS) is a fuzzy set with fuzzy membership function. Due to fuzzyness in membership function of T2 FS, the computational complexity is very high to deal with T2 FS. For this reason to deal with T2 FS, generally a T2 FS is converted to a type-1 fuzzy set (T1 FS) by some type reduction methods. Type reduction is the procedure by which a T2 FS is converted to the corresponding T1 FS, known as type reduced set (TRS). But till now there are very few reduction methods available in the literature. Centroid type reduction (Kernik and Mendel [63]) is an example of such type reduction method.

Geometric Defuzzification for T2 FS (Coupland and John [31]): Coupland and John [31] proposed a defuzzification method for T2 FSs with the help of geometric representation of a T2 FS. A geometric T2 FS from a discrete T2 FS is constructed (Coupland [30], Coupland and John [31])) by breaking down the membership function of the T2 FS into five areas and then each of the five areas is modeled by a collection of 3-D triangles where the edges of these triangles are connected to form a 3-D polyhedron. The final defuzzified value is found by calculating the center of area of the polyhedron which approximates the type-2 fuzzy membership function. The center of area of the polyhedron is obtained by taking weighted average of x-component of the centroid and the area of each of the triangles those form the polyhedron. In case of T2 FS having continuous domains of primary or secondary membership function, to apply geometric defuzzification method, first one have to discretize the continuous domains into finite number of points (preferably equidistant points) within the support of the corresponding membership functions. The approach of geometric representation of discrete T2 FS is limited to T2 FSs where all the secondary membership functions are convex.

Type-2 Fuzzy Variable: Before going to the definition of type-2 fuzzy variable we present some related definitions those are required to define a type-2 fuzzy variable.

Definition 2.7

(Fuzzy Possibility Space (FPS)). Let $\varGamma$ be the universe of discourse. An ample field (Wang [136]) $\mathcal {A}$ on $\varGamma$ is a class of subsets of $\varGamma$ that is closed under arbitrary unions, intersections, and complements in $\varGamma$.

Let $\tilde{P}os: \mathcal {A}\mapsto \mathfrak {R}([0,1])$ be a set function defined on $\mathcal {A}$ such that $\{\tilde{P}os(A)| \mathcal {A}\ni A ~atom\}$ is a family of mutually independent RFVs. Then $\tilde{P}os$ is called a fuzzy possibility measure (Liu and Liu [99]) if it satisfies the following conditions:

(P1) $\tilde{P}os(\emptyset )$ =$\tilde{0}$.

(P2) For any subclass $\{A_{i} | i\in I\}$ of $\mathcal {A}$ (finite, countable or uncountable),

$$\tilde{P}os\big (\bigcup _{i\in I}A_{i}\big ) = sup_{i\in I} \tilde{P}os(A_{i}).$$

The triplet $(\varGamma ,\mathcal {A},\tilde{P}os)$ is referred to as a fuzzy possibility space (FPS).

Definition 2.8

(Regular Fuzzy Variable (RFV)). For a possibility space $(\varTheta ,p ,Pos)$, a regular fuzzy variable (Liu and Liu [99]) $\tilde{\xi }$ is defined as a measurable map from $\varTheta$ to [0, 1] in the sense that for every $t\in [0,1]$, one has $\{\gamma \in \varTheta ~|~ \tilde{\xi }(\gamma )\le t\}\in p$.

A discrete RFV is represented as $\tilde{\xi }\sim \left( \begin{array}{cccc} r_{1} &{} r_{2} &{} ... &{} r_{n} \\ \mu _{1} &{} \mu _{2} &{} ... &{} \mu _{n} \\ \end{array}\right)$, where $r_{i}\in [0,1]$ and $\mu _{i}>0,~\forall i$ and max$_{i}\{\mu _{i}\}=1$.

If $\tilde{\xi }=(r_{1},r_{2},r_{3},r_{4})$ with $0\le r_{1}<r_{2}<r_{3}<r_{4}\le 1$, then $\tilde{\xi }$ is called a trapezoidal RFV.

If $\tilde{\xi }=(r_{1},r_{2},r_{3})$ with $0\le r_{1}<r_{2}<r_{3}\le 1$, then $\tilde{\xi }$ is called a triangular RFV.

Definition 2.9

(Type-2 Fuzzy Variable). As a fuzzy variable (type-1) is defined as a function from the possibility space to the set of real numbers, a type-2 fuzzy variable (T2 FV) is defined as a function from the fuzzy possibility space to the set of real numbers. If $(\varGamma ,\mathcal {A},\tilde{P}os)$ is a fuzzy possibility space (Liu and Liu [99]), then a type-2 fuzzy variable $\tilde{\xi }$ is defined as a map from $\varGamma$ to $\mathfrak {R}$ such that for any $t\in \mathfrak {R}$ the set $\{\gamma \in \varGamma ~|~\tilde{\xi }(\gamma )\le t\}\in \mathcal {A}$, i.e. a type-2 fuzzy variable (T2 FV) is a map from a fuzzy possibility space to the set of real numbers.

Then $\tilde{\mu }_{\tilde{\xi }}(x)$, called secondary possibility distribution function of $\tilde{\xi }$, is defined as a map $\mathfrak {R}\mapsto \mathfrak {R}[0,1]$ such that $\tilde{\mu }_{\tilde{\xi }}(x)=\tilde{Pos}\{\gamma \in \varTheta ~|~\tilde{\xi }(\gamma )=x\},~x\in \mathfrak {R}$. $\mu _{\tilde{\xi }}(x,u)$, called type-2 possibility distribution function, is a map $\mathfrak {R}\times J_{x}\mapsto [0,1]$, defined as $\mu _{\tilde{\xi }}(x,u)=Pos\{\tilde{\mu }_{\tilde{\xi }}(x)=u\},~(x,u)\in \mathfrak {R}\times J_{x}$, $J_{x}\subseteq [0,1]$ is the domain or support of $\tilde{\mu }_{\tilde{\xi }}(x)$, i.e., $J_{x}=\{u\in [0,1]~|~\mu _{\tilde{\xi }}(x,u)> 0\}$. Here $J_{x}$ may be called as primary possibility of the point x and for a particular value of x, say $x=x'$, $\tilde{\mu }_{\tilde{\xi }}(x')\sim \mu _{\tilde{\xi }}(x',u)$, $u\in J_{x'}$ gives the secondary possibility of $x'$.

The secondary possibility distribution of a particular value $x=x'$, i.e. $\tilde{\mu }_{\tilde{\xi }}(x')$ actually represents a regular fuzzy variable (RFV).

Definition 2.10

(Interval Type-2 Fuzzy Variable). If for a type-2 fuzzy variable $\tilde{\xi }$ we call the $\mu _{\tilde{\xi }}(x',u')$ as secondary possibility degree for a point $x=x'$ and $u'\in J_{x'}$, then if secondary possibility degrees for all the points with respective primary possibilities are 1, $\tilde{\xi }$ is said to be interval type-2 fuzzy variable (IT2 FV).

Example 2.4

Let $\tilde{\xi }$ is a T2 FV defined as

$$\begin{aligned} \tilde{\xi }=\left\{ \begin{array}{ll} 5, &{} \hbox {with possibility (0.2,0.4,0.6);} \\ 6, &{} \hbox {with possibility (0.4,0.6,0.8);} \\ 7, &{} \hbox {with possibility (0.1,0.3,0.5,0.7).} \end{array}\right. \end{aligned}$$

(43)

i.e., the possibilities that $\tilde{\xi }$ has the values 5 and 6 are $\tilde{\mu }_{\tilde{\xi }}(5)=(0.2,0.4,0.6)$ and $\tilde{\mu }_{\tilde{\xi }}(6)=(0.4,0.6,0.8)$ respectively, each of which is triangular RFV and possibility that $\tilde{\xi }$ takes the value 7 is $\tilde{\mu }_{\tilde{\xi }}(7)=(0.1,0.3,0.5,0.7)$ which is trapezoidal RFV. Obviously as $\tilde{\mu }_{\tilde{\xi }}(5)=(0.2,0.4,0.6)$ is triangular RFV, we have,

$$\mu _{\tilde{\xi }}(5,u)=\left\{ \begin{array}{ll} \frac{u-0.2}{0.2}, &{} \hbox {if}\, 0.2\le u\le 0.4; \\ 1, &{} \hbox {if}\, u=0.4; \\ \frac{0.6-u}{0.2}, &{} \hbox {if}\, 0.4\le u\le 0.6.\\ 0, &{} \hbox {otherwise;} \\ \end{array} \right. $$

from which we get the secondary possibilities for the point 5 and each values of u, $0.2\le u\le 0.6$. $\tilde{\xi }$ is depicted in Fig. 5.

Fig. 5.

Type-2 fuzzy variable $\tilde{\xi }$

Example 2.5

(Type-2 Triangular Fuzzy Variable). A type-2 triangular fuzzy variable (Qin et al. [127]) $\tilde{\xi }$ is represented by $(r_{1},r_{2},r_{3};\theta _{l},\theta _{r})$, where $r_{1}$, $r_{2}$, $r_{3}$ are real numbers and $\theta _{l},\theta _{r}\in [0,1]$ are two parameters characterizing the degree of uncertainty that $\tilde{\xi }$ takes a value x and the secondary possibility distribution function $\tilde{\mu }_{\tilde{\xi }}(x)$ of $\tilde{\xi }$ is defined by

$$\begin{aligned} \tilde{\mu }_{\tilde{\xi }}(x)=\big (\frac{x-r_{1}}{r_{2}-r_{1}}-\theta _{l}\min \big \{\frac{x-r_{1}}{r_{2}-r_{1}},\frac{r_{2}-x}{r_{2}-r_{1}}\big \},\frac{x-r_{1}}{r_{2}-r_{1}}, \frac{x-r_{1}}{r_{2}-r_{1}}+ \nonumber \\ + \theta _{r}\min \big \{\frac{x-r_{1}}{r_{2}-r_{1}},\frac{r_{2}-x}{r_{2}-r_{1}}\big \}\big ) \end{aligned}$$

(44)

for any $x\in [r_{1},r_{2}]$, and

$$\begin{aligned} \tilde{\mu }_{\tilde{\xi }}(x)=\big (\frac{r_{3}-x}{r_{3}-r_{2}}-\theta _{l}\min \big \{\frac{r_{3}-x}{r_{3}-r_{2}},\frac{x-r_{2}}{r_{3}-r_{2}}\big \},\frac{r_{3}-x}{r_{3}-r_{2}}, \frac{r_{3}-x}{r_{3}-r_{2}}+\nonumber \\ +\theta _{r}\min \big \{\frac{r_{3}-x}{r_{3}-r_{2}},\frac{x-r_{2}}{r_{3}-r_{2}}\big \}\big ) \end{aligned}$$

(45)

for any $x\in (r_{2},r_{3}]$.

A type-2 triangular fuzzy variable can be seen as an extension of a type-1 triangular fuzzy variable or simply a triangular fuzzy variable. In a triangular fuzzy variable (TFV) $(r_{1},r_{2},r_{3})$, the membership grade (possibility degree) of each point is a fixed number in [0,1]. However in a type-2 triangular fuzzy variable $\tilde{\xi }=(r_{1},r_{2},r_{3};\theta _{l},\theta _{r})$, the primary memberships (possibilities) of the points are no longer fixed values, instead they have a range between 0 and 1. Here $\theta _{l}$ and $\theta _{r}$ are used to represent the spreads of primary memberships of type-2 TFV. Obviously if $\theta _{l}=\theta _{r}=0$, then type-2 TFV $\tilde{\xi }$ becomes a type-1 TFV and the Eqs. (44) and (45) together become the membership function of a type-1 TFV. Now from Eqs. (44) and (45), $\tilde{\mu }_{\tilde{\xi }}(x)$ can be written as

$$\begin{aligned} \tilde{\mu }_{\tilde{\xi }}(x)= \left\{ \begin{array}{ll} \big (\frac{x-r_{1}}{r_{2}-r_{1}}-\theta _{l}\frac{x-r_{1}}{r_{2}-r_{1}},\frac{x-r_{1}}{r_{2}-r_{1}},\frac{x-r_{1}}{r_{2}-r_{1}}+\theta _{r}\frac{x-r_{1}}{r_{2}-r_{1}}\big ) , &{} \hbox {if}\,x\in [r_{1},\frac{r_{1}+r_{2}}{2}]; \\ \big (\frac{x-r_{1}}{r_{2}-r_{1}}-\theta _{l}\frac{r_{2}-x}{r_{2}-r_{1}},\frac{x-r_{1}}{r_{2}-r_{1}},\frac{x-r_{1}}{r_{2}-r_{1}}+\theta _{r}\frac{r_{2}-x}{r_{2}-r_{1}}\big ), &{} \hbox {if}\,x\in (\frac{r_{1}+r_{2}}{2},r_{2}]; \\ \big (\frac{r_{3}-x}{r_{3}-r_{2}}-\theta _{l}\frac{x-r_{2}}{r_{3}-r_{2}},\frac{r_{3}-x}{r_{3}-r_{2}},\frac{r_{3}-x}{r_{3}-r_{2}}+\theta _{r}\frac{x-r_{2}}{r_{3}-r_{2}}\big ), &{} \hbox {if}\,x\in (r_{2},\frac{r_{2}+r_{3}}{2}]; \\ \big (\frac{r_{3}-x}{r_{3}-r_{2}}-\theta _{l}\frac{r_{3}-x}{r_{3}-r_{2}},\frac{r_{3}-x}{r_{3}-r_{2}},\frac{r_{3}-x}{r_{3}-r_{2}}+\theta _{r}\frac{r_{3}-x}{r_{3}-r_{2}}\big ), &{} \hbox {if}\,x\in (\frac{r_{2}+r_{3}}{2},r_{3}]. \end{array}\right. \end{aligned}$$

(46)

Let us illustrate Example 2.5 numerically. Consider the type-2 triangular fuzzy variable $\tilde{\xi }=(2,3,4;0.5,0.8)$.

Then its secondary possibility distribution is given by

$$\begin{aligned} \tilde{\mu }_{\tilde{\xi }}(x)= \left\{ \begin{array}{ll} (0.5(x-2),x-2,1.8(x-2)), &{} \hbox {if}\,x\in [2,2.5]; \\ ((x-2)-0.5(3-x),x-2,(x-2)+0.8(3-x)), &{} \hbox {if}\,x\in (2.5,3]; \\ ((4-x)-0.5(x-3),4-x,(4-x)+0.8(x-3)), &{} \hbox {if}\,x\in (3,3.5]; \\ (0.5(4-x),4-x,1.8(4-x)), &{} \hbox {if}~x\in (3.5,4]. \end{array}\right. \end{aligned}$$

Here secondary possibility degree of each value of x is a triangular fuzzy variable (more precisely a triangular RFV), e.g., $\tilde{\mu }_{\tilde{\xi }}(2.5)=(0.25,0.5,0.9)$, $\tilde{\mu }_{\tilde{\xi }}(3.2)=(0.7,0.8,0.96)$, etc. So the domain of secondary possibility $\tilde{\mu }_{\tilde{\xi }}(2.5)$ varies from 0.25 to 0.9 and that of $\tilde{\mu }_{\tilde{\xi }}(3.2)$ varies from 0.7 to 0.96.

The FOU of $\tilde{\xi }$ is depicted in Fig. 6.

Fig. 6.

FOU of $\tilde{\xi }$.

Example 2.6

(Trapezoidal Interval Type-2 Fuzzy Variable). A trapezoidal interval type-2 fuzzy variable $\tilde{A}$ in the universe of discourse X can be represented by $\tilde{A}=(\tilde{A^U},\tilde{A^L})=((a_{1}^U,a_{2}^U,a_{3}^U,a_{4}^U;w^U),(a_{1}^L,a_{2}^L,a_{3}^L,a_{4}^L;w^L))$, where both $\tilde{A^U}$ and $\tilde{A^L}$ are trapezoidal fuzzy variables of height $w^U$ and $w^L$ respectively.

For example consider a trapezoidal IT2 FV $\tilde{A}=((2,4,6,8;1), (3,4.5$, 5.5, 7; 0.8)) which is depicted in Fig. 7.

Fig. 7.

Trapezoidal interval type-2 fuzzy variable $\tilde{A}$

The arithmetic operations between trapezoidal interval type-2 fuzzy variables $\tilde{A_{1}}=(\tilde{A_{1}^U},\tilde{A_{1}^L})=((a_{11}^U,a_{12}^U,a_{13}^U,a_{14}^U;w_{1}^U),(a_{11}^L,a_{12}^L,a_{13}^L,a_{14}^L;w_{1}^L))$ and $\tilde{A_{2}}=$ $(\tilde{A_{2}^U},\tilde{A_{2}^L})=((a_{21}^U,a_{22}^U,a_{23}^U,a_{24}^U;w_{2}^U),(a_{21}^L,a_{22}^L,a_{23}^L,a_{24}^L;w_{2}^L))$ are defined based on Chen and Lee [23, 24] as follows:

Addition operation: $\tilde{A_{1}}\oplus \tilde{A_{2}}=(\tilde{A_{1}^U},\tilde{A_{1}^L})\oplus (\tilde{A_{2}^U},\tilde{A_{2}^L})$

$=((a_{11}^U+a_{21}^U,a_{12}^U+a_{22}^U,a_{13}^U+a_{23}^U,a_{14}^U+a_{24}^U,min(w_{1}^U,w_{2}^U)), (a_{11}^L+a_{21}^L,a_{12}^L+a_{22}^L,a_{13}^L+a_{23}^L,a_{14}^L+a_{24}^L,min(w_{1}^L,w_{2}^L))),$

Multiplication operation: $\tilde{A_{1}}\otimes \tilde{A_{2}}=(\tilde{A_{1}^U},\tilde{A_{1}^L})\otimes (\tilde{A_{2}^U},\tilde{A_{2}^L})$

$=((a_{11}^U\times a_{21}^U,a_{12}^U\times a_{22}^U,a_{13}^U\times a_{23}^U,a_{14}^U\times a_{24}^U,min(w_{1}^U,w_{2}^U)), (a_{11}^L\times a_{21}^L,a_{12}^L\times a_{22}^L,a_{13}^L\times a_{23}^L,a_{14}^L\times a_{24}^L,min(w_{1}^L,w_{2}^L))).$

The arithmetic operations between trapezoidal interval type-2 fuzzy variable $\tilde{A_{1}}$ and a crisp value $k(> 0)$ are defined as follows:

$k\tilde{A_{1}}=((k\times a_{11}^U,k\times a_{12}^U,k\times a_{13}^U,k\times a_{14}^U;w_{1}^U),(k\times a_{11}^L,k\times a_{12}^L,k\times a_{13}^L,k\times a_{14}^L;w_{1}^L)),$

$\frac{\tilde{A_{1}}}{k}=((\frac{1}{k}\times a_{11}^U,\frac{1}{k}\times a_{12}^U,\frac{1}{k}\times a_{13}^U,\frac{1}{k}\times a_{14}^U;w_{1}^U),(\frac{1}{k}\times a_{11}^L,\frac{1}{k}\times a_{12}^L,\frac{1}{k}\times a_{13}^L,\frac{1}{k}\times a_{14}^L;w_{1}^L))$.

Critical Value (CV)-Based Reduction Method for Type-2 Fuzzy Variables (Qin et al. [127]): The CV-based reduction method is developed using the following definitions.

Critical Values (CVs) for RFVs: Qin et al. [127] introduced three kinds of critical values (CVs) of a RFV $\tilde{\xi }$. These are:

• (i) the optimistic CV of $\tilde{\xi }$, denoted by CV*[$\tilde{\xi }$], is defined as

  $$\begin{aligned} CV^{*}[\tilde{\xi }]=\sup _{\alpha \in [0,1]} [\alpha \wedge Pos\{\tilde{\xi }\ge \alpha \}] \end{aligned}$$

  (47)

• (ii) the pessimistic CV of $\tilde{\xi }$, denoted by CV$_{*}$[$\tilde{\xi }$], is defined as

  $$\begin{aligned} CV_{*}[\tilde{\xi }]= \sup _{\alpha \in [0,1]} [\alpha \wedge Nec\{\tilde{\xi }\ge \alpha \}] \end{aligned}$$

  (48)

• (iii) the CV of $\tilde{\xi }$, denoted by CV[$\tilde{\xi }$], is defined as

  $$\begin{aligned} CV[\tilde{\xi }]= \sup _{\alpha \in [0,1]} [\alpha \wedge Cr\{\tilde{\xi }\ge \alpha \}]. \end{aligned}$$

  (49)

Example 2.7

Let $\tilde{\xi }$ be a discrete RFV defined by

$$\tilde{\xi }=\left( \begin{array}{cccc} 0.2 &{} 0.4 &{} 0.5 &{} 0.7 \\ 0.3 &{} 0.7 &{} 1.0 &{} 0.6 \\ \end{array}\right) $$

Then for $\alpha \in [0,1],$

$$Pos\{\tilde{\xi }\ge \alpha \}=\sup _{r\ge \alpha }~\mu _{\tilde{\xi }}(r)= \left\{ \begin{array}{l@{\quad }l} 1, &{} \hbox {if}\, \alpha \le 0.5; \\ 0.6, &{} \hbox {if}\, 0.5<\alpha \le 0.7; \\ 0, &{} \hbox {if}\, 0.7<\alpha \le 1. \end{array}\right. $$

$$Nec\{\tilde{\xi }\ge \alpha \}=1-\sup _{r< \alpha }~\mu _{\tilde{\xi }}(r)= \left\{ \begin{array}{l@{\quad }l} 1, &{} \hbox {if}\, \alpha \le 0.2; \\ 0.7, &{} \hbox {if}\, 0.2<\alpha \le 0.4; \\ 0.3, &{} \hbox {if}\, 0.4<\alpha \le 0.5; \\ 0, &{} \hbox {if}\, 0.5<\alpha \le 1. \end{array}\right. $$

and so,

$$ Cr\{\tilde{\xi }\ge \alpha \}=\left\{ \begin{array}{l@{\quad }l} 1, &{} \hbox {if}\, \alpha \le 0.2; \\ 0.85, &{} \hbox {if}\, 0.2<\alpha \le 0.4; \\ 0.65, &{} \hbox {if}\, 0.4<\alpha \le 0.5; \\ 0.3, &{} \hbox {if}\, 0.5<\alpha \le 0.7; \\ 0, &{} \hbox {if}\, 0.7<\alpha \le 1. \end{array}\right. $$

Now from (47), (48) and (49) we have

$$\begin{aligned} CV^*[\tilde{\xi }]= & {} \sup _{\alpha \in [0,1]} [\alpha \wedge Pos\{\tilde{\xi }\ge \alpha \}]\\= & {} \sup _{\alpha \in [0,0.5]}[\alpha \wedge 1]~\vee \sup _{\alpha \in (0.5,0.7]}[\alpha \wedge 0.6]~\vee \sup _{\alpha \in (0.7,1]}[\alpha \wedge 0]\\= & {} 0.5~\vee ~0.6~\vee ~0=0.6\\ CV_{*}[\tilde{\xi }]= & {} \sup _{\alpha \in [0,1]} [\alpha \wedge Nec\{\tilde{\xi }\ge \alpha \}]\\= & {} \sup _{\alpha \in [0,0.2]}[\alpha \wedge 1]\vee \sup _{\alpha \in (0.2,0.4]}[\alpha \wedge 0.7]\vee \sup _{\alpha \in (0.4,0.5]}[\alpha \wedge 0.3]\vee \sup _{\alpha \in (0.5,1]}[\alpha \wedge 0]\\= & {} 0.2~\vee ~0.4~\vee ~0.3~\vee ~0=0.4 \end{aligned}$$

and

$$\begin{aligned} CV[\tilde{\xi }]= & {} \sup _{\alpha \in [0,1]} [\alpha \wedge Pos\{\tilde{\xi }\ge \alpha \}]\\= & {} \sup _{\alpha \in [0,0.2]}[\alpha \wedge 1]\vee \sup _{\alpha \in (0.2,0.4]}[\alpha \wedge 0.85]\vee \sup _{\alpha \in (0.4,0.5]}[\alpha \wedge 0.65]\vee \\&\sup _{\alpha \in (0.5,0.7]}[\alpha \wedge 0.3]\vee \sup _{\alpha \in (0.7,1]}[\alpha \wedge 0]\\= & {} 0.2\vee 0.4\vee 0.5\vee ~0.3\vee 0=0.5. \end{aligned}$$

The following theorems introduce the critical values (CVs) of trapezoidal and triangular RFVs.

Theorem 2.2

(Qin et al. [127]). Let $\tilde{\xi }=(r_{1},r_{2},r_{3},r_{4})$ be a trapezoidal RFV. Then we have

• (i) the optimistic CV of $\tilde{\xi }$ is

  $$\begin{aligned} CV^*[\tilde{\xi }]=r_{4}/(1+r_{4}-r_{3}), \end{aligned}$$

  (50)

• (ii) the pessimistic CV of $\tilde{\xi }$ is

  $$\begin{aligned} CV_{*}[\tilde{\xi }]=r_{2}/(1+r_{2}-r_{1}), \end{aligned}$$

  (51)

• (iii) the CV of $\tilde{\xi }$ is

  $$\begin{aligned} CV[\tilde{\xi }]= \left\{ \begin{array}{ll} \frac{2r_{2}-r_{1}}{1+2(r_{2}-r_{1})}, &{} \hbox {if}\, r_{2}> \frac{1}{2}; \\ \frac{1}{2}, &{} \hbox {if}\, r_{2}\le \frac{1}{2}< r_{3}; \\ \frac{r_{4}}{1+2(r_{4}-r_{3})}, &{} \hbox {if}\, r_{3}\le \frac{1}{2}. \end{array}\right. \end{aligned}$$

  (52)

Theorem 2.3

(Qin et al. [127]). Let $\tilde{\xi }=(r_{1},r_{2},r_{3})$ be a triangular RFV. Then we have

• (i) the optimistic CV of $\tilde{\xi }$ is

  $$\begin{aligned} CV^*[\tilde{\xi }]=r_{3}/(1+r_{3}-r_{2}), \end{aligned}$$

  (53)

• (ii) the pessimistic CV of $\tilde{\xi }$ is

  $$\begin{aligned} CV_{*}[\tilde{\xi }]=r_{2}/(1+r_{2}-r_{1}), \end{aligned}$$

  (54)

• (iii) the CV of $\tilde{\xi }$ is

  $$\begin{aligned} CV[\tilde{\xi }]= \left\{ \begin{array}{ll} \frac{2r_{2}-r_{1}}{1+2(r_{2}-r_{1})}, &{} \hbox {if}\, r_{2}> \frac{1}{2}; \\ \frac{r_{3}}{1+2(r_{3}-r_{2})}, &{} r_{2}\le \frac{1}{2}. \end{array}\right. \end{aligned}$$

  (55)

Now we discussed the CV-based reduction method.

The CV-Based Reduction Method: Because of fuzziness in membership function of T2 FS, computational complexity is very high to deal with T2 FS. A general idea to reduce its complexity is to convert a T2 FS into a T1 FS so that the methodologies to deal with T1 FSs can also be applied to T2 FSs. Qin et al. [127] proposed a CV-based reduction method which reduces a type-2 fuzzy variable to a type-1 fuzzy variable (may or may not be normal). Let $\tilde{\xi }$ be a T2 FV with secondary possibility distribution function $\tilde{\mu }_{\tilde{\xi }}(x)$ (which represents a RFV). The method is to introduce the critical values (CVs) as representing values for RFV $\tilde{\mu }_{\tilde{\xi }}(x)$, i.e., CV$^*$[$\tilde{\mu }_{\tilde{\xi }}(x)$], CV$_{*}$[$\tilde{\mu }_{\tilde{\xi }}(x)$] or CV[$\tilde{\mu }_{\tilde{\xi }}(x)$] and so corresponding type-1 fuzzy variables (T1 FVs) are derived using these CVs of the secondary possibilities. Then these methods are respectively called optimistic CV reduction, pessimistic CV reduction and CV reduction method.

Example 2.4 (Continued). The possibilities of each point of the T2 FV $\tilde{\xi }$ in Example 2.4, are triangular or trapezoidal RFVs. So from Theorems 2.2 and 2.3 we obtain

CV$^*$[$\tilde{\mu }_{\tilde{\xi }}(5)]=\frac{1}{2}$, CV$^*$[$\tilde{\mu }_{\tilde{\xi }}(6)]=\frac{2}{3}$, CV$^*$[$\tilde{\mu }_{\tilde{\xi }}(7)]=\frac{7}{12}$.

CV$_{*}$[$\tilde{\mu }_{\tilde{\xi }}(5)]=\frac{1}{3}$, CV$_{*}$[$\tilde{\mu }_{\tilde{\xi }}(6)]=\frac{1}{2}$, CV$_{*}$[$\tilde{\mu }_{\tilde{\xi }}(7)]=\frac{1}{4}$.

CV[$\tilde{\mu }_{\tilde{\xi }}(5)]=\frac{3}{7}$, CV[$\tilde{\mu }_{\tilde{\xi }}(6)]=\frac{4}{7}$, CV[$\tilde{\mu }_{\tilde{\xi }}(7)]=\frac{1}{2}$.

Then by optimistic CV, pessimistic CV and CV reduction methods, the T2 FV $\tilde{\xi }$ is reduced respectively to the following T1 FVs

$\left( \begin{array}{ccc} 5 &{} 6 &{} 7 \\ \frac{1}{2} &{} \frac{2}{3} &{} \frac{7}{12} \\ \end{array}\right)$, $\left( \begin{array}{ccc} 5 &{} 6 &{} 7 \\ \frac{1}{3} &{} \frac{1}{2} &{} \frac{1}{4} \\ \end{array}\right)$ and $\left( \begin{array}{ccc} 5 &{} 6 &{} 7 \\ \frac{3}{7} &{} \frac{4}{7} &{} \frac{1}{2} \\ \end{array}\right) .$

In the following theorem the optimistic CV, pessimistic CV and CV reductions of a type-2 triangular fuzzy variable are obtained. Since the secondary possibility distribution of a type-2 triangular fuzzy variable is a triangular RFV, so applying Theorem 2.3, Qin et al. [127] established the following theorem in which a type-2 triangular fuzzy variable is reduced to a type-1 fuzzy variable.

Theorem 2.4

(Qin et al. [127]). Let $\tilde{\xi }$ be a type-2 triangular fuzzy variable defined as $\tilde{\xi }=(r_{1},r_{2},r_{3};\theta _{l},\theta _{r})$. Then we have:

• (i) Using the optimistic CV reduction method, the reduction $\xi _{1}$ of $\tilde{\xi }$ has the following possibility distribution

  $$\begin{aligned} \mu _{\xi _{1}}(x)= \left\{ \begin{array}{l@{\quad }l} \frac{(1+\theta _{r})(x-r_{1})}{r_{2}-r_{1}+\theta _{r}(x-r_{1})}, &{} \hbox {if}\,x\in [r_{1},\frac{r_{1}+r_{2}}{2}]; \\ \frac{(1-\theta _{r})x+\theta _{r}r_{2}-r_{1}}{r_{2}-r_{1}+\theta _{r}(r_{2}-x)}, &{} \hbox {if}\,x\in (\frac{r_{1}+r_{2}}{2},r_{2}]; \\ \frac{(-1+\theta _{r})x-\theta _{r}r_{2}+r_{3}}{r_{3}-r_{2}+\theta _{r}(x-r_{2})}, &{} \hbox {if}\,x\in (r_{2},\frac{r_{2}+r_{3}}{2}]; \\ \frac{(1+\theta _{r})(r_{3}-x)}{r_{3}-r_{2}+\theta _{r}(r_{3}-x)}, &{} \hbox {if}\,x\in (\frac{r_{2}+r_{3}}{2},r_{3}]. \end{array}\right. \end{aligned}$$

  (56)

• (ii) Using the pessimistic CV reduction method, the reduction $\xi _{2}$ of $\tilde{\xi }$ has the following possibility distribution

  $$\begin{aligned} \mu _{\xi _{2}}(x)=\left\{ \begin{array}{l@{\quad }l} \frac{x-r_{1}}{r_{2}-r_{1}+\theta _{l}(x-r_{1})}, &{} \hbox {if}\,x\in [r_{1},\frac{r_{1}+r_{2}}{2}]; \\ \frac{x-r_{1}}{r_{2}-r_{1}+\theta _{l}(r_{2}-x)}, &{} \hbox {if}\,x\in (\frac{r_{1}+r_{2}}{2},r_{2}]; \\ \frac{r_{3}-x}{r_{3}-r_{2}+\theta _{l}(x-r_{2})}, &{} \hbox {if}\,x\in (r_{2},\frac{r_{2}+r_{3}}{2}]; \\ \frac{r_{3}-x}{r_{3}-r_{2}+\theta _{l}(r_{3}-x)} , &{} \hbox {if}\,x\in (\frac{r_{2}+r_{3}}{2},r_{3}]. \end{array}\right. \end{aligned}$$

  (57)

• (iii) Using the CV reduction method, the reduction $\xi _{3}$ of $\tilde{\xi }$ has the following possibility distribution

  $$\begin{aligned} \mu _{\xi _{3}}(x)= \left\{ \begin{array}{l@{\quad }l} \frac{(1+\theta _{r})(x-r_{1})}{r_{2}-r_{1}+2\theta _{r}(x-r_{1})}, &{} \hbox {if}\,x\in [r_{1},\frac{r_{1}+r_{2}}{2}]; \\ \frac{(1-\theta _{l})x+\theta _{l}r_{2}-r_{1}}{r_{2}-r_{1}+2\theta _{l}(r_{2}-x)}, &{} \hbox {if}\,x\in (\frac{r_{1}+r_{2}}{2},r_{2}]; \\ \frac{(-1+\theta _{l})x-\theta _{l}r_{2}+r_{3}}{r_{3}-r_{2}+2\theta _{l}(x-r_{2})}, &{} \hbox {if}\,x\in (r_{2},\frac{r_{2}+r_{3}}{2}]; \\ \frac{(1+\theta _{r})(r_{3}-x)}{r_{3}-r_{2}+2\theta _{r}(r_{3}-x)}, &{} \hbox {if}\,x\in (\frac{r_{2}+r_{3}}{2},r_{3}]. \end{array}\right. \end{aligned}$$

  (58)

Example 2.8

Consider the type-2 triangular fuzzy variable $\tilde{\xi }{=}(2, 3, 4$; 0.5, 0.8) whose FOU is depicted in Fig. 6.

Then its optimistic CV, pessimistic CV and CV reductions are shown in the Fig. 8.

Note 2.1: The reduced type-1 fuzzy variables from T2 FVs as obtained by CV-based reduction methods are not always normalized, i.e. are general fuzzy variables. For instance, from Example 2.4 (continued) we observe that the reductions of T2 FV $\tilde{\xi }$ are not normal. For such cases, generalized credibility measure $\tilde{Cr}$ is used instead of the credibility measure.

The generalized credibility measure $\tilde{Cr}$ of a fuzzy event $\{\tilde{\xi }\in B\}$, $B\subset \mathfrak {R}$ is defined as

$$\tilde{Cr}\{\tilde{\xi }\in B\}=\frac{1}{2}(\sup _{x\in \mathfrak {R}}~\mu _{\tilde{\xi }}(x)+\sup _{x\in B}~\mu _{\tilde{\xi }}(x)-\sup _{x\in B^c}~\mu _{\tilde{\xi }}(x)).$$

It is obvious that if $\tilde{\xi }$ is normalized (i.e. $\sup _{x\in \mathfrak {R}}~\mu _{\tilde{\xi }}(x)=1$), then $\tilde{Cr}$ coincides with usual credibility measure Cr.

Fig. 8.

(1) optimistic CV, (2) pessimistic CV, (3) CV reductions of $\tilde{\xi }$.

2.4 Rough Set

Here we introduced some basic idea of approximation of a subset of a certain universe by means of lower and upper approximation and the rough set theory. Suppose U is a non-empty finite set of objects called the universe and A is a non-empty finite set of attributes, then the pair $S=(U,A)$ is called information system. For any $B\subseteq A$ there is associated an equivalence relation I(B) defined as $I(B)=\{(x,y)\in U\times U \mid \forall a\in B, a(x)=a(y)\}$, where a(x) denotes the value of attribute a for element x. I(B) is called the B-indiscernibility relation. The equivalence classes of the B-indiscernibility relation are denoted by $[x]_{B}$.

For an information system $S=(U,A)$ and $B\subseteq A$, $X\subseteq U$ can be approximated using only the information contained in B by constructing the B-lower and B-upper approximations (Pawlak [122]) of X, denoted $\underline{B}X$ and $\overline{B}X$ respectively, where

$$\underline{B}X = \{x~|~[x]_{B}\subseteq X\}~and~ \overline{B}X = \{x~|~[x]_{B}\cap X\ne \phi \}.$$

Clearly, lower approximation $\underline{B}X$ is the definable (exact) set contained in X so that the objects in $\underline{B}X$ can be with certainty classified as members of X on the basis of knowledge in B, while the objects in $\overline{B}X$ can be only classified as possible members of X on the basis of knowledge in B. The B-boundary region of X is defined as

$$BN_{B}=\overline{B}X-\underline{B}X$$

and thus consists of those objects that we cannot decisively classify into X on the basis of knowledge in B. The boundary region of a crisp (exact) set is an empty set as the lower and upper approximation of crisp set are equal. A set is said to be rough if the boundary region is non-empty, i.e., if $BN_{B}\ne \phi$ then X is referred to as rough with respect to B.

Rough set can be also characterized numerically by the following coefficient

$$\alpha _{B}(X)=\frac{\mid \underline{B}X\mid }{\mid \overline{B}X\mid }$$

called the accuracy of approximation, where |X| denotes the cardinality of X. Obviously $0\le \alpha _{B}(X)\le 1$. If $\alpha _{B}(X)=1$, X is crisp with respect to B and if $\alpha _{B}(X)<1$, X is rough with respect to B.

Example 2.9

A simple information system (also known as attribute-value tables or information table) is shown in Table 1. This table contains information about patients suffering from a certain disease and objects in this table are patients, attributes can be, for example, headache, body temperature etc. Columns of the table are labeled by attributes (symptoms) and rows by objects (patients), whereas entries of the table are attribute values. Thus each row of the table can be seen as information about specific patient.

Table 1. An example of information system

From the table it is observed that patients p2, p3 and p5 have the same conditions with respect to the attribute Headache. So patients p2, p3 and p5 are indiscernible with respect to the attribute Headache. Similarly patients p3 and p6 are indiscernible with respect to attributes Muscle-pain and Flu, and patients p2 and p5 are indiscernible with respect to attributes Headache, Muscle-pain and Temperature. Hence, the attribute Headache generates two elementary sets $\{p2, p3, p5\}$ and $\{p1, p4, p6\}$, i.e., $I(Headache)=\{\{p2, p3, p5\},\{p1, p4, p6\}\}$. Similarly the attributes Headache and Muscle-pain form the following elementary sets: $\{p1, p4, p6\}$, $\{p2, p5\}$ and $\{p3\}$.

Now we observe that patient p2 and p5 indiscernible with respect to the attributes Headache, Muscle-pain and Temperature, but patient p2 has flu, whereas patient p5 does not, hence flu cannot be characterized in terms of attributes Headache, Muscle-pain and Temperature. Hence p2 and p5 are the boundary-line cases, which cannot be properly classified in view of the available knowledge. The remaining patients p1, p3 and p6 display symptoms (Muscle-pain and at least high temperature, which are must in a patient having flu as seen from the table) which enable us to classify them with certainty as having flu and patient p4 for sure does not have flu, in view of the displayed symptoms. Thus the lower approximation of the set of patients having flu is the set $\{p1, p3, p6\}$ and the upper approximation of this set is the set $\{p1, p2, p3, p5, p6\}$, whereas the boundary-line cases are patients p2 and p5. Now consider the concept “flu”, i.e., the set $X =\{p1, p2, p3, p6\}$ and the set of attributes B = Headache, Muscle-pain, Temperature. Then $\underline{B}X=\{p1,p3,p6\}$ and $\overline{B}X=\{p1, p2, p3, p5, p6\}$ and $BN_{B}=\overline{B}X-\underline{B}X=\{p2,p5\}\ne \phi$. So here X can be referred to as rough with respect to B. Also in this case we get $\alpha _{B}(X)=3/5$. It means that the concept “flu” can be characterized partially employing symptoms Headache, Muscle-pain and Temperature.

Rough Variable: The concept of rough variable is introduced by Liu [86]. The following definitions are based on Liu [86, 88].

Definition 2.11

Let $\varLambda$ be a nonempty set, $\mathcal {A}$ be a $\sigma$-algebra of subsets of $\varLambda$, $\varDelta$ be an element in $\mathcal {A}$, and $\pi$ be a nonnegative, real-valued, additive set function on $\mathcal {A}$. Then $(\varLambda ,\varDelta ,\mathcal {A},\pi )$ is called a rough space.

Definition 2.12

(Rough Variable). A rough variable $\xi$ on the rough space $(\varLambda ,\varDelta ,\mathcal {A},\pi )$ is a measurable function from $\varLambda$ to the set of real numbers $\mathfrak {R}$ such that for every Borel set B of $\mathfrak {R}$, we have $\{\lambda \in \varLambda ~|~\xi (\lambda )\in B\}\in \mathcal {A}$.

Then the lower and upper approximations of the rough variable $\xi$ are defined as follows:

$$\underline{\xi }=\{\xi (\lambda )~|~\lambda \in \varDelta \}~and~\overline{\xi }=\{\xi (\lambda )~|~\lambda \in \varLambda \}.$$

Definition 2.13

Let $\xi$ be a rough vector on the rough space $(\varLambda ,\varDelta ,\mathcal {A},\pi )$, and $f_{j} : \mathfrak {R}^n \rightarrow \mathfrak {R}$ be continuous functions, $j = 1,2,...,m$. Then the upper trust of the rough event characterized by $f_{j}(\xi )\le 0; j = 1,2,...,m$ is defined by

$$T\bar{r}\{f_{j}(\xi )\le 0_{,j = 1,2,...,m}\}=\frac{\pi \{\lambda \in \varLambda |f_{j}(\xi (\lambda ))\le 0,~j = 1,2,...,m\}}{\pi (\varLambda )},$$

and the lower trust of the rough event characterized by $f_{j}(\xi )\le 0; j = 1,2,...,m$ is defined by

$$T\underline{r}\{f_{j}(\xi )\le 0_{,j = 1,2,...,m}\}=\frac{\pi \{\lambda \in \varDelta |f_{j}(\xi (\lambda ))\le 0,~j = 1,2,...,m\}}{\pi (\varDelta )}.$$

If $\pi (\varDelta )=0$, then the upper trust and lower trust of the rough event are assumed to be equivalent, i.e., $T\bar{r}\{f_{j}(\xi )\le 0_{,j = 1,2,...,m}\}\equiv T\underline{r}\{f_{j}(\xi )\le 0_{,j = 1,2,...,m}\}.$

The trust of the rough event is defined as the average value of the lower and upper trusts, i.e.,

$$Tr\{f_{j}(\xi )\le 0_{,j = 1,2,...,m}\}{=}\frac{1}{2}(T\bar{r}\{f_{j}(\xi )\le 0_{,j = 1,2,...,m}\}+T\underline{r}\{f_{j}(\xi )\le 0_{,j = 1,2,...,m}\}).$$

Definition 2.14

Let $\xi$ be a rough variable on the rough space $(\varLambda ,\varDelta ,\mathcal {A},\pi )$ and $\alpha \in (0,1]$, then

$$\xi _{sup}(\alpha )=\sup \{r|Tr\{\xi \ge r\}\ge \alpha \}$$

is called $\alpha$-optimistic value to $\xi$; and

$$\xi _{inf}(\alpha )=\inf \{r|Tr\{\xi \le r\}\ge \alpha \}$$

is called $\alpha$-pessimistic value to $\xi$.

Definition 2.15

Let $\xi$ be a rough variable on the rough space $(\varLambda ,\varDelta ,\mathcal {A},\pi )$. The expected value of $\xi$ is defined by

$$E[\xi ]=\int _{0}^\infty Tr\{\xi \ge r\}dr-\int _{-\infty }^0 Tr\{\xi \le r\}dr.$$

Theorem 2.5

(Liu [88]). Let $\xi _{inf}(\alpha )$ and $\xi _{sup}(\alpha )$ be the $\alpha$-pessimistic and $\alpha$-optimistic values of the rough variable $\xi$, respectively.Then we have

• (a) $Tr\{\xi \le \xi _{inf}(\alpha )\ge \alpha \}$ and $Tr\{\xi \ge \xi _{sup}(\alpha )\ge \alpha \}$;

• (b) $\xi _{inf}(\alpha )$ is an increasing and left-continuous function of $\alpha$;

• (c) $\xi _{sup}(\alpha )$ is a decreasing and left-continuous function of $\alpha$;

• (d) if $0<\alpha \le 1$, then $\xi _{inf}(\alpha )=\xi _{sup}(1-\alpha )$ and $\xi _{sup}(\alpha )=\xi _{inf}(1-\alpha )$;

• (e) if $0<\alpha \le 0.5$, then $\xi _{inf}(\alpha )\le \xi _{sup}(\alpha )$;

• (f) if $0.5<\alpha \le 1$,then $\xi _{inf}(\alpha )\ge \xi _{sup}(\alpha )$.

Example 2.10

Consider that $\xi =([a,b],[c,d])$ be a rough variable with $c\le a<b\le d$, where [a, b] is the lower approximation and [c, d] is the upper approximation. This means the elements in [a, b] are certainly members of the variable and that of [c, d] are possible members of the variable. Here $\varDelta =\{\lambda |a\le \lambda \le b\}$ and $\varLambda =\{\lambda |c\le \lambda \le d\}$, $\xi (x)=x$ for all $x\in \varLambda$, $\mathcal {A}$ is the Borel algebra on $\varLambda$ and $\pi$ is the Lebesgue measure.

As an practical example consider the possible transportation cost of unit product to be transported from a source i to certain destination j through a conveyance k for a certain time period. But as transportation cost depends upon fuel price, labor charges, tax charges, etc. and each of which is fluctuate time to time, so it is not always possible to determine its exact value. Suppose four experts give the possible unit transportation cost for $i-j$ route via conveyance k, determined in a certain time period as intervals [3,5], [3.5,6], [4,5] and [4,6] respectively. Denotes $c_{ijk}$ as - ’the possible value of the unit transportation cost for $i-j$ route through conveyance k according to the all experts’. Then $c_{ijk}$ is not exact and can be approximated by means of lower and upper approximation. Here [4,5] can be taken as the lower approximation of $c_{ijk}$ as it is the greatest definable (exact) set that $c_{ijk}$ contain, i.e., every member of [4,5] is certainly a value of $c_{ijk}$ according to all experts. Here [3,6] is the upper approximation, as members of [3,6] may or may not be possible transportation cost according to all experts. So $c_{ijk}$ can be represented as the rough variable ([4,5],[3,6]).

For a given value r and $\xi =([a,b],[c,d])$, trust of rough events characterized by $\xi \le r$ and $\xi \ge r$ (Liu [86, 88]) are given by

$$\begin{aligned} Tr\{\xi \le r\}= \left\{ \begin{array}{l@{\quad }l} 0, &{} \hbox {if}\, r\le c; \\ \frac{r-c}{2(d-c)}, &{} \hbox {if}\, c\le r\le a; \\ \frac{1}{2}(\frac{r-a}{b-a}+\frac{r-c}{d-c}), &{} \hbox {if}\, a\le r\le b;\\ \frac{1}{2}(\frac{r-c}{d-c}+1), &{} \hbox {if}\, b\le r\le d; \\ 1, &{} \hbox {if}\, r\ge d. \end{array}\right. \end{aligned}$$

(59)

$$\begin{aligned} Tr\{\xi \ge r\}= \left\{ \begin{array}{l@{\quad }l} 0, &{} \hbox {if}\, r\ge d; \\ \frac{d-r}{2(d-c)}, &{} \hbox {if}\, b\le r\le d; \\ \frac{1}{2}(\frac{d-r}{d-c}+\frac{b-r}{b-a}), &{} \hbox {if}\, a\le r\le b;\\ \frac{1}{2}(\frac{d-r}{d-c}+1), &{} \hbox {if}\, c\le r\le a; \\ 1, &{} \hbox {if}\, r\le c. \end{array}\right. \end{aligned}$$

(60)

For rough variable $\xi =([4,5],[2,7])$, $Tr\{\xi \le r\}$ and $Tr\{\xi \ge r\}$ are depicted in Fig. 9.

Fig. 9.

The trust of the rough event characterized by (1) $\xi \le r$ and (2) $\xi \ge r$.

$\alpha$-optimistic value to $\xi =([a,b],[c,d])$ is

$$\begin{aligned} \xi _{sup}(\alpha )=\left\{ \begin{array}{ll} (1-2\alpha ) d+2\alpha c, &{} \hbox {if}\, \alpha \le ((d-b)/2(d-c)); \\ 2(1-\alpha ) d+(2\alpha -1)c, &{} \hbox {if}\, \alpha \ge ((2d-a-c)/2(d-c)); \\ \frac{d(b-a)+b(d-c)-2\alpha (b-a)(d-c)}{(b-a)+(d-c)}, &{} \hbox {otherwise.} \end{array}\right. \end{aligned}$$

(61)

$\alpha$-pessimistic value to $\xi$ is

$$\begin{aligned} \xi _{inf}(\alpha )= \left\{ \begin{array}{ll} (1-2\alpha ) c+2\alpha d, &{} \hbox {if}\, \alpha \le ((a-c)/2(d-c)); \\ 2(1-\alpha ) c+(2\alpha -1)d, &{} \hbox {if}\, \alpha \ge ((b+d-2c)/2(d-c)); \\ \frac{c(b-a)+a(d-c)+2\alpha (b-a)(d-c)}{(b-a)+(d-c)}, &{} \hbox {otherwise.} \end{array}\right. \end{aligned}$$

(62)

The expected value of $\xi$ is $E(\xi )=\frac{1}{4}(a+b+c+d)$.

2.5 Single-Objective Optimization

Single-Objective Linear Programming (SOLP)/Non-linear Programming (SONLP) Problem: If an optimization problem consists of only one objective function, then problem is called a single-objective mathematical programming (SOMP) problem. The minimization of a constrained SOMP problem can be formulated as:

$$\begin{aligned} \left\{ \begin{array}{ll} Find &{} x = (x_{1}, x_{2}, ...., x_{n})^T \\ which~ minimizes &{} f(x) \\ subject~to &{} x\in X \\ where~X= &{} x:\left\{ \begin{array}{ll} g_{j}(x)\le 0, &{} j=1,2,...,m; \\ x_{i}\ge 0, &{} i=1,2,...,n. \end{array}\right. \end{array}\right. \end{aligned}$$

(63)

where, objective function f(x) and constraints $g_{j}(x)$, $j = 1, 2, ....,m$ are functions defined on n-dimensional set.

When both the objective function and the constraints are linear, the above SOMP problem becomes a single-objective linear programming problem (SOLP). Otherwise, it is a single-objective non-linear programming problem (SONLP).

Feasible Solution: A decision variable vector x satisfying all the constraints is called a feasible solution to the problem. The collection of all such solutions forms the feasible region.

Optimal Solution: If a feasible solution $x^*$ of (63) be such that for each feasible point x, $f(x)\le f(x^*)$ for maximization problem and $f(x)\ge f(x^*)$ for minimization problem then $x^*$ is called an optimal solution of the problem.

Local Optimum: A feasible solution $x^*$ of (63) is said be local optimum if there exists an $\epsilon > 0$ such that $f(x)\ge f(x^*)$ for minimization problem and $f(x)\le f(x^*)$ for maximization problem, $\forall x\in X:~\parallel x-x^*\parallel <\epsilon$.

Global Optimum: A feasible solution $x^*$ of (63) is said be global optimum if $f(x)\ge f(x^*)$ for minimization problem and $f(x)\le f(x^*)$ for maximization problem $\forall x\in X$.

Necessary Condition for Optimality: The necessary condition for a feasible solution $x^*\in X$ of (63) to be optimal is that all the partial derivatives $\frac{\partial f(x)}{\partial x_{r}}$ are exist at $x = x^*$ and $\frac{\partial f(x)}{\partial x_{r}}=0$ for $r=1,2,...,n$.

Example 2.11

As an example of a single-objective problem we consider a simple transportation problem with 3 sources $(i=1,2,3)$ and 3 destinations $(j=1,2,3)$ as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} Minimize~Z= &{} \sum _{i=1}^3\sum _{j=1}^3~c_{ij}~x_{ij}, \\ subject~to &{} \sum _{j=1}^3 x_{ij}~\le a_{i},~~i=1,2,3, \\ &{} \sum _{i=1}^3 x_{ij}~~\ge b_{j},~~j=1,2,3, \\ x_{ij}\ge 0,~\forall ~ i,j, &{} \sum _{i=1}^3 a_{i}\ge \sum _{j=1}^3 b_{j}, \end{array} \right. \end{aligned}$$

(64)

where $c_{ij}$ is the cost for transportation of unit product from source i to destination j, $x_{ij}$ is decision variable which represents the quantity to be transported from i-th origin to j-th destination and so that the objective function Z represents the total transportation cost. The unit transportation costs are given as follows: $c_{11}=5$, $c_{12}=6$, $c_{13}=8$, $c_{21}=7$, $c_{22}=9$, $c_{23}=5$, $c_{31}=8$, $c_{32}=9$ and $c_{33}=7$. The availabilities at each sources and demands of each destinations are as follows: $a_{1}=36$, $a_{2}=20.8$, $a_{3}=28.6$, $b_{1}=22.8$, $b_{2}=31$, $b_{3}=30$.

2.6 Solution Techniques for Single-Objective Linear/Non-linear Problem

Generalized Reduced Gradient (GRG): The GRG technique is a method for solving NLP problems with equality as well as inequality constraints. Consider the NLP problem as:

$$\begin{aligned} \left\{ \begin{array}{ll} Find &{} x = (x_{1}, x_{2}, ...., x_{n})^T \\ which~ minimizes &{} f(x) \\ subject~to &{} x\in X \\ where~X= &{} x:\left\{ \begin{array}{ll} g_{j}(x)\le 0, &{} j=1,2,...,m; \\ h_{r}(x)=0, &{} r=1,2,...,p;\\ x_{i}\ge 0, &{} i=1,2,...,n. \end{array}\right. \end{array}\right. \end{aligned}$$

(65)

By adding a non-negative slack variable $s_{j}(\ge 0)$, $j = 1, 2, ...,m$ to each of the above inequality constraints, the problem (65) can be stated as,

$$\begin{aligned} \left\{ \begin{array}{ll} Minimize &{} f(x) \\ subject~to &{} x = (x_{1}, x_{2}, ...., x_{n})^T \in X \\ where~X= &{} x:\left\{ \begin{array}{ll} g_{j}(x)+s_{j}=0, &{} j=1,2,...,m; \\ h_{r}(x)=0, &{} r=1,2,...,p;\\ x_{i}\ge 0, &{} i=1,2,...,n.\\ s_{j}\ge 0, &{} j=1,2,...,m \end{array}\right. \end{array} \right. \end{aligned}$$

(66)

where the lower and upper bounds on the slack variables, $s_{j}$, $j = 1, 2, ...,m$ are taken as a zero and a large number (infinity) respectively.

Denote $s_{j}$ by $x_{n+j}$, $g_{j}(x)+s_{j}$ by $\xi _{j}$, $j = 1, 2, ...,m$ and $h_{r}(x)$ by $\xi _{m+r}$, $r=1,2,...,p$. Then the above problem (66) becomes

$$\begin{aligned} \left\{ \begin{array}{ll} Minimize &{} f(x) \\ subject~to &{} x = (x_{1}, x_{2}, ...., x_{n+m})^T \in X \\ where~X= &{} x:\left\{ \begin{array}{ll} \xi _{j}=0, &{} j=1,2,...,m+p; \\ x_{i}\ge 0, &{} i=1,2,...,n+m. \end{array}\right. \end{array} \right. \end{aligned}$$

(67)

This GRG technique is based on the idea of elimination of variables using the equality constraints. Theoretically, $(m+p)$ variables (dependent variables) can be expressed in terms of remaining $(n - p)$ variables (independent variables). Thus one can divide the $(n + m)$ decision variables arbitrarily into two sets as

$$x = (y, z)^T$$

where, y is $(n-p)$ design or independent variables and z is $(m+p)$ state or dependent variables and

$$y = (y_{1}, y_{2}, ...., y_{n-p})^T,~ z = (z_{1}, z_{2}, ...., z_{m+p})^T.$$

Here, the design variables are completely independent and the state variables are dependent on the design variables used to satisfy the constraints $\xi _{j}(x) = 0$, $(j = 1, 2,...,m+ p)$. Consider the first variations of the objective and constraint functions:

$$\begin{aligned} df(x)&=\sum _{i=1}^{n-p}\frac{\partial f}{\partial y_{i}} dy_{i}+\sum _{i=1}^{m+p}\frac{\partial f}{\partial z_{i}} dz_{i}=\nabla _{y}^T f dy+\nabla _{z}^T f dz\end{aligned}$$

(68)

$$\begin{aligned} d\xi _{j}(x)&= \sum _{i=1}^{n-p}\frac{\partial \xi _{j}}{\partial y_{i}} dy_{i}+\sum _{i=1}^{m+p}\frac{\partial \xi _{j}}{\partial z_{i}} dz_{i} \end{aligned}$$

(69)

$$\begin{aligned} or~d\xi&= C~dy+D~dz\\ where~\nabla _{y}^T f&= \big (\frac{\partial f}{\partial y_{1}},\frac{\partial f}{\partial y_{2}},...,\frac{\partial f}{\partial y_{n-p}}\big ) \nonumber \\ \nabla _{z}^T f&= \big (\frac{\partial f}{\partial z_{1}},\frac{\partial f}{\partial z_{2}},...,\frac{\partial f}{\partial z_{m+p}}\big )\nonumber \end{aligned}$$

(70)

$$C=\begin{bmatrix} \frac{\partial \xi _{1}}{\partial y_{1}}&...&...&...&\frac{\partial \xi _{1}}{\partial y_{n-p}} \\ \frac{\partial \xi _{2}}{\partial y_{1}}&...&...&...&\frac{\partial \xi _{2}}{\partial y_{n-p}} \\ ...&...&...&...&... \\ ...&...&...&...&... \\ \frac{\partial \xi _{m+p}}{\partial y_{1}}&...&...&...&\frac{\partial \xi _{m+p}}{\partial y_{n-p}} \\ \end{bmatrix},~D=\begin{bmatrix} \frac{\partial \xi _{1}}{\partial z_{1}}&...&...&...&\frac{\partial \xi _{1}}{\partial z_{m+p}} \\ \frac{\partial \xi _{2}}{\partial z_{1}}&...&...&...&\frac{\partial \xi _{2}}{\partial z_{m+p}} \\ ...&...&...&...&... \\ ...&...&...&...&... \\ \frac{\partial \xi _{m+p}}{\partial z_{1}}&...&...&...&\frac{\partial \xi _{m+p}}{\partial z_{m+p}} \\ \end{bmatrix}$$

$$dy=(dy_{1},dy_{2},...,dy_{n-p})^T$$

$$and~dz=(dz_{1},dz_{2},...,dz_{m+p})^T$$

Assuming that the constraints are originally satisfied at the vector x $(\xi (x) = 0)$, any change in the vector dx must correspond to $d\xi = 0$ to maintain feasibility at $x + dx$. Thus, Eq. (70) can be solved as

$$C~dy+D~dz=0$$

$$\begin{aligned} or~dz=-D^{-1}~Cdy \end{aligned}$$

(71)

The change in the objective function due to the change in x is given by the Eq. (68), which can be expressed, using Eq. (71) as

$$\begin{aligned} df(x)&=(\nabla _{y}^T f dy-\nabla _{z}^T f D^{-1}~C) dy\nonumber \\ or~\frac{df(x)}{dy}&=G_{R}\end{aligned}$$

(72)

$$\begin{aligned} where~G_{R}&=\nabla _{y}^T f dy-\nabla _{z}^T f D^{-1}~C \end{aligned}$$

(73)

is called the generalized reduced gradient. Geometrically, the reduced gradient can be described as a projection of the original n-dimensional gradient into the $(n - m)$ dimensional feasible region described by the design variables.

A necessary condition for the existence of minimum of an unconstrained function is that the components of the gradient vanish. Similarly, a constrained function assumes its minimum value when the appropriate components of the reduced gradient are zero. In fact, the reduced gradient $G_{R}$ can be used to generate a search direction S to reduce the value of the constrained objective function. Similarly, to the gradient $\nabla f$ that can be used to generate a search direction S for an unconstrained function. A suitable step length $\lambda$ is to be chosen to minimize the value of f(x) along the search direction. For any specific value of $\lambda$, the dependent variable vector z is updated using Eq. (70). Noting that Eq. (68) is based on using a linear approximation to the original non-linear problem, so the constraints may not be exactly equal to zero at $\lambda$, i.e., $d\xi \ne 0$. Hence, when y is held fixed, in order to have

$$\begin{aligned} \xi _{j}(x) + d\xi _{j}(x) = 0,~j = 1, 2, ...,m + p \end{aligned}$$

(74)

following must be satisfied.

$$\begin{aligned} \xi (x) + d\xi (x) = 0. \end{aligned}$$

(75)

Using Eq. (70) for $d\xi$ in Eq. (75), following is obtained

$$\begin{aligned} dz = D^{-1}(-\xi (x) - Cdy). \end{aligned}$$

(76)

The value dz given by Eq. (76) is used to update the value of z as

$$\begin{aligned} z_{update} = z_{current} + dz. \end{aligned}$$

(77)

The constraints evaluated at the updated vector x, and the procedure of finding dz using Eq. (76) is repeated until dz is sufficiently small.

2.7 Single-Objective Problem in Fuzzy Environment

When in a single-objective optimization problem, some of the or all the parameters in objective function and constraints are not precisely defined or completely known, then if such parameters are represented by fuzzy numbers(/variables), the problem is termed as single-objective optimization problem in fuzzy environment. Consider the following fuzzy programming problem,

$$\begin{aligned} \left\{ \begin{array}{ll} Min &{} f(x,\tilde{\xi }) \\ subject~to &{} g_{j}(x,\tilde{\xi })\le \tilde{b_{j}},~j=1,2,...,m \\ &{} x_{i}\ge 0,~i=1,2,...,n \\ \end{array} \right. \end{aligned}$$

(78)

where, $x = (x_{1}, x_{2}, ...., x_{n})^T$ is a decision vector,$\tilde{\xi }$ is a fuzzy vector, $f(x,\tilde{\xi })$ is a return function, and $g_{j}(x,\tilde{\xi })\le \tilde{b_{j}}$ are constraints, $j = 1,2,...,m$. It is not possible to minimize directly a fuzzy quantity $f(x,\tilde{\xi })$ and also the constraints $g_{j}(x,\tilde{\xi })\le \tilde{b_{j}}$, $j = 1,2,...,m$ do not produce a crisp feasible set. In order to solve the above fuzzy model several researchers proposed a number of different methods. Fuzzy expected value model (EVM) (Liu and Liu [94]), chance-constrained programming model (CCP) (Liu and Iwamura [92]), dependent-chance programming (DCP) (Liu [85]) are some of the such available techniques. We now provide short description of these techniques.

Expected Value Model: In order to obtain a solution (here a decision with minimum expected return) of (78), Liu and Liu [94] provided a spectrum of fuzzy expected value model (EVM) as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} Min &{} E[f(x,\tilde{\xi })] \\ subject~to &{} E[g_{j}(x,\tilde{\xi })-\tilde{b_{j}}]\le 0,~j=1,2,...,m \\ &{} x_{i}\ge 0,~i=1,2,...,n \\ \end{array} \right. \end{aligned}$$

(79)

For detail explanation, crisp equivalent form of the fuzzy EVM please see Liu and Liu [94], Liu [90], Yang and Liu [153].

Chance-Constrained Programming Model: This method is used to solve the problems with chance-constraints. In this method, the uncertain constraints are allowed to be violated such that constraints must be satisfied at some chance (/confidence) level. For example, since the fuzzy constraints $g_{j}(x,\tilde{\xi })\le \tilde{b_{j}},~j=1,2,...,m$ do not define a deterministic feasible set, a natural idea is to provide a confidence level $\alpha$ at which it is desired that the fuzzy constraints hold. A chance constrained programming for the minimization problem (78) with fuzzy parameters using possibility measure may be constructed as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} Min_{x}&{} (Min_{\bar{f}}~~\bar{f}) \\ subject~to &{} Pos\{f(x,\tilde{\xi })\le \bar{f}\}\ge \alpha , \\ &{} Pos\{\tilde{\xi }\mid ~g_{j}(x,\tilde{\xi })\le \tilde{b_{j}}\}\ge \alpha _{j},~j=1,2,...,m \\ &{} x_{i}\ge 0,~i=1,2,...,n \\ \end{array} \right. \end{aligned}$$

(80)

where, $\alpha$ is a predetermined confidence level so that Min $\bar{f}$ indicates the minimum value that the objective function achieves with possibility at least $\alpha$ $(0<\alpha \le 1)$. In other words we want to minimize the $\alpha$-optimistic return. $\alpha _{j}$ indicates the predetermined confidence level of satisfaction of the constraint.

A chance constrained programming for the minimization problem (78) with fuzzy parameters using credibility measure may be constructed as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} Min_{x}&{} (Min_{\bar{f}}~~\bar{f}) \\ subject~to &{} Cr\{f(x,\tilde{\xi })\le \bar{f}\}\ge \alpha , \\ &{} Cr\{g_{j}(x,\tilde{\xi })\le \tilde{b_{j}}\}\ge \alpha _{j},~j=1,2,...,m \\ &{} x_{i}\ge 0,~i=1,2,...,n \\ \end{array} \right. \end{aligned}$$

(81)

where, $\alpha$ is a predetermined confidence (credibility) level so that Min $\bar{f}$ indicates the minimum value that the objective function achieves with credibility degree(/level) at least $\alpha$ $(0<\alpha \le 1)$. In other words we want to minimize the $\alpha$-optimistic return. $\alpha _{j}$ indicates the predetermined credibility level of satisfaction of the constraint.

For detail explanation regarding the, crisp equivalent forms of the fuzzy CCP problem please see Liu and Iwamura [92], Mula et al. [116], Liu [84, 90], Yang and Liu [153] and Kundu et al. [74].

Dependent-Chance Programming: The idea of dependent-chance programming (DCP) is to optimize the chance of an uncertain event. Suppose for the minimization problem like (78), a decision maker will satisfy with a solution (decision vector x) for which the objective value is not exceed a certain value. So a decision maker may fixed a satisfying predetermined maximal objective value and maximize the credibility level that objective value is not exceed the predetermined value. Then with respect to a given predetermined maximal objective value $\bar{f}$ the dependent chance-constrained programming model for the problem (78) is formulated as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} Max&{} Cr\{f(x,\tilde{\xi })\le \bar{f}\} \\ subject~to &{} g_{j}(x,\tilde{\xi })\le \tilde{b_{j}},~j=1,2,...,m \\ &{} x_{i}\ge 0,~i=1,2,...,n \\ \end{array} \right. \end{aligned}$$

(82)

For detail explanation, crisp equivalent forms of the fuzzy CCP problem please see Liu [85], Liu [90], Yang and Liu [153].

2.8 Multi-objective Optimization

A general multi-objective programming problem (minimization problem) is of the following form:

$$\begin{aligned} \left\{ \begin{array}{ll} Find &{} x = (x_{1}, x_{2}, ...., x_{n})^T \\ which~ minimizes &{} F(x)=(f_{1}(x),f_{2}(x),...,f_{k}(x))^T \\ subject~to &{} x\in X \\ where~X= &{} x:\left\{ \begin{array}{ll} g_{j}(x)\le 0, &{} j=1,2,...,m; \\ x_{i}\ge 0, &{} i=1,2,...,n. \end{array}\right. \end{array} \right. \end{aligned}$$

(83)

where, $f_{1}(x),f_{2}(x),...,f_{k}(x)$ are $k\ge 2)$ objectives.

Complete Optimal Solution: A feasible solution $x^*$ is said to be a complete optimal solution to the multi-objective problem in (83) iff there exists $x^*\in X$ such that $f_{i}(x^*)\le f_{i}(x)$, $i = 1, 2,...,k$ for all $x\in X$. In general, the objective functions of the multi-objective problem conflict with each other, a complete optimal solution does not always exist and so Pareto (or non dominated) optimality concept is introduced.

Pareto Optimal Solution: A feasible solution $x^*$ is said to be a Pareto optimal solution to the (83) iff there does not exist another $x\in X$ such that $f_{i}(x)\le f_{i}(x^*)$ for all $i,~i = 1, 2,...,k$ and $f_{j}(x)< f_{j}(x^*)$ for at least one index $j,~j = 1,2,....,k$. An objective vector $F^*$ is Pareto-optimal if there does not exist another objective vector F(x) such that $f_{i}\le f_{i}^*$, for all $i,~i = 1,2,...,k$ and $f_{j}< f_{j}^*$ for at least one index j. Therefore, $F^*$ is Pareto optimal if the decision vector corresponding to it is Pareto optimal. Unless an optimization problem is convex, only locally optimal solution is guaranteed using standard mathematical programming techniques. Therefore, the concept of Pareto-optimality needs to be modified to introduce the notion of a locally Pareto-optimal solution for a non-convex problem as defined by Geoffrion [49].

Locally Pareto Optimal Solution: A feasible solution $x^*$ is said to be a locally Pareto optimal solution to the multi-objective problem (83) if and only if there exists an $r > 0$ such that $x^*$ is Pareto optimal in $X\cap N(x^*,r)$, where $N(x^*,r)$ is a r-neighborhood of $x^*$, i.e., there does not exist another $x\in X\cap N(x^*,r)$ such that $f_{i}(x)\le f_{i}(x^*)$.

Concept of Domination: Most evolutionary multi-objective optimization algorithms use the concept of domination. In these algorithms, two solutions are compared on the basis of whether one dominates the other solution or not. Let us use the operator $\sqsupseteq$ between two solutions i and j as $i\sqsupseteq j$ denotes that solution i is better than solution j on a particular objective. Similarly $i \sqsubseteq j$ for a particular objective implies that solution i is worse than solution j on this objective. With this assumption a solution x is said to dominate the other solution y, if both the following conditions hold.

The solution x is not worse than y in all the objectives.

The solution x is strictly better than y in at least one objective, i.e., $f_{j}(x)\sqsupseteq f_{j}(y)$ for at least one $j,~j=1, 2,...,k$. Now, let us introduce some linear/non-linear programming techniques which are used to achieve at least local Pareto optimal solutions of multi-objective optimization problem.

Example 2.12

In the single-objective problem (64) as presented in Sect. 2.5, the objective function is minimization of total transportation cost. Now in case of transportation of highly breakable items (e.g. glass-goods, toys, ceramic goods, etc.), the breakability issue also should be considered. Breaking of items may be due to bad condition of road, long distance of a certain route, etc. Then an additional objective function which represents minimization of total breaking items is imposed in the problem and the problem becomes multi-objective. Suppose $r_{ij}$ be the rate of breakability (/percentage of breakability) for transportation of goods from source i to destination j. Also suppose customer at destination compromises on receiving less amount than the demanded amount due to breaking of items. Then the problem becomes

$$\begin{aligned} \left\{ \begin{array}{ll} Minimize~Z= &{} {\sum }_{i=1}^3{\sum }_{j=1}^3~c_{ij}~x_{ij}, \\ \\ Minimize~Z'= &{} {\sum }_{i=1}^3{\sum }_{j=1}^3~r_{ij}~x_{ij}, \\ \\ subject~to &{} {\sum }_{j=1}^3 x_{ij}~\le a_{i},~~i=1,2,3, \\ &{} {\sum }_{i=1}^3 x_{ij}~~\ge b_{j},~~j=1,2,3, \\ x_{ij}\ge 0,~\forall ~ i,j, &{} {\sum }_{i=1}^3 a_{i}\ge {\sum }_{j=1}^3 b_{j}, \end{array} \right. \end{aligned}$$

(84)

where values of $r_{ij}$ are given by $r_{11}=2$, $r_{12}=1.5$, $r_{13}=1.2$, $r_{21}=1$, $r_{22}=1.2$, $r_{23}=1.5$, $r_{31}=2.5$, $r_{32}=2$, $r_{33}=1.5$. The values of the other parameters are same as the problem (64). The solution of such multi-objective problem is discussed in the next section and also in Sect. 3 with numerical example.

2.9 Solution Techniques for Multi-objective Linear/Non-linear Problem

Fuzzy Programming Technique: Zimmarmann [159] introduced fuzzy linear programming approach for solving problem with multiple objectives and he showed that fuzzy linear programming always gives efficient solutions and an optimal compromise solution. The steps to solve the multi-objective models using fuzzy programming technique are as follows:

Step 1: Solve the multi-objective problem (83) as a single objective problem using, each time, only one objective $f_{p}(p=1,2,...,k)$(ignore all other objectives) to obtain the optimal solution $X^{p*}={x_{i}^p}$ of k different single objective solid transportation problem.

Step 2: Calculate the values of all the k objective functions at all these k optimal solutions $X^{p*}~(p=1,2,...,k)$ and find the upper and lower bound for each objective given by $U_{p}=Max\{f_{p}(X^{1*}),f_{p}(X^{2*}),...,f_{p}(X^{k*})\}$ and $L_{p}=f_{p}(X^{p*})$, $p=1,2,...,k$ respectively.

Step 3: Then an initial fuzzy model is given by

$$\begin{aligned} \left\{ \begin{array}{ll} Find &{} x = (x_{1}, x_{2}, ...., x_{n})^T \\ subject~to &{} f_{p}(x)\le L_{p} \\ x\in X,~X= &{} x:\left\{ \begin{array}{ll} g_{j}(x)\le 0, &{} j=1,2,...,m; \\ x_{i}\ge 0, &{} i=1,2,...,n. \end{array}\right. \end{array}\right. \end{aligned}$$

(85)

where $x={x_{i}}$, $i=1,2,...,n$; $p=1,2,...,k$

Step 4: case(I). Construct linear membership function $\mu _{p}(f_{p})$ corresponding to p-th objective as

$$\mu _{p}(f_{p})=\left\{ \begin{array}{ll} 1, &{} \hbox {if}\, f_{p}\le L_{p}; \\ \frac{U_{p}-f_{p}}{U_{p}-L_{p}}, &{} \hbox {if}\, L_{p}<f_{p}<U_{p}; \\ 0, &{} \hbox {if}\, f_{p}\ge L_{p},~~~~~~~~~~~~~~~~~~~~~~\forall ~ p. \end{array}\right. $$

                  or,

case(II): Construct hyperbolic membership function $\mu _{p}^H(f_{p})$ corresponding to p-th objective as

$$\mu _{p}^H(f_{p})=1/2+1/2~\tanh [(\frac{U_{p}+L_{p}}{2}-f_{p})\alpha _{p}],\alpha _{p}=\frac{3}{(U_{p}-L_{p})/2}=\frac{6}{U_{p}-L_{p}}.$$

Step 5: For case(I), formulate fuzzy linear programming problem using max-min operator as

$$\begin{aligned} \left\{ \begin{array}{ll} Max &{} \lambda \\ subject~to &{} \lambda \le \mu _{p}(f_{p})=(U_{p}-f_{p})/(U_{p}-L_{p}),~\forall p \\ x\in X,~X= &{} x:\left\{ \begin{array}{ll} g_{j}(x)\le 0, &{} j=1,2,...,m; \\ x_{i}\ge 0, &{} i=1,2,...,n. \end{array}\right. \end{array}\right. \end{aligned}$$

(86)

$$\lambda \ge 0 ~and~ \lambda =min_{p}\{\mu _{p}(Z_{p})\}.$$

For case(II), formulate fuzzy programming problem with hyperbolic membership function as

$$\begin{aligned} \left\{ \begin{array}{ll} Max &{} \lambda \\ subject~to &{} 2\lambda -1\le \tanh [(\frac{U_{p}+L_{p}}{2}-f_{p})\alpha _{p}],~\forall p \\ x\in X,~X= &{} x: \left\{ \begin{array}{ll} g_{j}(x)\le 0, &{} j=1,2,...,m; \\ x_{i}\ge 0, &{} i=1,2,...,n. \end{array}\right. \\ \lambda \ge ~0. &{} . \\ \end{array}\right. \end{aligned}$$

(87)

Let $\lambda ^\prime =\tanh ^{-1}(2\lambda -1)$, then above problem becomes

$$\begin{aligned} \left\{ \begin{array}{ll} Max &{} \lambda \\ subject~to &{} \lambda ^\prime \le (\frac{U_{p}+L_{p}}{2}-f_{p})\alpha _{p},~\forall p \\ x\in X,~X= &{} x: \left\{ \begin{array}{ll} g_{j}(x)\le 0, &{} j=1,2,...,m; \\ x_{i}\ge 0, &{} i=1,2,...,n. \end{array}\right. \\ \lambda \ge ~0. &{} . \\ \end{array} \right. \end{aligned}$$

(88)

Then since $\tanh$ and $\tanh ^{-1}$ are strictly increasing functions, the above problem equivalently becomes,

$$\begin{aligned} \left\{ \begin{array}{ll} Max &{} \lambda ^\prime \\ subject~to &{} \lambda ^\prime +Z_{p}~\alpha _{p}\le (\frac{U_{p}+L_{p}}{2})~\alpha _{p},~\forall p \\ x\in X,~X= &{} x: \left\{ \begin{array}{ll} g_{j}(x)\le 0, &{} j=1,2,...,m; \\ x_{i}\ge 0, &{} i=1,2,...,n. \end{array} \right. \\ \lambda ^\prime \ge ~0. &{} \hbox {.} \\ \end{array} \right. \end{aligned}$$

(89)

Step-6: Now the reduced problems under case-(I) and case-(II) are solved by a linear optimization technique and in each case the optimum compromise solutions are obtained.

In case-(II), maximum overall satisfactory level of compromise is Max $\lambda = \lambda ^*=1/2+(\tanh \lambda ^{\prime *})/2.$

Global Criteria Method: Global criteria method gives a compromise solution for a multi-objective problem. Actually this method is a way of achieving compromise in minimizing the sum in deviations of the ideal solutions (minimum value of the each objectives in case of minimization problem) from the respective objective functions. The steps of this method to solve the multi-objective model (83) are as follows:

Step-1: Solve the multi-objective problem as a single objective problem using, each time, only one objective $f_{p}~(p=1,2,...,k)$ ignoring all other objectives.

Step-2: From the results of step-1, determine the ideal objective vector, say $(f_{1}^{\min },f_{2}^{\min },...,f_{k}^{\min })$ and corresponding values of $(f_{1}^{\max },f_{2}^{\max },...,f_{k}^{\max })$.

Step-3: Formulate the following auxiliary problem

$$\begin{aligned} \left\{ \begin{array}{ll} Find &{} x = (x_{1}, x_{2}, ...., x_{n})^T \\ which~ minimizes &{} GC \\ subject~to &{} x\in X \\ where~X= &{} x: \left\{ \begin{array}{ll} g_{j}(x)\le 0, &{} j=1,2,...,m; \\ x_{i}\ge 0, &{} i=1,2,...,n. \end{array}\right. \end{array} \right. \end{aligned}$$

(90)

where

$$\begin{aligned} GC=Min\bigg \{\sum _{t=1}^k\bigg (\frac{f_{t}(x)-f_{t}^{\min }}{f_{t}^{\min }}\bigg )^q\bigg \}^{\frac{1}{q}}, \end{aligned}$$

(91)

$$\begin{aligned} or,~GC=Min\bigg \{\sum _{t=1}^k\bigg (\frac{f_{t}(x)-f_{t}^{\min }}{f_{t}^{\max }-f_{t}^{\min }}\bigg )^q\bigg \}^{\frac{1}{q}}, \end{aligned}$$

(92)

where $1\le q\le \infty$. An usual value of q is 2. This method is then called global criterion method in $L_{2}$ norm.

Weighted Sum Method: The weighted sum method scalarizes a set of objectives into a single objective by multiplying each objective with users supplied weights. The weights of an objective are usually chosen in proportion to the objectives relative importance in the problem. However setting up an appropriate weight vector depends on the scaling of each objective function. It is likely that different objectives take different orders of magnitude. When such objectives are weighted to form a composite objective function, it would be better to scale them appropriately so that each objective possesses more or less the same order of magnitude. This process is called normalization of objectives. After the objectives are normalized, a composite objective function F(x) can be formed by summing the weighted normalized objectives and the multi-objective problem given in Eq. (83) is then converted to a single-objective optimization problem as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} Find &{} x = (x_{1}, x_{2}, ...., x_{n})^T \\ which~ minimizes &{} \sum _{i=1}^k~w_{i}f_{i}(x),~w_{i}\in [0,1] \\ subject~to &{} x\in X \\ where~X= &{} x: \left\{ \begin{array}{ll} g_{j}(x)\le 0, &{} j=1,2,...,m; \\ x_{i}\ge 0, &{} i=1,2,...,n. \end{array}\right. \end{array}\right. \end{aligned}$$

(93)

Here, $w_{i}$ is the weight of the i-th objective function. Since the minimum of the above problem does not change if all the weights are multiplied by a constant, it is the usual practice to choose weights such that their sum is one, i.e., $\sum _{i=1}^k~w_{i}=1$. Miettinen [109] proved that the solution of the weighted sum problem (2.71) is Pareto optimal if the weighting coefficients are positive, that is $w_{i} > 0$, $i = 1, 2,...,k$.

3 Some Transportation Models with Fuzzy (Type-1) Parameters

If more than one objective is to be considered and optimized at the same time in an STP, then the problem is called multi-objective solid transportation problem (MOSTP). If more than one type of item/product is to be transported through the conveyances in an STP, then the problem is called multi-item solid transportation problem (MISTP). Also in a solid transportation system it may happen that several objectives are present and several types of items are to be transported, then we call this problem multi-objective multi-item solid transportation problem (MOMISTP). Besides source, destination and conveyance capacity constraints in an STP, there may exist several other types of constraints. For example, budget constraints may arise due to limited budget, space constraints may arise due to limited space in warehouses, stores, etc.

Due to insufficient information, lack of evidence, fluctuating financial market, the available data of a transportation system such as transportation costs, resources, demands, conveyance capacities are not always crisp or precise. For example, transportation cost depends upon fuel price, labor charges, tax charges, etc., each of which are fluctuate time to time. So for a future transportation planning it is not always easy to predict surely the possible unit transportation cost of a route in a certain time period. Similarly supply of a source can not be always exact, because it depends upon the availability of manpower, raw-materials, market competition, product demands, etc. Also it may not always possible to get relevant precise data/random data with a known distribution. So such a TP becomes more realistic if these parameters are assumed to be flexible/imprise i.e. fuzzy nature. For example if value of certain parameter of a decision making problem is given in an interval, then practically each of the point in the interval may not have the same importance or possibility. So it will be more realistic if those parameters are expressed by fuzzy numbers like triangular, trapezoidal, etc.

To solve constrained/unconstrained optimization problem with fuzzy parameters, several researchers developed many methodologies. Liu and Iwamura [92] presented chance-constrained programming with fuzzy parameters. Liu and Liu [94] presented expected value model for fuzzy programming. Yang and Liu [153] applied expected value model, chance-constrained programming model and dependent-chance programming to a fixed charge STP in fuzzy environment. Liang [82] presented a fuzzy goal programming approach for solving integrated production/transportation planning decision problems with fuzzy multiple goals. Mula et al. [116] applied possibilistic programming approach to a material requirement planing problem with fuzzy constraints and fuzzy coefficients.

In this chapter, we have investigated two solid transportation models namely, a multi-objective solid transportation problem with budget constraint and a multi-objective multi-item solid transportation problem both in fuzzy environment.

3.1 Related Results

Theorem 3.1

(Yang and Liu [153]). Suppose that $\tilde{\xi }$ is a fuzzy number with continuous membership function $\mu _{\tilde{\xi }}(x)$, and $r_{0}=\sup \{r:\mu _{\tilde{\xi }}(r)=1\}$, $g(x,\tilde{\xi })=h(x)-\tilde{\xi }$. Then we have $Cr\{g(x,\tilde{\xi })\ge 0\}\ge \alpha$ if and only if $h(x)\ge F_{\alpha }$, where

$$F_{\alpha }=\left\{ \begin{array}{ll} \inf \{F|F=\mu _{\tilde{\xi }}^{-1}(2\alpha )\}, &{} \hbox {if}\, \alpha \le 0.5; \\ \inf \{F|F=\mu _{\tilde{\xi }}^{-1}(2(1-\alpha )),F>r_{0}\}, &{} \hbox {if}\, \alpha >0.5. \end{array}\right. $$

Theorem 3.2

(Yang and Liu [153]). Suppose that $\tilde{\xi }$ is a fuzzy number with continuous membership function $\mu _{\tilde{\xi }}(x)$, and $r_{0}=\inf \{r:\mu _{\tilde{\xi }}(r)=1\}$, $g(x,\tilde{\xi })=h(x)-\tilde{\xi }$. Then we have $Cr\{g(x,\tilde{\xi })\le 0\}\ge \alpha$ if and only if $h(x)\le F_{\alpha }$, where

$$F_{\alpha }=\left\{ \begin{array}{ll} \sup \{F|F=\mu _{\tilde{\xi }}^{-1}(2\alpha )\}, &{} \hbox {if}\, \alpha \le 0.5; \\ \sup \{F|F=\mu _{\tilde{\xi }}^{-1}(2(1-\alpha )),F<r_{0}\}, &{} \hbox {if}\, \alpha >0.5. \end{array}\right. $$

Theorem 3.3

(Liu [90]). Assume that the function $g(x,\xi )$ can be written as ,

$$g(x,\xi )=h_{1}(x)\tilde{\xi }_{1}+h_{1}(x)\tilde{\xi }_{2}+...+h_{t}(x)\tilde{\xi }_{t}+h_{0}(x)$$

where $\tilde{\xi }_{k}$ are trapezoidal fuzzy variables $(r_{k1},r_{k2},r_{k3},r_{k4})$, $k=1,2,...,t$, respectively. We define two functions $h_{k}^+(x)=h_{k}(x)\vee 0$ and $h_{k}^-(x)=-(h_{k}(x)\wedge 0)$ for k=1,2,...,t. Then we have

(a) when $\alpha \le 1/2$, $Cr\{g(x,\xi )\le 0\}\ge \alpha$ if and only if

$$(1-2\alpha )\sum _{k=1}^t [r_{k1}h_{k}^+(x)-r_{k4}h_{k}^-(x)]+2\alpha \sum _{k=1}^t [r_{k2}h_{k}^+(x)-r_{k3}h_{k}^-(x)]+h_{0}(x)\le 0;$$

(b) when $\alpha >1/2$, $Cr\{g(x,\xi )\le 0\}\ge \alpha$ if and only if

$$(2-2\alpha )\sum _{k=1}^t [r_{k3}h_{k}^+(x)-r_{k2}h_{k}^-(x)]+(2\alpha -1) \sum _{k=1}^t [r_{k4}h_{k}^+(x)-r_{k1}h_{k}^-(x)]+h_{0}(x)\le 0;$$

From the above theorem following corollaries are obtained.

Corollary 1:

If $\tilde{\xi }=(r_{1},r_{2},r_{3},r_{4})$ is a trapezoidal fuzzy variable and h(x) is a function of x, then $Cr\{h(x)\le \tilde{\xi }\}\ge \alpha$ if and only if $h(x)\le F_{\xi }$, where

$$F_{\xi }=\left\{ \begin{array}{ll} (1-2\alpha ) r_{4}+2\alpha r_{3}, &{} \hbox {if}\, \alpha \le \frac{1}{2}; \\ 2(1-\alpha ) r_{2}+(2\alpha -1) r_{1}, &{} \hbox {if}\, \alpha > \frac{1}{2}. \end{array} \right. $$

Proof:

$Cr\{h(x)\le \tilde{\xi }\}\ge \alpha \Leftrightarrow Cr\{-\tilde{\xi }+h(x)\le 0\}\ge \alpha \Leftrightarrow Cr\{\tilde{\xi '}+h(x)\le 0\}\ge \alpha$,

where $\tilde{\xi '}=-\tilde{\xi }=(-r_{4},-r_{3},-r_{2},-r_{1}).$

Then from the above theorem it follows that this inequality holds if and only if

$$(a) (1-2\alpha )(-r_{4})+2\alpha (-r_{3})+h(x)\le 0,~if\,\alpha \le \frac{1}{2}$$

$$(b)~2(1-\alpha )(-r_{2})+(2\alpha -1) (-r_{1})+h(x)\le 0,~if\,\alpha >\frac{1}{2}.$$

and hence the corollary follows.

Corollary 2:

If $\tilde{\xi }=(r_{1},r_{2},r_{3},r_{4})$ is a trapezoidal fuzzy variable and h(x) is a function of x, then $Cr\{h(x)\ge \tilde{\xi }\}\ge \alpha$ if and only if $h(x)\ge F_{\xi }$, where

$$F_{\xi }=\left\{ \begin{array}{ll} (1-2\alpha ) r_{1}+2\alpha r_{2}, &{} \hbox {if}\, \alpha \le \frac{1}{2}; \\ 2(1-\alpha ) r_{3}+(2\alpha -1) r_{4}, &{} \hbox {if}\, \alpha > \frac{1}{2}. \end{array} \right. $$

Proof:

$Cr\{h(x)\ge \tilde{\xi }\}\ge \alpha \Leftrightarrow Cr\{\tilde{\xi }-h(x)\le 0\}\ge \alpha .$

Then from the above theorem it follows that this inequality holds if and only if

$$(a) (1-2\alpha )r_{1}+2\alpha r_{2}-h(x)\le 0,~if\,\alpha \le \frac{1}{2}$$

$$(b)~2(1-\alpha )r_{3}+(2\alpha -1) r_{4}-h(x)\le 0,~if\,\alpha >\frac{1}{2}.$$

and hence the corollary follows.

Corollary 3:

If $\tilde{\xi }=(r_{1},r_{2},r_{3},r_{4})$ and $\tilde{\eta }=(t_{1},t_{2},t_{3},t_{4})$ are trapezoidal fuzzy variables and $h(x)\ge 0~\forall x$, then $Cr\{h(x)\tilde{\xi }\le \tilde{\eta }\}\ge \alpha$ if and only if

$$(a)(1-2\alpha )h(x)r_{1}+2\alpha h(x)r_{2}\le (1-2\alpha )t_{4}+2\alpha t_{3},~when~ \alpha \le \frac{1}{2}$$

$$(b)~2(1-\alpha )h(x)r_{3}+(2\alpha -1) h(x)r_{4}\le 2(1-\alpha )t_{2}+(2\alpha -1)t_{1},~when~ \alpha >\frac{1}{2}.$$

Proof: $Cr\{h(x)\tilde{\xi }\le \tilde{\eta }\}\ge \alpha \Leftrightarrow Cr\{(h(x)\tilde{\xi }-\tilde{\eta })\le 0\}\ge \alpha \Leftrightarrow Cr\{(h(x)\tilde{\xi }+\tilde{\eta '})\le 0\}\ge \alpha$, where $\tilde{\eta '}=-\tilde{\eta }=(-t_{4},-t_{3},-t_{2},-t_{1})$.

Then from the above theorem it follows that this inequality holds if and only if

$$(a)(1-2\alpha )(h(x)r_{1}-t_{4})+2\alpha (h(x)r_{2}-t_{3})\le 0,~when\,\alpha \le \frac{1}{2}$$

$$(b)~2(1-\alpha )(h(x)r_{3}-t_{2})+(2\alpha -1) (h(x)r_{4}-t_{1})+h(x)\le 0,~if\,\alpha >\frac{1}{2}.$$

and hence the corollary follows.

This is obvious that these three corollaries help us to determine crisp equivalences of various inequalities with fuzzy parameters.

3.2 A Defuzzification Method

Kikuchi [66] proposed a defuzzification method to find the most appropriate set of crisp numbers for a set of fuzzy numbers which satisfy a set of rigid relationships among them. The main idea of the method is to find the best set of crisp values satisfying the relationships those maximizes the minimum degree of membership that one of those values takes. Fuzzy linear programming is applied in this method. The method is summarized as follows.

Let $\tilde{X_{1}}$, $\tilde{X_{2}}$,...,$\tilde{X_{n}}$ are fuzzy numbers with membership functions $\mu _{\tilde{X_{1}}}$, $\mu _{\tilde{X_{2}}}$,...,$\mu _{\tilde{X_{n}}}$ respectively. Suppose we have to find corresponding crisp values $x_{1}$, $x_{2}$,...,$x_{n}$ those satisfy some relationships $R_{j}(x),~j\in \mathbb {N}$ among them. Then the following linear programming based on fuzzy linear programming is formulated.

$$Max~ \lambda $$

$$s.t.~~\mu _{\tilde{X_{i}}}(x_{i})\ge \lambda ,~i=1,2,...,n$$

and the relationships $R_{j}(x),~j\in \mathbb {N}$

$$x_{i},~\lambda \ge 0,~i=1,2,...,n.$$

where $\lambda$ is the minimum degree of membership that one of the values $x_{1}$, $x_{2}$,...,$x_{n}$ takes, i.e. $\lambda ^*=Max \lambda =Max~Min[\mu _{\tilde{X_{1}}}(x_{1}),\mu _{\tilde{X_{2}}}(x_{2}),...,\mu _{\tilde{X_{n}}}(x_{n})]$.

Kikuchi [66] applied this method to a traffic volume consistency problem taking all observed values as triangular fuzzy numbers. Dey and Yadav [36] modified this method with trapezoidal fuzzy numbers.

3.3 Model 3.1: Multi-objective Solid Transportation Problem Having Budget Constraint with Fuzzy Parameters

Here a multi-objective solid transportation problem (MOSTP) is formulated with unit transportation penalties/costs, supplies, demands and conveyance capacities as fuzzy numbers (variables). Here the several objectives may be minimization of total transportation costs, minimization of total deterioration of goods, etc. Also, apart from source, demand and capacity constraints, an extra constraint on the total transportation budget at each destination is imposed. Obviously these budget constraints are performed for the objective function which represents minimization of the total transportation cost. The following notations are used to formulate the model.

Notations:

• (i) $\tilde{c_{ijk}^p}$: Fuzzy unit transportation penalties from i-th source to j-th destination via k-th conveyance for the p-th objective.

• (ii) $x_{ijk}^p$: The decision variable which represents amount of product to be transported from i-th origin to j-th destination via k-th conveyance for the p-th objective.

• (iii) $\tilde{a_{i}}$: The fuzzy amount of the product available at the i-th origin.

• (iv) $\tilde{b_{j}}$: The fuzzy demand of the product of j-th destination.

• (v) $\tilde{e_{k}}$: Fuzzy transportation capacity of conveyance k.

• (vi) $Z_{p}$: The p-th objective.

• (vii) $\tilde{B_{j}^l}$: Available fuzzy budget amount for j-th destination for objective $Z_{l}$.

Mathematical Model: Mathematically the MOSTP with budget constraints having P objectives, m origins, n destinations and K conveyances is formulated as follows.

$$\begin{aligned} Min~Z_{p}=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~~\tilde{c_{ijk}^p}~x_{ijk}~~ ,p=1,2,...,P \end{aligned}$$

(94)

$$\begin{aligned} s.t.~ \sum _{j=1}^n\sum _{k=1}^K x_{ijk}~\le \tilde{a_{i}},~~i=1,2,...,m, \end{aligned}$$

(95)

$$\begin{aligned} \sum _{i=1}^m\sum _{k=1}^K x_{ijk}~~\ge \tilde{b_{j}},~~j=1,2,...,n, \end{aligned}$$

(96)

$$\begin{aligned} \sum _{i=1}^m\sum _{j=1}^n~x_{ijk}\le \tilde{e_{k}},~~k=1,2,...,K, \end{aligned}$$

(97)

$$\begin{aligned} \sum _{i=1}^m\sum _{k=1}^K \tilde{c_{ijk}^l}~x_{ijk}~~\le \tilde{B_{j}^l},~~j=1,2,...,n~,~l\in \{1,...,P\}, \end{aligned}$$

(98)

$$x_{ijk}\ge 0, \forall ~ i,j,k.$$

Here for $p=l$ (say), $l\in \{1,2,...,P\}$, $\tilde{c_{ijk}^l}$ represent unit transportation cost so that available fuzzy budget amount for j-th destination, i.e. $\tilde{B_{j}^l}$ is imposed for objective $Z_{l}$.

Solution Methodology: Chance-Constrained Programming: We apply the chance constrained programming (CCP) technique using credibility measure to the above model and then it is formulated as

$$\begin{aligned} Min [\bar{Z_{1}},\bar{Z_{2}},...,\bar{Z_{P}}] \end{aligned}$$

(99)

$$\begin{aligned} s.t.~Cr\{\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~~\tilde{c_{ijk}^p}~x_{ijk}\le \bar{Z_{p}}\}\ge \eta _{p},~p=1,2,...,P, \end{aligned}$$

(100)

$$\begin{aligned} Cr\{\sum _{j=1}^n\sum _{k=1}^K x_{ijk}~\le \tilde{a_{i}}\}\ge \alpha _{i},~~i=1,2,...,m, \end{aligned}$$

(101)

$$\begin{aligned} Cr\{\sum _{i=1}^m\sum _{k=1}^K x_{ijk}~~\ge \tilde{b_{j}}\}\ge \beta _{j},~~j=1,2,...,n, \end{aligned}$$

(102)

$$\begin{aligned} Cr\{\sum _{i=1}^m\sum _{j=1}^n~x_{ijk}\le \tilde{e_{k}}\}\ge \gamma _{k},~~k=1,2,...,K, \end{aligned}$$

(103)

$$\begin{aligned} Cr\{\sum _{i=1}^m\sum _{k=1}^K \tilde{c_{ijk}^l}~x_{ijk}~~\le \tilde{B_{j}^l}\}\ge \delta _{j}^l,~~j=1,2,...,n~,~l\in \{1,...,P\}, \end{aligned}$$

(104)

$$x_{ijk}\ge 0, \forall ~ i,j,k,$$

where $\eta _{p}$ indicates that we are going to optimize the $\eta _{p}$-critical value of the objective $Z_{p}(p=1,2,...,P)$, and $\alpha _{i}$, $\beta _{j}$, $\gamma _{k}$ and $\delta _{j}^l$ are predetermined credibility levels of satisfaction of the above constraints (101), (102), (103) and (104) respectively. In other words, the constraint (101) indicates that total amount transported from source i must be less than or equal to its supply capacity $\tilde{a_{i}}$ at the credibility level at least $\alpha _{i}$; the constraint (102) indicates that total amount transported to destination j must satisfy its requirement $\tilde{b_{j}}$ at the credibility at least $\beta _{j}$, the constraint (103) indicates that total amount transported through conveyance k must not be more than its capacity $\tilde{e_{k}}$ at the credibility at least $\gamma _{k}$ and the constraints (104) indicates that for the specific objective $Z_{l}$, total transportation costs for j-th destination must not exceed the available budget amount $\tilde{B_{j}^l}$ at the credibility at least $\delta _{j}^l$.

Crisp Equivalences: Let $\tilde{c_{ijk}^p}=(c_{ijk}^{p1},c_{ijk}^{p2},c_{ijk}^{p3},c_{ijk}^{p4})$,  $\tilde{a_{i}}=(a_{i}^1,a_{i}^2,a_{i}^3,a_{i}^4)$, $\tilde{b_{j}}=(b_{j}^1,b_{j}^2,b_{j}^3,b_{j}^4)$, $\tilde{e_{k}}=(e_{k}^1,e_{k}^2,e_{k}^3,e_{k}^4)$, $\tilde{B_{j}^l}=(B_{j}^{l1},B_{j}^{l2},B_{j}^{l3},B_{j}^{l4})$ are trapezoidal fuzzy numbers for all p, i, j and k.

Now since $\tilde{c_{ijk}^p}$ are trapezoidal fuzzy numbers and $x_{ijk}\ge 0$ for all i, j, k,  so $Z_{p}(x)=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~~\tilde{c_{ijk}^p}~x_{ijk}$ are also trapezoidal fuzzy numbers for any feasible solution x and given by $Z_{p}(x)=(r_{1}^p(x),r_{2}^p(x),r_{3}^p(x),r_{4}^p(x))$, where

$$\begin{aligned} r_{1}^p(x)=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~~c_{ijk}^{p1}~x_{ijk}~ ,~r_{2}^p(x)=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~~c_{ijk}^{p2}~x_{ijk}, \end{aligned}$$

(105)

$$\begin{aligned} r_{3}^p(x)=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~~c_{ijk}^{p3}~x_{ijk}~ ,~r_{4}^p(x)=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~~c_{ijk}^{p4}~x_{ijk}, \end{aligned}$$

(106)

$$p=1,2,...,P. $$

Then the objective $\bar{Z_{p}}$ in (99), i.e. $Min ~\bar{Z_{P}},$ s.t. $Cr\{Z_{p}(x)\le \bar{Z_{p}}\}\ge \eta _{p}$ is equivalently computed as $\bar{Z_{p}}=\inf \{r:Cr\{Z_{P}(x)\le r\}\ge \eta _{p}\}$ which is nothing but $\eta _{p}$ - pessimistic value to $Z_{p}$ $(i.e.~Z_{p_{inf}}(\eta _{p}))$ and so is equal to $Z'_{p}(x)$, where

$$Z'_{p}(x)=\left\{ \begin{array}{ll} (1-2\eta _{p})r_{1}^p(x)+2\eta _{p}~r_{2}^p(x), &{} \hbox {if}\,\alpha \le 0.5; \\ 2(1-\eta _{p})r_{3}^p(x)+(2\eta _{p}-1)r_{4}^p(x), &{} \hbox {if}\,\alpha >0.5. \end{array}\right. $$

Now from corollaries 1 and 2 of the Theorem 3.3, the constraint (101) and (102) and from corollary 1, the constraint (103) can be written respectively in equivalent crisp forms as

$$\begin{aligned} \sum _{j=1}^n\sum _{k=1}^K x_{ijk}~\le F_{\alpha _{i}},~i=1,2,...,m \end{aligned}$$

(107)

$$\begin{aligned} \sum _{i=1}^m\sum _{k=1}^K x_{ijk}~~\ge F_{\beta _{j}},~j=1,2,...,n \end{aligned}$$

(108)

$$\begin{aligned} \sum _{i=1}^m\sum _{j=1}^n~x_{ijk}\le F_{\gamma _{k}},~k=1,2,...,K \end{aligned}$$

(109)

where, $F_{\alpha _{i}}= \left\{ \begin{array}{ll} (1-2\alpha _{i})a_{i}^4+2\alpha _{i} a_{i}^3, &{} \hbox {if}\, \alpha _{i}\le 0.5; \\ 2(1-\alpha _{i})a_{i}^2+(2\alpha _{i}-1)a_{i}^1, &{} \hbox {if}\, \alpha _{i}>0.5. \end{array}\right.$

$F_{\beta _{j}}=\left\{ \begin{array}{ll} (1-2\beta _{j}) b_{j}^1+2\beta _{j} b_{j}^2, &{} \hbox {if}\, \beta _{j}\le 0.5; \\ 2(1-\beta _{j}) b_{j}^3+(2\beta _{j}-1)b_{j}^4, &{} \hbox {if}\, \beta _{j}>0.5. \end{array}\right.$

$F_{\gamma _{k}}=\left\{ \begin{array}{ll} (1-2\gamma _{k})e_{k}^4+2\gamma _{k} e_{k}^3, &{} \hbox {if}\, \gamma _{k}\le 0.5; \\ 2(1-\gamma _{k})e_{k}^2+(2\gamma _{k}-1)e_{k}^1, &{} \hbox {if}\, \gamma _{k}>0.5. \end{array}\right.$

Now the budget constraint (104) is in the form

$$Cr\{\sum _{i=1}^m\sum _{k=1}^K x_{ijk}~(c_{ijk}^{l1},c_{ijk}^{l2},c_{ijk}^{l3},c_{ijk}^{l4})+(-1)(B_{j}^{l1},B_{j}^{l2},B_{j}^{l3},B_{j}^{l4})\le 0\}\ge \delta _{j}^l$$

Since $x_{ijk}\ge 0$ for all i, j, k,  from Corollary 2 of the Theorem 3.3, it is obvious that this constraint will be active if and only if $g_{j}^l\le 0$, where

$$g_{j}^l={\left\{ \begin{array}{ll} \begin{aligned} (1-2\delta _{j}^l)(\sum _{i=1}^m\sum _{k=1}^K c_{ijk}^{l1}~x_{ijk}-B_{j}^{l4})+\\ +2\delta _{j}^l(\sum _{i=1}^m\sum _{k=1}^K c_{ijk}^{l2}~x_{ijk}-B_{j}^{l3}), \end{aligned} &{} \text{ if } \delta _{j}\le 0.5; \\ \begin{aligned} 2(1-\delta _{j}^l)(\sum _{i=1}^m\sum _{k=1}^Kc_{ijk}^{l3}~x_{ijk}-B_{j}^{l2})+\\ +(2\delta _{j}^l-1)(\sum _{i=1}^m\sum _{k=1}^Kc_{ijk}^{l4}~x_{ijk}-B_{j}^{l1}), \end{aligned} &{}\text{ if } \delta _{j}>0.5. \end{array}\right. }$$

So finally an equivalent crisp form of the above CCP model (99)–(104) formulated for the model (94)–(98) can be written as

$$Min[Z'_{1}(x),Z'_{2}(x),...,Z'_{P}(x)]$$

$$\begin{aligned} s.t.~~~ g_{j}^l\le 0,~j=1,2,...,n~, \end{aligned}$$

(110)

with the constraints (107), (108), (109),

$$x_{ijk}\ge 0 for~all~ i,j,k.$$

Now the problem (110) is a multi-objective problem and so can be solved by fuzzy programming technique, Global criteria method (cf. Sect. 2.9), etc.

Numerical Experiment: To illustrate the Model 3.1 ((94)–(98)), we consider an example where from the past record of a transport company, the possible values of the parameters such as the unit transportation costs, the supplies, the demands, the available conveyance capacities can not be precisely determined. For instance, unit transportation cost for a route is “about 6”, the supply of a source is “around 28–30”, etc. These linguistic data can be transferred into triangular or trapezoidal fuzzy numbers. For example if it is seen from the past record that most possible value of unit transportation cost of a route is 13 and it vary from 12 to 14 with less possibility, then it is “about 13” and represented by the fuzzy number (12,13,14)$\sim$(12,13,13,14). Similarly the most possible value of supply of a source ranges between 28 to 30 and is not less than 27 and greater than 32, i.e. it is “around 28-30” and represented by TrFN (27,28,30,32). For the current model, two sources, two destinations, two conveyances and two objectives are considered, i.e. $i,j,k,p=1,2$. The fuzzy penalties associated with the two objectives $Z_{1}$ and $Z_{2}$ are given in Tables 2 and 3 respectively. The values of all the parameters associated with two resources, two destinations, two conveyances and two objectives are given below. Also budget constraint is imposed on the objective $Z_{1}$ (i.e. $l=1$). $\tilde{a_{1}}=(37,40,46,48)$, $\tilde{a_{2}}=(28,32,35,37)$, $\tilde{b_{1}}=(28,29,30,31)$, $\tilde{b_{2}}=(31,33,34,35)$, $\tilde{e_{1}}=(27,29,32,34)$, $\tilde{e_{2}}=(39,41,44,47)$, $\tilde{B_{1}^1}=(480,485,491,497)$, and $\tilde{B_{2}^1}=(501,505,510,515).$

Table 2. Penalties (costs) $\tilde{c_{ijk}^1}$

Table 3. Penalties $\tilde{c_{ijk}^2}$

Now applying chance-constrained programming technique to solve the problem, we reconstruct the problem as model (99)–(104) and use corresponding crisp equivalent form (110). For this purpose, let us consider the credibility level $\alpha _{i}=0.9$ for the source constraints, $\beta _{j}=0.9$ for the demand constraints, $\gamma _{k}=0.95$ for the capacity constraints, $\delta _{j}^l=0.9$ for the budget constraints, where $i,j,k=1,2$, $l=1$ and let $\eta _{p}=0.9$ $(p=1,2)$, which implies that we want to minimize 0.9-critical value of the objectives. Then using (110), the proposed problem becomes

$$Min[Z'_{p}(x)]~~p=1,2$$

$$Z'_{p}(x)=0.2~r_{3}^p(x)+0.8~r_{4}^p(x)~~,p=1,2$$

$$ \sum _{j=1}^2\sum _{k=1}^2 x_{ijk}~\le F_{\alpha _{i}},~i=1,2$$

$$\begin{aligned} \sum _{i=1}^2\sum _{k=1}^2 x_{ijk}~~\ge F_{\beta _{j}},~j=1,2 \end{aligned}$$

(111)

$$\sum _{i=1}^2\sum _{j=1}^2~x_{ijk}\le F_{\gamma _{k}},~k=1,2$$

$$ 0.2(\sum _{i=1}^2\sum _{k=1}^2c_{ijk}^{13}~x_{ijk})+0.8(\sum _{i=1}^2\sum _{k=1}^2c_{ijk}^{14}~x_{ijk})\le (0.2 B_{j}^{12}+0.8 B_{j}^{11}),~j=1,2$$

where expression of $r_{3}^p(x)$ and $r_{4}^p(x)$ are same as in (106) for $i,j,k=1,2.$

With the given data, we have $F_{\alpha _{1}}=37.6$, $F_{\alpha _{2}}=28.8$, $F_{\beta _{1}}=30.8$, $F_{\beta _{2}}=34.6$, $F_{\gamma _{1}}=27.4$, $F_{\gamma _{1}}=39.4$

Solving this problem by fuzzy programming technique (with linear membership function) (cf. Sect. 2.9), the obtained optimum compromise solution is presented in Table 4. The solution is obtained by using the standard optimization solver - LINGO.

Table 4. Optimum results for Model (94)–(98)

$B_{1}^1$ and $B_{2}^1$ represent the budget values for j=1,2 respectively for objective $Z_{1}$ and $\lambda$ represents maximum overall satisfactory level of compromise.

3.4 Model 3.2: Multi-objective Multi-item Solid Transportation Problem with Fuzzy Parameters

A multi-objective multi-item solid transportation problem (MOMISTP) with fuzzy parameters is formulated in which several objectives (e.g., minimization of transportation costs, minimization of total deterioration of goods, etc.) are involved and also several types of items/goods are to be transported from sources to destinations through the conveyances. The following notations are used to formulate the model.

Notations:

• (i) $\tilde{c_{ijk}^{tp}}$: for the objective $Z_{t}$, fuzzy unit transportation penalty from i-th origin to j-th destination by k-th conveyance for p-th item.

• (ii) $x_{ijk}^p$: the decision variable that represents the amount of p-th item to be transported from i-th source to j-th destination by k-th conveyance.

• (iii) $\tilde{a_{i}^p}$: amount of p-th item represented by fuzzy number available at i-th origin

• (iv) $\tilde{b_{j}^p}$: fuzzy demand of j-th destination for p-th item

• (v) $\tilde{e_{k}}$: total fuzzy capacity of k-th conveyance.

Mathematical Model: An MOMISTP with R objectives, l different items, m origins, n destinations and K types of conveyances is formulated as follows:

$$ Min~Z_{t}=\sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~~\tilde{c_{ijk}^{tp}}~x_{ijk}^p~ ,t=1,2,...,R $$

$$\begin{aligned} s.t.~ \sum _{j=1}^n\sum _{k=1}^K x_{ijk}^p~\le & {} \tilde{a_{i}^p},~~i=1,2,...,m; p=1,2,...l,\nonumber \\ \sum _{i=1}^m\sum _{k=1}^K x_{ijk}^p~~\ge & {} \tilde{b_{j}^p},~~j=1,2,...,n; p=1,2,...,l, \\ \sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n~x_{ijk}^p\le & {} \tilde{e_{k}},~~k=1,2,...,K,\nonumber \\ x_{ijk}^p\ge & {} 0,~ \forall ~ i,j,k,p.\nonumber \end{aligned}$$

(112)

Defuzzification Process: Consider $\tilde{a_{i}^p}$, $\tilde{b_{j}^p}$ and $\tilde{e_{k}}$ ($\forall ~i,j,k,p$) as trapezoidal fuzzy numbers defined by $\tilde{a_{i}^p}=(a_{i}^{p1},a_{i}^{p2},a_{i}^{p3},a_{i}^{p4})$, $\tilde{b_{j}^p}=(b_{j}^{p1},b_{j}^{p2},b_{j}^{p3},b_{j}^{p4})$ and $\tilde{e_{k}}=(e_{k}^1,e_{k}^2,e_{k}^3,e_{k}^4)$ and their membership functions are $\mu _{\tilde{a_{i}^p}}$, $\mu _{\tilde{b_{j}^p}}$ and $\mu _{\tilde{e_{k}}}$ respectively. Now to solve the above problem, we first find corresponding defuzzified (crisp) values, say, $a_{ic}^p$, $b_{jc}^p$ and $e_{kc}$ ($\forall ~i,j,k,p$) so that for each item, total available resources greater than or equal to the total demands and also total conveyance capacities greater than or equal to the total demands for all items, i.e.

$$\sum _{i=1}^m~a_{ic}^p\ge \sum _{j=1}^n~b_{jc}^p~,~p=1,2,...,l ~ and ~\sum _{k=1}^K~e_{kc}\ge \sum _{p=1}^l\sum _{j=1}^n~b_{jc}^p.$$

Because defuzzified values of availabilities, demands and conveyance capacities must have to be satisfy these conditions to have a feasible solution of the above problem. For this purpose we apply the defuzzification method (cf Sect. 3.2) based on fuzzy linear programming.

The method is to introduce an auxiliary variable $\lambda$ and formulate the following linear programming.

$$Max~~\lambda $$

$$s.t.~~\mu _{\tilde{a_{i}^p}}(a_{ic}^p)\ge \lambda ,~\mu _{\tilde{b_{j}^p}}(b_{jc}^p)\ge \lambda ,~\mu _{\tilde{e_{k}}}(e_{kc})\ge \lambda ,$$

$$\sum _{i=1}^m~a_{ic}^p\ge \sum _{j=1}^n~b_{jc}^p,~\sum _{k=1}^K~e_{kc}\ge \sum _{p=1}^l\sum _{j=1}^n~b_{jc}^p,$$

$$\forall ~i,~j,~k,~p.$$

where $\lambda$ is the minimum degree of membership that one of the values of the variables $a_{ic}^p$, $b_{jc}^p$, $e_{kc}$ takes,

i.e. Max $\lambda$ = $\lambda ^*$ = Max Min $[\mu _{\tilde{a_{i}^p}}(a_{ic}^p),~\mu _{\tilde{b_{j}^p}}(b_{jc}^p),~\mu _{\tilde{e_{k}}}(e_{kc})]$, where

$$\mu _{\tilde{a_{i}^p}}(a_{ic}^p)=\left\{ \begin{array}{ll} \frac{a_{ic}^p-a_{i}^{p1}}{a_{i}^{p2}-a_{i}^{p1}}, &{} \hbox {if}\,a_{i}^{p1}\le a_{ic}^p\le a_{i}^{p2}; \\ 1, &{} \hbox {if}\,a_{i}^{p2}\le a_{ic}^p\le a_{ic}^{p3}; \\ \frac{a_{i}^{p4}-a_{ic}^p}{a_{i}^{p4}-a_{i}^{p3}}, &{} \hbox {if}\,a_{i}^{p3}\le a_{ic}^p\le a_{i}^{p4}. \end{array}\right. $$

and similarly for $\mu _{\tilde{b_{j}^p}}(b_{jc}^p)$ and $\mu _{\tilde{e_{k}}}(e_{kc})$.

Now if we denote left and right sides of the membership function $\mu _{\tilde{a_{i}^p}}(a_{ic}^p)$ by $\mu _{\tilde{a_{i}^p}}^l(a_{ic}^p)$ and $\mu _{\tilde{a_{i}^p}}^r(a_{ic}^p)$ respectively and so on for $\mu _{\tilde{b_{j}^p}}(b_{jc}^p)$ and $\mu _{\tilde{e_{k}}}(e_{kc})$, then the above programming becomes

$$Max~~\lambda $$

$$s.t.~~\mu _{\tilde{a_{i}^p}}^l(a_{ic}^p)\ge \lambda ,~\mu _{\tilde{a_{i}^p}}^r(a_{ic}^p)\ge \lambda $$

$$\mu _{\tilde{b_{j}^p}}^l(b_{jc}^p)\ge \lambda ,~ \mu _{\tilde{b_{j}^p}}^r(b_{jc}^p)\ge \lambda $$

$$\begin{aligned} \mu _{\tilde{e_{k}}}^l(e_{kc})\ge \lambda ,~\mu _{\tilde{e_{k}}}^r(e_{kc})\ge \lambda \end{aligned}$$

(113)

$$\sum _{i=1}^m~a_{ic}^p\ge \sum _{j=1}^n~b_{jc}^p,~\sum _{k=1}^K~e_{kc}\ge \sum _{p=1}^l\sum _{j=1}^n~b_{jc}^p,$$

$\forall ~i,~j,~k,~p.$

Solution Methodology: Consider that $\tilde{c_{ijk}^{tp}}$ are all independent trapezoidal fuzzy numbers represented as $(c_{ijk}^{tp1},c_{ijk}^{tp2},c_{ijk}^{tp3},c_{ijk}^{tp4})$. Now after obtaining the defuzzified values $a_{ic}^p$, $b_{jc}^p$ and $e_{kc}$ ($\forall ~i,j,k,p$) by above procedure (i.e. using (113)), the problem (112) becomes,

$$\begin{aligned} Min~Z_{t}=\sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~~\tilde{c_{ijk}^{tp}}~x_{ijk}^p~~ ,t=1,2,...,R \end{aligned}$$

(114)

Fig. 10.

Minimization of TrFN $\tilde{Z}$

$$\begin{aligned} s.t.~\sum _{j=1}^n\sum _{k=1}^K x_{ijk}^p~\le a_{ic}^p,~~i=1,2,...,m; p=1,2,...l \end{aligned}$$

(115)

$$\begin{aligned} \sum _{i=1}^m\sum _{k=1}^K x_{ijk}^p~~\ge b_{jc}^p,~~j=1,2,...,n; p=1,2,...,l \end{aligned}$$

(116)

$$\begin{aligned} \sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n~x_{ijk}^p\le e_{kc},~~k=1,2,...,K \end{aligned}$$

(117)

$$x_{ijk}^p\ge 0,~ \forall ~ i,j,k,p.$$

Now, we use following methods to solve this problem.

Method-1: Using the Concept-Minimum of Fuzzy Number: The objective functions in (114) are $Z_{t}=\sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~~\tilde{c_{ijk}^{tp}}~x_{ijk}^p~~ ,t=1,2,...,R$. Since $\tilde{c_{ijk}^{tp}}$ are trapezoidal fuzzy numbers and $x_{ijk}^p\ge 0$ for all i, j, k and p, so each $Z_{t}$ for $t=1,2,...,R$ is also a trapezoidal fuzzy number for any feasible solution and is given by $Z_{t}$=$(Z_{t}^1,Z_{t}^2,Z_{t}^3,Z_{t}^4)$ where

$Z_{t}^r=\sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~~\tilde{c_{ijk}^{tpr}}~x_{ijk}^p$ for $r=1,2,3,4$.

As it is not possible to minimize directly a fuzzy number $\tilde{Z}$, here we use a method proposed by Buckly et al. [14]. They applied this method to a fuzzy inventory control problem. The method is to convert min $\tilde{Z}$ into a multi-objective problem

$$Min \tilde{Z}= (Max~A_{L}(\tilde{Z}), Min~C(\tilde{Z}), Min~A_{R}(\tilde{Z})),$$

where $C(\tilde{Z})$ is the center of the core of the fuzzy number and $A_{L}(\tilde{Z})$, $A_{R}(\tilde{Z})$ are the area under graph of the membership function of $\tilde{Z}$ to the left and right of C(Z) (minimization of a TrFN $\tilde{Z}$ is shown in Fig. 10). If the support of $\tilde{Z}$ be [$u_{1},u_{3}$] and the center of the core of $\tilde{Z}$ be at $u_{2}$, then

$$A_{L}(\tilde{Z})=\int _{u_{1}}^{u_{2}}\mu _{\tilde{Z}}(x)~dx~and~A_{R}(\tilde{Z})=\int _{u_{2}}^{u_{3}}\mu _{\tilde{Z}}(x)~dx~.$$

Then this multi-objective problem is converted to a single objective problem as follows

$$\begin{aligned} Min \tilde{Z}= Min \{\lambda _{1}[M-A_{L}(\tilde{Z})]+\lambda _{2}C(\tilde{Z})+\lambda _{3}A_{R}(\tilde{Z})\}, \end{aligned}$$

(118)

where $\lambda _{l}> 0,$ for $l=1,2,3$, $\lambda _{1}+\lambda _{2}+\lambda _{3}=1$ and M is a large positive number so that Max $A_{L}(\tilde{Z})$ is equivalent to Min $[M-A_{L}(\tilde{Z})]$. The values of $\lambda _{l}$ are taken by decision maker or a sensitivity analysis can be done taking different values of $\lambda _{l}$ to choose appropriate values of $\lambda _{l}$.

Now for a trapezoidal fuzzy number $\tilde{Z}=(z^1,z^2,z^3,z^4)$, the membership function is

$$\mu _{\tilde{Z}}(x)=\left\{ \begin{array}{ll} \frac{x-z^1}{z^2-z^1}, &{} \hbox {if}\, z^1\le x\le z^2; \\ 1, &{} \hbox {if}\, z^2\le x\le z^3; \\ \frac{z^4-x}{z^4-z^3}, &{} \hbox {if}\, z^3\le x\le z^4; \\ 0, &{} \hbox {otherwise.} \end{array} \right. $$

So the core of $\tilde{Z}$ is $[z^2,z^3]$ and $C(\tilde{Z})=\frac{z^2+z^3}{2}$.

$$A_{L}(\tilde{Z})=\int _{z^1}^{\frac{z^2+z^3}{2}}\mu _{\tilde{Z}}(x)~dx=\int _{z^1}^{z^2}\frac{x-z^1}{z^2-z^1}~dx~+~\int _{z^2}^{\frac{z^2+z^3}{2}}1~dx=\frac{1}{2} (z^3-z^1),$$

$$A_{R}(\tilde{Z})=\int _{\frac{z^2+z^3}{2}}^{z^3}1~dx~+~\int _{z^3}^{z^4}\frac{z^4-x}{z^4-z^3}~dx=\frac{1}{2} (z^4-z^2).$$

Applying this method to the objective function (114) of the problem (114)–(117), the corresponding crisp form of the problem becomes

$$ Min \bar{Z_{t}}= \lambda _{1}[M-A_{L}(Z_{t})]+\lambda _{2}C(Z_{t})+\lambda _{3}A_{R}(Z_{t})~,t=1,2,...R,$$

$$\begin{aligned} A_{L}(Z_{t})=\frac{Z_{t}^3-Z_{t}^1}{2},~C(Z_{t})=\frac{Z_{t}^2+Z_{t}^3}{2},~A_{R}(Z_{t})=\frac{Z_{t}^4-Z_{t}^2}{2}, \end{aligned}$$

(119)

subject to the constraints (115)–(117),

$$x_{ijk}^p\ge 0,~ \forall ~ i,j,k,p,~~\lambda _{1}+\lambda _{2}+\lambda _{3}=1,~\lambda _{l}> 0,~l=1,2,3.$$

Though the choice of values of $\lambda _{l}$ depends upon decision maker(s), it should be kept in mind that, as the above problem is a minimization problem, our aim should be more in maximizing $A_{L}(Z_{t})$ (i.e. possibility of getting less values than $C(Z_{t})$) and minimizing $C(Z_{t})$ rather than in minimizing $A_{R}(Z_{t})$ (i.e. possibility of getting more values than $C(Z_{t})$).

Method-2: Using Expected Value: Here we minimize the expected value of the objective functions and then the problem (114)–(117) becomes

$$ Min~E[Z_{t}]=E[\sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~~\tilde{c_{ijk}^{tp}}~x_{ijk}^p]~~ ,t=1,2,...,R $$

$$\begin{aligned} s.t.~~ the~ constraints~(115)-(117), \end{aligned}$$

(120)

$$x_{ijk}^p\ge 0,~ \forall ~ i,j,k,p$$

which is equivalently written as

$$Min~E[Z_{t}]=\bar{Z_{t}}=\sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~~E[\tilde{c_{ijk}^{tp}}]~x_{ijk}^p~~ ,t=1,2,...,R $$

$$\begin{aligned} s.t.~~ the~ constraints~(115)-(117), \end{aligned}$$

(121)

$$x_{ijk}^p\ge 0,~ \forall ~ i,j,k,p.$$

Now the deterministic models (119) and (121) are multi-objective problems and so can be solved by fuzzy programming technique, Global criteria method (cf. Sect. 2.9), etc.

Note: Deterministic forms obtained using expected value model (EVM), chance-constrained programming model for an optimization problem with fuzzy parameters having interrelated constraints like in STP may not always possesses any feasible solution. For example if we construct the EVM for the problem (112) by using expected value to both the objective functions and the constraints then it becomes:

$$Min~E[Z_{t}]=E\big [\sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~~\tilde{c_{ijk}^{tp}}~x_{ijk}^p\big ]~~,t=1,2,...,R $$

$$\begin{aligned} s.t.~ E\big [\sum _{j=1}^n\sum _{k=1}^K x_{ijk}^p-\tilde{a_{i}^p}\big ]~\le & {} 0,~~i=1,2,...,m; p=1,2,...l,\nonumber \\ E\big [\sum _{i=1}^m\sum _{k=1}^K x_{ijk}^p-\tilde{b_{j}^p}\big ]~\ge & {} 0,~~j=1,2,...,n; p=1,2,...,l, \\ E\big [\sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n~x_{ijk}^p-\tilde{e_{k}}\big ]~\le & {} 0,~~k=1,2,...,K,\nonumber \end{aligned}$$

(122)

$$x_{ijk}^p\ge 0,~ \forall ~ i,j,k,p.$$

Then by the linearity property of expected value operator, the crisp equivalence form of this model becomes

$$ Min~E[Z_{t}]=\bar{Z_{t}}=\sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~~E[\tilde{c_{ijk}^{tp}}]~x_{ijk}^p~~ ,t=1,2,...,R $$

$$\begin{aligned} \nonumber s.t.~ \sum _{j=1}^n\sum _{k=1}^K x_{ijk}^p~\le & {} E[\tilde{a_{i}^p}],~~i=1,2,...,m; p=1,2,...l,\\ \sum _{i=1}^m\sum _{k=1}^K x_{ijk}^p~~\ge & {} E[\tilde{b_{j}^p}],~~j=1,2,...,n; p=1,2,...,l, \\ \nonumber \sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n~x_{ijk}^p\le & {} E[\tilde{e_{k}}],~~k=1,2,...,K, \end{aligned}$$

(123)

$$x_{ijk}^p\ge 0,~ \forall ~ i,j,k,p.$$

But in the above crisp equivalence form, the deterministic values of supplies, demands and conveyance capacities, i.e. $E[\tilde{a_{i}^p}]$, $E[\tilde{b_{j}^p}]$ and $E[\tilde{e_{k}}]$ respectively may not satisfy the required conditions for feasible solution, i.e. for each item, total supplies greater than or equal to the total demands and also total conveyance capacities greater than or equal to the total demands for all items. So this method gives a feasible solution only when the fuzzy supplies, demands and conveyance capacities are so that their respective expected values automatically satisfy those conditions.

Numerical Experiment: To illustrate numerically the Model 3.2 (112), we consider an example with $p=1,2=i,k;~j=1,2,3$ and the following data. The unit transportation penalties are given in Tables 5, 6, 7 and 8. $\tilde{a_{1}^1}=(21,24,26,28)$, $\tilde{a_{2}^1}=(28,32,35,37)$, $\tilde{b_{1}^1}=(14,16,19,22)$, $\tilde{b_{2}^1}=(17,20,22,25)$, $\tilde{b_{3}^1}=(12,15,18,21)$, $\tilde{a_{1}^2}=(32,34,37,39)$, $\tilde{a_{2}^2}=(25,28,30,33)$, $\tilde{b_{1}^2}=(20,23,25,28)$, $\tilde{b_{2}^2}=(16,18,19,22)$, $\tilde{b_{3}^2}=(15,17,19,21)$, $\tilde{e_{1}}=(46,49,51,53)$, $\tilde{e_{2}}=(51,53,56,59).$

Table 5. Penalties/costs $\tilde{c_{ijk}^{11}}$

Now to get the corresponding defuzzified values $a_{ic}^p$, $b_{jc}^p$, $e_{kc}$, $i=1,2,~j=1,2,3,~k=1,2,~p=1,2,$ we apply the fuzzy programming (113) and the obtained values are

$a_{1c}^1=23.7$, $a_{2c}^1=31.6$, $b_{1c}^1=15.8$, $b_{2c}^1=19.7$, $b_{3c}^1=14.7$, $a_{1c}^2=33.8$, $a_{2c}^2=27.7$, $b_{1c}^2=22.7$, $b_{2c}^2=17.8$, $b_{3c}^2=16.8$, $e_{1c}=51.2$, $e_{2c}=56.3$, with $\lambda =0.9$.

Table 6. Penalties/costs $\tilde{c_{ijk}^{12}}$

Table 7. Penalties/costs $\tilde{c_{ijk}^{21}}$

Table 8. Penalties/costs $\tilde{c_{ijk}^{22}}$

Results Using Minimum of Fuzzy Number (Method-1): To solve the above considered problem we convert the problem as in (119) and take $\lambda _{1}=\lambda _{2}=0.4$, $\lambda _{3}=0.2$ (as we concentrate more in maximizing $A_{L}(Z_{t})$ and minimizing $C(Z_{t})$ than in minimizing $A_{R}(Z_{t})$) and M=500.

Applying fuzzy linear programming (i.e. fuzzy programming with linear membership function) (cf. Sect. 2.9) we get the following results

$L_{1}=\min \bar{Z_{1}}=601.9~(A_{L}(Z_{1})=186,~C(Z_{1})=1095.75,~A_{R}(Z_{1})=190)$,

$U_{1}=656.73~(A_{L}(Z_{1})=196.05,~C(Z_{1})=1231.45,~A_{R}(Z_{1})=212.85)$,

$L_{2}=\min \bar{Z_{2}}=483.2~(A_{L}(Z_{2})=190.9,~C(Z_{1})=811.65,~A_{R}(Z_{1})=174.5)$,

$U_{2}=541.71~(A_{L}(Z_{2})=166.15,~C(Z_{2})=941.55,~A_{R}(Z_{2})=157.75)$,

and the optimal compromise solution is

$x_{111}^1=9$, $x_{221}^1=19.7$, $x_{132}^1=14.7$, $x_{212}^1=6.8$, $x_{111}^2=18.38394$, $x_{231}^2=4.116056$, $x_{122}^2=2.732113$, $x_{132}^2=12.68394$, $x_{212}^2=4.316056$, $x_{222}^2=15.06789$, $\lambda =0.753$.

$\bar{Z_{1}}=615.4325$, in which $A_{L}(Z_{1})=182.35$, $C(Z_{1})=1133.39$, $A_{R}(Z_{1})=175.0821$, so that the core of the optimum value of objective function $Z_{1}$ is [1039.232, 1227.548] and 1133.39 is the center of the core.

$\bar{Z_{2}}=497.6407$, in which $A_{L}(Z_{2})=183.092$, $C(Z_{2})=844.4438$, $A_{R}(Z_{2})=165.5$, so that the core of the optimum value of objective function $Z_{2}$ is [753.1357, 935.7518] and 844.4438 is the center of the core. The optimum values of $Z_{1}$ and $Z_{2}$ are shown in Figs. 11 and 12 respectively. Applying global criterion method in $L_{2}$ norm (cf. Sect. 2.9) the following results are obtained.

Fig. 11.

Optimum values of $Z_{1}$

$x_{111}^1=9$, $x_{221}^1=19.7$, $x_{132}^1=14.7$, $x_{212}^1=6.8$, $x_{111}^1=16.4902$, $x_{231}^2=6.0097$, $x_{122}^2=6.5195$, $x_{132}^2=10.7902$, $x_{212}^2=6.2097$, $x_{222}^2=11.2804$.

$\bar{Z_{1}}=618.0837$, in which $A_{L}(Z_{1})=182.35$, $C(Z_{1})=1138.12$, $A_{R}(Z_{1})=178.8695$, so that the core of the optimum value of objective function $Z_{1}$ is the interval [1043.019, 1233.229] and 1138.12 is the center of the core.

$\bar{Z_{2}}=495.3683$, in which $A_{L}(Z_{2})=182.1451$, $C(Z_{2})=837.8158$, $A_{R}(Z_{2})=165.5$, so that the core of the optimum value of objective function $Z_{2}$ is [745.5609, 930.0706] and 837.8158 is the center of the core.

It is observed from the optimal solutions of the objective functions that the decision makers have more information in hand about the objective function values.

Fig. 12.

Optimum values of $Z_{2}$

Results Using Expected Value of the Objective Function (Method-2): To minimize the expected value of the objective functions of the above considered problem, we reconstruct the problem as (120) and transform it to corresponding crisp equivalence form as (121).

Then applying fuzzy linear programming (cf. Sect. 2.9) we get the following result.

$L_{1}=\min \bar{Z_{1}}=1092.45$, $U_{1}=1248.85$, $L_{2}=\min \bar{Z_{2}}=800.45$, $U_{2}=923.45$ and the optimal compromise solution is

$x_{111}^1=3.1686,~x_{121}^1=5.8313,~x_{221}^1=13.8686,~x_{132}^1=14.7, ~x_{212}^1=12.6314,$ $x_{111}^2=22.7,~x_{221}^2=5.6314,~x_{122}^2=11.1,~x_{222}^2=1.0686,~x_{232}^2=16.8,~\lambda =0.6989,~\bar{Z_{1}}=1139.536,~\bar{Z_{2}}=837.4808$.

Applying global criterion method in $L_{2}$ (cf. Sect. 2.9) norm we get the following result.

$\bar{Z_{1}}^{\min }=1092.45$ and $\bar{Z_{2}}^{\min }=800.45$ and the compromise optimum solution is

$x_{111}^1=1.5624$, $x_{121}^1=7.4375$, $x_{221}^1=12.2625$, $x_{132}^1=14.7$, $x_{212}^1=14.2375$, $x_{111}^2=22.7$, $x_{221}^2=6.7$, $x_{231}^2=0.5375$, $x_{122}^2=11.1$, $x_{232}^2=16.2625$, $\bar{Z_{1}}=1144.894$ and $\bar{Z_{2}}=832.1250$.

Using the crisp equivalence form (123) of the expected value model (122) we can not find any feasible solution for this numerical example. However for any other example with suitable data set, this method can gives feasible solution.

Overview of the Results by Two Methods: We note that the optimal expected values of the objective functions $Z_{1}(=1139.536)$ and $Z_{2}(=837.4808)$ as obtained using expected value (method-2) and fuzzy programming technique, lie within the core [1039.232, 1227.548] and [753.1357, 935.7518] of $Z_{1}$ and $Z_{2}$ respectively as obtained using method-1 (method based on minimum of fuzzy number). Also the optimal expected values $Z_{1}$ and $Z_{2}$ that obtained by method-2 are close to the center of core 1133.39 and 844.4438 of $Z_{1}$ and $Z_{2}$ respectively that are obtained by method-1.

Fig. 13.

Discussion of results obtained by method-1 and method-2.

This discussion is given pictorially in Fig. 13. This is also true for the results obtained by using global criterion method.

3.5 Overall Conclusion

In Model 3.1, a MOSTP with fuzzy penalties, resources, demands, conveyance capacities and budget constraints has been formulated. Budget constraints with fuzzy budget amounts are imposed in the problem. The presented problem is solved using chance-constrained programming with credibility measure.

For the first time, a multi-objective multi-item solid transportation problem (Model 3.2) with fuzzy penalties, sources, demands and conveyance capacities is formulated and solved. For defuzzification, two methods (cf. Sects. 3.2 and 3.4 (Method-1), available in the literature and not applied so far in STP have been successfully applied in MOMISTP. Multi-objective problems are solved by two methods and results are compared.

The presented models can be extended to include space constraints, price discount on the basis of amount of transported units, etc. The methods, used for solution here are quite general in nature and these can be applied to other similar uncertain/impricise models in other areas such as inventory control, ecology, sustainable farm management, etc.

4 Some Transportation Models with Type-2 Fuzzy Parameters

In many real world problems, due to lack of input information, noises in data, linguistic information, multiple sources of the collected data, bad statistical analysis etc., it is sometimes difficult to determine exact membership grades to represent an uncertain parameter by ordinary fuzzy set and as a result type-2 fuzzy set (T2 FS) appear. Due to fuzziness in membership function, the computational complexity is very high to deal with T2 FS. For the high computational complexity of general T2 FS, till now the most widely used T2 FS is interval T2 FS (IT2 FS), which is a special case of general T2 FS.

In case of a T2 FS, generally complete defuzzification process consists of two parts - type reduction and defuzzification proper. Type reduction is a procedure by which a T2 FS is converted to the corresponding T1 FS, known as type reduced set (TRS). The TRS is then easily defuzzified to a crisp value. Karnik and Mendel [63] proposed a centroid type reduction method to reduce IT2 FS into T1 FS. But it is very difficult to apply this method to a general T2 FS. Because this method was derived from embedded sets representation theory in which a T2 FS is represented as the union of its T2 embedded sets, and this union consists of an astronomical number of T2 embedded sets, which results a very high computational complexity. Greenfield et al. [51] have proposed an extension of this procedure to discretised generalized type-2 fuzzy sets. Other researchers (Liu, [91]; Wu and Tan, [147]) have developed type reduction strategies for continuous generalized T2 FS. Coupland and John [31] proposed a geometric defuzzification method for T2 FSs by converting a T2 FS into a geometric T2 FS. In terms of possibility theory, Liu and Liu [99] defined a type-2 fuzzy variable as a map from a fuzzy possibility space to the set of real numbers. Qin et al. [127] introduced three kinds of reduction methods called optimistic CV, pessimistic CV and CV reduction methods for type-2 fuzzy variables (T2 FVs) based on CVs (critical values) of regular fuzzy variables.

At present, type-2 fuzzy set theories are being developed and applied in various fields such as group decision making system (Chen and Lee [23, 24], Chen et al. [21], Chen et al. [26]), neural network (Aliev et al. [5]), Portfolio selection problem (Hasuike and Ishi [54]), Pattern recognition (Mitchell [112]), data envelopment analysis (Qin et al. [127]), Ad hoc networks (Yuste et al. [155]), etc. Figueroa-Garca and Hernndez [43] first considered a transportation problem with interval type-2 fuzzy demands and supplies. At the best of our knowledge, we are the first to consider the transportation problems with type-2 fuzzy parameters. Thus this is an emerging area and is yet to be developed. In this chapter, we have proposed a defuzzification method of type-2 fuzzy variables. We have also introduced an interval approximation method of continuous type-2 fuzzy variables. We have formulated and solved two fixed charge transportation problems and a multi-item solid transportation problem with type-2 fuzzy parameters.

4.1 Related Theorem

The following theorem approaches to find crisp equivalent forms of constraints involving type-2 triangular fuzzy variables. This theorem is established using generalized credibility measure for the reduced fuzzy variable from type-2 triangular fuzzy variable by CV (critical value) reduction method.

Theorem 4.1

(Qin et al. [127]). Let $\xi _{i}$ be the reduction of the type-2 triangular fuzzy variable $\tilde{\xi _{i}}=(r_{1}^i,r_{2}^i,r_{3}^i;\theta _{l,i},\theta _{r,i})$ obtained by the CV reduction method for $i=1,2,...,n.$ Suppose $\xi _{1},\xi _{2},...,\xi _{n}$ are mutually independent, and $k_{i}\ge 0$ for $i=1,2,...,n.$

• (i) Given the generalized credibility level $\alpha \in (0,0.5]$, if $\alpha \in (0,0.25]$, then $\tilde{Cr}\{\sum _{i=1}^n~k_{i}\xi _{i}\le t\}\ge \alpha$ is equivalent to

  $$\begin{aligned} \sum _{i=1}^n~\frac{(1-2\alpha +(1-4\alpha )\theta _{r,i})k_{i}r_{1}^i+2\alpha k_{i}r_{2}^i}{1+(1-4\alpha )\theta _{r,i}}\le t, \end{aligned}$$

  (124)

  and if $\alpha \in (0.25,0.5]$, then $\tilde{Cr}\{\sum _{i=1}^n~k_{i}\xi _{i}\le t\}\ge \alpha$ is equivalent to

  $$\begin{aligned} \sum _{i=1}^n~\frac{(1-2\alpha )k_{i}r_{1}^i+(2\alpha +(4\alpha -1)\theta _{l,i})k_{i}r_{2}^i}{1+(4\alpha -1)\theta _{l,i}}\le t. \end{aligned}$$

  (125)

• (ii) Given the generalized credibility level $\alpha \in (0.5,1]$, if $\alpha \in (0.5,0.75]$, then $\tilde{Cr}\{\sum _{i=1}^n~k_{i}\xi _{i}\le t\}\ge \alpha$ is equivalent to

  $$\begin{aligned} \sum _{i=1}^n~\frac{(2\alpha -1)k_{i}r_{3}^i+(2(1-\alpha )+(3-4\alpha )\theta _{l,i})k_{i}r_{2}^i}{1+(3-4\alpha )\theta _{l,i}}\le t, \end{aligned}$$

  (126)

  and if $\alpha \in (0.75,1]$, then $\tilde{Cr}\{\sum _{i=1}^n~k_{i}\xi _{i}\le t\}\ge \alpha$ is equivalent to

  $$\begin{aligned} \sum _{i=1}^n~\frac{(2\alpha -1+(4\alpha -3)\theta _{r,i})k_{i}r_{3}^i+2(1-\alpha )k_{i}r_{2}^i}{1+(4\alpha -3)\theta _{r,i}}\le t. \end{aligned}$$

  (127)

Corollary 4.1:

From the above theorem, equivalent expressions of $\tilde{Cr}\{\sum _{i=1}^n~k_{i}\xi _{i}\ge t\}\ge \alpha$ are easily obtained, since

$$\begin{aligned} \tilde{Cr}\{\sum _{i=1}^n~k_{i}\xi _{i}\ge t\}\ge \alpha\Rightarrow & {} \tilde{Cr}\{\sum _{i=1}^n~-k_{i}\xi _{i}\le -t\}\ge \alpha \\\Rightarrow & {} \tilde{Cr}\{\sum _{i=1}^n~k_{i}\xi '_{i}\le t'\}\ge \alpha , \end{aligned}$$

where $\xi '_{i}=-\xi _{i}$ is the reduction of $-\tilde{\xi _{i}}=(-r_{3}^i,-r_{2}^i,-r_{1}^i;\theta _{r,i},\theta _{l,i})$ and $t'=-t$.

So from (i) of the above theorem, given the generalized credibility level $\alpha \in (0,0.5]$, if $\alpha \in (0,0.25]$, then $\tilde{Cr}\{\sum _{i=1}^n~k_{i}\xi _{i}\ge t\}\ge \alpha$, i.e. $\tilde{Cr}\{\sum _{i=1}^n~k_{i}\xi '_{i}\le t'\}\ge \alpha$ is equivalent to

$$\begin{aligned} \sum _{i=1}^n~\frac{(1-2\alpha +(1-4\alpha )\theta _{l,i})k_{i}(-r_{3}^i)+2\alpha k_{i}(-r_{2}^i)}{1+(1-4\alpha )\theta _{l,i}}\le t'=-t, \end{aligned}$$

(128)

which implies

$$\begin{aligned} \sum _{i=1}^n~\frac{(1-2\alpha +(1-4\alpha )\theta _{l,i})k_{i}r_{3}^i+2\alpha k_{i}r_{2}^i}{1+(1-4\alpha )\theta _{l,i}}\ge t, \end{aligned}$$

(129)

and if $\alpha \in (0.25,0.5]$, then $\tilde{Cr}\{\sum _{i=1}^n~k_{i}\xi _{i}\ge t\}\ge \alpha$ is equivalent to

$$\begin{aligned} \sum _{i=1}^n~\frac{(1-2\alpha )k_{i}(-r_{3}^i)+(2\alpha +(4\alpha -1)\theta _{r,i})k_{i}(-r_{2}^i)}{1+(4\alpha -1)\theta _{r,i}}\le -t \end{aligned}$$

(130)

which implies

$$\begin{aligned} \sum _{i=1}^n~\frac{(1-2\alpha )k_{i}r_{3}^i+(2\alpha +(4\alpha -1)\theta _{r,i})k_{i}r_{2}^i}{1+(4\alpha -1)\theta _{r,i}}\ge t.\end{aligned}$$

(131)

The equivalent expressions for other values of $\alpha$ are similarly obtained.

4.2 Theoretical Developments

Defuzzification of Type-2 Fuzzy Variables ([75]): Here we have introduced a defuzzification process of type-2 fuzzy variables. This method consists of two parts. First CV-based reduction method (Sect. 2.3) is applied to transform the type-2 fuzzy variables into corresponding type-1 fuzzy variables. Then, to get corresponding defuzzified (crisp) values, centroid method described in Sect. 2.2 is applied to these reduced type-1 fuzzy variables. For continuous case the formula $\int _{-\infty }^{\infty } x \mu _{\tilde{A}}(x) dx/\int _{-\infty }^{\infty } \mu _{\tilde{A}}(x) dx$ is used while $\sum _{x} x \mu _{\tilde{A}}(x)/\sum _{x} \mu _{\tilde{A}}(x)$ ia applied for discrete case.

The entire defuzzification process is shown in Fig. 14 and illustrated with the following two examples.

Fig. 14.

Defuzzification of a type-2 fuzzy variable

Example 4.1

Let us consider $\tilde{A}=\{(x,\tilde{\mu }_{\tilde{A}}(x)):x\in X\}$ where $X=\{4,5,6\}$ and the primary memberships (possibilities) of the points of X are, respectively, $J_{4}=\{0.3,0.4,0.6\}$, $J_{5}=\{0.6,0.8,0.9\}$, and $J_{6}=\{0.5,0.6,0.7,0.8\}$. The secondary possibility of the point 4 is

$\tilde{\mu }_{\tilde{A}}(4)=\mu _{\tilde{A}}(4,u)=(0.6/0.3)+(1.0/0.4)+(0.7/0.6)\sim \left( \begin{array}{ccc} 0.3 &{} 0.4 &{} 0.6 \\ 0.6 &{} 1.0 &{} 0.7 \\ \end{array} \right)$,

which represents a regular fuzzy variable (RFV). Similarly

$\tilde{\mu }_{\tilde{A}}(5)=\mu _{\tilde{A}}(5,u)=(0.7/0.6)+(1.0/0.8)+(0.8/0.9)\sim \left( \begin{array}{ccc} 0.6 &{} 0.8 &{} 0.9 \\ 0.7 &{} 1.0 &{} 0.8 \\ \end{array} \right)$,

$\tilde{\mu }_{\tilde{A}}(6)=\mu _{\tilde{A}}(6,u)=(0.3/0.5)+(0.4/0.6)+(1.0/0.7)+(0.5/0.8)\sim \left( \begin{array}{cccc} 0.5 &{} 0.6 &{} 0.7 &{} 0.8 \\ 0.3 &{} 0.4 &{} 1.0 &{} 0.5 \\ \end{array} \right)$.

So discrete type-2 fuzzy variable $\tilde{A}$ is given by

$$\begin{aligned} \tilde{A}=\left\{ \begin{array}{ll} 4, &{} \hbox {with membership}\, \tilde{\mu }_{\tilde{A}}(4); \\ 5, &{} \hbox {with membership}\, \tilde{\mu }_{\tilde{A}}(5); \\ 6, &{} \hbox {with membership}\, \tilde{\mu }_{\tilde{A}}(6). \end{array}\right. \end{aligned}$$

(132)

For this T2 FV $\tilde{A}$, $\tilde{\mu }_{\tilde{A}}(4)$, $\tilde{\mu }_{\tilde{A}}(5)$ and $\tilde{\mu }_{\tilde{A}}(6)$ are discrete RFVs. So the CVs of these RFVs can be obtained by using the formula (47), (48) and (49) (cf. Sect. 2.3) as illustrated in Example 2.7, e.g., from (47), we have $CV^{*}[\tilde{\mu }_{\tilde{A}}(4)]=\sup _{\alpha \in [0,1]} [\alpha \wedge Pos\{\tilde{\mu }_{\tilde{A}}(4)\ge \alpha \}]$, where

$$\begin{aligned} Pos\{\tilde{\mu }_{\tilde{A}}(4)\ge \alpha \}=\left\{ \begin{array}{ll} 1, &{} \hbox {if} \alpha \le 0.4; \\ 0.7, &{} \hbox {if} 0.4<\alpha \le 0.6; \\ 0, &{} \hbox {if} 0.6<\alpha \le 1. \end{array} \right. \end{aligned}$$

(133)

so that

$$\begin{aligned} CV^*[\tilde{\mu }_{\tilde{A}}(4)]= & {} \sup _{\alpha \in [0,0.4]}[\alpha \wedge 1]~\vee \sup _{\alpha \in (0.4,0.6]}[\alpha \wedge 0.7]~\vee \sup _{\alpha \in (0.6,1]}[\alpha \wedge 0]\nonumber \\= & {} 0.4~\vee ~0.6~\vee ~0=0.6. \end{aligned}$$

(134)

In this way, from (47), (48) and (49) (cf. Sect. 2.3) we obtain CV$^*$[$\tilde{\mu }_{\tilde{A}}(4)]=0.6$, CV$^*$[$\tilde{\mu }_{\tilde{A}}(5)]=0.8$, CV$^*$[$\tilde{\mu }_{\tilde{A}}(6)]=0.6$,

CV$_{*}$[$\tilde{\mu }_{\tilde{A}}(4)]=0.4$, CV$_{*}$[$\tilde{\mu }_{\tilde{A}}(5)]=0.6$, CV$_{*}$[$\tilde{\mu }_{\tilde{A}}(6)]=0.6$,

CV[$\tilde{\mu }_{\tilde{A}}(4)]=0.4$, CV[$\tilde{\mu }_{\tilde{A}}(5)]=0.65$, CV[$\tilde{\mu }_{\tilde{A}}(6)]=0.6$.

Then applying optimistic CV, pessimistic CV and CV reduction methods (Sect. 2.3), the T2 FV $\tilde{A}$ is reduced respectively to the following T1 FVs

$\left( \begin{array}{ccc} 4 &{} 5 &{} 6 \\ 0.6 &{} 0.8 &{} 0.6 \\ \end{array} \right)$, $\left( \begin{array}{ccc} 4 &{} 5 &{} 6 \\ 0.4 &{} 0.6 &{} 0.6 \\ \end{array} \right)$ and $\left( \begin{array}{ccc} 4 &{} 5 &{} 6 \\ 0.4 &{} 0.65 &{} 0.6 \\ \end{array} \right) .$

Then applying centroid method to these T1 FVs we get the corresponding complete defuzzified (crisp) values 5, 5.125 and 5.121 respectively. For practical use, which of the defuzzified values should be considered, it is up to the decision maker. However we recommend to take the defuzzified value (e.g., 5.121 for this example) obtained by applying the centroid method to the reduced T1 FV as derived using CV reduction method. This is because optimistic CV and pessimistic CV reduction methods are developed using possibility and necessity measure respectively, while CV reduction method uses credibility measure which is the average of possibility and necessity measures.

Example 4.2

Consider the T2 FV $\tilde{\xi }$ presented in Example 2.4 in Sect. 2.3, Chap. 2. Also in Example 2.4 (continued), applying optimistic CV, pessimistic CV and CV reduction method to $\tilde{\xi }$ we already obtain the corresponding reduced type-1 fuzzy variables as $\left( \begin{array}{ccc} 5 &{} 6 &{} 7 \\ \frac{1}{2} &{} \frac{2}{3} &{} \frac{7}{12} \\ \end{array} \right)$, $\left( \begin{array}{ccc} 5 &{} 6 &{} 7 \\ \frac{1}{3} &{} \frac{1}{2} &{} \frac{1}{4} \\ \end{array} \right)$ and $\left( \begin{array}{ccc} 5 &{} 6 &{} 7 \\ \frac{3}{7} &{} \frac{4}{7} &{} \frac{1}{2} \\ \end{array} \right)$ respectively.

Then applying centroid method to these T1 FVs we get the corresponding complete defuzzified (crisp) values 6.0476, 5.923 and 6.0476 respectively.

Comparison with geometric defuzzification method (Coupland and John [31]):

Applying the geometric defuzzification method (cf. Sect. 2.3) to Example 4.1 we find the defuzzified value of the discrete type-2 fuzzy variable $\tilde{A}$ as 5.158 as compared to 5.121, obtained by the above proposed method.

Since the domains of the secondary possibilities (memberships) of all the points of the type-2 fuzzy variable $\tilde{\xi }$ of Example 4.2 are continuous over [0,1], so to apply geometric defuzzification method we have to dicretize the continuous domains. We discretize the continuous domains of the secondary possibilities of the points of $\tilde{\xi }$ with equidistant 0.05 and applying geometric defuzzification method we obtain defuzzified value 6.1403 of $\tilde{\xi }$, compared to earlier result 6.0476.

Nearest Interval Approximation of Continuous Type-2 Fuzzy Variables ([76]). Here we have proposed a method of approximation of continuous type-2 fuzzy variable by crisp interval. For this purpose we first find the CV-based reductions of the type-2 fuzzy variable. Then we derive the corresponding $\alpha$-cuts of these CV-based reductions. Finally applying interval approximation method (Grzegorzewski [52]) to the $\alpha$-cuts we find approximate crisp intervals. The entire method is shown in the Fig. 15.

Fig. 15.

Nearest interval approximation of continuous T2 fuzzy variable.

Example 4.3

Now we illustrate the above method with type-2 triangular fuzzy variable. Let $\tilde{\xi }$ be a type-2 triangular fuzzy variable defined as $\tilde{\xi }=(r_{1},r_{2},r_{3};\theta _{l},\theta _{r})$. Then from Theorem 2.4 (cf. Sect. 2.3) we have the optimistic CV reduction, pessimistic CV reduction and CV reduction of $\tilde{\xi }$ as $\xi _{1}$, $\xi _{2}$ and $\xi _{3}$ respectively with the possibility distributions given by (56), (57) and (58) (cf. Sect. 2.3). Now using the definition of $\alpha$-cut of a fuzzy number we find $\alpha$-cuts of the reductions of $\tilde{\xi }$.

$\alpha$-cut of the optimistic CV reduction $\xi _{1}$ of $\tilde{\xi }$: Applying the definition of $\alpha$-cut of a fuzzy variable we find the $\alpha$-cut of the reduction $\xi _{1}$ as $[\xi _{1L}(\alpha ),\xi _{1R}(\alpha )]$, where,

$$\begin{aligned} \xi _{1L}(\alpha )=\left\{ \begin{array}{ll} \frac{(1+\theta _{r})r_{1}+(r_{2}-r_{1}-\theta _{r}r_{1})\alpha }{(1+\theta _{r})-\theta _{r}\alpha }, &{} 0\le \alpha \le 0.5; \\ \frac{(r_{1}-\theta _{r}r_{2})+(r_{2}-r_{1}+\theta _{r}r_{2})\alpha }{(1-\theta _{r})+\theta _{r}\alpha }, &{} 0.5<\alpha \le 1. \end{array}\right. \end{aligned}$$

(135)

$$\begin{aligned} \xi _{1R}(\alpha )=\left\{ \begin{array}{ll} \frac{(r_{3}-\theta _{r}r_{2})-(r_{3}-r_{2}-\theta _{r}r_{2})\alpha }{(1-\theta _{r})+\theta _{r}\alpha }, &{} 0.5\le \alpha \le 1; \\ \frac{(1+\theta _{r})r_{3}-(r_{3}-r_{2}+\theta _{r}r_{3})\alpha }{(1+\theta _{r})-\theta _{r}\alpha }, &{} 0\le \alpha <0.5. \end{array} \right. \end{aligned}$$

(136)

$\alpha$-cut of the pessimistic CV reduction $\xi _{2}$ of $\tilde{\xi }$: $\alpha$-cut of the reduction $\xi _{2}$ is obtained as $[\xi _{2L}(\alpha ),\xi _{2R}(\alpha )]$, where,

$$\begin{aligned} \xi _{2L}(\alpha )=\left\{ \begin{array}{ll} \frac{r_{1}+(r_{2}-r_{1}-\theta _{l}r_{1})\alpha }{1-\theta _{l}\alpha }, &{} 0\le \alpha \le 0.5; \\ \frac{r_{1}+(r_{2}-r_{1}+\theta _{l}r_{2})\alpha }{1+\theta _{l}\alpha }, &{} 0.5<\alpha \le 1. \end{array}\right. \end{aligned}$$

(137)

$$\begin{aligned} \xi _{2R}(\alpha )=\left\{ \begin{array}{ll} \frac{r_{3}-(r_{3}-r_{2}-\theta _{l}r_{2})\alpha }{1+\theta _{l}\alpha }, &{} 0.5\le \alpha <1; \\ \frac{r_{3}-(r_{3}-r_{2}+\theta _{l}r_{3})\alpha }{1-\theta _{l}\alpha }, &{} 0\le \alpha <0.5. \end{array} \right. \ \end{aligned}$$

(138)

$\alpha$-cut of the CV reduction $\xi _{3}$ of $\tilde{\xi }$: $\alpha$-cut of the reduction $\xi _{3}$ is obtained as $[\xi _{3L}(\alpha ),\xi _{3R}(\alpha )]$, where,

$$\begin{aligned} \xi _{3L}(\alpha )=\left\{ \begin{array}{ll} \frac{(1+\theta _{r})r_{1}+(r_{2}-r_{1}-2\theta _{r}r_{1})\alpha }{(1+\theta _{r})-2\theta _{r}\alpha }, &{} 0\le \alpha \le 0.5; \\ \frac{(r_{1}-\theta _{l}r_{2})+(r_{2}-r_{1}+2\theta _{l}r_{2})\alpha }{(1-\theta _{l})+2\theta _{l}\alpha }, &{} 0.5<\alpha \le 1. \end{array}\right. \end{aligned}$$

(139)

$$\begin{aligned} \xi _{3R}(\alpha )=\left\{ \begin{array}{ll} \frac{(r_{3}-\theta _{l}r_{2})-(r_{3}-r_{2}-2\theta _{l}r_{2})\alpha }{(1-\theta _{l})+2\theta _{l}\alpha }, &{} 0.5\le \alpha \le 1; \\ \frac{(1+\theta _{r})r_{3}-(r_{3}-r_{2}+2\theta _{r}r_{3})\alpha }{(1+\theta _{r})-2\theta _{r}\alpha }, &{} 0\le \alpha <0.5. \end{array} \right. \end{aligned}$$

(140)

Now we know that nearest interval approximation of a fuzzy number (Grzegorzewski [52]) $\tilde{A}$ with $\alpha$-cut $[A_{L}(\alpha ),A_{R}(\alpha )]$ is given by (cf. Sect. 2.2) $C_{d}(\tilde{A})=[C_{L},C_{R}]$, where $C_{L}=\int _{0}^1A_{L}(\alpha )d\alpha$ and $C_{R}=\int _{0}^1A_{R}(\alpha )d\alpha$.

Using this method for the $\alpha$-cuts of optimistic CV, pessimistic CV or CV reduction of $\tilde{\xi }$ we can find the nearest interval approximation of $\tilde{\xi }$ as follows.

Nearest interval approximation of $\tilde{\xi }$ using $\alpha$-cut of the optimistic CV reduction $\xi _{1}$ of $\tilde{\xi }$: In this case the nearest interval approximation of $\tilde{\xi }$ is obtained as $[C_{L},C_{R}]$ where,

$$\begin{aligned} C_{L}&=\int _{0}^1\xi _{1L}(\alpha )d\alpha \nonumber \\&= \int _{0}^{0.5} \frac{(1+\theta _{r})r_{1}+(r_{2}-r_{1}-\theta _{r}r_{1})\alpha }{(1+\theta _{r})-\theta _{r}\alpha }d\alpha \nonumber \\&\quad +\int _{0.5}^1\frac{(r_{1}-\theta _{r}r_{2})+(r_{2}-r_{1}+\theta _{r}r_{2})\alpha }{(1-\theta _{r})+\theta _{r}\alpha }d\alpha = C_{L1}+C_{L2}, \end{aligned}$$

(141)

$$C_{L1}=\frac{(1+\theta _{r})r_{1}}{\theta _{r}}\ln \big (\frac{1+\theta _{r}}{1+0.5\theta _{r}}\big )-\frac{r_{2}-r_{1}-\theta _{r}r_{1}}{\theta _{r}^2} \big [0.5\theta _{r}-(1+\theta _{r})\ln \big (\frac{1+\theta _{r}}{1+0.5\theta _{r}}\big )\big ],$$

$$C_{L2}=-\frac{r_{1}-\theta _{r}r_{2}}{\theta _{r}}\ln (1-0.5\theta _{r})+\frac{r_{2}-r_{1}+\theta _{r}r_{2}}{\theta _{r}^2}\big [0.5\theta _{r}+(1-\theta _{r})\ln (1-0.5\theta _{r})\big ].$$

$$\begin{aligned} \nonumber C_{R}&=\int _{0}^1\xi _{1R}(\alpha )d\alpha \\ \nonumber&= \int _{0}^{0.5}\frac{(1+\theta _{r})r_{3}-(r_{3}-r_{2}+\theta _{r}r_{3})\alpha }{(1+\theta _{r})-\theta _{r}\alpha }d\alpha \\ \nonumber&\quad + \int _{0.5}^1\frac{(r_{3}-\theta _{r}r_{2})-(r_{3}-r_{2}-\theta _{r}r_{2})\alpha }{(1-\theta _{r})+\theta _{r}\alpha }d\alpha \\&= C_{R1}+C_{R2}, \end{aligned}$$

(142)

$$C_{R1}=\frac{(1+\theta _{r})r_{3}}{\theta _{r}}\ln \big (\frac{1+\theta _{r}}{1+0.5\theta _{r}}\big )+\frac{r_{3}-r_{2}+\theta _{r}r_{3}}{\theta _{r}^2} \big [0.5\theta _{r}-(1+\theta _{r})\ln \big (\frac{1+\theta _{r}}{1+0.5\theta _{r}}\big )\big ],$$

$$C_{R2}=-\frac{r_{3}-\theta _{r}r_{2}}{\theta _{r}}\ln (1-0.5\theta _{r})-\frac{r_{3}-r_{2}-\theta _{r}r_{2}}{\theta _{r}^2}\big [0.5\theta _{r}+(1-\theta _{r})\ln (1-0.5\theta _{r})\big ].$$

We call this interval as optimistic interval approximation of $\tilde{\xi }$.

Nearest interval approximation of $\tilde{\xi }$ using $\alpha$-cut of the pessimistic CV reduction $\xi _{2}$ of $\tilde{\xi }$: In this case the nearest interval approximation of $\tilde{\xi }$ is obtained as $[C_{L},C_{R}]$ where,

$$\begin{aligned} \nonumber C_{L}&=\int _{0}^1\xi _{2L}(\alpha )d\alpha \\ \nonumber&= \int _{0}^{0.5}\frac{r_{1}+(r_{2}-r_{1}-\theta _{l}r_{1})\alpha }{1-\theta _{l}\alpha }d\alpha +\int _{0.5}^1\frac{r_{1}+(r_{2}-r_{1}+\theta _{l}r_{2})\alpha }{1+\theta _{l}\alpha }d\alpha \\&= C_{L1}+C_{L2}, \end{aligned}$$

(143)

$$C_{L1}=-\frac{r_{1}}{\theta _{l}}\ln (1-0.5\theta _{l})-\frac{r_{2}-r_{1}-\theta _{l}r_{1}}{\theta _{l}^2}\big [0.5\theta _{l}+\ln (1-0.5\theta _{l})\big ],$$

$$C_{L2}=\frac{r_{1}}{\theta _{l}}\ln \big (\frac{1+\theta _{l}}{1+0.5\theta _{l}}\big )+\frac{r_{2}-r_{1}+\theta _{l}r_{2}}{\theta _{l}^2}\big [0.5\theta _{l}-\ln \big (\frac{1+\theta _{l}}{1+0.5\theta _{l}}\big )\big ].$$

$$\begin{aligned} \nonumber C_{R}= & {} \int _{0}^1\xi _{2R}(\alpha )d\alpha \\ \nonumber= & {} \int _{0}^{0.5}\frac{r_{3}-(r_{3}-r_{2}+\theta _{l}r_{3})\alpha }{1-\theta _{l}\alpha }d\alpha +\int _{0.5}^1\frac{r_{3}-(r_{3}-r_{2}-\theta _{l}r_{2})\alpha }{1+\theta _{l}\alpha }d\alpha \\= & {} C_{R1}+C_{R2}, \end{aligned}$$

(144)

$$C_{R1}=-\frac{r_{3}}{\theta _{l}}\ln (1-0.5\theta _{l})+\frac{r_{3}-r_{2}+\theta _{l}r_{3}}{\theta _{l}^2}\big [0.5\theta _{l}+\ln (1-0.5\theta _{l})\big ],$$

$$C_{R2}=\frac{r_{3}}{\theta _{l}}\ln \big (\frac{1+\theta _{l}}{1+0.5\theta _{l}}\big )-\frac{r_{3}-(r_{3}-r_{2}-\theta _{l}r_{2}}{\theta _{l}^2}\big [0.5\theta _{l}-\ln \big (\frac{1+\theta _{l}}{1+0.5\theta _{l}}\big )\big ].$$

We call this interval as pessimistic interval approximation of $\tilde{\xi }$.

Nearest interval approximation of $\tilde{\xi }$ using $\alpha$-cut of the CV reduction $\xi _{3}$ of $\tilde{\xi }$: In this case the nearest interval approximation of $\tilde{\xi }$ is obtained as $[C_{L},C_{R}]$ where,

$$\begin{aligned} \nonumber C_{L}&=\int _{0}^1\xi _{3L}(\alpha )d\alpha \\ \nonumber&= \int _{0}^{0.5}\frac{(1+\theta _{r})r_{1}+(r_{2}-r_{1}-2\theta _{r}r_{1})\alpha }{(1+\theta _{r})-2\theta _{r}\alpha }d\alpha \\ \nonumber&\quad +\int _{0.5}^1\frac{(r_{1}-\theta _{l}r_{2})+(r_{2}-r_{1}+2\theta _{l}r_{2})\alpha }{(1-\theta _{l})+2\theta _{l}\alpha }\\&= C_{L1}+C_{L2}, \end{aligned}$$

(145)

$$C_{L1}=\frac{(1+\theta _{r})r_{1}}{2\theta _{r}}\ln (1+\theta _{r})-\frac{r_{2}-r_{1}-2\theta _{r}r_{1}}{4\theta _{r}^2}\big [\theta _{r}-(1+\theta _{r})\ln (1+\theta _{r})\big ],$$

$$C_{L2}=\frac{r_{1}-\theta _{l}r_{2}}{2\theta _{l}}\ln (1+\theta _{l})+\frac{r_{2}-r_{1}+2\theta _{l}r_{2}}{4\theta _{l}^2}\big [\theta _{l}-(1-\theta _{l})\ln (1+\theta _{l})\big ].$$

$$\begin{aligned} \nonumber C_{R}&=\int _{0}^1\xi _{3R}(\alpha )d\alpha \\ \nonumber&= \int _{0}^{0.5}\frac{(1+\theta _{r})r_{3}-(r_{3}-r_{2}+2\theta _{r}r_{3})\alpha }{(1+\theta _{r})-2\theta _{r}\alpha }d\alpha \\ \nonumber&\quad + \int _{0.5}^{1}\frac{(r_{3}-\theta _{l}r_{2})-(r_{3}-r_{2}-2\theta _{l}r_{2})\alpha }{(1-\theta _{l})+2\theta _{l}\alpha }d\alpha \\&= C_{R1}+C_{R2}, \end{aligned}$$

(146)

$$C_{R1}=\frac{(1+\theta _{r})r_{3}}{2\theta _{r}}\ln (1+\theta _{r})+\frac{r_{3}-r_{2}+2\theta _{r}r_{3}}{4\theta _{r}^2}\big [\theta _{r}-(1+\theta _{r})\ln (1+\theta _{r})\big ],$$

$$C_{R2}=\frac{r_{3}-\theta _{l}r_{2}}{2\theta _{l}}\ln (1+\theta _{l})-\frac{r_{3}-r_{2}-2\theta _{l}r_{2}}{4\theta _{l}^2}\big [\theta _{l}-(1-\theta _{l})\ln (1+\theta _{l})\big ].$$

We call this interval as credibilistic interval approximation of $\tilde{\xi }$.

For example consider the type-2 triangular fuzzy variable $\tilde{\xi }=(2,3,4;0.5,0.8)$ whose FOU is depicted in Fig. 6 and its optimistic CV, pessimistic CV and CV reductions are shown in the Fig. 8 (Sect. 2.3). We find nearest interval approximation of $\tilde{\xi }$. From Eqs. (141), (142), (143), (144), (145) and (146), the optimistic, pessimistic and credibilistic interval approximations of $\tilde{\xi }$ are obtained as

$$[2.4086,3.5913],~[2.5567,3.4432]~and~[2.4925,3.5074]$$

respectively. These results are shown in the Fig. 16.

Fig. 16.

Interval approximation of $\tilde{\xi }$ using (1) optimistic CV, (2) pessimistic CV, (3) CV reductions.

4.3 Model 4.1: Fixed Charge Transportation Problem with Type-2 Fuzzy Cost Parameters

Here a fixed charge transportation problem (FCTP) with unit transportation costs and fixed(/additional) costs as type-2 fuzzy variables is formulated.

Notations:

• (i) $\tilde{c_{ij}}$: The unit transportation cost from i-th source to j-th destination represented by type-2 fuzzy variable.

• (ii) $\tilde{d_{ij}}$: Fixed(/additional) cost associated with route (i, j) represented by type-2 fuzzy variable.

• (iii) $x_{ij}$: The decision variable which represents amount of product to be transported from i-th origin to j-th destination.

• (iv) Z: The objective function.

• (v) $a_{i}$: The amount of the product available at the i-th origin.

• (vi) $b_{j}$: The demand of the product at j-th destination.

Mathematical Model: A FCTP with m sources and n destinations and direct costs and fixed cost parameters as T2 FVs is as follows:

$$\begin{aligned} Min~Z=\sum _{i=1}^m\sum _{j=1}^n~(\tilde{c_{ij}}~x_{ij}+\tilde{d_{ij}}y_{ij}),\end{aligned}$$

(147)

$$\begin{aligned} subject~to~\sum _{j=1}^n x_{ij}~\le & {} a_{i},~~i=1,2,...,m,\end{aligned}$$

(148)

$$\begin{aligned} \sum _{i=1}^m x_{ij}~~\ge & {} b_{j},~~j=1,2,...,n, \end{aligned}$$

(149)

$$\begin{aligned} x_{ij}\ge 0,~y_{ij}=\left\{ \begin{array}{ll} 1, &{} \hbox {if}\, x_{ij}>0; \\ 0, &{} \hbox {otherwise.} \end{array} \right. ~\forall ~ i,j,\end{aligned}$$

(150)

$$\begin{aligned} \sum _{i=1}^m a_{i}\ge \sum _{j=1}^n b_{j} \end{aligned}$$

(151)

It is obvious that the fixed charge $\tilde{d_{ij}}$ will be costed for a route (i, j) only if any transportation activity is assigned to that route. So $y_{ij}$ is defined such that if $x_{ij}>0$ then $y_{ij}=1$, otherwise it will be 0.

4.4 Defuzzifiaction

Since the unit transportation costs $\tilde{c_{ij}}$s and the fixed(/additional) costs $\tilde{d_{ij}}$s in the above model are T2 FVs, we apply defuzzification method presented in Sect. 4.2. We first apply CV-based reduction method to transform the T2 FVs into corresponding T1 FVs and then centroid method to the reduced T1 FVs to get corresponding defuzzified (crisp) values. Taking these defuzzified (crisp) cost values, the problem can be then easily solved using any standard optimization solver.

Numerical Experiment: In this section the presented model and methods are illustrated numerically. To illustrate the Model 4.1 ((147)–(151)), we consider an example with three sources and two destinations, i.e., $i =1,2,3$ and $j =1,2$.

The unit transportation costs $\tilde{c_{ij}}$ are the following discrete type-2 fuzzy variables.

$\tilde{c_{11}}=\left\{ \begin{array}{ll} 2, &{} \hbox {with} \tilde{\mu }_{\tilde{c_{11}}}(2)=(0.2,0.4,0.6,0.8); \\ 4, &{} \hbox {with} \tilde{\mu }_{\tilde{c_{11}}}(4)=(0.5,0.7,0.9); \\ 5, &{} \hbox {with} \tilde{\mu }_{\tilde{c_{11}}}(5)=(0.3,0.5,0.7). \end{array}\right.$

$\tilde{c_{12}}=\left\{ \begin{array}{ll} 7, &{} \hbox {with} \tilde{\mu }_{\tilde{c_{12}}}(7)=(0.4,0.6,0.7); \\ 8, &{} \hbox {with} \tilde{\mu }_{\tilde{c_{12}}}(8)=(0.5,0.7,0.8); \\ 9, &{} \hbox {with} \tilde{\mu }_{\tilde{c_{12}}}(9)=(0.7,0.9,1). \end{array} \right.$

$\tilde{c_{21}}=\left\{ \begin{array}{ll} 4, &{} \hbox {with} \tilde{\mu }_{\tilde{c_{21}}}(4)=\left( \begin{array}{ccc} 0.3 &{} 0.5 &{} 0.7 \\ 0.4 &{} 1 &{} 0.7 \\ \end{array} \right) ; \\ 5, &{} \hbox {with} \tilde{\mu }_{\tilde{c_{21}}}(5)=\left( \begin{array}{ccc} 0.6 &{} 0.8 &{} 0.9 \\ 0.5 &{} 0.9 &{} 1 \\ \end{array} \right) ; \\ 7, &{} \hbox {with} \tilde{\mu }_{\tilde{c_{21}}}(7)=\left( \begin{array}{ccc} 0.5 &{} 0.7 &{} 0.8 \\ 0.4 &{} 1 &{} 0.7 \\ \end{array} \right) . \end{array}\right.$

$\tilde{c_{22}}=\left\{ \begin{array}{ll} 6, &{} \hbox {with} \tilde{\mu }_{\tilde{c_{22}}}(6)=(0.4,0.5,0.7,0.8); \\ 7, &{} \hbox {with} \tilde{\mu }_{\tilde{c_{22}}}(7)=(0.6,0.8,0.9); \\ 9, &{} \hbox {with} \tilde{\mu }_{\tilde{c_{22}}}(9)=(0.4,0.6,0.7). \end{array} \right.$

$\tilde{c_{31}}=\left\{ \begin{array}{ll} 3, &{} \hbox {with} \tilde{\mu }_{\tilde{c_{31}}}(3)=(0.3,0.4,0.6); \\ 5, &{} \hbox {with} \tilde{\mu }_{\tilde{c_{31}}}(5)=(0.7,0.9,1); \\ 6, &{} \hbox {with} \tilde{\mu }_{\tilde{c_{31}}}(6)=(0.4,0.6,0.7). \end{array} \right.$

$\tilde{c_{32}}=\left\{ \begin{array}{ll} 8, &{} \hbox {with} \tilde{\mu }_{\tilde{c_{32}}}(8)=(0.3,0.5,0.6); \\ 9, &{} \hbox {with} \tilde{\mu }_{\tilde{c_{32}}}(9)=(0.5,0.7,0.8,0.9); \\ 10, &{} \hbox {with} \tilde{\mu }_{\tilde{c_{32}}}(10)=(0.5,0.6,0.8). \end{array}\right.$

The supplies $a_{i}$ and demands $b_{j}$ are as follows:

$a_{1}=20$, $a_{2}=14$, $a_{3}=18$, $b_{1}=28$, $b_{2}=21$.

For convenience of computing we suppose that the fixed charge $\tilde{d_{ij}}=0.5 \tilde{c_{ij}}$.

Solution Using Proposed Defuzzification Method (cf. Sect. 4.2 ): To solve the above problem we first find corresponding defuzzified (crisp) values of the type-2 fuzzy cost parameters $\tilde{c_{ij}}$. For this purpose we first apply CV reduction method to reduce type-2 fuzzy variables $\tilde{c_{ij}}$ to type-1 fuzzy variables, then applying centroid method we get the corresponding crisp values. We denote these crisp values as $c_{ij}^c$ which are obtained as

$c_{11}^c=3.6956$, $c_{12}^c=8.1071$, $c_{21}^c=5.4615$, $c_{22}^c=7.36$, $c_{31}^c=4.8523$ and $c_{32}^c=9.0482$.

Now using these crisp costs values, the optimum solution of the problem is obtained by the standard optimization solver - LINGO and given in Table 9.

Solution Using Geometric Defuzzification (cf. Sect. 2.3 ): Using geometric defuzzification method we obtain the defuzzified values of the type-2 fuzzy cost parameters $\tilde{c_{ij}}$ as follows.

$c_{11}^c=3.6896$, $c_{12}^c=8.219$, $c_{21}^c=5.6355$, $c_{22}^c=7.5651$, $c_{31}^c=4.65$ and $c_{32}^c=9.1932$.

Using these defuzzified cost values, the optimum solution of the problem is obtained and presented in Table 9.

Table 9. Optimum results for model-4.1

So from the above two results, we see that the optimum allocations (i.e., values of $x_{ij}s$) as obtained by the two approaches are the same. However the optimum objective value (minimum transportation cost) as obtained using the geometric defuzzification method is something more than that of using proposed defuzzification method.

4.5 Model 4.2: Fixed Charge Transportation Problem with Type-2 Fuzzy Costs, Supplies and Demands

Notations:

• (i) $\tilde{c_{ij}}$: The unit transportation costs from i-th source to j-th destination represented by type-2 fuzzy variable.

• (ii) $\tilde{d_{ij}}$: Fixed(/additional) cost associated with route (i, j) represented by type-2 fuzzy variable.

• (iii) $x_{ij}$: The decision variable which represents amount of product to be transported from i-th origin to j-th destination.

• (iv) Z: The objective function.

• (v) $\tilde{a_{i}}$: The amount of the product available at the i-th origin represented by type-2 fuzzy variable.

• (vi) $\tilde{b_{j}}$: The demand of the product at j-th destination represented by type-2 fuzzy variable.

Mathematical Model: A FCTP with m sources, n destinations and unit transportation costs, fixed costs, supplies and demands as T2 FVs is formulated as follows:

$$\begin{aligned} Min~Z=\sum _{i=1}^m\sum _{j=1}^n~(\tilde{c_{ij}}~x_{ij}+\tilde{d_{ij}}y_{ij}), \end{aligned}$$

(152)

$$\begin{aligned} subject~to~\sum _{j=1}^n x_{ij}~\le & {} \tilde{a_{i}},~~i=1,2,...,m,\end{aligned}$$

(153)

$$\begin{aligned} \sum _{i=1}^m x_{ij}~~\ge & {} \tilde{b_{j}},~~j=1,2,...,n, \end{aligned}$$

(154)

$$\begin{aligned} x_{ij}\ge 0,~ y_{ij}=\left\{ \begin{array}{ll} 1, &{} \hbox {if}\, x_{ij}>0; \\ 0, &{} \hbox {otherwise.} \end{array} \right. ~\forall ~ i,j \end{aligned}$$

(155)

Solution Methodology: Chance-Constrained Programming Using Generalized Credibility: Suppose that $\tilde{c'_{ij}}$, $\tilde{d'_{ij}}$, $\tilde{a'_{i}}$ and $\tilde{b'_{j}}$ are the reduced T1 FVs (may not be normalized) of the T2 FVs $\tilde{c_{ij}}$, $\tilde{d_{ij}}$, $\tilde{a_{i}}$ and $\tilde{b_{j}}$ respectively according to CV-based reduction method. Now to solve the above problem we formulate a chance-constrained programming model with these reduced fuzzy parameters. Chance-constrained programming with fuzzy (type-1) parameters was introduced by Liu and Iwamura [92] using possibility measure. Latter it is developed (Liu [90], Yang and Liu [153], Kundu et al. [74]) by using credibility measure. But since the reduced fuzzy parameters $\tilde{c'_{ij}}$, $\tilde{d'_{ij}}$, $\tilde{a'_{i}}$ and $\tilde{b'_{j}}$ may not be normalized, so usual credibility measure can not be used and hence using generalized credibility (Note 2.1, Sect. 2.3), as the problem is minimization problem, the following chance-constrained programming model is formulated:

$$\begin{aligned} Min_{x}~(Min_{\bar{f}}~~\bar{f}) \end{aligned}$$

(156)

$$\begin{aligned} subject~to~\tilde{Cr}\{\sum _{i=1}^m\sum _{j=1}^n~(\tilde{c'_{ij}}~x_{ij}+\tilde{d'_{ij}}y_{ij})\le \bar{f}\}\ge \alpha \end{aligned}$$

(157)

$$\begin{aligned} \tilde{Cr}\{\sum _{j=1}^n x_{ij}~\le \tilde{a'_{i}}\}\ge \alpha _{i},~~i=1,2,...,m \end{aligned}$$

(158)

$$\begin{aligned} \tilde{Cr}\{\sum _{i=1}^m x_{ij}~~\ge \tilde{b'_{j}}\}\ge \beta _{j},~~j=1,2,...,n \end{aligned}$$

(159)

$$\begin{aligned} x_{ij}\ge 0,~ y_{ij}= \left\{ \begin{array}{ll} 1, &{} \hbox {if}\, x_{ij}>0; \\ 0, &{} \hbox {otherwise.} \end{array}\right. ~\forall ~ i,j \end{aligned}$$

(160)

where Min $\bar{f}$ indicates the minimum possible value that the objective function less or equal to it with generalized credibility at least $\alpha$ $(0<\alpha \le 1)$. $\alpha _{i}$, $\beta _{j}$ $(0<\alpha _{i}, \beta _{j}\le 1)$ are the predetermined generalized credibility levels of satisfaction of the source and destination constraints respectively for all i, j.

Crisp Equivalences: Suppose that the $\tilde{c_{ij}}$, $\tilde{d_{ij}}$, $\tilde{a_{i}}$ and $\tilde{b_{j}}$ are all mutually independent type-2 triangular fuzzy variables defined by $\tilde{c_{ij}}=(c_{ij}^1,c_{ij}^2,c_{ij}^3;\theta _{l,ij},\theta _{r,ij})$, $\tilde{d_{ij}}=(d_{ij}^1,d_{ij}^2,d_{ij}^3;\theta '_{l,ij},\theta '_{r,ij})$, $\tilde{a_{i}}=(a_{i}^1,a_{i}^2,a_{i}^3;\theta _{l,i},\theta _{r,i})$ and $\tilde{b_{j}}=(b_{j}^1,b_{j}^2,b_{j}^3;\theta _{l,j},\theta _{r,j})$. Also let $\tilde{c'_{ij}}$, $\tilde{d'_{ij}}$, $\tilde{a'_{i}}$ and $\tilde{b'_{j}}$ are the corresponding reductions by the CV reduction method.

Then from Theorem 4.1 and its corollary, the chance-constrained model formulation (156)–(160) of Model-4.2 (i.e., (152)–(155)) can be turned into the following crisp equivalent (for proof see the Appendix) parametric programming problems:

Case-I: $0<\alpha \le 0.25$: Then the equivalent parametric programming problem for the model representation (156)–(160) is

$$\begin{aligned} Min~\sum _{i=1}^m\sum _{j=1}^n\big [\frac{(1-2\alpha +(1-4\alpha )\theta _{r,ij})c_{ij}^1x_{ij}+2\alpha c_{ij}^2x_{ij}}{1+(1-4\alpha )\theta _{r,ij}}~+\nonumber \\ \frac{(1-2\alpha +(1-4\alpha )\theta '_{r,ij})d_{ij}^1y_{ij}+2\alpha d_{ij}^2y_{ij}}{1+(1-4\alpha )\theta '_{r,ij}}\big ] \end{aligned}$$

(161)

$$\begin{aligned} subject~to~~\sum _{j=1}^n~x_{ij}\le & {} F_{a_{i}},~i=1,2,...,m \end{aligned}$$

(162)

$$\begin{aligned} \sum _{i=1}^m~x_{ij}\ge & {} F_{b_{j}},~j=1,2,...,n \end{aligned}$$

(163)

$$\begin{aligned} x_{ij}\ge 0,~ y_{ij}=\left\{ \begin{array}{ll} 1, &{} \hbox {if}\, x_{ij}>0; \\ 0, &{} \hbox {otherwise.} \end{array} \right. ~\forall ~ i,j, \end{aligned}$$

(164)

where $F_{a_{i}}$ and $F_{b_{j}}$ are given by (177) and (178) respectively.

Case-II: $0.25<\alpha \le 0.5$: Then the equivalent parametric programming problem for the model (156)–(160) is

$$\begin{aligned} Min~\sum _{i=1}^m\sum _{j=1}^n\big [\frac{(1-2\alpha )c_{ij}^1x_{ij}+(2\alpha +(4\alpha -1)\theta _{l,ij})c_{ij}^2x_{ij}}{1+(4\alpha -1)\theta _{l,ij}}~+\nonumber \\ \frac{(1-2\alpha )d_{ij}^1y_{ij}+(2\alpha +(4\alpha -1)\theta '_{l,ij})d_{ij}^2y_{ij}}{1+(4\alpha -1)\theta '_{l,ij}}\big ] \end{aligned}$$

(165)

$$\begin{aligned} subject~to~~\sum _{j=1}^n~x_{ij}\le & {} F_{a_{i}},~i=1,2,...,m \end{aligned}$$

(166)

$$\begin{aligned} \sum _{i=1}^m~x_{ij}\ge & {} F_{b_{j}},~j=1,2,...,n \end{aligned}$$

(167)

$$\begin{aligned} x_{ij}\ge 0,~ y_{ij}= \left\{ \begin{array}{ll} 1, &{} \hbox {if}\, x_{ij}>0; \\ 0, &{} \hbox {otherwise.} \end{array}\right. ~\forall ~ i,j \end{aligned}$$

(168)

Case-III: $0.5<\alpha \le 0.75$: Then the equivalent parametric programming problem for the model (156)–(160) is

$$\begin{aligned} Min~\sum _{i=1}^m\sum _{j=1}^n\big [\frac{(2\alpha -1)c_{ij}^3x_{ij}+(2(1-\alpha )+(3-4\alpha )\theta _{l,ij})c_{ij}^2x_{ij}}{1+(3-4\alpha )\theta _{l,ij}}~+\nonumber \\ \frac{(2\alpha -1)d_{ij}^3y_{ij}+(2(1-\alpha )+(3-4\alpha )\theta '_{l,ij})d_{ij}^2y_{ij}}{1+(3-4\alpha )\theta '_{l,ij}}\big ] \end{aligned}$$

(169)

$$\begin{aligned} subject~to~~\sum _{j=1}^n~x_{ij}\le & {} F_{a_{i}},~i=1,2,...,m \end{aligned}$$

(170)

$$\begin{aligned} \sum _{i=1}^m~x_{ij}\ge & {} F_{b_{j}},~j=1,2,...,n \end{aligned}$$

(171)

$$\begin{aligned} x_{ij}\ge 0,~ y_{ij}=\left\{ \begin{array}{ll} 1, &{} \hbox {if}\, x_{ij}>0; \\ 0, &{} \hbox {otherwise.} \end{array} \right. ~\forall ~ i,j \end{aligned}$$

(172)

Case-IV: $0.75<\alpha \le 1$: Then the equivalent parametric programming problem for the model (156)–(160) is

$$\begin{aligned} Min~\sum _{i=1}^m\sum _{j=1}^n\big [\frac{(2\alpha -1+(4\alpha -3)\theta _{r,ij})c_{ij}^3x_{ij}+2(1-\alpha )c_{ij}^2x_{ij}}{1+(4\alpha -3)\theta _{r,ij}}~+\nonumber \\ \frac{(2\alpha -1+(4\alpha -3)\theta '_{r,ij})d_{ij}^3y_{ij}+2(1-\alpha )d_{ij}^2y_{ij}}{1+(4\alpha -3)\theta '_{r,ij}}\big ] \end{aligned}$$

(173)

$$\begin{aligned} subject~to~~\sum _{j=1}^n~x_{ij}\le & {} F_{a_{i}},~i=1,2,...,m \end{aligned}$$

(174)

$$\begin{aligned} \sum _{i=1}^m~x_{ij}\ge & {} F_{b_{j}},~j=1,2,...,n \end{aligned}$$

(175)

$$\begin{aligned} x_{ij}\ge 0,~ y_{ij}=\left\{ \begin{array}{ll} 1, &{} \hbox {if}\, x_{ij}>0; \\ 0, &{} \hbox {otherwise.} \end{array}\right. ~\forall ~ i,j, \end{aligned}$$

(176)

where,

$$\begin{aligned} F_{a_{i}}=\left\{ \begin{array}{ll} \frac{(1-2\alpha _{i}+(1-4\alpha _{i})\theta _{l,i})a_{i}^3+2\alpha _{i} a_{i}^2}{1+(1-4\alpha _{i})\theta _{l,i}}, &{} \hbox {if }\,0<\alpha _{i}\le 0.25; \\ \frac{(1-2\alpha _{i})a_{i}^3+(2\alpha _{i}+(4\alpha _{i}-1)\theta _{r,i})a_{i}^2}{1+(4\alpha _{i}-1)\theta _{r,i}}, &{} \hbox {if }\,0.25<\alpha _{i}\le 0.5; \\ \frac{(2\alpha _{i}-1)a_{i}^1+(2(1-\alpha _{i})+(3-4\alpha _{i})\theta _{r,i})a_{i}^2}{1+(3-4\alpha _{i})\theta _{r,i}}, &{} \hbox {if }\,0.5<\alpha _{i}\le 0.75; \\ \frac{(2\alpha _{i}-1+(4\alpha _{i}-3)\theta _{l,i})a_{i}^1+2(1-\alpha _{i})a_{i}^2}{1+(4\alpha _{i}-3)\theta _{l,i}}, &{} \hbox {if }\,0.75<\alpha _{i}\le 1. \end{array}\right. \end{aligned}$$

(177)

$$\begin{aligned} F_{b_{j}}=\left\{ \begin{array}{ll} \frac{(1-2\beta _{j}+(1-4\beta _{j})\theta _{r,j})b_{j}^1+2\beta _{j} b_{j}^2}{1+(1-4\beta _{j})\beta _{r,j}}, &{} \hbox {if }\,0<\beta _{j}\le 0.25; \\ \frac{(1-2\beta _{j})b_{j}^1+(2\beta _{j}+(4\beta _{j}-1)\theta _{l,j})b_{j}^2}{1+(4\beta _{j}-1)\theta _{l,j}}, &{} \hbox {if }\,0.25<\beta _{j}\le 0.5; \\ \frac{(2\beta _{j}-1)b_{j}^3+(2(1-\beta _{j})+(3-4\beta _{j})\theta _{l,j})b_{j}^2}{1+(3-4\beta _{j})\theta _{l,j}}, &{} \hbox {if }\,0.5<\beta _{j}\le 0.75; \\ \frac{(2\beta _{j}-1+(4\beta _{j}-3)\theta _{r,j})b_{j}^3+2(1-\beta _{j})b_{j}^2}{1+(4\beta _{j}-3)\theta _{r,j}}, &{} \hbox {if }\,0.75<\beta _{j}\le 1. \end{array}\right. \end{aligned}$$

(178)

Numerical Experiment: To illustrate the Model 4.2 ((152)–(155)) numerically, consider a problem having three sources and two destinations with the following type-2 fuzzy data.

$\tilde{a_{1}}=(16,18,20;0.5,0.8)$, $\tilde{a_{2}}=(15,16,18;0.4,0.6)$, $\tilde{a_{3}}=(14,15,16;0.6,0.9)$

$\tilde{b_{1}}=(20,22,24;0.5,0.5)$, $\tilde{b_{2}}=(18,19,20;0.6,0.8).$

The direct and fixed costs for this problem are given in Table 10.

Table 10. Direct costs and fixed costs

The predetermined general credibility levels for the chance-constrained programming model (156)–(160) as formulated to solve the Model-4.2 are taken as $\alpha =0.9$, $\alpha _{i}=0.9$, $\beta _{j}=0.9$, $i=1,2,3$; $j=1,2$.

Now using (173)–(176), the equivalent parametric programming problem becomes

$$\begin{aligned} Min~\sum _{i=1}^3\sum _{j=1}^2\big [\frac{(0.8+0.6\theta _{r,ij})c_{ij}^3x_{ij}+0.2c_{ij}^2x_{ij}}{1+0.6\theta _{r,ij}}~+ \end{aligned}$$

$$\begin{aligned} \frac{(0.8+0.6\theta '_{r,ij})d_{ij}^3y_{ij}+0.2d_{ij}^2y_{ij}}{1+0.6\theta '_{r,ij}}\big ] \end{aligned}$$

(179)

$$\begin{aligned} subject~to~~\sum _{j=1}^2~x_{ij}\le & {} F_{a_{i}},~i=1,2,3 \end{aligned}$$

(180)

$$\begin{aligned} \sum _{i=1}^3~x_{ij}\ge & {} F_{b_{j}},~j=1,2 \end{aligned}$$

(181)

$$\begin{aligned} x_{ij}\ge 0,~ y_{ij}=\left\{ \begin{array}{ll} 1, &{} \hbox {if}\, x_{ij}>0; \\ 0, &{} \hbox {otherwise.} \end{array} \right. ~\forall ~ i,j \end{aligned}$$

(182)

where $F_{a_{1}}=16.30$, $F_{a_{2}}=15.16$, $F_{a_{3}}=14.14$, $F_{b_{1}}=23.69$ and $F_{b_{2}}=19.86$ are obtained from Eqs. (177) and (178).

Solving this, the optimum results are $x_{12}=16.3$, $x_{21}=13.11$, $x_{31}=10.58$, $x_{32}=3.56$ and the objective function value (minimum transportation cost)= 239.5014.

4.6 Sensitivity Analysis for the Numerical Experiment Of Model 4.2

A sensitivity analysis for the numerical experiment of Model-4.2 is presented to show the efficiency and logically correctness of the crisp equivalent form and solution approaches of the presented problem. For some different generalized credibility levels for the objective function, source constraints and destination constraints of the model representation (156)–(160) formulated to solve the Model 4.2, the changes in the objective function value (minimum transportation cost) are presented in the Table 11.

It is observed from the Table 11 that for fixed credibility levels of the objective function and the source constraints, i.e., for fixed $\alpha$ and $\alpha _{i}(i=1,2,3)$, minimum transportation cost increases with the increased credibility levels $(\beta _{j},j=1,2)$ of the destination constraints. The reason of this fact is that as the credibility levels $\beta _{j}$ increase, the defuzzified amount of the demands $(F_{b_{j}},j=1,2)$ are also increased (e.g., for $\beta _{j}=0.7$, $F_{b_{1}}=22.27$, $F_{b_{2}}=19.35$ and for $\beta _{j}=0.8$, $F_{b_{1}}=23.27$, $F_{b_{2}}=19.65$) and as a result total transported amount also increases.

Now for fixed $\alpha$ and $\beta _{j}(j=1,2)$, minimum transportation cost increases with the increased credibility levels $(\alpha _{i},i=1,2,3)$ of the source constraints. The interesting fact is that in this case, though total transported amounts are the same but still transportation cost increases as the credibility levels $\alpha _{i}(i=1,2,3)$ increase. The reason is that, as the credibility levels $\alpha _{i}(i=1,2,3)$ increase, the defuzzified amount of the availabilities $(F_{a_{i}},i=1,2,3)$ decrease (e.g., for $\alpha _{i}=0.7,$ $F_{a_{1}}=17.31,$ $F_{a_{2}}=15.64,$ $F_{a_{3}}=14.66$ and for $\alpha _{i}=0.8$, $F_{a_{1}}=16.72,$ $F_{a_{2}}=15.37,$ $F_{a_{3}}=14.35$) and as a result for the fixed demand, the allocation options of the product (to the less cost path) decrease.

Table 11. Changes in transportation cost for different credibility levels

Also we observe from the Table 11 that for fixed $\alpha _{i}(i=1,2,3)$ and $\beta _{j}(j=1,2)$ minimum transportation cost increases as the credibility level $\alpha$ increases. This is because in this case defuzzified cost coefficients of the objective function increase with increased credibility level $\alpha$.

4.7 Model 4.3: Multi-item Solid Transportation Problem Having Restriction on Conveyances with Type-2 Fuzzy Parameters

Here, we formulate a multi-item solid transportation problem (MISTP) with restriction on some items and conveyances in the sense that some specific items prohibited to be transported through some particular conveyances. In this problem the transportation parameters, e.g., unit transportation costs, supplies, demands, conveyance capacities are type-2 triangular fuzzy variables.

Notations:

• (i) $\tilde{c_{ijk}^p}$: The unit transportation costs from i-th source to j-th destination by k-th conveyance for p-th item, represented by type-2 fuzzy variable.

• (ii) $x_{ijk}^p$: The decision variable which represents amount of p-th item to be transported from i-th origin to j-th destination by k-th conveyance.

• (iii) Z: The objective function.

• (iv) $\tilde{a_{i}^p}$: The amount of the p-th item available at the i-th origin, represented by type-2 fuzzy variable.

• (v) $\tilde{b_{j}^p}$: The demand of the p-th item at j-th destination, represented by type-2 fuzzy variable.

• (vi) $\tilde{e_{k}}$: Total transportation capacity of conveyance k, represented by type-2 fuzzy variable.

Mathematical Model: Let l items are to be transported from m origins (or sources) $O_{i}~(i=1,2,...,m)$ to n destinations $D_{j}~(j=1,2,...,n)$ by means of K different modes of transportation (conveyance). Also there are some restrictions on some specific items and conveyances such a way that some items can not be transported through some conveyances. Let us denote $I_{k}$ as the set of items which can be transported through conveyance k $(k=1,2,...,K)$. We use notation $p~(=1,2,...,l)$ to denote the items. Then the mathematical formulation of the problem is as follows:

$$\begin{aligned} Min~Z=\sum _{p\in I_{1}}\sum _{i=1}^m\sum _{j=1}^n\tilde{c_{ij1}^p}~x_{ij1}^p~+\sum _{p\in I_{2}}\sum _{i=1}^m\sum _{j=1}^n\tilde{c_{ij2}^p}~x_{ij2}^p~+...+\sum _{p\in I_{K}}\sum _{i=1}^m\sum _{j=1}^n\tilde{c_{ijK}^p}~x_{ijK}^p, \end{aligned}$$

where $|I_{1}\bigcup I_{2}\bigcup ... \bigcup I_{K}|=l$

$$\begin{aligned} =\sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~~d_{ijk}^p.(\tilde{c_{ijk}^p}~x_{ijk}^p), \end{aligned}$$

(183)

$$\begin{aligned} subject~to~\sum _{j=1}^n\sum _{k=1}^K d_{ijk}^p~x_{ijk}^p~\le & {} \tilde{a_{i}^p},~~i=1,2,...,m; p=1,2,...l,\end{aligned}$$

(184)

$$\begin{aligned} \sum _{i=1}^m\sum _{k=1}^K d_{ijk}^p~x_{ijk}^p~~\ge & {} \tilde{b_{j}^p},~~j=1,2,...,n; p=1,2,...,l, \end{aligned}$$

(185)

$$\begin{aligned} \sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n~d_{ijk}^p~x_{ijk}^p\le & {} \tilde{e_{k}},~~k=1,2,...,K, \end{aligned}$$

(186)

$$\begin{aligned} x_{ijk}^p\ge 0,~ \forall ~ i,j,k,p \end{aligned}$$

(187)

where $d_{ijk}^p$ is defined as $d_{ijk}^p=\left\{ \begin{array}{ll} 1, &{} \hbox {if}\, p\in I_{k}; \\ 0, &{} \hbox {otherwise.} \end{array}\right.$ $\forall ~i,j,k,p.$

Solution Methodology 1: Chance-Constrained Programming Using Generalized Credibility: Suppose that $\tilde{c_{ijk}^{p'}}$, $\tilde{a_{i}^{p'}}$, $\tilde{b_{j}^{p'}}$ and $\tilde{e'_{k}}$ are the reduced fuzzy (type-1) variables from type-2 fuzzy variables $\tilde{c_{ijk}^p}$, $\tilde{a_{i}^p}$, $\tilde{b_{j}^p}$ and $\tilde{e_{k}}$ respectively based on CV-based reduction method. Now to solve the above problem we formulate a chance-constrained programming model with these reduced fuzzy parameters. Since the reduced fuzzy parameters $\tilde{c_{ijk}^{p'}}$, $\tilde{a_{i}^{p'}}$, $\tilde{b_{j}^{p'}}$ and $\tilde{e'_{k}}$ may not be normalized, so using generalized credibility for the objective function as well as for the constraints the following chance constrained programming model is formulated for the above problem (183)–(187).

$$\begin{aligned} Min_{x}~(Min_{\bar{f}}~~\bar{f}) \end{aligned}$$

(188)

$$\begin{aligned} \tilde{Cr}\{\sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~~d_{ijk}^p.(\tilde{c_{ijk}^{p'}}~x_{ijk}^p)\le \bar{f}\}\ge \alpha , \end{aligned}$$

(189)

$$\begin{aligned} s.t.~\tilde{Cr}\{\sum _{j=1}^n\sum _{k=1}^K d_{ijk}^p~x_{ijk}^p~\le & {} \tilde{a_{i}^{p'}}\}\ge \alpha _{i}^p,~~i=1,2,...,m; p=1,2,...l,\end{aligned}$$

(190)

$$\begin{aligned} \tilde{Cr}\{\sum _{i=1}^m\sum _{k=1}^K d_{ijk}^p~x_{ijk}^p~\ge & {} \tilde{b_{j}^{p'}}\}\ge \beta _{j}^p,~~j=1,2,...,n; p=1,2,...,l, \end{aligned}$$

(191)

$$\begin{aligned} \tilde{Cr}\{\sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n~d_{ijk}^p~x_{ijk}^p\le & {} \tilde{e'_{k}}\}\ge \gamma _{k},~~k=1,2,...,K, \end{aligned}$$

(192)

$$\begin{aligned} x_{ijk}^p\ge 0,~d_{ijk}^p=\left\{ \begin{array}{ll} 1, &{} \hbox {if}\,p\in I_{k}; \\ 0, &{} \hbox {otherwise.} \end{array}\right. \forall ~ i,j,k,p \end{aligned}$$

(193)

where Min $\bar{f}$ indicates the minimum value that the objective function achieves with generalized credibility at least $\alpha$ $(0<\alpha \le 1)$. $\alpha _{i}^p$, $\beta _{j}^p$ and $\gamma _{k}$ are predetermined generalized credibility levels of satisfaction of the respective constraints for all i, j, k, p.

Crisp Equivalence: We consider $\tilde{c_{ijk}^p}$, $\tilde{a_{i}^p}$, $\tilde{b_{j}^p}$ and $\tilde{e_{k}}$ are all mutually independent type-2 triangular fuzzy variables as $\tilde{c_{ijk}^p}=(c_{ijk}^{p1},c_{ijk}^{p2},c_{ijk}^{p3};\theta _{l,ijk}^p,\theta _{r,ijk}^p)$, $\tilde{a_{i}^p}=(a_{i}^{p1},a_{i}^{p2},a_{i}^{p3};\theta _{l,i}^p,\theta _{r,i}^p)$, $\tilde{b_{j}^p}=(b_{j}^{p1},b_{j}^{p2},b_{j}^{p3};\theta _{l,j}^p,\theta _{r,j}^p)$ and $\tilde{e_{k}}=(e_{k}^1,e_{k}^2,e_{k}^3;\theta _{l,k},\theta _{r,k})$. Then from Theorem-4.1 and its corollary, the chance-constrained model formulation (188)–(193) is turned into the following crisp equivalent parametric programming problems:

Case-I: $0<\alpha \le 0.25$: The equivalent parametric programming problem for model (188)–(193) is

$$\begin{aligned} Min~\sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K d_{ijk}^p\big [\frac{(1-2\alpha +(1-4\alpha )\theta _{r,ijk}^p)c_{ijk}^{p1}x_{ijk}^p+2\alpha c_{ijk}^{p2}x_{ijk}^p}{1+(1-4\alpha )\theta _{r,ijk}^p}\big ], \end{aligned}$$

(194)

$$\begin{aligned} sub.~to~~\sum _{j=1}^n\sum _{k=1}^K d_{ijk}^p~x_{ijk}^p\le & {} F_{a_{i}^p},~i=1,2,...,m;~p=1,2,...l, \end{aligned}$$

(195)

$$\begin{aligned} \sum _{i=1}^m\sum _{k=1}^K d_{ijk}^p~x_{ijk}^p\ge & {} F_{b_{j}^p},~j=1,2,...,n;~p=1,2,...l, \end{aligned}$$

(196)

$$\begin{aligned} \sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n~d_{ijk}^p~x_{ijk}^p\le & {} F_{e_{k}},~k=1,2,...,K, \end{aligned}$$

(197)

$$\begin{aligned} x_{ijk}^p\ge 0,~d_{ijk}^p=\left\{ \begin{array}{ll} 1, &{} \hbox {if}\,p\in I_{k}; \\ 0, &{} \hbox {otherwise.} \end{array} \right. \forall ~ i,j,k,p, \end{aligned}$$

(198)

where $F_{a_{i}^p}$, $F_{b_{j}^p}$ and $F_{e_{k}}$ are given by (214), (215) and (216) respectively.

Case-II: $0.25<\alpha \le 0.5$: Then the equivalent parametric programming problem for model (188)–(193) is

$$\begin{aligned} Min~\sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K d_{ijk}^p\big [\frac{(1-2\alpha )c_{ijk}^{p1}x_{ijk}^p+(2\alpha +(4\alpha -1)\theta _{l,ijk}^p)c_{ijk}^{p2}x_{ijk}^p}{1+(4\alpha -1)\theta _{l,ijk}^p}\big ] \end{aligned}$$

(199)

$$\begin{aligned} sub.~to~~\sum _{j=1}^n\sum _{k=1}^K d_{ijk}^p~x_{ijk}^p\le & {} F_{a_{i}^p},~i=1,2,...,m;~p=1,2,...l, \end{aligned}$$

(200)

$$\begin{aligned} \sum _{i=1}^m\sum _{k=1}^K d_{ijk}^p~x_{ijk}^p\ge & {} F_{b_{j}^p},~j=1,2,...,n;~p=1,2,...l, \end{aligned}$$

(201)

$$\begin{aligned} \sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n~d_{ijk}^p~x_{ijk}^p\le & {} F_{e_{k}},~k=1,2,...,K, \end{aligned}$$

(202)

$$\begin{aligned} x_{ijk}^p\ge 0,~d_{ijk}^p=\left\{ \begin{array}{ll} 1, &{} \hbox {if}\, p\in I_{k}; \\ 0, &{} \hbox {otherwise.} \end{array}\right. \forall ~ i,j,k,p. \end{aligned}$$

(203)

Case-III: $0.5<\alpha \le 0.75$: Then the equivalent parametric programming problem for model (188)–(193) is

$$\begin{aligned} Min~\sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K d_{ijk}^p\big [\frac{(2\alpha -1)c_{ijk}^{p3}x_{ijk}^p+(2(1-\alpha )+(3-4\alpha )\theta _{l,ijk}^p)c_{ijk}^{p2}x_{ijk}^p}{1+(3-4\alpha )\theta _{l,ijk}^p}\big ] \end{aligned}$$

(204)

$$\begin{aligned} sub.~to~~\sum _{j=1}^n\sum _{k=1}^K d_{ijk}^p~x_{ijk}^p\le & {} F_{a_{i}^p},~i=1,2,...,m;~p=1,2,...l, \end{aligned}$$

(205)

$$\begin{aligned} \sum _{i=1}^m\sum _{k=1}^K d_{ijk}^p~x_{ijk}^p\ge & {} F_{b_{j}^p},~j=1,2,...,n;~p=1,2,...l, \end{aligned}$$

(206)

$$\begin{aligned} \sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n~d_{ijk}^p~x_{ijk}^p\le & {} F_{e_{k}},~k=1,2,...,K, \end{aligned}$$

(207)

$$\begin{aligned} x_{ijk}^p\ge 0,~d_{ijk}^p= \left\{ \begin{array}{ll} 1, &{} \hbox {if}\, p\in I_{k}; \\ 0, &{} \hbox {otherwise.} \end{array}\right. \forall ~ i,j,k,p. \end{aligned}$$

(208)

Case-IV: $0.75<\alpha \le 1$: Then the equivalent parametric programming problem for model (188)–(193) is

$$\begin{aligned} Min~\sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K d_{ijk}^p\big [\frac{(2\alpha -1+(4\alpha -3)\theta _{r,ijk}^p)c_{ijk}^{p3}x_{ijk}^p+2(1-\alpha )c_{ijk}^{p2}x_{ijk}^p}{1+(4\alpha -3)\theta _{r,ijk}^p}\big ] \end{aligned}$$

(209)

$$\begin{aligned} sub.~to~~\sum _{j=1}^n\sum _{k=1}^K d_{ijk}^p~x_{ijk}^p\le & {} F_{a_{i}^p},~i=1,2,...,m;~p=1,2,...l, \end{aligned}$$

(210)

$$\begin{aligned} \sum _{i=1}^m\sum _{k=1}^K d_{ijk}^p~x_{ijk}^p\ge & {} F_{b_{j}^p},~j=1,2,...,n;~p=1,2,...l, \end{aligned}$$

(211)

$$\begin{aligned} \sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n~d_{ijk}^p~x_{ijk}^p\le & {} F_{e_{k}},~k=1,2,...,K, \end{aligned}$$

(212)

$$\begin{aligned} x_{ijk}^p\ge 0,~d_{ijk}^p= \left\{ \begin{array}{ll} 1, &{} \hbox {if}\, p\in I_{k}; \\ 0, &{} \hbox {otherwise.} \end{array}\right. \forall ~ i,j,k,p \end{aligned}$$

(213)

where,

$$\begin{aligned} F_{a_{i}^p}= \left\{ \begin{array}{ll} \frac{(1-2\alpha _{i}^p+(1-4\alpha _{i}^p)\theta _{l,i}^p)a_{i}^{p3}+2\alpha _{i}^p a_{i}^{p2}}{1+(1-4\alpha _{i}^p)\theta _{l,i}^p}, &{} \hbox {if}\,0<\alpha _{i}^p\le 0.25; \\ \frac{(1-2\alpha _{i}^p)a_{i}^{p3}+(2\alpha _{i}^p+(4\alpha _{i}^p-1)\theta _{r,i}^p)a_{i}^{p2}}{1+(4\alpha _{i}^p-1)\theta _{r,i}^p}, &{} \hbox {if}\,0.25<\alpha _{i}^p\le 0.5; \\ \frac{(2\alpha _{i}^p-1)a_{i}^{p1}+(2(1-\alpha _{i}^p)+(3-4\alpha _{i}^p)\theta _{r,i}^p)a_{i}^{p2}}{1+(3-4\alpha _{i}^p)\theta _{r,i}^p}, &{} \hbox {if}\,0.5<\alpha _{i}^p\le 0.75; \\ \frac{(2\alpha _{i}^p-1+(4\alpha _{i}^p-3)\theta _{l,i}^p)a_{i}^{p1}+2(1-\alpha _{i}^p)a_{i}^{p2}}{1+(4\alpha _{i}^p-3)\theta _{l,i}^p}, &{} \hbox {if}\,0.75<\alpha _{i}^p\le 1. \end{array}\right. \end{aligned}$$

(214)

$$\begin{aligned} F_{b_{j}^p}=\left\{ \begin{array}{ll} \frac{(1-2\beta _{j}^p+(1-4\beta _{j}^p)\theta _{r,j}^p)b_{j}^{p1}+2\beta _{j}^p b_{j}^{p2}}{1+(1-4\beta _{j}^p)\beta _{r,j}^p}, &{} \hbox {if}\,0<\beta _{j}^p\le 0.25; \\ \frac{(1-2\beta _{j}^p)b_{j}^{p1}+(2\beta _{j}^p+(4\beta _{j}^p-1)\theta _{l,j}^p)b_{j}^{p2}}{1+(4\beta _{j}^p-1)\theta _{l,j}^p}, &{} \hbox {if}\, 0.25<\beta _{j}^p\le 0.5; \\ \frac{(2\beta _{j}p-1)b_{j}^{p3}+(2(1-\beta _{j}^p)+(3-4\beta _{j}^p)\theta _{l,j}^p)b_{j}^{p2}}{1+(3-4\beta _{j}^p)\theta _{l,j}^p}, &{} \hbox {if}\,0.5<\beta _{j}^p\le 0.75; \\ \frac{(2\beta _{j}^p-1+(4\beta _{j}^p-3)\theta _{r,j}^p)b_{j}^{p3}+2(1-\beta _{j}^p)b_{j}^{p2}}{1+(4\beta _{j}^p-3)\theta _{r,j}^p}, &{} \hbox {if}\,0.75<\beta _{j}^p\le 1. \end{array}\right. \end{aligned}$$

(215)

$$\begin{aligned} F_{e_{k}}=\left\{ \begin{array}{ll} \frac{(1-2\gamma _{k}+(1-4\gamma _{k})\theta _{l,k})e_{k}^3+2\gamma _{k} e_{k}^2}{1+(1-4\gamma _{k})\theta _{l,k}}, &{} \hbox {if}\,0<\gamma _{k}\le 0.25; \\ \frac{(1-2\gamma _{k})e_{k}^3+(2\gamma _{k}+(4\gamma _{k}-1)\theta _{r,k})e_{k}^2}{1+(4\gamma _{k}-1)\theta _{r,k}}, &{} \hbox {if}\,0.25<\gamma _{k}\le 0.5; \\ \frac{(2\gamma _{k}-1)e_{k}^1+(2(1-\gamma _{k})+(3-4\gamma _{k})\theta _{r,k})e_{k}^2}{1+(3-4\gamma _{k})\theta _{r,k}}, &{} \hbox {if}\,0.5<\gamma _{k}\le 0.75; \\ \frac{(2\gamma _{k}-1+(4\gamma _{k}-3)\theta _{l,k})e_{k}^1+2(1-\gamma _{k})e_{k}^2}{1+(4\gamma _{k}-3)\theta _{l,k}}, &{} \hbox {if}\,0.75<\gamma _{k}\le 1. \end{array}\right. \end{aligned}$$

(216)

Solution Methodology 2: Using Nearest Interval Approximation: Consider costs $\tilde{c_{ijk}^p}$, supplies $\tilde{a_{i}^p}$, demands $\tilde{b_{j}^p}$ and conveyance capacities $\tilde{e_{k}}$ are all mutually independent type-2 triangular fuzzy variables defined by $\tilde{c_{ijk}^p}=$

$(c_{ijk}^{p1},c_{ijk}^{p2},c_{ijk}^{p3};\theta _{l,ijk}^p,\theta _{r,ijk}^p)$, $\tilde{a_{i}^p}=$ $(a_{i}^{p1},a_{i}^{p2},a_{i}^{p3};\theta _{l,i}^p,\theta _{r,i}^p)$, $\tilde{b_{j}^p}=$ $(b_{j}^{p1},b_{j}^{p2},b_{j}^{p3};\theta _{l,j}^p,\theta _{r,j}^p)$ and $\tilde{e_{k}}=(e_{k}^1,e_{k}^2,e_{k}^3;\theta _{l,k},\theta _{r,k})$. Then we find nearest interval approximations (credibilistic interval approximation, cf. Sect. 4.2) of $\tilde{c_{ijk}^p}$, $\tilde{a_{i}^p}$, $\tilde{b_{j}^p}$ and $\tilde{e_{k}}$, suppose these are $[c_{ijkL}^p,c_{ijkR}^p]$, $[a_{iL}^p,a_{iR}^p]$, $[b_{jL}^p,b_{jR}^p]$ and $[e_{kL},e_{kR}]$ respectively. Then with these nearest interval approximations, the Model (183)–(183) becomes

$$\begin{aligned} Min~Z=\sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~~d_{ijk}^p.([c_{ijkL}^p,c_{ijkR}^p]~x_{ijk}^p) \end{aligned}$$

(217)

$$\begin{aligned} subject~to~ \sum _{j=1}^n\sum _{k=1}^K d_{ijk}^p~x_{ijk}^p~\le & {} [a_{iL}^p,a_{iR}^p],~~i=1,2,...,m; p=1,2,...l,\end{aligned}$$

(218)

$$\begin{aligned} \sum _{i=1}^m\sum _{k=1}^K d_{ijk}^p~x_{ijk}^p~~\ge & {} [b_{jL}^p,b_{jR}^p],~~j=1,2,...,n; p=1,2,...,l, \end{aligned}$$

(219)

$$\begin{aligned} \sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n~d_{ijk}^p~x_{ijk}^p\le & {} [e_{kL},e_{kR}],~~k=1,2,...,K, \end{aligned}$$

(220)

$$\begin{aligned} x_{ijk}^p\ge 0,~d_{ijk}^p=\left\{ \begin{array}{ll} 1, &{} \hbox {if}\,p\in I_{k}; \\ 0, &{} \hbox {otherwise.} \end{array} \right. \forall ~ i,j,k,p. \end{aligned}$$

(221)

Deterministic Form: We first obtain deterministic forms of the uncertain constraints using the idea of possibility degree of interval number (Zhang et al. [161]) representing certain degree by which one interval is larger or smaller than another. Now we denote the left hand side expressions of the source, destination and conveyance capacity constraints, i.e. (218), (219) and (220) respectively of the model (217)–(221) by $S_{i}^p$, $D_{j}^p$ and $E_{k}$ respectively. Here the right hand sides of these constraints are interval numbers and left sides are crisp, then the possibility degree of satisfaction of these constraints are defined as

$$P_{S_{i}^p\le [a_{iL}^p,a_{iR}^p]}=\left\{ \begin{array}{ll} 1, &{} S_{i}^p\le a_{iL}^p; \\ \frac{a_{iR}^p-S_{i}^p}{a_{iR}^p-a_{iL}^p}, &{} a_{iL}^p< S_{i}^p\le a_{iR}^p; \\ 0, &{} S_{i}^p> a_{iR}^p. \end{array} \right. $$

$$P_{D_{j}^p\ge [b_{jL}^p,b_{jR}^p]}=\left\{ \begin{array}{ll} 0, &{} D_{j}^p< b_{jL}^p; \\ \frac{D_{j}^p-b_{jL}^p}{b_{jR}^p-b_{jL}^p}, &{} b_{jL}^p\le D_{j}^p< b_{jR}^p; \\ 1, &{} D_{j}^p> b_{jR}^p. \end{array} \right. $$

$$P_{E_{k}\le [e_{kL},e_{kR}]}=\left\{ \begin{array}{ll} 1, &{} E_{k}\le e_{kL}; \\ \frac{e_{kR}-E_{k}}{e_{kR}-e_{kL}}, &{} e_{kL}< E_{k}\le e_{kR}; \\ 0, &{} E_{k}> e_{kR}. \end{array} \right. $$

Now if the constraints are allowed to be satisfied with some predetermined possibility degree level $\alpha _{i}^p$, $\beta _{j}^p$ and $\gamma _{k}$ $(0\le \alpha _{i}^p,\beta _{j}^p,\gamma _{k}\le 1)$ respectively, i.e. $P_{S_{i}^p\le [a_{iL}^p,a_{iR}^p]}\ge \alpha _{i}^p$, $P_{D_{j}^p\ge [b_{jL}^p,b_{jR}^p]}\ge \beta _{j}^p$ and $P_{E_{k}\le [e_{kL},e_{kR}]}\ge \gamma _{k}$ $\forall ~i,j,k,p$, then the equivalent deterministic inequalities of the respective constraints are obtained as follows:

$$\begin{aligned} S_{i}^p\le & {} a_{iR}^p-\alpha _{i}^p(a_{iR}^p-a_{iL}^p),~i=1,2,...,m;~p=1,2,...,l, \end{aligned}$$

(222)

$$\begin{aligned} D_{j}^p\ge & {} b_{jL}^p+\beta _{j}^p(b_{jR}^p-b_{jL}^p),~j=1,2,...,n;~p=1,2,...,l,\end{aligned}$$

(223)

$$\begin{aligned} E_{k}\le & {} e_{kR}-\gamma _{k}(e_{kR}-e_{kL}),~k=1,2,...,K. \end{aligned}$$

(224)

Now to deal with objective function we find minimum possible objective function value (say $\underline{Z}$) and maximum possible objective function value (say $\overline{Z}$) for the interval costs $[c_{ijkL}^p,c_{ijkR}^p]$, by solving the following two problems:

$$\begin{aligned}&\underline{Z}= Min_{c_{ijkL}^p\le c_{ijk}^p\le c_{ijkR}^p} [Min~\sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~d_{ijk}^p(c_{ijk}^p~x_{ijk}^p)]\end{aligned}$$

(225)

$$\begin{aligned}&\overline{Z}= Max_{c_{ijkL}^p\le c_{ijk}^p\le c_{ijkR}^p} [Min~\sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~d_{ijk}^p(c_{ijk}^p~x_{ijk}^p)] \end{aligned}$$

(226)

subject to the above constraints (4.99)–(4.101) for both cases.

So we get the range of the optimal value of the objective function of the problem (217)–(221) as $[\underline{Z},\overline{Z}]$. Assume that the solution of the problem (225) is $x^\prime =\{x_{ijk}^{p^\prime }\}$ with corresponding costs $c^\prime =\{c_{ijk}^{p^\prime }\}$ and the solution of the problem (226) is $x^{\prime \prime }=\{x_{ijk}^{p^{\prime \prime }}\}$ with corresponding costs $c^{\prime \prime }=\{c_{ijk}^{p^{\prime \prime }}\}$, $\forall ~i,j,k,p.$

Now we find compromise optimal solution by treating above problems (225) and (226) together as bi-objective problem and applying fuzzy linear programming (Zimmermann [159]) as follows:

Let us denote

$Z_{1}=\sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~d_{ijk}^p(c_{ijk}^{p^\prime }~x_{ijk}^p)$ and

$Z_{2}=\sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~d_{ijk}^p(c_{ijk}^{p^{\prime \prime }}~x_{ijk}^p)$, so that $Z_{1}(x_{ijk}^{p^\prime })=\underline{Z}$ and $Z_{2}(x_{ijk}^{p^{\prime \prime }})=\overline{Z}$.

Now we find lower and upper bound for both the objective as $L_{1}=Z_{1}(x_{ijk}^{p^\prime })$, $U_{1}=Z_{1}(x_{ijk}^{p^{\prime \prime }})$ and $L_{2}=Z_{2}(x_{ijk}^{p^{\prime \prime }})$, $U_{2}=Z_{2}(x_{ijk}^{p^\prime })$ respectively.

Then construct the following two membership function for the objective functions respectively as

$$\mu _{1}(Z_{1})=\left\{ \begin{array}{ll} 1, &{} \hbox {if}\, Z_{1}\le L_{1}; \\ \frac{U_{1}-Z_{1}}{U_{1}-L_{1}}, &{} \hbox {if}\, L_{1}<Z_{1}<U_{1}; \\ 0, &{} \hbox {if}\, Z_{1}\ge U_{1}. \end{array} \right. ~ and~ \mu _{2}(Z_{2})=\left\{ \begin{array}{ll} 1, &{} \hbox {if}\, Z_{2}\le L_{2}; \\ \frac{U_{2}-Z_{2}}{U_{2}-L_{2}}, &{} \hbox {if}\, L_{2}<Z_{2}<U_{2}; \\ 0, &{} \hbox {if}\, Z_{2}\ge U_{2}. \end{array} \right. $$

Finally solve the following problem

$$Max~\lambda $$

$$\begin{aligned} subject~to~\mu _{1}(Z_{1})\ge \lambda ,~\mu _{2}(Z_{2})\ge \lambda \end{aligned}$$

(227)

$$\begin{aligned} \text { and the constraints } (222){-}(224) \end{aligned}$$

$$0\le \lambda \le 1.$$

Solving this we get the optimal solution, say $x_{ijk}^{p*}$, $\forall ~i,j,k,p$ which minimizes both the objectives $Z_{1},Z_{2}$ with certain degree $\lambda =\lambda ^*$ (say) and values of the objectives $Z_{1},Z_{2}$ at $x_{ijk}^{p*}$ give the range of the objective value, say $[\underline{Z}^*,\overline{Z}^*]$.

Numerical Experiment: Consider the Model 4.3 ((183)–(187)) with 3 $(p=1,2,3)$ items, 4 $(k=1,2,3,4)$ conveyances, sources $i=1,2$ and destinations $j=1,2,3$. Also $I_{1}=\{1,2\}$, $I_{2}=\{1,2,3\}$, $I_{3}=\{3\}$, $I_{4}=\{1,2\}$.

The transportation costs are given in the Tables 12, 13 and 14.

Table 12. Costs $\tilde{c_{ijk}^{1}}$

Table 13. Costs $\tilde{c_{ijk}^{2}}$

Table 14. Costs $\tilde{c_{ijk}^{3}}$

The supplies, demands and conveyance capacities are as follows:

$a_{1}^1=(21,24,25;0.5,0.5)$, $a_{2}^1=(26,28,30;0.6,0.8)$, $b_{1}^1=(10,12,14;0.7,0.9)$, $b_{2}^1=(12,13,15;0.4,0.7)$, $b_{3}^1=(9,12,15;0.4,0.6)$,

$a_{1}^2=(26,28,31;0.5,1)$, $a_{2}^2=(20,24,26;0.6,0.8)$, $b_{1}^2=(14,16,17;0.4,0.6)$, $b_{2}^2=(11,13,15;0.8,0.5)$, $b_{3}^2=(10,11,12;0.5,0.5)$,

$a_{1}^3=(24,26,28;0.6,0.9)$, $a_{2}^3=(32,35,37;0.8,0.5)$, $b_{1}^3=(16,18,20;0.4,0.6)$, $b_{2}^3=(12,14,16;0.6,1)$, $b_{3}^3=(12,15,17;0.5,0.5)$,

$e_{1}=(34,36,38;0.5,1)$, $e_{2}=(46,49,51;0.6,0.8)$, $e_{3}=(28,30,32;0.7,0.9)$, $e_{4}=(40,43,44;0.5,0.5)$.

Solution Using Chance-Constrained Programming (c.f. Sect. 4.7 ): The predetermined general credibility levels for objective function and constraints are taken as $\alpha =0.9$, $\alpha _{i}^p=0.9$, $\beta _{j}^p=0.9$, $\gamma _{k}=0.9$, $p=1,2,3$, $i=1,2$, $j=1,2,3$, $k=1,2,3,4$. Then using (209)–(213) the equivalent deterministic form of the problem becomes

$$\begin{aligned} Min~\sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K d_{ijk}^p\big [\frac{(0.8+0.6\theta _{r,ijk}^p)c_{ijk}^{p3}x_{ijk}^p+0.2c_{ijk}^{p2}x_{ijk}^p}{1+0.6\theta _{r,ijk}^p}\big ] \end{aligned}$$

$$\begin{aligned} sub. to~~\sum _{j=1}^n\sum _{k=1}^K d_{ijk}^p~x_{ijk}^p\le & {} F_{a_{i}^p},~i=1,2,...,m;~p=1,2,...l, \end{aligned}$$

(228)

$$\begin{aligned} \sum _{i=1}^m\sum _{k=1}^K d_{ijk}^p~x_{ijk}^p\ge & {} F_{b_{j}^p},~j=1,2,...,n;~p=1,2,...l, \\ \sum _{p=1}^l\sum _{i=1}^m\sum _{j=1}^n~d_{ijk}^p~x_{ijk}^p\le & {} F_{e_{k}},~k=1,2,...,K, \end{aligned}$$

$$x_{ijk}^p\ge 0,~d_{ijk}^p=\left\{ \begin{array}{ll} 1, &{} \hbox {if}\,p\in I_{k}; \\ 0, &{} \hbox {otherwise.} \end{array}\right. \forall ~ i,j,k,p,$$

where, $F_{a_{1}^1}=21.46$, $F_{a_{2}^1}=26.29$, $F_{a_{1}^2}=26.30$, $F_{a_{2}^2}=20.58$, $F_{a_{1}^3}=24.29$, $F_{a_{2}^3}=32.40$, $F_{b_{1}^1}=13.74$, $F_{b_{2}^1}=14.71$, $F_{b_{3}^1}=14.55$, $F_{b_{1}^2}=16.85$, $F_{b_{2}^2}=14.69$, $F_{b_{3}^2}=11.84$, $F_{b_{1}^3}=19.70$, $F_{b_{2}^3}=15.75$, $F_{b_{3}^3}=16.69$, $F_{e_{1}}=34.30$, $F_{e_{2}}=46.44$, $F_{e_{3}}=28.28$, $F_{e_{4}}=40.46$.

Solving this problem using LINGO solver, based upon Generalized Reduced Gradient (GRG) algorithm, we get the optimum solution as follows:

$x_{111}^1=6.75$, $x_{211}^1=6.99$, $x_{231}^1=5.07$, $x_{232}^1=9.48$,$x_{124}^1=14.71$, $x_{211}^2=3.65$, $x_{231}^2=$11.84, $x_{122}^2=13.1$,$x_{114}^2=13.2$, $x_{224}^2=1.59$, $x_{122}^3=7.17$, $x_{132}^3=8.54$, $x_{232}^3=8.15$, $x_{123}^3=8.58$, $x_{213}^3=19.7$ and minimum transportation cost (objective value)= 1093.482.

Solution Using Nearest Interval Approximation (c.f. Sect. 4.7 ): The nearest interval approximations (credibilistic) of the given triangular type-2 fuzzy parameters are calculated using the formula (145) and (146).

Table 15. Costs $\tilde{c_{ijk}^{1}}$

Table 16. Costs $\tilde{c_{ijk}^{2}}$

Table 17. Costs $\tilde{c_{ijk}^{3}}$

The corresponding unit transportation costs as obtained are presented in Tables 15, 16 and 17 and supplies, demands, capacities are as follows:

$a_{1}^1=[22.50,24.50]$, $a_{2}^1=[26.9904,29.0095]$, $b_{1}^1=[10.9910,13.0089]$,

$b_{2}^1=[12.4920,14.0158]$, $b_{3}^1=[10.4835,13.5164]$,

$a_{1}^2=[26.9767,29.5348]$, $a_{2}^2=[21.9809,25.0095]$, $b_{1}^2=[14.9890,16.5054]$, $b_{2}^2=[12.0148,13.9851]$, $b_{3}^2=[10.50,11.50]$,

$a_{1}^3=[24.9861,27.0138]$, $a_{2}^3=[33.5222,35.9851]$, $b_{1}^3=[16.9890,19.0109]$, $b_{2}^3=[12.9820,15.0179]$, $b_{3}^3=[13.50,16.0]$,

$e_{1}=[34.9767,37.0232]$, $e_{2}=[47.4856,50.0095]$, $e_{3}=[28.9910,31.0089]$, $e_{4}=[41.50,43.50]$.

Consider that the possibility degree of satisfaction of each of the source, destination and conveyance capacity constraints with interval right hand sides is 0.9. Then the equivalent deterministic forms of all the constraints are obtained using (222)–(224). Now subject to these deterministic constraints we find minimum and maximum possible value of the objective function by solving (225) and (226) and corresponding optimal solutions are obtained as follows:

$\underline{Z}=725.9498$; $x_{131}^1=13.2131$, $x_{211}^1=10.5682$, $x_{112}^1=2.2388$, $x_{122}^1=7.2480$, $x_{222}^1=6.6154$, $x_{231}^2=11.4$, $x_{122}^2=10.8787$, $x_{114}^2=16.3537$, $x_{224}^2=2.9093$, $x_{122}^3=4.4302$, $x_{132}^3=10.3745$, $x_{232}^3=5.3754$, $x_{123}^3=10.3840$, $x_{213}^3=18.8087$ and $\overline{Z}=950.1511$; $x_{111}^1=8.8365$, $x_{211}^1=3.9705$, $x_{231}^1=10.6858$, $x_{122}^1=13.8634$, $x_{232}^1=2.5272$, $x_{211}^2=0.2883$, $x_{231}^2=11.4$, $x_{122}^2=11.1671$, $x_{114}^2=16.0654$, $x_{224}^2=2.6209$, $x_{122}^3=4.4302$, $x_{132}^3=10.3745$, $x_{232}^3=5.3754$, $x_{123}^3=10.3840$, $x_{111}^3=18.8087$.

We now apply fuzzy linear programming to obtain an unique optimum allocation. We get $L_{1}=725.9498$, $U_{1}=741.4106$, $L_{2}=950.1511$, $U_{2}=956.9979$ and hence compromise optimal solution as

$x_{111}^1=0.2095$, $x_{131}^1=8.6270$, $x_{211}^1=12.5975$, $x_{231}^1=2.3472$, $x_{122}^1=13.8634$, $x_{232}^1=2.2388$, $x_{231}^2=11.4$, $x_{122}^2=10.8787$, $x_{114}^2=16.3537$, $x_{224}^2=2.9093$, $x_{122}^3=4.4302$, $x_{132}^3=10.3745$, $x_{232}^3=5.3754$, $x_{123}^3=10.3840$, $x_{213}^3=18.8087$, $\lambda =0.987$, $\underline{Z}^*=726.1475$, $\overline{Z}^*=950.2386$.

4.8 Overall Conclusion

In this section, a defuzzification method of general type-2 fuzzy variable is outlined and compared numerically with geometric defuzzification method. A nearest interval approximation for continuous T2 FV is also introduced. Interval approximation method has been illustrated with type-2 triangular fuzzy variable. For the first time, two FCTPs and a MISTP with type-2 fuzzy parameters have been formulated and solved. Chance-constrained programming problems for a FCTP and MISTP with type-2 triangular fuzzy variables are formulated and solved. The MISTP with type-2 triangular fuzzy parameters is also solved using interval approximations of type-2 triangular fuzzy variables. Now-a-days, the volume and complexity of the collected data in various fields is growing rapidly. In order to describe and extract the useful information hidden in uncertain data and to use this data properly in practical problems, many researchers have proposed a number of improved theories including type-2 fuzzy set. The methodologies used in this chapter are quite general and these can be applied to the decision making problems in different areas with type-2 fuzzy parameters. The presented models can be extended to different types of transportation problems including price discounts, transportation time constraints, breakable/deteriorating items, etc.

5 Transportation Mode Selection Problem with Linguistic Terms

5.1 Introduction

Solid transportation problem (STP) is a problem of transporting goods from some sources to some destinations through several types of conveyances (modes of transportation) and the objective may be minimization of cost, time, maximization of profit, etc. But cost or time may not be the only criteria for selecting modes. There may be several other criteria for which all modes may not be equally preferable in a transportation system. Generally the available modes of transportation are rail, road, water, air, pipeline etc. Choice of modes depends upon several parameters (criteria) such as transportation cost, time, distance, product characteristics (e.g. weight, volume, value, life cycle etc.), flexibility, safety factor, inventory cost, etc. The main difficulty to select best mode is the conflicting nature of the modes under different criteria, i.e., under certain criteria, a mode may be superior than another but may not be under another criteria. Also all the criteria related to a transportation system may not have equal priority. For example generally faster modes are preferable than slower modes for time saving, but for product having low value to weight ratio, slower modes are preferable for transportation cost saving and in this case time has less priority than transportation cost. The product having short life cycle need rapid transportation modes, because here the main priority is time saving. So the tusk is to select overall best transportation mode with respect to all the selection criteria in a transportation system. Obviously multi-criteria (/attribute) decision making (MCDM/MADM), which is a procedure to determine best alternative among some feasible alternatives, can be an efficient method to solve transportation mode selection problem. In literature there are several articles available related to transportation mode selection problem (Kiesmüller et al. [65], Kumru and Kumru [71], Monahan and Berger [113], Tuzkaya and Önüt [134], Eskigun et al. [41], Wang and Lee [138]).

Multi-criteria (/attribute) decision making (MCDM/MADM) (Anand et al. [7], Baleentis and Zeng [10], Chen and Lee [23, 24], Chen et al. [26], Dalalah et al. [32], Ding and Liang [37], Fu [45], Wang and Lee [139], Wang and Parkan [32], Wu and Chen [148]), is a method to select most convenient alternative among some available alternatives with respect to some evaluation criteria provided by decision maker(s) for a particular problem. This type of problems are often called multi-criteria(/attribute) group decision making (MCGDM/MAGDM) problem in presence of several decision makers. The evaluation ratings of the alternatives with respect to the criteria and criteria weights as provided by the decision makers are generally linguistic terms (e.g., very high, medium, fair, good, etc.). Human judgements are not always precise and also a word does not have the same meaning to different people and is therefore uncertain. Zadeh [157, 158] first used a fuzzy set (Zadey [156]) to model a word. Many researchers (Anand et al. [7], Cheng and Lin [28], Dalalah et al. [32], Ding and Liang [37], Dursun et al. [39], Hatami-Marbini and Tavana [55], Tuzkaya and Önüt [134], Wang and Lee [139], Wang and Parkan [142]) developed MCDM problems where type-1 fuzzy sets(/numbers) are used to describe linguistic uncertainties rather than just single numeric value. Then the problem is called fuzzy multi-criteria decision making (FMCDM) problem in which evaluation ratings and criteria weights are fuzzy numbers.

Fuzzy analytical hierarchy process (FAHP) (Anand et al. [7], Chan, N. Kumar [16], Mikhailov and Tsvetinov [111]), Fuzzy analytical network process (FANP) (Ertay et al. [40], Mikhailov and Sing [110], Tuzkaya and Önüt [134]), fuzzy preference relation based decision making (Lee [78], Wang [137]), fuzzy TOPSIS method (Chen [20], Wang and Elhag [141], Wang et al. [140], Wang and Lee [139]) are some available methods for solving FMCDM problems. The main drawback of the FAHP and FANP methods is that these methods consist of large number of fuzzy pair-wise comparison which makes the methods difficult for computation. Lee’s (Lee [78]) method using extended fuzzy preference relation is computationally efficient, but in case of two alternatives, whatever the ratings of the two alternatives are, this method always gives total performance index of one alternative as 1 and that of another 0. So it is difficult to compare the alternatives with each other in the sense how much one is preferable than another and to use the performance indices in any further requirements. In fuzzy TOPSIS method of Wang and Elhag [141], for each member of fuzzy decision matrix, different $\alpha$-level sets are to be evaluated and for each different $\alpha$-levels, two NLP models are to be solved. So to find accurate result, large number of $\alpha$-levels are to be set and then corresponding time complexity becomes high. Fuzzy TOPSIS of Wang et al. [140] is less complex, but the positive and negative ideal solutions as derived by Max and Min operations under fuzzy environment may not be founded on feasible alternatives.

Ranking of fuzzy number is an important issue in group decision making, specially for decision making with linguistic terms, which are generally represented by fuzzy numbers. There are several methods of fuzzy ranking (Abbasbandy and Asady [1], Cheng [27], Chu and Tsao [29], Fortems and Roubens [44], Liu [90], Lee [78], Liou and Wang [100]) available in the literature, each of which has some advantages and disadvantages. Also many ranking methods are based on defuzzification (e.g., expected value (Liu [90]), centroid (Wang et al. [143]), magnitude (Abbasbandy and Hajjari [2]) of fuzzy number) in which, from fuzzy numbers corresponding crisp quantities are obtained using some utility functions and fuzzy numbers are ranked according to these crisp values. Drawback of defuzzification is that it tends to loss some information and thus is unable to grasp the sense of uncertainty. For example, expected value (Liu and Liu [90]) of a trapezoidal fuzzy number $(r_{1},r_{2},r_{3},r_{4})$ is just the average $(r_{1}+r_{2}+r_{3}+r_{4})/4$, though each $r_{i}$ does not have the same membership (/possibility) degree. Some of the techniques (Abbasbandy and Asady [1], Chen [19]; Liou and Wang [100]) are case dependent and produce different results in different cases for certain fuzzy numbers. Also some methods are found to be logically incorrect. For example, Asady and Zendehnam’s [8] distance minimization method and Chen’s [19] method are seemed to be logically incorrect as shown by Abbasbandy and Hajjari [2] and Liou and Wang [100] respectively.

Mendel [102] explained using Popper’s Falsificationism that modeling word using type-1 fuzzy set is not scientifically correct. Mendel [102, 103] also explained that a sensible way to model a word is to using interval type-2 fuzzy set (IT2 FS). There are some methodologies, such as the interval approach (Liu and Mendel [95], the person membership function approach (Mendel [104]) and the interval end-points approach (Mendel and Wu [108]) available to obtain mathematical models for IT2 FS for words. Chen and Lee [23, 24] developed fuzzy multiple attributes group decision-making methods (FMAGDM) based on ranking IT2 FSs and interval type-2 TOPSIS method respectively where linguistic weights are represented by IT2 FSs. Chen et al. [26], Chen and Wang [25] developed FMAGDM method based on ranking IT2 FSs.

In this section, a new ranking method of fuzzy numbers is developed using a ranking function which we define using credibility measure. This ranking function is bounded over [0,1] so that it is easy to compare two fuzzy numbers with each other. We also provide a method of ranking interval type-2 fuzzy variables (IT2 FVs) using a ranking function which we define with the help of generalized credibility measure. Then we propose two computationally efficient fuzzy MCGDM (FMCGDM) methods, first one based on proposed ranking method of fuzzy numbers and the second one based on the proposed ranking method of IT2 FVs. We discuss how to assign weights of modes if a decision maker wish, to a STP in addition to the main criteria. The proposed FMCGDM methods are applied to two transportation mode selection problems where evaluation ratings and criteria weights are expressed by linguistic terms.

5.2 Theoretical Developments

In the following Subsects. 5.4 and 5.6 we have developed two fuzzy multi-criteria group decision making process, first one based on ranking fuzzy numbers and second one based on ranking interval type-2 fuzzy variables. For the construction of the methods we need some results which are given below.

Theorem 5.1:

For any two trapezoidal fuzzy numbers $\tilde{A}=(a_{1},a_{2},a_{3},a_{4})$ and $\tilde{B}=(b_{1},b_{2},b_{3},b_{4})$, $Cr\{\tilde{A}\le \tilde{B}\}\ge \alpha$ if and only if

$$(1-2\alpha )(a_{1}-b_{4})+2\alpha (a_{2}-b_{3})\le 0~~for~\alpha \le 0.5$$

$$2(1-\alpha )(a_{3}-b_{2})+(2\alpha -1)(a_{4}-b_{1})\le 0~~for~\alpha > 0.5.$$

Proof: $Cr\{\tilde{A}\le \tilde{B}\}\ge \alpha \Leftrightarrow$ $Cr\{(\tilde{A}-\tilde{B})\le 0\}\ge \alpha \Leftrightarrow Cr\{(\tilde{A}+\tilde{B'})\le 0\}\ge \alpha$, where $\tilde{B'}=-\tilde{B}=(-b_{4},-b_{3},-b_{2},-b_{1})$.

Then the theorem follows from Theorem 3.3 (Sect. 3).

Corollary 5.1

For any two trapezoidal fuzzy numbers $\tilde{A}=(a_{1},a_{2},a_{3},a_{4})$ and $\tilde{B}=(b_{1},b_{2},b_{3},b_{4})$, $Cr\{\tilde{A}\ge \tilde{B}\}\ge \alpha$ if and only if

$$(1-2\alpha )(a_{4}-b_{1})+2\alpha (a_{3}-b_{2})\ge 0~~for~\alpha \le 0.5$$

$$2(1-\alpha )(a_{2}-b_{3})+(2\alpha -1)(a_{1}-b_{4})\ge 0~~for~\alpha > 0.5.$$

Theorem 5.2:

For any two triangular fuzzy numbers $\tilde{A}=(a_{1},a_{2},a_{3})$ and $\tilde{B}=(b_{1},b_{2},b_{3})$, $Cr\{\tilde{A}\le \tilde{B}\}\ge \alpha$ if and only if

$$(1-2\alpha )(a_{1}-b_{3})+2\alpha (a_{2}-b_{2})\le 0~~for~\alpha \le 0.5$$

$$2(1-\alpha )(a_{2}-b_{2})+(2\alpha -1)(a_{3}-b_{1})\le 0~~for~\alpha > 0.5.$$

Corollary 5.2

For any two triangular fuzzy numbers $\tilde{A}=(a_{1},a_{2},a_{3})$ and $\tilde{B}=(b_{1},b_{2},b_{3})$, $Cr\{\tilde{A}\ge \tilde{B}\}\ge \alpha$ if and only if

$$(1-2\alpha )(a_{3}-b_{1})+2\alpha (a_{2}-b_{2})\ge 0~~for~\alpha \le 0.5$$

$$2(1-\alpha )(a_{2}-b_{2})+(2\alpha -1)(a_{1}-b_{3})\ge 0~~for~\alpha > 0.5.$$

5.3 A New Approach for Ranking of Fuzzy Numbers

To rank fuzzy numbers $\tilde{A}$ and $\tilde{B}$, we propose to find the possible credibility degree to which $\tilde{A}\ge \tilde{B}$ or $\tilde{A}\le \tilde{B}$. For this purpose we find the maximum satisfied credibility degree that $\tilde{A}\ge \tilde{B}$ or maximum satisfied credibility degree that $\tilde{A}\le \tilde{B}$, i.e.

$$\begin{aligned} Max_{\alpha \in [0,1]} [Cr\{\tilde{A}\ge \tilde{B}\}=\alpha ] \end{aligned}$$

(229)

$$\begin{aligned} or,~Max_{\alpha \in [0,1]} [Cr\{\tilde{A}\le \tilde{B}\}=\alpha ]. \end{aligned}$$

(230)

We denote (229) by $M_{\alpha }(\tilde{A}\ge \tilde{B})$ and (230) by $M_{\alpha }(\tilde{A}\le \tilde{B})$.

Suppose for two fuzzy numbers $\tilde{A}$ and $\tilde{B}$, $M_{\alpha }(\tilde{A}\ge \tilde{B})=\alpha ^\prime$, then we say that $\tilde{A}\ge \tilde{B}$ with credibility $\alpha ^\prime$.

Example 5.1

Suppose $\tilde{A}$ and $\tilde{B}$ be two trapezoidal fuzzy numbers defined by $\tilde{A}=(a_{1},a_{2},a_{3},a_{4})$ and $\tilde{B}=(b_{1},b_{2},b_{3},b_{4})$. Then from Corollary 5.1 it follows that $M_{\alpha }(\tilde{A}\ge \tilde{B})$=$Max_{\alpha \in [0,1]} [Cr\{\tilde{A}\ge \tilde{B}\}=\alpha ]$ is obtained by solving

$$Max ~\alpha $$

$$\begin{aligned} (1-2\alpha )(a_{4}-b_{1})+2\alpha (a_{3}-b_{2})\ge 0~~for~0\le \alpha \le 0.5\\ 2(1-\alpha )(a_{2}-b_{3})+(2\alpha -1)(a_{1}-b_{4})\ge 0~~for~0.5<\alpha \le 1\nonumber \end{aligned}$$

(231)

$$0\le \alpha \le 1.$$

As our object is to find maximum possible credibility degree $\alpha$, an easy way of solving (231) is that first solve Max $\alpha$ with respect to the second constraint, if such $\alpha$ $(0.5<\alpha \le 1)$ exist then this is the required solution and if it does not exist then solve Max $\alpha$ with respect to the first constraint.

If we consider $\tilde{A}=(4,6,7,9)$ and $\tilde{B}=(2,3,5,7)$, then

$M_{\alpha }(\tilde{A}\ge \tilde{B})$=$Max_{\alpha \in [0,1]} [Cr\{\tilde{A}\ge \tilde{B}\}=\alpha ]=0.625$.

Example 5.2

Suppose $\tilde{A}$ and $\tilde{B}$ be two triangular fuzzy numbers defined by $\tilde{A}=(a_{1},a_{2},a_{3})$ and $\tilde{B}=(b_{1},b_{2},b_{3})$. Then from Corollary 5.2 it follows that $M_{\alpha }(\tilde{A}\ge \tilde{B})$=$Max_{\alpha \in [0,1]} [Cr\{\tilde{A}\ge \tilde{B}\}=\alpha ]$ is obtained by solving

$$Max ~\alpha $$

$$\begin{aligned} (1-2\alpha )(a_{3}-b_{1})+2\alpha (a_{2}-b_{2})\ge 0~~for~0\le \alpha \le 0.5\\ 2(1-\alpha )(a_{2}-b_{2})+(2\alpha -1)(a_{1}-b_{3})\ge 0~~for~0.5<\alpha \le 1\nonumber \end{aligned}$$

(232)

$$0\le \alpha \le 1.$$

For example if $\tilde{A}=(2,4,6)$ and $\tilde{B}=(3,5,6)$ then

$M_{\alpha }(\tilde{A}\ge \tilde{B})$=$Max_{\alpha \in [0,1]} [Cr\{\tilde{A}\ge \tilde{B}\}=\alpha ]=0.375$.

Ranking Function: We define ranking function R to rank one fuzzy number $\tilde{A}$ upon another fuzzy number $\tilde{B}$ as follows:

$$\begin{aligned} R(\tilde{A},\tilde{B})=\left\{ \begin{array}{ll} M_{\alpha }(\tilde{A}\ge \tilde{B}), &{} \hbox {if it exist;} \\ 0, &{} \hbox {otherwise.} \end{array}\right. \end{aligned}$$

(233)

Table 18. Comparative results of Example 5.3

Obviously

$$\begin{aligned} R(\tilde{B},\tilde{A})=\left\{ \begin{array}{ll} M_{\alpha }(\tilde{A}\le \tilde{B}), &{} \hbox {if it exist;} \\ 0, &{} \hbox {otherwise.} \end{array}\right. \end{aligned}$$

(234)

It follows from the definition of $R(\tilde{A},\tilde{B})$ and self-duality property of the credibility measure that R is reciprocal, i.e., $R(\tilde{A},\tilde{B})=1-R(\tilde{B},\tilde{A})$. Also from (231) and (232) it is clear that R is transitive for trapezoidal or triangular fuzzy numbers, i.e. $R(\tilde{A},\tilde{B})\ge 1/2$ and $R(\tilde{B},\tilde{C})\ge 1/2$ $\Rightarrow$ $R(\tilde{A},\tilde{C})\ge 1/2$ for any trapezoidal or triangular fuzzy numbers $\tilde{A}$, $\tilde{B}$, $\tilde{C}$. So R is total ordering and satisfies all the criteria proposed by Yuan [154]. For any two fuzzy numbers $\tilde{A}$ and $\tilde{B}$, the ranking of $\tilde{A}$, $\tilde{B}$ is done as follows:

• (i) $\tilde{A}\succ \tilde{B}$ iff $R(\tilde{A},\tilde{B})>1/2.$

• (ii) $\tilde{A}\prec \tilde{B}$ iff $R(\tilde{A},\tilde{B})<1/2.$

• (iii) But if $R(\tilde{A},\tilde{B})=1/2$, then it is difficult to determine which is larger and which is smaller. In this case we may conclude $\tilde{A}\sim \tilde{B}$.

Example 5.3

Consider the following sets.

Set 1: $\tilde{A}=(4,6,7,9)$, $\tilde{B}=(2,3,5,7)$;

Set 2: $\tilde{A}=(3,3.5,4)$, $\tilde{B}=(2,3.3,5)$

Set 3: $\tilde{A}=(2,4,5,6)$, $\tilde{B}=(2,3,5,7)$

A comparative results of our proposed method and several other methods are presented in Table 18.

Remark:

From the Table 18 we observe that when value of $R(\tilde{A},\tilde{B})$ (i.e. the credibility that $\tilde{A}\ge \tilde{B}$) in our proposed method is far from 0.5 (larger or smaller than 0.5), then all the methods give the same result. For example for Set 1, $R(\tilde{A},\tilde{B})=0.625$ and all methods give the same result that $\tilde{A}\succ \tilde{B}$. But as the credibility becomes close to 0.5, all methods do not give the same result. For example for the Set 3, results of our proposed method, Expected value (Liu [90]), Sign distance for $p=1$ (Abbasbandy and Asady [1]), Lee’s [78], Liou and Wang’s [100], Fortems and Roubens’s [44] methods are $\tilde{A}\sim \tilde{B}$, but Sign distance for $p=2$ (Abbasbandy and Asady [1]), Cheng distance (Cheng [27]) methods give $\tilde{A}\prec \tilde{B}$ and Chu and Tsao’s [29], Abbasbandy and Hajjari’s [2] methods furnish $\tilde{A}\succ \tilde{B}$.

5.4 The Proposed FMCGDM Method Based on Ranking Fuzzy Numbers

Suppose $A_{1}, A_{2}, ..., A_{m}$ are m alternatives and these alternatives are evaluated on basis of the criteria $C_{1}, C_{2},...,C_{n}$ by the decision makers $D_{l}, l=1,2,...,p$. Suppose rating of $A_{i}$ based on criteria $C_{j}$ according to the decision maker $D_{l}$ is $\tilde{A}_{ij}^l$ which is represented by fuzzy number, where $i=1,2,...,m$, $j=1,2,...,n$ and $l=1,2,...,p$. Let $\tilde{w}_{j}^l$ be the fuzzy weight of the criteria $C_{j}$ indicating its importance given by the decision maker $D_{l}$ for all j and l. The proposed fuzzy MCGDM method to rank the alternatives is as follows:

Step-1: Construct the decision matrix $\tilde{D}=[\tilde{A}_{ij}]_{m\times n}$ where each $\tilde{A}_{ij}$ is the average of the ratings of alternative $A_{i}$ given by the decision makers $D_{l}, l=1,2,...,p$ based on criteria $C_{j}$, i.e.,

$$\begin{array}{cccc} C_{1}&C_{2}&....&C_{n} \end{array}$$

$$\tilde{D}=\begin{array}{c} A_{1} \\ A_{2} \\ \vdots \\ A_{m} \end{array} \begin{bmatrix} \tilde{A}_{11}&\tilde{A}_{12}&...&\tilde{A}_{1n} \\ \tilde{A}_{21}&\tilde{A}_{22}&...&\tilde{A}_{2n} \\ \vdots&\vdots&\vdots&\vdots \\ \tilde{A}_{m1}&\tilde{A}_{m2}&...&\tilde{A}_{mn}\\ \end{bmatrix},$$

where

$$\begin{aligned} \tilde{A}_{ij}=\frac{\tilde{A}_{ij}^1\oplus \tilde{A}_{ij}^2\oplus ...\oplus \tilde{A}_{ij}^p}{p}. \end{aligned}$$

(235)

Calculate the average weights $w_{j}$ of the each criteria $C_{j}$ by averaging their weights given by the decision makers $D_{l}, l=1,2,...,p$, i.e.

$$\begin{aligned} \tilde{w}_{j}=(\tilde{w}_{j}^1\oplus \tilde{w}_{j}^2\oplus ....\oplus \tilde{w}_{j}^p)/p. \end{aligned}$$

(236)

Step-2: Normalize the decision matrix $\tilde{D}$. Suppose $\tilde{D^\prime }=[\tilde{A_{ij}^\prime }]_{m\times n}$ be the normalized decision matrix (normalizing process is shown in the end of this method).

Step-3: Derive the relative preference (/performance) matrix $P=[r_{ij}]_{m\times n}$, where

$$\begin{aligned} r_{ij}=\sum _{k\ne i}~R(\tilde{A_{ij}^\prime },\tilde{A_{kj}^\prime }), \end{aligned}$$

(237)

R is the ranking function as defined in (233). $r_{ij}$ is called the relative preference index of the alternative $A_{i}$ with respective to all the remaining alternatives for the criteria $C_{j}$.

Step-4: Calculate the fuzzy weighted relative preference of the each alternative by

$$\begin{aligned} A_{i}^*=\sum _{j=1}^n~r_{ij}\otimes \tilde{w_{j}},~i=1,2,...,m. \end{aligned}$$

(238)

Step-5: Find the total preference index of each alternative by

$$\begin{aligned} r_{i}=\sum _{k\ne i}~R(\tilde{A_{i}^*},\tilde{A_{k}^*}),~i=1,2,...,m. \end{aligned}$$

(239)

Step-6: Normalize the preference indices $r_{i}$ to obtain preference weights of the alternatives that sum to 1 by

$$\begin{aligned} w_{i}^P=\frac{r_{i}}{\sum _{j}^m r_{j}},~i=1,2,..,m. \end{aligned}$$

(240)

Step-7: Rank alternatives according to their weights $w_{i}^P,$ $i=1,2,...,m.$

The process of normalization of $\tilde{D}=[\tilde{A_{ij}}]_{m\times n}$ is shown below in case when $\tilde{A_{ij}}$ are triangular fuzzy numbers:

Fig. 17.

Flow-chart of the proposed FMCGDM method

Suppose each $\tilde{A_{ij}}$ is a triangular fuzzy number defined by $\tilde{A_{ij}}=(a_{ij}^L,a_{ij}^M,a_{ij}^U)$, then

$$\tilde{A_{ij}^\prime }=\big (\frac{a_{ij}^L}{a_{j}^*},\frac{a_{ij}^M}{a_{j}^*},\frac{a_{ij}^U}{a_{j}^*}\big ),~where~a_{j}^*=\max _{i}\{a_{ij}^U\},$$

where j is the benefit criteria or the ratings are given in favor of the criteria (i.e. in positive sense).

But if j is a cost criteria and $\tilde{A_{ij}}$ is given as amount of cost but not as rating, then normalization is done as follows:

$$\tilde{A_{ij}^\prime }=\big (\frac{a_{j}^*}{a_{ij}^U},\frac{a_{j}^*}{a_{ij}^M},\frac{a_{j}^*}{a_{ij}^L}\big ),~where~a_{j}^*=\min _{i}\{a_{ij}^L\}.$$

The flow-chart of the above method is presented in Fig. 17.

5.5 A Method of Ranking Trapezoidal Interval Type-2 Fuzzy Variables

Some Results on Generalized Trapezoidal Fuzzy Variables: In Sect. 2, we already mentioned that if a fuzzy variable is not normal, i.e. for generalized fuzzy variable, generalized credibility measure $\tilde{Cr}$ has to be used instead of the usual credibility measure. For a generalized trapezoidal fuzzy variable $\tilde{\xi }=(a,b,c,d;w)$, $\tilde{Cr}\{\tilde{\xi }\le x\}$ is obtained as follows:

$$\begin{aligned} \tilde{Cr}\{\tilde{\xi }\le x\}= & {} \frac{1}{2}(w+\sup _{r\le x}~\mu _{\tilde{\xi }}(x)-\sup _{r>x}~\mu _{\tilde{\xi }}(x))\\= & {} \frac{1}{2}\{w+0-w\}=0,~if~ x\le a\\= & {} \frac{1}{2}\{w+\frac{w(x-a)}{b-a}-w\}=\frac{w(x-a)}{2(b-a)},~if~ a\le x\le b\\= & {} \frac{1}{2}\{w+w-w\}=\frac{w}{2},~if~ b\le x\le c\\= & {} \frac{1}{2}\{w+w-\frac{w(d-x)}{d-c}\}=\frac{w(x+d-2c)}{2(d-c)},~if~c\le x\le d\\= & {} \frac{1}{2}\{w+w-0\}=w,~if~ x\ge d, \end{aligned}$$

i.e.,

$$\begin{aligned} \tilde{Cr}\{\tilde{\xi }\le x\}= \left\{ \begin{array}{ll} 0, &{} \hbox {if}\, x\le a; \\ \frac{w(x-a)}{2(b-a)}, &{} \hbox {if}\,a\le x\le b; \\ \frac{w}{2}, &{} \hbox {if}\,b\le x\le c; \\ \frac{w(x+d-2c)}{2(d-c)}, &{} \hbox {if}\,c\le x\le d; \\ w, &{} \hbox {if}\,x\ge d. \end{array}\right. \end{aligned}$$

(241)

Theorem 5.3:

If $\tilde{\xi }=(a,b,c,d;w)$ is generalized trapezoidal fuzzy variable and $0< \alpha \le 1$, then $Cr\{\tilde{\xi }\le x\}\ge \alpha$ is equivalent to

$$(i)~\frac{1}{w}((w-2\alpha )a+2\alpha b)\le x,~if\,\alpha \le \frac{w}{2},$$

$$(ii)~\frac{1}{w}(2(w-\alpha )c+(2\alpha -w) d)\le x,~if~ \alpha >\frac{w}{2}.$$

Proof:

It is clear from 241 that if $\alpha \le \frac{w}{2}$, then $Cr\{\tilde{\xi }\le x\}\ge \alpha$ implies $\frac{w(x-a)}{2(b-a)}\ge \alpha$, i.e. $\frac{1}{w}((w-2\alpha )a+2\alpha b)\le x$ and if $\alpha >\frac{w}{2}$, then $Cr\{\tilde{\xi }\le x\}\ge \alpha$ implies $\frac{w(x+d-2c)}{2(d-c)}\ge \alpha$, i.e. $\frac{1}{w}(2(w-\alpha )c+(2\alpha -w) d)\le x$.

Theorem 5.4:

If $\tilde{A_{1}}=(a_{1},a_{2},a_{3},a_{4};w_{1})$ and $\tilde{A_{2}}=(b_{1},b_{2},b_{3},b_{4};w_{2})$ be two generalized trapezoidal fuzzy variables and $0< \alpha \le 1$, then $\tilde{Cr}\{\tilde{A_{1}}\le \tilde{A_{2}}\}\ge \alpha$ if

$$(w-2\alpha )(a_{1}-b_{4})+2\alpha (a_{2}-b_{3})\le 0~~for~\alpha \le w/2$$

$$2(w-\alpha )(a_{3}-b_{2})+(2\alpha -w)(a_{4}-b_{1})\le 0~~for~\alpha > w/2,$$

where $w=min(w_{1},w_{2})$.

Proof:

$-\tilde{A_{2}}=(-b_{4},-b_{3},-b_{2},-b_{1};w_{2})$ and so $\tilde{A_{1}}-\tilde{A_{2}}=(a_{1}-b_{4},a_{2}-b_{3},a_{3}-b_{2},a_{4}-b_{1};min(w_{1},w_{2}))$. Now $Cr\{\tilde{A_{1}}\le \tilde{A_{2}}\}\ge \alpha \Leftrightarrow$ $Cr\{(\tilde{A_{1}}-\tilde{A_{2}})\le 0\}\ge \alpha$ and hence the theorem follows from Theorem 5.3.

Corollary 5.3:

If $\tilde{A_{1}}=(a_{1},a_{2},a_{3},a_{4};w_{1})$ and $\tilde{A_{2}}=(b_{1},b_{2},b_{3},b_{4};w_{2})$ be two generalized trapezoidal fuzzy variables and $0< \alpha \le 1$, then $\tilde{Cr}\{\tilde{A_{1}}\ge \tilde{A_{2}}\}\ge \alpha$ if

$$(w-2\alpha )(a_{4}-b_{1})+2\alpha (a_{3}-b_{2})\ge 0~~for~\alpha \le w/2$$

$$2(w-\alpha )(a_{2}-b_{3})+(2\alpha -w)(a_{1}-b_{4})\ge 0~~for~\alpha > w/2,$$

where $w=min(w_{1},w_{2})$.

Ranking Function and Relative Preference Index: Here we define a ranking function which can be used to rank two generalized fuzzy variables, say $\tilde{A_{1}}$ and $\tilde{A_{2}}$. For this purpose we find the possible credibility (generalized) degree to which $\tilde{A_{1}}\ge \tilde{A_{2}}$ or $\tilde{A_{1}}\le \tilde{A_{2}}$, i.e. we find the maximum satisfied credibility degree that $\tilde{A_{1}}\ge \tilde{A_{2}}$ or maximum satisfied credibility degree that $\tilde{A_{1}}\le \tilde{A_{2}}$, i.e.

$$\begin{aligned} Max_{\alpha \in [0,w]} [\tilde{Cr}\{\tilde{A_{1}}\ge \tilde{A_{2}}\}=\alpha ] \end{aligned}$$

(242)

$$\begin{aligned} or,~Max_{\alpha \in [0,w]} [\tilde{Cr}\{\tilde{A_{1}}\le \tilde{A_{2}}\}=\alpha ], \end{aligned}$$

(243)

where w is minimum of heights of $\tilde{A_{1}}$ and $\tilde{A_{2}}$, so $0<w\le 1$.

We denote (242) by $M_{\alpha }(\tilde{A_{1}}\ge \tilde{A_{2}})$ and (242) by $M_{\alpha }(\tilde{A_{1}}\le \tilde{A_{2}})$.

Suppose for two generalized fuzzy numbers $\tilde{A_{1}}$ and $\tilde{A_{2}}$, $M_{\alpha }(\tilde{A_{1}}\ge \tilde{A_{2}})=\alpha ^\prime$, then we say that $\tilde{A_{1}}\ge \tilde{A_{2}}$ with credibility $\alpha ^\prime$.

Suppose $\tilde{A_{1}}=(a_{1},a_{2},a_{3},a_{4};w_{1})$ and $\tilde{A_{2}}=(b_{1},b_{2},b_{3},b_{4};w_{2})$ be two generalized trapezoidal fuzzy variables and $w=min(w_{1},w_{2})$. Then from Corollary 5.3 it follows that $M_{\alpha }(\tilde{A_{1}}\ge \tilde{A_{2}})$=$Max_{\alpha \in [0,w]} [\tilde{Cr}\{\tilde{A_{1}}\ge \tilde{A_{2}}\}=\alpha ]$ is obtained by solving

$$Max ~\alpha $$

$$\begin{aligned} s.t.~(w-2\alpha )(a_{4}-b_{1})+2\alpha (a_{3}-b_{2})\ge 0~~for~0\le \alpha \le w/2\\ 2(w-\alpha )(a_{2}-b_{3})+(2\alpha -w)(a_{1}-b_{4})\ge 0~~for~w/2<\alpha \le w\nonumber \end{aligned}$$

(244)

$$0\le \alpha \le w.$$

As the objective is to find maximum possible credibility degree $\alpha$, so to solve 244, one may first find Max $\alpha$ with respect to the second constraint, if such $\alpha$ $(w/2<\alpha \le w)$ exist then this is the required solution and if it does not exist then find Max $\alpha$ satisfying the first constraint.

Example 5.4:

As an example consider $\tilde{A_{1}}=(5,7,8,9;1)$ and $\tilde{A_{2}}=(4,5,6,9;0.8)$, then $w=0.8$ and solving (5.16) for this example we have

$M_{\alpha }(\tilde{A_{1}}\ge \tilde{A_{2}})$=$Max_{\alpha \in [0,w]} [Cr\{\tilde{A_{1}}\ge \tilde{A_{2}}\}=\alpha ]=0.48$.

Ranking Function: We define a ranking function that can be used to rank two generalized fuzzy variable $\tilde{A_{1}}$ and $\tilde{A_{2}}$ as follows:

$$\begin{aligned} R(\tilde{A_{1}}\ge \tilde{A_{2}})=\left\{ \begin{array}{ll} M_{\alpha }(\tilde{A_{1}}\ge \tilde{A_{2}}), &{} \hbox {if it exist;} \\ 0, &{} \hbox {otherwise.} \end{array}\right. \end{aligned}$$

(245)

Obviously

$$\begin{aligned} R(\tilde{A_{1}}\le \tilde{A_{2}})=\left\{ \begin{array}{ll} M_{\alpha }(\tilde{A_{1}}\le \tilde{A_{1}}), &{} \hbox {if it exist;} \\ 0, &{} \hbox {otherwise.} \end{array}\right. \end{aligned}$$

(246)

It follows from the definition of $R(\tilde{A_{1}},\tilde{A_{2}})$ and self-duality property of the credibility measure that $R(\tilde{A_{1}}\ge \tilde{A_{2}})=w-R(\tilde{A_{1}}\le \tilde{A_{2}})$. In particular if $\tilde{A_{1}}$ and $\tilde{A_{2}}$ are normalized, i.e. $w=1$, then R is reciprocal. Also from (244) it is clear that R is transitive for generalized trapezoidal fuzzy variables, i.e. $R(\tilde{A_{1}},\tilde{A_{2}})\ge w/2$ and $R(\tilde{A_{2}},\tilde{A_{3}})\ge w/2$ $\Rightarrow$ $R(\tilde{A_{1}},\tilde{A_{3}})\ge w/2$ for any trapezoidal fuzzy variables $\tilde{A_{1}}$, $\tilde{A_{1}}$, $\tilde{A_{1}}$. So R is total ordering and satisfies all the criteria of fuzzy ranking proposed by Yuan [154]. For any two generalized fuzzy variables $\tilde{A_{1}}$ and $\tilde{A_{2}}$, the ranking of $\tilde{A_{1}}$, $\tilde{A_{2}}$ is done as follows:

• (i) $\tilde{A_{1}}\succ \tilde{A_{2}}$ iff $R(\tilde{A_{1}}\ge \tilde{A_{2}})>w/2.$

• (ii) $\tilde{A_{1}}\prec \tilde{A_{2}}$ iff $R(\tilde{A_{1}}\ge \tilde{A_{2}})<w/2.$

• (iii) But if $R(\tilde{A_{1}}\ge \tilde{A_{2}})=w/2$, then rank them including their heights, i.e., $\tilde{A_{1}}\sim \tilde{A_{2}}$ also if $w_{1}=w_{2}$, $\tilde{A_{1}}<\tilde{A_{2}}$ also if $w_{1}<w_{2}$ and $\tilde{A_{1}}>\tilde{A_{2}}$ also if $w_{1}>w_{2}$.

Now to include the three subcases of the equality case $R(\tilde{A_{1}}\ge \tilde{A_{2}})=w/2$ and for any further use of ranking values, we define relative preference index $r_{i}$ of each $\tilde{A_{i}}$ by adding an additional value based on their heights to the ranking value $R(\tilde{A_{i}}\ge \tilde{A_{j}})$ as follows:

$$r_{i}=R(\tilde{A_{i}}\ge \tilde{A_{j}})+\frac{w_{i}-w}{2},~i\ne j,~i,j=1,2,$$

$w=min(w_{1},w_{2})$. Then the fuzzy variables $\tilde{A_{i}}$ are ranked based on relative preference indices $r_{i}$.

The Method of Ranking Trapezoidal Interval Type-2 Fuzzy Variables: Suppose $\tilde{A_{i}}, i=1,2,...,n$ are n trapezoidal interval type-2 fuzzy variables, where $\tilde{A_{i}}=(\tilde{A_{i}^U},\tilde{A_{i}^L})=((a_{i1}^U,a_{i2}^U,a_{i3}^U,a_{i4}^U;w_{i}^U),(a_{i1}^L,a_{i2}^L,a_{i3}^L,a_{i4}^L;w_{i}^L))$. Denote $w_{M}^U=min_{i}\{w_{i}^U\}$ and $w_{M}^L=min_{i}\{w_{i}^L\}$. The proposed procedure of ranking $\tilde{A_{i}}, i=1,2,...,n$ is as follows:

First find upper relative preference index $r_{i}^U$ of each $\tilde{A_{i}}$ by

$$r_{i}^U=\sum _{k\ne i}~R(\tilde{A_{i}^U}\ge \tilde{A_{k}^U})+\frac{w_{i}^U-w_{M}^U}{2},~i=1,2,...,n$$

and lower relative preference index $r_{i}^L$ of each $\tilde{A_{i}}$ by

$$r_{i}^L=\sum _{k\ne i}~R(\tilde{A_{i}^L}\ge \tilde{A_{k}^L})+\frac{w_{i}^L-w_{M}^L}{2},~i=1,2,...,n.$$

Then the relative preference index $r_{i}$ of each $\tilde{A_{i}}$ is calculated by

$$r_{i}=\frac{r_{i}^U+r_{i}^L}{2},~i=1,2,...,n.$$

Rank $\tilde{A_{i}}$ according to the value of $r_{i}$, i.e. the larger the value of $r_{i}$, the better the ranking order of $\tilde{A_{i}}$.

Example 5.5:

Consider trapezoidal interval type-2 fuzzy variables

$A_{1}=((0.4,0.7,0.9,1.2;1),(0.5,0.7,0.9,1.1;0.9))$,

$A_{2}=((0.3,0.5,0.6,0.9;1),(0.4,0.55,0.65,0.8;0.9))$

and $A_{3}=((0.6,0.8,1.1,1.4;1),(0.7,0.9,1,1.2;0.9))$. Then $w_{i}^U=1$, $w_{i}^L=0.9,~i=1,2,3$ and so $w_{M}^U=1$ and $w_{M}^L=0.9$. Now,

$r_{1}^U=R(\tilde{A_{1}^U}\ge \tilde{A_{2}^U})+R(\tilde{A_{1}^U}\ge \tilde{A_{3}^U})+\frac{w_{1}^U-w_{M}^U}{2}=0.583+0.5+0=1.083$,

$r_{1}^L=R(\tilde{A_{1}^L}\ge \tilde{A_{2}^L})+R(\tilde{A_{1}^L}\ge \tilde{A_{3}^L})+\frac{w_{1}^L-w_{M}^L}{2}=0.514+0.45+0=0.964$ and so $r_{1}=1.023$

Similarly we obtain $r_{2}^U=0.717$, $r_{2}^L=0.515$, $r_{2}=0.616$ and $r_{3}^U=1.2$, $r_{3}^L=1.221$, $r_{3}=1.2105$. Hence $A_{3}\succ A_{1}\succ A_{2}$.

A Comparison of the Above Ranking Result: We now compare the above ranking result of the interval type-2 fuzzy variables $A_{1}$, $A_{2}$ and $A_{3}$ with few existing methods as given in Table 19.

Table 19. Comparative results of Example 5.5

5.6 Proposed Fuzzy MCGDM Based on Ranking Interval Type-2 Fuzzy Variables

Suppose $A_{1}, A_{2}, ..., A_{m}$ are m alternatives and these alternatives are evaluated on basis of the criteria $C_{1}, C_{2},...,C_{n}$ by the decision makers $D_{l}, l=1,2,...,p$. Suppose rating of $A_{i}$ based on criteria $C_{j}$ according to the decision maker $D_{l}$ is $\tilde{A}_{ij}^l$ which is represented by trapezoidal interval type-2 fuzzy variable, where $i=1,2,...,m$, $j=1,2,...,n$ and $l=1,2,...,p$. Let $\tilde{w}_{j}^l$ be the weight of the criteria $C_{j}$ indicating its importance given by the decision maker $D_{l}$, where $\tilde{w}_{j}^l$ is represented by interval type-2 fuzzy variable for all j and l. The proposed fuzzy MCGDM method to rank the alternatives is as follows:

Step 1: Construct the decision matrix $\tilde{D}=[\tilde{A}_{ij}]_{m\times n}$ where each $\tilde{A}_{ij}$ is the average of the ratings of alternative $A_{i}$ given by the decision makers $D_{l}, l=1,2,...,p$ based on criteria $C_{j}$, i.e.,

$$~~~~~~~~~~~\begin{array}{cccc} C_{1}&C_{2}&....&C_{n} \end{array}$$

$$ \tilde{D}=\begin{array}{c} A_{1} \\ A_{2} \\ \vdots \\ A_{m} \end{array} \begin{bmatrix} \tilde{A}_{11}&\tilde{A}_{12}&...&\tilde{A}_{1n} \\ \tilde{A}_{21}&\tilde{A}_{22}&...&\tilde{A}_{2n} \\ \vdots&\vdots&\vdots&\vdots \\ \tilde{A}_{m1}&\tilde{A}_{m2}&...&\tilde{A}_{mn}\\ \end{bmatrix},$$

where

$$\begin{aligned} \tilde{A}_{ij}=\frac{\tilde{A}_{ij}^1\oplus \tilde{A}_{ij}^2\oplus ...\oplus \tilde{A}_{ij}^p}{p}. \end{aligned}$$

(247)

Suppose each $\tilde{A}_{ij}$ is represented by $\tilde{A_{ij}}=(\tilde{A_{ij}^U},\tilde{A_{ij}^L})$ with heights of $\tilde{A_{ij}^U}$ and $\tilde{A_{ij}^L}$ as $w_{ij}^U$ and $w_{ij}^L$ respectively.

Calculate the average weights $w_{j}$ of the each criteria $C_{j}$ by averaging their weights given by the decision makers $D_{l}, l=1,2,...,p$, i.e.

$$\begin{aligned} \tilde{w}_{j}=(\tilde{w}_{j}^1\oplus \tilde{w}_{j}^2\oplus ....\oplus \tilde{w}_{j}^p)/p. \end{aligned}$$

(248)

Step 2: Derive the upper relative preference matrix $RP^U=[r_{ij}^U]_{m\times n}$, where $r_{ij}^U$ are the upper relative preference indices of alternatives $A_{i}$ based on criteria $C_{j}$, i.e.,

$$\begin{aligned} r_{ij}^U=\sum _{k\ne i}~R(\tilde{A}_{ij}^U\ge \tilde{A}_{kj}^U)+\frac{w_{ij}^U-w_{Mj}^U}{2},~1\le i\le m,~1\le j\le n \end{aligned}$$

(249)

and similarly the lower relative preference matrix $RP^L=[r_{ij}^L]_{m\times n}$, where

$$\begin{aligned} r_{ij}^L=\sum _{k\ne i}~R(\tilde{A}_{ij}^L\ge \tilde{A}_{kj}^L)+\frac{w_{ij}^L-w_{Mj}^L}{2},~1\le i\le m,~1\le j\le n, \end{aligned}$$

(250)

$w_{Mj}^U=min_{i}\{w_{ij}^U\}$ and $w_{Mj}^L=min_{i}\{w_{ij}^L\}$, $w_{ij}^U$ and $w_{ij}^L$ are the heights of the upper and lower membership of $\tilde{A}_{ij}^l$ respectively.

Finally derive the relative preference matrix $RP=[r_{ij}]_{m\times n}$, where $r_{ij}=\frac{r_{ij}^U+r_{ij}^L}{2}$, $1\le i\le m,~1\le j\le n$.

Step 3: Calculate the fuzzy weighted relative preference of each alternative by employing the importance weights of the criteria as follows:

$$\begin{aligned} \tilde{A_{i}^*}=r_{11}\cdot \tilde{w}_{1}\oplus r_{12}\cdot \tilde{w}_{2}\oplus ...\oplus r_{1n}\cdot \tilde{w}_{n}=(\tilde{A_{i}^{*U}},\tilde{A_{i}^{*L}})~(say),~~i=1,2,...,n. \end{aligned}$$

(251)

Step 4: Find the final upper preference index of each alternative by

$$\begin{aligned} r_{i}^U=\sum _{k\ne i}~R(\tilde{A_{i}^{*U}}\ge \tilde{A_{k}^{*U}})+\frac{w_{i}^U-w_{M}^U}{2},~i=1,2,...,m. \end{aligned}$$

(252)

and the final lower preference index

$$\begin{aligned} r_{i}^L=\sum _{k\ne i}~R(\tilde{A_{i}^{*L}}\ge \tilde{A_{k}^{*L}})+\frac{w_{i}^L-w_{M}^L}{2},~i=1,2,...,m, \end{aligned}$$

(253)

where $w_{i}^U$, $w_{i}^L$ are the heights of $\tilde{A_{i}^{*U}}$, $\tilde{A_{i}^{*L}}$ respectively and $w_{M}^U=\min _{i}\{w_{i}^U\}$, $w_{M}^L=\min _{i}\{w_{i}^L\}$. Then final preference index $r_{i}$ of each alternative is obtained by $r_{i}=\frac{r_{i}^U+r_{i}^L}{2}$, $i=1,2,...,m$.

Now the alternatives $A_{i}$ can be ranked according to their ranking values $r_{i}$. However for better comparison we find preference weights of the alternatives that sum to 1 as in the following step.

Step 5: Obtain preference weights $W_{i}$ of the alternatives that sum to 1 by normalizing the preference indices $r_{i}$ as

$$\begin{aligned} W_{i}=\frac{r_{i}}{\sum _{j=1}^m r_{j}},~i=1,2,...,m, \end{aligned}$$

(254)

where $0\le W_{i}\le 1$ and $\sum _{i=1}^m~W_{i}=1.$

Rank the alternatives $A_{i}$ according to their preference weights $W_{i},~i=1,2,...,m$.

5.7 Problem 5.1: A Transportation Mode Selection Problem with Linguistic Weights and Ratings Generated by Fuzzy Numbers and Its Application to STP

Suppose in a solid transportation problem (STP) there are two modes of transportation (conveyances) available - rail and road. Along with the main criteria (transportation cost), decision makers want to rate the two modes with respect to some other criteria, which are also very important for a transportation policy. Three decision makers $D_{1}$, $D_{2}$, $D_{3}$ select five main criteria- cost (C), speed/time (S), product characteristics (P), flexibility (F) and safety factor (SF). Also there are subcriteria associated with each main criteria as follows:

• (1) Cost (C): This main criterion contains cost factors that are involved in transportation system.

  • $C_{1}$: Transportation cost for shipment of goods from source to destination.

  • $C_{2}$: Cost of damages to freight incurred at the transportation or transshipment stages.

  • $C_{3}$: Fixed cost (transport equipment, maintenance, terminal facilities, etc.).

• (2) Speed/time (S): This criterion contains time related subcriteria.

  • $S_{1}$: The average speed that the conveyance can provide.

  • $S_{2}$: The time consumed for loading, storing and unloading process.

  • $S_{3}$: The ratio of the distance between supply and demand points to the transportation time.

  • $S_{4}$: Time reliability, i.e. the past record for delivering in time.

• (3) Product characteristics (P): This criteria involved with product related features.

  • $P_{1}$: The weight of the freight permissible.

  • $P_{2}$: The volume of the freight permissible.

  • $P_{3}$: Value to weight of the freight.

• (4) Flexibility (F): This criterion contains subcriteria involving capacity, route, time schedule flexibility.

  • $F_{1}$: The ability to change the transportation route for unexpected cause during transportation.

  • $F_{2}$: The ability to change the volume and weight capacity of the vehicles.

  • $F_{3}$: The ability to change the predetermined time schedule.

• (5) Safety factor (SF): This criterion contains safety problem related features.

  • $SF_{1}$: The accidental rate in a determined time period.

  • $SF_{2}$: The rate of product being damaged during transportation.

The decision makers compare the criteria with each other and gives the importance weights for each criteria. The linguistic terms and related fuzzy numbers (Lee [78], Wang and Elhag [141]) for criteria weights and evaluation ratings are shown in Table 20. The linguistic importance weights of the main and subcriteria are given in Tables 21 and 23 respectively. The average fuzzy weights of the main criteria are obtained using Tables 20 and 21 by averaging their weights given by the three decision makers and presented in Table 22. Similarly using Tables 20 and 23, the average fuzzy weights of the subcriteria are obtained and presented in Table 24. The average weight of the each subcriterion is then multiplied by the corresponding main criterion weight and presented in Table 25 and thus effective weight of the each subcriterion is obtained. Denotes these effective weights of the subcriteria j by $\tilde{w}_{j},~j=1,2,...,15$, where $j=1$ indicates the criterion $C_{1}$, $j=2$ indicates the criterion $C_{2}$ and in this way $j=15$ indicates the criterion $SF_{2}$. The evaluation ratings of the transportation modes - rail and road as determined by the decision makers based on the selection criteria are given in Table 26. Based on the Table 26, the group fuzzy decision matrix is derived by averaging the ratings of the decision makers and is presented in Table 27. So this decision matrix is denoted by $\tilde{D}=[\tilde{A}_{ij}]_{2\times 15}$, where $i=1,2$ indicate the alternatives rail and road respectively, $j=1$ indicates the criterion $C_{1}$, $j=2$ indicates the criterion $C_{2}$ and in this way $j=15$ indicates the criterion $SF_{2}$. Now we apply our proposed FMCGDM method (cf. Sect.5.4) based on ranking fuzzy numbers step by step as follows:

Step-1: The fuzzy group decision matrix (Table 27) is normalized and shown in Table 28.

Step-2: Based on Table 28, the relative preference matrix $[r_{ij}]_{2\times 15}$ is derived using Eq. (237) and shown in Table 29. For example, $r_{11}=R(\tilde{A_{11}^\prime },\tilde{A_{21}^\prime })=M_{\alpha }(\tilde{A_{11}^\prime }\ge \tilde{A_{21}^\prime })=0.833$, obtained by solving (232) where $\tilde{A_{11}}=(0.83,0.97,1)$, $\tilde{A_{21}}=(0.57,0.77,0.93)$ and $r_{21}=R(\tilde{A_{21}^\prime },\tilde{A_{11}^\prime })=1-R(\tilde{A_{11}^\prime },\tilde{A_{21}^\prime })=1-r_{11}=0.167.$

Step-3: Fuzzy weighted relative preferences of the two alternatives are calculated through Tables 29 and 25 using Eq. (238) and shown in Table 30.

Step-4: From Table 30, using Eq. (239) total preference indices of the two alternatives are obtained and shown in Table 31.

Step-5: Normalizing the preference indices according to Eq. (240) the preference weights of the two alternatives are obtained as $w_{1}^P=0.586$ for rail and $w_{2}^P=0.414$ for road.

From the above results we observe that for the current problem rail mode is preferred than road and weights of rail and road are 0.586 and 0.414 respectively. So sum of the weights is 1 and these weights can be used for any further requirements.

Table 20. Linguistic terms and related fuzzy numbers of criteria weights and evaluation ratings

Table 21. Linguistic importance weights of the main criteria

Table 22. Average weights of the main criteria

Table 23. Linguistic importance weights of the subcriteria

Table 24. Average weights of the subcriteria

Table 25. Average weights of the subcriteria multiplied by the corresponding main criteria weights

Table 26. Linguistic ratings of the alternatives with respect to each criteria

Table 27. Fuzzy group decision matrix

Table 28. Normalized group fuzzy decision matrix

Table 29. Relative preference matrix

Table 30. Fuzzy weighted relative preferences of the alternatives

Table 31. Total preference indices

Table 32. Comparative results of presented problem 5.1.

Table 33. Penalties (costs) $\tilde{c_{ijk}}$

Comparison with Some Other Methods: We solve the above problem by three existing methods- Lee’s [78] method based on extended fuzzy preference relation, fuzzy TOPSIS of Wang and Lee [139] and method of Cheng and Lin [28] based on fuzzy Delphi method and the results are presented in Table 32. Lee’s method gives total performance index of rail mode as 1 and that of road 0 so that rail mode is preferable than road for this problem. Wang and Lee’s method gives the closeness coefficient of rail as 1 and that of road 0 so that by this method rail mode is preferable than road. Actually in case of two alternatives, whatever the ratings of the alternatives and criteria weights are, these two methods always give total performance index or closeness coefficient of one alternative as 1 and that of another 0. Cheng and Lin’s method gives the defuzzified values of the aggregate fuzzy evaluations (here aggregate triangular fuzzy numbers) for rail and road as 6.854 and 6.791 respectively. Hence both the three methods give same preference as obtained by our proposed method, i.e. rail mode is preferred than road for the current problem.

5.8 Assigning the Preference Weights of the Different Modes into The STP

How to Assign: Suppose in a STP, K types of modes of transportation (conveyances) available for transportation. If objective function of a STP is minimization of transportation cost, then obviously transportation cost be the main criterion of choosing conveyances for certain route. However, if it is observed that besides main criterion there are also some other criteria such as speed/time, flexibility, safety factor of conveyances, etc. those are also vary important for a particular problem, then the decision maker may seek to find overall importance weights of the modes with respect all the criteria. Then assign the weights of the modes to the main objective function of the problem so that optimal transportation policy is according to the main criterion in addition to the other selected important criteria. Suppose $w_{k}^P$ is the weights of the conveyance $k(=1,2,...,K)$ as obtained by the FMCGDM method under some predetermined criteria. These transportation mode weights are assigned to the STP so that the amounts of goods transported through conveyances are according to their weights in addition to the main criterion such as cost or time etc. Actually the main aim is to transport the goods through the best mode as maximum as possible. The objective function of the STP is

$$\begin{aligned} Max/Min~Z=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~c_{ijk}~x_{ijk}. \end{aligned}$$

• (i) If the problem is a maximization problem, i.e. $c_{ijk}$ represents profit, amount etc., then to find optimum result (values of $x_{ijk}$’s), assign $w_{k}^P$ in the objective function as follows:

  $$\begin{aligned} Max~Z^\prime =\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~w_{k}^P(c_{ijk}~x_{ijk}). \end{aligned}$$

  and then find the actual value of Z (total profit, amount, etc.) using the values of obtained $x_{ijk}$’s and corresponding $c_{ijk}$’s.

• (ii) If the problem is a minimization problem, i.e. $c_{ijk}$ represents transportation cost, etc., then to find optimum result (values of $x_{ijk}$’s), assign $w_{k}^P$ in the objective function as follows:

  $$\begin{aligned} Min~Z^\prime =\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~\frac{1}{w_{k}^P}(c_{ijk}~x_{ijk}), \end{aligned}$$

  because higher value of $w_{k}^P$ (i.e., lower value of $1/w_{k}^P$) ensures the possibility of increasing the amount of goods transported through the conveyance k. Now the actual value of Z (total transportation cost) is derived using the values of obtained $x_{ijk}$’s and corresponding $c_{ijk}$’s.

Numerical Illustration: Consider a STP with three sources $(i=1,2,3)$, three destinations $(j=1,2,3)$ and two conveyances $(k=1,2)$. Here conveyance $k=1$ indicates rail and $k=2$ indicates road. The unit transportation costs $(c_{ijk})$ are presented in Table 33 and the availabilities $(a_{i})$, demands $(b_{j})$ are given below.

$a_{1}=35$, $a_{2}=30$, $a_{3}=42$, $b_{1}=32$, $b_{2}=36$, $b_{3}=35$, $e_{1}=60$, $e_{2}=52$.

So mathematically the problem becomes

$$\begin{aligned} Min~Z=\sum _{i=1}^3\sum _{j=1}^3\sum _{k=1}^2~(c_{ijk}~x_{ijk}), \end{aligned}$$

$$\begin{aligned} s.t.~ \sum _{j=1}^3\sum _{k=1}^2 x_{ijk}~\le & {} a_{i},~~i=1,2,3,\nonumber \\ \sum _{i=1}^3\sum _{k=1}^2 x_{ijk}~~\ge & {} b_{j},~~j=1,2,3, \\ \sum _{i=1}^3\sum _{j=1}^3~x_{ijk}\le & {} e_{k},~~k=1,2,\nonumber \end{aligned}$$

(255)

$$x_{ijk}\ge 0,~ \forall ~ i,j,k.$$

Now introducing weights of the transportation modes in the objective function, the problem becomes

$$\begin{aligned} Min~Z^\prime =\sum _{i=1}^3\sum _{j=1}^3\sum _{k=1}^2~\frac{1}{w_{k}^P}(c_{ijk}~x_{ijk}), \end{aligned}$$

$$\begin{aligned} s.t.~ \sum _{j=1}^3\sum _{k=1}^2 x_{ijk}~\le & {} a_{i},~~i=1,2,3,\nonumber \\ \sum _{i=1}^3\sum _{k=1}^2 x_{ijk}~~\ge & {} b_{j},~~j=1,2,3, \\ \sum _{i=1}^3\sum _{j=1}^3~x_{ijk}\le & {} e_{k},~~k=1,2,\nonumber \end{aligned}$$

(256)

$$x_{ijk}\ge 0,~ \forall ~ i,j,k,$$

where $w_{1}^P=0.586$ (for rail) and $w_{2}^P=0.414$ (for road).

Solving the problem (256) we have

$x_{111}=20$, $x_{121}=10$, $x_{331}=30$, $x_{132}=5$, $x_{222}=26$, $x_{312}=12$ and $Min Z=4\cdot 20+6\cdot 10+6\cdot 30+4\cdot 5+6\cdot 26+4\cdot 12=544.$

Now solving the problem without mode weights (problem (255)), we have

$x_{111}=19.5$, $x_{121}=6$, $x_{331}=25.5$, $x_{132}=9.5$, $x_{222}=30$, $x_{312}=12.5$ and $Min Z=4\cdot 19.5+6\cdot 6+6\cdot 25.5+4\cdot 9.5+6\cdot 30+4\cdot 12.5=535$.

Remark:

We see that in case of the problem without mode weights, total transported amount through rail is 51 and through road is 52. Where as for the problem with mode weights total transported amount through rail is 60 and through road is 43. This is as per expectation because here rail mode has higher preference weight than road. Also we observe that the problem without mode weights provides less transportation cost. So it is up to the decision makers whether they decide to determine transportation policy only according to the main criterion (i.e. cost) or according to all other criteria including the main criterion.

Table 34. Linguistic terms and related fuzzy variables of criteria weights

Table 35. Linguistic terms and related fuzzy variables of evaluation ratings

5.9 Problem 5.2: A Transportation Mode Selection Problem with Linguistic Weights and Ratings Generated by IT2 FVs

Suppose in a transportation system there are two modes of transportation (conveyances) available - rail and road. Besides the main criterion (transportation cost), decision makers want to rate the two modes with respect to some other criteria, which are also very important for a transportation policy. The selection criteria are already presented in Sect. 5.3 for the Problem 5.1.

The decision makers compare the criteria with each other and gives the importance weights for each criteria. The linguistic terms and related fuzzy variables (Anand et al. [7], Chen and Lee [23, 24]) for criteria weights and evaluation ratings are shown in Tables 34 and 35 respectively. The linguistic importance weights of the main and subcriteria as given by the decision makers are same as presented in Tables 21 and 23 respectively. Average fuzzy weights of the main criteria and subcriteria are obtained by averaging the related IT2 fuzzy variables (based on Eq. (248)) of the criteria weights. For example, average weight of the cost criteria C is found ((0.83,0.97,0.97,1;1),(0.9,0.97,0.97,0.98;0.9)), obtained by averaging the related fuzzy variables of the linguistic weights VH, H and VH. Similarly the average weight of the subcriteria $C_{1}$ is found ((0.83,0.97,0.97,1;1), (0.9,0.97,0.97,0.98;0.9)). The average weight of the each subcriterion is then multiplied by the corresponding main criteria weight and thus effective weight of the each subcriterion is obtained. For example, effective weight of the subcriterion $C_{1}$ is obtained ((0.69,0.94,0.94,1;1),(0.81,0.94,0.94,0.96;0.9)) by multiplying the average weight of the subcriterion $C_{1}$ with the weight of the corresponding main criteria C. In this way we find the effective weights of all the subcriteria as follows.

$C_{1}$: ((0.69,0.94,0.94,1;1),(0.81,0.94,0.94,0.96;0.9)),

$C_{2}$: ((0.52,0.8,0.8,0.97;1),(0.53,0.8,0.8,0.88;0.9)),

$C_{3}$: ((0.52,0.8,0.8,0.97;1),(0.53,0.8,0.8,0.88;0.9)),

$S_{1}$: ((0.34,0.64,0.64,0.9;1),(0.49,0.64,0.64,0.71;0.9)),

$S_{2}$: ((0.32,0.58,0.58,0.87;1),(0.44,0.58,0.58,0.72)),

$S_{3}$: ((0.4,0.69,0.69,0.94),(0.53,0.69,0.69,0.81;0.9)),

$S_{4}$: ((0.27,0.52,0.52,0.81;1),(0.39,0.52,0.52,0.66;0.9)),

$P_{1}$: ((0.19,0.4,0.4,0.7;1),(0.28,0.4,0.4,0.54;0.9)),

$P_{2}$: ((0.19,0.4,0.4,0.7;1),(0.28,0.4,0.4,0.54;0.9)),

$P_{3}$: ((0.25,0.49,0.49,0.81;1),(0.36,0.49,0.49,0.64;0.9)),

$F_{1}$: ((0.14,0.32,0.32,0.59;1),(0.22,0.32,0.32,0.45;0.9)),

$F_{2}$: ((0.11,0.29,0.29,0.54;1),(0.22,0.29,0.29,0.4;0.9)),

$F_{3}$: ((0.14,0.32,0.32,0.59),(0.22,0.32,0.32,0.45;0.9)),

$SF_{1}$: ((0.13,0.31,0.31,0.58),(0.21,0.31,0.31,0.44;0.9)),

$SF_{2}$: ((0.18,0.4,0.4,0.69),(0.28,0.4,0.4,0.53;0.9)).

The evaluation ratings of the transportation modes - rail and road as determined by the decision makers based on the selection criteria are same as presented in Table 26.

Table 36. Fuzzy group decision matrix

Table 37. Relative preference matrix

Table 38. Fuzzy weighted relative preferences of the alternatives

Table 39. Final preference indices and preference weights

Now we apply our proposed FMCGDM method based on ranking interval type-2 fuzzy variables step by step (cf. Sect. 5.6) as follows:

Step-1: Based on the Eq. (247), the group fuzzy decision matrix is derived by averaging the linguistic ratings of the decision makers and is presented in Table 36. The average effective weights of all the subcriteria are already obtained in the above.

Step-2: Upper and lower relative preference indices, i.e., $r_{ij}^U$ and $r_{ij}^L$ of the alternatives (rail and road) with respect to each subcriteria are obtained from Table 36 using Eqs. (249) and (250) respectively and presented in Table 37. Then the relative preference indices $r_{ij}$ of the alternatives are obtained by averaging their upper and lower relative preference indices as presented in Table 37.

Step-3: Then the fuzzy weighted relative preferences of the alternatives rail and road are calculated by employing the effective weights of the subcriteria as Eq. (251) and presented in Table 38.

Step-4: From Table 38, the final upper preference indices $r_{i}^U$ and lower preference indices $r_{i}^L$ of the alternatives are obtained using Eqs. (252) and (253) respectively and final preference indices $r_{i}$ are calculated by averaging them. These results are presented in Table 39.

Step-5: Preference weights $(W_{i})$ of the alternatives that sum to 1 are obtained by normalizing the preference indices $r_{i}$ and shown in Table 39.

From Table 39 we observe that weights of rail and road are 0.63 and 0.37 respectively and so for the current problem rail mode is preferred than road.

5.10 Overall Conclusion

Selection of suitable transportation modes is a major issue in transportation systems. There may exist large number of conflicting criteria for selecting convenient modes. Also human judgments are usually imprecise (i.e., linguistic, interval etc.) rather than precise numeric values.

In this section, we have proposed a computationally efficient fuzzy multi-criteria group decision making (FMCGDM) method (cf. Sect. 5.4) based on ranking fuzzy numbers. For this purpose we have defined a ranking function (cf. Sect. 5.3) based on credibility measure to rank a fuzzy number over another fuzzy number. The proposed fuzzy MCGDM method is applied (cf. Sect. 5.7) to find most convenient transportation mode alternatives in which the evaluation ratings and criteria weights are expressed in linguistic terms generated by fuzzy numbers. Also this method gives the weights of the alternatives which can be used for further requirements. The mode weights as founded by the method are assigned to a STP so that best mode can be used as maximum as possible.

In Sect. 5.5, a new method of ranking IT2 FVs based on generalized credibility measure is proposed. In Sect. 5.6, we have presented a new FMCGDM method based on the proposed ranking method of IT2 FVs. The proposed FMCGDM method is applied to a transportation mode selection problem (cf. Sect. 5.9) in which the evaluation ratings and criteria weights are expressed in linguistic terms generated by trapezoidal IT2 FVs.

The proposed methods are computationally efficient and we expect that these methods may have potential applications in many industry based FMCGDM problems in the future.

6 Solid Transportation Models with Transportation Cost Parameters as Rough Variables

6.1 Introduction

Traditionally the solid transportation problem (STP) (Haley [53], Gen et al. [48], Jiménez and Verdegay [60], Li et al. [81]) is modeled taking total supply capacity of all the conveyances and it is assumed that this total capacity is available for utilization for all source to destination routs whatever be the amount of product allocated in the routs for transportation. But in many practical situations this may not always happen. Practically most of time full vehicles, e.g., trucks, rail coaches are to be booked and the availability of each type of conveyance at each source may not be the same and vehicles available at one source may not be utilized at another source due to long distance between them or some other problems. Also fulfillment of capacity of a vehicle effects the optimal transportation policy. These practical situations motivated us to formulate some useful solid transportation models.

Rough set theory is one of the most convenient and accepted tool to deal with uncertainty. Though transportation problems in various types of uncertain environments such as fuzzy, random are studied by many researchers, there are very few research papers about TP in rough uncertain environment. Since rough set theory is proposed by Pawlak [121], it is developed by many researchers (Pawlak [122], Pawlak and Skowron [124], Polkowski [125], Liu and Zhu [96]) in theoretical aspect and applied into many practical fields such as data envelopment analysis (DEA) (Shafiee and Shams-e-alam [131], Xu et al. [151]), data mining (Lin et al. [83]), multi-criteria decision analysis (Dembczynski et al. [35], Pawlak and Slowinski [123]), medical diagnosis (Hirano and Tsumoto [56], Tsumoto [133], Zhang et al. [163]), neural network (Azadeh et al. [9], Zhang et al. [162]), etc. Liu [86] proposed the concept rough variable which is a measurable function from rough space to the set of real numbers. Liu [87] discussed some inequalities of rough variables and convergence concept of sequence of rough variables. Liu and Zhu [97] introduced rough variable with values in measurable spaces. Liu [86, 88] studied some rough programming models with rough variables as parameters. Xu and Yao [150] studied a two-person zero-sum matrix games with payoffs as rough variables. Tao and Xu [132] developed a rough multi-objective programming for dealing with multi-objective solid transportation problem assuming that the feasible region is not fixed but flexible due to imprecise parameters. Xu et al. [151] proposed a rough DEA model to solve a supply chain performance evaluation problem with rough parameters. Xiao and Lai [149] considered power-aware VLIW instruction scheduling problem with power consumption parameters as rough variables. Mondal et al. [114] considered a production-repairing inventory model with fuzzy rough variables. But at the best of our knowledge none studied STPs with any of the parameters as rough variables before Kundu et al. [73].

In this section, we formulate solid transportation model with vehicle capacity and an additional cost which is incurred due to not fulfilling the vehicle capacity. The unit transportation costs and unit additional costs in the models are taken as rough variables. To solve the said models with transportation costs as rough variables we have presented rough chance-constrained programming, rough expected value and rough dependent-chance programming models.

6.2 Model 6.1: New Solid Transportation Model with Vehicle Capacity

We first describe and formulate the model deterministically and then consider the model with rough cost parameters.

Notations:

• (i) $c_{ijk}$: The unit transportation costs from i-th source to j-th destination via k-th conveyance according to full utilization of the vehicle capacity.

• (ii) $x_{ijk}$: The decision variable which represents amount of product to be transported from i-th origin to j-th destination via k-th conveyance.

• (iii) Z: The objective function.

• (iv) $a_{i}$: The amount of the product available at the i-th origin.

• (v) $b_{j}$: The demand of the product at j-th destination.

• (vi) $q_{k}$: The capacity of singe vehicle of k-th type conveyance.

• (vii) $z_{ijk}$: The frequency (number of required vehicles) of conveyance k for transporting goods from source i to destination j via conveyance k.

• (viii) $\epsilon _{ijk}$: Total additional (penalty) cost for $i-j-k$ route due to not fulfilling the vehicle capacity.

Description of the Problem and Model Formulations: In traditional STP, total transportation capacity of conveyances is taken and the problem is solved assuming that this total capacity can be utilized for all routes whatever the allocation of products is in the routes. But in many real transportation systems, full vehicles (e.g. trucks for road transportation, coaches for rail transportation, etc.) are to be booked and number of vehicles required are according to amount of product to be transported through a particular route. The difficulty in this case arises when the amount of allocated product is not sufficient to fill up the capacity of the vehicle, because then extra cost is incurred despite the unit transportation cost due to not fulfilling the vehicle capacity. Here we formulate some solid transportation models with vehicle capacity to deal with such situations.

Suppose $q_{k}$ be the capacity of singe vehicle of k-th type conveyance. Let $z_{ijk}$ be the frequency (number of required vehicles) of conveyance k for transporting goods from source i to destination j via conveyance k and $x_{ijk}$ (decision variable) be the corresponding amount of goods. Then $z_{ijk}$ is a decision variable which takes only positive integer or zero. Also we have

$$x_{ijk}\le z_{ijk}\cdot q_{k}.$$

Now in such vehicle transportation system obviously calculation of unit transportation cost is according to the full utilization of the capacity of the vehicle. That is for a particular route $i-j-k$ if the unit transportation cost $c_{ijk}$ is according to full utilization of the vehicle capacity $q_{k}$ then an extra cost (penalty) will be added if the capacity $q_{k}$ is not fully utilized. Determination of additional cost for deficit amount depends upon the relevant transportation authority. Two cases may arise, either authority do not want to compromise for deficit amount and so direct cost $c_{ijk}$ is also represent the additional cost for unit deficit amount, or they agree to compromise and fixed an additional cost for unit deficit amount. For calculating additional cost first deficit amount of goods is to be calculated for each route. This can be done by two ways - calculating deficit amount for $i-j-k$ route directly as $(z_{ijk}\cdot q_{k}-x_{ijk})$ or by calculating the empty ratio (Yang et al. [152]) of each vehicle of k-th type conveyance for transporting goods from source i to destination j as

$$d_{ijk}=\left\{ \begin{array}{ll} 0, &{} \hbox {if}\, \frac{x_{ijk}}{q_{k}}=[\frac{x_{ijk}}{q_{k}}]; \\ 1-(\frac{x_{ijk}}{q_{k}}-[\frac{x_{ijk}}{q_{k}}]), &{} \hbox {otherwise.} \end{array} \right. $$

Then the amount of deficit amount for $i-j-k$ route is given by $q_{k}\cdot d_{ijk}$. Now if $u_{ijk}$ represents additional cost for unit amount of deficit from source i to destination j via conveyance k, then additional cost for this route is given by

$$\epsilon _{ijk}=u_{ijk}(z_{ijk}\cdot q_{k}-x_{ijk})~or~ \epsilon _{ijk}=u_{ijk}\cdot q_{k}\cdot d_{ijk}.$$

The total additional (penalty) cost for the problem is

$$C(x)=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~\epsilon _{ijk}.$$

So the STP model becomes

$$\begin{aligned} Min~Z=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~(c_{ijk}~x_{ijk}+\epsilon _{ijk}) \end{aligned}$$

$$\begin{aligned} s.t.~ \sum _{j=1}^n\sum _{k=1}^K x_{ijk}~\le & {} a_{i},~~i=1,2,...,m,\nonumber \\ \sum _{i=1}^m\sum _{k=1}^K x_{ijk}~\ge & {} b_{j},~~j=1,2,...,n, \\ x_{ijk}\le & {} z_{ijk}\cdot q_{k},~i=1,2,...,m; j=1,2,...,n; k=1,2,...,K,\nonumber \end{aligned}$$

(257)

$$\sum _{i=1}^ma_{i}\ge \sum _{j=1}^nb_{j},~x_{ijk}\ge 0,~z_{ijk}\in Z^+, \forall ~ i,j,k.$$

In the above model it is assumed that there are sufficient number of vehicles of each type of conveyance available to transport the required amount of goods (i.e., there is no restriction on number of available vehicles of each type of conveyances). If number of vehicles of conveyances limited to certain number, suppose $Q_{k}$ for k-th type conveyance then an another constraint

$$\sum _{i=1}^m\sum _{j=1}^n~z_{ijk}\le Q_{k},~k=1,2,...,K$$

is added to the model (257), then the above model becomes

$$\begin{aligned} Min~Z=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~(c_{ijk}~x_{ijk}+\epsilon _{ijk}) \end{aligned}$$

$$\begin{aligned} s.t.~ \sum _{j=1}^n\sum _{k=1}^K x_{ijk}~\le & {} a_{i},~~i=1,2,...,m,\nonumber \\ \sum _{i=1}^m\sum _{k=1}^K x_{ijk}~\ge & {} b_{j},~~j=1,2,...,n, \\ x_{ijk}\le & {} z_{ijk}\cdot q_{k},~i=1,2,...,m; j=1,2,...,n; k=1,2,...,K,\nonumber \\ \sum _{i=1}^m\sum _{j=1}^n~z_{ijk}\le & {} Q_{k},~k=1,2,...,K,\nonumber \end{aligned}$$

(258)

$$\sum _{i=1}^ma_{i}\ge \sum _{j=1}^nb_{j},~x_{ijk}\ge 0,~z_{ijk}\in Z^+, \forall ~ i,j,k.$$

This limitation of number of vehicles can effect the optimal transportation policy. For example unavailability of sufficient number of vehicles of certain type of conveyance may force to use another type of conveyance which costs higher than the previous.

The hierarchical structures of the model (258) is shown in the Fig. 18.

Fig. 18.

The hierarchical structures of the model (258).

In the above two models it is assumed that total available vehicles can be utilized in each source as they required. But in reality in each source, the availability of different vehicles may not be the same and the vehicles available at one source may not be utilized for another source due to long distance between them. So there may be a situation arises that in a certain source there are more than sufficient number of particular vehicles available to transport product to destinations but at the same time in an another source there are less number of that vehicles available than the requirement. As a result it may happen that vehicle having less transportation cost leaving from certain source to destination without being fully loaded, while vehicle having comparably high transportation cost leaving from another source to destination with fully loaded. So it is realistic to include a constraint defining source-wise vehicle availability. Suppose at source i, the number of available vehicles of k-th type conveyance is $V_{i}^k$ and vehicles at each source can not be shared to other sources.

Fig. 19.

The hierarchical structures of the model (259).

Then the constraints

$$\sum _{j=1}^n z_{ijk}\le V_{i}^k,~i=1,2,...,m; k=1,2,...,K$$

is added to the model (257) and so the model becomes

$$\begin{aligned} Min~Z=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~(c_{ijk}~x_{ijk}+\epsilon _{ijk}) \end{aligned}$$

$$\begin{aligned} \nonumber s.t.~ \sum _{j=1}^n\sum _{k=1}^K x_{ijk}~\le & {} a_{i},~~i=1,2,...,m, \\ \sum _{i=1}^m\sum _{k=1}^K x_{ijk}~\ge & {} b_{j},~~j=1,2,...,n, \\ \nonumber x_{ijk}\le & {} z_{ijk}\cdot q_{k},~i=1,2,...,m; j=1,2,...,n; k=1,2,...,K,\\ \nonumber \sum _{j=1}^n z_{ijk}\le & {} V_{i}^k,~i=1,2,...,m; k=1,2,...,K, \end{aligned}$$

(259)

$$\sum _{i=1}^ma_{i}\ge \sum _{j=1}^nb_{j},~x_{ijk}\ge 0,~z_{ijk}\in Z^+, \forall ~ i,j,k.$$

The hierarchical structures of the model (259) is shown in the Fig. 19.

6.3 The Model with Unit Transportation and Additional Costs (Penalty) as Rough Variables

Consider the unit transportation costs $c_{ijk}$ and as well as unit additional costs $u_{ijk}$ for the model (257) are rough variables represented by $c_{ijk}=$ $([c_{ijk}^2,c_{ijk}^3],$ $[c_{ijk}^1,c_{ijk}^4])$, $c_{ijk}^1\le c_{ijk}^2<c_{ijk}^3\le c_{ijk}^4$ and $u_{ijk}=([u_{ijk}^2,u_{ijk}^3],[u_{ijk}^1,u_{ijk}^4])$, $u_{ijk}^1\le u_{ijk}^2<u_{ijk}^3\le u_{ijk}^4$. Then, the objective function of the model (257), given by $Z=$ $\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~ (c_{ijk}~x_{ijk}+\epsilon _{ijk})$, $\epsilon _{ijk}=u_{ijk}(z_{ijk}\cdot q_{k}-x_{ijk})$ becomes a rough variable defined as $Z=([Z^2,Z^3],[Z^1,Z^4])$, where

$$\begin{aligned} Z^r=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~(c_{ijk}^r~x_{ijk}+\epsilon _{ijk}^r),~r=1,2,3,4, \end{aligned}$$

(260)

$\epsilon _{ijk}^r=u_{ijk}^r(z_{ijk}\cdot q_{k}-x_{ijk}),~r=1,2,3,4.$

Rough Chance-Constrained Programming Model: For the above problem with rough objective function one can not directly minimize it. The main idea of chance-constrained method is that a uncertain constraint is allowed to violet ensuring that it must be hold at some chance/confidence level. We apply the idea of chance-constrained programming (CCP) to the objective function of the model (257) with rough costs (i.e. rough objective function) with the help of trust measure. Since the problem is a minimization problem, we minimize the smallest objective $\bar{Z}$ satisfying $Tr\{Z\le \bar{Z}\}\ge \alpha$, where $\alpha \in (0,1]$ is a specified trust (confidence) level, i.e., we minimize the $\alpha$-pessimistic value $Z_{inf}(\alpha )$ of Z. This implies that the optimum objective value will below the $\bar{Z}$ with a trust level at least $\alpha$. So the rough CCP becomes

$$\begin{aligned} Min~(Min~\bar{Z}) \end{aligned}$$

(261)

$$\begin{aligned} s.t.~Tr\{Z\le \bar{Z}\}\ge & {} \alpha ,\nonumber \\ \sum _{j=1}^n\sum _{k=1}^K x_{ijk}~\le & {} a_{i},~~i=1,2,...,m, \end{aligned}$$

(262)

$$\begin{aligned} \sum _{i=1}^m\sum _{k=1}^K x_{ijk}~\ge & {} b_{j},~~j=1,2,...,n, \end{aligned}$$

(263)

$$\begin{aligned} x_{ijk}\le & {} z_{ijk}\cdot q_{k},~i=1,2,...,m; j=1,2,...,n; k=1,2,...,K,\end{aligned}$$

(264)

$$\begin{aligned} \sum _{i=1}^ma_{i}\ge & {} \sum _{j=1}^nb_{j},~x_{ijk}\ge 0,~z_{ijk}\in Z^+, \forall ~ i,j,k. \end{aligned}$$

(265)

Now we also formulate another rough CCP for the model (257) with rough costs, to minimize the greatest objective $\underline{Z}$ satisfying $Tr\{Z\ge \underline{Z}\}\ge \alpha$, where $\alpha \in (0,1]$ is a specified trust (confidence) level, i.e., we minimize the $\alpha$-optimistic value $Z_{sup}(\alpha )$ of Z. In other words, we minimize maximum $\underline{Z}$ so that the optimum objective value will greater or equal to the $\underline{Z}$ with a trust level at least $\alpha$. So the rough CCP becomes

$$\begin{aligned} Min~(Max~\underline{Z}) \end{aligned}$$

$$\begin{aligned} s.t.~Tr\{Z\ge \underline{Z}\}\ge \alpha , \end{aligned}$$

(266)

and the constraints (262)–(265).

Deterministic Forms: From the definition of $\alpha$-pessimistic value (Definition 2.14, Sect. 2.4), the above CCP (261)–(265) equivalently becomes

$$\begin{aligned} Min~Z' \end{aligned}$$

$$\begin{aligned} s.t. ~the~ constraints ~(262)-(265), \end{aligned}$$

(267)

where

$$\begin{aligned} Z'&= Z_{inf}(\alpha )\nonumber \\&= \left\{ \begin{array}{ll} (1-2\alpha ) Z^1+2\alpha Z^4, &{} \hbox {if}\, \alpha \le ((Z^2-Z^1)/2(Z^4-Z^1)); \\ 2(1-\alpha ) Z^1+(2\alpha -1)Z^4, &{} \hbox {if}\, \alpha \ge ((Z^3+Z^4-2Z^1)/2(Z^4-Z^1)); \\ \frac{Z^1(Z^3-Z^2)+Z^2(Z^4-Z^1)+2\alpha (Z^3-Z^2)(Z^4-Z^1)}{(Z^3-Z^2)+(Z^4-Z^1)}, &{} \hbox {otherwise.} \end{array}\right. \end{aligned}$$

From the definition of $\alpha$-optimistic value, the above CCP (266) equivalently becomes

$$\begin{aligned} Min~Z'' \end{aligned}$$

$$\begin{aligned} s.t. ~the~ constraints ~(262)-(265), \end{aligned}$$

(268)

where

$$\begin{aligned}Z''&= Z_{sup}(\alpha )\\&= \left\{ \begin{array}{ll} (1-2\alpha ) Z^4+2\alpha Z^1, &{} \hbox {if}\, \alpha \le ((Z^4-Z^3)/2(Z^4-Z^1)); \\ 2(1-\alpha ) Z^4+(2\alpha -1)Z^1, &{} \hbox {if}\, \alpha \ge ((2Z^4-Z^2-Z^1)/2(Z^4-Z^1)); \\ \frac{Z^4(Z^3-Z^2)+Z^3(Z^4-Z^1)-2\alpha (Z^3-Z^2)(Z^4-Z^1)}{(Z^3-Z^2)+(Z^4-Z^1)}, &{} \hbox {otherwise.} \end{array}\right. \end{aligned}$$

Since for $0.5<\alpha \le 1$, $Z_{inf}(\alpha )\ge Z_{sup}(\alpha )$, so solving the problems (267) and (267) with trust level $\alpha$ $(0.5<\alpha \le 1)$ we conclude that optimum objective value lie within the range $[Z'',Z']$ with the trust level at least $\alpha$.

In case of models (258) and (259) with unit transportation and additional costs as rough variables, rough CCP can be developed same way as above.

Rough Expected Value Model: We find the expected value for the objective function of the model (257) with rough costs, so the problem becomes

$$\begin{aligned} Min~E[Z]=E[\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~~c_{ijk}~x_{ijk}+\epsilon _{ijk}] ,\end{aligned}$$

(269)

$$\begin{aligned} s.t. ~the~ constraints ~(262)-(265). \end{aligned}$$

Deterministic Forms: From the expected value of a rough variable (Definition 2.15, Example 2.9, Sect. 2.4), the deterministic form of the above problem (269) becomes

$$\begin{aligned} Min~E[Z]=(Z^1+Z^2+Z^3+Z^4)/4 ,\end{aligned}$$

(270)

$$\begin{aligned} s.t. ~the~ constraints ~(262)-(265), \end{aligned}$$

$$where~Z^r=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~(c_{ijk}^r~x_{ijk}+\epsilon _{ijk}^r),~r=1,2,3,4,$$

.

Rough Dependent-Chance Programming Model: The idea of dependent-chance programming is to optimize the chance of an uncertain event. Suppose in view of previous experiment, a decision maker will satisfy with a transportation plan for which the total transportation cost is not exceed a certain value. So a decision maker may fixed a satisfying predetermined maximal objective value, i.e. total transportation cost and maximize the trust value that total transportation cost is not exceed the predetermined cost. So to obtain the most trastable transportation plan with respect to a given predetermined maximal cost $\bar{Z}$ the dependent chance-constrained programming model for the model (257) with rough objective function is formulated as follows:

$$\begin{aligned} Max~Tr\{Z=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~(c_{ijk}~x_{ijk}+\epsilon _{ijk})\le \bar{Z}\} , \end{aligned}$$

(271)

$$\begin{aligned} s.t. ~the~ constraints ~(262)-(265), \end{aligned}$$

Deterministic Forms: The deterministic form of the objective function of (271) can be obtained by the trust of a rough event as discussed in Example 2.9, Sect. 2.4. $Tr\{Z=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^K~(c_{ijk}~x_{ijk}+\epsilon _{ijk})\le \bar{Z}\}$, where $Z=([Z^2,Z^3],[Z^1,Z^4])$, $Z^r$ is given by (260), can be written as the following function:

$$\begin{aligned} Z'=\left\{ \begin{array}{ll} 0, &{} \hbox {if}\, \bar{Z}\le Z^1; \\ \frac{\bar{Z}-Z^1}{2(Z^4-Z^1)}, &{} \hbox {if}\, Z^1\le \bar{Z}\le Z^2; \\ \frac{1}{2}(\frac{\bar{Z}-Z^2}{Z^3-Z^2}+\frac{\bar{Z}-Z^1}{Z^4-Z^1}), &{} \hbox {if}\, Z^2\le \bar{Z}\le Z^3;\\ \frac{1}{2}(\frac{\bar{Z}-Z^1}{Z^4-Z^1}+1), &{} \hbox {if}\, Z^3\le \bar{Z}\le Z^4; \\ 1, &{} \hbox {if}\, \bar{Z}\ge Z^4. \end{array}\right. \end{aligned}$$

(272)

So deterministic form of the above problem (271) becomes Max $Z'$ with respect to the constraints (262)–(265).

6.4 Numerical Experiments

Models with Unit Transportation and Additional Costs as Crisp Numbers: Here we demonstrate the models with crisp cost parameters for better understanding and to show the efficiency of the models. Consider a problem with three sources $(i=1,2,3)$, three destinations $(j=1,2,3)$, two types of conveyances $(k=1,2)$. The unit transportation costs are given in Table 40. The availabilities at each sources, demands of each destinations and capacity of single vehicle of each type of conveyances are given in Table 41.

Table 40. Unit transportation costs $c_{ijk}$

Table 41. Availabilities, demands and vehicle capacity.

Table 42. Optimum results for model (257)

For convenience suppose additional costs for unit deficit amount is $u_{ijk}=0.8\cdot c_{ijk}$.

Now if there are sufficient number of vehicles of each type conveyances available as required (i.e., there is no restriction on number of available vehicles of each type of conveyances), then for the above problem solving the model (257) we have the solution given in Table 42.

So total number of required vehicles of conveyance $k=1$ is 10 and that of conveyance $k=2$ is 11.

Now as we say earlier, it may happen that number of vehicles of certain type of conveyance is so limited that it is not sufficient to fulfill its requirement for a transportation system.

Suppose in the above example the number of available vehicles of conveyance $k=1$ is 14 and that of conveyance $k=2$ is 10, i.e., $Q_{1}=14$ and $Q_{2}=10$. Then with the same data as given in Tables 40 and 41, solving the model (258) we have the solution given in Table 43.

Table 43. Optimum results for model (258)

It should be mentioned that here in case of model (258), if number of available vehicles of each type of conveyances at each source are greater or equal to as required in model (257), i.e., if $Q_{1}\ge 10$ and $Q_{2}\ge 11$ then model (258) gives the same result as model (257).

Now to demonstrate model (259), consider the same data as given in Tables 40 and 41 and suppose availability of vehicles of each type conveyances at each sources are $V_{1}^1=5$, $V_{1}^2=3$, $V_{2}^1=4$, $V_{2}^2=6$, $V_{3}^1=4$, $V_{3}^2=5$.

Then solving the model (259) we have the solution as presented in Table 44.

Table 44. Optimum results for model (259)

Models with Unit Transportation and Additional Costs as Rough Variables: Consider the model (257) with three sources $(i=1,2,3)$, three destinations $(j=1,2,3)$, two types of conveyances $(k=1,2)$. The unit transportation costs are rough variables as given in Tables 45 and 46.

The availabilities at each sources, demands of each destinations and capacity of single vehicle of each type of conveyances are same as in Table 41.

For convenience suppose additional costs for unit deficit amount is $u_{ijk}=0.8\cdot c_{ijk}$.

Table 45. Unit transportation costs $c_{ij1}$

Table 46. Unit transportation costs $c_{ij2}$

Solution Using Rough CCP: Now constructing rough CCP as (261)–(265) with trust level $\alpha =0.9$, we have corresponding deterministic form using (267) as follows:

$$\begin{aligned} Min~Z' \end{aligned}$$

$$\begin{aligned} s.t.~\sum _{j=1}^3\sum _{k=1}^2 x_{ijk}~\le & {} a_{i},~~i=1,2,3,\nonumber \\ \sum _{i=1}^3\sum _{k=1}^2 x_{ijk}~\ge & {} b_{j},~~j=1,2,3, \\ x_{ijk}\le & {} z_{ijk}\cdot q_{k},~i=1,2,3; j=1,2,3; k=1,2,\nonumber \end{aligned}$$

(273)

$$~x_{ijk}\ge 0,~z_{ijk}\in Z^+, \forall ~ i,j,k.$$

where,

$$Z'= \left\{ \begin{array}{ll} -0.8 Z^1+1.8 Z^4, &{} \hbox {if}\, 0.9\le ((Z^2-Z^1)/2(Z^4-Z^1)); \\ 0.2 Z^1+0.8Z^4, &{} \hbox {if}\, 0.9 \ge ((Z^3+Z^4-2Z^1)/2(Z^4-Z^1)); \\ \frac{Z^1(Z^3-Z^2)+Z^2(Z^4-Z^1)+1.8(Z^3-Z^2)(Z^4-Z^1)}{(Z^3-Z^2)+(Z^4-Z^1)}, &{} \hbox {otherwise.} \end{array}\right. $$

$$Z^r=\sum _{i=1}^3\sum _{j=1}^3\sum _{k=1}^2~(c_{ijk}^r~x_{ijk}+\epsilon _{ijk}^r),~r=1,2,3,4,$$

$\epsilon _{ijk}^r=0.8 c_{ijk}^r(z_{ijk}\cdot q_{k}-x_{ijk}),~r=1,2,3,4.$

Solving this problem we get the solution presented in Table 47.

Table 47. Optimum results for model (257) with transportation costs as rough variables using rough CCP

From this solution we conclude that the objective value will less or equal to 630.2688 with trust level at least 0.9.

We now construct rough CCP as (266) with trust level $\alpha =0.9$ and then we have corresponding deterministic form using (268) as follows:

$$\begin{aligned} Min~Z'' \end{aligned}$$

$$\begin{aligned} s.t.~\sum _{j=1}^3\sum _{k=1}^2 x_{ijk}~&\le a_{i},~~i=1,2,3,\nonumber \\ \sum _{i=1}^3\sum _{k=1}^2 x_{ijk}~&\ge b_{j},~~j=1,2,3, \\ x_{ijk}&\le z_{ijk}\cdot q_{k},~i=1,2,3; j=1,2,3; k=1,2,\nonumber \end{aligned}$$

(274)

$$x_{ijk}\ge 0,~z_{ijk}\in Z^+, \forall ~ i,j,k.$$

where,

$$Z''=\left\{ \begin{array}{ll} -0.8 Z^4+1.8 Z^1, &{} \hbox {if}\, 0.9\le ((Z^4-Z^3)/2(Z^4-Z^1)); \\ 0.2 Z^4+0.8Z^1, &{} \hbox {if}\, 0.9 \ge ((2Z^4-Z^2-Z^1)/2(Z^4-Z^1)); \\ \frac{Z^4(Z^3-Z^2)+Z^3(Z^4-Z^1)-1.8(Z^3-Z^2)(Z^4-Z^1)}{(Z^3-Z^2)+(Z^4-Z^1)}, &{} \hbox {otherwise.} \end{array}\right. $$

Solving this we get $Min Z''=471.427$. So the objective value will greater or equal to 471.427 with trust level at least 0.9.

As we know for $0.5<\alpha \le 1$, $Z_{inf}(\alpha )\ge Z_{sup}(\alpha )$, here our results $(Z'>Z'')$ shows this truth. Finally we can conclude that the optimum objective value lie within the range [471.427, 630.2688] with trust level at least 0.9.

Table 48. Optimum results using rough expected value

Solution Using Rough Expected Value: To solve the current problem using rough expected value, we use the rough expected value model (269). Then using its deterministic form (270) and solving it we get the solution presented in Table 48.

So we see that the expected objective value lie within the range of objective value as obtained by rough CCP.

Solution Using Rough Dependent CCP: The objective of this model is that for a predetermined maximal objective value find a solution with maximum satisfied trust level so that the optimum objective value is not more than that predetermined value. For the current problem, suppose the decision maker satisfied with a transportation plan for which the objective value is not exceed 600. So construct the problem as (271) with $\bar{Z}=600$. Then using (272) we find the maximum trust level Max$~\alpha =\alpha '=0.843$ and the corresponding transportation planing is presented in Table 49.

Table 49. Optimum results using rough dependent CCP

6.5 Overall Conclusion

This section presents solid transportation model for the transportation system where full vehicles are used for transportation so that unit transportation costs are determined according to full utilization of the vehicle capacity. To deal with different situations like availability of each type of conveyances, whether the available vehicles at one source can be utilized at another source or not, this presented model is extended to different models with different constraints. STP with different types of uncertain variables such as fuzzy, random, fuzzy random are discussed by many researchers, but STP with rough variables is not discussed before. In this paper we only assume the unit transportation costs as rough variables, the STP with all the parameters, i.e., costs, availabilities, demands, conveyance capacities as rough variables may be taken as a future work.

7 Overall Contribution and Future Extension

In this thesis, we have discussed several useful transportation models in different uncertain (e.g. fuzzy, type-2 fuzzy, rough, linguistic) environments. The thesis broadly addresses the following major sub-topics, namely:

• Transportation modeling with fuzzy parameters.

• Transportation modeling with type-2 fuzzy parameters.

• Transportation modeling with rough parameters.

• Transportation mode selection with linguistic information.

In Sect. 3 of this Article, a multi-objective solid transportation problem with type-1 fuzzy parameters is formulated and solved. In this problem, a fuzzy budget amount for each destination is imposed so that total transportation cost should not exceed that budget amount. In the budget constraint, both left and right sides have fuzzy quantity. To deal with such type of constraints, a deterministic form is derived by the idea of chance-constraint. Here, we have also formulated a general model (MOMISTP) to deal with transportation problem with multiple objectives and several types of goods to be transported. In this problem the corresponding parameters are taken as fuzzy numbers. A defuzzification process to find crisp values of corresponding fuzzy resources, demands and conveyance capacities is introduced so that the conditions that total available resources and total conveyance capacities are greater than or equal to the total demands must be satisfied. We have discussed that some well established methods like expected value model may not yield any feasible solution for the problem having constraints with such type of conditional relations. The idea of minimum of fuzzy numbers is also applied to the fuzzy objective function and we obtained fuzzy solution for the objective function with coefficients as fuzzy numbers.

For high computational complexity, there are very few methods available to deal with type-2 fuzzy set. In Sect. 4, we have proposed a defuzzification method of type-2 fuzzy variables. We have also introduced an interval approximation method of continuous type-2 fuzzy variables. For the first time, different transportation problems with type-2 fuzzy parameters are formulated and solved. Defuzzification method is applied to solve a FCTP with type-2 fuzzy cost parameters. A chance-constrained programming model is formulated using generalized credibility measure to solve a FCTP with type-2 fuzzy parameters. A MISTP having restriction on conveyances is formulated with type-2 fuzzy parameters. A deterministic form for the problem is obtained by applying interval analysis using the interval approximations of continuous type-2 fuzzy variables.

In Sect. 5, we have proposed a computationally efficient fuzzy MCGDM method based on a ranking function which is defined based on credibility measure to rank a fuzzy number over another fuzzy number. The proposed FMCGDM method is successfully applied to transportation mode selection problem with linguistic terms generated by fuzzy numbers. We have also proposed a computationally efficient fuzzy MCGDM method based on a ranking interval type-2 fuzzy variables. This proposed FMCGDM method is applied to a transportation mode selection problem where linguistic ratings of the alternatives and criteria weights are represented by IT2 FVs.

In remaining part of the this Article (Sect. 6), a practical solid transportation model is formulated considering per trip capacity for each type of conveyances. This is applicable for the system in which full vehicles, e.g. trucks, rail coaches are to be booked for transportation of products so that transportation cost is determined on the basis of full conveyances. We have represented fluctuating cost parameters by rough variables. To solve the problem with rough cost parameters, we have used rough chance constrained programming model, rough expected value model and rough dependent-chance programming model developed on the basis of trust measure theory.

Future Extension: Improvement/development in existing transportation models is a major issue in transportation research. To overcome different types of increased complexities and new challenges model should be adaptively changed and solution strategies should be developed. The transportation models presented in the thesis also can be extended to form different types of realistic models. For example, for transportation of several types of items, optimal distribution of available vehicle capacity among the items is a very important issue. In such case, space constraints can be implemented considering amount of goods, preferability of goods to be transported, availability of vehicle capacity, etc. For transportation of highly breakable items (e.g. glass-goods, toys, ceramic goods, etc.), the breakability issue should be considered. Also safety of transportation of goods through a particular route (specially in roadways due to land slide, insurgency, robbery, bad road, etc.) is also very important in the transportation system. So consideration of safety factor of the routes may be taken into account as an additional objective or a constraint.

In Sect. 4, the interval approximation method of continuous type-2 fuzzy variables is illustrated with type-2 triangular fuzzy variable. This interval approximation method can be applied to other T2 FVs such as type-2 normal fuzzy variable, type-2 gamma fuzzy variable, etc.

In Sect. 6, the solid transportation model is formulated with only the unit transportation costs as rough variables, the STP with all the parameters, i.e., costs, availabilities, demands, conveyance capacities as rough variables may be taken as a future work.

The models formulated in this dissertation can be formulated and solved in fuzzy random, random fuzzy, fuzzy rough and bifuzzy environments with unit transportation costs, sources, demands, conveyance capacities, etc. as the corresponding imprecise parameters/variables.