Keywords

11.1 Introduction

Recently, microgrids have been emerging as a framework for testing future smart grid issues in small scale. MGs are local grids that comprise different technologies such as power electronics converters; distributed generations, energy-storage systems, and telecommunications which can operate connected to the traditional centralized grid, but also could operate autonomously in islanded mode [1].

However, apart from these obvious benefits of MGs, their introduction into the traditional distribution network raises many new challenges; with one of the most important being the frequency and voltage participation in islanded operation mode. Control strategies have an important role to provide global stability in MGs. This problem has been investigated in recent years. In order to enhance the reliability and performances of the droop-controlled voltage source inverters (VSIs), virtual impedance control algorithms have developed providing the inverters with hot-swap operation, harmonic power sharing, and robustness for large-line power impedance variations [2–4]. Droop control is a kind of cooperative control that allows parallel connection of VSIs sharing active and reactive powers. It can be seen as a primary power control of a synchronous machine. However, droop control still has several drawbacks such as poor harmonic current sharing and high dependence on the power line impedances. In order to improve these drawbacks, a hierarchical control concept from the traditional power system has been introduced for MGs in [5–7]. The first level of this hierarchy is primary control which is strictly local and deals with the inner voltage and current control loops and droop control of the individual DGs, in order to adjust the frequency and amplitude according to active and reactive power of the units. Secondary control is conceived to compensate frequency and voltage deviations produced inside the MG by the virtual inertias and output virtual impedances of primary control. Tertiary control is responsible for global optimization of the MG and managing power flow between MGs and the distribution network of the main grid [7]. In all of these literatures, a central secondary control (CSC) has been used in order to manage the MG. The centralized control strategy has an inherent drawback of the single point of failure, i.e., all DGs measure signals of interest and send them to a common single MG central controller (MGCC), an MGCC failure terminates the secondary control action for all units [8].

In this paper, a networked hierarchical control for multiple parallel VSI system was developed. A new approach of distributed secondary control (DSC) strategy is proposed to implement it in a distributed way along the local control with communication systems. This kind of distributed control strategies are also named as networked control systems (NCS). A simple networked control scheme based on the industrial network for the DSC of MGs is presented. This way, every DG has its own local secondary control which can produce appropriate control signal for the primary control level by using the measurements of other DGs in each sample time.

This paper is organized as follows: Sect. 11.2 provides a networked hierarchical control structure for the MGs. The DSC of islanded MGs and its modeling and small-signal stability analysis are presented in Sect. 11.3. Section 11.4 provides simulation results of an islanded MG evaluating the proposed algorithm for DSC. Section 11.5 concludes this paper and outlines future research directions.

11.2 Networked Hierarchical Control Structure of MGs

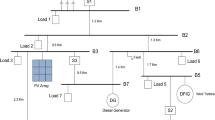
MGs for standalone and grid-connected applications have been considered in the past as separate approaches. Nevertheless, nowadays, it is necessary to conceive flexible MGs that are able to operate in both grid-connected and islanded modes. Thus, the study of topologies, architectures, planning, and configurations of MGs are necessary [9]. This paper deals with the hierarchical control of MGs consisting of the same three control levels as presented in large power systems. Such a kind of system is supposed to operate over large synchronous machines with high inertias and inductive networks. However, in power electronic-based MGs, there are no inertias and the nature of the networks is mainly resistive. Consequently, there are important differences between both systems that we have to take into account when designing their control schemes. This three-level hierarchical control is organized as follows. The primary control deals with the inner control of the DG units, adding virtual inertias and controlling their output impedances. The secondary control is conceived to restore the frequency and amplitude deviations produced inside the MG by the virtual inertias and output virtual impedances. The tertiary control regulates the power flow between the grid and the MG at the point of common coupling (PCC). In this paper, we use networked control system (NCS) for MGs. From the NCS perspective, DSC requires that every DG obtains the global average of the parameters of interest, i.e., frequency, voltage, and active and/or reactive power, in order to derive the local control signals. The provision of global averages is the task of underlying communication infrastructure. Several communication technologies have been introduced for NCSs, both wired and wireless [10]. Figure 11.1 illustrates the architecture of networked hierarchical control for islanded MG.

Fig. 11.1
figure 1

The architecture of networked hierarchical control for islanded MGs

Full size image

As shown, secondary control is locally embedded in each DG unit, similar to primary control; however, the local secondary control requires an underlying communication network to operate properly. In turn, the local secondary controllers operate on these parameters, regulating the frequency and voltage of the system and sharing power between the units.

11.3 Distributed Secondary Control of Islanded MGs

Conventional CSC is only responsible for restoring frequency and voltage inside the whole MG using common measurements of the system. However, DSC using the proposed communication algorithm is able to not only control frequency and voltage but also share power between units in the MG.

11.3.1 Frequency/Voltage Control and Power Sharing

In the distributed strategy, each DG has its own local secondary control to regulate the frequency. In this sense, each unit measures its frequency at each sampling instant, averaging the received information from other units and then sending its average \( \bar{f}_{\text{MG}} \) to the other units through the communication network. The averaged data are compared with the nominal frequency of \( f_{\text{MG}}^{*} \) and sent to the secondary controller of DGi to restore the frequency as follows:

$$ \delta f_{s} = k_{\text{pf}} (f_{\text{MG}}^{*} - \bar{f}_{\text{MG}} ) + k_{\text{if}} \int {(f_{\text{MG}}^{*} - \bar{f}_{\text{MG}} )} {\text{d}}t $$
(11.1)

where k pf and k if are the control parameters of the PI compensator of unit i, and δf s is the secondary control signal sent to the primary control level in order to remove the frequency deviations.

Similar approach can be used as in the distributed frequency control one, in which each inverter will measure the voltage error, and tries to compensate the voltage deviation caused by the Q-V droop. In this secondary voltage control strategy, after calculating the average value of voltage \( \bar{E}_{\text{MG}} \) that is based on the information exchanged over the communication network, every local secondary controller measures the voltage error and compares it with the voltage reference \( E_{\text{MG}}^{*} \). In the next step, the local secondary controller sends control signal δEs to the primary level of control as a set point to compensate for the voltage deviation. The voltage restoration control loop of DG i can be expressed as follows:

$$ \delta E_{s} = k_{\text{pE}} (E_{\text{MG}}^{*} - \bar{E}_{\text{MG}} ) + k_{\text{iE}} \int {(E_{\text{MG}}^{*} - \bar{E}_{\text{MG}} )} {\text{d}}t $$
(11.2)

With k pE and k iE are the PI controller parameters of the voltage secondary control. In a low R/X MG, reactive power is difficult to be precisely shared between units using Q-V droop control, since voltage is not common in the whole system as opposed to frequency. A solution is to implement a distributed average power sharing in the secondary loop, where the averaging is performed through the communication network. The averaging power process is done in each DG, so that finally, as the information is common, all of them will have the same reference. Therefore, the reactive power sharing can be expressed as

$$ \delta Q_{s} = k_{\text{pQ}} (Q_{i} - \bar{Q}_{\text{MG}} ) + k_{\text{iQ}} \int {(Q_{i} - \bar{Q}_{\text{MG}} )} {\text{d}}t $$
(11.3)

where k pQ and k iQ are the PI controller parameters, Q i is the locally calculated reactive power (which can be active power in the case of high-resistive-line MGs), \( \bar{Q}_{\text{MG}} \) is the average power obtained through the communication network, and δQ s is the control signal produced by the secondary control in each sample instant and afterward sent to the primary loop.

11.3.2 Modeling and Small-Signal Stability Analysis

Figure 11.2 shows the equivalent circuit of n inverters connected to an AC bus. It is assumed that the output impedance of the inverters is mainly inductive (θ = 90°). In order to analyze the stability of the system and to adjust the parameters of DSC, a small-signal model has been developed. In this situation, the active power and reactive power injected into the bus by every inverter are expressed as the following equations [11]:

Fig. 11.2
figure 2

Small-signal representation of frequency\voltage control\reactive power sharing

Full size image
$$ P_{i} = \frac{{E_{i} V\sin \phi_{i} }}{{X_{i} }};\quad Q_{i} = \frac{{E_{i} V\cos \phi_{i} - V^{2} }}{{X_{i} }} $$
(11.4)

where E i and V are the amplitudes of the ith inverter output voltage and the common bus voltage, \( \phi_{i} \) is the power angle of the inverter, and X i is the magnitude of the output reactance for the ith inverter. From the above equations, it can be seen that if the phase difference between E i and V is small enough, the active power is strongly influenced by power angle \( \phi_{i} \), and the reactive power flow depends on the voltage amplitude difference. Consequently, the frequency and the amplitude of the inverter output voltage can be expressed by the droops control method as [11].

$$ \left\{ \begin{gathered} \omega_{i} = \omega^{ * } - k_{p} P_{i} \hfill \\ E_{i} = E^{ * } - k_{q} Q_{i} \hfill \\ \end{gathered} \right. $$
(11.5)

where ω ∗and E ∗are the output voltage frequency and amplitude references, and kp and kq are the droop frequency and amplitude coefficients. As aforementioned, the outputs of secondary control obtained through (11.1–11.3) are added to the droops to shift the droop lines in order to restore the frequency and voltage of the system and to share the power between the units. Therefore, (11.5) are updated as,

$$ \left\{ \begin{aligned} \omega_{i} = & \,\omega^{ * } - k_{p} p_{i} + \delta \omega_{s} \\ E_{i} = & \,E^{ * } - k_{q} Q_{i} + \delta E_{s} + \delta Q_{s} \\ \end{aligned} \right. $$
(11.6)

So a small-signal model is obtained by linearizing (11.4–11.6) at operating points P ie, Q ie, E ie, Ve, and \( \phi_{\text{ie}} \) as follows:

$$ \left\{ \begin{aligned}\Delta \omega_{i} (s) =\, &\Delta \omega^{ * } (s) - k_{p}\Delta p_{i} (s) +\Delta \omega_{s} (s) \\\Delta E_{i} (S) =\, &\Delta E^{ * } (s) - k_{q}\Delta Q_{i} (s) +\Delta E_{s} (S)+\Delta Q_{s} (s) \\ \end{aligned} \right. $$
(11.7)
$$ \Delta \phi_{i} = \int {\Delta \omega_{i} {\text{d}}t} $$
(11.8)
$$ \Delta p_{i} (s) = G\Delta \phi_{i} (s) $$
(11.9)
$$ \Delta Q_{i} (s) = H\Delta E_{i} (s) + F\Delta V(s) $$
(11.10)

where

$$ \begin{aligned} G = \frac{{E_{\text{ie}} V_{e} \, \cos \phi_{\text{ie}} }}{{X_{i} }},\;\;\;\;H = \frac{{2E_{\text{ie}}- V_{e} \, \cos \phi_{\text{ie}} }}{{X_{i} }},\;\;\;\; F = - \frac{{E_{\text{ie}} \cos \phi_{\text{ie}} }}{{X_{i} }} \\ \end{aligned} $$
(11.11)

Figure 11.2 show the small-signal representation of frequency and voltage control and reactive power sharing control model. The dynamics of the system around the operating point may be expressed in state-space form as follows:

$$ \dot{x}(t) = Ax(t) $$
(11.12)

The frequency control model, \( x = [x_{1} ,x_{2} ,x_{3} ,x_{4} ]^{T} \) and A is

$$ A = \left[ {\begin{array}{*{20}c} { - \frac{1}{{\tau_{p} }} \, } & 0 & 0 & G \\ { - \frac{{k_{p} }}{{\tau_{p} }}} & { - \frac{{1 + k_{pf} }}{\tau }} & 1 & 0 \\ 0 & { - \frac{{k_{if} }}{\tau }} & 0 & 0 \\ { - \frac{{k_{p} }}{{\tau_{p} }}} & { - \, \frac{{k_{pf} }}{\tau }} & 1 & 0 \\ \end{array} } \right] $$
(11.13)

To realize the droop functions, it is necessary to employ low-pass filters (LPFs) in order to calculate the active and reactive power from the instantaneous power. The state variables x 1, x 2, x 3, and x 4 are assigned to the output of LPF, PLL, PI controller, and the integral term of the power angle, respectively.

For voltage control, \( x = [x_{1} ,x_{2} ]^{T} \) and A is

$$ A = \left[ {\begin{array}{*{20}c} {\frac{{1 + k_{pE} + k_{q} H}}{{\tau_{p} (1 + k_{pE} )}}} & {\frac{H}{{1 + k_{pE} }}} \\ {\frac{{k_{q} k_{i} E}}{{\tau_{p} (1 + k_{pE} )}}} & { - \, \frac{{k_{i} E}}{{1 + k_{pE} }}} \\ \end{array} } \right] $$
(11.14)

where x 1 and x 2 are chosen as the state variable of LPF and PI controller. Note that in the related analysis, the communication delay and packet losses were assumed to be negligible.

11.4 Simulation Results

For the calculation of plant parameters (G, H, and F), we can choose E ie = 1 per unit, Ve = 1 per unit, and ϕ ie = 0. Moreover, we assume X i  = 0.001 per unit. Other needed parameters can be found in reference [12].

Figure 11.3 shows the trajectory of the low-frequency eigenvalues of both the frequency and voltage models as a function of the secondary control parameters. From the figure we can see that as the proportional terms of PI controllers are increased, the eigenvalues of the system move toward an unstable region, making the system more oscillatory and eventually leading to instability. However, the integral term parameter has no significant effect on the dynamics of the system. Similar analysis can be performed for the other parameters of the presented model.

Fig. 11.3
figure 3

Trace of eigenvalues as a function of secondary control parameters. a Frequency control of increasing kpf. b Frequency control of increasing kif. c Voltage control of increasing kpE. d Voltage control of increasing kiE

Full size image

11.5 Conclusions

In this paper, the evaluation of the hierarchical control is presented and discussed. A new approach of distributed secondary control based on network for islanded MGs has been proposed. The primary control includes the droop method and the virtual impedance loops, in order to share active and reactive power. The secondary control restores the frequency and amplitude deviations produced by the primary control. The modeling, controller design, and stability analysis for the microgrids consist of a number of voltage source inverters (VSIs) operating in parallel are derived. Simulation results show the good performance of the MG system using the proposed DSC method. Finally, an impact analysis of communications in frequency and active power control in hierarchic multi-MG structures, considering both packet delays and losses is the next work to be done.