Keywords

1 Introduction

Optimum control theory has been applied in many areas of science, from engineering to economics. An algorithm that provides (approximate) solutions to optimum control problems for nonlinear dynamic systems with different kinds of stochastics is OPTCON, which was first introduced in [3]. An extension has been developed in [2], which includes passive learning or open-loop feedback control policies.

OPTCON was implemented in MATLAB and can deliver numerical solutions to problems with real economic data. Two such applications are described and analyzed in this paper. We develop two macroeconomic models of the Slovenian economy, a nonlinear model called SLOVNL and a (comparable) linear model called SLOVL. The algorithm with both open-loop and open-loop feedback strategies is applied to these models and the influence of the control scheme and the nonlinearity of the model on the optimum solution is investigated in some optimization experiments.

2 The Problem

The OPTCON algorithm is designed to provide approximate solutions to optimum control problems with a quadratic objective function (a loss function to be minimized) and a nonlinear multivariate discrete-time dynamic system under additive and parameter uncertainties. The intertemporal objective function is formulated in quadratic tracking form, which is quite often used in applications of optimum control theory to econometric models. It can be written as

$$\begin{aligned} J=E \left[ \sum ^T_{t=1}L_t(x_t,u_t) \right] , \end{aligned}$$
(1)

with

$$\begin{aligned} L_t(x_t,u_t)=\frac{1}{2}\left( \begin{array}{c} x_t-\tilde{x}_t\\ u_t-\tilde{u}_t\\ \end{array} \right) 'W_t\left( \begin{array}{c} x_t-\tilde{x}_t\\ u_t-\tilde{u}_t\\ \end{array}\right) . \end{aligned}$$
(2)

\(x_t\) is an \(n\)-dimensional vector of state variables that describes the state of the economic system at any point in time \(t\). \(u_t\) is an \(m\)-dimensional vector of control variables, \(\tilde{x}_t\in R^n\) and \(\tilde{u}_t\in R^m\) are given ‘ideal’ (desired, target) levels of the state and control variables respectively. \(T\) denotes the terminal time period of the finite planning horizon. \(W_t\) is an \(((n+m)\times (n+m))\) matrix, specifying the relative weights of the state and control variables in the objective function. \(W_t\) (or \(W\)) is symmetric.

The dynamic system of nonlinear difference equations has the form

$$\begin{aligned} x_t=f(x_{t-1},x_t, u_t, \theta , z_t)+\varepsilon _t, t=1, ..., T, \end{aligned}$$
(3)

where \(\theta \) is a \(p\)-dimensional vector of parameters the values of which are assumed to be constant but unknown to the decision maker (parameter uncertainty), \(z_t\) denotes an \(l\)-dimensional vector of non-controlled exogenous variables, and \(\varepsilon _t\) is an \(n\)-dimensional vector of additive disturbances (system error). \(\theta \) and \(\varepsilon _t\) are assumed to be independent random vectors with expectations \(\hat{\theta }\) and \(O_n\) respectively and covariance matrices \(\Sigma ^{\theta \theta }\) and \(\Sigma ^{\varepsilon \varepsilon }\) respectively. \(f\) is a vector-valued function fulfilling some differentiability assumptions, \(f^i(.....)\), is the \(i\)-th component of \(f(.....)\), \(i=1, ..., n\).

3 The Optimum Control Algorithm

The OPTCON1 algorithm [3] determines policies belonging to the class of open-loop controls. It either ignores the stochastics of the system altogether or assumes the stochastics to be given once and for all at the beginning of the planning horizon. The nonlinearity problem is tackled iteratively, starting with a tentative path of state and control variables. The tentative path of the control variables is given for the first iteration. In order to find the corresponding tentative path for the state variables, the nonlinear system is solved numerically. After the tentative path is found, the iterative approximation of the optimal solution starts. The solution is sought from one time path to another until the algorithm converges or the maximal number of iterations is reached. During this search the system is linearized around the previous iteration’s result as a tentative path and the problem is solved for the resulting time-varying linearized system. The criterion for convergence demands that the difference between the values of current and previous iterations be smaller than a pre-specified number. The approximately optimal solution of the problem for the linearized system is then used as the tentative path for the next iteration, starting off the procedure all over again.

The more recent version OPTCON2 [2] incorporates both open-loop and open-loop feedback (passive-learning) controls. The idea of passive learning corresponds to actual practice in applied econometrics: at the end of each time period, the model builder (the control agent) observes what has happened, that is, the current values of state variables, and uses this information to re-estimate the model and hence improve his/her knowledge of the system.

The passive-learning strategy implies observing current information and using it in order to adjust the optimization procedure. For the purpose of comparing open-loop and open-loop feedback results, it is not possible to observe current and true values, so one has to resort to Monte Carlo simulations. Large numbers of random time paths for the additive and multiplicative errors are generated, representing what new information could look like in reality. In this way ‘quasi-real’ observations are created and both types of controls, open-loop and passive-learning (open-loop feedback), are compared.

4 The SLOVNL Model

We estimated two simple macroeconometric models for Slovenia, one nonlinear (SLOVNL) and one linear (SLOVL). The SLOVNL model (SLOVenian model, Non-Linear version) is a small nonlinear econometric model of the Slovenian economy consisting of 8 equations, 4 behavioral equations and 4 identities. SLOVNL includes 8 state variables, 3 control variables, 4 exogenous non-controlled variables and 16 unknown (estimated) parameters. We used quarterly data for the time periods 1995:1 to 2006:4; this data base with 48 observations admits a full-information maximum likelihood (FIML) estimation of the expected values and the covariance matrices for the parameters and the system errors. The starting period for the optimization is 2004:1; the terminal period is 2006:4 (12 periods).

figure a

The objective function penalizes deviations of objective variables from their ‘ideal’ (desired, target) values. The ‘ideal’ values of the state and control variables (\(\tilde{x}_t\) and \(\tilde{u}_t\) respectively) are chosen as shown in Table 1. The ‘ideal’ values for most variables are defined in terms of growth rates (denoted by % in Table 1) starting from the last given observation (2003:4). For \(Pi4\) and \(TaxRate\), constant ‘ideal’ values are used; for \(STIRLN\), a linear decrease of 0.25 per quarter is assumed to be the goal.

Table 1. ‘Ideal’ values of objective variables, SLOVNL
Full size table
Table 2. Weights of objective variables, SLOVNL
Full size table

The weights for the variables, i.e. the constant matrix \(W\) in the objective function, are first chosen as shown in Table 2a (‘raw’ weights) to reflect the relative importance of the respective variable in the (hypothetical) policy maker’s objective function. These ‘raw’ weights have to be scaled or normalized according to the levels of the respective variables to make the weights comparable. The normalized (‘correct’) weights are shown in Table 2b.

5 The SLOVL Model

To analyse the impact of the nonlinearity of the system we developed a linear pendant to the SLOVNL model. This ‘sister model’ is called SLOVL (SLOVenian model, Linear version) and consists of 6 equations, 4 of them behavioral and 2 identities. The model includes 6 state variables, 3 exogenous non-controlled variables, 3 control variables, and 15 unknown (estimated) parameters. We used the same data base as for SLOVNL and a specification as close as possible to that of SLOVNL in order to make comparisons between the results of the algorithm for a linear and a nonlinear model. Again, we used full-information maximum likelihood (FIML) to estimate the expected values and the covariance matrices for the parameters and the system errors. The starting and the terminal period for the optimization are again 2004:1 and 2006:4.

figure d

The objective function is analogous as for SLOVNL, where the ‘ideal’ values of the state and control variables (\(\tilde{x}_t\) and \(\tilde{u}_t\) respectively) are chosen as shown in Table 3. For the weights for the variables, Table 4a shows the ‘raw’ weights and Table 4b gives the normalized weights.

Table 3. ‘Ideal’ values of objective variables, SLOVL
Full size table
Table 4. Weights of objective variables, SLOVL
Full size table

6 Optimization Experiments

The OPTCON2 algorithm is applied to the two econometric models SLOVNL and SLOVL. Two different experiments are run for both models: in experiment 1, two open-loop solutions are compared, a deterministic one where the variances and covariances of the parameters are ignored, and a stochastic one where the estimated parameter covariance matrix is taken into account. In experiment 2, the properties of the open-loop and the open-loop feedback solutions are compared. Furthermore, by comparing the results for the SLOVNL and the SLOVL models we want to analyze the impact of nonlinearity on the properties of the optimal solution.

6.1 Experiment 1: Open-Loop Optimal Policies

For experiment 1, two different open-loop solutions are calculated: a deterministic and a stochastic one. The deterministic solution assumes that all parameters of the model are known with certainty and are equal to the estimated values. In the stochastic case, the covariance matrix of the parameters as estimated by FIML is used but no updating of information occurs during the optimization process.

The results (for details, see [1, 2]) show that both the deterministic and the stochastic solutions follow the ‘ideal’ values fairly well but fiscal policies are less expansionary and hence real \(GDP\) is mostly below its ‘ideal’ values. The values of the objective function show a considerable improvement in system performance obtained by optimization and only moderate costs of uncertainty.

An interesting result is that the deterministic and the stochastic open-loop solutions are very similar. Furthermore, one can see that the SLOVL model is a good ‘linear approximation’ of the nonlinear SLOVNL model because the results for both models are nearly identical. This fact can be used for isolating the impact of nonlinearity on finding the optimum control solution, especially for the case of open-loop feedback policies.

6.2 Experiment 2: Open-Loop Feedback Optimal Policies

The aim of experiment 2 consists in comparing open-loop (OL) and open-loop feedback (OLF) optimal stochastic controls. Figures 1 and 2 show the results of a representative Monte Carlo simulation, displaying the value of the objective function arising from applying OPTCON2 to the SLOVNL and the SLOVL models respectively, under 1000 independent random Monte Carlo runs. The graphs plot the values of the objective function for OL policies (x-axis) and OLF policies (y-axis) against each other. In the ‘zoom in’ panels of the figures, we cut the axes so as to show the mass of the points and omitting ‘outliers’, i.e. results where the value of the objective function becomes extremely large.

Fig. 1.
figure 1

OL and OLF control, value of objective function; SLOVNL; 1000 Monte Carlo runs; left: ‘normal’, right: ‘zoom in’

Full size image
Fig. 2.
figure 2

OL and OLF control, value of objective function; SLOVL; 1000 Monte Carlo runs; left: ‘normal’, right: ‘zoom in’

Full size image

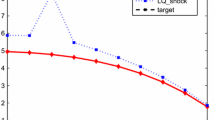
One can see that in most cases the values of the objective function for the open-loop feedback solution are smaller than the values of the open-loop solution, indicated by a greater mass of dots below the 45 degree line. This means that open-loop feedback controls give better results (lower values of the cost function) in the majority of the cases investigated. For the SLOVNL model, the OLF policy gives better results than the OL policy in 66.4 % of the cases, for the SLOVL model in 65.4 % of the cases considered here.

However, one can also see from these figures (especially in the left-hand panels with a ‘normal’ view) that there are many cases where either control scheme results in very high losses, indicated by dots which are significantly distant from the main mass of the dots. These cases are called ‘outliers’ and can be seen even more clearly in Fig. 3. This figure shows the same results of the 1000 independent Monte Carlo runs for each model (SLOVNL and SLOVL) separately, but for each Monte Carlo run. The OLF and OL objective function values are plotted in Fig. 3 together on the y-axis in each Monte Carlo run, the number of which is shown on the x-axis. Diamonds represent open-loop feedback results and squares represent open-loop results.

Fig. 3.
figure 3

Open-loop vs. open-loop feedback control, value of objective function (1000 Monte Carlo runs) (left: SLOVNL, right: SLOVL)

Full size image

The results mean that (passive) learning does not necessarily improve the quality of the final results; it may even worsen them. One reason for this is the presence of the two types of stochastic disturbances: additive (random system error) and multiplicative error (‘structural’ error in the parameters). The decision maker cannot distinguish between realizations of errors in the parameters and in the equations as he just observes the resulting state vector. Based on this information, he learns about the values of the parameter vector, but he may be driven away from the ‘true’ parameter vector due to the presence of the random system error.

6.3 On the Impact of Nonlinearity

In the previous section we saw that there is a severe problem of what we called ‘outliers’ - cases with very high losses or values of the objective function. In a similar framework of optimum stochastic control, [4] investigated numerical reasons for outliers. It was not possible to confirm that the sources of the problem found by these authors were decisive for the outlier problem in our framework. We suspect that there are other reasons for the outliers. One possible reason is the stochastics of the dynamic system itself. In our SLOVNL and SLOVL models all the parameters (including all the intercepts) are considered to be stochastic, which may make this reason more likely to work.

The second possible reason is based on the nonlinear nature of the models for which the OPTCON algorithm was created. The SLOVL model was created mainly in order to test this possibility. The graphical results in the previous section show that the outliers occur in the linear as well as in the nonlinear model version. Moreover, in some of the experiments with 1000 Monte Carlo runs for the SLOVNL model, it turned out that the algorithm did not converge in some runs. In these cases, the algorithm starts to diverge and results in some non-reasonable or even complex numbers for some variables. In the 1000 Monte Carlo runs experiment considered above this happened six times. On the contrary, under the SLOVL model, not one single case of non-convergence out of the 1000 Monte Carlo runs occurred. Thus we arrive at the conclusion that nonlinearity is not the reason for the ‘outliers’, but it can worsen the problem.

7 Conclusion

A comparison of open-loop control (without learning) and open-loop feedback control (with passive learning) shows that open-loop feedback control outperforms open-loop control in the majority of the cases investigated for the two small econometric models of Slovenia. But it suffers from a problem of ‘outliers’ which is present for both policy schemes. When comparing the results for the nonlinear SLOVNL model and the linear SLOVL model, we found that the nonlinearity of the system is not responsible for the ‘outliers’ but may worsen their influence in some cases.