Magic Loops and the Dynamic Controllability of Simple Temporal Networks with Uncertainty

Abstract

A Simple Temporal Network with Uncertainty (STNU) is a structure for representing and reasoning about temporal constraints and uncontrollable-but-bounded temporal intervals called contingent links. An STNU is dynamically controllable (DC) if there exists a strategy for executing its time-points that guarantees that all of the constraints will be satisfied no matter how the durations of the contingent links turn out. The fastest algorithm for checking the dynamic controllability of STNUs is based on an analysis of the graphical structure of STNUs. This paper (1) presents a new method for analyzing the graphical structure of STNUs, (2) determines an upper bound on the complexity of certain structures—the indivisible semi-reducible negative loops; (3) presents an algorithm for generating loops—the magic loops—whose complexity attains this upper bound; and (4) shows how the upper bound can be exploited to speed up the process of DC-checking for certain networks.

1 Background

Agent-based applications invariably involve actions and temporal constraints. Dechter et al. [1] introduced Simple Temporal Networks (STNs) to facilitate the management of temporal constraints. Vidal and Ghallab [14] were the first to incorporate actions with uncertain durations into an STN-like framework, and to define a notion of dynamic controllability. Morris et al. [6] developed the most widely accepted formalization of Simple Temporal Networks with Uncertainty (STNUs) and dynamic controllability. Morris and Muscettola [7] developed an $O(N^5)$-time algorithm for checking the dynamic controllability of STNUs. Morris [5] presented an $O(N^4)$-time DC-checking algorithm based on an analysis of the structure of STNU graphs; it is the fastest DC-checking algorithm to date. This paper presents a new way of analyzing the structure of STNU graphs, and shows how it can be used to speed up DC checking for some networks.

The rest of this section summarizes the definitions and results for STNs, STNUs and dynamic controllability that will be used in the rest of the paper.

1.1 Simple Temporal Networks

Dechter et al. [1] introduced Simple Temporal Networks (STNs) and presented the basic theoretical results for them. An STN is a pair, $(\mathcal {T}, \mathcal {C})$, where $\mathcal {T}$ is a set of time-point variables (or time-points) and $\mathcal {C}$ is a set of constraints, each having the form, $Y - X \le \delta$, for some $X, Y \in \mathcal {T}$, and real number $\delta$. Typically, the time-points in $\mathcal {T}$ represent starting or ending times of actions, or abstract coordination times. The constraints in $\mathcal {C}$ can accommodate release, deadline, duration and inter-action constraints. An STN is consistent if there exists a set of values for its time-points that together satisfy all of its constraints.

For any STN, $\mathcal {S}= (\mathcal {T}, \mathcal {C})$, there is a corresponding graph, $\mathcal {G}$, where the nodes in $\mathcal {G}$ correspond to the time-points in $\mathcal {T}$, and for each constraint, $Y-X \le \delta$, in $\mathcal {C}$, there is an edge in $\mathcal {G}$ of the form, $X \mathop {\longrightarrow }\limits ^{\delta } Y$. For convenience, this paper calls the constraints and edges in an STN ordinary constraints and edges.

The all-pairs, shortest-paths (APSP) matrix for $\mathcal {G}$ is called the distance matrix for $\mathcal {S}$ (or $\mathcal {G}$) and is denoted by $\mathcal {D}$. Thus, for any $X$ and $Y$ in $\mathcal {T}$, $\mathcal {D}(X,Y)$ equals the length of the shortest path from $X$ to $Y$ in the graph $\mathcal {G}$. If $\mathcal {D}$ has nothing but zeros down its main diagonal, then $\mathcal {D}$ is said to be consistent.

Theorem 1

(Fundamental Theorem of STNs). For any STN $\mathcal {S}$, with graph $\mathcal {G}$, and distance matrix $\mathcal {D}$, the following are equivalent: (1) $\mathcal {S}$ is consistent; (2) $\mathcal {G}$ has no negative loops; and (3) $\mathcal {D}$ is consistent.

1.2 STNs with Uncertainty

Some applications involve actions whose durations are uncontrollable, but none-theless guaranteed to fall within known bounds. For example, when I turn on my laptop, I do not control how long it will take to load its operating system; however, I know that it will take anywhere from one to four minutes. A Simple Temporal Network with Uncertainty (STNU) augments an STN to include contingent links that represent this kind of uncontrollable-but-bounded temporal interval [6]. A contingent link has the form, $(A,x,y,C)$, where $A$ and $C$ are time-points and $0 < x < y < \infty$. $A$ is called the activation time-point; $C$ is called the contingent time-point. Intuitively, the duration of the interval from $A$ to $C$ is uncontrollable, but guaranteed to fall within the interval $[x,y]$. Typically, an agent controls the execution of the activation time-point $A$, but only observes the subsequent execution of the contingent time-point $C$ in real time.¹

Formally, an STNU is a triple, $(\mathcal {T}, \mathcal {C}, \mathcal {L})$, where $(\mathcal {T}, \mathcal {C})$ is an STN, and $\mathcal {L}$ is a set of contingent links. $N$ is used to denote the number of time-points in an STNU, $K$ the number of contingent links. The most important property of an STNU is whether it is dynamically controllable (DC)—that is, whether there exists a strategy for executing the non-contingent time-points that guarantees that all of the constraints in the network will be satisfied no matter how the contingent durations turn out. The strategy is dynamic in that its execution decisions are allowed to react to past observations, but not present or future observations. The formal semantics for dynamic controllability is quite complicated, but it need not be presented here because a more convenient—and equivalent—graphical characterization is available, as follows.

Fig. 1.

The ordinary and labeled edges associated with a contingent link, $(A,x,y,C)$.

Graph for an STNU. Let $\mathcal {S}= (\mathcal {T}, \mathcal {C}, \mathcal {L})$ be an STNU. The graph for $\mathcal {S}$ contains all edges from the STN, $(\mathcal {T}, \mathcal {C})$, as well as additional edges derived from the contingent links in $\mathcal {L}$. In particular, for each contingent link $(A,x,y,C) \in \mathcal {L}$, the graph contains the edges shown in Fig. 1. The ordinary edges, $A \mathop {\longrightarrow }\limits ^{y} C$ and $C \mathop {\longrightarrow }\limits ^{{-}x} A$, represent the constraints, $C - A \le y$ and $A - C \le -x$ (i.e., $C - A \in [x,y]$). The other edges are labeled edges representing uncontrollable possibilities. In particular, $A \mathop {\longrightarrow }\limits ^{c\,:\,x} C$, which is called a lower-case (LC) edge, represents the possibility that the contingent duration might take on its minimum value, $x$; and $C \mathop {\longrightarrow }\limits ^{C\,:\,-y} A$, which is called an upper-case (UC) edge, represents the possibility that the contingent duration might take on its maximum value, $y$.

Because the graph of an STNU contains ordinary, lower-case and upper-case edges, paths in an STNU graph can be quite complicated. However, as shall be seen, the so-called semi-reducible paths are particularly important. For expository convenience, the definition of a semi-reducible path is postponed; however, the SR-distance matrix, $\mathcal {D}^*$, can be defined now as the all-pairs, shortest-semi-reducible-paths matrix for an STNU graph (i.e., for any time-points $X$ and $Y$, $\mathcal {D}^*(X,Y)$ equals the length of the shortest semi-reducible path from $X$ to $Y$).

Theorem 2

(Fundamental Theorem of STNUs). For any STNU $\mathcal {S}$, with graph $\mathcal {G}$, and SR-distance matrix $\mathcal {D}^*$, the following are equivalent: (1) $\mathcal {S}$ is dynamically controllable; (2) $\mathcal {G}$ has no semi-reducible negative loops; and (3) $\mathcal {D}^*$ is consistent.²

1.3 DC-Checking Algorithms

In view of Theorem 2, the problem of determining whether an STNU is dynamically controllable can be answered by computing the SR-distance matrix $\mathcal {D}^*$. If, during the process, a negative entry along the main diagonal is ever discovered—which would correspond to a semi-reducible negative loop—then the network cannot be dynamically controllable. Algorithms for determining whether an STNU is dynamically controllable are called DC-checking algorithms.

Two polynomial-time DC-checking algorithms have been presented so far in the literature: the $O(N^5)$-time algorithm of Morris and Muscettola [7], henceforth called the $N^5$ algorithm; and the $O(N^4)$-time algorithm of Morris [5], henceforth called the $N^4$ algorithm. The $N^5$ algorithm uses a set of rules to generate new edges in the graph, effectively a new kind of constraint propagation that accommodates labeled edges. After at most $O(N^2)$ rounds of edge generation, the algorithm is guaranteed to have computed the matrix $\mathcal {D}^*$ or determined that it is inconsistent. Since each round takes $O(N^3)$ time, the overall complexity is $O(N^5)$. The $N^4$ algorithm uses the same edge-generation rules but, as will be seen, restricts their application to “reducing away” LC edges. This restricted form of edge-generation is sufficient to compute the matrix $\mathcal {D}^*$ or determine that it is inconsistent. Based on an analysis of the structure of semi-reducible negative loops, the $N^4$ algorithm requires only $K \le N$ rounds of edge-generation. Since each round can be done in $O(N^3)$ time, its overall time-complexity is $O(N^4)$.

Edge-generation Rules. Intuitively, the ordinary constraints in an STNU are constraints that the agent in charge of executing time-points wants to satisfy. In contrast, the lower-case and upper-case edges represent uncontrollable possibilities that could potentially threaten the satisfaction of the ordinary constraints. Typically, to eliminate such threats, the agent must satisfy additional constraints—or, in graphical terms, add new edges to the graph. Toward that end, Morris and Muscettola [7] presented the five edge-generation rules in Table 1, where pre-existing edges are denoted by solid arrows and newly generated edges are denoted by dashed arrows. Each rule takes two pre-existing edges as input and generates a single edge as output. Incidentally, applicability conditions of the form, $Y \not \equiv Z$, should be construed as stipulating that $Y$ and $Z$ must be distinct time-point variables, not as constraints on the values of those variables.

Table 1. The edge-generation rules from Morris and Muscettola [7].

The rules only generate new ordinary or upper-case edges, never new lower-case edges. The generated ordinary edges represent additional constraints that must be satisfied to avoid threatening the satisfaction of the original constraints. The generated upper-case edges represent additional conditional constraints that the agent must satisfy. A generated UC edge of the form, $Y \mathop {\longrightarrow }\limits ^{C\,:\,-w} A$, represents a conditional constraint that can be glossed as: “As long as the contingent duration $C-A$ might take on its maximum value, then $A-Y \le -w$ (i.e., $Y \ge A + w$) must be satisfied (i.e., $Y$ must wait at least $w$ after $A$).”

Path Transformations. Morris [5] showed that the process of edge generation can also be viewed as one of path transformation or path reduction. For example, suppose a path $\mathcal {P}$ contains two adjacent edges, $e_1$ and $e_2$, to which one of the first four edge-generation rules can be applied to generate a new edge $e$, as illustrated in the lefthand side of Fig. 2. Let $\mathcal {P}^\prime$ be the path obtained from $\mathcal {P}$ by replacing $e_1$ and $e_2$ by the new edge $e$. We say that $\mathcal {P}$ has been transformed into (or reduced to) $\mathcal {P}^\prime$. Similarly, if $\mathcal {P}$ contains a UC edge $E$ to which the Label-Removal rule can be applied to generate a new ordinary edge $E^o$, then $\mathcal {P}$ can be transformed by replacing $E$ by $E^o$. Finally, any sequence of zero or more such transformations also counts as a path transformation. The righthand side of Fig. 2 illustrates a two-step transformation of a path $\mathcal {P}$, using the No-Case and Lower-Case rules.

Fig. 2.

Two examples of transforming a path $\mathcal {P}$ into a path $\mathcal {P}^\prime$.

Importantly, path transformations preserve unlabeled length (i.e., the length of the path ignoring any alphabetic labels on its edges). This follows directly from the fact that each edge-generation rule preserves unlabeled length.

Morris [5] introduced semi-reducible paths, which play a central role in the determination of dynamic controllability. For convenience, we present the definition of semi-reducible paths in terms of OU-edges and OU-paths.

Definition 1

(OU-edge, OU-path, Semi-reducible path, SRN loop). An OU-edge is an edge that is either ordinary or upper-case. An OU-path is a path consisting solely of OU-edges. A path in an STNU graph is called semi-reducible if it can be transformed into an OU-path. A semi-reducible loop with negative unlabeled length is called an SRN loop.

Note that the path, $\mathcal {P}$, on the righthand side of Fig. 2 is semi-reducible, since it can be transformed into the OU-path, $\mathcal {P}^\prime$.

The $N^4$ DC-checking Algorithm. The $N^4$ algorithm takes a two-step approach to determining whether an STNU has any SRN loops. In Step 1, it generates the OU-edges that could arise from the transformation of semi-reducible paths into OU-paths. The dashed edges in Fig. 2 are examples of such edges. In Step 2, it gathers the OU-edges from Step 1—minus any alphabetic labels—into an STN, $\mathcal {S}^\dagger$. It then computes the corresponding distance matrix, $\mathcal {D}^\dagger$, which turns out to equal the SR-distance matrix, $\mathcal {D}^*$, for the original STNU.

To illustrate Step 1, suppose $\mathcal {P}$ is a semi-reducible path consisting of original STNU edges, including at least one LC edge $e$, as shown in Fig. 3. Since $\mathcal {P}$ is semi-reducible, there must be a sequence of reductions by which $\mathcal {P}$ is transformed into an OU-path. Thus, sometime during that transformation, the Lower-Case or Cross-Case rule must be applied to $e$ and some other edge $e^\prime$ to yield a new OU-edge $\tilde{e}$, effectively removing $e$ from the path. We say that $e$ has been “reduced away”. To enable this, the original path $\mathcal {P}$ must have a sub-path, $\mathcal {P}_e$, immediately following $e$, such that $\mathcal {P}_e$ reduces to the edge $e^\prime$, as shown in Fig. 3. The concatenation of the LC edge $e$ with the sub-path $\mathcal {P}_e$ is called a lower-case reducing sub-path (LCR sub-path); edges such as $\tilde{e}$ that are generated by transforming an LCR sub-path into a single edge, are called core edges [3].

Fig. 3.

Reducing away a lower-case edge, $e$.

In view of the above, every occurrence of an LC edge, $e$, in any semi-reducible path, $\mathcal {P}$, must belong to an LCR sub-path in $\mathcal {P}$. Equivalently, the edges in any semi-reducible path, $\mathcal {P}$, that do not belong to an LCR sub-path must be OU-edges from the original STNU. Thus, Step 1 of the $N^4$ algorithm searches for LCR sub-paths and the core edges they generate. Crucially, this search does not require exhaustively applying the edge-generation rules from Table 1. Instead, as will be seen, the search can be limited to extension sub-paths, which have an important nesting property. After Step 1, the algorithm has a set, $\mathcal {E}$, of OU-edges.

For Step 2, note that there is a one-to-one correspondence between shortest semi-reducible paths in the original STNU and shortest paths consisting of edges in $\mathcal {E}$. In particular, if $\mathcal {P}$ is a shortest semi-reducible path, then it can be transformed into a path, $\mathcal {P}^\prime$, whose edges are in $\mathcal {E}$; and since path transformations preserve unlabeled length, $|\mathcal {P}| = |\mathcal {P}^\prime |$. Conversely, if $\mathcal {P}^\prime$ is a shortest path with edges in $\mathcal {E}$, then, by “unwinding” the transformations that generated the edges in $\mathcal {E}$, $\mathcal {P}^\prime$ can be “un-transformed” into a semi-reducible path $\mathcal {P}$, with $|\mathcal {P}^\prime | = |\mathcal {P}|$.

Next, since alphabetic labels are irrelevant to the computation of unlabeled lengths, let $\mathcal {E}^\dagger$ be the set of ordinary edges obtained by stripping any alphabetic labels from the edges in $\mathcal {E}$; let $\mathcal {S}^\dagger$ be the corresponding STN; and let $\mathcal {D}^\dagger$ be the corresponding distance matrix. Then $\mathcal {D}^\dagger$ is equal to the all-pairs, shortest-paths matrix for paths with edges in $\mathcal {E}$, and hence $\mathcal {D}^\dagger = \mathcal {D}^*$. Thus, the $N^4$ algorithm concludes that the original STNU is DC iff $\mathcal {D}^\dagger$ is consistent.

2 Modifying Morris’ Analysis

To simplify his mathematical analysis, Morris [5] introduces two kinds of instantaneous reactivity into the semantics of dynamic controllability. First, he allows contingent links of the form, $(A,0,y,C)$, in which the lower bound on the contingent duration is zero. This effectively allows scenarios in which it is uncertain whether the temporal interval between a cause and its effect will be instantaneous. Second, he allows an agent to react instantaneously to an observation of a contingent execution. Although these sorts of instantaneous reactions may be applicable to some domains, this author prefers to stick with the more realistic assumptions of the original semantics—and the edge-generation rules in Table 1—in which both the lower bounds of contingent durations and agent reaction times must be positive. The rest of this section shows how Morris’ approach can be modified to conform to the original semantics of dynamic controllability.

Given his assumptions, Morris changed the conditions for the Lower-Case rule to $v < 0$ (i.e., he eliminated the case, $v=0$). The reason is that when $v=0$, the edge, $S \mathop {\longrightarrow }\limits ^{v} T$, represents the constraint, $T - S \le 0$ (i.e., $T \le S$), which expresses that $T$ must execute no later than the contingent time-point $S$. If able to react instantaneously, an agent need only wait for $S$ to execute and then instantaneously execute $T$. Thus, no additional constraint is required to guard against $S$ executing early. If unable to react instantaneously, then the new edge from $Q$ to $T$ is needed. Similar remarks apply to the Cross-Case rule.

Extension Sub-paths. Let $e$ be some LC edge in a path, $\mathcal {P}$; and let $e_1, e_2, \ldots$ be the sequence of edges immediately following $e$ in $\mathcal {P}$. If $e$ can be reduced away in $\mathcal {P}$, then it may be that there are many values of $m \ge 1$ for which the sub-path, $e_1, e_2, \ldots , e_m$, could be used to reduce away $e$. For example, the LC edge from $Q$ to $R$ in Fig. 2 can be reduced away not only by the two-edge sub-path from $R$ to $T$, as shown in the figure, but also by the three-edge sub-path from $R$ to $U$. In such cases, the extension sub-path, defined below, will turn out to be the sub-path that can reduce away $e$ for which the value of $m$ is the smallest.

Definition 2

(Extension sub-path; moat edge). Let $e$ be an LC edge in a path $\mathcal {P}$. Let $e_1, e_2, \ldots$ be the sequence of edges that immediately follow $e$ in $\mathcal {P}$. For each $i \ge 1$, let $\mathcal {P}_e^i$ be the sub-path of $\mathcal {P}$ consisting of the edges, $e_1, \ldots , e_i$. If it exists, let $m$ be the smallest integer such that either: (1) $|\mathcal {P}_e^m| < 0$; or (2) $|\mathcal {P}_e^m| = 0$ and $\mathcal {P}_e^m$ is not a loop. Then the extension sub-path (ESP) for $e$ in $\mathcal {P}$, notated $\mathcal {P}_e$, is the sub-path $\mathcal {P}_e^m$; and its last edge, $e_m$, is called the moat edge for $e$ in $\mathcal {P}$. If no such $m$ exists, then $e$ has no ESP or moat edge in $\mathcal {P}$.³

For the LC edge from $Q$ to $R$ in Fig. 2, the extension sub-path is the two-edge path labeled $\mathcal {P}_e$; and the moat edge is the edge from $S$ to $T$.

Structure of ESPs. Given the setup in Definition 2, $m$ is the smallest value for which $|\mathcal {P}_e^m| < 0$ or $\mathcal {P}_e^m$ is a zero-length non-loop. Conversely, for any $i < m$, either $|\mathcal {P}_e^i| > 0$ or $\mathcal {P}_e^i$ is a zero-length loop. This implies that any ESP must consist of zero or more loops of length zero, followed by a (non-empty) sub-path that has no prefixes that are zero-length loops. These observations motivate the following.

Definition 3

(Pesky prefix; nice path). A pesky prefix of $\mathcal {P}$ is a non-empty prefix of $\mathcal {P}$ that is a loop of length $0$. A nice path is one having no pesky prefixes.

In general, an ESP may have zero or more pesky prefixes, followed by a non-empty nice path.⁴ Figure 4 shows an ESP with two pesky prefixes, one nested inside the other, followed by a non-empty nice suffix.

Fig. 4.

An extension sub-path with two pesky prefixes.

Nesting Property for ESPs. The following lemma confirms that ESPs as defined in Definition 2 have the nesting property highlighted by Morris [5].⁵

Lemma 1

(Nesting Property for ESPs). Let $\mathcal {P}_1$ and $\mathcal {P}_2$ be two ESPs within the same path $\mathcal {P}$. Then $\mathcal {P}_1$ and $\mathcal {P}_2$ are either disjoint (i.e., share no edges) or one is nested inside (i.e., is a sub-path of) the other.

Breaches and Usable/Unusable Moat Edges. Suppose that $\mathcal {P}$ is a path that contains an occurrence of a lower-case edge, $e$, that derives from a contingent link, $(A,x,y,C)$. Thus, $e$ has the form, $A \mathop {\longrightarrow }\limits ^{c\,:\,x} C$. Suppose further that $e$ has an extension sub-path, $\mathcal {P}_e$, in $\mathcal {P}$. The existence of an ESP for $e$ in $\mathcal {P}$ turns out to be a necessary, but insufficient condition for reducing away $e$ in $\mathcal {P}$. For example, using Fig. 3 as a reference, if the edge, $e^\prime$, into which $\mathcal {P}_e$ is transformed, happens to be an upper-case edge with alphabetic label $C$ (i.e., that matches the lower-case label on $e$), then the Cross-Case rule cannot be applied to $e$ and $e^\prime$, blocking the reducing away of $e$. (Recall the condition, $R \not \equiv S$, for the Cross-Case rule.) Such moat edges are called unusable. (It could also be said that $\mathcal {P}_e$ is unusable.) The following definitions specify the characteristics of usable/unusable moat edges.

Definition 4

(Breach; usable/unusable moat edge). Let $e$ be an LC edge for a contingent link, $(A,x,y,C)$; let $\mathcal {P}_e$ be the ESP for $e$ in some path $\mathcal {P}$; and let $e_m$ be the corresponding moat edge. Any occurrence in $\mathcal {P}_e$ of an upper-case edge labeled by $C$ is called a breach. If $\mathcal {P}_e$ has no breaches, it is called breach-free. If $e_m$ is a breach and $|\mathcal {P}_e| < -x$, then $e_m$ is said to be unusable; else, it is usable.

Theorem 3 shows the crucial role of usable moat edges for semi-reducible paths [5].

Theorem 3

A path $\mathcal {P}$ is semi-reducible if and only if each of its lower-case edges has a usable moat edge in $\mathcal {P}$.

Since a pesky prefix, by definition, has length zero, extracting a pesky prefix from an extension sub-path cannot affect its length. In addition, since a pesky prefix cannot constitute the entirety of an extension sub-path, extracting a pesky prefix cannot affect the moat edge. Therefore, the usability of a moat edge cannot be affected by extracting a pesky prefix from an ESP and, hence, the semi-reducibility of a path cannot be affected by extracting pesky prefixes.

Corollary 1

Let $\mathcal {P}$ be any path. Let $\mathcal {P}^\prime$ be the path obtained from $\mathcal {P}$ by extracting all pesky prefixes from any extension sub-paths within $\mathcal {P}$. Then $\mathcal {P}$ is semi-reducible if and only if $\mathcal {P}^\prime$ is semi-reducible.

Given this result, the rest of this paper presumes that all pesky prefixes are extracted from any path without affecting its semi-reducibility.

Fig. 5.

A semi-reducible path with nested ESPs.

Corollary 2

Any semi-reducible path, $\mathcal {P}$, can be transformed into an OU-path using a sequence of reductions whereby each LC edge $e$ in $\mathcal {P}$ is reduced away by its corresponding extension sub-path $\mathcal {P}_e$.

Figure 5 illustrates a semi-reducible path with nested extension sub-paths. In the figure, lower-case edges are shown with a distinctive arrow type, ESPs are shaded, and the core edges are dashed.

Morris [5] proved that an STNU with $K$ contingent links has an SRN loop if and only if it has a breach-free SRN loop in which extension sub-paths are nested to a depth of at most $K$. Thus, his $N^4$ DC-checking algorithm performs $K$ rounds of searching for breach-free extension sub-paths that could be used to reduce away lower-case edges, each round effectively increasing the nesting depth of the extension sub-paths it considers. The core edges generated in this way are then collected—minus any upper-case labels—into an STN, $\mathcal {S}^\dagger$, as previously described, to compute the distance matrix, $\mathcal {D}^\dagger$, which equals the all-pairs, shortest-semi-reducible-paths matrix for the original STNU.

3 Indivisible SRN Loops

This section introduces a new approach to analyzing the structure of semi-reducible negative loops. The key feature of the approach is its focus on the number of occurrences of lower-case edges in what it calls indivisible SRN loops (or iSRN loops). As will be seen, for the purposes of DC checking, it suffices to restrict attention to iSRN loops. However, the main result of this section is that the number of occurrences of LC edges in any iSRN loop in any STNU having $K$ contingent links is at most $2^K-1$.

Definition 5

For any path, $\mathcal {P}$, the number of occurrences of lower-case edges in $\mathcal {P}$ is denoted by $\#\mathcal {P}$.

Fig. 6.

An indivisible SRN loop, $\mathcal {P}$.

Suppose that $\mathcal {P}$ is an SRN loop and $\mathcal {Q}$ is a sub-loop of $\mathcal {P}$ that also happens to be an SRN loop (i.e., $\mathcal {Q}$ is an SRN sub-loop of $\mathcal {P}$). Since every LC edge in $\mathcal {Q}$ also belongs to $\mathcal {P}$, it follows that $\#\mathcal {Q}\le \#\mathcal {P}$. However, if $\mathcal {P}$ is an indivisible SRN loop, then $\#\mathcal {Q}$ must equal $\#\mathcal {P}$. That is, no SRN sub-loop of an iSRN loop $\mathcal {P}$ can have fewer occurrences of LC edges than $\mathcal {P}$.

Definition 6

(iSRN loop). Let $\mathcal {P}$ be an SRN loop. $\mathcal {P}$ is called an indivisible SRN loop (or iSRN loop) if $\#\mathcal {Q}= \#\mathcal {P}$ for every SRN sub-loop $\mathcal {Q}$ of $\mathcal {P}$.

Figure 6 shows an example of an SRN loop, $\mathcal {P}$, that has no SRN sub-loops and, thus, is indivisible. $\mathcal {P}$ contains three occurrences of LC edges (two from $A$ to $B$, one from $C$ to $D$); thus, $\#\mathcal {P}= 3$. $\mathcal {P}$ is semi-reducible because each LC edge has a corresponding breach-free extension sub-path that can be used to reduce it away. In addition, $|\mathcal {P}| = -7 < 0$. Finally, although $\mathcal {P}$ has many sub-loops, two of which are shaded in the figure, none of them are SRN sub-loops. For example, the lefthand shaded sub-loop is not semi-reducible and the righthand shaded sub-loop is non-negative. Thus, $\mathcal {P}$ is an iSRN loop.

Lemma 2, below, shows that for DC checking, it suffices to restrict attention to iSRN loops. The iSRN loop, $\mathcal {P}^\prime$, is obtained by recursively extracting SRN sub-loops until, eventually, an iSRN loop is found.

Lemma 2

If an STNU $\mathcal {S}$ has an SRN loop $\mathcal {P}$, then $\mathcal {S}$ also has an iSRN loop $\mathcal {P}^\prime$. Furthermore, $\mathcal {P}^\prime$ can be chosen such that $\# \mathcal {P}^\prime \le \# \mathcal {P}$.

The search for an upper bound on the number of occurrences of LC edges in any iSRN loop begins by focusing on root-level LCR sub-paths (i.e., LCR sub-paths that are not contained within any other). This notion can be defined since, by Lemma 1, ESPs in any semi-reducible path must be disjoint or nested.

Definition 7

(Root-level). Let $e$ be an occurrence of an LC edge in a semi-reducible path $\mathcal {P}$; and let $\mathcal {P}_e$ be the extension sub-path for $e$ in $\mathcal {P}$. If $\mathcal {P}_e$ is not contained within any other ESP in $\mathcal {P}$, then $\mathcal {P}_e$ is called a root-level ESP in $\mathcal {P}$; $e$ is called a root-level LC edge in $\mathcal {P}$; and the LCR sub-path formed by concatenating $e$ and $\mathcal {P}_e$ is called a root-level LCR sub-path.

Theorem 4 bounds the number of root-level LCR sub-paths in any iSRN loop.

Theorem 4

Any iSRN loop in any STNU with $K$ contingent links has at most $K$ root-level LCR sub-paths.

Theorem 5, below, bounds the depth of nesting of LCR sub-paths (or, equivalently, ESPs) in an iSRN loop. It extends Morris’ result that if an STNU with $K$ contingent links has an SRN loop, then it has a breach-free SRN loop whose extension sub-paths are nested to a depth of at most $K$.

Theorem 5

Let $\mathcal {P}$ be an iSRN loop in an STNU having $K$ contingent links. Then $\mathcal {P}$ is breach-free and has LCR sub-paths nested to a depth of at most $K$.

Although Theorem 5 bounds the nesting depth of LCR sub-paths in an iSRN loop, it does not limit the number of LC edges within any root-level LCR sub-path. Theorem 6, below, shows that any non-trivial iSRN loop must have an LC edge that occurs exactly once—and at the root level. Theorem 6 provides the key for the inductive proof of Theorem 7, below, the main result of this section.

Theorem 6

If $\mathcal {P}$ is an iSRN loop that contains at least one lower-case edge, then $\mathcal {P}$ must have a root-level LC edge that occurs exactly once in $\mathcal {P}$.

Theorem 7

If $\mathcal {P}$ is an iSRN loop in an STNU with $K$ contingent links, then $\# \mathcal {P}\le 2^K-1$.

Finally, Theorem 8 shows that the ordinary edges associated with contingent links (cf. Fig. 1) can be ignored for the purposes of DC checking. Although this does not affect the worst-case complexity of DC checking, it has the potential to limit the branching factor of edge generation in practice.

Theorem 8

Any STNU having an SRN loop has an iSRN loop that contains none of the ordinary edges associated with contingent links.

4 Magic Loops

Section 3 showed that the number of LC edges in any iSRN loop is at most $2^K-1$. This section defines a magic loop as any iSRN loop that has exactly $2^K-1$ occurrences of LC edges. It then presents an algorithm for constructing such loops, thereby proving that the $2^K-1$ bound is tight. Interestingly, the STNUs used to generate these magic loops have only $2K +1$ time-points (two time-points for each contingent link, plus one extra time-point) and $4K$ edges.

Definition 8

(Magic Loop). A magic loop of order $K$ is any iSRN loop that (1) belongs to an STNU having $K$ contingent links; and (2) contains exactly $2^K-1$ occurrences of LC edges

The algorithm for constructing magic loops is recursive. For each $K \ge 1$, it defines an STNU, $\mathcal {S}_K$, that contains a magic loop, $\mathcal {M}_K$, of order $K$. The STNUs and magic loops employ edges whose lengths are specified by numerical parameters, such as $x_i, y_i, \alpha _i, \beta _i, \gamma _i,$ and $\delta _i$, where $1 \le i \le K$. All of these parameters have positive integer values; thus, any negative values are specified with explicit negative signs, as in: $-y_i, -\alpha _i$ or $-\gamma _i$. Each magic loop, $\mathcal {M}_K$, also has several sub-paths, called $\phi _i$, $\chi _i$ and $\omega _i$. These sub-paths have important properties that are exploited in the proofs. Whereas all of the parameters are positive, the lengths of the sub-paths, $\phi _i, \chi _i$ and $\omega _i$, are invariably negative. For convenience, the rest of this section uses $k$ instead of $K$, and $*$ instead of $k+1$. Thus, for example, $\mathcal {S}_*$ is shorthand for $\mathcal {S}_{K+1}$.

Fig. 7.

The STNU $\mathcal {S}_1$ (left) and magic loop $\mathcal {M}_1$ (right).

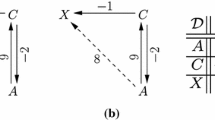
For the base case, the STNU $\mathcal {S}_1$ and its magic loop $\mathcal {M}_1$ are shown in Fig. 7. $\mathcal {M}_1$ contains two sub-loops, neither of which is an SRN loop; thus, $\mathcal {M}_1$ is an iSRN loop. Also, $\mathcal {M}_1$ contains $2^1-1 = 1$ occurrence of an LC edge; thus, $\mathcal {M}_1$ is a magic loop of order $1$.

For the recursive case, suppose $\mathcal {S}_k$ is an STNU with $k$ contingent links with the form shown at the left of Fig. 8, and $\mathcal {M}_k$ is a magic loop of order $k$ with the form shown at the right of Fig. 8. Note that $\mathcal {S}_1$ and $\mathcal {M}_1$ have the desired forms.

Fig. 8.

The generic form of $\mathcal {S}_k$ (left) and $\mathcal {M}_k$ (right).

The values of $\gamma _k$, $|\phi _k|$ and $|\chi _k|$ suffice to generate the values of the parameters, $\alpha _*, \beta _*, \gamma _*, \delta _*, x_*$ and $y_*$, which are determined sequentially, as shown in Rules 1–6 of Table 2. (Recall that the asterisk is used as a shorthand for $k+1$.) Once these values are in hand, the STNU, $\mathcal {S}_*$, is built out of $\mathcal {S}_k$ as shown in Fig. 9; and the magic loop, $\mathcal {M}_*$, is created with the structure shown in Fig. 10.

Notice, too, that $\mathcal {M}_*$ introduces a single, new lower-case edge associated with a contingent link, $(A_*, x_*, y_*, C_*)$. Since each $\chi _k$ sub-path has $2^k - 1$ occurrences of LC edges, the total number of occurrences of LC edges in $\mathcal {M}_*$ is $1 + 2(2^k - 1) = 2^{k+1} - 1$, as desired. Figure 11 shows the STNU $\mathcal {S}_2$ and magic loop $\mathcal {M}_2$ generated using these parameters; the LCR sub-paths are shaded for convenience.

Finally, Theorem 9, below, shows that for each $k \ge 1$, the loop, $\mathcal {M}_k$, is indeed a magic loop; and Theorem 10 shows that for each $k \ge 1$, the only iSRN loops in $\mathcal {S}_k$ are necessarily magic loops; thus, there are no iSRN loops in $\mathcal {S}_k$ having fewer than $2^k-1$ occurrences of lower-case edges. Taken together, these theorems show that magic loops are not only worst-case scenarios in terms of the number of occurrences of LC edges in an iSRN loop, but also that there are STNUs for which this worst-case scenario is the only case.

Theorem 9

For each $k \ge 1$, the loop, $\mathcal {M}_k$, is a magic loop of order $k$ (i.e., an iSRN loop having exactly $2^k-1$ occurrences of lower-case edges).

Theorem 10

Let $\mathcal {S}_k$ be the STNU as described in this section for some $k \ge 1$. Every SRN loop in $\mathcal {S}_k$ has at least $2^k -1$ occurrences of LC edges.

Table 2. Rules for generating parameters for the case $k+1$.

Fig. 9.

Building the STNU, $\mathcal {S}_*$, from $\mathcal {S}_k$.

Fig. 10.

The structure of $\mathcal {M}_*$, a magic loop of order $k+1$.

Fig. 11.

STNU $\mathcal {S}_2$ (top) and magic loop $\mathcal {M}_2$ (bottom).

5 Speeding up DC Checking

This section presents a recursive $O(N^3)$-time pre-processing algorithm that exploits the $2^K-1$ bound on the number of occurrences of LC edges in iSRN loops. For certain networks, this pre-processing algorithm decreases the computation time for the $N^4$ DC-checking algorithm from $O(N^4)$ to $O(N^3)$.

Let $\mathcal {S}$ be an STNU having $K$ contingent links. The pre-processing algorithm computes, for each contingent time-point, $C_j$, an upper bound on the number of distinct contingent time-points that can co-occur in any iSRN loop in $\mathcal {S}$ that contains $C_j$. The largest of these upper bounds then serves as an upper bound, $UB$, on the number of distinct contingent time-points—and hence the number of distinct LC edges—that can co-occur in any single iSRN loop in $\mathcal {S}$. Since any iSRN loop having at most $UB$ distinct lower-case edges can be viewed as an iSRN loop in an STNU having exactly $UB$ contingent links, such a loop can have extension sub-paths nested to a depth of at most $UB$ (cf. Theorem 5). Thus, $UB$ also provides an upper bound on the number of rounds needed for the $N^4$ algorithm to check the dynamic controllability of $\mathcal {S}$.

In cases where $UB < K$, the pre-processing algorithm can provide significant savings. Indeed, for some STNUs, $UB = 1$, implying the need for only one $O(N^3)$-time round of the $N^4$ algorithm, even though the unaware $N^4$ algorithm might still perform $K$ rounds at a cost of $O(N^4)$. At the other extreme, for some STNUs, $UB = K$, in which case, the pre-processing algorithm provides no benefit. However, since the pre-processing algorithm runs in $O(N^3)$ time, it does not introduce a significant overhead for the $N^4$ algorithm, whose first step is an $O(N^3)$-time computation of a distance matrix.

In more detail. Given an STNU, $\mathcal {S}$, with $K$ contingent links, the algorithm begins by computing:

• $2^K-1$, the max. number of occurrences of LC edges in any iSRN loop in $\mathcal {S}$;

• $\varDelta$, the max. value of $y-x$ among all contingent links, $(A,x,y,C)$, in $\mathcal {S}$; and

• $\mathcal {D}^\diamond$, the APSP matrix for the OU-paths in $\mathcal {S}$, computable in $O(N^3)$ time.

Next, for each pair of distinct contingent time-points, $C_i$ and $C_j$, it computes:

• $LB _{ij} \ = \ \mathcal {D}^\diamond (C_i,C_j) + \mathcal {D}^\diamond (C_j,C_i) - (2^K-1)\varDelta$.

As will be shown, if $\mathcal {P}$ is any iSRN loop in $\mathcal {S}$ that contains both $C_i$ and $C_j$, then $|\mathcal {P}| \ge LB _{ij}$ (i.e., $LB _{ij}$ is a Lower Bound for the lengths of iSRN loops that contain both $C_i$ and $C_j$). Thus, if $LB _{ij} \ge 0$, it follows that $C_i$ and $C_j$ cannot co-occur in any iSRN loop in $\mathcal {S}$. But in that case, any iSRN loop—if such exists—can have at most $K-1$ distinct LC edges and, thus, no more than $2^{(K-1)}-1$ occurrences of LC edges.

If the upper bound on the number of occurrences of LC edges in iSRN loops in $\mathcal {S}$ can be lowered in this way, the algorithm recursively seeks to identify additional combinations of contingent time-points that cannot co-occur within any iSRN loop. It terminates when no further combinations can be found.

Fig. 12.

The iSRN loop, $\mathcal {P}$ (left), and its OU-cousin, $\mathcal {P}^\circ$ (right).

Consider the scenario in Fig. 12, where the lefthand loop is an iSRN loop, $\mathcal {P}$, that contains a pair of distinct contingent time-points, $C_i$ and $C_j$. Note that the sub-path from $C_i$ to $C_j$ is called $\mathcal {P}_{ij}$, and the sub-path from $C_j$ to $C_i$ is called $\mathcal {P}_{ji}$. Next, define the ordinary cousin of an LC edge, $A \mathop {\longrightarrow }\limits ^{c\,:\,x} C$, to be the corresponding ordinary edge, $A \mathop {\longrightarrow }\limits ^{y} C$, for the contingent link $(A,x,y,C)$ (cf. Fig. 1). The righthand loop, $\mathcal {P}^\circ$, in Fig. 12 is the same as $\mathcal {P}$, except that any occurrences of LC edges have been replaced by their ordinary cousins. Since $\mathcal {P}^\circ$ may yet contain upper-case edges, we call it the OU-cousin of $\mathcal {P}$. Notice that $\mathcal {P}^\circ$ is the concatenation of the OU-cousins of $\mathcal {P}_{ij}$ and $\mathcal {P}_{ji}$. Furthermore, since $\mathcal {P}^\circ _{ij}$ and $\mathcal {P}^\circ _{ji}$ are OU-paths, it follows that their lengths are bounded below by the corresponding OU-distance-matrix entries, whence:

$$\begin{aligned} \mathcal {D}^\diamond (C_i,C_j) + \mathcal {D}^\diamond (C_j,C_i) \ \le \ |\mathcal {P}^\circ _{ij}| + |\mathcal {P}^\circ _{ji}| \ = \ |\mathcal {P}^\circ | \end{aligned}$$

(1)

Now, by Theorem 7, since $\mathcal {P}$ is an iSRN loop, $\#\mathcal {P}\le 2^K-1$. Thus, the difference in the lengths of $\mathcal {P}$ and $\mathcal {P}^\circ$ is bounded as follows:

$$\begin{aligned} \varDelta _\mathcal {P}\ = \ |\mathcal {P}^\circ | - |\mathcal {P}| \ \le \ \#\mathcal {P}(2^K-1)\varDelta \ \le \ (2^K-1)\varDelta \end{aligned}$$

(2)

where $\varDelta$ is the maximum value of $y-x$ over all the contingent links in the STNU. Combining the inequalities (1) and (2) then yields:

• $|\mathcal {P}| \ \ge \ |\mathcal {P}^\circ | - (2^K-1)\varDelta \ \ge \ \mathcal {D}^\diamond (C_i,C_j) + \mathcal {D}^\diamond (C_j,C_i) - (2^K-1)\varDelta$

Since this inequality must hold whenever $\mathcal {P}$ is an iSRN loop in which the distinct contingent time-points, $C_i$ and $C_j$, both occur, it follows that if

• $\mathcal {D}^\diamond (C_i,C_j) + \mathcal {D}^\diamond (C_j,C_i) - (2^K-1)\varDelta \ \ge \ 0$

then there cannot be any such loop. ($|\mathcal {P}|$ must be negative if $\mathcal {P}$ is an iSRN loop.)

Next, for each pair of contingent time-points, $C_i$ and $C_j$, let $\mathcal {F}(i,j) = \mathcal {D}^\diamond (C_i,C_j) + \mathcal {D}^\diamond (C_j,C_i)$. Then the preceding rule, which is the main rule used by the pre-processing algorithm, can be re-stated as:

• If $C_i$ and $C_j$ are distinct contingent time-points such that $\mathcal {F}(i,j) \ge (2^K-1)\varDelta$, then $C_i$ and $C_j$ cannot both occur in the same iSRN loop.

Pseudo-code for the pre-processing algorithm is given in Table 3. For each contingent time-point, $C_i$, it defines the following variables:

• $\mathrm {ctr}_i$, an upper bound (initially $\mathrm {ctr}_i = K$) on the number of distinct contingent time-points that can co-occur in any iSRN loop that contains $C_i$.

• $L_i$, a list of entries from row $i$ of the $\mathcal {F}$ matrix, sorted into decreasing order.

As the algorithm runs, any entry, $(i,j,\mathcal {F}(i,j))$ from $L_i$, for which $\mathcal {F}(i,j) \ge (2^{\mathrm {ctr}_i}-1)\varDelta$, signals that $C_j$ could not occur in the same iSRN loop with $C_i$. Such entries are popped off $L_i$ and pushed onto the global queue. As each entry from the global queue is processed, the corresponding $\mathrm {ctr}_i$ value decreases, which may lead to further entries moving from $L_i$ to the global queue. The algorithm terminates whenever the global queue is emptied, at which point no further reductions in $\mathrm {ctr}_i$ values can be made. The algorithm returns the maximum $\mathrm {ctr}_i$ value, which specifies the maximum number of distinct contingent time-points that can co-occur in any iSRN loop in the given STNU. The Appendix proves that the algorithm’s worst-case running time is $O(N^3)$.

In best-case scenarios, the pre-processing algorithm results in all off-diagonal entries in $\mathcal {F}$ being crossed out, implying that there can be no nesting of LCR paths in any iSRN loop. In such cases, it is only necessary to do one $O(N^3)$-time round of the $N^4$ algorithm to ascertain whether the STNU is dynamically controllable. The benefit in such cases can be dramatic, for if the network contains even one semi-reducible path having $K$ levels of nesting, then the unaided $N^4$ algorithm would needlessly perform $K$ rounds of processing in $O(N^4)$ time.

Table 3. Pseudo-code for the pre-processing algorithm.

6 Conclusions

This paper presented a new way of analyzing the structure of STNU graphs with the aim of speeding up DC checking. It proved that the number of occurrences of lower-case edges in iSRN loops is bounded above by $2^K-1$. It presented an algorithm for constructing STNUs that contain iSRN loops that attain this upper bound, thereby showing that the bound is tight. Given their highly convoluted structure, such loops are called magic loops. And it presented an $O(N^3)$-time pre-processing algorithm that exploits the $2^K-1$ bound to speed up DC checking for some networks. Thus, the paper makes theoretical and practical contributions.

Other researchers have sought to speed up the process of DC checking using incremental algorithms. Stedl and Williams [11] developed Fast-IDC, an incremental algorithm that maintains the dispatchability of an STNU after the insertion of new constraints or the tightening of existing constraints. Shah et al. [10] extended Fast-IDC to accommodate the removal or weakening of constraints. Although intended to be applied incrementally, their algorithm showed orders of magnitude improvement over an earlier pseudo-polynomial DC-checking algorithm when evaluated empirically, checking dynamic controllability from scratch. It would be interesting to see if their work could be applied to generate an incremental version of the Morris’ $N^4$ algorithm.

Others have extended the concept of dynamic controllability to accommodate various combinations of probability, preference and disjunction. Tsamardinos [12] augmented contingent durations with probability density functions and provided a method that, under certain restrictions, finds “the schedule that maximizes the probability of executing the plan in a way that respects the temporal constraints.” Tsamardinos et al.  [13] developed algorithms to compute lower and upper bounds for the probability of a legal plan execution. Morris et al. [8] used probability density functions to represent the uncertainties associated with contingent durations, but also incorporated preferences over event durations. Rossi et al. [9] augmented STNUs with preferences (but not probabilities) and defined the Simple Temporal Problem with Preferences and Uncertainty (STPPU) and notions of weak, strong and dynamic controllability.

Effinger et al. [2] defined dynamic controllability for temporally-flexible reactive programs that include the following constructs: “conditional execution, iteration, exception handling, non-deterministic choice, parallel and sequential composition, and simple temporal constraints”. They presented a DC-checking algorithm for temporally-flexible reactive programs that frames the problem as an “AND/OR search tree over candidate program executions.”