Generalized Lagrange Identity for Discrete Symplectic Systems and Applications in Weyl–Titchmarsh Theory

Abstract

In this paper we consider discrete symplectic systems with analytic dependence on the spectral parameter. We derive the Lagrange identity, which plays a fundamental role in the spectral theory of discrete symplectic and Hamiltonian systems. We compare it to several special cases well known in the literature. We also examine the applications of this identity in the theory of Weyl disks and square summable solutions for such systems. As an example we show that a symplectic system with the exponential coefficient matrix is in the limit point case.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In this paper we consider a $2n$-dimensional discrete symplectic system

whose coefficient matrix ${\mathbb S}_k(\lambda )\in {\mathbb C}^{2n\times 2n}$ is analytic in the spectral parameter $\lambda \in {\mathbb C}$ in a neighborhood of $0$ and satisfies a symplectic-type identity, i.e.,

$$\begin{aligned} {\mathbb S}_k(\lambda )=\sum _{j=0}^\infty \lambda ^j{\fancyscript{S}}_k^{[j]}, \quad {\mathbb S}_k^*(\lambda )\,{\fancyscript{J}}\,{\mathbb S}_k(\bar{\lambda })={\fancyscript{J}}, \quad {\fancyscript{J}}=\left( \begin{matrix} 0 &{} \ I \\ -I &{} \ 0 \end{matrix}\right) . \end{aligned}$$

(1)

The superscript $^*$ denotes the conjugate transpose and $M^*(\lambda ):=[M(\lambda )]^*$. For the applications we will in addition assume that a certain weight matrix $\varPsi (\lambda )\in {\mathbb C}^{2n\times 2n}$ is positive semidefinite. The terminology “symplectic system” refers to the fact that ${\mathbb S}_k(\lambda )$ and the fundamental matrix of system (S$_\lambda$) are complex symplectic (also called conjugate symplectic or ${\fancyscript{J}}\!$-unitary) when $\lambda$ is real, i.e., they satisfy the identity $M^*\!\!\!{\fancyscript{J}}M={\fancyscript{J}}$.

For convenience we write system (S$_\lambda$) as two $n$-dimensional equations with $z_k(\lambda )=(x_k^*(\lambda ),\ u_k^*(\lambda ))^*$ and ${\mathbb S}_k(\lambda )=\begin{pmatrix}{\fancyscript{A}}_k(\lambda ) &{} {\fancyscript{B}}_k(\lambda )\\ {\fancyscript{C}}_k(\lambda ) &{} {\fancyscript{D}}_k(\lambda )\end{pmatrix}$. System (S$_\lambda$) was studied in the literature in several special cases. In [2–4, 6, 9] the first equation in (S$_\lambda$) does not depend on $\lambda$ and the second equation is linear in $\lambda$, which by [2, Remark 3(iii)] gives the form

$$\begin{aligned} z_{k+1}(\lambda )=\begin{pmatrix}{\fancyscript{A}}_k &{} {\fancyscript{B}}_k \\ {\fancyscript{C}}_k-\lambda W_k{\fancyscript{A}}_k &{} {\fancyscript{D}}_k-\lambda W_k{\fancyscript{B}}_k\end{pmatrix} z_k(\lambda ), \end{aligned}$$

(2)

where ${\fancyscript{S}}_k:=\begin{pmatrix}{\fancyscript{A}}_k &{} {\fancyscript{B}}_k \\ {\fancyscript{C}}_k &{} {\fancyscript{D}}_k\end{pmatrix}$ is complex symplectic, $W_k$ is Hermitian, and $W_k\ge 0$. Note that system (2) covers also the classical second order Sturm–Liouville equation

$$\begin{aligned} -\varDelta (R_k\varDelta y_k(\lambda ))+Q_ky_{k+1}(\lambda )=\lambda W_ky_{k+1}(\lambda ) \end{aligned}$$

(3)

with Hermitian matrices $R_k,Q_k,W_k\in {\mathbb C}^{n\times n}$, invertible $R_k$, and $W_k>0$, see Example 1. System (S$_\lambda$) with a general linear dependence on $\lambda$

$$\begin{aligned} z_{k+1}(\lambda )=({\fancyscript{S}}_k+\lambda {\fancyscript{V}}_k)\,z_k(\lambda ) \end{aligned}$$

(4)

was studied in [18, 19], where the matrix ${\fancyscript{S}}_k$ is complex symplectic, ${\fancyscript{V}}_k^*\!{\fancyscript{J}}{\fancyscript{S}}_k$ is Hermitian and positive semidefinite, and ${\fancyscript{V}}_k^*\!{\fancyscript{J}}{\fancyscript{V}}_k=0$. In [15, 16] the linear Hamiltonian difference system

$$\begin{aligned} \varDelta \left( \begin{matrix} x_k(\lambda ) \\ u_k(\lambda ) \end{matrix}\right) =\left( \begin{matrix} A_k &{} B_k+\lambda W_k^{[1]} \\ C_k-\lambda W_k^{[2]} &{} -A_k^* \end{matrix}\right) \left( \begin{matrix} x_{k+1}(\lambda ) \\ u_k(\lambda ) \end{matrix}\right) \end{aligned}$$

(5)

is considered with the matrices $A_k,B_k,C_k,W_k^{[1]},W_k^{[2]}\in {\mathbb C}^{n\times n}$, ${\tilde{A}}_k:=(I-A_k)^{-1}$ exists, $B_k,C_k,W_k^{[1]},W_k^{[2]}$ are Hermitian, and $W_k^{[1]}\ge 0$, $W_k^{[2]}\ge 0$. Upon expanding the forward difference in (5), we can verify that system (5) corresponds to a discrete symplectic system (S$_\lambda$) with quadratic dependence on $\lambda$. Another linear Hamiltonian system

$$\begin{aligned} \varDelta \left( \begin{matrix} x_k(\lambda ) \\ u_k(\lambda ) \end{matrix}\right) =\lambda {\fancyscript{J}}H_k\left( \begin{matrix} x_{k+1}(\lambda ) \\ u_k(\lambda ) \end{matrix}\right) , \qquad H_k:=\left( \begin{matrix} -C_k &{} \ A_k^* \\ A_k &{} \ B_k \end{matrix}\right) , \end{aligned}$$

(6)

with $H_k\in {\mathbb C}^{2n\times 2n}$ Hermitian and ${\tilde{A}}_k(\lambda ):=(I-\lambda A_k)^{-1}$ is studied in [13, 14]. Upon expanding the latter inverse into a power series we get the analytic dependence on $\lambda$ in the coefficient matrix of system (6). More generally, the linear Hamiltonian system corresponding to

$$\begin{aligned} \varDelta \left( \begin{matrix} x_k(\lambda ) \\ u_k(\lambda ) \end{matrix}\right) ={\fancyscript{J}}(H_k^{[0]}+\lambda H_k^{[1]}) \left( \begin{matrix} x_{k+1}(\lambda ) \\ u_k(\lambda ) \end{matrix}\right) \end{aligned}$$

with Hermitian $H_k^{[0]},H_k^{[1]}\in {\mathbb C}^{2n\times 2n}$ is considered in [5]. Finally, a discrete symplectic system (S$_\lambda$) with analytic dependence on $\lambda$ and ${\fancyscript{S}}_k^{[0]}=I$ is studied in [7]. The latter paper also motivated the present study.

All the above mentioned references are devoted to various results in the spectral theory of the corresponding system. As it is known, the Lagrange identity plays a fundamental role in these investigations. This identity connects the ${\fancyscript{J}}\!$-skew-product of two solutions of system (S$_\lambda$) with the associated weight matrix $\varPsi _k(\lambda )$. In this paper we prove a general form of the Lagrange identity for system (S$_\lambda$) with analytic dependence on $\lambda \in {\mathbb C}$ and calculate the corresponding weight matrix explicitly in terms of the coefficients of (S$_\lambda$). This result includes the Lagrange identities for the above mentioned special systems. As a consequence we obtain the ${\fancyscript{J}}\!$-monotonicity of the fundamental matrix $\varPhi _k(\lambda )$ of (S$_\lambda$), which is used in [7] for proving the Krein traffic rules for the eigenvalues of $\varPhi _k(\lambda )$. We also investigate applications of the generalized Lagrange identity in the discrete Weyl–Titchmarsh theory. In particular, we show that under an appropriate Atkinson condition involving the weight matrix $\varPsi _k(\lambda )$, the theory of eigenvalues, Weyl disks, and square summable solutions developed in [18, 19] for system (4) remains valid without any change also for system (S$_\lambda$) with the analytic dependence on $\lambda$.

2 Lagrange Identity

Consider system (S$_\lambda$) with complex $2n\times 2n$ matrix ${\mathbb S}_k(\lambda )$ such that (1) holds. The parameter $\lambda \in {\mathbb C}$ is restricted to $|\lambda |<\varepsilon$ for some $\varepsilon >0$ ($\varepsilon =\infty$ is allowed), which bounds the region of convergence of ${\mathbb S}_k(\lambda )$ in (1) for all $k\in [0,\infty )_{\scriptscriptstyle {\mathbb Z}}:=[0,\infty )\cap {\mathbb Z}$. It follows that the matrices ${\fancyscript{S}}_k^{[j]}$, $j\in [0,\infty )_{\scriptscriptstyle {\mathbb Z}}$, satisfy the identities

$$\begin{aligned} {\fancyscript{S}}_k^{[0]*}\!\!{\fancyscript{J}}{\fancyscript{S}}_k^{[0]}&={\fancyscript{J}}\end{aligned}$$

(7)

$$\begin{aligned} \sum _{j=0}^m {\fancyscript{S}}_k^{[j]*}\!\!{\fancyscript{J}}{\fancyscript{S}}_k^{[m-j]}&=0, \qquad m\in {\mathbb N} \end{aligned}$$

(8)

for all $k\in [0,\infty )_{\scriptscriptstyle {\mathbb Z}}$. We note that $|\det \,{\fancyscript{S}}_k^{[0]}|=1$, as the determinant of any complex symplectic matrix is a complex unit. The second identity in (1) implies that ${\mathbb S}_k(\lambda )$ is invertible and hence

$$\begin{aligned} {\mathbb S}_k^{-1}(\lambda )=-{\fancyscript{J}}\,{\mathbb S}_k^*(\bar{\lambda }){\fancyscript{J}}=-\sum _{j=0}^\infty \lambda ^j{\fancyscript{J}}{\fancyscript{S}}_k^{[j]*}\!{\fancyscript{J}}. \end{aligned}$$

Remark 1

From ${\mathbb S}_k(\lambda )\,{\mathbb S}_k^{-1}(\lambda )=I$ we then obtain the identity ${\mathbb S}_k(\lambda )\,{\fancyscript{J}}\,{\mathbb S}_k^*(\bar{\lambda })={\fancyscript{J}}$ or equivalently

$$\begin{aligned} {\fancyscript{S}}_k^{[0]}\!{\fancyscript{J}}{\fancyscript{S}}_k^{[0]*}={\fancyscript{J}}, \qquad \sum _{j=0}^m {\fancyscript{S}}_k^{[j]}\!{\fancyscript{J}}{\fancyscript{S}}_k^{[m-j]*}=0, \qquad m\in {\mathbb N}. \end{aligned}$$

First we study the ${\fancyscript{J}}\!$-skew product of two coefficient matrices with different values of the spectral parameter. This lemma gives a main tool for the proof of the Lagrange identity.

Lemma 1

Assume (7)–(8). Then for every $\lambda ,\nu \in {\mathbb C}$ with $|\lambda |<\varepsilon$, $|\nu |<\varepsilon$,

$$\begin{aligned} {\mathbb S}_k^*(\lambda ){\fancyscript{J}}\,{\mathbb S}_k(\nu )={\fancyscript{J}}+(\bar{\lambda }-\nu )\,\varOmega _k(\bar{\lambda },\nu ), \end{aligned}$$

$k\in [0,\infty )_{\scriptscriptstyle {\mathbb Z}}$, where the $2n\times 2n$ matrix $\varOmega (\bar{\lambda },\nu )$ is defined by

$$\begin{aligned} \varOmega _k(\bar{\lambda },\nu ):=\sum _{m=0}^\infty \sum _{j=0}^m {\bar{\lambda }}^{m-j}\nu ^j \sum _{l=0}^j {\fancyscript{S}}_k^{[m-l+1]*}\!\!\!{\fancyscript{J}}{\fancyscript{S}}_k^{[l]}. \end{aligned}$$

(9)

Moreover, for $\nu =\lambda$ the matrix $\varOmega _k(\bar{\lambda },\lambda )$ is Hermitian for all $k\in [0,\infty )_{\scriptscriptstyle {\mathbb Z}}$.

Proof

We fix $|\lambda |<\varepsilon$, $|\nu |<\varepsilon$, and $k\in [0,\infty )_{\scriptscriptstyle {\mathbb Z}}$. The power series for ${\mathbb S}_k^*(\lambda )$ and ${\mathbb S}_k(\nu )$ converge absolutely, so that the terms in the product ${\mathbb S}_k^*(\lambda ){\fancyscript{J}}\,{\mathbb S}_k(\nu )$ can be re-arranged to the separate powers of ${\bar{\lambda }}^{m-j}\nu ^j$, that is,

$$\begin{aligned} {\mathbb S}_k^*(\lambda ){\fancyscript{J}}\,{\mathbb S}_k(\nu )=\sum _{m=0}^\infty \sum _{j=0}^m {\bar{\lambda }}^{m-j}\nu ^j {\fancyscript{S}}_k^{[m-j]*}\!\!\!{\fancyscript{J}}{\fancyscript{S}}_k^{[j]}. \end{aligned}$$

By using identity (8) for each $m\in {\mathbb N}$, we replace the term $\nu ^m{\fancyscript{S}}_k^{[0]*}\!\!\!{\fancyscript{J}}{\fancyscript{S}}_k^{[m]}$ by

$$\begin{aligned} -\nu ^m\,\big ( {\fancyscript{S}}_k^{[m]*}\!\!\!{\fancyscript{J}}{\fancyscript{S}}_k^{[0]}+{\fancyscript{S}}_k^{[m-1]*}\!\!\!{\fancyscript{J}}{\fancyscript{S}}_k^{[1]}+\dots +{\fancyscript{S}}_k^{[1]*}\!\!\!{\fancyscript{J}}{\fancyscript{S}}_k^{[m-1]} \big ). \end{aligned}$$

Thus, with the aid of (7) we get

$$\begin{aligned} {\mathbb S}_k^*(\lambda ){\fancyscript{J}}\,{\mathbb S}_k(\nu )&= {\fancyscript{J}}+\sum _{m=1}^\infty \sum _{j=1}^m ({\bar{\lambda }}^j-\nu ^j)\,\nu ^{m-j}{\fancyscript{S}}_k^{[j]*}\!\!\!{\fancyscript{J}}{\fancyscript{S}}_k^{[m-j]}. \end{aligned}$$

Upon factoring $\bar{\lambda }-\nu$ out of each term ${\bar{\lambda }}^j-\nu ^j$ and collecting the remaining products with the same powers of ${\bar{\lambda }}$ and $\nu$, we get

$$\begin{aligned} {\mathbb S}_k^*(\lambda ){\fancyscript{J}}\,{\mathbb S}_k(\nu )&= {\fancyscript{J}}+(\bar{\lambda }-\nu ) \sum _{m=1}^\infty \sum _{j=1}^m \bigg ( \sum _{l=1}^j {\bar{\lambda }}^{j-l}\nu ^{l-1} \bigg ) \nu ^{m-j}{\fancyscript{S}}_k^{[j]*}\!\!\!{\fancyscript{J}}{\fancyscript{S}}_k^{[m-j]} \nonumber \\&= {\fancyscript{J}}+(\bar{\lambda }-\nu )\,\varOmega _k(\bar{\lambda },\nu ), \end{aligned}$$

where $\varOmega _k(\bar{\lambda },\nu )$ is given in (9). Finally, for $\nu :=\lambda$ we get by using ${\fancyscript{J}}^*=-{\fancyscript{J}}$ and identities (8) that the matrix $\varOmega _k(\bar{\lambda },\lambda )$ is Hermitian. This latter fact is also shown in [7, Proposition 1]. $\square$

The following theorem provides the main result of this section. Its relationship to known discrete Lagrange identities in the literature is discussed in Sect. 3.

Theorem 1

(Lagrange identity) Assume (7)–(8) and fix $\lambda ,\nu \in {\mathbb C}$ with $|\lambda |<\varepsilon$, $|\nu |<\varepsilon$. For any two solutions $z(\lambda )$ and $z(\nu )$ of systems (S$_\lambda$) and (S$_{\nu }$), respectively, we have for all $k\in [0,\infty )_{\scriptscriptstyle {\mathbb Z}}$

$$\begin{aligned}&\varDelta \big (z_k^*(\lambda ){\fancyscript{J}}z_k(\nu )\big )=(\bar{\lambda }-\nu )\,\,z_k^*(\lambda )\,\varOmega _k(\bar{\lambda },\nu )\,z_k(\nu ),\end{aligned}$$

(10)

$$\begin{aligned} z_{k+1}^*(\lambda )&{\fancyscript{J}}z_{k+1}(\nu )=z_0^*(\lambda ){\fancyscript{J}}z_0(\nu )+(\bar{\lambda }-\nu ) \sum _{j=0}^k z_j^*(\lambda )\,\varOmega _j(\bar{\lambda },\nu )\,z_j(\nu ). \end{aligned}$$

(11)

Proof

Given that $z_{k+1}(\lambda )={\mathbb S}_k(\lambda )\,z_k(\lambda )$ and $z_{k+1}(\nu )={\mathbb S}_k(\nu )\,z_k(\nu )$ for all $k\in [0,\infty )_{\scriptscriptstyle {\mathbb Z}}$, we obtain from Lemma 1 that

$$\begin{aligned} \varDelta \big (z_k^*(\lambda ){\fancyscript{J}}z_k(\nu )\big )&= z_k^*(\lambda )\,\big [{\mathbb S}_k^*(\lambda ){\fancyscript{J}}\,{\mathbb S}_k(\nu )-{\fancyscript{J}}\big ]\,z_k(\nu ) \\&= (\bar{\lambda }-\nu )\,\,z_k^*(\lambda )\,\varOmega _k(\bar{\lambda },\nu )\,z_k(\nu ). \end{aligned}$$

The summation of (10) over the interval $[0,k]_{\scriptscriptstyle {\mathbb Z}}$ then yields (11). $\square$

Motivated by Lemma 1, we define for $k\in [0,\infty )_{\scriptscriptstyle {\mathbb Z}}$ the Hermitian $2n\times 2n$ matrix

$$\begin{aligned} \varPsi _k(\lambda ):=\varOmega _k(\bar{\lambda },\lambda )=\sum _{m=0}^\infty \sum _{j=0}^m {\bar{\lambda }}^{m-j}\lambda ^j \sum _{l=0}^j {\fancyscript{S}}_k^{[m-l+1]*}\!\!\!{\fancyscript{J}}{\fancyscript{S}}_k^{[l]}. \end{aligned}$$

(12)

The following identities show that $\varPsi _k(\lambda )$ is the correct weight matrix for the spectral theory of system (S$_\lambda$), see the examples and applications in Sects. 3 and 4.

Corollary 1

For every $\lambda \in {\mathbb C}$ with $|\lambda |<\varepsilon$ and $k\in [0,\infty )_{\scriptscriptstyle {\mathbb Z}}$ we have

$$\begin{aligned} \varDelta \big (z_k^*(\lambda ){\fancyscript{J}}z_k(\lambda )\big )=-2i\,\mathrm{im}(\lambda )\,z_k^*(\lambda )\,\varPsi _k(\lambda )\,z_k(\lambda ), \end{aligned}$$

(13)

$$\begin{aligned} z_{k+1}^*(\lambda ){\fancyscript{J}}z_{k+1}(\lambda )=z_0^*(\lambda ){\fancyscript{J}}z_0(\lambda )-2i\,\mathrm{im}(\lambda ) \sum _{j=0}^k z_j^*(\lambda )\,\varPsi _j(\lambda )\,z_j(\lambda ), \end{aligned}$$

(14)

$$\begin{aligned} z_k^*(\lambda ){\fancyscript{J}}z_k(\bar{\lambda })=z_0^*(\lambda ){\fancyscript{J}}z_0(\bar{\lambda }). \end{aligned}$$

(15)

Remark 2

When $|\lambda |<\varepsilon$ and $\lambda \in {\mathbb R}$, we have

$$\begin{aligned} \varPsi _k(\lambda )=\sum _{m=0}^\infty \sum _{j=0}^m \lambda ^m \sum _{l=0}^j {\fancyscript{S}}_k^{[m-l+1]*}\!\!\!{\fancyscript{J}}{\fancyscript{S}}_k^{[l]}=-{\mathbb S}_k^*(\lambda ){\fancyscript{J}}\,\dot{\mathbb S}_k(\lambda ) =\dot{{\mathbb S}}_k^*(\lambda ){\fancyscript{J}}\,{\mathbb S}_k(\lambda ), \end{aligned}$$

where the dot denotes the derivative with respect to $\lambda$. The weight matrix

$$\begin{aligned} {\fancyscript{J}}\,\dot{\mathbb S}_k(\lambda ){\fancyscript{J}}\,{\mathbb S}_k^*(\lambda ){\fancyscript{J}}={\mathbb S}_k^{*-1}(\lambda )\,\varPsi _k(\lambda )\,{\mathbb S}_k^{-1}(\lambda ) \end{aligned}$$

was used in [11, 17] in the oscillation theory of systems (S$_\lambda$) with general nonlinear dependence on $\lambda$.

3 Special Examples

In this section we show the connection of the generalized Lagrange identity in Theorem 1 to several special cases known in the literature. We also demonstrate that a positive definite weight matrix $\varPsi _k(\lambda )$ can be obtained when ${\mathbb S}_k(\lambda )$ is quadratic in $\lambda$.

Example 1

In the simplest case, i.e., for the second order Sturm–Liouville difference equation (3), the Lagrange identity is

$$\begin{aligned} \varDelta \big [ y_k^*(\lambda )\,R_k\varDelta y_k(\nu )-(\varDelta y_k^*(\lambda ))\,R_ky_k(\nu ) \big ]=(\bar{\lambda }-\nu )\,\,y_{k+1}^*(\lambda )\,W_k\,y_{k+1}(\nu ), \end{aligned}$$

see e.g. [1, Theorem 4.2.1] or [10, Theorem 2.2.3]. This can be seen from (10) and (9), in which $\varepsilon =\infty$, $x_k:=y_k$, $u_k:=R_k\varDelta y_k$, $z_k=(x_k^*,\ u_k^*)^*$, and use the formula $x_{k+1}=x_k+R_k^{-1}u_k$. The coefficient matrix of (S$_\lambda$) is ${\mathbb S}_k(\lambda ):={\fancyscript{S}}_k+\lambda {\fancyscript{V}}_k$ with

$$\begin{aligned} {\fancyscript{S}}_k:={\fancyscript{S}}_k^{[0]}&=\left( \begin{matrix} I &{} \ R_k^{-1} \\ Q_k &{} \ I+Q_kR_k^{-1} \end{matrix}\right) , \quad {\fancyscript{V}}_k:={\fancyscript{S}}_k^{[1]}=-\left( \begin{matrix} 0 &{} \ \ 0 \\ W_k &{} \ \ W_kR_k^{-1} \end{matrix}\right) , \\ \varOmega (\bar{\lambda },\nu )&={\fancyscript{V}}_k^*\!\!{\fancyscript{J}}{\fancyscript{S}}_k=\left( \begin{matrix} I,&R_k^{-1} \end{matrix}\right) ^{\!*}\,W_k\,\left( \begin{matrix} I,&R_k^{-1} \end{matrix}\right) =\varPsi _k(\lambda ), \end{aligned}$$

and ${\fancyscript{S}}_k^{[j]}:=0$ for $j\ge 2$. Note that Eqs. (7) and (8) with $m\in \{1,2\}$ hold, since $R_k,Q_k,W_k$ are assumed to be Hermitian.

Example 2

Consider system (4) with general linear dependence on $\lambda$. In this case ${\fancyscript{S}}_k^{[0]}:={\fancyscript{S}}_k$, ${\fancyscript{S}}_k^{[1]}:={\fancyscript{V}}_k$, ${\fancyscript{S}}_k^{[j]}:=0$ for $j\ge 2$, $\varepsilon =\infty$, and $\varOmega _k(\bar{\lambda },\nu )={\fancyscript{V}}_k^*\!\!{\fancyscript{J}}{\fancyscript{S}}_k=\varPsi _k(\lambda )$ is constant in $\lambda$ and Hermitian. Identities (7) and (8) with $m\in \{1,2\}$ are

$$\begin{aligned} {\fancyscript{S}}_k^*\!\!{\fancyscript{J}}{\fancyscript{S}}_k={\fancyscript{J}}, \quad {\fancyscript{S}}_k^*\!\!{\fancyscript{J}}{\fancyscript{V}}_k+{\fancyscript{V}}_k^*\!\!{\fancyscript{J}}{\fancyscript{S}}_k=0, \quad {\fancyscript{V}}_k^*\!\!{\fancyscript{J}}{\fancyscript{V}}_k=0. \end{aligned}$$

(16)

The Lagrange identity in (10) is, compare with [19, Theorem 2.6],

$$\begin{aligned} \varDelta \big (z_k^*(\lambda ){\fancyscript{J}}z_k(\nu ) \big )&= (\bar{\lambda }-\nu )\,\,z_k^*(\lambda )\,{\fancyscript{V}}_k^*\!\!{\fancyscript{J}}{\fancyscript{S}}_k\,z_k(\nu ) \nonumber \\&= (\bar{\lambda }-\nu )\,\,z_{k+1}^*(\lambda )\,{\fancyscript{J}}{\fancyscript{V}}_k{\fancyscript{J}}{\fancyscript{S}}_k^*\!\!{\fancyscript{J}}z_{k+1}(\nu ). \end{aligned}$$

(17)

Observe that by (16) the matrix ${\fancyscript{V}}_k$ is singular. Hence, $\varOmega _k(\bar{\lambda },\nu )$ and $\varPsi _k(\lambda )$ are in this case singular as well. Moreover, $\det \,{\mathbb S}_k(\lambda )=\det {\fancyscript{S}}_k$ and thus $|\det \,{\mathbb S}_k(\lambda )|=1$.

Example 3

System (2) represents a special case of Example 2, namely

$$\begin{aligned} {\fancyscript{S}}_k:={\fancyscript{S}}_k^{[0]}=\left( \begin{matrix} {\fancyscript{A}}_k &{} {\fancyscript{B}}_k \\ {\fancyscript{C}}_k &{} {\fancyscript{D}}_k \end{matrix}\right) , \quad {\fancyscript{V}}_k:={\fancyscript{S}}_k^{[1]}=-\left( \begin{matrix} 0 &{} \ 0 \\ W_k{\fancyscript{A}}_k &{} \ W_k{\fancyscript{B}}_k \end{matrix}\right) , \\ \varOmega _k(\bar{\lambda },\nu )={\fancyscript{V}}_k^*\!\!{\fancyscript{J}}{\fancyscript{S}}_k=\left( \begin{matrix} {\fancyscript{A}}_k,&{\fancyscript{B}}_k \end{matrix}\right) ^*\,W_k\,\left( \begin{matrix} {\fancyscript{A}}_k,&{\fancyscript{B}}_k \end{matrix}\right) =\varPsi _k(\lambda ). \end{aligned}$$

In this case the Lagrange identity in (10) or (17) has the form

$$\begin{aligned} \varDelta \big (z_k^*(\lambda ){\fancyscript{J}}z_k(\nu ) \big )=(\bar{\lambda }-\nu )\,\,x_{k+1}^*(\lambda )\,W_k\,x_{k+1}(\nu ), \end{aligned}$$

(18)

where $z(\lambda )=(x^*(\lambda ),\ u^*(\lambda ))^*$ and $z(\nu )=(x^*(\nu ),\ u^*(\nu ))^*$. Identity (18) is used in [6, Lemma 2.3] and [4, Lemma 2.6].

Example 4

In this example we discuss the symplectic analogue (or a generalization to the symplectic system) of the linear Hamiltonian system (5), which was studied in [15, 16]. We take system (S$_\lambda$) with a special quadratic dependence on $\lambda$

$$\begin{aligned} z_{k+1}(\lambda )=\left( \begin{matrix} {\fancyscript{A}}_k &{} \ {\fancyscript{B}}_k+\lambda {\fancyscript{A}}_kW_k^{[2]} \\ {\fancyscript{C}}_k-\lambda W_k^{[1]}\!{\fancyscript{A}}_k &{} \ {\fancyscript{D}}_k+\lambda {\fancyscript{C}}_kW_k^{[2]}-\lambda W_k^{[1]}({\fancyscript{B}}_k+\lambda {\fancyscript{A}}_kW_k^{[2]}) \end{matrix}\right) z_k(\lambda ), \end{aligned}$$

(19)

where $W_k^{[1]}$ and $W_k^{[2]}$ are Hermitian. That is, ${\mathbb S}_k(\lambda )={\fancyscript{S}}_k+\lambda {\fancyscript{V}}_k+\lambda ^2{\fancyscript{W}}_k$ with $\varepsilon =\infty$,

$$\begin{aligned} {\fancyscript{S}}_k:={\fancyscript{S}}_k^{[0]}=\left( \begin{matrix} {\fancyscript{A}}_k &{} \ {\fancyscript{B}}_k \\ {\fancyscript{C}}_k &{} \ {\fancyscript{D}}_k \end{matrix}\right) , \quad {\fancyscript{W}}_k:={\fancyscript{S}}_k^{[2]}={\fancyscript{J}}\widetilde{W}_k{\fancyscript{S}}_k{\fancyscript{J}}\widehat{W}_k=\left( \begin{matrix} 0 &{} \ 0 \\ 0 &{} \ -W_k^{[1]}\!{\fancyscript{A}}_kW_k^{[2]} \end{matrix}\right) , \\ {\fancyscript{V}}_k:={\fancyscript{S}}_k^{[1]}={\fancyscript{J}}\widetilde{W}_k{\fancyscript{S}}_k+{\fancyscript{S}}_k{\fancyscript{J}}\widehat{W}_k =\left( \begin{matrix} 0 &{} \ {\fancyscript{A}}_kW_k^{[2]} \\ -W_k^{[1]}{\fancyscript{A}}_k &{} \ {\fancyscript{C}}_kW_k^{[2]}-W_k^{[1]}{\fancyscript{B}}_k \end{matrix}\right) , \quad \quad \quad \\ \varOmega _k(\bar{\lambda },\nu )=\widehat{W}_k+(I-\bar{\lambda }\widehat{W}_k{\fancyscript{J}})\,{\fancyscript{S}}_k^*\,\widetilde{W}_k\,{\fancyscript{S}}_k\,(I+\nu \!{\fancyscript{J}}\widehat{W}_k),\quad \quad \quad \quad \quad \quad \quad \quad \end{aligned}$$

and ${\fancyscript{S}}_k^{[j]}:=0$ for $j\ge 3$. The Hermitian $2n\times 2n$ matrices $\widetilde{W}_k:={\text {diag}}\{W_k^{[1]},0\}$ and $\widehat{W}_k:={\text {diag}}\{0,W_k^{[2]}\}$ are block diagonal. We can see that in this case $\varPsi _k(\lambda )=\varOmega _k(\bar{\lambda },\lambda )$ is Hermitian but no longer constant in $\lambda$, as was the case in Examples 1–3. The above coefficients satisfy identities (7) and (8) with $m\in \{1,2,3,4\}$, i.e.,

$$\begin{aligned} {\fancyscript{S}}_k^*\!\!{\fancyscript{J}}{\fancyscript{S}}_k={\fancyscript{J}}, \qquad {\fancyscript{S}}_k^*\!\!{\fancyscript{J}}{\fancyscript{V}}_k+{\fancyscript{V}}_k^*\!\!{\fancyscript{J}}{\fancyscript{S}}_k&=0, \qquad {\fancyscript{V}}_k^*\!\!{\fancyscript{J}}{\fancyscript{W}}_k + {\fancyscript{W}}_k^*{\fancyscript{J}}{\fancyscript{V}}_k = 0 \\ {\fancyscript{S}}_k^*\!\!{\fancyscript{J}}{\fancyscript{W}}_k+{\fancyscript{V}}_k^*\!\!{\fancyscript{J}}{\fancyscript{V}}_k+{\fancyscript{W}}_k^*\!\!{\fancyscript{J}}{\fancyscript{S}}_k&=0, \qquad {\fancyscript{W}}_k^*\!\!{\fancyscript{J}}{\fancyscript{W}}_k=0. \end{aligned}$$

The Lagrange identity in (10) now reads as

$$\begin{aligned} \varDelta \big (z_k^*(\lambda ){\fancyscript{J}}z_k(\nu ) \big ) = (\bar{\lambda }-\nu )\,\big [x_{k+1}^*(\lambda )\,W_k^{[1]}\,x_{k+1}(\nu )+u_k^*(\lambda )\,W_k^{[2]}\,u_k(\nu )\big ], \end{aligned}$$

(20)

where $z(\lambda )=(x^*(\lambda ),\ u^*(\lambda ))^*$ and $z(\nu )=(x^*(\nu ),\ u^*(\nu ))^*$. Identity (20) can be found in [16, Lemma 2.2]. We note that we can factorize ${\mathbb S}_k(\lambda )$ and $\varOmega _k(\bar{\lambda },\nu )$ as

$$\begin{aligned} {\mathbb S}_k(\lambda )&= \left( \begin{matrix} I &{} \ \ 0 \\ -\lambda W_k^{[1]} &{} \ \ I \end{matrix}\right) \left( \begin{matrix} {\fancyscript{A}}_k &{} \ {\fancyscript{B}}_k \\ {\fancyscript{C}}_k &{} \ {\fancyscript{D}}_k \end{matrix}\right) \left( \begin{matrix} I &{} \ \ \lambda W_k^{[2]} \\ 0 &{} \ \ I \end{matrix}\right) , \\ \varOmega _k(\bar{\lambda },\nu )&= \left( \begin{matrix} {\fancyscript{A}}_k^* &{} \ \ 0 \\ {\fancyscript{B}}_k^*+\bar{\lambda }W_k^{[2]}\!{\fancyscript{A}}_k^* &{} \ \ I \end{matrix}\right) \left( \begin{matrix} W_k^{[1]} &{} \ 0 \\ 0 &{} \ W_k^{[2]} \end{matrix}\right) \left( \begin{matrix} {\fancyscript{A}}_k &{} \ \ {\fancyscript{B}}_k+\nu {\fancyscript{A}}_kW_k^{[2]} \\ 0 &{} \ \ I \end{matrix}\right) . \end{aligned}$$

Therefore, $\det \,{\mathbb S}_k(\lambda )=\det {\fancyscript{S}}_k$ and $|\det \,{\mathbb S}_k(\lambda )|=1$ as in Example 2, and

$$\begin{aligned} \det \,\varPsi _k(\lambda )=\det \,\varOmega _k(\bar{\lambda },\nu )=|\det {\fancyscript{A}}_k|^2\times \det \,W_k^{[1]}\times \det \,W_k^{[2]}. \end{aligned}$$

(21)

Equation (21) shows that the determinant of the weight matrix $\varPsi _k(\lambda )$ does not depend on $\lambda$. Moreover, $\varPsi _k(\lambda )$ is invertible if and only if ${\fancyscript{A}}_k$, $W_k^{[1]}$, $W_k^{[2]}$ are invertible. And in this case the matrix $\varPsi _k(\lambda )$ is positive definite if and only if $W_k^{[1]}$ and $W_k^{[2]}$ are positive definite. However, an invertible (positive definite) weight matrix $\varPsi _k(\lambda )$ can occur only when system (19) corresponds to a linear Hamiltonian system (5) with invertible (positive definite) $W_k^{[1]}$ and $W_k^{[2]}$, because in this case ${\fancyscript{A}}_k={\tilde{A}}_k$ is invertible. The other coefficients of (19) are then given by ${\fancyscript{B}}_k={\tilde{A}}_kB_k$, ${\fancyscript{C}}_k=C_k{\tilde{A}}_k$, and ${\fancyscript{D}}_k=C_k{\tilde{A}}_kB_k+I-A_k^*$, see [16, Formula (2.3)].

Example 5

Consider the linear Hamiltonian difference system (6), in which

$$\begin{aligned} Sco_k^{[0]}:&=I, \quad {\fancyscript{S}}_k^{[1]}:={\fancyscript{J}}H_k, \quad {\fancyscript{S}}_k^{[j]}:=\left( \begin{matrix} A_k^j &{} \ \ A_k^{j-1}B_k \\ C_kA_k^{j-1} &{} \ C_kA_k^{j-2}B_k \end{matrix}\right) ,\quad j\ge 2, \\&\varOmega _k(\bar{\lambda },\nu )=D_k^*(\lambda )\,H_k\,D_k(\nu ), \quad D_k(\lambda ):=\left( \begin{matrix} {\tilde{A}}_k(\lambda ) &{} \ \lambda {\tilde{A}}_k(\lambda )\,B_k \\ 0 &{} \ I \end{matrix}\right) , \end{aligned}$$

where ${\tilde{A}}_k(\lambda ):=(I-\lambda A_k)^{-1}$, see [7, p. 5]. Therefore, the dependence of ${\mathbb S}_k(\lambda )$ on $\lambda$ is analytic with $\varepsilon =\inf \{1/{\text {sprad}}(A_k),\ k\in [0,\infty )_{\scriptscriptstyle {\mathbb Z}}\}$, provided this infimum is positive, where ${\text {sprad}}(M)=\max \{|\mu |,\ \mu \, {\text {is an eigenvalue of}}\,M\}$ denotes the spectral radius of $M$. The Lagrange identity in (10) is, compare with [13, Formula (9)],

$$\begin{aligned} \varDelta \big (z_k^*(\lambda ){\fancyscript{J}}z_k(\nu ) \big ) = (\bar{\lambda }-\nu )\,\left( \begin{matrix} x_{k+1}(\lambda ) \\ u_k(\lambda ) \end{matrix}\right) ^{\!\!\!*}\!H_k\left( \begin{matrix} x_{k+1}(\nu ) \\ u_k(\nu ) \end{matrix}\right) . \end{aligned}$$

Example 6

In [7, 8], the discrete symplectic system (S$_\lambda$) with ${\fancyscript{S}}_k^{[j]}:=(1/j!)\,R_k^j$ for $j\in [0,\infty )_{\scriptscriptstyle {\mathbb Z}}$ is studied, where $R_k\in {\mathbb C}^{2n\times 2n}$ satisfies $R_k^*{\fancyscript{J}}+{\fancyscript{J}}R_k=0$. This means that the coefficient matrix ${\mathbb S}_k(\lambda )$ is of exponential type, i.e., $\varepsilon =\infty$ and

$$\begin{aligned} {\mathbb S}_k(\lambda )=\sum _{j=0}^\infty \frac{\lambda ^j}{j!}\,R_k^j=\exp (\lambda R_k). \end{aligned}$$

(22)

By [7, p. 6] or [8, Sect. 2], we then have

$$\begin{aligned} \varOmega _k(\bar{\lambda },\nu )\!=\!\!\sum _{j=1}^\infty (-1)^j\,\frac{(\bar{\lambda }-\nu )^{2j-1}}{(2j)!}\,(R_k^*)^j\!\!{\fancyscript{J}}R_k^j - \sum _{j=0}^\infty (-1)^j\,\frac{(\bar{\lambda }-\nu )^{2j}}{(2j+1)!}\,(R_k^*)^j\!\!{\fancyscript{J}}R_k^{j+1}\!\!\!. \end{aligned}$$

The Lagrange identity has the same form as in (10) with the above $\varOmega _k(\bar{\lambda },\nu )$.

4 Weyl–Titchmarsh Theory

In this section we discuss the applications of the Lagrange identity from Theorem 1 in the Weyl–Titchmarsh theory for system (S$_\lambda$) with analytic dependence on $\lambda$. We assume that the Hermitian weight matrix $\varPsi _k(\lambda )$ defined in (12) satisfies

$$\begin{aligned} \varPsi _k(\lambda )\ge 0, \qquad k\in [0,\infty )_{\scriptscriptstyle {\mathbb Z}}. \end{aligned}$$

(23)

In [19] we have recently developed the Weyl–Titchmarsh theory for system (4), i.e., for system (S$_\lambda$) with general linear dependence on $\lambda$. In this section we show that most of the results in [19] remain valid also for the analytic dependence on $\lambda$, when we modify the corresponding Atkinson-type condition to this more general setting. One of the crucial properties is that the fundamental matrix $\varPhi _k(\lambda )$ of (S$_\lambda$) satisfies

$$\begin{aligned} \varPhi _k^*(\lambda )\,{\fancyscript{J}}\,\varPhi _k(\bar{\lambda })={\fancyscript{J}}\end{aligned}$$

(24)

for all $k\in [0,\infty )_{\scriptscriptstyle {\mathbb Z}}$ whenever (24) holds at the initial point $k=0$. Note that identity (24) now follows from (15) in Corollary 1. In the subsequent paragraphs we review the most important results, which are in particular connected to the theory of square summable solutions of (S$_\lambda$).

In [19] we identified the minimal requirements for the solutions of (S$_\lambda$) to satisfy the Atkinson condition. In this way we obtained the weak and strong Atkinson conditions, which are needed for different statements in the Weyl–Titchmarsh theory. For completeness we reformulate these conditions in the setting of this paper. Let $\varPhi _k(\lambda )=(Z_k(\lambda ),\ \widetilde{Z}_k(\lambda ))$ be the partition of the fundamental matrix of system (S$_\lambda$) into $2n\times n$ solutions, which are given by the initial conditions $Z_0(\lambda )=\alpha ^*$ and $\widetilde{Z}_0(\lambda )=-{\fancyscript{J}}\alpha ^*$ for some fixed $\alpha \in {\mathbb C}^{n\times 2n}$ with $\alpha {\fancyscript{J}}\alpha ^*=0$ and $\alpha \alpha ^*=I$. The solution $\widetilde{Z}(\lambda )$ is called the natural conjoined basis of (S$_\lambda$) and the spectral properties of the associated eigenvalue problem are formulated in terms of this natural conjoined basis. Let us fix for a moment an index $N\in [1,\infty )_{\scriptscriptstyle {\mathbb Z}}$.

Hypothesis 1

(Finite weak Atkinson condition) For all $\lambda \in {\mathbb C}$ with $|\lambda |<\varepsilon$ and every column $z(\lambda )$ of the natural conjoined basis $\widetilde{Z}(\lambda )$ of (S$_\lambda$) we assume that

$$\begin{aligned} \sum _{k=0}^N z_k^*(\lambda )\,\varPsi _k(\lambda )\,z_k(\lambda )>0. \end{aligned}$$

(25)

If $\beta \in {\mathbb C}^{n\times 2n}$ with $\beta {\fancyscript{J}}\beta ^*=0$ and $\beta \beta ^*=I$ is also fixed, then we consider the symplectic eigenvalue problem

$$\begin{aligned} (\mathrm{S}_\lambda ), \quad k\in [0,N]_{\scriptscriptstyle {\mathbb Z}}, \quad \alpha \,z_0(\lambda )=0, \quad \beta \,z_{N+1}(\lambda )=0. \end{aligned}$$

(26)

It follows as in [19, Theorem 2.8] that under Hypothesis 1 the eigenvalues of (26) are real, isolated, and they are characterized by $\det \,\beta \,\widetilde{Z}_{N+1}(\lambda )=0$. The corresponding eigenfunctions are then of the form $\widetilde{Z}(\lambda )\,d$ with nonzero $d\in {\text {Ker}}\beta \,\widetilde{Z}_{N+1}(\lambda )$.

The $M(\lambda )$-function for system (S$_\lambda$) is defined by $M_k(\lambda ):=-[\beta \,\widetilde{Z}_k(\lambda )]^{-1}\beta \,Z_k(\lambda )$ and it satisfies the properties in [19, Lemma 2.10 and Theorem 2.13]. In particular, $M_k^*(\lambda )=M_k(\bar{\lambda })$ and $M_k(\lambda )$ is analytic in $\lambda$. Define the Weyl solution $\chi (\lambda ,M)$ of (S$_\lambda$) corresponding to $M\in {\mathbb C}^{n\times n}$ and the Hermitian matrix function ${\fancyscript{E}}(\lambda ,M)$ by

$$\begin{aligned} \chi _k(\lambda ,M):=\varPhi _k(\lambda )\,\left( \begin{matrix} I,&\ M^* \end{matrix}\right) ^{\!*}, \quad {\fancyscript{E}}_k(\lambda ,M):=i\,\delta (\lambda )\,\chi _k^*(\lambda ,M){\fancyscript{J}}\chi _k(\lambda ,M), \end{aligned}$$

(27)

where $\delta (\lambda ):={\text {sgn}}\,\text {im}(\lambda )$. The Weyl disk $D_k(\lambda )$ and the Weyl circle $C_k(\lambda )$ are then defined as the sets

$$\begin{aligned} D_k(\lambda ):=\big \{M\in {\mathbb C}^{n\times n},\ {\fancyscript{E}}_k(\lambda ,M)\le 0 \big \}, \quad C_k(\lambda ):=\big \{M\in {\mathbb C}^{n\times n},\ {\fancyscript{E}}_k(\lambda ,M)=0 \big \}. \end{aligned}$$

It follows that the results in [19, Sect. 3] regarding the Weyl disks and Weyl circles hold exactly in the same form, but now under the following assumption.

Hypothesis 2

(Infinite weak Atkinson condition) There exists $N_0\in {\mathbb N}$ such that for all $\lambda \in {\mathbb C}$ with $|\lambda |<\varepsilon$ every column $z(\lambda )$ of $\widetilde{Z}(\lambda )$ satisfies (25) with $N=N_0$.

We summarize the main properties of the Weyl disks in the following.

Theorem 2

Let $\lambda \in {\mathbb C}\setminus {\mathbb R}$ with $|\lambda |<\varepsilon$ and suppose that (23) and Hypothesis 2 hold. Then for every $k\ge N_0+1$ the Weyl disk and Weyl circle satisfy

$$\begin{aligned} D_k(\lambda )&= \big \{ P_k(\lambda )+R_k(\lambda )\,VR_k(\bar{\lambda }),\ V\in {\mathbb C}^{n\times n},\ V^*V\le I \big \}, \\ C_k(\lambda )&= \big \{ P_k(\lambda )+R_k(\lambda )\,UR_k(\bar{\lambda }),\ U\in {\mathbb C}^{n\times n},\ U^*U=I \big \}, \end{aligned}$$

where the center $P_k(\lambda )$ and the matrix radius $R_k(\lambda )$ are defined by

$$\begin{aligned} P_k(\lambda ):=-{\fancyscript{H}}_k^{-1}(\lambda )\,{\fancyscript{G}}_k(\lambda ), \qquad R_k(\lambda ):={\fancyscript{H}}_k^{-1/2}(\lambda ) \end{aligned}$$

(28)

with ${\fancyscript{H}}_k(\lambda )$ and ${\fancyscript{G}}_k(\lambda )$ given by ${\fancyscript{H}}_k(\lambda ):=i\,\delta (\lambda )\,{\widetilde{Z}}_k^*(\lambda ){\fancyscript{J}}\widetilde{Z}_k(\lambda )$ and ${\fancyscript{G}}_k(\lambda ):=i\,\delta (\lambda )\,{\widetilde{Z}}_k^*(\lambda ){\fancyscript{J}}Z_k(\lambda )$. Moreover, the Weyl disks $D_k(\lambda )$ are closed, convex, and $D_{k+1}(\lambda )\subseteq D_k(\lambda )$ for all $k\ge N_0+1$.

Proof

The proof follows the same arguments as in [19, Theorem 3.8]. We note that by (14) in Corollary 1 we have

$$\begin{aligned} {\fancyscript{H}}_k(\lambda )=2\,|\text {im}(\lambda )| \sum _{j=0}^{k-1}{\widetilde{Z}}_j^*(\lambda )\,\varPsi _j(\lambda )\,\widetilde{Z}_j(\lambda ). \end{aligned}$$

(29)

This shows that under Hypothesis 2 the matrices ${\fancyscript{H}}_k(\lambda )$ are Hermitian and positive definite for $k\ge N_0+1$, so that the center $P_k(\lambda )$ and the matrix radius $R_k(\lambda )$ are well defined. $\square$

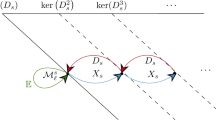
The properties of the Weyl disks $D_k(\lambda )$ in Theorem 2 and formula (29) imply that for $k\rightarrow \infty$ there exists the limiting Weyl disk $D_+(\lambda ):=\bigcap _{k\ge N_0+1}D_k(\lambda )$, which is closed and convex and which satisfies

$$\begin{aligned} D_+(\lambda )=\big \{ P_{\!+}(\lambda )+R_+(\lambda )\,VR_+(\bar{\lambda }),\ V\in {\mathbb C}^{n\times n},\ V^*V\le I \big \}, \end{aligned}$$

where the limiting center and the limiting matrix radius are complex $n\times n$ matrices

$$\begin{aligned} P_{\!+}(\lambda ):=\lim _{k\rightarrow \infty }P_k(\lambda ), \qquad R_+(\lambda ):=\lim _{k\rightarrow \infty }R_k(\lambda )\ge 0, \end{aligned}$$

compare with [19, Theorem 3.9 and Corollary 3.11]. The elements of the limiting Weyl disk are characterized in the following result.

Theorem 3

Let $\lambda \in {\mathbb C}\setminus {\mathbb R}$ with $|\lambda |<\varepsilon$ and suppose that (23) and Hypothesis 2 hold. The matrix $M\in {\mathbb C}^{n\times n}$ belongs to $D_+(\lambda )$ if and only if

$$\begin{aligned} \sum _{k=0}^\infty \chi _k^*(\lambda ,M)\,\varPsi _k(\lambda )\,\chi _k(\lambda ,M)\le \frac{\mathrm{im}(M)}{\mathrm{im}(\lambda )}, \end{aligned}$$

(30)

where $\chi (\lambda ,M)$ is the Weyl solution of $\mathrm{{(S}}_\lambda$) corresponding to $M$ defined in (27).

Proof

The proof follows by applying identity (14) in Corollary 1 to ${\fancyscript{E}}_k(\lambda ,M)$, see also [19, Corollary 3.12]. $\square$

We now discuss the number of square summable solutions of (S$_\lambda$) with analytic dependence on $\lambda$. As the weight matrix $\varPsi _k(\lambda )$ now depends on $\lambda$, we define for $\lambda \in {\mathbb C}$ with $|\lambda |<\varepsilon$ the semi-inner product and the semi-norm

$$\begin{aligned} \langle z,\widetilde{z} \rangle _{\varPsi (\lambda )}:=\sum _{k=0}^\infty z_k^*\,\varPsi _k(\lambda )\,\widetilde{z}_k, \quad \Vert z\Vert _{\varPsi (\lambda )}:=\sqrt{\langle z,z \rangle _{\varPsi (\lambda )}}=\bigg ( \sum _{k=0}^\infty z_k^*\,\varPsi _k(\lambda )\,z_k \bigg )^{\!\!1/2}\!\!\!\!, \end{aligned}$$

and the corresponding space of all square summable sequences with respect to $\varPsi (\lambda )$

$$\begin{aligned} \ell _{\varPsi (\lambda )}^2:=\big \{ \{z_k\}_{k=0}^\infty ,\ z_k\in {\mathbb C}^{2n},\ \Vert z\Vert _{\varPsi (\lambda )}<\infty \big \}. \end{aligned}$$

(31)

Observe that the space $\ell _{\varPsi (\lambda )}^2$ now also depends on $\lambda$. However, in some special cases this space can be taken independent on $\lambda$, as it is shown for systems (2), (3), (4) in Examples 1–3. Also, in view of (20) in Example 4 we may consider for systems (19) or (5) the space

$$\begin{aligned} \ell _{W^{[1]},W^{[2]}}^2:=\bigg \{ \big \{z_k=(x_k^*,u_k^*)^*\big \}_{k=0}^\infty , \ \sum _{k=0}^\infty \big ( x_{k+1}^*\,W_k^{[1]}x_{k+1}+u_k^*\,W_k^{[2]}u_k \big ) <\infty \bigg \}, \end{aligned}$$

which does not depend on $\lambda$. Given the space $\ell _{\varPsi (\lambda )}^2$ in (31), its subspace of all square summable solutions of (S$_\lambda$) is denoted by

$$\begin{aligned} {\mathcal N}(\lambda ):=\big \{ z\in \ell _{\varPsi (\lambda )}^2,\ z=\{z_k\}_{k=0}^\infty \ {\text {solves}} ({\text{ S }}_\lambda )\big \}. \end{aligned}$$

Under assumption (23) and Hypothesis 2, the result in Theorem 3 implies that $n\le \dim {\mathcal N}(\lambda )\le 2n$ for all $\lambda \in {\mathbb C}\setminus {\mathbb R}$ with $|\lambda |<\varepsilon$, see also [19, Theorem 4.2]. The two extreme cases are then called as the limit point case when $\dim {\mathcal N}(\lambda )=n$, and the limit circle case when $\dim {\mathcal N}(\lambda )=2n$. The cases when $\dim {\mathcal N}(\lambda )$ is between $n+1$ and $2n-1$ are called intermediate. It follows that the results in [19, Theorem 4.2, Corollary 4.15] hold for system (S$_\lambda$) with analytic dependence on $\lambda$ in exactly the same form under the appropriate weak or strong Atkinson type condition. We summarize the main result regarding the number of linearly independent square summable solutions of (S$_\lambda$) in the following theorem.

Theorem 4

Let $\lambda \in {\mathbb C}\setminus {\mathbb R}$ with $|\lambda |<\varepsilon$ and suppose that (23) and Hypothesis 2 hold. Then system $(S_\lambda )$ has exactly $n+{\text {rank}}\,R_+(\lambda )$ linearly independent square summable solutions, i.e.,

$$\begin{aligned} \dim {\mathcal N}(\lambda )=n+{\text {rank}}\,R_+(\lambda ), \end{aligned}$$

where $R_+(\lambda )$ is the matrix radius of the limiting Weyl disk $D_+(\lambda )$.

Proof

We refer to the proof of [19, Theorem 4.9] for the details. $\square$

As a consequence of Theorem 4 we obtain the characterization of the limit point case and limit circle case for system (S$_\lambda$) with analytic dependence on $\lambda$ in terms of the limiting matrix radius $R_+(\lambda )$.

Corollary 2

Let $\lambda \in {\mathbb C}\setminus {\mathbb R}$ with $|\lambda |<\varepsilon$ and suppose that (23) and Hypothesis 2 hold. System $(S_\lambda )$ is in the limit point case if and only if $R_+(\lambda )=0$, and in this case $D_+(\lambda )=\{P_{\!+}(\lambda )\}$ and $D_+(\bar{\lambda })=\{P_{\!+}(\bar{\lambda })\}$. System $\mathrm{(S}_\lambda )$ is in the limit circle case if and only if $R_+(\lambda )$ is invertible.

In a similar way, the results in [18] regarding the Weyl–Titchmarsh theory for system (S$_\lambda$) with jointly varying endpoints remain valid also for the analytic dependence on $\lambda$, when we assume the following finite or infinite strong Atkinson type condition.

Hypothesis 3

(Finite strong Atkinson condition) For all $\lambda \in {\mathbb C}$ with $|\lambda |<\varepsilon$, every nontrivial solution $z(\lambda )$ of (S$_\lambda$) satisfies (25).

Hypothesis 4

(Infinite strong Atkinson condition) There exists $N_0\in {\mathbb N}$ such that for all $\lambda \in {\mathbb C}$ with $|\lambda |<\varepsilon$ every nontrivial solution $z(\lambda )$ of (S$_\lambda$) satisfies (25) with $N=N_0$.

We illustrate the Weyl–Titchmarsh theory of system (S$_\lambda$) with analytic dependence on $\lambda$ by the following interesting example.

Example 7

In this example we show that the discrete symplectic system

$$\begin{aligned} z_{k+1}(\lambda )=\exp (\lambda \!{\fancyscript{J}})\,z_k(\lambda ). \end{aligned}$$

(32)

is in the limit point case for every $\lambda \in {\mathbb C}\setminus {\mathbb R}$. Moreover, we calculate the unique $2n\times n$ solution (up to an invertible multiple) of (32) whose columns lie in $\ell _{\varPsi (\lambda )}^2$ and thus form a basis of ${\mathcal N}(\lambda )$. System (32) is an exponential symplectic system from Example 6, where $\varepsilon =\infty$, ${\mathbb S}_k(\lambda ):=\exp (\lambda \!{\fancyscript{J}})$ is given in (22) with $R_k:={\fancyscript{J}}$. This matrix satisfies the conditions $R_k^*{\fancyscript{J}}+{\fancyscript{J}}R_k=0$ in Example 6, so that by (22) we have ${\mathbb S}_k(\lambda )=\exp (\lambda \!{\fancyscript{J}})=(\cos \lambda )\,I+(\sin \lambda ){\fancyscript{J}}$. Note that this matrix does not depend on $k$.

For simplicity we perform the calculations below in the scalar case, i.e., for $n=1$. The general case follows with the same arguments upon multiplication by the $n\times n$ or $2n\times 2n$ identity matrices at appropriate places. The fundamental matrix $\varPhi _k(\lambda )$ of (32) with $\varPhi _0(\lambda )=I$ is given by

$$\begin{aligned} \varPhi _k(\lambda )=\exp (k\lambda \!{\fancyscript{J}})=(\cos k\lambda )\,I+(\sin k\lambda ){\fancyscript{J}}=\left( \begin{matrix} \cos k\lambda &{} \ \sin k\lambda \\ -\sin k\lambda &{} \ \cos k\lambda \end{matrix}\right) \end{aligned}$$

for every $k\in [0,\infty )_{\scriptscriptstyle {\mathbb Z}}$. Since $\varPhi _0(\lambda )=I$, we take $\alpha :=(1,\ 0)$, so that $\alpha {\fancyscript{J}}\alpha ^*=0$ and $\alpha \alpha ^*=1$ are satisfied. It follows that the natural conjoined basis of (32) is determined by the second column of $\varPhi (\lambda )$, i.e., $\widetilde{Z}_k(\lambda )=((\cos k\lambda )^*,\ (\sin k\lambda )^*)^*$. Since the powers of ${\fancyscript{J}}$ repeat in a cycle of length four, the weight matrix $\varPsi _k(\lambda )=\varOmega (\bar{\lambda },\lambda )$ is given in Example 6 as (we substitute $x:=\text {im}(\lambda )$)

$$\begin{aligned} \varPsi _k(\lambda )&= \frac{1}{2x} \sum _{j=0}^\infty \frac{(2x)^{2j+1}}{(2j+1)!}\,\,I + \frac{1}{2x} \sum _{j=1}^\infty \frac{(2x)^{2j}}{(2j)!}\,\,\,i{\fancyscript{J}}= \frac{\sinh \,2x}{2x}\,\,I+\frac{\cosh \,2x-1}{2x}\,\,i{\fancyscript{J}}\\&= \frac{\sinh \,x}{x}\,\big [ (\cosh \,x)\,I+(\sinh \,x)\,i{\fancyscript{J}}\big ] = \frac{\sinh \,x}{x}\,\left( \begin{matrix} \cosh x &{} \ i\sinh \,x \\ -i\sinh x &{} \ \cosh \,x \end{matrix}\right) >0, \end{aligned}$$

where we used the formulas for hyperbolic functions $\sinh \,2x=2\sinh \,x\,\cosh \,x$, $\cosh \,2x=2\cosh ^2x-1$, and the identity $\cosh ^2x-\sinh ^2x=1$. By the definition of ${\fancyscript{H}}_k(\lambda )$ and ${\fancyscript{G}}_k(\lambda )$ in Theorem 2,

$$\begin{aligned} {\fancyscript{H}}_k(\lambda )&= i\,\delta (\lambda )\,(\sin k\bar{\lambda }\,\cos k\lambda -\cos k\bar{\lambda }\,\sin k\lambda )=\sinh \,(2k\,|\text {im}(\lambda )|), \\ {\fancyscript{G}}_k(\lambda )&= -i\,\delta (\lambda )\,(\sin k\bar{\lambda }\,\sin k\lambda +\cos k\bar{\lambda }\,\cos k\lambda )=-i\,\delta (\lambda )\,\cosh \,(2k\,\text {im}(\lambda )), \end{aligned}$$

where we used the identities $\cosh \,x=\cos \,ix$ and $i\sinh \,x=\sin \,ix$ relating the hyperbolic and trigonometric functions. The same value for ${\fancyscript{H}}_k(\lambda )$ is of course obtained from formula (29) after some calculations. Therefore, Hypothesis 2 is satisfied with $N_0=1$, and by (28)

$$\begin{aligned} P_k(\lambda )=i\,\coth \,(2k\,\text {im}(\lambda )), \qquad R_k(\lambda )=1/\sqrt{\sinh \,(2k\,|\text {im}(\lambda )|)}. \end{aligned}$$

The center and radius of the limiting disk $D_+(\lambda )$ are then

$$\begin{aligned} P_{\!+}(\lambda )=\lim _{k\rightarrow \infty }P_k(\lambda )=i\,\delta (\lambda ), \qquad R_+(\lambda )=\lim _{k\rightarrow \infty }R_k(\lambda )=0, \end{aligned}$$

so that system (32) is in the limit point case for every $\lambda \in {\mathbb C}\setminus {\mathbb R}$. From Corollary 2 and Theorem 3 we obtain that $\dim {\mathcal N}(\lambda )=1$, and the space ${\mathcal N}(\lambda )$ of square integrable solutions of system (32) is generated by the Weyl solution

$$\begin{aligned} \chi _k(\lambda ,P_{\!+}(\lambda ))&= \varPhi _k(\lambda )\,\left( \begin{matrix} I \\ P_{\!+}(\lambda ) \end{matrix}\right) =\left( \begin{matrix} \cos \,k\lambda +i\,\delta (\lambda )\,\sin \,k\lambda \\ -\sin \,k\lambda +i\,\delta (\lambda )\,\cos \,k\lambda \end{matrix}\right) \\&= \left( \begin{matrix} 1 \\ i\,\delta (\lambda ) \end{matrix}\right) \,e^{\,i\,\delta (\lambda )\,k\lambda }, \end{aligned}$$

for which (we again substitute $x:=\text {im}(\lambda )$)

$$\begin{aligned} \big \Vert \,\chi (\lambda ,P_{\!+}(\lambda ))\,\big \Vert _{\varPsi (\lambda )}^2&= \sum _{k=0}^\infty \chi _k^*(\lambda ,P_{\!+}(\lambda ))\,\varPsi _k(\lambda )\,\chi _k(\lambda ,P_{\!+}(\lambda )) \\&= \frac{2\sinh \,x}{x}\times [\cosh \,x-\delta (\lambda )\,\sinh \,x] \times \sum _{k=0}^\infty e^{-2\,|x|k} \\&= \frac{2\sinh \,x}{x}\times [\cosh \,x-\delta (\lambda )\,\sinh \,x] \times \frac{1}{1-e^{-2\,|x|}}=\frac{1}{|\,x\,|}. \end{aligned}$$

This shows that $\big \Vert \,\chi (\lambda ,P_{\!+}(\lambda ))\,\big \Vert _{\varPsi (\lambda )}=1/\sqrt{|\text {im}(\lambda )|}<\infty$, and so indeed we have $\chi (\lambda ,P_{\!+}(\lambda ))\in \ell _{\varPsi (\lambda )}^2$ for every $\lambda \in {\mathbb C}\setminus {\mathbb R}$. On the other hand, we also have

$$\begin{aligned} \big \Vert \,\widetilde{Z}(\lambda )\,\big \Vert _{\varPsi (\lambda )}^2&= \sum _{k=0}^\infty \widetilde{Z}_k^*(\lambda )\,\varPsi _k(\lambda )\,\widetilde{Z}_k(\lambda ) \overset{(29)}{=} \frac{1}{2\,|\text {im}(\lambda )|} \,\lim _{k\rightarrow \infty }{\fancyscript{H}}_k(\lambda ) \\&=\frac{1}{2\,|\text {im}(\lambda )|} \,\lim _{k\rightarrow \infty }\sinh (2k\,|\text {im}(\lambda )|)=\infty , \end{aligned}$$

so that $\tilde{Z}(\lambda )\not \in \ell _{\varPsi (\lambda )}^2$. Thus, again we get that $\dim {\mathcal N}(\lambda )=1$. Similarly, in arbitrary dimension $n$ we get that the $n$ columns of the Weyl solution $\chi (\lambda ,P_{\!+}(\lambda ))$ are linearly independent and they belong to $\ell _{\varPsi (\lambda )}^2$, while the $n$ columns of the natural conjoined basis $\widetilde{Z}(\lambda )$ are linearly independent and they do not belong to $\ell _{\varPsi (\lambda )}^2$. Hence, $\dim {\mathcal N}(\lambda )=n$ and system (32) is in the limit point case for all $\lambda \in {\mathbb C}\setminus {\mathbb R}$.

Finally, as a consequence of (14) we obtain the ${\fancyscript{J}}\!$-monotonicity of the fundamental matrix of (S$_\lambda$). We recall the terminology from [12, p. 7] saying that a matrix $M\in {\mathbb C}^{2n\times 2n}$ is ${\fancyscript{J}}\!$-nondecreasing if $i\,M^*\!\!\!{\fancyscript{J}}M\ge i\!{\fancyscript{J}}$, and it is ${\fancyscript{J}}\!$-nonincreasing if $i\,M^*\!\!\!{\fancyscript{J}}M\le i\!{\fancyscript{J}}$. Similarly we define the corresponding notions of a ${\fancyscript{J}}\!$-increasing and ${\fancyscript{J}}\!$-decreasing matrix. These concepts are used in [12] to study the stability zones for continuous time periodic linear Hamiltonian systems. In a similar way, such stability zones are studied in [13, 14] for discrete linear Hamiltonian systems (6) and in [7] for discrete symplectic systems (S$_\lambda$) with ${\fancyscript{S}}_k^{[0]}=I$.

Corollary 3

Fix $\lambda \in {\mathbb C}$ with $|\lambda |<\varepsilon$ and assume (23). Let $\varPhi (\lambda )$ be a fundamental matrix of system $(S_\lambda )$ such that $\varPhi _0(\lambda )$ is complex symplectic, i.e., $\varPhi _0^*(\lambda ){\fancyscript{J}}\,\varPhi _0(\lambda )={\fancyscript{J}}$. Then for every $k\in [0,\infty )_{\scriptscriptstyle {\mathbb Z}}$ the matrix $\varPhi _k(\lambda )$ is ${\fancyscript{J}}\!$-nondecreasing or ${\fancyscript{J}}\!$-nonincreasing depending on whether $\text {im}(\lambda )>0$ or $\text {im}(\lambda )<0$. Moreover, under Hypothesis 4 the ${\fancyscript{J}}\!$-monotonicity of $\varPhi _k(\lambda )$ is strict for $k\ge N_0+1$.

Proof

By applying (14) to the fundamental matrix $\varPhi _k(\lambda )$ we get

$$\begin{aligned} i\,\varPhi _k^*(\lambda ){\fancyscript{J}}\,\varPhi _k(\lambda )-i\!{\fancyscript{J}}=2\,\text {im}(\lambda ) \sum _{j=0}^{k-1} \varPhi _j^*(\lambda )\,\varPsi _j(\lambda )\,\varPhi _j(\lambda ). \end{aligned}$$

(33)

By (23), the sum in (33) is nonnegative, so that $\varPhi _k(\lambda )$ is ${\fancyscript{J}}\!$-nondecreasing when $\text {im}(\lambda )>0$, and it is ${\fancyscript{J}}\!$-nonincreasing when $\text {im}(\lambda )<0$. Moreover, under Hypothesis 4 the sum in (33) is positive definite for $k\ge N_0+1$, so that $\varPhi _k(\lambda )$ is ${\fancyscript{J}}\!$-increasing when $\text {im}(\lambda )>0$, and it is ${\fancyscript{J}}\!$-decreasing when $\text {im}(\lambda )<0$. $\square$