Realtime Simulation-in-the-Loop Control for Agile Ground Vehicles

Abstract

In this paper we present a system for real-time control of agile ground vehicles operating in rough 3D terrain replete with bumps, berms, loop-the-loops, skidding, banked-turns and large jumps. The proposed approach fuses local-planning and feedback trajectory-tracking in a unified, simulation-based framework that operates in real-time. Experimentally we find that fast physical simulation-in-the-loop enables impressive control over difficult 3D terrain. The success of the proposed method can be attributed to the fact that it takes advantage of the full expressiveness of the inherently non-linear, terrain-dependent, highly dynamic systems involved. Performance is experimentally validated in a motion capture lab on a high-speed non-holonomic vehicle navigating a 3D map provided by an offline perception system.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

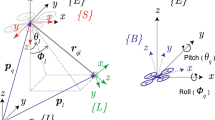
We presentKeivan, Nima Sibley, Gabe a unified approach to both planning and control that leverages accurate physical simulation to perform both tasks jointly and in real-time. Physical simulation is beneficial because it can model not only complex vehicle dynamics, but also vehicle-terrain interaction. For instance, simulation can include complex 3D surface models, varying friction models, realistic contact models – indeed anything deemed necessary to more faithfully predict reality. Our approach is based on the insight that if simulation is sufficiently fast and accurate, it can be used to predict system state farther into the future. This allows us to servo on errors between desired future performance and simulated future performance. One may think of this as closing the loop using an accurate, long-range process model (Fig. 1).

Fig. 1.

Long jump and loop-the-loop experiment. A feasible trajectory is first solved through waypoints using a boundary value solver on a 3D scanned terrain model (right). The trajectory is then tracked and executed by the real-time feedback controller (left).

For both feasible trajectory-generation and feedback-control we employ an optimization-based boundary-value solver. The solver takes as input a starting configuration, a terrain model, and a goal. The goal can be either a waypoint or a desired trajectory. The aim is to find a command sequence, $c(\mathbf {p})$, that will drive, in simulation and in reality, the vehicle from the start to the goal, over the intervening terrain. The command sequence itself is a low-degree-of-freedom generator parameterized by $\mathbf {p}$, such as a polynomial, spline, etc. The solver is used to find the parameters that yield a desired command sequence. We find that this approach allows accurate real-time planning and control in full 3D environments, with complex vehicle dynamics and terrain interaction, including slipping, jumping and driving upside-down.

The use of motion primitives [17] and stochastic search methods such as RRT and RRT* [12, 13] and probabilistic methods such as PRMs [2, 4] and POMDPs have resulted in algorithms that successfully navigate complex obstacle fields even in higher order configuration space. A major advantage of these methods is that they can employ nonlinear dynamics models thereby enabling physically accurate planning in complex environments without approximation or linearization. However, this advantage comes at a performance price as stochastic methods invariably sample infeasible trajectories. Conversely, optimization based methods [10] employ effective initial guesses and numerical or analytical optimization techniques to rapidly converge on optimal paths. However due to the reliance on the accuracy of the initial guess, these methods are susceptible to failure or suboptimal performance depending on the quality of this guess. The quality, optimality and methodology of the plans notwithstanding, their open loop performance in real robots is inevitably impaired by the existence of imperfections or extraneous inputs that may not have been included in the dynamics model. Therefore for real-life applications, some form of closed loop control is desired.

In contrast to simulation-in-the-loop or model-predictive control, traditional feedback systems use static and/or dynamic feedback of the state to determine the controls for the next time steps. To aid stability analysis, traditional approaches also typically model the system with simplified, analytically treatable, vehicle models. Recent developments have resulted in methods allowing the calculation of Lyapunov functions for nonlinear systems [11] and defining graphs of Lyapunov-stable regions around states as in the case of LQR-Trees [20]. These methods rely on the linearization of the state transfer function in order to obtain analytically tractable control policies, and the automatic recovery of stability regions. Linearized time-varying systems often entail substantial gain-tuning, which is known to be an arduous and time consuming process, especially due to their non-intuitive nature [6]. In contrast, with simulation-in-the-loop based approaches, we find that it is possible to automatically learn physically meaningful parameters that lead directly to improved system performance – that is, learning to make simulation match reality.

Recent developments in model predictive control (MPC) [9] and learning-based model predictive control (LBMPC) [3] both implement model-based control schemes and infer the underlying model parameters. Likewise, our system relies on accurate models of the physical parameters that define the system. In our case, these models are learned beforehand using online non-linear regression [15]. We find that expressive models learned via online regression are advantageous as they allow accurate simulation, farther into the future, over difficult and challenging terrain.

2 Methodology

The proposed approach relies on simulating the effect of applying a sequence of linear and angular velocity commands which are defined by a low-degree of freedom control-function, $c\left( \mathbf {p}\right)$. Feasible trajectories are generated by solving a boundary value problem for the parameterized control function that links two waypoints – i.e., the command sequence that will move the car between these two waypoints. To control the vehicle we repeatedly minimize the difference between a forward-simulated vehicle and the desired trajectory. This approach leverages accurate simulation of the vehicle and terrain dynamics at the expense of a model which is not analytically differentiable. Therefore, in order to generate a control law to optimize either the boundary or the trajectory cost, we will rely on finite-difference estimations of the gradient of the vehicle model, in a least-squares optimization setting.

Fig. 2.

(a) Planning to a waypoint: $e_{b}$ is the boundary residual between a trajectory and the waypoint $\mathbf {x}_{f}$. (b) Trajectory tracking: $e_{t}$ is the trajectory residual calculated between the simulation $\varPsi$ and the reference trajectory over a finite horizon $t_{l}$. Control delay compensation is shown where the delay is $t_{d}$ (For more refer to Sect. 2.3).

2.1 Optimization

The boundary error as shown in Fig. 2a, is used when planning feasible trajectories between waypoints and is formulated as:

$$ e_{b}=\begin{Vmatrix}\mathbf {x}_{lf}\boxminus \varPsi _{l}\left( \mathbf {c\left( \mathbf {p}\right) },\mathbf {x}_{i},t_{f}\right) \end{Vmatrix}_{2} $$

We define the function $\varPsi _{l}\left( \mathbf {c},\mathbf {x}_{i},t_{f}\right)$ as representing the numeric simulation, where $c\left( \mathbf {p}\right)$ is the control function defined by parameters $\mathbf {p}$, $\mathbf {x}_{i}$ is the starting state, and $t_{f}$ is the time instant for which we desire the state of the vehicle. $\varPsi _{l}$ returns the state $\phi _{lt_{f}}=\begin{bmatrix}\mathbf {T}_{lv}~\mathbf {v}\end{bmatrix}$ where $\mathbf {v}\in \mathbb {R}^{3}$ is the velocity vector in local coordinates and $\mathbf {T}_{lv}\in \mathbb {R}^{4\times 4}$ is the transformation matrix from vehicle to the local coordinates. The local coordinates are defined by the average of the initial and final waypoint terrain normals. $\mathbf {x}_{f}=\begin{bmatrix}\mathbf {T}_{lv}~\mathbf {v}\end{bmatrix}$ is the desired state at the end of the trajectory in local coordinates, set by a waypoint. The optimization minimizes the weighted square norm of the error vector by varying the parameter vector $\mathbf {p}$, and consequently the control function that drives the vehicle forward in time. The operator $\boxminus$ calculates the velocity and $se\left( 3\right)$ pose error between two vehicle states.

The trajectory cost is shown in Fig. 2b and is used to track a reference trajectory. The error vector is taken between samples on the simulated trajectory (defined by $\varPsi _{l})$ and a finite horizon over the reference trajectory, $\mathcal {X}=\left\{ \mathbf {x}_{0}...\mathbf {x}_{n}\right\}$:

$$ e_{t}=\begin{Vmatrix}\sum \nolimits _{j=0}^{n}w_{j}\mathbf {x}_{lj}\boxminus \varPsi _{l}\left( \mathbf {c},\mathbf {x}_{i},t_{j}\right) +t_{f}\end{Vmatrix}_{2} $$

Where $t_{l}$ is the duration of the finite horizon and is included in the error to favor time optimal solutions, that is the optimization will search for the shortest path that converges to the trajectory being tracked. This error is a weighted average between the reference trajectory set $\mathcal {X}$ and the simulated trajectory given by $\varPsi$. The weighting imposed by the set $\mathcal {W=}\left\{ w_{0}...w_{n}\right\} , \sum \mathcal {W}=1$ is required to ensure more importance is placed at the end of the trajectory rather than the beginning, since due to the non-holonomic constraints, the initial cost cannot be minimized. In our implementation, a simple linear weighting scheme was used from the beginning to the end of the trajectory.

The optimization attempts to minimize the error vector by the weighted least squares optimization $\left( J^{T}WJ\right) \mathbf {p}=J^{T}W\mathbf {r}$ where $W$ is a diagonal matrix of weights for each individual row of the error vector and $\mathbf {r}$ is the error vector. The weight matrix is required as we are optimizing cartesian poses, angles and velocities in the same vector, and a rational weighting scheme based on the importance of the relative units is required for efficient optimization. These weights can also reflect the fact that certain degrees of freedom are more important to minimize than others (i.e. in-plane yaw, vs. pitch and roll).

The Jacobian is defined as $J=\partial \mathbf {e}/\partial \mathbf {p}$. Due to the inclusion of the simulation function $\varPsi$ in the error vector, the Jacobian cannot be evaluated analytically and must be obtained through finite differences. In order to obtain real-time performance, we calculate the Jacobian via a multi-threaded simulation scheme, whereby each column of the Jacobian (which corresponds to an evaluation of the simulation function $\varPsi$) is undertaken in a separate thread. Due to the extreme nonlinearity caused by the terrain, a parallelized trust region damping scheme is used.

In the trajectory cost function, we have used the set $\mathcal {X}$ to represent the reference trajectory. The duration of this set, denoted as $t_{l}$, represents the finite horizon for which we optimize when tracking a feasible trajectory. As time itself is a cost in the optimization and $t_{l}$ is allowed to change (due to the change in $\mathbf {x}_{f}$), the solutions will favor time-optimal trajectories, if they can be planned without increasing the trajectory cost. The choice of initial $t_{l}$ however, has an impact on convergence. If $t_{l}$ is too small, there will be insufficient time and space for the vehicle to be able to close the gap on the trajectory. In the pathological case, this can lead to a local minimum whereby $t_{l}$ cannot be incrementally increased by the optimization, and convergence will fail. Conversely, if $t_{l}$ is set too large, there may be insufficient expressivity in the command sequence to solve solutions that adhere to the reference trajectory. This problem has been studied in the literature and heuristics-based methods exist to find the optimal finite horizon [8]. In our solution, we have experimentally determined $t_{l}=0.4s$ as a suitable horizon duration to initialize the solution. The optimization will then attempt to reduce (and may potentially increase) the finite horizon time.

2.2 Control Parametrization

Our vehicle model is controlled via steering and acceleration commands. As stated previously, we are interested in a low degree of freedom control function, $\mathbf {c}=C\left( \mathbf {p}\right)$ which generates an expressive command sequence.

Here $\mathbf {p}$ is a vector which parametrizes the command sequence, which is then discretized for simulation. In our previous work [15] we had employed the use of cubic curvature polynomials [13] to parametrize steering. However, cubic curvature polynomials require expensive optimizations in order to generate command sequences given the boundary conditions. This necessitates the use of pre-calculated lookup tables and an additional optimization in order to produce an initial guess for real-time planning. Therefore, in the proposed methodology, we have employed the use of 2D bezier curves for steering, and a constant acceleration parameter to control velocity. Bezier curves have been used extensively in path planning for autonomous vehicles [5, 14] due to the ease with which one can extract the path curvature given the control points and final pose. The desired quality for the chosen parameterization (cubic-curvature, bezier curves, etc.) is that (a) the resulting command sequence is “expressive” – i.e., it can actually cause the vehicle to move in a desired fashion, and (b) that it is parameterized by few degrees of freedom – to facilitate fast finite differences optimization. In Appendix A we detail how we have used bezier curves to this effect.

2.3 Feedfoward

An advantage of the simulation-in-the-loop approach is that it provides easy access to physically meaningful parameters like terrain surface and vehicle configuration. These can be used for feedforward compensation to help the optimization avoid local minima that litter the cost landscape. We employed the use of three feedforward terms in our implementation: gravity, wheel friction and control-delay.

Gravity feedforward is useful to mitigate the effects of steep and undulating terrain. A simple gravity feedforward model was implemented as

$$ a_{g}=\frac{1}{m}\sum _{i=1}^{4}\mathbf {n_{i}}F_{i}.\mathbf {v}_{x} $$

where $\mathbf {n_{i}}$ is the surface normal at the point of contact of wheel $i$, $F_{i}$ is the normal force at contact for wheel $i$, $\mathbf {v}_{x}$ is the axis orientation vector for the vehicle chassis and $m$ is the mass of the vehicle.

Friction feedforward is used to compensate for wheel resistance. The acceleration compensation for friction is calculated as

$$ a_{f}=\frac{1}{m}\sum _{i=1}^{4}\mu F_{i} $$

where $\mu$ is the friction coefficient and $F_{i}$ is the normal force of wheel $i$. Once $a_{g}$ and $a_{f}$ are calculated for the current time step, they are fed forward into the acceleration parameter $a$ of the next time step. The final acceleration used in the simulation is given by $a_{totoal}=a+a_{g}+a_{f}$ where $a$ is the parameter used in the optimization. This type of terrain-aware feed-forward compensation (which uses terms such as $F_{i}$ and $\mathbf {n}_{i}$) is made possible by a full physical simulation of the vehicle and terrain dynamics.

Control delay feedforward is used to compensate for both delayed state estimation and delays in the control pipeline. Compensating for these phenomenon increases stability. In order to compensate for control delay, we make use of a control queue which serves to store all commands that are sent to the vehicle. The current state of the vehicle $\mathbf {x}_{i}^{-}$ can then be transformed to the compensated state $\mathbf {x}_{i}$ as follows

$$ \mathbf {x}_{i}=\varPsi \left( \mathbf {c}_{q}\left( t_{i}-t_{d}:t_{i}\right) ,\mathbf {x}_{i}^{-},t_{d}\right) $$

Where $\varPsi$ is the simulation function as defined in Sect. 2.1. To compensate for control delay, we simulate the vehicle forward by the control delay duration $t_{d}$, using the control queue $\mathbf {c}_{q}\left( t_{i}-t_{d}:t_{i}\right)$, which contains the commands sent to the car from time $t_{i}-t_{d}$ up to the current time $t\mathbf {_{i}}$. The augmented state $\mathbf {x}_{i}$ is then used to generate the next set of commands. In this fashion, we are predicting the pose of the vehicle at the time after which the current commands will begin executing ($t_{i}+t_{d})$, using commands already in the execution pipeline ($\mathbf {c}_{q})$.

2.4 Vehicle Modeling

Our experiments use a modified racing remote-control vehicle with rear-wheel electric propulsion, rack and pinion steering and spring/damper suspension. The parameters described in the models below are learnt automatically using an online nonlinear regression [15]. In order to accurately simulate the dynamics of our vehicle, and fully consider the uneven terrain, we use a double track vehicle model with suspension dynamics, as detailed in [7]. The chassis is modeled as a rigid body with forces and moments imparted due to wheel contacts and motor torques. The wheel forces are modeled using spring/damper dynamics as $F_{w}=kx+c\dot{x}$ where $c$ is the damping coefficient, $k$ is the spring stiffness and $x$ is the deviation from the spring rest state. As $F_{w}$ acts along the suspension axis, moments are induced about the center of gravity of the vehicle. To obtain $x$ and $\dot{x}$, we leverage an off the shelf physics simulation engine [1] along with a scanned 3D model of the terrain, represented as a dense triangle mesh, to calculate the wheel position and velocities.

When accelerating or braking, the electric motor applies a torque to the rear wheels which is proportional to the current passing through the motor winding. This current is itself dependent on the voltage applied to the motor as well as the current rotor speed. The motor controller hardware employed applies a voltage across the rotor terminals for a given input signal. Therefore, the torque applied to the rear wheels is modeled as $T=V.C_{T_{stall}}-\omega .C_{\omega }$ where $V$ is the voltage applied to the motor, $C_{T_{stall}}$ is a constant relating the stall torque of the motor to the applied voltage, $\omega$ is the motor speed and $C_{\omega }$ defines the slope with which the torque diminishes as the motor gains speed. The torque resulting from this equation is then applied to the rear wheel axles. As expected, this rear-wheel torque also induces an opposing torque about the CG, resulting in “wheelies” if the applied torque is too high.

To enforce non-holonomic constraints, sideways motion from the wheels must be eliminated. We therefore enforce a constraint on the relative velocities of the wheels and the terrain, which applies a force to enforce the non-holonomic constraints of the vehicle, and prevent lateral slip. However in practice, slip conditions can cause violations of non-holonomic constraints. To model these phenomena, we use the Magic Tire Model [16] which defines the maximum lateral force applicable as a function of the normal force $F_{w}$, the slip angle and 4 coefficients.

Fig. 3.

All experiments are performed on the figure-8 trajectory in Fig. 4. The RMSE error is taken as the average trajectory residual taken over two consecutive laps of the figure-8 consisting of a weighted combination of translation, heading and velocity error. (a) Trajectory error with varying velocity setpoints, showing the effect of tire slip model at higher velocities. (b) Effects of planning frequency on the error. (c) Effects of incorrect control delay feedforward on RMSE. (d) The effects of gravity feedforward. Large errors are apparent for both solutions at the start of the trajectory due to initial convergence, and on the ramp when gravity feedforward has been turned off.

3 Results

The local planner and trajectory tracker were experimentally tested on a wide array of challenging environments including jumps, loop-the-loops and quarter pipes. The experiments were carried out on a small high-speed autonomous robot in a motion capture environment. In order to build an accurate model of the vehicle, a machine learning based approach to model identification was used in conjunction with the accurate simulation model in order to infer the difficult to measure parameters such as tire model coefficients, friction coefficients and electric motor torque parameters. For state estimation, global pose estimates from a Vicon motion capture system operating at 120 Hz were fused with IMU measurements at 400 Hz in a sliding window filter in order to obtain accurate pose and velocity estimates. The local planning and trajectory tracking were performed in real-time on an Intel i7 laptop with 4 hyper-threaded cores. Re-planning rates with the specified hardware was between 40 and 60 Hz depending on the terrain.

Fig. 4.

Experimental figure 8 over flat terrain and quarter pipe, showing boundary value solution trajectory

For results on solving and tracking the aforementioned challenging environments, please refer to the video submission. In order to qualitatively explore the effects of parameters on the performance of the real-time trajectory tracker, a number of experiments were performed over the figure-8 trajectory shown in Fig. 4. A feasible trajectory was solved between a series of manually placed waypoints, and the controller was subsequently used to track the trajectory with the experimental vehicle.

In Fig. 3a, the effects of the tire model described in Sect. 2.4 on the tracking error are shown. At higher speeds, there is significant slip between the plastic wheels and the carpet floor. Furthermore, the acceleration applied reduces the normal forces on the front wheels, increasing slip. The inclusion of the tire model allows the optimization to fold in these effects and correct the steering. Figure 3b shows the effect of planning frequency on the error. It is apparent that stable performance is observed down to re-planning rates of 5 Hz, however this is at the expensive of higher tracking error. Figure 3c demonstrates the effect of control delay feedforward on tracking accuracy. The control delay of the system was determined via model identification to be 0.11s. The negative effect on tracking accuracy as the control delay parameter deviates from the true value is due to the inability to properly compensate the control inputs for delays. Figure 3d demonstrates the effect of gravity feedforward on tracking accuracy. The plot demonstrates two separate runs with sections taking place on the ramp. It can be seen that when gravity feedforward is not used, there is a large increase in tracking error on the ramp. Due to the increased acceleration required to maintain velocity on the incline, the lack of gravity feedforward leads to bad initialization and convergence problems.

4 Discussion

Our approach to local planning and control is different in that it does not make use of an analytically differentiable model to provide a feedback command-sequence. Rather, we solve an optimization problem involving the full simulation. This approach works not only for obtaining feasible paths given the boundary conditions (i.e. local planning), but also in the case of trajectory tracking. In the latter case, continuous re-planning based on an accurate vehicle and terrain model provides stability and accurate tracking even without an explicit feedback law. This tracking stability is observed down to very low re-planning frequencies.

However, that is not to say that continuous re-planning does not constitute feedback control. On the contrary, perturbations are folded into subsequent plans as they are sensed by the state estimation. However, the level of detail folded into the simulation ensures that unexpected perturbations are rare, as all extraneous effects of the terrain and vehicle model are already considered.

Indeed, traditional guarantees about stability, given a perturbation are no longer possible due to the lack of an analytical model, however our results show that convergence is fast and reliable for a wide range of terrain and vehicle conditions including large jumps, loop-the-loops, quarter pipes, bumps and berms. These situations all pose challenges to traditional control schemes including linear and nonlinear MPC, due to the non-analytical terrain term. Even though a feedback controller designed with an analytical model would yield guarantees of stability, if the terrain were to be sufficiently perturbed, divergence of control would be inevitable. However, with simulation-in-the-loop the knowledge obtained from simulating the future would provide powerful predictions of the failure modes, and would also facilitate triggering of abort maneuvers.

Furthermore, the use of an accurate simulation model replaces gains in traditional control schemes with physically meaningful model parameters. Whereas tuning LQR, PID and other feedback control schemes involves the calculation and setting of abstract gains relating to error and control amplitudes, the only parameters that need to be tuned in the proposed methodology are the model parameters, which have physical meanings.

5 Conclusions

We have presented a unified approach to planning and control based on fast physical simulation-in-the-loop. To find feasible trajectories between waypoints, we solve a boundary-value-problem that depends on a low degree-of-freedom but highly expressive control function that drives a simulated vehicle forward in time. To track the reference trajectory, a trajectory-cost is repeatedly minimized using the same optimization. Similar to receding horizon or model predictive control, constant re-planning provides feedback to mitigate deviation from the desired trajectory, however we avoid simplifying the underlying model. Simulation-in-the-loop can include any phenomenon worth modeling, such as 3D terrain, complex tire models, friction, slipping and jumping. Simulation also provides a means to fold in perturbations before they happen, and to preemptively adjust the control sequence accordingly. The results show that this methodology is able to control a high-speed autonomous vehicle through challenging terrain such as large jumps, skids, steep banks and loop-the-loops.

Appendix A

We define the bezier curve $\mathbf {P}(s),\, s\in [0,1]$ as $\mathbf {P}(s)=\sum _{i=0}^{n}B_{i}^{n}(s)\mathbf {P}_{i}$ where $\mathbf {P}_{i}\in \mathbb {R}^{2}$ is the $i$th control point. We have initially parametrized the bezier curve with the variable $s$ rather than the traditional $t$, as we desire the final curve to indeed be parametrized by time, which we represent as $t$. The relationship between $s$ and $t$ depends on the evolution of the vehicle velocity. As we have proposed a constant acceleration parameter $a$, we can parametrize the bezier curve w.r.t time as $\mathbf {P}(s(t))$ where $s(t)=t/t_{total}=t/(2d/(v_{i}+v_{f})$, $d$ is the distance along the bezier curve, and $v_{i}$ and $v_{f}$ are the initial and final velocities respectively. The curvature of the bezier curve at any value of $t$ defined as $\kappa \left( t\right)$ can then be calculated using the analytical first and second derivatives of the curve in $x$ and $y$ [5]. The steering angle $\theta _{s}$ can then be obtained from $\kappa$, based on a simplified symmetric bicycle steering model with zero slip [18] $\theta _{s}=tan^{-1}\left( l\kappa \right)$ where $l$ is the wheel base.

The order of the bezier curve is chosen such that sufficient expressivity exists to satisfy boundary conditions. For trajectory tracking, a major requirement is $C^{2}$ continuity. This is needed to ensure maximum feasibility of steering commands, as the actuators cannot be discontinuously controlled, when switching from one command sequence to the next. To independently constrain the curvature on the boundary of a bezier curve, three control points are required [19], therefore we use fifth degree bezier curves $\left( n=6\right)$ in order to independently satisfy the constraint at both ends of the curve.

Given the bezier curve control points, the parameter vector $\mathbf {p^{\prime }}$ can be expressed as $\mathbf {p^{\prime }}=\begin{bmatrix}\mathbf {P}_{0},&...&,\mathbf {P}_{6}&a\end{bmatrix}^{T}$ where $\mathbf {P}_{0},...,\mathbf {P}_{6}\in \mathbb {R}^{2}$ are the control points. $\mathbf {p^{\prime }}$ is defined by 13 parameters: 2 for each control point and 1 for acceleration. There are three gauge freedoms associated with transforms in $\mathbb {SE}2$, reducing the actual parameter space to 10. However, properties of the bezier curve can be exploited to further reduce the number of parameters. Given the initial projected 2D pose ($\mathbf {x}_{i_{proj}}=\begin{bmatrix}x_{i}~y_{i}~\theta _{i}~\kappa _{i}\end{bmatrix},$ as described below), the position, heading and curvature of the vehicle can be constrained (the curvature is constrained by the current curvature $\kappa _{i}$). Consequently, the first three control points can be parametrized using only $h_{i}$ and $a_{i}$ (refer to [19]). Fixing $x_{i}$, $y_{i}$ and $\theta _{i}$ also removes the gauge freedoms of the control points. At the other end of the bezier curve, $\mathbf {x}_{f_{proj}}=\begin{bmatrix}x_{f}~y_{f}~\theta _{f}~\kappa _{f}\end{bmatrix}$ is used to reduce the parameter space of the final 3 control points from 6 to 3, as the end curvature is also constrained by $k_{f}$ to enforce $C^{2}$ continuity. This leaves the parameters $h_{i}$, $a_{i}$, $h_{f}$ and $a_{f}$. To further reduce the parameter space, these values were set as follows: $h_{i}=a_{i}=h_{f}=a_{f}=\frac{1}{5}\begin{Vmatrix}\begin{bmatrix}x_{f}&y_{f}\end{bmatrix}-\begin{bmatrix}x_{i}&y_{i}\end{bmatrix}\end{Vmatrix}$ where the factor of $1/5$ times the distance between the start and end points was empirically determined to result in adequate control laws for a wide range of start and goal positions, headings and curvatures. Therefore, the initial parameter space $\mathbf {p}$ can be obtained from the reduced parameter space: $\mathbf {p^{\prime }}=\mathcal {B}(\mathbf {p,}\mathbf {x}_{i_{proj}},\kappa _{f})$ where $\mathbf {p}=\begin{bmatrix}x_{f}~y_{f}~\theta _{f}~a\end{bmatrix}^{T}$, and $\mathcal {B}$ is a function which maps the reduced parameter space to the full 5th degree bezier control points. Note that $\mathcal {B}\left( \right)$ requires the initial state $\mathbf {x_{i}}$ to constrain the first three control points, and the final curvature $\kappa _{f}$ to constrain the last 3 points according to $\mathbf {p}$. Therefore the command-sequence used in the optimization is defined as $\mathbf {c}=C\left( \mathbf {x}_{i},\mathcal {B}(\mathbf {p,}\mathbf {x}_{i_{proj}},\kappa _{f})\right)$.

The control law parametrization scheme detailed previously uses bezier curves in $\mathbb {R}^{2}$. While control commands generated from these curves would perfectly steer an ideal vehicle in $\mathbb {R}^{2}$, the same statement can not be made for a vehicle in $\mathbb {R}^{3}$ driving over rough terrain. For this reason, we are interested in initializing the steering command-sequence in a way which places us in the basin of attraction of the optimization that follows.

To initialize the bezier curve, we project the pose of the vehicle onto a plane in $\mathbb {R}^{2}$, the normal of which is calculated as the average of the terrain normals at the start and end of the trajectory. This serves to maximize the likelihood that following the curvature of the bezier curve will lead the vehicle to follow the shape of the curve. We define the projection as $\mathbf {x}_{proj}\in \mathbb {R}^{4}=\mathcal {P}(\mathbf {T}_{pw}\mathbf {x}_{w},\kappa )$. Where $x_{proj}$ is the state vector in projected $\mathbb {R}^{2}$ coordinates defined as $\begin{bmatrix}x~y~\theta ~\kappa \end{bmatrix}$, $\mathbf {T}_{pw}$ is the $\mathbb {R}^{4\times 4}$ transformation matrix from world coordinates to the projection plane coordinates (obtained from the terrain normals), and $\mathcal {P}$ is the projection function, which takes the $x$ and $y$ components, and projects the vehicle theta onto the plane. Once both $\mathbf {x}_{i_{proj}}$ and $\mathbf {x}_{f_{proj}}$ have been obtained, a bezier curve can be initialized using the aforementioned re-parametrization function $\mathcal {B}(\mathbf {p^{\prime }},\mathbf {x}_{i_{proj}},\kappa _\mathbf {f})$, which returns the initial bezier control points.