Keywords

1 Introduction

The application of mobile robots in industrial and commercial settings has become increasingly common in recent years. Mobile robots have the ability to move through the environment autonomously and therefore save time and effort when completing mundane or dangerous tasks. We have seen recent applications of UGVs in cooperation with unmanned aerial vehicles (UAV) conducting search and localization tasks [12], another application might be the use of UGVs in military services [14] or in rescue operations and disaster robotics as described by Jorge et al. [7]. Accomplishing these challenging tasks usually require more advanced algorithms which obtain data from various sources and the task of navigation is a more complicated one.

In general, autonomous navigation in an environment with some type of uncertainty (e.g., unknown obstacles, different weather conditions, terrain conditions, etc.) requires two different consecutive motion planning algorithms – global and local path planners. The point of a global path planner (GPP) is to find an approximate path through the environment which seems to be feasible on a large scale using more general data which can be offline or online map data. On the other hand, the local path planner uses sensors that provide data from immediate proximity. These sensors can be, for example, LIDAR, cameras, ultrasonic sensors, radars, IMUs or any other sensor used for typical SLAM algorithms. Many of the experimental vehicles already contain all of the above sensors (e.g. [4, 13]), which makes the task easier. The local planner then finds a path through the environment which not only avoids obstacles that do not have to be present on a global map but also can react to changes in the environment (e.g., moving obstacles).

In further sections, we propose a global path planning algorithm for an UGV which uses offline map data containing digital terrain and digital surface models of the environment. This data is usually well known and is fairly accurate to allow for good global path planning on a large scale. In this paper, we will use map data with a resolution of one meter and size ranging from one to two kilometers square. Size of the map data depends on the path planning goal as well as on the computational hardware and the time window in which the algorithm needs to find the path.

1.1 Review of the Literature

Designing a GPP for a UGV moving through a difficult terrain is a complex task involving selection and preparation of map data which will be used as an input to the path planner. This preparation might include initial traversability assessment and obstacle detection to already exclude some areas of the map which might not be searched by the path planning algorithm. The algorithm itself is mostly an enhanced version of standard algorithms which complies with nonholonomic constrains of the vehicle and further evaluates its stability in terrain and respects dynamics of the vehicle as well.

Map data can be obtained, for example, in the form of elevation maps combined with maps of roads, settlements, waterways, vegetation, and so on, or in the form of aerial scans of the ground for example from a UAV. Rybanský et al. describe the process of combining multiple maps to characterize the traversability in each location of the map [22]. The optimal path is then planned using traction coefficients of the vehicle and geometric coefficients. Another approach for classifying traversability using deceleration coefficients is presented in [10]. A very similar topic is covered in [1] where the traversability over microreliefs is determined by the geometric features of the vehicle. Situation where the map is obtained from a UAV working in collaboration with UGV and exploring the terrain ahead to plan the optimal path is described in [21]. Another application of map data in the form of the pointcloud obtained from UAV is in [3]. Where the traversibility of the map is classified only by geometrical features, for example, slope, elevation difference and roughness.

Many of the typical GPP algorithms use A* [5] or RRT algorithm [17] to find a path between two points resulting in a holonomic path which does not have to be suitable for a UGV especially if the vehicle in question is not a small one. Some of the typical nonholonomic planning algorithms are Hybrid A* [2, 19, 29], RRT* [11], algorithms using Reeds Shepp curves [8] or Dubins path [30]. A different approach is energy-optimal trajectory planning described in [28] or in [15] a length-optimal trajectory algorithm for an UAV is presented. These path planners ensure that the resulting path will be suitable for a vehicle with given kinematics and nonholonomic constrains. However, even this may not be sufficient for a vehicle moving through a challenging terrain where other factors come into play, like limitations of the vehicle powertrain, wheel slipping, losing contact with the ground, tipping over, sliding of the vehicle on a slippery terrain or getting stuck in mud or sand and so on.

Another step to make these nonholonomic path planners more suitable for planning a path through a non-planar terrain is to add some information about the terrain traversability. This information might be a simple one, for example, the limitation of the maximal slope angle as in [16] where Muñoz et al. present their approach based on A* algorithm to plan a path in digital terrain map (DTM). More sophisticated traversibility classification methods are used in [11] and [3]. In the first mentioned one, Krüsi et al. use RRT and RRT* planners in combination with traversibility classification based on the surface roughness and maximal roll and pitch angles. In the latter, Fedorenko et al. use only RRT and the same traversibility classification methods as in the previous work to plan a path in the pointcloud data obtained from a UAV. The Hybrid A* algorithm is used by Thoresen et al. [29] in combination with the fast marching grid heuristic to plan a path in already known traversibility map.

Path planners that are able to combine kinematic and dynamic constrains belong to the category of kinodynamic planners. These planners may either improve the previously mentioned nonholonomic path planners (PRM [9], RRT [18]) or come up with their own unique approach of path generation as in [27]. They also greatly differ in a complexity of the dynamic model and influences that it takes into account depending on the targeted application and computational power. Some researchers simplify the vehicle to the point mass [9, 25] therefore assume that all wheels are in permanent contact with the ground and that there is no slip between the wheel and the ground. Others take into consideration the whole 3D dynamics and six degrees of freedom motion of the vehicle [27]. Another difference is in the way how the surface is represented Shiller et al. in [25] represents the surface as a B patch where as Kobilarov et al. in [9] assumes that the surface is composed of angled planar sections. Some works take into account other influences such as different soil types and their interaction with the tires [26].

Based on these related works and our goal, which is to create a global path planner able to find a path in considerable large areas based on aerial laser scans of the terrain, we will extend the Hybrid A* algorithm by using a simplified dynamic model of the vehicle to asses the traversability of the terrain and to obtain a near time optimal path. This approach will secure that the resulting path meets kinematic and dynamic constrains and it is easily modifiable to account for various influences. This method might be also suitable for the enhancement of the current applications which already use Hybrid A* algorithm.

2 Implementation

This section describes the input conditions for our research, limits, theoretical basement and the final algorithm of the solution.

2.1 Terrain Map

To be able to perform the global path planning, map data is required. In this case, two types of map data were obtained – digital terrain model (DTM) and digital surface model (DSM), both in the triangular irregular network (TIN) format. DTM in the version called DMR 5G contains data specifying only the terrain profile without any structures, trees and obstacles. DSM in the version called DMP 1G contains a height profile including the latter. Difference between these two types of maps is depicted in the Fig. 1. DMR 5G and DMP 1G maps are published by Czech Office for Surveying, Mapping and Cadastre (ČÚZK).

Fig. 1.
figure 1

DTM vs. DSM map comparison

Full size image

These types of maps can be obtained from UAV drones, enforcing the idea of cooperation between UAV and UGV. The data itself is obtained using a LIDAR scan of the ground, obtaining the DSM and interpolating between the lowest points to produce the DTM. More advanced algorithms can also use radar or sonar to improve the quality of mapping or in the latter case to also get the DTM data of underwater sections.

An essential step that affects the final result is the postprocessing of the data. The main goals of the postprocessing are:

  • grid interpolation,

  • obstacle detection.

Since the raw data is in the TIN format, it needs to be transformed into an uniform grid which is more convenient for path planning. This transformation is done via linear interpolation. This interpolation introduces an error that causes an inaccurate representation of the true terrain. However, this effect is negligible considering the size of the search area and the fact that we are designing a global planner, in which case some inaccuracies are permissible. The error also decreases with the grid resolution, which was set to 1 m.

To detect obstacles, we use the fact that the DSM map contains the obstacles and the DTM map does not. Therefore, we subtract the DTM map from the DSM and locations with nonzero elevation, with some tolerance margin, correspond to the location of obstacles. The resulting map with separated obstacles can be seen in the Fig. 2.

Since the input map data contains information only about the elevation of the terrain, we assume that the surface of the terrain is smooth and uniform throughout the map. Although this assumption might be violated in many cases additional map data can be included with minor modifications of the path finding algorithm.

Fig. 2.
figure 2

Obstacle classification based on DTM and DSM subtraction

Full size image

2.2 Hybrid A* Algorithm

The proposed path planner uses a modified Hybrid A* algorithm which is based on the standard A* algorithm [6]. The A* algorithm is well known and its grid-based version will be only briefly described to clarify used notation.

A* algorithm works with two sets of nodes: open O and closed C. Each iteration of the algorithm starts with a selection of the most promising node out of the open set. At the beginning, only the start node is in the open set. This node is selected based on its total cost \(f = g + h\) consisting of two parts, where g cost represents the total cost required to get from the start node to the current node. The second part is the heuristic cost h which represents the cost estimate of getting from the current node to the goal. The better this heuristic cost is, the fewer nodes are required to be expanded and the faster the whole algorithm is. This node is then expanded to find further possible movements. In a grid-based A*, the expansion is either to four neighbouring cells or to all eight adjacent cells. These child nodes are then checked for collision with obstacles and checked if they are already in the close set or in the open set with a higher cost. Then they are added to the open set and the whole process repeats unless the goal is reached or there are no more nodes to expand.

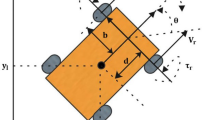
The original Hybrid A* algorithm described in [2] was designed for path planning of autonomous nonholonomic vehicles in DARPA Urban Challenge in 2007. It improves the A* algorithm in a way that the expansion is done not only for four or eight neighbouring cells but by motion primitives generated using a kinematic model of the respective vehicle as can be seen in the Fig. 3 assuming movement with constant velocity. It, therefore, transforms the input in the joint space of the nonholonomic vehicle to the search space \((x, y, \psi )\). Where x and y is a Cartesian position of the vehicle and \(\psi \) is the yaw angle of the vehicle. Each node of the graph, therefore, stores not only its discrete state but also the continuous state of the vehicle together with the respective cost.

Fig. 3.
figure 3

Node expansion for Hybrid A* algorithm

Full size image

Choosing a node for expansion is done in the same way as in the case of original A*. Only cost functions are modified.

g function represents the distance between the current node and the child node, which also includes penalties for reversing and changing the direction of movement.

h function original algorithm uses two heuristic functions. The first function calculates the distance from a current state to the goal state, ignoring obstacles but respecting the nonholonomic nature of the vehicle.

The second heuristic function provides the shortest distance from a current state to the goal state, ignoring nonholonomic constraints but considering obstacles. The resulting h cost is taken as the maximum of both outputs of the upper mentioned heuristic functions.

Another addition to the standard A* algorithm is the analytical expansion, where the Reed-Shepp curve is calculated from the current state to the goal and the node is added only if the calculated path is obstacle-free. This addition improves the precision and performance of the algorithm. It should be noted that this analytical expansion is calculated only for some nodes and the frequency of this calculation is increasing towards the goal.

2.3 Nonholonomic Path Planner with Dynamic Model

The proposed algorithm for global path planning in an elevation grid map is based on the Hybrid A* algorithm described in the previous section. Unlike the original algorithm, this method does not expect the vehicle to move with a constant velocity but the velocity is based on a simplified dynamic model. Therefore, the search space of the algorithm is \((x, y, \psi , v)\), where v is the longitudinal velocity of the vehicle.

Each expanded node N of the graph holds the following information:

$$\begin{aligned} N = (\tilde{x}, \tilde{y}, x, y, \psi , v, d, \delta , g, f) \end{aligned}$$
(1)

where \(\tilde{x}\) and \(\tilde{y}\) are discrete vehicle coordinates corresponding with centers of individual grid cells G of the map, d is a vehicle direction, where 1 represents forward movement and \(-1\) reverse movement and \(\delta \) is a steering angle. We also denote \(\boldsymbol{n} = (x, y)\) as a vector of continuous positions of the node N.

Expansion

The purpose of the expansion is to find new possible movements of the vehicle from the current node \(N_0\). A node with the lowest cost f is chosen from the open set O for expansion. Children of this node lie on the end of the motion primitives. These primitives are generated based on a bicycle kinematic model [20]. This model was chosen as a simplification of the Ackermann model, where the front and the rear wheels of the bicycle lie in the middle of the front and rear axis of the four-wheel vehicle. Each motion primitive has the same length p and is calculated for a fixed steering angle \(\delta \) of the front wheel. The range of these steering angles is a user input into the planner.

Fig. 4.
figure 4

Kinematic bicycle model

Full size image

Calculation of the motion primitive from node \(N_0\) to the child node \(N_1\) is covered by Eqs. (2)–(7) and depicted in the Fig. 4. The continuous vehicle position \(\boldsymbol{n_1}\) in node \(N_1\) is obtained from the Eq. (6) and its yaw angle is based on the Eq. (7). These equations differ if the vehicle is going straight or if it is turning. Position in node \(N_1\) is derived as position \(\boldsymbol{n_0}\) in node \(N_0\) to which the difference between positions \(\boldsymbol{n_0}\) and \(\boldsymbol{n_1}\) in local vehicle coordinate system is added. This difference is rotated by angle \(\psi _0\) to the global coordinate system using rotation matrix \(\boldsymbol{R}\). Calculation of the yaw angle is straightforward; if the vehicle is not turning, the yaw angle is preserved. Otherwise, the turning angle \(\varphi \) is added. This turning angle depends on the radius of curvature \(r_N\) which is based on the simple geometrical formulas (2) and (3).

$$\begin{aligned} r_B = \frac{l}{\tan \delta } \end{aligned}$$
(2)
$$\begin{aligned} r_N = \sqrt{l_r^2 + r_B^2} \end{aligned}$$
(3)
$$\begin{aligned} \varphi = p/r_N \end{aligned}$$
(4)
$$\begin{aligned} \boldsymbol{R} = \begin{bmatrix} \cos \, \psi _0 &{} \quad -\sin \, \psi _0 \\ \sin \, \psi _0 &{} \qquad \cos \, \psi _0 \\ \end{bmatrix} \end{aligned}$$
(5)
$$\begin{aligned} \boldsymbol{n_1} = {\left\{ \begin{array}{ll} \boldsymbol{n_1} + \boldsymbol{R} \begin{bmatrix} r_N \sin \, \varphi \\ r_N (1 - \cos \, \varphi ) \end{bmatrix} &{} \text {if } \delta \ne 0 \\[10pt] \boldsymbol{n_1} + \boldsymbol{R} \begin{bmatrix} p \\ 0 \end{bmatrix}&\text {otherwise} \end{array}\right. } \end{aligned}$$
(6)
$$\begin{aligned} \psi _1 = {\left\{ \begin{array}{ll} \psi _0 + \varphi &{} \text {if } \delta \ne 0 \\ \psi _0 &{} \text {otherwise} \end{array}\right. } \end{aligned}$$
(7)

G Function

Unlike most of the derivations of the A* algorithm, the output of our g function is not the distance between two nodes, which might be penalized in numerous ways, but time. This time is calculated based on a mass point equation of motion (10).

We will use the simplified dynamic model of the vehicle where the vehicle is considered as a point mass. Due to the coarse resolution of the map data and lack of any information about the surface of the terrain, we will neglect the assessment of the vehicle stability and we will assume no slip and permanent contact between the wheels and the ground.

Based on our kinematic model of the bicycle, the path between two consecutive nodes can be either a straight line or a circular arc. Since each node N may have a different elevation, based on its corresponding node G, the path between nodes might be inclined. This transforms the circular arc path into the part of a helix as can be seen in the Fig. 5. In the same way, the straight-line path might be angled towards the horizontal plane.

The helical path can be transformed into the orthogonal triangle provided we neglect the wheel slip and centripetal forces. In this orthogonal triangle, the legs represent the length of the motion primitive p and the elevation difference \(\mathrm {\varDelta } H\), the hypotenuse is the actual length of the slope s. Using this simplification, both turning and going straight can be assessed in the same way.

To calculate the length of the slope s the Eq. 8 is used, where \(\varDelta H\) is the elevation difference between grid cells \(G_1\) a \(G_0\). The slope angle is given by Eq. 9.

$$\begin{aligned} s = \sqrt{{\mathrm {\varDelta } H}^2 + p^2} \end{aligned}$$
(8)
$$\begin{aligned} \theta = \mathrm {atan}\frac{\mathrm {\varDelta } H}{p} \end{aligned}$$
(9)

The following equations of motion are based on the Fig. 6. Since we neglect the rotation of the wheel and consider the whole vehicle as a point mass, the only relevant equation of motion for our case is Eq. (10) in direction of \(X_l\) of the local coordinate system. Members of Eq. (10) are calculated based on Eqs. (11)–(15). Symbols used in the following equations are described in the Table 1. There are two types of dissipative forces in our model. The first one is the torque \(M_\mathrm {f}\) representing rolling resistance and the second one is \(F_\mathrm {b}\) which depends on the velocity and represents all other losses.

Fig. 5.
figure 5

Vehicle path

Full size image
Table 1. Table of symbols
Full size table
Fig. 6.
figure 6

Free-body diagram of a vehicle on a slope

Full size image
$$\begin{aligned} X_l: ma&= 4F_\mathrm {m} - 4\frac{M_\mathrm {f}}{r} - F_\mathrm {g} \, \sin \theta - F_\mathrm {b} \end{aligned}$$
(10)
$$\begin{aligned} F_\mathrm {m}&= \frac{M_\mathrm {m}}{r} \end{aligned}$$
(11)
$$\begin{aligned} M_\mathrm {f}&= F_\mathrm {N} \xi \end{aligned}$$
(12)
$$\begin{aligned} F_\mathrm {N}&= \frac{F_\mathrm {g} \cos \theta }{4} \end{aligned}$$
(13)
$$\begin{aligned} F_\mathrm {g}&= m g \end{aligned}$$
(14)
$$\begin{aligned} F_\mathrm {b}&= b v^2 \end{aligned}$$
(15)

We can numerically solve Eq. (10) to obtain the position and velocity throughout time. Based on these values, we can determine if the vehicle reached the node \(N_1\), how long did it take and what was the velocity of the vehicle at that time. This velocity will be used for the calculation of g cost from the node \(N_1\) to its child nodes. The resulting g cost corresponds to time required to move from \(N_0\) to \(N_1\). If the node \(N_1\) is unreachable, g cost is set to a high value.

H Function. Since the g cost represents time, the output of the h function has to be time as well. The original H* algorithm uses two heuristic functions as described in Sect. 2.2. These heuristics are well suited for the conditions of the autonomous car moving through mostly flat areas with known obstacles. In our case, the classified obstacles are only obstacles resulting from the difference of DSM and DTM maps, these are vegetation, buildings and other man-made structures, as described in Sect. 2.1. Therefore, all terrain obstacles such as cliffs, ridges, hills, etc. are not considered as obstacles. Since we designed our path planner for a vehicle moving through challenging terrain where terrain obstacles are dominant, the original heuristics were not very beneficial.

Our heuristic function (16) calculates time required to move from the child node to the goal as an Euclidean distance divided by the maximum allowable velocity \(v_\mathrm {max}\) of the vehicle. The Euclidean distance is a spatial distance considering also the elevation of the child node and the goal.

$$\begin{aligned} h = \frac{\sqrt{(\boldsymbol{n}_\mathrm {g} - \boldsymbol{n}_1)^2 + (H_\mathrm {g} - H_1)^2}}{v_\mathrm {max}} \end{aligned}$$
(16)

3 Experiments

We decided to test our algorithm in locations with a challenging terrain where our dynamic model can be fully evaluated and where it can be also compared to a known optimal path. Therefore, locations of quarries were chosen since they provide a difficult terrain and roads for mining vehicles which can be used for comparison. We used DSM and DTM maps of three quarry sites located in the Czech Republic for testing, namely quarries in Jakubčovice nad Odrou, Mokrá–Horákov and Dolní Kounice.

For the purpose of the following tests, a 4WD (wheel drive) vehicle with the following parameters was chosen (Table 2).

Table 2. Vehicle parameters
Full size table

During each step of expansion, five motion primitives with length p of 2 m were generated for both forward and reverse direction with maximal steering angle \(\delta \) of 40\(^\circ \).

The algorithm was programmed in MATLAB® and the experiments were conducted on the PC running Ubuntu 20.04 with Intel® XeonTMCPU E3-1245 v3 @ 3.40 GHz and 16 GB of RAM.

Map data from the query in Dolní Kounice were used for the first experiment. Locations of the start and goal nodes together with a found path and expanded nodes are shown in Fig. 7a. For comparison, there is an aerial view of the quarry in the Fig. 7b. The aerial view does not match with the map data due to different dates of capturing data. It can be seen that there are classified obstacles at the bottom of the quarry near the start node and that the start node is surrounded by steep slopes from three sides. Therefore, the only way to the goal leads through the obstacles and via a side road on the left side of the quarry. Calculation of the path took 17 s and 78 956 nodes were expanded.

Fig. 7.
figure 7

Quarry in Dolní Kounice

Full size image

The second experiment presented in this paper was conducted with data from the quarry in Mokrá–Horákov (see Fig. 8). This quarry has an interesting layout with two quarries separated by a narrow passageway. Calculation of the path took 114 s and 474 139 nodes were expanded.

The last experiment presents the influence of the driving torque \(M_\mathrm {m}\) on the planned path. This experiment was conducted on map data from a quarry in Jakubčovice nad Odrou. The experiment was conducted for three different settings of the driving torque with the same position of the start and goal nodes in all three conditions. The lowest driving torque was set to a value which still enables the vehicle to successfully find a path. The middle value was the same as in the previous experiments and the highest setting was set to more than double of the standard driving torque.

4 Results

The result of the first experiment can be seen in the Fig. 7a. The proposed planner was able to find a way through the bottom of the query and successfully avoided all classified obstacles. It also found a side road leading towards the top of the query while avoiding cliffs and steep slopes. This evaluation was done solely based on the simplified dynamic model of the vehicle.

In the second experiment, the planner found a way through the narrow section separating both quarries and precisely followed the same road towards the goal which is regularly used by mining trucks. The result of this experiment is in the Fig. 8a. Finding a way through narrow sections is a difficult task for all planners, especially in our case where the movement of the vehicle is constrained by the kinematic model and by the number of generated motion primitives. This causes that the vehicle cannot reach an arbitrary yaw angle and therefore it has to alternate between left and right turns to reach a goal in certain directions.

Fig. 8.
figure 8

Quarry in Mokrá–Horákov

Full size image
Fig. 9.
figure 9

Comparison of different driving torque settings

Full size image

Results of the last experiment are shown in the Fig. 9. It can be seen that if the driving torque is set low, it will result in the situation shown in the Fig. 9a. In this case, the vehicle was able to reach the goal but it had to take a longer “zigzag” path while going up the hill to minimize the slope angle and therefore the torque required to move. The middle Fig. 9b depicts a situation where the vehicle has a reasonably set driving torque. The planned path follows the existing road and tends to the goal. In the last presented case shown in the Fig. 9c, the driving torque is set too high which results in the planned path going almost directly towards the goal. This result is correct but may not be feasible for a real vehicle since our model does not account for the tipping over of the vehicle. If the driving torque was set even higher, the resulting path would be a straight line connecting the start and goal nodes.

5 Discussion

Based on the results presented in the previous subsection, the algorithm proved to be capable of finding a global path while respecting all constraints. The aim of this paper is to present an idea of extending the Hybrid A* algorithm by a simplified dynamic model of the vehicle which is used for traversability assessment and obtaining a near time optimal path.

To improve the performance of the planner and preserve the simplicity of the whole algorithm, some simplifications of the vehicle model were made. These simplifications are acceptable since the proposed planner is meant to be a global planner and all errors resulting from the simplifications should be handled by the local planner of the vehicle. Nevertheless, there is still space for further improvements described below.

The whole algorithm can be improved by incorporating the findings of other researchers. For example, the used grid map can be expanded by additional layers in [22] which will provide information about settlements, roads, waterways, vegetation, soils, etc. This information can be incorporated either directly into the dynamic model or as additional heuristics.

Another improvement might be to smooth out and post-process the found path as in [2]. Since the expansion of each node is only to several discrete locations, the resulting path is usually not smooth and might frequently change the steering angle.

Further improvements can be directed towards the dynamic model of the vehicle which could take into account other influences mentioned for example in [27] and [9]. It could also consider the real center of gravity of the vehicle and its dimensions, so any tip-over of the vehicle could be penalised, this would prevent the situation shown in the Fig. 9c. Addition of side forces could help to better describe the turning motion of the vehicle.

An addition to the dynamic model could be a collision model of the vehicle as presented in [1] which could better assess collisions between a vehicle and microrelief objects.

For the final application the algorithm has to be greatly optimised and rewritten to C++ to improved its performance. Another possibility is to parallelize certain parts of the algorithm, especially the expansion section can benefit from it.

6 Conclusion

A kinodynamic global path planner has been presented in this paper. This path planner operates on a grid map with obstacles and elevation data in each cell of the grid. This grid map is based on TIN data obtained either from a UAV or publicly available DTM and DSM maps.

A modified Hybrid A* algorithm was used as a graph search method, where the total cost of movement from the start node to the goal node is expressed a time. Therefore, the resulting path is time optimal. The evaluation of the cost required to move from one node to the other was based on the dynamic simulation of the simplified dynamic vehicle model. This ensures that the resulting path not only complies with the nonholonomic constraints of the vehicle but also with the limitations of the vehicle powertrain. Inclusion of the dynamic model of the vehicle which is numerically solved and which can be further expanded to include other influences into the simulation is the main innovation of this work.

The proposed planner was tested on map data of several quarries which provide challenging terrain for testing the algorithm with numerous terrain obstacles. These terrain obstacles are not classified as physical obstacles and have to be identified by the dynamic simulation. The planner was able to find paths that correspond to the regular roads used in these quarries. These roads can be considered time-optimal and is proven that these roads are traversable for nonholonimic mining vehicles.