Source Localization and Tracking: A Sparsity-Exploiting Maximum a Posteriori Based Approach

Abstract

In this work, we explore the potential of sparse recovery algorithms for localization and tracking the direction-of-arrivals (DOA) of multiple targets using a limited number of noisy time samples collected from a small number of sensors. In target tracking problems, the targets are assumed to be moving with a small random angular acceleration. We show that the target tracking problem can be posed as a problem of recursively reconstructing a sequence of sparse signals where the support of the signals changing slowly with time. Here, one can use the support of last signal as a priori information to estimate the behavior of current signal. In particular, we propose a maximum a posteriori (MAP)-based approach to deal with the sparse recovery problem arising in tracking and detection of DOAs. We consider both narrowband and broadband scenarios. Numerical simulations demonstrate the effectiveness of the proposed algorithm. We found that the proposed algorithm can resolve and track closely spaced DOAs with a small number of sensors.

Research is supported by the Australian Research Council.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Direction of arrival (DOA) estimation using sensor array has been an active research area [20, 25, 37], playing an important role in smart antennas, next generation mobile communication systems, various type of imaging systems and target tracking applications. Many algorithms have been developed, see [37] and references therein. The algorithms like Capon [6], pose the DOA estimation problem as a beamforming problem. Here one designs adaptive filterbanks to obtain nonparametric estimate of the spatial spectrum. The popular alternative to this is the subspace algorithms like MUSIC [35], ESPRIT [33] or weighted subspace fitting [36, 41]. The subspace algorithms which exploit the low-rank structure of the noise-free signal. The maximum-likelihood estimation [25] is another efficient technique, but requires accurate initialization to ensure global convergence. All these methods rely on the statistical properties of the data, and hence requires a large number of time samples.

Conventional DOA estimation techniques cannot exploit the target moving statistics into their formulation and hence their performance degrade when a large number of DOAs moving in a field of interest [45]. Recently, several approaches have been developed for tracking targets [4, 8, 30, 31, 44, 45]. The maximum likelihood (ML) methods [30, 31, 45] have good statistical properties and are robust in target tracking with a relatively small number of samples. The works in [30, 31] incorporate the target motion dynamics in ML estimation and computes the the DOA parameters at each time subinterval and refine the ML estimates through Kalman filtering. The concept of Multiple Target States (MTS) has been introduced in [45] to describe the target motion. The DOA tracking is implemented through updating the MTS by maximizing the likelihood function of the array output. However, ML-based algorithms have high computational cost in general [8]. A recursive expectation and maximization (EM) [12] algorithm has been used in [8] to improve computational efficiency of ML algorithms. Cyclostationarity property of the moving targets has been exploited in [44]. In target tracking, the change in DOA from last time frame to the current time frame is computed by exploiting the difference of the averaged cyclic cross correlation of array output. Target tracking in clutter environment is also addressed in [4].

Sparse signal representation has been applied for spectral analysis [10, 14–16, 26, 34]. In [34], a Cauchy-prior is used to enforce sparsity in a temporal spectrum. A recursive weighted least-squares algorithm called FOCUSS has been developed in [16] for source localization. Fuchs [14, 15] formulates the source localization problem as a sparse recovery problem in the beam-space domain. DOA estimation has been posed into joint-sparse recovery problem in [10, 19, 26]. $\ell _1$-SVD [26] combines the singular value decomposition (SVD) step of the subspace algorithms with a sparse recovery method based on $\ell _1$-norm minimization. The $\ell _1$-SVD algorithm can handle closely spaced correlated sources if the number of sources is known. An alternative strategy called joint $\ell _{2,0}$ approximation of DOA (JLZA-DOA) is proposed in [19]. The algorithm represents the snapshots of sensors as some jointly sparse [18] linear combinations of the columns of a manifold matrix. The resulting optimization problem of JLZA-DOA has been solved using a convex–concave procedure. JLZA is further extended to deal with the joint sparse problem with multiple measurement matrices arising in broadband DOA estimation, where the manifold matrices for different frequency bands are different. This allows a sensor spacing larger than the smallest half-wavelength of the broadband signal, which in turn results in a significant improvement in the DOA resolution performance. However, these algorithms have been designed for stationary DOA estimation.

There are two aims of the work: (i) develop an efficient algorithm for stationary DOA estimation and, (ii) adopt the algorithm for multiple target tracking. We pose target tracking as a problem of tracking a sparse signal $\mathbf {x}(t)$. Here the field of interest is discretized into a fine grid consisting of a large number ($n$) of potential DOAs, and $\mathbf {x}(t)$ is an $n$ dimensional complex valued vector, where the $i$th component of $\mathbf {x}(t)$ is essentially the signal received from the $i$th point on the DOA-grid at time $t$. Since there are only a small number of targets at any time $t$, the vector $\mathbf {x}(t)$ is sparse, and the support of $\mathbf {x}(t)$ gives the locations of the targets. As the targets move, the support of $\mathbf {x}(t)$ changes with time $t$. If this change is slow enough, then from the estimate of $\mathbf {x}(t-1)$ we can make a fairly accurate prediction of the support of $\mathbf {x}(t)$. Recent papers [24, 39, 40] in compressive sensing (CS) with partially known support demonstrate that such prior knowledge about the support can be used to significantly lower the number of data samples needed for reconstruction.

While the algorithms for CS with partially known support work well for slowly varying support, these methods cannot be used if the target speed is above a particular threshold. To alleviate this problem we propose a MAP estimation approach. At time $t$ we use the past estimates of $\mathbf {x}(\tau ), \ \tau < t$, to construct a a priori predictive probability density function of $\mathbf {x}(t)$. This prior is such that the components of $\mathbf {x}(t)$ which are close to the predicted future location of DOA, will have large magnitude with very high probability. On the other hand, a component of $\mathbf {x}(t)$ which are far from the predicted location is of large magnitude with a very small probability. Subsequently, we use this prior and the array measurements at time $t$ to derive a MAP estimate of $\mathbf {x}(t)$.

We demonstrate the performance of our method on minimum-redundancy linear arrays [27]. In a minimum-redundancy array, the inter-element spacing is not necessarily required to maintain the half wavelength of the receiving narrowband signal. We can resolve relatively large number of DOAs with small sensors and time samples. Moreover, such array arrangement leads to an increase in the resolution of DOA estimation.

Similar to [19], we enforce joint sparsity in DOA estimation for narrowband and broadband signals. In broadband case, this joint sparsity allows a sensor spacing larger than the smallest half-wavelength of the signal, which in turn results in a significant improvement in the DOA resolution performance. This is possible because the spatial aliasing effect can be suppressed by enforcing the joint sparsity of the recovered spatial spectrum across the whole frequency range under consideration.

The chapter is structured as follows. In Sect. 9.2, narrowband stationary DOA estimation is considered. The DOA estimation problem is set as an underdetermined sparse recovery problem. Some state-of-the-art sparsity-based DOA estimation techniques have been discussed, and a MAP-based DOA estimation framework has been developed. Section 9.3 considers the narrowband DOA tracking problem. We formulate MAP framework in DOA tracking. We also demonstrate a possible way to adopt a conventional sparsity-based DOA estimation technique in tracking problem. The proposed MAP approach has been extended for broadband DOA estimation in Sect. 9.4. Finally, in Sect. 9.5 we present some simulation results.

2 Stationary Narrowband DOA Estimation

2.1 Background

Consider $k$ narrow-band signals $\{ s_j(t) \}_{j=1}^k$ incident on a sensor array, consisting of $m$ omnidirectional sensors. Let

$$ \mathbf {y}(t)=[\mathbf {y}_1(t) \cdots \mathbf {y}_m (t)]', $$

where $\mathbf {y}_j(t)$ is the signal recorded after demodulation by the $j$th sensor and $\mathbf {y}'$ denotes the transpose of $\mathbf {y}$. Defining

$$ \mathbf {s}(t)=[s_1(t) \cdots s_k (t) ]', $$

and using the narrowband observation model [20, 25], we have

$$\begin{aligned} \mathbf {y}(t) = A(\theta ) \mathbf {s}(t) + e(t). \end{aligned}$$

(9.1)

Here $A(\theta )$ is the manifold matrix, $\theta$ is the DOA vector containing the directions of arrival of individual signals, i.e., the $j$th component $\theta _j$ of $\theta$ gives the DOA of the signal $s_j(t)$, and $e(t)$ denotes the measurement noise. The manifold matrix consists of the steering vectors $\{ a(\theta _j) \}_{j=1}^k$:

$$ A(\theta ) = [a(\theta _1) \cdots a(\theta _k)]. $$

The mapping $a(\theta )$ depends on the array geometry and the wave velocity, which are assumed to be known for any given $\theta$. The problem is to find $\theta$ and $k$ from $\{ \mathbf {y}_j(t) \}_{j=1}^m$.

2.2 Connection to the Blind Source Separation

Blind source separation (BSS) involves recovering unobserved signals from a set of their mixtures [1, 21, 32]. For instance, the signal received by an antenna is a superposition of signals emitted by all the sources which are in its receptive filed. Let us consider $k$ signals $\{ s_j(t) \}_{j=1}^k$ incident on a sensor array, consisting of $k$ sensors. Let

$$ \hat{\mathbf {y}}(t)=[\hat{\mathbf {y}}_1(t) \cdots \hat{\mathbf {y}}_k (t)]', $$

where $\hat{\mathbf {y}}_j(t)$ is the signal recorded by the $j$th sensor. The model of sensor output be [1, 21]:

$$\begin{aligned} \hat{\mathbf {y}}(t) = \hat{A} \mathbf {s}(t) + \hat{e}(t). \end{aligned}$$

(9.2)

where $\hat{A}\in \mathbb {R}^{k\times k}$ is an unknown nonsingular mixing matrix. Without knowing the properties of the source signals and the mixing matrix, we want to estimate the source signals from the observations $\hat{\mathbf {y}}(t)$ via some linear transformation of the form [1]

$$\begin{aligned} \hat{\mathbf {s}}(t)=B \hat{\mathbf {y}}(t) \end{aligned}$$

(9.3)

where $\hat{\mathbf {s}}(t)=[ \hat{s}_1(t) \cdots \hat{s}_k (t) \ ]'$, and $B\in \mathbb {R}^{k \times k}$ is a de-mixing matrix. However, without any information about $\hat{A}$ or $\mathbf {s}(t)$, it is impossible to estimate $\hat{\mathbf {s}}(t)$. In BSS, different assumptions have been made on $\mathbf {s}(t)$. For example, independent component analysis (ICA)-based approach assumes that the sources $\mathbf {s}(t)$ are statistically independent [21]. The goal of ICA is to find the transformation matrix $B$ such that the random variables $\hat{s}_1(t), \ldots , \hat{s}_k (t)$ are as independent as possible [32].

There are interesting similarities between the BSS model in (9.2) and the DOA estimation model in (9.1). In the DOA estimation problem (see (9.1)), we have to estimate the source signals, while the matrix $A(\theta )$ and $\mathbf {s}(t)$ are unknown. Unlike BSS, DOA estimation model assumes that the construction of matrix $A(\theta )$ depends on the sensor array geometry and DOA of source signals. Since, the sensor array geometry is known, if one can estimate the DOA of sources, it is possible to construct $A(\theta )$, and hence estimation of $\mathbf {s}(t)$. It is not necessary the sources to be statistically independent [43]. Hence, DOA estimation can be viewed as a semi-BSS problem. Recently, BSS techniques have been applied for DOA estimation [9, 22, 29].

2.3 DOA Estimation as a Joint-Sparse Recovery Problem

We divide the whole area of interest into some discrete set of “potential locations”. In this work, we consider the far-field scenario and hence the discrete set be a grid of directions-of-arrival angles. Let the set of all potential DOAs be $\mathbb {G} = \{ \bar{\theta }_1, \ldots , \bar{\theta }_n\}$, where typically $n \gg k$. The choice of $\mathbb {G}$ is similar to that used in the Capon or MUSIC algorithms. Collect the steering vectors for each element of $\mathbb {G}$ in

$$ \Phi = [a(\bar{\theta }_1) \cdots a(\bar{\theta }_n)]. $$

Since $\mathbb {G}$ is known, $\Phi$ is known and is independent of $\theta$. Now, represent the signal field at time $t$ by $\mathbf {x}(t) \in \mathbb {C}^{n}$, where the $j$th component $\mathbf {x}_j(t)$ of $\mathbf {x}(t)$ is nonzero only if $\bar{\theta }_j = \theta _{\ell }$ for some $\ell$, and in that case $\mathbf {x}_j(t) = \mathbf {s}_{\ell }(t)$. Then one has a model

$$\begin{aligned} \mathbf {y}(t) = \Phi \mathbf {x}(t) + \bar{e}(t), \end{aligned}$$

(9.4)

where $\bar{e}(t)$ is the residual due to measurement noise and model-errors. Since $k \ll n$, $\mathbf {x}(t)$ is sparse. Note that the equality $\bar{\theta }_j = \theta _{\ell }$ may not hold exactly for any $\ell \in \{ 1,2,\ldots ,k \}$ in practice. Nevertheless, by making $\mathbb {G}$ dense enough, one can ensure $\bar{\theta }_j \approx \theta _{\ell }$ closely, and the remaining modeling error is absorbed in the residual term $\bar{e}(t)$. We model the elements of $\bar{e}(t)$ as mutually independent, and identically complex Gaussian distributed random variables with zero mean and variance $1/\lambda$, where $\lambda$ is a positive real number.

The model, (9.4) lets us pose the problem of estimating $k$ and $\theta$ as that of estimating a sparse $\mathbf {x}(t)$ which can be solved using CS [13] framework. If there is a reliable algorithm to recover the sparse $\mathbf {x}(t)$ from $\mathbf {y}(t)$ using (9.4), then all but a few components of the final solution $\mathbf {x}(t)$ will have very small magnitudes. Thus, if the $j$th component $x_j(t)$ is a dominant component in the recovered $\mathbf {x}(t)$, then we infer that at time $t$, there is a source with DOA $\bar{\theta }_j$, with an associated signal $x_j(t)$. Finally, the number of these dominant spikes gives $k$.

A $k$ sparse $\mathbf {x}(t)$ can be recovered uniquely from (9.4) if $k \le m/2$, and every $m$ columns of $\Phi$ form a basis of $\mathbb {C}^m$. The latter is called the unique representation property, and is closely connected to the concept of an un-ambiguous array. Apart from the limit on $k$, the single snapshot setting in (9.4) is sensitive to noise. Since noise is ubiquitous in practical problems, we turn to the so-called joint sparse formulation [18]. In practice, we have several snapshots $\{\mathbf {y}(t)\}_{t=1}^N$. Using (9.4), we can write

$$\begin{aligned} Y := [\mathbf {y}(1) \cdots \mathbf {y}(N)] = \Phi X + E, \end{aligned}$$

(9.5)

where $X = [\mathbf {x}(1) \cdots \mathbf {x}(N)]$ is a sparse matrix, and $E = [\bar{e}_1 \cdots \bar{e}_N]$. If the DOA vector $\theta$ is time-invariant over the period of measurement, then for all $t$ the nonzero dominant peaks in $\mathbf {x}(t)$ occur at the same locations corresponding to the actual DOAs. In other words, only $k$ rows of $X$ are nonzero. Such a matrix is called jointly $k$-sparse. Hence the DOA estimation problem can be posed as the multiple measurement vectors (MMV) problem [18] of finding a jointly sparse $X$ from $Y$.

2.4 Results on the Joint-Sparse Recovery Problem

Assume that $E = 0$, and $Y, X$ are real-valued.¹ The conditions for the existence of a unique solution to the MMV problem is demonstrated by the following lemma [11].

Lemma 1

Let rank $(Y)=r \le m$, and every $m$ columns of $\Phi$ form a basis of $\mathbb {R}^m$. Then a solution to (9.5) with $k$ nonzero rows is unique provided that $k\le \lceil (m+r)/2 \rceil -1$, where $\lceil .\rceil$ denotes the ceiling operation.

We pose DOA estimation as a MMV problem. Assume that $N>m$, and the matrix

$$ X = [\mathbf {x}(1) \cdots \mathbf {x}(N)] $$

has rank $k$. Then according to Lemma 1, the DOAs can be estimated uniquely using the joint sparse framework if $k \le m-1$. It is interesting that all the subspace algorithms, e.g., MUSIC or ESPRIT, have the same limitation.

As described in [19], an $\ell _{2,0}$-norm-based minimization approach can be used to solve the MMV problem arising in DOA estimation. However, since zero norm leads to an NP-hard problem, different relaxations used in literature.

2.5 DOA Estimation Using $\ell _1$ Optimization

$\ell _1$-SVD [26] is an efficient algorithm that uses $\ell _{2,1}$-based optimization to solve the DOA estimation problem. In presence of noise, $\ell _1$-SVD algorithm considers the following way to solve $X$ given $Y$ in (9.5)

$$\begin{aligned} \min _{X} \Vert Y-\Phi X\Vert _F^2+\varsigma \Vert X\Vert _{2,1}, \end{aligned}$$

(9.6)

where $||X||_{2,1}$ is the mixed norm

$$\begin{aligned} || X ||_{2,1} = \sum _{i=1}^n \sqrt{ \sum _{j=1}^N | x_i(j) |^2 } = \sum _{i=1}^n ||X(i,:)||_2, \end{aligned}$$

(9.7)

and $\varsigma >0$ is a tuning factor whose value depends on noise present in the signal. Note that we use the Matlab notation $X(i,:)$ to denote the $i$th row of $X$.

The computation time needed to optimization in (9.6) increases with increasing $N$. To reduce both the computational complexity and sensitivity to noise, $\ell _1$-SVD uses SVD of the data matrix $Y\in \mathbb {C}^{m\times N}$. Similar to other subspace algorithms (i.e., MUSIC) the $\ell _1$-SVD keeps the signal subspace.

2.6 MAP Approach for DOA Localization

In this section we develop a maximum a posteriori (MAP) estimation approach for stationary DOA estimation. Recall that individual columns of $E$ are modeled as mutually independent and identically complex Gaussian distributed random vectors with zero mean and covariance matrix $1/\lambda I$. Using (9.5) the conditional density of $Y$ given $X$ is given by

$$\begin{aligned} p(Y|X) = \left( \frac{\lambda }{2 \pi } \right) ^{mN} \exp \{ - \lambda || Y - \Phi X ||_F^2/2 \}. \end{aligned}$$

(9.8)

Now suppose we know a priori density $p(X)$ of $X$. Then MAP proposes to estimate $X$ by maximizing the conditional density $p(X|Y)$ given the observed data $Y$ with respect to $X$. This is same as maximizing the joint log-likelihood function [23]

$$\begin{aligned} \log p(Y | X) + \log p(X). \end{aligned}$$

(9.9)

Next we propose a suitable candidate for $p(X)$. Recall that $X$ is row sparse. Furthermore it is reasonable to postulate the rows of $X$ are mutually independent, because the locations of individual targets are independent. In practice, it is common to assume that the elements in a row $X(i,:)$ are independent and identically distributed. The independence follows from the choice of the sampling frequency used in practical arrays. The identical distribution follows because the energy of a target signal remains the same over $N$ snapshots. Now for a given $i$, we have two possibilities:

• With a high probability $1{-}q$ there is no target at $\bar{\theta }_i$, and so the elements of $X(i,:)$ are basically of very small energy (contributed by noise and model errors), say $\mu$. We model $X(i,:)$ in this case as a complex Gaussian distributed random vector with mean zero and covariance matrix $\mu ^2 I$.

• Otherwise (with a low probability $q$), there is a target at $\bar{\theta }_i$ so that the elements of $X(i,:)$ have relatively large energy $\rho \gg \mu$ contributed by the target signal. We model $X(i,:)$ in this case as a complex Gaussian distributed random vector with mean zero and covariance matrix $\rho ^2 I$.

Consequently, $p(X)$ is a product of Gaussian mixture densities

$$\begin{aligned} p(X) = \prod _{i=1}^n \left\{ \frac{q}{(2 \pi \rho )^N} \exp \left( \frac{ -||X(i,:)||_2^2}{ 2 \rho ^2 } \right) + \frac{1-q}{(2 \pi \mu )^N} \exp \left( \frac{ -||X(i,:)||_2^2 }{ 2 \mu ^2 } \right) \right\} . \end{aligned}$$

(9.10)

In this work we set $q=k/n$. Such a Gaussian mixture model has been used in simulations [28] and performance analysis [17] in CS literature. Using (9.10) we can write

$$\begin{aligned} -\ln [ p(X) ] = \sum _{i=1}^n \left( \frac{ -||X(i,:)||_2^2}{ 2 \rho ^2 } - \ln \left[ 1 + r \exp \left\{ -\frac{ ||X(i,:)||_2^2 }{2\sigma ^2} \right\} \right] \right) + \mathrm {constant} \end{aligned}$$

(9.11)

where the “constant” absorbs the terms independent of $X$, and

$$\begin{aligned} r = \frac{(1-q)\rho ^N}{q \mu ^N}, \quad \frac{1}{\sigma ^2} = \frac{1}{\mu ^2} - \frac{1}{\rho ^2}. \end{aligned}$$

(9.12)

Combining (9.11) with (9.8) and (9.9), we can write the criterion function

$$\begin{aligned} \wp (X)=\sum _{i=1}^n\left( \frac{ || X(i,:)||_2^2}{2 \rho ^2} - \ln \left[ 1 + r_i \exp \left\{ -\frac{|| X(i,:)||_2^2}{2\sigma ^2} \right\} \right] \right) +\frac{\lambda }{2}\Vert Y-\Phi X\Vert _F^2, \end{aligned}$$

(9.13)

which we need to minimize with respect to $X$. The reader may have noticed that while moving from (9.11) to (9.13) we have replaced $r$ by $r_i$. Indeed for stationary DOA estimation case $r_i = r, \ \forall i$. Having different $r_i$ for different values of $i$ will be useful in tracking moving targets, where it will suffice to minimize the same cost function (9.13). Considering the more general case at this stage allows us to use the results in the next section in the tracking problem.

2.7 Solution Strategy

Like many optimization problems encountered in CS literature [7, 38], minimizing (9.13) is a nonconvex problem. To deal with the nonconvex optimization problem we use the concept of graduated nonconvexity (GNC) [2, 3]. GNC is a deterministic annealing method for approximating the global solution for nonconvex minimization problems. Here we construct a sequence of functions $\wp _j(X), j=0,1,2,\ldots ,w$ such that

• $\wp _0(X)$ is quadratic;

• $|\wp _{j+1}(X) - \wp _{j}(X)|$ is small in the neighborhood of the minimizer ${X}^{(j)}$ of $\wp _{j}(X)$;

• $\wp _{w}(X) = \wp (X)$ for a user chosen integer $w$.

Because $\wp _0(X)$ is quadratic, we can compute ${X}^{(0)}$ using the standard analytical expression. Then as $|\wp _{1}(X) - \wp _{0}(X)|$ is small in the neighborhood of ${X}^{(0)}$, by initializing a numerical algorithm to minimize $\wp _{1}(X)$ at ${X}^{(0)}$ one has a high probability of converging to ${X}^{(1)}$. If we continue this process of initializing the numerical algorithm to optimize $\wp _{j+1}(X)$ at our estimate of ${X}^{(j)}$ obtained by numerically optimizing $\wp _{j}(X)$, then one can expect that ${X}^{(w)}$ is likely to be the minimizer of $\wp _w(X)$.

The sequence of functions $\wp _j(X), j=0,1,2,\ldots ,w$ are constructed as follows. We choose an appropriate real number ${\sigma }_1$ (more details on how the choices are made will follow shortly), and define

$$\begin{aligned} \wp _0(X)&= \sum _{i} \frac{ \Vert X(i,:)\Vert _2^2 }{ 2 \rho ^2 } + \frac{\lambda }{2}\Vert Y-\Phi X\Vert _F^2 \end{aligned}$$

(9.14)

$$\begin{aligned} \wp _j(X)&= \wp _0(X) - \sum _{i} \ln \left[ 1 + r_i \exp \left\{ -\frac{\Vert X(i,:)\Vert _2^2}{2\sigma _j^2} \right\} \right] \quad j = 1,2,3,\ldots ,w; \end{aligned}$$

(9.15)

where

$$\begin{aligned}{\sigma }_j&= ({\sigma }/{\sigma }_1)^{j/w} {\sigma }_1, \end{aligned}$$

and $w$ is a user chosen integer. The parameter ${\sigma }_j$ controls the degree of nonconvexity in ${\wp }_j$. As we increase the value of $j$ form $0$ to $w$, we gradually transform ${\wp }_j$ from a convex function ${\wp }_0$ to our desired likelihood function ${\wp }_w$. If $w$ is sufficiently large, then the change from ${\wp }_{j-1}$ to ${\wp }_j$ is small, and so is the change from $X^{(j-1)}$ to $X^{(j)}$.

Next we derive an expression for $X^{(0)}$. Let $R$ be a diagonal matrix such that $R_{ii} ={\rho }^2.$ Recall that $X^{(0)}$ is the minimum point of $\wp _0$. Hence, if we differentiate (9.14) with respect to $X$ and evaluate at $X^{(0)}$, we must get zero. Hence

$$\begin{aligned} X^{(0)} = (R+\lambda \Phi ^* \Phi )^{-1}(\lambda \Phi ^* Y). \end{aligned}$$

(9.16)

Note that we denote the conjugate transpose of $\Phi$ by $\Phi ^*$.

We can reduce the cost of computing $X^{(0)}$ if we use an alternative expression for $X^{(0)}$, which is obtained by applying matrix inversion lemma in the right hand side of (9.16)

$$\begin{aligned} X^{(0)}&=R^{-1}\Phi ^*( I/\lambda +\Phi R^{-1}\Phi ^*)^{-1}Y. \end{aligned}$$

(9.17)

where $I$ is a $m \times m$ identity matrix. Computing $X^{(0)}$ via (9.16) requires inverting an $m \times m$ matrix. On the other hand we must invert an $n\times n$ matrix if we compute $X^{(0)}$ via (9.17).

The parameter ${\sigma }_1$ controls the degree of nonconvexity in ${\wp }_1$. If we take ${\sigma }_1 \rightarrow \infty$, then the logarithmic term in (9.15) tends to $\ln (1+r)$, making ${\wp }_1$ a quadratic function. In practice, we take

$$ {\sigma }_1 \ge 5 \max _{i}\Vert X(i,:)^{(0)}\Vert _2, $$

This ensures $\exp \{-\Vert X(i,:)^{(0)}\Vert _2^2/(2{\sigma }_1^2) \} \ge 0.99$ for all $i$. Consequently, $\exp \{-\Vert X(i,:)^{(0)}\Vert _2^2/(2{\sigma }_1^2) \} \approx 1$ for all $X$ satisfying $||X-{X}^{(0)}||_F < ||{X}^{(1)}-{X}^{(0)}||_F$ [28].

2.8 Minimizing $\wp _j$

In this section we explore some properties of $X^{(j)}$, and develop a numerical algorithm to compute it. Define

$$\begin{aligned} \xi _j(X(i,:)) = \frac{1}{ \rho ^2} + \frac{ r_i \exp \left( -\frac{\Vert X(i,:) \Vert _2^2}{2\sigma ^2_j} \right) }{ \sigma _j^2 \left[ 1 + r_i \exp \left( - \frac{\Vert X(i,:) \Vert _2^2}{2\sigma _j^2} \right) \right] }, \end{aligned}$$

(9.18)

and an $n \times n$ diagonal matrix $W_j(X)$ as

$$ W_j(X) = \mathrm {diag} \{ \ \xi _j ( X(1,:) ) \ \ \xi _j ( X(2,:) ) \cdots \xi _j ( X(m,:) ) \ \}. $$

From (9.18) it is readily verified that $\xi _j \{ X(i,:) \} > 0$ for all $i$. Hence $W_j(X)$ is a positive definite matrix.

Now we can verify that

$$\begin{aligned} \frac{\partial \wp _j (X) }{\partial X} = W_j( X ) X - \lambda \Phi ^*(Y-\Phi X ). \end{aligned}$$

(9.19)

Since $X^{(j)}$ is the minimum point of $\wp _j$, setting $X = X^{(j)}$ in (9.19) we get

$$\begin{aligned} X^{(j)} = g_j(X^{(j)}) \end{aligned}$$

(9.20)

where

$$\begin{aligned} g_j(X) := \{ W_j( X ) + \lambda \Phi ^* \Phi \} ^{-1} \{ \lambda \Phi ^* Y \}. \end{aligned}$$

(9.21)

Also, a calculation similar to (9.17) gives

$$\begin{aligned} g_j(X) := W^{-1}_j(X){\Phi ^*} \left[ I/\lambda +\Phi W^{-1}_j (X){\Phi ^*} \right] ^{-1}Y. \end{aligned}$$

(9.22)

The equation $X = g_j(X)$ is nonlinear, and cannot be solved analytically. One possibility is to use a fixed point iteration. However, the convergence of the fixed point iteration is not guaranteed. Nevertheless, using (9.19) and (9.21) we have

$$\begin{aligned} g_j(X) - X = - \{ W_j( X^{(j)} ) + \lambda \Phi ^* \Phi \} ^{-1} \frac{\partial \wp _j (X) }{\partial X}. \end{aligned}$$

(9.23)

Since $W_j$ is a positive definite matrix, and $\lambda >0$, the matrix $W_j( X^{(j)} ) + \lambda \Phi ^* \Phi$ is positive definite. Hence (9.23) implies that $\wp _j(X)$ is decreasing along the vector $g_j(X) -X$. In fact moving to $g_j(X)$ from $X$ is same as taking the Newton step associated with some convex–concave procedure to minimize $\wp _j(X)$ [19].

Table 9.1 MAP for narrowband DOA estimation

2.9 Numerical Algorithm for Solving MAP Optimization

The MAP optimization strategy is given in Table 9.1. We assume that the values of $\rho$, and $\mu$ are known. In fact, simulation results demonstrate that the accurate values of $\rho$, and $\mu$ are not necessary. Instead, an approximation of these values are sufficient [17]. Using initial $X^{(0)}$ we calculate $\sigma _1$, and in Step 3 some parameters including $w$ are set. In each iteration, we find a step-length $\kappa$ along the decent-direction $g_j(X)-X$ using the standard backtracking strategy (step 4–5) [5]. We set $\beta =0.5$, which is very common [5]. The inner-iteration for updating $X$ for a given $j$ terminates when the relative change in the magnitude of $X$ is below $\eta$, see step 7. Hence for a smaller $\eta$ more accurate solutions are sought in expense of higher computation time. According to our experimental study, having $\eta = 0.02$ makes a good tradeoff. Upon convergence of each inner iteration, we increment $j$ (step 7). Note that choosing a larger $w$ helps the optimization problem in (9.15) to move slowly from convex to its desire nonconvex form. Thus we have lower probability to get trapped in local minimum. However, a larger $w$ increases the number of outer iterations (step 4–7) of the algorithm, and hence the computation time. Our experimental study suggests that choosing $w = 20$ makes a good tradeoff between solution accuracy and computation time. Upon convergence for $j=w$, PMAP stops its iterations. The value of $\lambda$ depends on noise variance. In our simulation, we set $\lambda =5$ [19].

2.10 Acceleration via QR Factorization

Typically, the matrix $X \in \mathbb {C}^{n \times N}$ in (9.5) is large, as $n$ is a large number (we need $n=360$ to achieve $0.5^{\circ }$ spatial resolution). If the number of data samples $N$ is large, the algorithm may become very slow. To accelerate the algorithm, we use the QR factorization $Y/\sqrt{N} = \bar{R}Q$, where $\bar{R}\in \mathbb {C}^{m \times m}$ is a nonsingular upper triangular matrix, and $Q\in \mathbb {C}^{m \times N}$ is such that $QQ^* = I$. When $E=0$, then

$$\begin{aligned} \mathrm {row \ span}\{X\} \subset \mathrm {row \ span}\{Q\}. \end{aligned}$$

(9.24)

Consequently, $\Vert Y-\Phi X\Vert _F^2 = \Vert \bar{R} -\Phi \bar{X} \Vert ^2_F$, where $\bar{X} = XQ^* \in \mathbb {C}^{n \times m}$ must be jointly row-sparse, and is of significantly smaller size than $X$. Hence, it is more efficient to estimate $\bar{X}$ via minimizing

$$\begin{aligned} \wp (\bar{X})=\sum _{i=1}^n\left( \frac{\Vert \bar{X}(i,:)\Vert _2^2}{2 \rho ^2} - \ln \left[ 1 + r_i \exp \left\{ -\frac{\Vert \bar{X}(i,:)\Vert _2^2}{2\sigma ^2} \right\} \right] \right) +\frac{\lambda }{2}\Vert \bar{R}-\Phi \bar{X}\Vert _F^2. \end{aligned}$$

(9.25)

Following (9.10), it is readily verified that $\bar{X}$ and $X$ have identical a priori density function.

3 Narrowband Target Tracking

3.1 Problem Formulation

Suppose $k$ number of targets are moving in a plane. We wish to

• Detect the targets; and

• Track the DOAs of the targets with a time resolution $\tau$, so that the algorithm will yield estimates DOAs at time instant $0,\tau , 2\tau , 3 \tau , \ldots$.

Let $f_c$ be the sampling frequency at the sensors. We assume that over each interval $[\ell \tau ,\ell \tau +\frac{N}{f_c}),$ the change of $\theta _i(t)$ is negligible, i.e.,

$$\begin{aligned} \theta (t)\approx \theta (\ell \tau ); \ \ t\in \left[ \ell \tau ,\ell \tau +\frac{N}{f_c}\right) \end{aligned}$$

(9.26)

where $N$ is the number of snapshots used to detect and estimate the DOAs at time $\ell \tau$. The above is a common assumption made by many state-of-the-art target tracking algorithms [4, 30, 31, 44]. Hence under this assumption, the $N$ snapshots of sensor data in (9.1) can be expressed as

$$\begin{aligned} y(t) \approx A(\theta (\ell \tau )) \mathbf {s}(t) + e(t), \ \ \ \ t\in \left[ \ell \tau ,\ell \tau +\frac{N}{f_c} \right) . \end{aligned}$$

(9.27)

Just as in (9.5) we can now formulate a stationary target tracking problem at time instant $\ell \tau$, where we need to recover a joint sparse matrix

$$ X_{\ell } = [\mathbf {x}(\ell \tau ) \ \ \mathbf {x}(\ell \tau + 1/f_c) \ \ \mathbf {x}\{ \ell \tau + (N-1)/f_c \}] $$

given the snapshot matrix

$$ Y_{\ell } = [\mathbf {y}(\ell \tau ) \ \ \mathbf {y}(\ell \tau + 1/f_c) \ \ \mathbf {y}\{ \ell \tau + (N-1)/f_c \}] $$

such that $Y_{\ell } = \Phi X_{\ell } + E_{\ell }$ holds. To solve this problem we can always use the stationary DOA estimation methods discussed before. However, when we track the targets the algorithm is inherently recursive. This means while estimating $X_{\ell }$, we already know estimates of $X_{\ell -1}, X_{\ell -2}, \ldots$. If we can use this prior knowledge efficiently, we can work with a significantly smaller $N$ making the assumption (9.26) a feasible one. In addition it is possible to work with larger number of targets. In order to exploit the prior information available in the estimates of $X_{\ell -1}, X_{\ell -2}, \ldots$, we need to consider a dynamic of model for target motion. This is discussed next.

3.2 Dynamic Model for the Target Motion

In this contribution, we stick to the most commonly used ‘small acceleration’ model used in the target tracking literature. For any target $i$, we assume that its angular acceleration $\ddot{\theta }_i(t)$ is a Wiener process with a small incremental variance. Note that we denote the first order derivative of $\theta (t)$ with respect to $t$ by $\dot{\theta }(t)$, and the second order derivative is denoted by $\ddot{\theta }(t)$.

For a generic DOA $\theta (t)$, it is straightforward to write down the state space equations for $\theta (t)$ in terms of the state

$$\begin{aligned} \mathbf {s}(t) = [\theta (t) \ \ \dot{\theta }(t) ]'. \end{aligned}$$

(9.28)

We have

$$\begin{aligned} \dot{\mathbf {s}}(t) = \left[ \begin{array}{cc} 0 &{} 1 \\ 0 &{} 0 \end{array}\right] \mathbf {s}(t) + \left[ \begin{array}{c} 0 \\ w(t) \end{array}\right] , \quad \theta (t) = [1 \ \ 0 ] \ \mathbf {s}(t), \end{aligned}$$

(9.29)

where $w(t)$ denotes the Wiener process with an incremental variance $\gamma$. Now we can discretize (9.29) with a time resolution $\tau$, and it is wellknown that the equivalent discrete-time model is given by

$$\begin{aligned} \mathbf {s}_1 (\ell + 1) = \left[ \begin{array}{cc} 1 &{} \tau \\ 0 &{} 1 \end{array}\right] \mathbf {s}_1(\ell ) + \mathbf {w}_1(\ell ), \quad \theta (\ell \tau ) = [1 \ \ 0 ] \ \mathbf {s}_1(\ell ), \end{aligned}$$

(9.30)

where we write $\mathbf {s}_1(\ell ) := \mathbf {s}(\ell \tau )$ for short; $\mathbf {w}_1(\ell )$ is a discrete-time, zero mean white noise sequence such that

$$\begin{aligned} \mathsf{E}\{ \mathbf {w}_1 \mathbf {w}'_1 \} = \gamma \left[ \begin{array}{cc} \tau ^3/3 &{} \tau ^2/2 \\ \tau ^2/2 &{} \tau \end{array}\right] . \end{aligned}$$

(9.31)

Using (9.30), (9.31) and after a few steps of algebra one can show that

$$\begin{aligned} \theta (\ell \tau ) = 2 \theta (\ell \tau - \tau ) - \theta (\ell \tau - 2 \tau ) + w_2(\ell ), \end{aligned}$$

(9.32)

where $w_2$ is a scalar valued discrete-time first order moving average process with zero mean and

$$\begin{aligned} \mathsf{E}\{ w_2 \} = 0, \quad \mathsf{E}\{ w_2^2 (\ell ) \} = \frac{2 \gamma \tau ^3}{3}, \quad \mathsf{E}\{ w_2 (\ell ) w_2 (\ell - 1) \} = \frac{\gamma \tau ^3}{6}. \end{aligned}$$

(9.33)

3.3 Extension of $\ell _1$-SVD for DOA Tracking

Using (9.32) we can use the estimates of $X_{\ell -1}, X_{\ell -2}, \ldots$ to make predictions about $X_{\ell }$. Then we wish to incorporate this prediction in the MAP framework described above. However, before doing so, we consider how we could naturally extend $\ell _1$-SVD method for tracking by using an approach called CS with partially known support [24, 39, 40]. The idea is to use the past estimates $X_{\ell -1}, X_{\ell -2}, \ldots$ to estimate the support of $X_{\ell }$, and use that information to estimate a joint sparse $X_{\ell }$.

Suppose that until time $t = (\ell - 1) \tau$ the tracking algorithm has detected $k$ targets. The estimated DOAs for the $i$th target at time$(\ell - j) \tau$ is denoted by $\hat{\theta }_i(\ell - j)$. From (9.32) we know

$$\begin{aligned} \mathsf{E}\{ \theta _i (\ell \tau ) \} = 2 \hat{\theta }_i(\ell - 1) - \hat{\theta }_i(\ell - 2). \end{aligned}$$

(9.34)

At this stage we neglect the second order statistics of $w_2(\ell )$, because the standard methods for CS with partially known support does not have any provisions to do so. Nevertheless, while discussing MAP approach in the next section, we will use the second order statistics of $w_2(\ell )$.

Define $\mathbb {I} := \{ 1,2,\ldots ,n \}$. Recall that $n$ is the number of points on the DOA-grid $\mathbb {G} = \{ \bar{\theta }_1, \bar{\theta }_2, \ldots , \bar{\theta }_n \}$. CS with partially known support requires us to predict the support $T(\ell )$ of $X_{\ell }$ defined as

$$ T_{\ell } := \{ i \in \mathbb {I} : ||X_{\ell } (i,:)||_2 \ne 0 \}. $$

We do so as follows. For each $i$ we identify the point of $\mathbb {G}$ which is the nearest to $\mathsf{E}\{ \theta _i (\ell \tau ) \}$ and denotes the associated index by $\iota _i$:

$$ \iota _i = \arg \min _{j \in \mathbb {I}} \ | \bar{\theta }_j - \mathsf{E}\{ \theta _i (\ell \tau ) \}|. $$

Then form

$$ T_{\ell } = \{ \iota _1, \iota _2, \ldots , \iota _k \}. $$

Different CS-based algorithms have been developed to exploit the support information in sparse recovery process [24, 39, 40]. Least squares CS-residual (LS-CS) [39] is a two step procedure. First, a least squares (LS) estimate $\bar{X}_{\ell }$ of $X_{\ell }$ is computed assuming that the support of $X_{\ell }$ is $T_{\ell }$. To explain the details, let

$$ \Phi _{+} = [ \Phi (:,\iota _1) \ \ \Phi (:,\iota _2) \cdots (:,\iota _k) \ ] $$

and

$$ X_+ = [\Phi ^*_+ \Phi _+ ]^{-1} \Phi ^*_+ Y. $$

Note that $X_+$ is a $k \times N$ matrix, and we form $\bar{X}_{\ell }$ as follows:

$$\begin{aligned} \bar{X}_{\ell }(i,:) = \left\{ \begin{array}{ll} X_+(j,:), &{} \mathrm {if \ } i = \iota _j \mathrm { \ for \ some \ } j \in \{ 1, \ldots , k \}, \\ 0, &{} \mathrm {otherwise}. \end{array}\right. \end{aligned}$$

(9.35)

Next calculate the associated residual

$$ \bar{Y}=Y - \Phi _{T_{\ell }} \bar{X}_{\ell }. $$

In the subsequent step, LS-CS uses a CS algorithm to find a sparse solution $\hat{X}_{\ell }$ such that $\bar{Y}_{\ell } =\Phi \hat{X}_{\ell }$. The final estimate is $\bar{X}_{\ell }+\hat{X}_{\ell }$. Adapting recently proposed modified-CS [40] to our problem, this step requires us to solve

$$\begin{aligned} \hat{X}_{\ell } = \arg \min _{X} \ \Vert Y-\Phi X\Vert _F^2 + \varsigma \sum \limits _{i \in \mathbb {I} \setminus T_{\ell }} ||X(i,:)||_2. \end{aligned}$$

(9.36)

We refer the modification of $\ell _1$-SVD as $\ell _1$-SVD-MCS. It might be worthwhile to note the difference between (9.6) and (9.36), and see how easily $\ell _1$-SVD in (9.6) is adapted to the framework of CS with partially known support.

3.4 MAP for Tracking

The MAP algorithm can be used for tracking problem with a small modification in the expression for $p(X)$ given in (9.10). Here we have the option to use the estimates of $X_{\ell -1}, X_{\ell -2}, \ldots$ to obtain a better prior density $p(X)$.

As before, suppose that until time $t = (\ell - 1) \tau$, the tracking algorithm has detected $k$ targets. Then according to (9.32) the conditional density of $\theta _i(\ell \tau )$ evaluated at $\theta$ is proportional to

$$ \eta _i (\theta ) = \exp \left\{ - \frac{ \left[ \theta - 2 \hat{\theta }_i(\ell -1) + \hat{\theta }_i (\ell -2) \right] ^2 }{4 \gamma \tau ^3 / 3 } \right\} . $$

It is natural to use this conditional density as a measure of the probability that $\theta _i(\ell \tau )$ is close to a grid point $\bar{\theta }_j$. In particular, if the $i$th target was the only target detected, then the probability $q_j$ that we will find that target at the grid point $\bar{\theta }_j$ is evaluated as

$$ \frac{ \eta _i(\bar{\theta }_j) }{ \sum _{j \in \mathbb {I}} \eta _i(\bar{\theta }_j) }. $$

When we have $k$ targets in the field, then the probability $q_j$ of finding a target at grid point $\bar{\theta }_j$ is given by

$$\begin{aligned} q_j = 1- \prod _{i=1}^k \left\{ 1- \frac{ \eta _i(\bar{\theta }_j) }{ \sum _{j \in \mathbb {I}} \eta _i(\bar{\theta }_j). } \right\} , \end{aligned}$$

(9.37)

The above expression for (9.37) works when no new target can appear in the field, and none of the existing targets can disappear. Nevertheless, we can generalize (9.37) to relax these requirements. Let

• $\alpha$ be the probability that an existing target disappears; and

• $\beta$ be the probability that a new target appears in the field at a grid point.

Now we modify (9.37) to accommodate the possibility that a new target may appear in the field and an existing target may disappear. The event that “the $i$th target is not presesent at $\bar{\theta }_j$” is the union of two mutually exclusive events:

• 1. The target has actually disappeared from the field (with probability $\alpha$); and

• 2. The target is still there in the field (with probability $1 - \alpha$), but it is not at $\bar{\theta }_j$. The probability of this event is

$$ (1- \alpha ) \left\{ 1- \frac{ \eta _i(\bar{\theta }_j) }{ \sum _{j \in \mathbb {I}} \eta _i(\bar{\theta }_j) } \right\} . $$

Now combining the probabilities of (1) and (2), the resultant probability that “the $i$th target is not present at $\bar{\theta }_j$” is

$$ \alpha + (1- \alpha ) \left\{ 1- \frac{ \eta _i(\bar{\theta }_j) }{ \sum _{j \in \mathbb {I}} \eta _i(\bar{\theta }_j) } \right\} . $$

Then the probability that none of the existing targets is present at $\bar{\theta }_j$ and no new target appears at $\bar{\theta }_j$ is

$$ (1 - \beta ) \prod _{i=1}^k \left[ \alpha + (1- \alpha ) \left\{ 1- \frac{ \eta _i(\bar{\theta }_j) }{ \sum _{j \in \mathbb {I}} \eta _i(\bar{\theta }_j) } \right\} \right] . $$

Thus, to accommodate the possibility that a new target may appear in the field and an existing target may disappear (9.37) is modified accordingly to

$$\begin{aligned} q_j = 1- (1 - \beta ) \prod _{i=1}^k \left[ \alpha + (1- \alpha ) \left\{ 1- \frac{ \eta _i(\bar{\theta }_j) }{ \sum _{j \in \mathbb {I}} \eta _i(\bar{\theta }_j) } \right\} \right] , \ \ j \in \mathbb {I} \end{aligned}$$

(9.38)

Once we know $q_i, \ \forall i \in \mathbb {I}$, we can replace $q$ by $q_i$ in (9.10) to get

$$\begin{aligned} p(X) = \prod _{i=1}^n \left\{ \frac{q_i}{(2 \pi \rho )^N} \exp \left( \frac{ -||X(i,:)||_2^2}{ 2 \rho ^2 } \right) + \frac{1-q_i}{(2 \pi \mu )^N} \exp \left( \frac{ -||X(i,:)||_2^2 }{ (2 \mu ^2) } \right) \right\} , \end{aligned}$$

(9.39)

which in turn gives

$$\begin{aligned} -\ln [ p(X) ] = \sum _{i=1}^n \left( \frac{ -||X(i,:)||_2^2}{ 2 \rho ^2 } - \ln \left[ 1 + r_i \exp \left\{ -\frac{ ||X(i,:)||_2^2 }{2\sigma ^2} \right\} \right] \right) + \mathrm {constant} \end{aligned}$$

(9.40)

where

$$\begin{aligned} r_i = \frac{(1-q_i)\rho ^N}{q_i \mu ^N}, \quad \frac{1}{\sigma ^2} = \frac{1}{\mu ^2} - \frac{1}{\rho ^2}. \end{aligned}$$

(9.41)

Combining (9.40) with (9.8) and (9.9), we again arrive at the criterion function (9.13). However, unlike the stationary case, now all $r_i$ are different from each other. Nevertheless, we can follow the procedure in Sect. 9.2.7 to develop a minimization problem and use the algorithm in Table 9.1 for estimation of $X(\ell )$. In this work, we set $\alpha =0.01,\beta =0.01$.

4 Extension of MAP Framework for Broadband DOA Estimation

We consider the procedure proposed in [19] for broadband DOA estimation. The broadband signal has been splitted into several narrowband signals by using a bank of narrowband filters. Subsequently, the narrowband model (9.5) is applied to each narrowband filter output. Suppose that we have narrowband data at frequencies $\{ \omega _i \}_{i=1}^K$, and let $\Phi _i$ be the “over-complete” manifold matrix at frequency $\omega _i$. Then, the narrowband model at frequency $\omega _i$ is of the form

$$ Y_i = \Phi _i X_i + E_i, \quad i \in \{ 1,2,\ldots ,K\}. $$

Here, $E_i$ is the additive noise at frequency $\omega _i$ and $X_i$ is the jointly row-sparse signal matrix at frequency $\omega _i$. Now,

$$ \mathbf{X}:= [X_1 \ \ X_2 \cdots X_K ] $$

is jointly row-sparse. This is because if $X_i(\ell ,:)$ is nonzero for some $\ell$, then there is source signal at frequency $\omega _i$ at direction $\bar{\theta }_{\ell }$. Therefore, we would expect signals at other frequencies from the direction $\bar{\theta }_{\ell }$ as well, making $X_i(\ell ,:)$ nonzero for all $i$.

Now to resolve broadband DOA in MAP framework we need to develop a priori density $p(\mathbf{X})$ of $\mathbf{X}$. We assume that the energy of a target at all frequency bands $\{\omega _j\}_{j=1}^K$ is almost similar. Nevertheless, the following approach can be extended easily when signal energy is different at different frequency band. Then as described in Sect. 9.2.6, we have two probabilities for every index $i$: (i) with very small probability $q_i$, there is a target at $\bar{\theta }_i$, and hence the elements of $\mathbf{X}(i,:)$ have relatively large energy $\rho$. We model $\mathbf{X}(i,:)$ as a complex Gaussian distributed random vector with zero mean and covariance matrix $\rho ^2I$; (ii) with probability $1-q_i$, the elements of $\mathbf{X}(i,:)$ have small energy $\mu \ll \rho$. Hence, $p(\mathbf{X})$ is a product of Gaussian mixture densities

$$\begin{aligned} p(\mathbf{X})=\prod _{i=1}^n\left\{ \frac{ q_i }{(2 \pi \rho ^2)^{KN} } \exp \left( - \frac{\Vert \mathbf{X}(i,:)\Vert _2^2}{2 \rho ^2 }\right) + \frac{ 1-q_i }{(2 \pi \mu ^2)^{KN} } \exp \left( - \frac{\Vert \mathbf{X}(i,:)\Vert _2^2}{2 \mu ^2 }\right) \right\} . \end{aligned}$$

(9.42)

Then following (9.8)–(9.13), we can end up the the criterion function

$$\begin{aligned} \wp (\mathbf{X})&=\sum _{i=1}^n\left( \frac{\Vert \mathbf{X}(i,:)\Vert _2^2}{2 \rho ^2} - \ln \left[ 1 + r_i \exp \left\{ -\frac{\Vert \mathbf{X}(i,:)\Vert _2^2}{2\sigma ^2} \right\} \right] \right) +\frac{\lambda }{2}\sum _{i=1}^K\Vert Y_i-\Phi _i X_i\Vert _F^2 \end{aligned}$$

(9.43)

where, $r_i = \dfrac{(1-q_i)\rho ^{KN}}{q_i \mu ^{KN}},$

which need to minimize with respect to $\mathbf{X}$, and $\sigma$ are defined in (9.12).

For minimizing (9.43), we follow the GNC procedure of Sect. 9.2.7 and generate $w$ number of suboptimization problem $\{\wp _j(\mathbf{X})\}_{j=1}^w$. Then following the calculation (9.18)–(9.23), it can be shown that $\wp _j(\mathbf{X})$ is decreasing along $\mathbf {g}_j(\mathbf{X})-\mathbf{X}$, where

$$\begin{aligned} \mathbf {g}_j(\mathbf{X})=[g_j^{(1)}(\mathbf{X}) \ g_j^{(2)}(\mathbf{X}) \ \cdots \ g_j^{(K)}(\mathbf{X})],\end{aligned}$$

(9.44)

$$\begin{aligned} g_j^{(i)}(\mathbf{X})= W^{-1}_j(\mathbf{X}){\Phi _i^*} \left[ I/\lambda +\Phi _i W^{-1}_j (\mathbf{X}){\Phi _i^*} \right] ^{-1}Y_i. \end{aligned}$$

(9.45)

Using the direction we can develop a broadband DOA estimation algorithm. The final algorithm is given in Table 9.2.

Table 9.2 MAP for broadband DOA estimation

4.1 Jamming Signal Mitigation

The noise term ${e}(t)$ in (9.1) is the residual noise due to measurement noise and model error. In general, it is assumed that the noise has uniform distribution and smaller magnitude than the source signal. However, there exists some other types of noisy signals; like, jamming signal. Jamming and deception is the intentional emission of radio frequency signals to interfere with the operation of a radar by saturating its receiver with noise or false information. In general, jamming signals come from fixed directions and have magnitude many times larger than actual source signal [42]. Hence, jamming signals hinder actual source. However, due to larger magnitude, it is easier to know the direction of jamming signal in priori. To mitigate from jamming, we will use the crude estimate of the direction of the jamming signal as a ‘partially known support’ of the sparse signal $\mathbf{X}$. Let the jammer direction be supported on $T_j$. Then the value of $q_i$ in (9.42) will be very high if $q_i\in T_j$. We then search any target in rest of the support of $\mathbf{X}$. In our experiments we set $q_i=0.99$ when $q_i\in T_j$.

5 Simulation Results

We compare the performance of MAP-based approach with $\ell _1$-SVD [26], Capon’s method [6], and $\ell _1$-SVD-MCS (see (9.36)). We use four sensors and follow the procedure of minimum-redundancy array [27] for the linear array arrangement. The interelement spacings are $d,3d$ and $2d$, respectively. For narrowband DOA estimation, the value of $d$ is equal to the half wavelength of receiving narrowband signal. For broadband signal we consider two types of the value of $d$ for two classes of algorithms. Similar to [19], MAP algorithm can allow a sensor spacing larger than the half wavelength associated with the highest frequency in the broadband signal. Hence, we set the value of $d$ to be $1.5$ times the smallest wavelength in the broadband signal. However, $\ell _1$-SVD and Capon cannot allow larger $d$. Hence we set the value of $d$ equals to $0.5$ times the smallest wavelength in the broadband signal. The algorithms starts with a uniform grid with $0.5^{\circ }$ resolution, i.e., $n=360$, and $\Phi \in \mathbb {C}^{4 \times 360}$. In DOA tracking simulation, we select starting DOA locations first. The future DOA locations are generated using (9.30). The starting $\dot{\theta }(t)=0.5^0$ and $\gamma =0.05$. The simulations are performed using MATLAB7.

5.1 Narrowband DOA Estimation and Tracking

Each narrowband signal is generated from a zero mean Gaussian distribution. The measurements are corrupted by temporally and spatially uncorrelated zero-mean noise sequence. At first we consider stationary DOA estimation. We assume the number of DOAs $k$ is unknown.

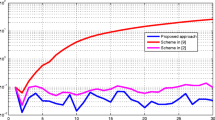
Figure 9.1a shows the spatial spectrum plots of the different algorithms when two uncorrelated sources are placed at $10^{\circ }$ and $15^{\circ }$. We take $N=50$ snapshots and $\mathrm {SNR}=2\,\mathrm {dB}$. Capon algorithm cannot separate sources. It indicates one source at $12^{\circ }$. $\ell _1$-SVD can separate two sources at $10^{\circ }$ and $13^{\circ }$. Hence detection bias is $2^{\circ }$. MAP algorithm can separate sources at $9.5^{\circ }$ and $15^{\circ }$. Hence bias in only $0.5^{\circ }$. Next, we investigate the impact of the noise power on the performance of algorithms. Here, we simulate two uncorrelated sources at $10^{\circ }$ and $15^{\circ }$. We keep the value of $N$ fixed at $50$ and vary the noise power. For each SNR, we carry out 100 independent simulations, and the results are shown in Fig. 9.1b, where we plot the frequency at which the different algorithms separate the sources against noise. Note that MAP outperforms the $\ell _1$-SVD. The plots for Capon is not shown, as they are unable to resolve the sources when $N < 140$.

Fig. 9.1

Separating two uncorrelated sources at $10^{\circ }$ and $15^{\circ }$ by different algorithms. a Spatial spectrum obtained by different algorithms. Signal $\mathrm {SNR}=2\,\mathrm {dB}$, $N=50$. b Frequency of separating sources versus SNR

Figure 9.2 shows the results when we simulate two strongly correlated sources at $10^{\circ }$ and $15^{\circ }$ with a correlation coefficient $0.99$. $\mathrm {SNR}=6\,\mathrm {dB}$ and $N=50$. Note that MAP can locate the sources clearly, while other methods generates single peak and failed separating sources.

Fig. 9.2

Separating two correlated sources at $10^{\circ }$ and $15^{\circ }$ by different algorithms. $\mathrm {SNR}=6\,\mathrm {dB}$, $N=50$

Fig. 9.3

DOA tracking for three targets. $\mathrm {SNR}=4\,\mathrm {dB}$, $N=50$. ‘$-$’ actual track, ‘$+$’ estimated track. a MAP, b $\ell _1$-SVD-MCS, c $\ell _1$-SVD, d Capon

Fig. 9.4

DOA tracking for three targets. $\mathrm {SNR}=4\,\mathrm {dB}$, $N=50$. ‘$-$’ actual track, ‘$+$’ estimated track. a MAP, b $\ell _1$-SVD-MCS, c $\ell _1$-SVD, d Capon

Fig. 9.5

Broadband DOA estimation results for three sources are located at $-10^{\circ }, 15^{\circ }$ and $20^{\circ }$. $\mathrm {SNR}=6\,\mathrm {dB}$, $N=100$. a MAP, b $\ell _1$-SVD, c Capon

Narrowband DOA tracking results are shown in Fig. 9.3. We consider three uncorrelated moving sources. The starting location of sources are $-20^{\circ },5^{\circ }$ and $10^{\circ }$ respectively. The average $\mathrm {SNR}=4\,dB$ and $N=50$. As can be seen in Fig. 9.3a MAP can track the sources almost accurately. There is a little error tracking the first source between time index $35$ and $45$. $\ell _1$-SVD-MCS can track sources until time index $25$. The interesting observation is that once $\ell _1$-SVD-MCS loses track of DOAs, it cannot back to the track again. As illustrated in Fig. 9.3b, after time index $25$, $\ell _1$-SVD-MCS cannot track second and third DOAs anymore. Instead, it generates some random walk around the track of first source. $\ell _1$-SVD can track the first source only. Capon also tracks first source. However, it generates another fictitious path from $40^{\circ }$ to $20^{\circ }$.

We consider another route in Fig. 9.4. The starting DOA locations are $-20^{\circ },5^{\circ }$ and $15^{\circ }$, respectively. In this scenario the first source crosses the route of other two sources. It is difficult to keep track of sources when they cross each other. Figure 9.4a illustrates that MAP is able to keep tracking the sources. In some cases, the estimated route of some sources are displaced from the actual route, however, MAP algorithm can back to the actual route of sources immediately. As before, $\ell _1$-SVD-MCS can track the sources until time index $25$. The algorithm loses the track of sources when the first and second sources cross each other. $\ell _1$-SVD and Capon failed tracking sources. Until time index $25$, both algorithms track the first sources, however, they start tracking the second source after time index $25$.

Fig. 9.6

Separating a broadband DOA in presence of jamming signal. The jamming signal comes from $1^0$ and actual source is at $20^0$. $N=100$

5.2 Broadband DOA Estimation and Tracking

Broadband sources are generated using the procedure [19]. Each source consists of $10$ sinusoids with frequencies randomly chosen from the interval $[1, 2.5]$ GHz. The received signal is sampled at $7.5$ GHz. The sampled data is filtered through a bank of first-order bandpass filters of the form

$$\begin{aligned} H_{\omega }(z) = \frac{(1-r) \mathrm {e}^{\mathrm {i}\omega }}{z - r \mathrm {e}^{\mathrm {i}\omega }} \end{aligned}$$

(9.46)

It can be shown that $H_{\omega }$ is a narrow-band filter centered at digital frequency $\omega$ (which is related to the analog frequency via the standard relationship). The bandwidth of the filter is controlled by $r$, where $0 < r < 1$. Taking $r \rightarrow 1$ makes the bandwidth smaller, but makes the filter less stable. We take $r = 0.99$. The filterbank consists of $50$ filters with center frequencies uniformly distributed over the interval $[1, 2.5]$ GHz.

Fig. 9.7

Broadband DOA tracking for four targets. $\mathrm {SNR}=4\,dB$, $N=100$. ‘$-$’ actual track, ‘$+$’ estimated track. a MAP, b $\ell _1$-SVD-MCS, c Capon

We simulate three broadband sources at $-10^{\circ },15^{\circ }$ and $20^{\circ }$ in Fig. 9.5. The $\mathrm {SNR}=6\,dB$ and $N=100$. As can be seen in Fig. 9.5, MAP algorithm separate three sources fairly accurately. The detected peaks are sharp and clear. $\ell _1$-SVD generates many spurious peaks and failed to locate the actual DOA locations. Capon roughly generates two peaks at $-9^{\circ }$ and $19^{\circ }$. However, It generates many other random peaks.

Figure 9.6 shows the source detection performance in presence of jamming signal. In this setup, a jammer sending signal at an angle $1^0$ with a $\mathrm {SNR}=40\,dB$. The actual source located at $20^0$ transmitting signal with $\mathrm {SNR}=2\,dB$. As can be seen, the proposed modification of MAP for jamming signal (MAP-Mod) in Sect. 9.4.1 can detect the actual source. However, when we are applying the conventional MAP, it detects jamming signal only.

Broadband DOA tracking results are shown in Fig. 9.7. We consider four moving sources. The starting location of sources are $-10^{\circ },15^{\circ }, 20^{\circ }$ and $30^{\circ }$, respectively. The $\mathrm {SNR}=4\,dB$ and $N=50$. As can be seen in Fig. 9.7a MAP can track the sources with reasonable accuracy.

6 Conclusion

A sparse signal reconstruction perspective for source localization and tracking has been proposed. We started with a scheme for localizing narrowband sources and developed a tractable MAP-based optimization approach which can exploit the joint-sparsity arises in the source localization problem. The scheme has been extend for wideband source localization. However, the resulting optimization was nonconvex. Hence, we propose an approach similar to the concept of GNC to cope with the issue. We described how to efficiently mitigate the local minima of the nonconvex optimization through an automatic method by choosing the regularization parameter. We then adopt the MAP formulation for narrowband and wideband source tracking scenario. In source tracking formulation, we utilize the information of current location and moving direction of DOA to estimate its future location. We modify the proposed MAP formulation so that it can use the information efficiently. Finally, we examined various aspects of our approach by using numerical simulations. Several advantages over existing source localization methods were identified, including increased resolution, no need for accurate initialization, and improved robustness to noise.

Some of the interesting questions for future research include an investigation of the applicability of GNC-based sparse recovery algorithms, which have a lower computational cost, to blind source localization. A theoretical study for determining the sequence $\wp _j(X)$ in (9.15) so that the algorithm can avoid local minima will be helpful.