Reliability Analysis for System with Random Failure Threshold

Abstract

Based on the degradation model and failure threshold probability distribution, the reliability analysis for system with random failure threshold is presented in this paper. The actual failure point of engineering system is unpredictable or random because of the system’s various uncertainties; which bring us a challenge to consider this problem in practical reliability analysis. An integrated methodology for reliability analysis with random failure threshold is developed in this paper, and both the degradation rate and the failure threshold uncertainty are considered in the deduction process. Moreover, the reliability analysis procedure for system with random failure threshold is given based on this method. In the end, the developed reliability analysis is demonstrated by an electro-hydrostatic actuator (EHA) system application example.

56.1 Introduction

The safety–critical nature of some systems used in aircraft, space, and some other application, specifies that the system’s key function should be guaranteed in the presence of subsystem failure. These mission-critical systems’ reliability is very important to the whole system safety; any drawback in design stage will bury some “bombs” to stop the continuous service. For completing the reliability index allocated by the father system, almost all the key component in the safety–critical system’s reliability will be analyzed thoroughly in complex system’s “V” style development procedure [1], both choosing the high-reliability component or optimizing the system structure will increase the reliability index.

Previous works by lots of scholars in this field have been focused on fault diagnosis, reliability analysis, and prognostic [2–6], which are rooted in the performance degradation model or path. Wang [7] establishes the mathematical model of quad redundant actuator (QRA), investigates the force equalization algorithm and carries out the performance degradation, simulation, and reliability analysis under the first failure and the second failure. Alejandro [8] proposes an integrated methodology for the reliability and dynamic performance analysis of fault-tolerant systems. Armen [9] gives a decomposition approach together with a linear programming formulation, which allows determination of bounds on the reliability of complex systems with manageable computational effort. Hao [10] considers the reliability modeling for the complex and dependent failure, and develops reliability models and preventive maintenance policies for such system, but in the soft failures model, only the established threshold is considered. Li [11] defines the vector-universal generating function and gives the operator to analyze the reliability of multi-state system with multiple performance parameter, and then proposes the procedure of reliability analysis based on this function. Arun [12] gives a reliability analysis of nuclear component cooling water system by the semi-Markov process model, because this model has potential to solve a reliability block diagram with a mixture of repairable and nonrepairable component. Utkin [13] considers the uncertainty of component reliability, which cannot describe the component behavior fully, and then gives the second-order uncertainty model for system reliability assessment, but in the aspect of system failure, we can sum this uncertainty in threshold uncertainty most of the time. Aven [14] discusses the use of uncertainty importance measures in reliability and risk analysis, and introduces a new type of combined sets of measures based on an integration of a traditional measure and a related uncertainty importance measure.

Nowadays, the reliability technology research for such hybrid or complex system has focus on the performance degeneracy system’s analysis. From the foregoing research, it is clear that various efforts have been made on such areas. However, there has less attention being paid to the uncertainty of threshold in engineering practice. According to the uncertainty of system degradation rate and the failure threshold in the complex operation environment, it’s necessary to consider the uncertainty items in the reliability analysis.

During the conventional reliability analysis, no matter for engineer or designer, the failure threshold is defined by experience and fixed. However, this assumption may not be valid in most situations, the failure threshold which the plant will shutdown is varied because of different operational environment, individual diversity, operator practice, etc. [15], the definitive value of failure cannot be given, the random failure threshold in actual operation presents challenging item to analyze the system reliability.

In this paper, the authors consider two specific subjects which are inevitable in practice engineering, e.g., both uncertainties in system degradation rate and failure threshold, and then deduce the reliability analysis approach based on continuous smooth performance degradation process. During this process, the uncertainties are considered in a probabilistic or statistical way. In the end, we demonstrate the reliability analysis process on a realistic example: the EHA device. As the key component in flight control system, EHA is very important for both the flight performance and reliability, but its reliability contains more uncertainty because of its servo or follow-up characteristic [16]. The individual which works in flight control system shows uncertainty or difference with nominal characteristic. The example simulates the uncertainty in the failure threshold and degradation rate, and then utilizes the approach presented in this paper to analyze the system reliability as the system parameter cannot be given definitely.

The remainder of this paper is organized as follows. Section 56.2 presents the degradation model used in the following reliability analysis. Section 56.3 deduces the reliability analysis based on degradation model with random failure threshold. Moreover in Sect. 56.4, the system reliability analysis procedure is given. And then an example about the EHA is simulated and implemented to show the validity of the approach in Sect. 56.5. Finally, Sect. 56.6 summarizes the paper and offers some remarks.

56.2 Degradation Model

In practice engineering, almost all the complex systems are hybrid systems, e.g., they are composed by several different major subsystems. System failure can be reflected by the performance level’s decreasing, the continuous system performance degradation is an aging process. This type of failure is just called as the soft failure [10], and the performance point which the system fails is defined as failure threshold.

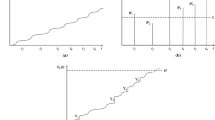
We can depict this process as the Fig. 56.1, the system will fails in the point which the whole performance degradation exceeds the actual failure threshold ${\text{Th}}_{\text{true}}$. In Fig. 56.1, the value d in different time t can be created by a system attribute parameter which can reflect the system performance, and the time t could be the real time or run cycles for system work.

Fig. 56.1

System degradation failure process

The degradation path in Fig. 56.1 is assumed to describe as

$$ x(t) = \alpha + \beta t . $$

(56.1)

where $\alpha$ is the system initial degradation value, and assumed to be constant, $\beta$ is the system degradation rate, which follows the normal distribution $\beta \sim N\left( {\mu_{\beta } ,\sigma_{\beta }^{2} } \right)$, and $\mu_{\beta }$, $\sigma_{\beta }$ are mean value and variance of degradation rate respectively.

According to the statement above, the ${\text{Th}}_{\text{true}}$ is failure threshold which actual failure occurs. Actually, the system failure threshold is given by engineer or designer with experience or accelerated life test, and the actual failure threshold ${\text{Th}}_{\text{true}}$ varies as the different environment. In this paper, we assume it to follow the normal distribution ${\text{Th}} \sim N\left( {\mu_{\text{Th}} ,\sigma_{\text{Th}}^{2} } \right)$, where $\mu_{\text{Th}}$, $\sigma_{\text{Th}}$ are mean value and variance of the failure threshold respectively.

56.3 Reliability Analyses for System with Random Failure Threshold

The reliability analysis for the hybrid system with complex system uncertainties should considers the various factors in system performance degeneracy process. For the system degradation process depicted by the Fig. 56.1, the probability that the system regress to less than some specified value $X$ at the time t is

$$ \Pr \left( {x(t) < X} \right) = \Pr \left( {\left( {\alpha + \beta t} \right) < X} \right) = \Pr \left( {\beta < \frac{X - \alpha }{t}} \right) . $$

(56.2)

As the degradation rate $\beta \sim N(\mu_{\beta } ,\sigma_{\beta }^{2} )$, so

$$ \Pr \left( {\beta < \frac{X - \alpha }{t}} \right) = \varPhi \left( {\frac{{\frac{X - \alpha }{t} - \mu_{\beta } }}{{\sigma_{\beta } }}} \right) = \varPhi \left( {\frac{{X - \alpha - \mu_{\beta } t}}{{t\sigma_{{_{\beta } }} }}} \right) . $$

(56.3)

If the failure threshold is known to be ${\text{Th}}_{\text{true}}$, the probability that the system is available or reliable before the time t is

$$ \Pr \left( {x(t) < {\text{Th}}_{\text{tre}} } \right) = \varPhi \left( {\frac{{{\text{Th}}_{\text{true}} - \alpha - \mu_{\beta } t}}{{t\sigma_{\beta } }}} \right) . $$

(56.4)

The probability distribution above is presented under the assumption that the ${\text{Th}}_{\text{true}}$ is known. Generally, the failure threshold is acquired by the engineer with experience or accelerated life test. We can assume that the ${\text{Th}}_{\text{true}}$ follows a normal distribution ${\text{Th}} \sim N\left( {\mu_{\text{Th}} ,\sigma_{\text{Th}}^{2} } \right)$.

Using the total probability formula

$$ \Pr \left( B \right) = \sum\limits_{i = 1}^{\infty } {\Pr \left( {A_{i} } \right)} P\left( {B/A_{i} } \right) . $$

(56.5)

Under the condition that the system will be failed in the failure threshold $({\text{Th}}_{d} ,{\text{Th}}_{u} )$, the probability $R_{s} (t)$ that the system will be reliable before the time t is

$$\begin{aligned} R_{s} (t) &= \int_{{{\text{Th}}_{d} }}^{{{\text{Th}}_{u} }} {\Pr \left( {{\text{Th}} = {\text{Th}}_{\text{true}} } \right)\int_{ - \infty }^{{\frac{{{\text{Th}}_{\text{true}} - \alpha - \mu_{t} t}}{{t\sigma_{\beta } }}}} {\frac{1}{{\sqrt {2\pi } }}e^{{ - \frac{{x^{2} }}{2}}} {\text{d}}x} } \\ &= \int\limits_{{{\text{Th}}_{d} }}^{{{\text{Th}}_{u} }} {\frac{1}{{\sqrt {2\pi } \sigma_{\text{Th}} }}} e^{{ - \frac{{(y - \mu_{\text{Th}} )^{2} }}{{2\sigma_{\text{Th}}^{2} }}}} \left( {\varPhi \left( {\frac{{y - a - t\mu_{\beta } }}{{t\sigma_{\beta } }}} \right)} \right){\text{d}}y \end{aligned}$$

(56.6)

where the $\varPhi ( \cdot )$ is the standard normal distribution function.

Because the failure threshold follows the normal distribution ${\text{Th}} \sim N\left( {\mu_{\text{Th}} ,\sigma_{\text{Th}}^{2} } \right)$, we can choose the upper and lower bound of threshold as $\mu_{\text{Th}} \pm 3\sigma_{\text{Th}}$, which guarantees the interval confidence up to 99.73 %.

56.4 The Reliability Analysis System Development Procedure

The Eq. (56.6) gives the probability that the system will be reliable before the time t in Sect. 56.3. So, through the experience or some other approaches, if we can get some system’s designated parameter for Eq. (56.6) in detailed, then the system’s reliability and some key factor’s effect on reliability can be analyzed.

Based on the probability equation above, the reliability analysis system development procedure can be listed as follow.

Step 1:

Analyze the subsystem or experience case, acquire the corresponding physical parameter data of the whole system operation process which varies from good to regression, and ends to system function failed.

Step 2:

Preprocess and identify the data, compare its error with the system parameter under ideal condition, and acquire the error or degradation model $x(t) = \alpha + \beta t$, including the initial degradation $\alpha$, and the mean value $\mu_{\beta }$, variance $\sigma_{\beta }$ of the degradation rate $\beta$.

Step 3:

Analyze the system failure point in degradation process, and then acquire the failure threshold ${\text{Th}} \sim N\left( {\mu_{\text{Th}} ,\sigma_{\text{Th}}^{2} } \right)$, including the threshold mean value $\mu_{\text{Th}}$, threshold variance $\sigma_{\text{Th}}$.

Step 4:

Compute the reliability and failure rate curves by the Eq. (56.6).

56.5 Numerical Examples: An Aircraft’s EHA Case

56.5.1 EHA Modeling and Simulation

According to flight control system’s actuating mechanism and the servo actuator’s mechanical wear characteristic, servo actuator’s performance or reliability is very important to the flight control system or aircraft, it has been seen as the key component in flight control system. Moreover, the EHA is widespread availability in the flight control field, which is composed by the controller or electric motor, piston, actuating cylinder, and the position feedback device.

As the Fig. 56.2 shows, the motor modulates the speed of rotation to change the flow, and then controls the piston’s position or control surface deflection.

Fig. 56.2

The simplified scheme of EHA driving the flight control surface

The EHA’s classical and main fault modes are relative to the mechanical and hydraulic component, which can be reflected by the system response. Based on the EHA’s physical characteristic analysis, the common fault mode contains motor demagnetization, actuator mechanical damage, and hydraulic cylinder friction exception. Especially the third fault mode, as the mechanical contact between piston and cylinder, it’s the main fault in EHA. The friction will changes the Motor damping factor $B_{m}$, Piston damping factor $B_{p}$ and Pump’s leak out factor $C_{t}$. In this example, we choose this fault mode to represent the system’s main fault, and analyze the reliability of it.

For gaining the physical parameter data of the whole system operation process which varies from good to regression, the EHA simulation model on Simulink is completed as the Fig. 56.3, whose explanation in detail can be found in [16].

Fig. 56.3

Simulation models for EHA

When the normal EHA system is motivated by the step command, the response of the system is showed in the Fig. 56.4. In Fig. 56.4, we can observe that the system tracking result is good.

Fig. 56.4

EHA model’s response in the normal condition

Using the simulation model above, we can simulate the key parameters’ variation which leads the system performance to failure level. In this process, the failure threshold of EHA is assumed to be stochastic, and the summed error of parameter from the normal value is chosen to be degradation value. Figure 56.5 gives the three parameters’ value point with stochastic failure threshold in 10 times system performance degradation simulation and average summed errors of the three parameters compared with the nominal value, the degradation interval in this simulation is assumed to 1,000 h in flight.

Fig. 56.5

The physical parameter decay and degradation path in simulation

56.5.2 Reliability Analysis

According to the data above, the parameter in Eq. (56.6) for reliability analysis with random failure threshold of EHA can be given as in Table 56.1, which is assumed to be known by experience in this reliability analysis.

Table 56.1 Parameter values for EHA’s reliability analysis

Using the Eq. (56.6), the reliability function $R_{s} (t)$ or probability that the system will be reliable before the time t is given in Fig. 56.6. In this situation, just like the Sect. 56.3’s explanation, we choose the upper and lower bound of the threshold to be $\mu_{\text{Th}} \pm 3\sigma_{\text{Th}}$.

Fig. 56.6

EHA’s reliability curves

And with the system mean life time definition ${\text{MTBF}}$

$$ {\text{MTBF}} = \int_{0}^{\infty } {R(t){\text{d}}t} . $$

(56.7)

We can compute the MTBF of EHA is $1.0224 \times 10^{4}$ h, this result is fit to the degradation process in the simulation as the Fig. 56.6.

56.6 Conclusions

In this article, the reliability analysis based on the degradation model with random failure threshold is developed for complex or key system, which actual failure threshold is unknown or has uncertainty in engineering. Using the total probability formula, the failure threshold interval is directed into the computation on system reliability. The reliability analysis is demonstrated on the realistic example about the EHA’s reliability analysis system development in aeronautical engineering, which shows the validation of the method presented in this paper.