Relativistic Effective Core Potentials

Abstract

The basic ideas of the effective core potential approach allowing for valence-only quantum chemical calculations implicitly including the most important relativistic effects are briefly outlined. The model potential and pseudopotential variants are described in their forms mostly applied for molecular electronic structure calculations. Effective core polarization potentials allowing to overcome some of the basic approximations underlying the effective core potential approach are also discussed.

Introduction

The effective core potential (ECP) approach is one of the oldest and still one of the most frequently used methods in relativistic quantum chemistry [1, 2]. Following chemical intuition, an atom is partitioned into a core and a valence electron system. The chemically inert core of the atom is considered to be frozen. It is removed from the explicit quantum chemical treatment, and its influence on a valence electron is modeled by an effective Hamiltonian, i.e., the ECP [3]. Thus, basic approximations underlying the ECP approach are the core-valence separation and the frozen-core approximation. On the one hand, ECPs lead to significant savings in the computations, especially for heavier atoms, since compared to an all-electron (AE) treatment only the smaller number of valence electrons has to be described explicitly. On the other hand, the corresponding valence-only model Hamiltonian can be constructed by replacing the relativistic operators with their nonrelativistic analogues, e.g., the nonrelativistic kinetic energy and the nonrelativistic Coulomb interaction, and still accounting for relativistic contributions implicitly by a suitable parametrization of the ECP to relativistic reference data.

The accuracy of a specific ECP thus depends on the accuracy of the underlying relativistic AE Hamiltonian it is designed to model. It also depends to a certain extent on the electronic structure method used to generate the suitable AE reference data for the adjustment of the ECP parameters. Last but not least, it is determined by the size of the core modeled by the ECP as well as by the chosen analytical ansatz for the ECP. In most approaches the ECP for a many-valence electron system is constructed as a sum over effective one-electron operators. Depending on whether the radial nodal structure of the AE valence orbitals is kept or simplified in the valence-only scheme, one works within the model potential (MP) [4] or the pseudopotential (PP) [5] approach.

The formal transformation from valence orbitals with the correct number of radial nodes used at the AE or MP level to the so-called pseudo-valence orbitals of the PP schemes exhibiting less radial nodes allows for the usage of smaller valence basis sets and thus leads to considerable computational savings. However, the elimination of radial nodes from the valence orbitals also leads to changes in the electron interaction between the valence electrons, which is not in all cases sufficiently compensated by the PP parametrization. Therefore, when using the same core-valence separation, the MP approach is potentially more accurate than the PP approach. Concerning the latter, aside from smaller frozen-core errors, small-core PPs usually exhibit smaller errors due to the pseudo-orbital transformation than large-core ones and are thus preferred for accurate calculations.

When going from an atom to a molecule, it is usually assumed that the atomic contributions behave additively, i.e., the molecular ECP is a superposition of the atomic ECPs. This assumption allows for an atomic parametrization of the ECPs, as well as an atomic optimization of the corresponding valence basis sets. In view of the about 120 elements in the periodic table as well as the various possible choices for the core size and the modeled relativistic Hamiltonian, this assumption is mandatory for efficiently generating consistent sets of ECPs which can be applied for all combinations of elements occurring in molecules.

Corrections to the assumption of superposition of atomic ECPs are nevertheless necessary for large cores, which exhibit in addition to the leading Coulomb repulsion between the cores modeled as point charges also deviations in their Coulomb interaction due to their extended and polarizable electron distributions as well as a noticeable additional repulsion due to the Pauli principle. Typically, the corresponding Pauli repulsion and mutual charge distribution penetration corrections can be approximated by those pairwise interactions between frozen spherical atomic cores, which go beyond their simple Coulomb point charge repulsion [6].

The ECPs further can be combined with so-called core polarization potentials (CPPs) , which are effective one- and two-electron operators and allow to correct somewhat for both the frozen-core approximation and the core-valence separation [7]. CPPs thus take into account the static polarizabilities of the atomic cores, as well as their dynamic polarizabilities, i.e., core-valence correlation [8]. In contrast to ECPs, the CPPs for many-valence electron systems are not merely sums of one-electron operators. Moreover, although constructed from atomic contributions, the molecular CPPs are not just superpositions of atomic terms. CPPs can be adjusted to both AE and experimental reference data.

Besides a parametrization based on ab initio AE reference data, the PP approach, usually then applied in combination with CPPs, also offers the possibility to adjust the free parameters in the analytical ansatz for the PP to experimental data [3]. Semiempirical energy-adjusted PPs based on experimental data for one-valence electron atoms and ions were derived for main group elements [9] as well as transition metals in configurations with closed d¹⁰ shells [6]. Difficulties arise for transition metals with open d and f shells, since due to the difficulties to accurately account for valence electron correlation effects a rigorous semiempirical adjustment is only possible for one-valence electron systems. However, when going from the corresponding one-valence electron ions to the neutral atom, large frozen-core errors arise, especially for elements with open d and f shells. Therefore, due to their more general applicability to all elements of the periodic table, the current article mainly focuses on the ab initio PP approaches.

The present article will briefly discuss the at present most frequently used ECPs, as well as CPPs, for standard molecular quantum chemical calculations. PPs used for quantum Monte Carlo (QMC) calculations or PPs used in connection with plane wave basis sets for density functional theory (DFT) calculations of solids are not described here. The list of references provided in this article is merely a selection of some representative articles, and as such it is incomplete. Further information on the topic, including the items omitted here, can be found in numerous review articles; cf., e.g., Schwerdtfeger [10] or Cao and Dolg [11] and the references cited therein.

General Considerations

A fundamental question before setting up an ECP approach is which AE Hamiltonian should be modeled by it. Various approximate relativistic many-electron schemes are at hand nowadays to generate suitable AE reference data for the ECP adjustment. In order to avoid any bias by finite basis sets, it is desirable to work with atomic structure codes using a finite difference scheme and to optimize suitable valence basis sets after the ECP has been constructed.

All-Electron Reference Approach

Consider a generic AE Hamiltonian for an atom with n electrons, i.e.,

$$\displaystyle{ \hat{H} =\sum _{ i=1}^{n}\hat{h}(i) +\sum _{ i=j+1}^{n}\sum _{ j=1}^{n-1}\hat{g}(i,j), }$$

(1)

where i and j stand for electron indices. Here and in the following, the expression X(i) denotes the dependence of the preceding term X on the position vector $\mathbf{r}_{i}$, whereas the dependence on only the distance is denoted by X(r _i ). Atomic units are used in the equations.

For a relativistic calculation, the one-electron operator $\hat{h}$ might be chosen as the Dirac (D) Hamiltonian

$$\displaystyle{ \hat{h}_{D}(i) = c\hat{\boldsymbol{\alpha }}_{i} \cdot \hat{\mathbf{p}}_{i} + (\hat{\boldsymbol{\beta }}_{i} -\mathbf{I}_{4})c^{2} + \hat{V }(r_{ i}), }$$

(2)

where the rest energy c ² of the electron was subtracted in order to get the same zero of energy as in the nonrelativistic case. Here, c stands for the velocity of light (c  ≈  137.0359895 a.u.). I ₄ corresponds to the 4 × 4 unit matrix. $\boldsymbol{\hat{\alpha }}$ and $\hat{\boldsymbol{\beta }}$ denote the 4 × 4 Dirac matrices

$$\displaystyle{ \boldsymbol{\hat{\alpha }} = \left (\begin{array}{ccc} {\boldsymbol{0}}_{2}& \boldsymbol{\hat{\sigma }} \\ \boldsymbol{\hat{\sigma }} &\boldsymbol{{0}}_{2} \end{array} \right )\qquad \text{and}\qquad \hat{\boldsymbol{\beta }} = \left (\begin{array}{ccc} \ \mathbf{I}_{2}& \ \mathbf{0}_{2} \\ \ \mathbf{0}_{2}& -\mathbf{I}_{2} \end{array} \right ), }$$

(3)

which can be written in terms of the three-component vector of the 2 × 2 Pauli matrices $\boldsymbol{\hat{\sigma }}$,

$$\displaystyle{ \hat{\boldsymbol{\sigma }}_{x} = \left (\begin{array}{ccc} 0&\ 1\\ 1 &\ 0 \end{array} \right ),\qquad \hat{\boldsymbol{\sigma }}_{y} = \left (\begin{array}{ccc} 0& - i\\ i & \ 0 \end{array} \right ),\qquad \hat{\boldsymbol{\sigma }}_{z} = \left (\begin{array}{ccc} 1& \ 0\\ 0 & -1 \end{array} \right ), }$$

(4)

the 2 × 2 unit matrix I ₂, and the 2 × 2 zero matrix 0 ₂. $\hat{\mathbf{p}}_{i} = -i\hat{{\boldsymbol \nabla }}_{i}$ is the momentum operator acting on the i-th electron, with the vector differential (del or nabla) operator $\hat{{\boldsymbol \nabla }}_{i} = (\partial /\partial x_{i},\partial /\partial y_{i},\partial /\partial z_{i})$.

Frequently, instead of the Coulomb point charge model

$$\displaystyle{ \hat{V }(r) = -\frac{Z} {r} }$$

(5)

a finite nuclear model is used, e.g., a Gaussian-type charge distribution

$$\displaystyle{ \rho _{\lambda }(r) =\rho _{0,\lambda }\ \mathrm{exp}(-\eta _{\lambda }r^{2})\qquad \text{with}\qquad 4\pi \ \int _{ 0}^{\infty }dr\ r^{2}\rho _{ \lambda }(r) = Z_{\lambda }. }$$

(6)

The parameter η _λ can be determined from the nuclear radius R _λ , which is related to the nuclear mass according to

$$\displaystyle\begin{array}{rcl} & & \eta _{\lambda } = 3/(2R_{\lambda }^{2})\qquad \text{with}\qquad R_{\lambda } = 2.2677 \times 10^{-5}M_{\lambda }^{1/3}.{}\end{array}$$

(7)

Other nuclear models, e.g., a hard sphere nucleus or a nucleus with a Fermi-type charge distribution, are also in use. It is important to note that the accuracy of modern ECPs can be so high that the parametrization can also include finite nucleus effects which are noticeable for heavy elements.

For the two-electron terms $\hat{g}$, the simplest choice is the nonrelativistic Coulomb (C) interaction

$$\displaystyle{ \hat{g}_{C}(i,j) = \frac{1} {r_{ij}}. }$$

(8)

Inclusion of the magnetic interaction between the electrons leads to the Gaunt (G) interaction

$$\displaystyle{ \hat{g}_{CG}(i,j) = \frac{1} {r_{ij}} -\frac{\boldsymbol{\hat{\alpha }}_{i} \cdot \boldsymbol{\hat{\alpha }}_{j}} {r_{ij}}, }$$

(9)

which includes the most important correction of the nonrelativistic Coulomb (C) interaction. Including the retardation of the interaction due to the finite velocity of light leads to the Breit (B) interaction in its low-frequency limit for the exchanged photon

$$\displaystyle{ \hat{g}_{CB}(i,j) = \frac{1} {r_{ij}} - \frac{1} {2r_{ij}}\left [\boldsymbol{\hat{\alpha }}_{i} \cdot \boldsymbol{\hat{\alpha }}_{j} + \frac{(\boldsymbol{\hat{\alpha }}_{i} \cdot \mathbf{r}_{ij})(\boldsymbol{\hat{\alpha }}_{j} \cdot \mathbf{r}_{ij})} {r_{ij}^{2}} \right ]. }$$

(10)

Inserted together with the Dirac Hamiltonian $\hat{h}_{D}$ (Eq. 2) into the generic Hamiltonian (Eq. 1), these three choices for $\hat{g}$ lead to the Dirac-Coulomb (DC), Dirac-Coulomb-Gaunt (DG), and Dirac-Coulomb-Breit (DCB) Hamiltonian, respectively. For heavy atoms, the latter Hamiltonian has to be augmented to include also low-order effects from quantum electrodynamics (QED), i.e., a frequency-dependent expression of the Breit interaction, the electron self-energy, and the vacuum polarization, leading to the best Hamiltonian which can currently be applied routinely in atomic structure calculations, e.g., using computer codes such as GRASP (general relativistic atomic structure package) [12]. These are usually carried out at the multi-configuration finite difference Dirac-Hartree-Fock (MCDHF) level to obtain suitable reference data for the determination of the ECPs.

When answering the initial question which relativistic Hamiltonian the valence-only approach should model, one has to consider the errors inherent to the ECP approach as well as possible errors due to the use of finite basis sets and the applied computational method in practical calculations. It is well known that the total nonrelativistic energy of an atom roughly increases with the nuclear charge to the second power, whereas relativistic corrections to it increase with the nuclear charge to the fourth power. In contrast to this, for a fixed number of valence electrons, the elements of a group of the periodic table are treated on equal footing within the ECP schemes, and the corresponding ECP errors are roughly the same for all members of the group. Thus, whereas for light elements the DC point nucleus Hamiltonian or approximations to it are usually sufficiently accurate, reference data based on at least the finite nucleus DCB Hamiltonian becomes mandatory for heavy elements. Since nowadays atomic electronic structure codes featuring the DC and DCB Hamiltonians are at hand, modern ECPs use the corresponding AE reference data. Some older, but nevertheless still very popular, sets of ECPs are based on approximate relativistic schemes such as the Wood-Boring [13] or Cowan-Griffin [14] relativistic HF approaches.

Table 1 lists relative energies of selected low-lying electronic states of roentgenium (Rg, eka-Au, Z = 111) calculated at the HF and MCDHF level using various forms of the Hamiltonian. The corresponding differential effects, i.e., contributions to the energy differences, are provided in Table 2. It is clear that for an element as heavy as Rg relativistic contributions arising from the Dirac one-particle Hamiltonian Δ _DC are huge and have to be included. This is also obvious from the corresponding huge orbital contraction (7s_1∕2 vs. 7s) and noticeable expansion (6d_5∕2 vs. 6d) of the valence orbitals depicted in Fig. 1. However, also the contributions due to a finite nuclear model Δ _fn , the Breit two-electron interaction Δ _B , and even low-order quantum electrodynamic contributions Δ _QED are above the accuracy typically achieved for modern ECP approaches in such energy differences, i.e., 0.01 eV or better.

Table 1 Energies (eV) relative to the ground J level of selected low-lying electronic states of roentgenium (Rg) (Z = 111) [12]

Table 2 Various contributions to energies (eV) relative to the ground J level of selected low-lying electronic states of roentgenium (Rg) (Z = 111) [12]

Fig. 1

Large components of the relativistic 6d_3∕2, 6d_5∕2, and 7s_1∕2 MCDHF/DC AE spinors of roentgenium (Rg) (Z = 111) in its 6d⁹ 7s² ground state configuration in comparison to corresponding nonrelativistic HF orbitals [12]. For the corresponding orbital energies, cf. Fig. 2

Frozen-Core Approximation

The most straightforward approach to formally reduce the explicit treatment to the valence electron system is the frozen-core approximation. The valence-only Hamiltonian can be written as

$$\displaystyle{ \hat{H}_{v} =\sum _{ i=1}^{n_{v} }\left [\hat{t}(i) + \hat{V }_{cv}(i)\right ] +\sum _{ i=j+1}^{n_{v} }\sum _{j=1}^{n_{v}-1}\hat{g}(i,j). }$$

(11)

Here n _v denotes the number of explicitly treated valence electrons, which adds up with the number of core electrons n _c to the total number of electrons n = n _v + n _c . $\hat{t}$ represents the kinetic energy operator in the one-electron Hamiltonian $\hat{h}$ in Eq. 1, and $\hat{V }_{cv}$ is the nonlocal potential for the interaction of a valence electron with the nucleus and the fixed core electron system. Besides the Coulomb potential arising from the nucleus, the latter contains a sum over Coulomb operators $\hat{J}_{k}$ and exchange operators $\hat{K}_{k}$ constructed from the n _c ∕2 doubly occupied core orbitals, i.e., in the case of a point nucleus, it reads

$$\displaystyle{ \hat{V }_{cv}(i) = -\frac{Z} {r_{i}} +\sum _{ k=1}^{n_{c}/2}\left [2\hat{J}_{ k}(i) -\hat{K}_{k}(i)\right ]. }$$

(12)

Clearly, the computational savings are small, if they are present at all, since the core orbitals have to be determined in advance and the full primitive AE basis sets are required to correctly describe the valence orbitals. However, atomic frozen-core AE calculations are a useful tool to assess the potential accuracy of ECPs applying a corresponding core definition .

Atomic Effective Core Potentials

Effective core potentials are constructed to model the DCB finite nucleus Hamiltonian, or some approximation of it, by using a parametrized valence-only Hamiltonian circumventing or at least simplifying the explicit construction of $\hat{V }_{cv}$ from AE solutions. Hereby, a suitable compromise between computational efficiency and accuracy is sought. The valence-only Hamiltonian is thus kept simple, but still offers enough flexibility to compensate the approximations underlying the ECP approach by a suitable adjustment to AE reference data. In most of the ECP schemes, the nonrelativistic kinetic energy is used in $\hat{h}$, and the nonrelativistic Coulomb interaction between electrons is assumed for $\hat{g}$. In the resulting, formally nonrelativistic valence-only model Hamiltonian

$$\displaystyle{ \hat{H}_{v} = -\frac{1} {2}\sum _{i=1}^{n_{v} }\nabla _{i}^{2} +\sum _{ i=j+1}^{n_{v} }\sum _{j=1}^{n_{v}-1} \frac{1} {r_{ij}} +\sum _{ i}^{n_{v} }\hat{V }_{cv}(i) }$$

(13)

the core-electron interaction terms $\hat{V }_{cv}$ have to be chosen so that results of calculations using the underlying AE Hamiltonian are reproduced as closely as possible in calculations using a corresponding method for approximately solving the Schrödinger equation, e.g., by matching results of AE calculations at the DHF level and corresponding ECP calculations at the two-component HF level. The whole machinery of nonrelativistic quantum mechanics can be used if a spin-free form of $\hat{V }_{cv}$ is used. Either spin-orbit (SO) coupling is neglected or averaged out at the level of the AE reference calculations prior to the parametrization of a one-component ECP, or the two-component ECP adjusted to AE reference data including SO effects is averaged after the adjustment. The resulting scalar-relativistic valence-only Hamiltonians might lead to slightly different results .

Choice of the Core

A basic question, besides which Hamiltonian the valence-only approach should model, is how large the atomic core to be replaced by the ECP should be. Larger cores make the calculations less expensive, whereas smaller cores usually allow for a higher accuracy due to smaller frozen-core errors as well as a better transferability from the atom to the molecule. A suitable compromise has to be found for routine calculations. Criteria for assigning shells to the core and valence space, respectively, are orbital energies and the shape of the corresponding radial functions. Some hints for an efficient choice of the core can also be obtained by performing atomic AE frozen-core calculations. It frequently turns out that the chemical core, e.g., the core implied by the ordering of the elements in the periodic system, is not a very accurate choice, and smaller cores are preferable.

A spatial criterium for separating core and valence orbitals based on the extension of the radial functions leads to smaller cores and usually to more accurate valence-only schemes than the energetic criterium based on orbital energies, which favors larger cores. Thus, a separation including all occupied shells of a given main quantum number n, as well as those with higher main quantum numbers, in the valence is favored nowadays. In the case of nd (n = 3, 4, 5, 6) transition metals, this corresponds to ns, np, nd, and (n + 1)s in the valence space, whereas for nf elements (n = 4 lanthanides, n = 5 actinides) ns, np, nd, nf, (n + 1)s, (n + 1)p, (n + 1)d, and (n + 2)s are attributed to the valence space for accurate parametrizations [15]. For heavy main group elements, e.g., those which have one or more filled d shells, a choice analogous to the one made for the transition metals provides a sufficiently high accuracy.

Table 3 lists frozen-core errors for a small-core (1s – 5f) and medium-core (1s – 6p) approximation for roentgenium (Rg). Only the small-core choice can provide an accuracy of 0.01 eV or better. The medium-core approximation is suggested by the orbital energies plotted in Fig. 2, both at the nonrelativistic and the relativistic level. However, the radial overlap of 6d and the 6s, 6p semicore orbitals is obviously too large to allow high accuracy, and, e.g., noticeable errors in energy differences depending on the 6d occupation number arise. Clearly, the large-core (1s – 6d) option is not possible for Rg due to the relativistically induced d⁹s¹ ground state configuration. The differential relativistic effect in the d¹⁰s¹ - d⁹s¹ energy difference amounts to more than 9 eV; cf. Table 2. Figure 2 shows the strong stabilization of 7s and the destabilization of 6d due to dominating direct and indirect relativistic effects, respectively. The corresponding orbital contraction and respective expansion are visualized by the 〈r〉 expectation values in Fig. 3. The large-core choice is also too inaccurate for the lighter homologue Au despite its d¹⁰s¹ ground state configuration, but it works reasonably well for the still lighter members of the group Ag and especially Cu [6].

Fig. 2

Orbital energies of roentgenium (Rg) (Z = 111) in its 6d⁹ 7s² ground state configuration from nonrelativistic HF and relativistic MCDHF/DC AE calculations [12]

Fig. 3

Radial expectation values 〈r〉 of roentgenium (Rg) (Z = 111) in its 6d⁹ 7s² ground state configuration from nonrelativistic HF and relativistic MCDHF/DC AE calculations [12]

Table 3 Frozen-core errors (eV) in total MCDHF/DC energies relative to the ground J level of selected low-lying electronic states of roentgenium (Rg) (Z = 111) using the Rg d⁹ s² ground state configuration core orbitals [12]

In special cases it is even possible to define open-shell cores, which correspond to an average over all states arising from the core electron configuration. In the case of lanthanides as well as (heavier) actinides, the f-in-core approximation can be successfully used in electronic structure calculations to treat an atom/ion with a given valency, corresponding to a fixed f occupation number, in molecules [11].

Nodes or No Nodes?

Another important question is if the radial nodal structure of the AE valence orbitals should be kept in the valence-only scheme or if a formal transformation to pseudo-valence orbitals with less radial nodes should be performed. Keeping the radial nodal structure unchanged has the advantage of being able to use unchanged AE operators in the calculations, whereas for pseudo-valence orbitals at least the operators sampling mainly the core region have to be transformed or effective operators have to be constructed. A typical and important example is the SO term of Pauli-type relativistic Hamiltonians, e.g., the Wood-Boring Hamiltonian, which exhibit a Z∕r ³ dependence. If such operators are used in calculations with pseudo-valence orbitals, the (effective) nuclear charge Z is merely an adjustable parameter and loses it physical meaning. It also turned out, especially for large cores, that valence correlation energies as well as, e.g., multiplet splittings are more accurate when the radial nodal structure of the valence orbitals is kept unchanged. This is related to a possible overestimation of exchange integrals, especially between valence orbitals for which a different number of radial nodes was removed [16]. On the other hand, it was found that for energy differences of chemical interest the related errors often cancel [17].

The main advantage of using pseudo-valence orbitals is the reduced basis set requirements, since the oscillations of the valence orbitals in the core region resulting from explicit orthogonality constraints with respect to the core orbitals are replaced by a smooth shape. A comparison between AE valence orbitals [12] and the corresponding pseudo-valence orbitals of an energy-consistent PP [18] is provided for roentgenium in Figs. 4 and 5. As seen from Fig. 4, the pseudo-valence orbitals virtually agree with the corresponding AE valence orbitals in the spatial valence region, e.g., for distances of more than 1.5 Bohr from the nucleus. In the spatial core region, which is emphasized by the logarithmic scale of the r axis in Fig. 5, the pseudo-valence orbitals decay quickly and smoothly when approaching the nucleus. The two options, keeping the number of radial nodes unchanged and reducing it, lead to the model potential (MP) [4] and pseudopotential (PP) [19, 20] approach, respectively.

Fig. 4

Large components of the 6d_3∕2, 6d_5∕2, and 7s_1∕2 MCDHF/DC AE spinors of roentgenium (Rg) (Z = 111) in its 6d⁹ 7s² ground state configuration in comparison to corresponding pseudo-valence orbitals of a MCDHF/DC+B-adjusted small-core PP (Q = 19) [12, 18]

Fig. 5

As in Fig. 4, but for a logarithmic scale of the radius r

Pseudopotentials

Pseudopotentials (PPs) , in a semiempirical form, were historically the first [3] and, in their ab initio form, are still the most widely used [10] ingredients for the core-electron interaction $\hat{V }_{cv}$ in the valence-only Hamiltonian (Eq. 13) of an atom. The theoretical foundation for the PP approach was set in 1959 by Phillips and Kleinman within an effective one-valence electron framework [5]. A generalization to many-valence electron cases was provided in 1968 by Weeks and Rice [21]. In the so-called generalized Phillips-Kleinman (GPK) equation, the valence electron Hamiltonian $\hat{H}_{v}$ is supplemented by the GPK PP $\hat{V }^{GPK}$,

$$\displaystyle{ \left (\hat{H}_{v} + \hat{V }^{\mathrm{GPK}}\right )\mathinner{\vert \varPhi _{ p}\rangle } = E_{v}\mathinner{\vert \varPhi _{p}\rangle }. }$$

(14)

Here, E _v denotes the total valence energy, and | Φ _p 〉 is a many-electron pseudo-valence eigenfunction. The term pseudo used here means that, e.g., Φ _p is built from orbitals which may have a different radial nodal structure than the AE valence orbitals. The original AE valence eigenfunction Φ _v is assumed to fulfill the following Schrödinger equation:

$$\displaystyle{ \hat{H}_{v}\mathinner{\vert \varPhi _{v}\rangle } = E_{v}\mathinner{\vert \varPhi _{v}\rangle }. }$$

(15)

Φ _v and Φ _p are related by a projection operator $1 -\hat{P}_{c}$, which projects out any core components in the wave function it acts on, i.e.,

$$\displaystyle{ \mathinner{\vert \varPhi _{v}\rangle } = (1 -\hat{P}_{c})\mathinner{\vert \varPhi _{p}\rangle }. }$$

(16)

By substituting Φ _v in Eq. 15 by this expression, acting from the left with $1 -\hat{P}_{c}$, exploiting the idempotency of $\hat{P}_{c}$, and comparing to Eq. 14, one arrives the following expression for the GPK PP

$$\displaystyle{ \hat{V }^{\mathrm{GPK}} = -\hat{H}_{ v}\hat{P}_{c} -\hat{P}_{c}\hat{H}_{v} + \hat{P}_{c}\hat{H}_{v}\hat{P}_{c} + E_{v}\hat{P}_{c}, }$$

(17)

which is a nonlocal, energy-dependent many-electron operator still requiring the notion of the solutions for the core electron system.

Eqs. 14, 15, 16, and 17 are by no means easier to solve than corresponding frozen-core HF AE equations. They demonstrate, however, that the correct total valence energy can be obtained by a valence electron eigenfunction which has a simplified form, e.g., a simpler radial nodal structure of the underlying orbitals. An explicit orthogonality of the core and valence electron wave functions is not required anymore. This can be more easily seen by looking at the case of a single valence electron outside a closed-shell core treated at the HF level. The valence Hamiltonian $\hat{H}_{v}$ then reduces to a Fock operator $\hat{F}$; the AE and pseudo-valence wave functions Φ _v and Φ _p then correspond to the AE valence and PP pseudo-valence orbitals φ _v and φ _p , respectively. The total valence energy E _v is replaced by the valence orbital energy ε _v . Assuming that the core orbitals φ _c are also eigenfunctions of the Fock operator $\hat{F}$ with eigenvalues ε _c , one can set up the so-called Phillips-Kleinman (PK) equation

$$\displaystyle{ \left (\hat{F} +\sum _{c}(\epsilon _{v} -\epsilon _{c})\mathinner{\vert \varphi _{c}\rangle }\mathinner{\langle \varphi _{c}\vert }\right )\mathinner{\vert \varphi _{p}\rangle } =\epsilon _{v}\mathinner{\vert \varphi _{p}\rangle }. }$$

(18)

Any pseudo-valence orbital φ _p which is a mixture of the original AE valence orbital φ _v and the core orbitals φ _c satisfies this equation and yields the correct eigenvalue ε _v . One can now seek solutions for which the energetically lowest one is free of radial nodes and thus requires only a reduced basis set for an accurate description.

However, for practical calculations, both the PK and the GPK equations are of no use, since in both cases the core-type solutions also have to be known. Moreover, restricting the pseudo-valence orbitals to be linear combinations of the original valence orbitals and the core orbitals leads to too compact radial functions and to related errors in molecular calculations, e.g., too short bond distances and too high binding energies. Therefore, for practical applications, further simplifications are necessary, and, in principle, the (formal) admixture of virtual orbitals has also to be allowed when building the pseudo-valence orbitals.

Essentially all PP approaches neglect the many-electron character and the energy dependence of the PK and GPK potentials, i.e., they use sums of effective one-electron Hamiltonians. The leading term of the core-valence interaction is the Coulomb interaction between the core, assumed as a point charge Q = Z − n _c , and the valence electron i

$$\displaystyle{ \hat{V }_{cv}^{PP}(i) = -\frac{Q} {r_{i}} +\varDelta \hat{ V }_{cv}(i). }$$

(19)

The analytical forms of the correction $\varDelta \hat{V }_{cv}$ are discussed in the following .

Local Form

Historically, a local potential of Yukawa type was used by Hellmann [3] in his 1935 study of the K atom:

$$\displaystyle{ \varDelta \hat{V }_{cv}(i) = \frac{2.74} {r} e^{-1.16r}. }$$

(20)

One disadvantage of the local ansatz is, e.g., that the valence energies for a given pseudo-main quantum number $\tilde{n}$ increase with the angular momentum quantum number l. This ordering is not always fulfilled, e.g., the (n−1)d^{1 2}D states of Ca⁺, Sr⁺, and Ba⁺ are found experimentally below the np^{1 2}P states.

Semilocal Form

For the deviation from the Coulomb potential, a semilocal form is used in modern PPs [20], e.g., for scalar-relativistic calculations, the ansatz is

$$\displaystyle{ \varDelta \hat{V }_{cv}(i) =\sum _{ l=0}^{l=\infty }V _{ l}(r_{i})\hat{P}_{l}(i). }$$

(21)

Here, $\hat{P}_{l}$ denotes an angular momentum projection operator based on spherical harmonics | lm〉

$$\displaystyle{ \hat{P}_{l}(i) =\sum _{ m=-l}^{m=l}\mathinner{\vert lm\rangle }\mathinner{\langle lm\vert }. }$$

(22)

Usually, the radial potentials V _l are very similar for angular momenta which are higher than those present in the core. Thus, a simpler approximate ansatz can be used, i.e.,

$$\displaystyle{ \varDelta \hat{V }_{cv}(i)\cong V _{L}(r_{i}) +\sum _{ l=0}^{L-1}[V _{ l}(r_{i}) - V _{L}(r_{i})]\hat{P}_{l}(i), }$$

(23)

where L − 1 denotes the largest angular momentum of any of the core orbitals.

Relativistic calculations including SO coupling require a modified semilocal ansatz [22, 23] such as

$$\displaystyle{ \varDelta \hat{V }_{cv}(i) =\sum _{ l=0}^{l=\infty }\sum _{ j=\vert l-\frac{1} {2} \vert }^{j=l+\frac{1} {2} }V _{lj}(r_{i})\hat{P}_{lj}(i), }$$

(24)

where now $\hat{P}_{lj}$ denotes the projector on spinor spherical harmonics | ljm > 

$$\displaystyle{ \hat{P}_{lj}(i) =\sum _{ m=-j}^{m=j}\mathinner{\vert ljm\rangle }\mathinner{\langle ljm\vert }. }$$

(25)

Again, the summation over angular symmetry may be truncated at L, when L − 1 stands for the highest angular quantum number present in the core, i.e.,

$$\displaystyle{ \varDelta \hat{V }_{cv}(i)\cong V _{L}(r_{i}) +\sum _{ l=0}^{l=L-1}\sum _{ j=\vert l-\frac{1} {2} \vert }^{j=l+\frac{1} {2} }[V _{lj}(r_{i}) - V _{L}(r_{i})]\hat{P}_{lj}(i). }$$

(26)

SO coupling usually lowers the symmetry and therefore makes quantum chemical investigations more expensive. It is thus advisable to use SO coupling as late as possible in the calculations. The options are, e.g., to perform a SO-CI after standard SO averaged configuration interaction (CI) or coupled cluster (CC) calculations for the interacting states in the basis of correlated scalar-relativistic (LS or Λ S) states, to perform the SO-CI in the basis of determinants and thus include electron correlation and SO coupling on the same footing, or to include it from the very beginning in the SCF process. The latter one-step approach is closest to modeling the underlying two- or four-component Hamiltonian, but it is also more costly than the two previous two-step procedures.

For the two-step procedures in which SO coupling is treated after the scalar-relativistic HF or even CI level, the relativistic PP in Eqs. 24 or 26 is splitted up in a spin-free (spin-dependent terms neglected or averaged, av) and a spin-dependent (spin-orbit, so) part

$$\displaystyle{ \varDelta \hat{V }_{cv}(i) =\varDelta \hat{ V }_{av}(i) +\varDelta \hat{ V }_{so}(i). }$$

(27)

The one-component PP $\varDelta \hat{V }_{av }$ can be obtained from the two-component one by applying the relations for the projection operators

$$\displaystyle{ \hat{P}_{l}(i) =\sum _{j}\hat{P}_{lj}(i) =\hat{ P}_{l,\vert l-\frac{1} {2} \vert }(i) +\hat{ P}_{l,l+\frac{1} {2} }(i) }$$

(28)

and radial potentials

$$\displaystyle{ V _{l}(r_{i}) = \frac{1} {2l + 1}[lV _{l,\vert l-\frac{1} {2} \vert }(r_{i}) + (l + 1)V _{l,l+\frac{1} {2} }(r_{i})]. }$$

(29)

The scalar-relativistic PP $\varDelta \hat{V }_{av}$ formally corresponds to the PPs defined in Eqs. 21 or 23. The corresponding SO term reads as

$$\displaystyle{ \varDelta \hat{V }_{so}(i) =\sum _{ l=1}^{L-1}\frac{\varDelta V _{l}(r_{i})} {2l + 1} [l\hat{P}_{l,l+1/2}(i) - (l + 1)\hat{P}_{l,l-1/2}(i)]. }$$

(30)

Here, Δ V _l is the difference between the relativistic radial potentials for the corresponding l value

$$\displaystyle{ \varDelta V _{l}(r_{i}) = V _{l,l+\frac{1} {2} }(r_{i}) - V _{l,\vert l-\frac{1} {2} \vert }(r_{i}). }$$

(31)

A simpler form of the SO PP $\varDelta \hat{V }_{so}$, which is especially suited for use in SO-CI calculations following a scalar-relativistic HF solution, was proposed by Pitzer and Winter [24]:

$$\displaystyle{ \varDelta \hat{V }_{so}(i) =\sum _{ l=1}^{L-1}\frac{2\varDelta V _{l}(r_{i})} {2l + 1} \hat{P}_{l}(i)\hat{\mathbf{l}}_{i} \cdot \hat{\mathbf{s}}_{i}\hat{P}_{l}(i). }$$

(32)

An alternative way to include SO coupling in PP calculations is the usage of a Pauli-type SO operator

$$\displaystyle{ \varDelta \hat{V }_{so}(i) = \frac{\alpha ^{2}} {2} \frac{Z_{\mathrm{eff}}} {r_{i}^{3}} \hat{\mathbf{l}}_{i} \cdot \hat{\mathbf{s}}_{i}. }$$

(33)

In contrast to Eq. 32, this form of the SO term is not variationally stable and can only be used in perturbation theory. Moreover, due to the altered shape of the pseudo-valence orbitals in the core region, the parameter Z _eff takes values which are far from those of an effective nuclear charge.

The angular parts of the ECPs given in Eqs. 23 and 26 are fixed in the semilocal ansatz. The radial potentials however have to be parametrized. In order to be able to perform calculations on multicenter systems, where mainly Gaussian basis sets are applied, the radial potentials are usually represented by linear combinations of Gaussian functions multiplied by powers of r

$$\displaystyle{ V _{m}(r_{i}) =\sum _{k}A_{km}r_{i}^{n_{km} }e^{-a_{km}r_{i}^{2} }\qquad \text{with}\qquad m = l,lj,L. }$$

(34)

The free parameters A _km , a _km have to be determined by a suitable adjustment to AE reference data, as will be discussed in section “Adjustment”. For integrability, n _km  ≥ −2 is required. Integrals over semilocal PPs as well as the corresponding SO terms for Cartesian Gaussian basis functions were derived, e.g., by McMurchie and Davidson [25] and Pitzer and Winter  [24, 26].

Nonlocal Form

The integral evaluation over semilocal pseudopotential operators is quite involved and may become quite costly if many centers in the system are bearing PPs. Pélissier et al. therefore proposed a transformation of the atomic semilocal part $V _{l}\hat{P}_{l}$ of the PPs in Eqs. 21 and 23 into a nonlocal form [27]

$$\displaystyle{ \hat{\tilde{V }}_{l}(i) =\sum _{j}\sum _{k}A_{jk}\mathinner{\vert g_{j}(i)\rangle }\mathinner{\langle g_{k}(i)\vert }. }$$

(35)

Here, the | g _j 〉 are orthonormalized linear combinations of Cartesian Gaussian functions

$$\displaystyle{ \left < \mathbf{r}\vert g_{j}\right > =\sum _{k}B_{jk}x^{l_{jx} }y^{l_{jy} }z^{l_{jz} }e^{-b_{jk}r^{2} }\qquad \text{with}\qquad l_{jx} + l_{jy} + l_{jz} = l. }$$

(36)

The parameters in Eq. 35 can be determined by minimizing the sum S of squared differences of matrix elements over $\hat{\tilde{V }}_{l}$ and V _l for a large atom-centered basis set { | χ _j 〉} of appropriate angular symmetry l

$$\displaystyle{ S =\sum _{jk}\left (\mathinner{\langle \chi _{j}\vert }\hat{\tilde{V }}_{l}\mathinner{\vert \chi _{k}\rangle } -\mathinner{\langle \chi _{j}\vert }V _{l}\mathinner{\vert \chi _{k}\rangle }\right )^{2}. }$$

(37)

The nonlocal operator $\hat{\tilde{V }}_{l}$ can further be cast into a simpler form by diagonalizing the matrix of the coefficients A _jk :

$$\displaystyle{ \hat{\tilde{V }}_{l}(i) =\sum _{j}\bar{A}_{j}\mathinner{\vert \bar{g}_{j}(i)\rangle }\mathinner{\langle \bar{g}_{j}(i)\vert }. }$$

(38)

Here, $\bar{A}_{j}$ and $\mathinner{\vert \bar{g}_{j}\rangle }$ denote the resulting eigenvalues and eigenvectors of the [A _jk ] matrix in the original { | g _j 〉} basis. The integral evaluation in molecular calculations is thus reduced to the calculation of overlap integrals between the molecular basis and the expansion basis $\{\mathinner{\vert \bar{g}\rangle }\}$. Similarly, the evaluation of derivatives of PP matrix elements with respect to the nuclear coordinates, which are needed in energy gradients for geometry optimizations, involves only the computation of derivatives of these overlap integrals .

Adjustment

For the adjustment of the free parameters in the radial PPs of the semilocal ansatz, two approaches differing in the type of AE reference data are in use today, i.e., the shape-consistent approach based on one-particle energies and wave functions (e.g., orbital energies and orbitals or spinor energies and spinors) or the energy-consistent approach relying exclusively on total valence energies. Thus, whereas the shape-consistent approach makes use of quantities defined only within an effective one-particle picture, the energy-consistent approach is based on quantum mechanically observable energy differences, i.e., excitation energies, ionization potentials, and electron affinities, and makes no use of wave function information.

Shape-Consistent Approach

The main idea of the shape-consistent approach [28, 29] is to select one suitable atomic reference state, to keep the orbital energy ε _p of the PP calculation at the value of the AE reference calculation ε _v and to reproduce with the pseudo-valence orbital φ _p, lj exactly the radial shape of the AE valence orbital φ _v, lj in the spatial valence region, e.g., outside a reasonably chosen critical radius (r ≥ r _c ). In the spatial core region (r < r _c ), the pseudo-valence orbital is represented by an auxiliary function f _lj , i.e.,

$$\displaystyle{ \varphi _{p,lj}(r) = \left \{\begin{array}{rcl} \varphi _{v,lj}(r)&\mathrm{for}&r \geq r_{c} \\ f_{lj}(r)&\mathrm{for}&r < r_{c} \end{array} \right.\qquad \text{and}\qquad \epsilon _{p,lj} =\epsilon _{v,lj}. }$$

(39)

Usually, a polynomial is used for f _lj , which is required to be radially nodeless and smooth, fulfills certain matching conditions at r _c , and leads to a normalized pseudo-valence orbital. In the case of reference data taken from, e.g., MCDHF/DC calculations, the renormalized upper (large) components of the spinors are used for φ _v, lj . The lower (small) components influence the radial density mainly in the core region, which is modified by the usage of f _lj anyhow, and can thus be neglected.

Once the pseudo-valence orbital φ _p, lj has been constructed, the radial part V _lj (r) of the corresponding semilocal PP $\varDelta \hat{V }_{cv}$ can be determined for each lj-value from the radial Fock equation for the chosen atomic reference state:

$$\displaystyle{ \left [-\frac{1} {2} \frac{d^{2}} {dr^{2}} + \frac{l(l + 1)} {2r^{2}} + V _{lj}^{PP}(r) +\hat{ W}_{ p,lj}(\{\varphi _{p^{{\prime}},l^{{\prime}}j^{{\prime}}}\})\right ]\varphi _{p,lj}(r) =\epsilon _{v,lj}\varphi _{p,lj}(r). }$$

(40)

Here, the radial kinetic energy operator is represented by the first two terms in the square brackets, whereas the last term $\hat{W}_{p,lj}$ stands for the effective valence Coulomb and exchange potential acting on φ _p, lj . The radial potential V _lj can be determined pointwise on a grid by inversion. It is usually approximated by a linear combination of Gaussian functions, possibly multiplied by powers of r; cf. Eq. 34. By repeating this procedure for each lj-combination, the complete PP in semilocal form can be constructed. The construction of scalar-relativistic PPs and their radial potentials V _l , e.g., based on Cowan-Griffin [14] HF reference data, is performed in analogous fashion using the AE valence orbital φ _v, l and its orbital energy ε _v, l .

In order to generate compact Gaussian expansions for the radial potentials V _l or V _lj , Durand and Barthelat proposed to minimize the following operator norm [30, 31]:

$$\displaystyle{ \vert \vert \hat{\mathcal{O}}\vert \vert = \left < \varphi _{p}\vert \hat{\mathcal{O}}^{2}\vert \varphi _{ p}\right >^{1/2}\quad \text{with}\quad \hat{\mathcal{O}} = \tilde{\epsilon }_{ v}\vert \tilde{\varphi }_{p}\left > \right <\tilde{\varphi }_{p}\vert -\epsilon _{v}\vert \varphi _{p}\left > \right <\varphi _{p}\vert. }$$

(41)

Here, the quantities without tilde correspond to the exact V _l or V _lj from a radial Fock equation such as Eq. 40, whereas those with tilde are calculated with an analytical potential $\tilde{V }_{l}$ or $\tilde{V }_{lj}$.

One advantage of the shape-consistent approach is that (in optimal cases) only one converged reference state is needed to derive a PP. Thus, even derivations of 0-valence electron potential modeling, e.g., rare gas elements, are possible. On the other hand, the restriction to one reference state may also lead to a bias of the PP between this state and others which might be equally important. Here, a suitable averaging might help. Another drawback is the requirement that the pseudo-valence orbitals in Eq. 39 have to be nodeless due to the necessary inversion of the radial Fock Eq. 40. Thus, the adjustment sometimes has to be performed for highly charged ions, which might lead to noticeable frozen-core errors when the PP is applied for the neutral atom or lower charged ions. Prescriptions to overcome this restriction were advised in the generalized relativistic effective core potential (GRECP) ansatz [32]. However, due to the necessary extension of the semilocal PP by nonlocal terms, the approach leads to a more complicated valence-only Hamiltonian and is thus not widely used.

The most popular shape-consistent PP sets using the semilocal ansatz, which is applicable for most standard quantum chemistry codes, are those of Hay and Wadt [33], Christiansen and collaborators [34], and Stevens, Krauss, and coworkers [35]. Whereas the first set is based on scalar-relativistic Cowan-Griffin AE HF calculations, the latter two sets use DHF/DC AE reference data. The set of Christiansen and collaborators covers essentially all elements of the periodic table. For a complete list of references to these PP sets , cf. Ref. [11].

Energy-Consistent Approach

In the energy-consistent approach [10, 15], first an analytical ansatz for the radial potentials V _l or V _lj in the PP is made. The free parameters therein are then adjusted to reproduce best the total valence energies of a multitude of electronic states of the neutral atom and its (not too highly charged) ions. This is usually achieved by minimizing the following quantity:

$$\displaystyle\begin{array}{rcl} S =\sum _{I}w_{I}(E_{I}^{PP} - E_{ I}^{AE} +\varDelta E_{\mathrm{ shift}})^{2}:=\mathrm{ min}.& &{}\end{array}$$

(42)

Here, E _I ^AE and E _I ^PP represent the total valence energies for a state I at the AE and PP level. The weights w _I could in principle be used to increase the accuracy for states of special interest, but they are usually set to one or to values leading to equal weights for all configurations included in the fit. The global shift Δ E _shift amounts usually to a small fraction of the total valence energies. It allows for each state I a systematic deviation of the total PP valence energy from the AE reference value (e.g., the sum of all valence ionization potentials for the ground state), but usually leads to much better energy differences between the states included in the adjustment (e.g., the lower ionization potentials, excitation energies, and the electron affinity).

A disadvantage of the energy-consistent approach is that a quite large number of states, which are partly not necessarily of direct physical interest, have to be included in the adjustment. For example, in order to describe semicore shells well, energetically high-lying states with excitations and ionizations from these have to be included in the reference data set. Sometimes, the reference data set has to be unwillingly restricted due to convergence difficulties. On the other hand, one advantage is that a large number of states of interest can be described in a balanced way and that the reference energies might also include contributions which are not treated self-consistently at the AE reference level, e.g., the Breit interaction or QED contributions.

Energy-consistent PPs adjusted to Wood-Boring AE HF reference data are available for most main groups as well as d- and f-transition metals. More recent parametrizations are based on MCDHF/DC+B or even MCDHF/DC+B+QED AE reference data and are available for heavy main group elements [36], d-transition metals [37, 38], some actinides [15], as well as some superheavy elements [39]. For a complete list of references to these PP sets, cf. Ref.  [11].

Model Potentials

Model potentials (MPs) [4], in contrast to pseudopotentials, retain the correct radial nodal structure of the AE valence orbitals. They are based on the Huzinaga-Cantu equation [40]

$$\displaystyle{ \left (\hat{F} +\sum _{c}(-2\epsilon _{c})\mathinner{\langle \varphi _{c}\vert }\mathinner{\vert \varphi _{c}\rangle }\right )\mathinner{\vert \varphi _{v}\rangle } =\epsilon _{v}\mathinner{\vert \varphi _{v}\rangle } }$$

(43)

and bridge the gap between PPs and AE frozen-core calculations. A shift operator added to the Fock operator $\hat{F}$, i.e., the second term in parentheses in Eq. 43, moves the energies of the core orbitals upward by − 2ε _c , so that a desired valence orbital is the lowest energy solution. Hereby, unlike in the PP approach where core and virtual orbitals are admixed to the valence orbital to yield a nodeless pseudo-valence orbital, the MP valence orbital keeps the nodal structure of the corresponding AE valence orbital. It is obvious that the primitive basis sets used in MP calculations have to be larger than those of PP calculations.

The interaction between a valence electron i and the atomic core is written in the MP approach as

$$\displaystyle{ \hat{V }_{cv}^{\mathrm{MP}}(i) = -\frac{Q} {r_{i}} +\varDelta \hat{ V }_{C}(i) +\varDelta \hat{ V }_{X}(i) +\hat{ P}(i). }$$

(44)

Here, $\varDelta \hat{V }_{C}(i)$ is the Coulomb (C) interaction between the core electrons and the valence electron

$$\displaystyle{ \varDelta \hat{V }_{C}(i) = -\frac{n_{c}} {r_{i}} + 2\sum _{c}\hat{J}_{c}(i) }$$

(45)

and $\varDelta \hat{V }_{X}(i)$ stands for the corresponding exchange (X) interaction

$$\displaystyle{ \varDelta \hat{V }_{X}(i) = -\sum _{c}\hat{K}_{c}(i). }$$

(46)

$\hat{J}_{c}(i)$ and $\hat{K}_{c}(i)$ denote for the Coulomb and exchange operators for the core orbital | φ _c 〉. The shift operator

$$\displaystyle{ \hat{P}(i) =\sum _{c}(-2\epsilon _{c})\mathinner{\vert \varphi _{c}(i)\rangle }\mathinner{\langle \varphi _{c}(i)\vert } }$$

(47)

prevents the MP valence orbitals to collapse into core-like solutions .

Ab Initio Model Potentials

One of the most successful variants of the MP approach is the ab initio model potentials (AIMPs) developed by Seijo, Barandiarán, and coworkers [41]. The Coulomb interaction of a valence electron and the core is represented by a local spherically symmetric potential

$$\displaystyle{ \varDelta \hat{V }_{C}(i) =\varDelta V _{C}(r_{i}) = \frac{1} {r_{i}}\sum _{k}C_{k}e^{-\alpha _{k}r_{i}^{2} }. }$$

(48)

A least-squares fit to the AE potential is used to determine the parameters α _k , C _k under the constraint ∑ _k C _k = Z − Q = n _c enforcing the correct asymptotic behavior. A spectral representation is used for the nonlocal exchange part

$$\displaystyle{ \varDelta \hat{V }_{X}(i) =\sum _{p,q}\mathinner{\vert \chi _{p}(i)\rangle }A_{pq}\mathinner{\langle \chi _{q}(i)\vert }. }$$

(49)

This MP operator yields the same Coulomb and exchange (one-center) integrals as the AE reference calculation, provided that sufficiently accurate expansions are used in Eqs. 48 and 49. The shift operator in Eq. 47 is constructed with core orbitals represented in sufficiently large AE basis sets.

Scalar-relativistic effects are taken into account implicitly. Using a Cowan-Griffin [14] scalar-relativistic AE reference calculation, the parameters in the Coulomb term (Eq. 45) and the shift operator (Eq. 47) are modified accordingly. In addition, the spectral representation of the mass-velocity and Darwin terms are added to the nonlocal representation of the exchange part (Eq. 49).

In order to take also SO coupling into account, an effective one-electron operator similar to the form proposed by Pitzer and Winter [24] for PPs is added [42]:

$$\displaystyle{ \varDelta \hat{V }_{cv,so}(i) =\sum _{l}\left (\sum _{k}\frac{B_{lk}} {r_{i}^{2}} e^{-\beta _{lk}r_{i}^{2} }\right )\hat{P}_{l}(i)\hat{\mathbf{l}}_{i} \cdot \hat{\mathbf{ s}}_{i}\hat{P}_{l}(i). }$$

(50)

Here, $\hat{\mathbf{l}}_{i} =\hat{\mathbf{ r}}_{i} \times \hat{\mathbf{ p}}_{i}$ and $\hat{\mathbf{s}}_{i}$ denote the operators of orbital angular momentum and spin, respectively. The coefficients B _lk and exponents β _lk are determined by means of a least-squares fit to the radial components of the Wood-Boring [13] AE SO term.

Model Core Potentials

The model core potential (MCP) approach advocated by Klobukowski and coworkers [43, 44] uses a simpler, entirely local approximation for the Coulomb and exchange terms than the AIMP approach, i.e.,

$$\displaystyle{ \varDelta \hat{V }_{C}(i) +\varDelta \hat{ V }_{X}(i) = -\frac{Q} {r_{i}}\sum _{k}A_{k}r_{i}^{n_{k} }e^{-\alpha _{k}r_{i}^{2} }. }$$

(51)

The values of n _k are restricted to 0 and 1. The model potential parameters A _k and α _k are determined by a simultaneous fit to orbital energies and corresponding radial functions for a given reference state .

Molecular Effective Core Potentials

The molecular valence-only Hamiltonian for a system with N atoms

$$\displaystyle{ \hat{H}_{v} = -\frac{1} {2}\sum _{i=1}^{n_{v} }\nabla _{i}^{2} +\sum _{ i=j+1}^{n_{v} }\sum _{j=1}^{n_{v}-1} \frac{1} {r_{ij}} +\sum _{ i}^{n_{v} }\hat{V }_{cv}(i) + V _{cc} }$$

(52)

is usually constructed by using a superposition of the atomic potentials

$$\displaystyle{ \hat{V }_{cv}(i) =\sum _{ I=1}^{N}\hat{V }_{ cv}^{I}(i). }$$

(53)

Here and in the following, I and J stand for nuclear indices. The interaction between the nuclei and cores I, J

$$\displaystyle{ V _{cc} =\sum _{ J=I+1}^{N}\sum _{ I=1}^{N-1}\left [\frac{Q_{I}Q_{J}} {r_{IJ}} +\varDelta V _{cc}^{IJ}(r_{ IJ})\right ] }$$

(54)

has as leading term the Coulomb interaction between the point charges Q _I and Q _J , which equal the nuclear charges or the core charges depending on whether the centers are treated at the AE or ECP level. The pairwise corrections Δ V _cc ^IJ(r _IJ ) describe deviations from the Coulomb repulsion of the point charges, e.g., for mutually penetrating cores, where besides modified electrostatic contributions also orthogonality constraints and the Pauli repulsion between the electron shells localized on different cores have to be considered.

For large cores, the point charge approximation used in Eq. 54 is not sufficiently accurate, and core-core/nucleus repulsion corrections have to be added, e.g.,

$$\displaystyle{ \varDelta V _{cc}^{IJ}(r_{ IJ}) = B_{IJ}e^{-b_{IJ}r_{IJ} }. }$$

(55)

The parameters B _IJ , b _IJ can be fitted to the deviations of the core-core and/or core-nucleus interactions from the point charge model as obtained from AE HF or DHF calculations for pairs of interacting frozen cores [6].

Core Polarization Potentials

For large, easily polarizable cores, a core polarization potential (CPP) $\hat{V }_{\mathrm{cpp}}$ can be added to the Hamiltonians (Eqs. 13 and 52) in order to account for static core polarization effects occurring already at the HF level as well as for dynamic core polarization effects related to core-valence correlation, i.e.,

$$\displaystyle{ \hat{V }_{\mathrm{cpp}} = -\frac{1} {2}\sum _{I}\alpha _{I}\hat{\mathbf{f}}_{I}^{2}. }$$

(56)

Here, α _I is the static dipole polarizability of the core I, and $\hat{\mathbf{f}}_{I}$ denotes the electric field produced by all valence electrons as well as all other cores and nuclei at the core I

$$\displaystyle{ \hat{\mathbf{f}}_{I} = -\sum _{i} \frac{\mathbf{r}_{iI}} {r_{iI}^{3}} +\sum _{J\neq I}Q_{J} \frac{\mathbf{r}_{JI}} {r_{JI}^{3}}. }$$

(57)

For short distances between the polarizing particles and the polarized core, problems arise due to the breakdown of this expression. The electric field is therefore multiplied by a cutoff function F, i.e.,

$$\displaystyle{ \hat{\mathbf{f}}_{I} = -\sum _{i} \frac{\mathbf{r}_{iI}} {r_{iI}^{3}}F(r_{iI},\delta _{e}^{I}) +\sum _{ J\neq I}Q_{J} \frac{\mathbf{r}_{JI}} {r_{JI}^{3}}F(r_{JI},\delta _{c}^{I}). }$$

(58)

A suitable ansatz for F was proposed by Meyer and coworkers [8] in the framework of AE calculations and was successfully adopted for large-core PPs [7]:

$$\displaystyle{ F(r_{iI},\delta ^{I}) = [1 - exp(-\delta ^{I}r_{ iI}^{2})]^{n}\qquad \text{with}\qquad x = i,I. }$$

(59)

The dipole polarizability α _I of the core I can be, e.g., evaluated at the coupled HF or DHF level, whereas the cutoff parameter δ _I can be fitted to match ionization potentials of one-valence electron systems from correlated calculations. Alternatively, the parameters can also be taken from experimental data, if this is available with sufficiently high accuracy.

It should be noted that unlike the ECPs (PPs, MPs), the CPP of a many-valence electron atom has one- and two-electron contributions and the CPP for a multicenter system is not a simple superposition of atomic one-electron potentials. The square of the electric field $\hat{\mathbf{f}}_{I}$ in Eq. 56 leads to modified electron-electron and core-core/nuclei interactions. Integrals over the above CPP operator for Cartesian Gaussian basis functions have been derived and implemented by Schwerdtfeger and Silberbach [45].

The usage of CPPs is especially popular for semiempirical large-core PPs, e.g., when treating alkaline and alkaline earth elements as one- and two-valence electron atoms, respectively [7, 46]. CPPs are also used in combination with semiempirical large-core PPs for main group elements [9] or when treating the group 11 and 12 metals with closed d¹⁰ shell as one- and two-valence electron atoms, respectively [6]. In the latter case, the extension to include higher-order effects, e.g., the quadrupole polarizability, has also been explored [47]. Their usage of CPPs together with ab initio small-core PPs as well as with MPs in general has not yet been sufficiently investigated, despite their quite successful applications at the AE level [8].

Valence Basis Sets

For the MP approach, the computational savings arising from the use of specially optimized valence basis sets are relatively small, since the MP valence orbitals keep all radial nodes which are present in their AE counterparts. The situation is quite different for the PP approach, since here the number of radial nodes in the pseudo-valence orbitals is reduced for most angular quantum numbers with respect to the AE case. Since the shape of the PP in the core region is to a certain extent arbitrary, each PP requires an individually optimized valence basis set. The usage of (truncated) AE basis sets or valence basis sets adopted from another PP may lead to significant errors in the total valence energies and in consequence possibly also to errors in the calculated atomic and molecular properties. The PP approach has the advantage to lead to relatively small basis set superposition errors. This advantage however may be lost when basis sets not optimized for the specific PP are used. Many of the published sets of PPs come together with corresponding valence basis sets, which therefore should be used in unchanged form or might be further extended, e.g., by adding diffuse, polarization, and correlation functions.

During the last decades, it became quite popular to use series of basis sets, e.g., in order to estimate the basis set limit from results of, e.g., double-, triple-, and quadruple-zeta quality by extrapolation techniques. For energy-consistent PPs, two types of such systematic basis sets have been developed for a large number of elements, i.e., the correlation-consistent generalized contracted basis sets of Peterson and collaborators (e.g., cc-pVXZ-PP and cc-pwCVXZ-PP, X = D, T, Q, 5) [36–38] and the error-balanced segmented contracted basis sets of Weigend and coworkers (def2-XVP and dhf-XVP, X = S, TZ, QZ) [48, 49]. The focus in the latter basis sets was also put on their performance in two-component HF and DFT calculations (dhf-XVP-2c, X = S, TZ, QZ). Further references to these and other basis sets for ECPs are provided in Ref. [11].

Calibration

A successful adjustment of an ECP for an atom at a certain level of theory, e.g., at the HF or DHF level, does not guarantee its success in calculations using different computational methods, e.g., correlated approaches, or when the ECP is used in a molecular environment. Calibration calculations with a rigorous comparison to results of accurate AE calculations, preferentially using the Hamiltonian the ECP aims to model and basis sets of comparable quality, or experimental data are therefore mandatory for ECPs.

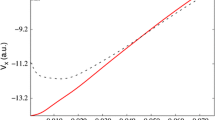
Figure 6 summarizes results for the ground state of Cu₂ when Cu is treated as a one-valence electron ion [6]. The underlying large-core PP replacing the 1s² …3d¹⁰ core is designed to model scalar-relativistic DHF/DC results. The core-core repulsion correction elongates the bond by more than 0.3 Bohr, whereas the inclusion of static core polarization and core-valence correlation by means of a CPP shortens the bond by more than 0.2 Bohr. After including valence correlation with a local correlation density functional, the bond distance agrees within 0.1 Bohr with the experimental value. The better performance of the PP at the HF level without any corrections is most likely due to error cancellations. This becomes obvious from the corresponding results for the binding energy and the vibrational frequency, which approach the experimental values very systematically upon adding the corrections.

Fig. 6

Equilibrium distance R _e , binding energy D _e , and vibrational frequency ω _e of Cu₂ from HF calculations with a DHF/DC-adjusted one-valence electron PP, including a core-core (cc) repulsion correction, a core polarization potential (CPP), and valence correlation (corr) by means of the Vosko-Wilk-Nusair local correlation functional [6]. Experimental values are indicated by the horizontal dashed lines

An example for a correlated atomic calibration study of a MCDHF/DC+B-adjusted small-core PP for the roentgenium atom is provided in Table 4. AE DCB Fock-space coupled cluster (FSCC) results of Eliav et al. [50] using very large basis sets are compared to corresponding PP MRCI data using standard basis sets [18], which are applicable also in molecular calculations [39]. The agreement with the AE reference data is on the average within 0.15 eV (3 %) provided that, as necessary in the FSCC approach, the spinors are taken from the closed-shell d¹⁰ s^{2 1}S₀ anion ground state. Larger deviations occur when spinors individually optimized for each configuration are used in the PP MRCI calculations, which points to substantial relaxation effects not covered by the FSCC approach. The deviations between AE and PP data in these calculations are much larger than in the PP fit: in the case of Rg, the energy adjustment was performed for 37 nonrelativistic configurations corresponding to 309 J levels. The mean absolute errors in the total valence energies were below 0.01 eV both for the nonrelativistic configurations and the J levels.

Table 4 Electron affinity (EA), excitation energies (EE), and ionization potentials (IP) of roentgenium (Rg) (Z = 111) from MRCI PP calculations in comparison to AE DCB FSCC results (eV) [18, 50]

Table 5 lists results for the equilibrium distance and the force constant of the monohydride of roentgenium using the same MCDHF/DC+B-adjusted small-core PP for roentgenium in two-component HF and MP2 calculations [39]. Comparison is made to corresponding AE DHF/DCG results, i.e., the Gaunt term was used instead of the full Breit term. In view of the very large relativistic bond length contraction of about 0.5 Å the obtained accuracy of better than 0.004 Å (0.27 %) of the PP results for the bond distances is quite satisfactory. The agreement of the force constants is better than 0.25 %.

Table 5 Bond distances R _e (Å) and force constants k _e (N/m) for the monohydride of roentgenium from AE and PP calculations [39]

Summary

The effective core potential approach, i.e., its model potential and pseudopotential variants, and the effective core polarization potential approach have been briefly reviewed. Despite the development of efficient, i.e., not too costly but still accurate, relativistic all-electron schemes, effective core potentials will still remain the workhorse for relativistic quantum chemical calculations on larger systems. The possibility to include besides the Dirac relativity also the Breit interaction as well as quantum electrodynamic effects implicitly in the calculations for heavy elements renders the approach quite attractive, besides the computational savings due to the reduced number of electrons to deal with.