Braneworld Black Holes

Abstract

In this article we review the present status of the numerical construction of black holes in the Randall–Sundrum II braneworld model. After reviewing the new numerical methods to solve the elliptic Einstein equations, we numerically construct a black hole solution in five-dimensional anti-de Sitter (AdS₅) space whose boundary geometry is conformal to the four-dimensional Schwarzschild solution. We argue that such a solution can be viewed as the infinite radius limit of a braneworld black hole, and we provide convincing evidence for its existence. By deforming this solution in AdS we can then construct braneworld black holes of various sizes. We find that standard 4d gravity on the brane is recovered when the radius of the black hole on the brane is much larger than the radius of the bulk AdS space.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

String theory is the best candidate for a theory of quantum gravity but its mathematical consistency requires the existence of extra spatial dimensions beyond the three that we observe. Almost a century ago Kaluza and Klein (KK) offered an attractive way of dealing with these extra (and yet unobserved) dimensions and obtain an effective theory at low energies which is compatible with observations: if these extra dimensions are compact and sufficiently small (naturally of the Planck radius, ℓ _P  ∼ 10⁻³³ cm) then, in four dimensions, they should manifest in experiments as a tower of massive particles with masses ∼ 1∕ℓ _P and therefore not detectable in present day particle accelerators.

In [1, 2] Randall and Sundrum proposed a remarkable alternative to KK compactification in which the extra dimensions are non-compact. In the Randall–Sundrum infinite braneworld model (henceforth RSII) [2] one takes two copies of AdS₅ and glues them together along a common boundary, the brane. This hypersurface (the brane) represents our 4d world and all Standard Model particles are pinned there, except for gravity which can propagate in all dimensions. This model provides a natural solution to the hierarchy problem since gravity is dissolved in the extra dimension. This construction is motivated by String Theory, where dynamical (d + 1)-dimensional objects, known as d-branes, with gauge fields living on their worldvolume, are fundamental objects in the theory.

Considering small fluctuations of the metric around the aforementioned background, Randall and Sundrum showed that there exists a zero mode of the graviton localised on the brane, together with continuum of massive KK modes. Moreover, it was shown [3, 4] that in the linearised regime, an observer living on the brane would experiment standard 4d gravity plus power law corrections, as opposed to the exponential corrections that arise in standard KK theory.

However, to validate the RSII model as viable description of our universe, one has to consider the strong field regime. In particular, one would like to check if there exist black holes in this model and, if so, understand their properties and compare them to astrophysical observations. Chamblin et al. [5] was the first one to consider black holes in RSII, but their solutions are singular and therefore unphysical. On the other hand, Emparan et al. [6] constructed an explicit (and regular) braneworld black hole solution in 3 + 1 bulk dimensions and verified that standard 3d gravity is recovered on the brane. The phenomenologically more interesting case of a 4 + 1 braneworld black hole remained elusive to analytical methods and numerical techniques were used to construct such solutions. However, the works of Kudoh et al. [7–10] did not succeed to numerically construct black holes on branes in the phenomenologically interesting regime. In fact, Yoshino [9] even conjectured that no non-extremal braneworld black holes of any size should exist.

Braneworld black holes can be understood using the AdS/CFT correspondence as quantum corrected black holes [11]. Using free field theory intuition and motivated by the previous unsuccessful attempts to numerically construct static braneworld black holes, Emparan et al. [11] conjectured that no large (compared to the size of the parent AdS space) static non-extremal braneworld black holes could exist since they would Hawking radiate and therefore be dynamical. However, Fitzpatrick et al. [12] provided counterarguments. We should point of that authors of [13–15] constructed the near horizon geometry of extremal braneworld black holes of any size. These black holes evade the non-existence conjecture because being extremal they do not Hawking radiate in the first place.

This was the status of braneworld black holes before the work of Figueras et al. [16, 17]. In this article, we will review and improve these works, which show that not only large braneworld black holes exist, but also that 4d gravity on the brane is recovered. Recently, Abdolrahimi et al. [18] appeared (see also [19]) which uses a different numerical method than that of [16, 17]. Furthermore, their results support those of [16, 17], which is rather non-trivial. Therefore, the present evidence suggests that the RSII model seems to provide a viable description of our universe even in the strong gravity regime.

2 The Harmonic Einstein Equations

In this section we review the numerical method that we used to construct the braneworld black holes. This method was first proposed in [20] to construct static spacetimes containing black holes and then extended in [21] to the stationary case (see [22] for review). Recently the method has been further extended to construct stationary spacetimes with non-Killing horizons [23] (see also [24]).

For simplicity, we start considering the Einstein vacuum equations in D-dimensions:

$$\displaystyle{ R_{ab} = 0. }$$

(1)

As we shall see shortly, adding a cosmological constant (positive or negative) and/or matter is straightforward. Furthermore, in this article we will only consider static spacetimes $(\mathcal{M},g)$.

Naively, it appears that in (1) there are as many equations as metric components and hence one would be tempted to think that they completely determine the metric. However, closer inspection reveals that this is not the case; the reason is that because of the underlying diffeomorphism invariance of the the theory, for any metric the corresponding Ricci tensor satisfies the Bianchi identity. In the general situation, the Bianchi identity contains D equations, and hence in (1) there are only $D(D - 1)/2$ non-trivial equations, rendering the problem for the metric underdetermined. The difficulty with (1) is that this is not an elliptic equation for the metric. More precisely, (1) is only an elliptic equation for the dynamical degrees of freedom but pure gauge modes are annihilated by the principle symbol of the operator. Therefore, we have to fix the gauge in order to turn (1) into an elliptic equation that can be solved numerically. The proposal of [20] is just one particular choice of gauge, but as we shall see shortly, it has great advantages as far as the numerical implementation is concerned.

The proposal of [20] is as follows. Instead of considering (1) on $(\mathcal{M},g)$, we consider a modified set of equations known as the “harmonic” or “DeTurck” Einstein equations:

$$\displaystyle{ R_{ab} -\nabla _{(a}\xi _{b)} = 0,{\qquad \xi }^{a} = {g}^{bc}(\varGamma _{ bc}^{a} -\bar{\varGamma }_{ bc}^{a}), }$$

(2)

where $\bar{\varGamma }$ is a fixed reference connection on $\mathcal{M}$, which for simplicity we take to be the Levi–Civita connection of a reference metric $\bar{g}$ on $\mathcal{M}$. The virtue of (2) is that the principle symbol of the operator is simply $P = -\frac{1} {2}{g}^{ab}\partial _{ a}\partial _{b}$ and hence, for any Riemannian metric g, (2) is a manifestly elliptic equation for the metric components and, as such, can be solved as a standard boundary value problem.

Clearly (2) is equivalent to (1) iff ξ ^a = 0 everywhere on the spacetime manifold $\mathcal{M}$.¹ This is precisely the gauge condition that we shall be imposing and it provides D local equations for the spacetime coordinates. More precisely, ξ ^a = 0 is equivalent to $\varDelta _{g}{x}^{a} = {H}^{a}$, where Δ _g is the scalar Laplacian and the source H ^a is specified in terms of the reference metric $\bar{g}$ as ${H}^{a} = -{g}^{bc}\bar{\varGamma }_{ bc}^{a}$. Therefore, the gauge choice that we are implementing is closely related to the celebrated generalised harmonic gauge [25–28]. There is, however, an important difference: whilst in generalised harmonic gauge one prescribes the sources H ^a, which in general are not tensors on $\mathcal{M}$, in our method the sources depend on both the metric g and the reference metric $\bar{g}$.

Whilst a solution to the Einstein equations (1) in our gauge ξ ^a = 0 solves the harmonic Einstein equations (2), the converse is not true. In fact, there can exist solutions to (2) with ${\xi }^{a}\neq 0$ and these are known as Ricci solitons. Since our ultimate goal is to solve (2) as a boundary value problem and find Einstein metrics instead of Ricci solitons, we have to supplement (2) with boundary conditions compatible with ξ ^a = 0 at the boundary whilst preserving the ellipticity of the problem.² We will come back to this point when we consider the concrete problem of numerically constructing braneworld black holes. Having specified suitable boundary conditions, the existence of Ricci solitons on $\mathcal{M}$ is constrained by the fact that ${\xi }^{a}$ has to satisfy the following manifestly elliptic equation:

$$\displaystyle{ {\nabla }^{2}{\xi }^{a} + R_{\ b}^{a}{\xi }^{b} = 0. }$$

(3)

This is a well-posed boundary value problem for ${\xi }^{a}$ and, for boundary conditions compatible with ${\xi }^{a} = 0\vert _{\partial \mathcal{M}}$, it always admits the zero solution.

Before we continue the discussion about the existence of Ricci solitons, we note that adding a cosmological constant term to the Einstein equations (1) does not change the character of the equations because such a term has no derivatives of the metric. Obviously the same is true for the harmonic Einstein equations (2). Therefore, from now on we will consider the harmonic Einstein equations augmented with a cosmological constant term, since these are the equations that we will have to solve for finding black holes on branes:

$$\displaystyle{ R_{ab}^{H} \equiv R_{ ab} -\varLambda \, g_{ab} -\nabla _{(a}\xi _{b)} = 0. }$$

(4)

It turns out that in favourable circumstances and for suitable boundary conditions one can prove that no Ricci solitons exist on $\mathcal{M}$. For instance, Bourguignon [30] proved that there are no Ricci solitons on a compact manifold without boundaries for any choice of gauge fixing vector ${\xi }^{a}$. More recently, Figueras et al. [16] proved a similar statement for non-compact and static spacetimes with different asymptotics of interest (flat, Kaluza-Klein and AdS). Their argument is as follows. Contracting (3) with $\xi _{a}$ and using (4) one finds

$$\displaystyle{ {\nabla }^{2}\phi {+\xi }^{a}\partial _{ a}\phi = -2\,\varLambda \,\phi + 2\,({\nabla {}^{a}\xi }^{b})(\nabla _{ a}\xi _{b}),\qquad \phi {=\xi }^{a}\xi _{ a}. }$$

(5)

For static spacetimes with a non-positive cosmological constant ($\varLambda \leq 0$), the right hand side of this equation is non-negative and its solutions are governed by a maximum principle. Therefore, if $\phi$ is non-constant, its maximum must be attained at the boundary and the normal outer gradient there must be positive. Then, imposing suitable regularity conditions and for flat, Kaluza-Klein or AdS asymptotic boundary conditions, one shows that ϕ = 0 at $\partial \mathcal{M}$, from which it follows that ϕ = 0 everywhere. From this and the fact that the metric is static, one then deduces that ${\xi }^{a} = 0$ everywhere on $\mathcal{M}$.

As we shall see later in the context of the numerical construction of braneworld black holes, the result of Figueras et al. [16] does not apply for the boundary conditions that one has to impose on the brane and in this case the existence of Ricci solitons cannot be ruled out a priori. However, because (4) is elliptic, then for fixed boundary conditions there exists a locally (in the space of solutions) unique solution. Therefore, it should always be possible to tell an Einstein metric from a Ricci soliton. In practice, a posteriori we can check whether ${\xi }^{a} \rightarrow 0$ in the continuum limit. Needless to say, in the numerical results that we will present later we found no evidence of Ricci solitons.

2.1 Methods for Solving the Harmonic Einstein Equations

In this subsection we will briefly review two general algorithms for solving the harmonic Einstein equations (2). The first one is based on relaxation whilst the second one is based on a root finding algorithm.

A standard algorithm to solve a non-linear elliptic equation is to simulate the associated diffusion equation; then, fixed points of the diffusion equation are solutions to the original elliptic equation. In the present context of solving the harmonic Einstein equations (4), the metric is evolved according to the diffusion equation

$$\displaystyle{ \frac{\partial } {\partial \lambda }\,g_{ab}(\lambda ) = -2\,R_{ab}^{H}, }$$

(6)

where λ is the diffusion time. In the mathematics literature, (6) is known as the Ricci–DeTurck equation and it is diffeomorphic to Hamilton’s famous Ricci flow equation. It is worth noting we want to solve (2) to find static (or stationary) spacetimes containing a black hole, and therefore the metric g Lorentzian. However, because (2) is elliptic then (6) is a well-posed parabolic equation.

The great advantage of this algorithm is that it is very easy to implement and, because it is diffeomorphic to Ricci flow, it does not depend on the choice of reference metric. However, as discussed in [20], some black hole spacetimes may be unstable fixed points of Ricci flow. The stability of a fixed point under the Ricci–DeTurck flow is determined by the spectrum of the Lichnerowicz operator, $\varDelta _{L}$, about the fixed point. If Δ _L admits negative modes, then small perturbations about the fixed point grow exponentially with the diffusion time and any initial data that does not coincide with the fixed point metric will be diverted away from the latter. It is well known that for some black hole spacetimes, Δ _L admits negative modes [31]. Even in this situation one may still use (6) to find Einstein metrics, but the initial data has to be suitably fine-tuned so that the flow happens on a hypersurface (in the space of geometries) orthogonal to the negative modes. See [20] for more details.

The other standard algorithm to solve (2) (or (4)), is Newton’s method. This algorithm is more difficult to implement in practice than Ricci flow and its basin of attraction depends on the choice of reference metric. On the other hand, it is insensitive to the presence of negative modes and it converges much faster to the fixed point. In this method, one starts with an initial guess ${g}^{(\mathit{old})}$ that does not solve (2) and then iteratively corrects it:

$$\displaystyle{ g_{ab}^{(\mathit{new})} = g_{ ab}^{(\mathit{old})} +\epsilon \, h_{ ab},\qquad (\varDelta _{H}h)_{ab} = -R_{ab}^{H}[{g}^{(\mathit{old})}], }$$

(7)

where Δ _H is the linearisation of R _ab ^H around a given background metric (not necessarily Einstein) and ε is a parameter (generically between 0 and 1) that controls the size of the correction. Newton’s method is basically a root finding algorithm and if the initial guess is sufficiently close to the actual solution, Newton’s method will converge to it. The performance of Newton’s method is not affected by the presence of positive or negative modes of Δ _H ; only zero modes could cause problems, but because the problem is elliptic, boundary conditions should remove all of them (in fact, this is how an elliptic problem is defined).

3 An Aside: AdS/CFT on Black Hole Backgrounds

In this section we will use AdS/CFT to construct the gravitational dual of $\mathcal{N} = 4$ super Yang-Mills (SYM) on the background of the 4d Schwarzschild black hole in a certain vacuum state. At this stage such a solution may seem unrelated to the problem of constructing braneworld black holes, but as we shall see later, large braneworld black holes can be understood as perturbations of this solution.

3.1 Setup

We want to find a static solution to the Einstein equations in five dimensions with a negative cosmological constant that is asymptotically locally AdS, with a metric on the conformal boundary in the same conformal class as 4d Schwarzschild. Furthermore, far from the conformal boundary we want the spacetime to approach the Poincare horizon of AdS. With these assumptions, the isometry group of the spacetime is R × SO(3), and the most general metric with this symmetry (which is closed under diffeomorphisms that preserve it) is given by

$$\displaystyle\begin{array}{rcl}{ \mathit{ds}}^{2}& =& \ \frac{{\ell}^{2}} {f{(x)}^{2}}\bigg(-4\,{r}^{2}\,f{(r)}^{2}\,{\mathit{dt}}^{2} + {x}^{2}\,g(x)\,{e}^{S}\,d\varOmega _{ (2)}^{2} \\ & & + \frac{4} {f{(r)}^{2}}\,{e}^{T+{r}^{2}\,A }\,{\mathit{dr}}^{2} + \frac{4} {g(x)}\,{e}^{S+{x}^{2}\,B }\,{\mathit{dx}}^{2} + \frac{2\,r\,x\,F} {f(r)} \,\mathit{dr}\,\mathit{dx}\bigg),{}\end{array}$$

(8)

where $f(\xi ) = 1 {-\xi }^{2}$ and $g(x) = 2 - {x}^{2}$, and the range of the coordinates is $r,x \in [0,1]$. The functions $X =\{ T,S,A,B,F\}$ are assumed to be smooth functions of r and x, and they are the unknowns. With our choice of coordinates, r = 0 and x = 0 correspond to location of the horizon of the black hole and the axis of symmetry respectively, and smoothness there requires that all functions X have to satisfy Neumann boundary conditions. r = 1 is the Poincare horizon and we impose a Dirichlet boundary condition X = 0 there so that the metric reduces to that of the Poincare horizon of AdS₅. Finally, x = 1 corresponds to the conformal boundary of AdS and we impose X = 0 there so that the induced metric is conformal to that of 4d Schwarzschild.

Finally, in order to solve the Einstein–DeTurck equation (4) we have to specify a reference metric. In the original work of Figueras et al. [16], the background metric was taken to be (8) with X = 0. However, one can show that in this gauge, the solution near the boundary of AdS (x = 1) has logs (and therefore it is not smooth), which leads to a poor convergence of the spectral code at sufficiently high resolution. In order to cure this deficiency, in the present work we take the reference metric to be (8) with $T = S = A = 0$, $B = -\frac{18} {5} f{(r)}^{2}f{(x)}^{2}$ and $F = -\frac{6} {5}f{(r)}^{2}f{(x)}^{3}$. One can show that in this gauge there are no logs at the order that affected [16] but we cannot rule out the presence of logs at higher orders.

Henceforth we set the radius of AdS to be one, ℓ = 1. In addition, note that because in AdS/CFT we only have to specify a representative of the conformal class of boundary metrics, we can set, without loss of generality, the radius of the boundary Schwarzschild solution to be one.

3.2 Results

In this subsection we briefly summarise our results for this AdS/CFT solution. Firstly we present the numerical solution. As we shall see later in the discussion of braneworld black holes, it is important to show that this AdS/CFT solution exists and it is smooth. Secondly we will consider the dual stress tensor.

Fig. 1

Embedding of the horizon of the AdS/CFT solution as a surface of revolution into four-dimensional hyperbolic space H ₄, ${\mathit{ds}}^{2}(\mathbf{H}_{4}) = \frac{1} {{z}^{2}} ({\mathit{dz}}^{2} +{ \mathit{dR}}^{2} + {R}^{2}\,d\varOmega _{(2)}^{2})$. Here z is the standard Poincare coordinate so that z = 0 is the boundary of H ₄, which coincides with the boundary of AdS

We have solved (4) numerically using a pseudospectral collocation approximation and Newton’s algorithm as described in Sect. 2.1. We have performed convergence tests and our numerical solution convergences exponentially (with the number of grid points) to the continuum, at least as far as we were able to check. This is the expected behaviour if a smooth solution exists. Moreover, for the data presented here, the maximal fractional error in the Einstein equations is better than 10⁻⁹, so these are extremely accurate numerical solutions.

In Fig. 1 we present the embedding of the horizon, as a surface of revolution, into four-dimensional hyperbolic space, H ₄. As this figure shows, at z = 0 (i.e., the boundary of AdS) the horizon has radius one, as it should since the boundary black hole has radius one by our choice of boundary conditions. In addition, one can see that the horizon extends from the boundary into to the bulk, and at some finite value of z the 2-sphere shrinks to zero size smoothly.

One can use the standard holographic renormalisation prescription [32] to extract the boundary stress tensor. The details of the calculation can be found in [16] and the result is:

$$\displaystyle\begin{array}{rcl} & & \langle T_{i}^{ j}\rangle = \frac{N_{c}^{2}} {{2\pi }^{2}{R}^{4}}\mathrm{diag}\bigg\{\frac{3\,R_{0}} {4\,R} \bigg(1 -\frac{7\,R_{0}} {12\,R} -\frac{R_{0}^{2}} {2\,{R}^{2}}\bigg) + t_{4}(R), \\ & & \frac{357\,R_{0}^{2}} {80\,{R}^{2}} \bigg(1\,-\,\frac{18\,R_{0}^{2}} {17\,R} \bigg) -\big (t_{4}(R)\,+\,2\,s_{4}(R)\big),-\frac{3\,R_{0}} {8\,R} \bigg(1\,+\,\frac{161\,R_{0}} {30\,R} -\frac{34\,R_{0}^{2}} {5\,{R}^{2}} \bigg) + s_{4}(R), \\ & & -\frac{3\,R_{0}} {8\,R} \bigg(1 + \frac{161\,R_{0}} {30\,R} -\frac{34\,R_{0}^{2}} {5\,{R}^{2}} \bigg) + s_{4}(R)\bigg\}, {}\end{array}$$

(9)

where R is the standard Schwarzschild radial coordinate³ and t ₄ and s ₄ can be extracted from the near boundary (x → 1) expansion of the metric:

$$\displaystyle\begin{array}{rcl} T& \approx & \frac{1} {5}\left (4 - 13{r}^{2} + 9{r}^{4}\right ){\left (1 - {x}^{2}\right )}^{2} -\frac{18} {11}{\left (1 - {r}^{2}\right )}^{2}{\left (1 - {x}^{2}\right )}^{3} +{ \left (1 - {x}^{2}\right )}^{4}t_{ 4}(r)+\ldots, {}\\ S& \approx & \frac{1} {10}\left (23 - 41{r}^{2} + 18{r}^{4}\right ){\left (1 - {x}^{2}\right )}^{2} -\frac{18} {11}{\left (1 - {r}^{2}\right )}^{2}{\left (1 - {x}^{2}\right )}^{3} +{ \left (1 - {x}^{2}\right )}^{4}s_{ 4}(r)+\ldots,{}\\ \end{array}$$

where here t ₄ and s ₄ should be viewed as functions of the compact radial coordinate r used in (8). We want to emphasise that with our choice of gauge, terms in the expansions above up to 5th order do not contain logs. The same is true for the remaining metric coefficients (not shown here).

Fig. 2

$\langle T_{t}^{t}\rangle$ (black), $\langle T_{R}^{R}\rangle$ (red) and $\langle T_{\varOmega }^{\varOmega }\rangle$ (blue) components of the stress tensor as functions of the Schwarzschild radial coordinate R. The dots correspond to the values of our interpolated data and the solid lines simply serve to guide the eye. Note that $\langle T_{t}^{t}\rangle =\langle T_{R}^{R}\rangle$ at R = R ₀ (the horizon) which is necessary and sufficient for the regularity of the stress tensor there. For $R \rightarrow \infty$ the various components of $\langle T_{i}^{\ j}\rangle$ decay as $\sim {R}^{-5}$

Note that the stress tensor (9) is traceless and conserved as consequence of the bulk Einstein equations. Therefore, t ₄ and s ₄ are not independent; they are related by a differential equation which expresses nothing but the conservation of (9). In Fig. 2 we plot the various components of the stress tensor of the dual field theory. First it is worth noting that the stress tensor is static, finite and regular everywhere in our domain. This is non-trivial since, as we now explain, it corresponds to the expectation value of the stress tensor of $\mathcal{N} = 4$ SYM in the background of the 4d Schwarzschild black in the Unruh state. Note that our boundary conditions are such that the bulk solution far from the black hole horizon approaches the Poincare horizon of AdS ₅. From the boundary point of view, this corresponds to the vacuum of the theory (i.e., zero temperature) and not a thermal state. The latter is given by the Hartle-Hawking vacuum and from the bulk point of view, it can be obtained by putting a finite temperature horizon in the IR. The so called static “black funnel” provides an example of a field theory in a black hole background in the Hartle-Hawking state and it has been recently constructed in [33]. With our boundary conditions, the stress tensor is regular on both the future and past event horizons and hence it cannot correspond to the Boulware state either since in the latter case, the dual stress tensor should be singular [34]. Therefore, we conclude that our stress tensor should correspond to the Unruh vacuum. This may seem puzzling at first sight because one usually associates the Unruh state to an evaporating black hole and therefore to a dynamical (as opposed to static) situation. The reason why our stress tensor is static is that our computation, which uses classical gravity in the bulk, only captures the leading order O(N _c ²) piece of the stress tensor, not the full quantum stress tensor. Time-dependence should only show up as an O(1) effect and it can only be detected including 1-loop graviton corrections in the bulk.

This AdS/CFT solution explicitly shows that strong coupling effects significantly alter the behaviour of quantum fields in black hole backgrounds. In particular, the arguments of Emparan et al. [11] against the existence of braneworld black holes should apply to this situation as well and this example shows that they are incorrect. Therefore, there is no reason why braneworld black holes should not exist.

4 Braneworld Black Holes

In this section we consider the numerical construction of braneworld black holes. The results in this section will be discussed in detail in a forthcoming paper [35]. In Sect. 4.1 we will argue that large braneworld black holes can be understood as perturbations of the AdS/CFT solution presented in Sect. 3. In Sect. 4.2 we present the details of our numerical construction of braneworld black holes and compare them to the previous results of [17]. In Sect. 4.3 we present our main results.

4.1 Large Braneworld Black Holes from AdS/CFT

Consider the AdS/CFT solution presented in Sect. 3 in Fefferman-Graham coordinates. In the near boundary expansion (z → 0), one has

$$\displaystyle\begin{array}{rcl} & &{ \mathit{ds}}^{2} = \frac{1} {{z}^{2}}({\mathit{dz}}^{2} +\tilde{ g}(z,x)\,{\mathit{dx}}^{\mu }{\mathit{dx}}^{\nu }),\;\quad \tilde{g}_{\mu \nu }(z,x) = g_{\mu \nu }^{(0)}(x) {}\\ & & +\frac{{z}^{2}} {2} \left (R_{\mu \nu }^{(0)}(x) -\frac{1} {6}\,g_{\mu \nu }^{(0)}(x){R}^{(0)}(x)\right ) + {z}^{4}\left (g_{\mu \nu }^{(4)}(x) + t_{\mu \nu }(x)\right ) + 2\,{z}^{4}\,\log z\,\,h_{\mu \nu }^{(4)}(x) {}\\ & & +O({z}^{6}). {}\\ \end{array}$$

Here g _{μ ν} ⁽⁰⁾ is the boundary metric and R _{μ ν} ⁽⁰⁾ and R ⁽⁰⁾ are the associated Ricci tensor and Ricci scalar respectively. t _{μ ν} is related to the vev of the stress tensor of the dual CFT by $\langle T_{\mu \nu }^{\mathit{CFT}}\rangle = t_{\mu \nu }/(4\pi \,G_{5})$ and the expressions for g _{μ ν} ⁽⁴⁾ and $h_{\mu \nu }^{(4)}$ can be found in [32]. In our setting g _{μ ν} ⁽⁰⁾ is the metric of the 4d Schwarzschild solution $g_{\mu \nu }^{\mathit{Schw}}$, which implies that $R_{\mu \nu }^{(0)} = 0$, R ⁽⁰⁾ = 0 and $h_{\mu \nu }^{(4)} = 0$.

Now assume that there exists a solution in AdS such that its boundary metric is given by the 4d Schwarzschild solution plus a small perturbation, $g_{\mu \nu }^{(0)} = g_{\mu \nu }^{\mathit{Schw}} {+\epsilon }^{2}\,h_{\mu \nu }$ where ε is a small parameter.⁴ In addition, as in Sect. 3, far from the horizon the solution should asymptote to the Poincare horizon of AdS₅. In this set up, we now slice the spacetime with an infinitely thin brane (as in the RSII model) located at z = ε. de Haro et al. [36] (see also [17]) showed that in order for this be possible, such a perturbation has to satisfy the induced Einstein equations on the brane with a source given by the expectation value of the CFT stress tensor obtained in Sect. 3:

$$\displaystyle{ \delta G_{\mu \nu }[h] = 16\,\pi G_{4}\langle T_{\mu \nu }^{\mathit{CFT}}\rangle. }$$

(10)

Moreover, the induced metric on the brane is given by the Schwarzschild geometry, with a radius which is parametrically larger than the radius of the bulk AdS spacetime ℓ plus a small perturbation:

$$\displaystyle{ \gamma _{\mu \nu } ={ \frac{{\ell}^{2}} {\epsilon }^{2}}(g_{\mu \nu }^{\mathit{Schw}} {+\epsilon }^{2}\,h_{\mu \nu }). }$$

(11)

Therefore, if such a perturbation exists, then one can construct arbitrarily large braneworld black holes. In the next subsection we shall see how this can be done numerically.

4.2 Numerical Construction

In the previous subsection we have argued that large braneworld black holes can be viewed as perturbations of the AdS/CFT solution constructed in Sect. 3. Therefore, in order to numerically construct the braneworld black holes we shall use a metric ansatz which is close to (8):

$$\displaystyle\begin{array}{rcl}{ \mathit{ds}}^{2}& =& \frac{{\ell}^{2}} {\varDelta {(r,x)}^{2}}\bigg(-4\,{r}^{2}\,f{(r)}^{2}\,{e}^{T}\,{\mathit{dt}}^{2} + {x}^{2}g(x)\,{e}^{S}\,d\varOmega _{ (2)}^{2} + \frac{4} {f{(r)}^{2}}\,{e}^{T+{r}^{2}f(r)A }{\mathit{dr}}^{2} \\ & & + \frac{4} {g(x)}\,{e}^{S+{x}^{2}B }\,{\mathit{dx}}^{2} + \frac{2\,r\,x} {f(r)}\,F\,\mathit{dr}\,\mathit{dx}\bigg), {}\end{array}$$

(12)

where $\varDelta (r,x) = (1 - {x}^{2}) +\epsilon (1 - {r}^{2})$. Here ε is a parameter that effectively measures the ratio between the radius of AdS₅ and the radius of the black hole on the brane. Hence, taking ε → 0 in (12) corresponds to having an infinitely large braneworld black hole and we recover the AdS/CFT solution, (8).

Using the ansatz (12) we numerically solve the equations of motion (4) subject to suitable boundary conditions. As a reference metric we took (12) with X = 0. The boundary conditions are as in Sect. 3 except at x = 1, where we impose the Israel junction conditions, $K_{\mu \nu } = \frac{1} {\ell} \gamma _{\mu \nu }$. This imposes conditions on T, S, A. In addition we fix F = 0 and ξ ^x = 0. These boundary conditions give rise to a regular elliptic problem and in particular they imply $\partial _{n}\xi _{r} = \frac{2} {\ell} \xi _{r}$ on the brane (where ∂ _n denotes the normal derivative), which is compatible with obtaining an Einstein solution with ${\xi }^{a} = 0$ everywhere on $\mathcal{M}$. We note that with these boundary conditions the soliton non-existence result of [16] does not apply and a posteriori we have to check that our solution is an Einstein metric and not a Ricci soliton. We have performed such checks and found no evidence of Ricci solitons.

4.3 Results

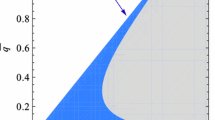
Following [17] we solved the equations of motion numerically using pseudospectral collocation approximation (using Newton’s method) and taking the same number of grid points N in the r and x directions. To characterise the numerical errors we consider the maximum value of $\vert R/20 + 1\vert$ in the whole domain, including the brane. This quantity should be exactly zero for an Einstein metric and hence it tells us about the vanishing of both ξ ^a and its gradients in the continuum limit. In Fig. 3 we show two representative plots for the ε = 0. 5, 1 solutions, which roughly correspond to black holes of size ∼ 2 and ∼ 1 respectively. As these plots show, $\vert R/20 + 1\vert _{max}$ does not vanish in the continuum limit and therefore our numerical solutions do not approximate a continuum solution and should be discarded. Moreover, the smaller the value of ε (i.e., the larger the black hole on the brane), the higher the resolution that is needed in order to see this lack of convergence. Note that depending on the size of the black hole on the brane, $\vert R/20 + 1\vert _{max}$ exhibits a spike at a certain value of N. One can see that this is due to the appearance of a numerical non-smooth near zero mode; it would be interesting to understand if our boundary conditions can be improved in order to get rid off these unphysical modes.

Fig. 3

Maximum (absolute) value of the normalised Ricci scalar over the whole domain (including the brane) as a function of the number of grid points for the ε = 0. 5, 1 solutions obtained with pseudospectral methods. This quantity should vanish in the continuum limit but the plots show that it does not

By plotting $R/20 + 1$ over the whole domain one sees that this lack of convergence is due to some oscillations that appear to be localised on the brane and do not go away in the continuum limit. Such a phenomenon is known as the Gibbs phenomenon and it is known to occur when one tries to approximate a non-smooth function with smooth polynomials, as in a pseudospectral collocation approximation. Since in Sect. 3 we convincingly showed the existence of the AdS/CFT solution, from which large braneworld black holes can be perturbatively constructed, we believe that this lack of convergence is just due to a poor choice of gauge. One might think that this lack of smoothness comes from the presence of logs near the brane, but this does not seem to be case. Indeed, we have performed the same calculation but choosing the same reference metric as in Sect. 3 (which has smoother near boundary behaviour) or in d = 6 (where no logs are expected) and found similar results. It would be interesting to understand in detail where this lack of smoothness comes from.

Fig. 4

$\vert R/20 + 1\vert _{max}$ against the number of grid points for the ε = 0. 01 (purple), 0. 1 (green), 1 (blue), 10 (red) and 100 (yellow) solutions, together with the fits (dashed) assuming exact third order convergence. As this plot shows, we have good third order convergence for braneworld black holes of all sizes

Since spectral methods seem to fail because of the lack of smoothness of the solutions, we have constructed braneworld black holes in d = 5, 6 using 3rd and 4th order finite differences respectively. In either case we have found good convergence (see Fig. 4 for the 5d results) to the continuum and, more importantly, the finite difference code is able to find solutions in a region of parameter space (i.e., small black holes) where the spectral code fails. Moreover, for the highest resolution solutions that we have constructed, the numerical errors of the finite difference solutions are smaller than those of the spectral solutions. However, higher order finite difference methods do not converge, which suggests that in our gauge the d = 5(6) solutions are only C ³(C ⁴).⁵ Summarising, our finite difference solutions converge to the continuum according the order of the approximation, therefore providing good evidence that the continuum solutions do exist. However, in our gauge they do not appear to be very smooth and hence the spectral approximation fails.

There are various reasons why [17] could not observe this lack of convergence. First, the metric ansatz used in this other paper is different from ours, and therefore the gauge is different. As we have argued above, this lack of convergence should be a gauge issue and therefore different gauges should give rise to different convergence properties of the numerical solutions. Secondly, and perhaps more fundamentally, the resolutions used in [17] were quite modest and as we have seen above, the lack of convergence only becomes apparent at sufficiently large N. Finally, Figueras and Wiseman [17] monitored $\phi {=\xi }^{a}\xi _{a}$ to estimate the numerical error and one can see that this quantity is better behaved than $\vert R/20 + 1\vert$.

Fig. 5

$\mathcal{A}_{H}{/\ell}^{3}$ vs. R ₄∕ℓ in a log–log plot. For small braneworld black holes, the area function approaches that of the 5d asymptotically flat Schwarzschild solution (in red). For large braneworld black holes it approaches of a 4d Schwarzschild solution which extends one AdS length into the bulk (in blue)

Finally, in Fig. 5 we display the area of the horizon of the full five-dimensional black hole as a function of the radius of the black hole on the brane. On this plot we also display the behaviour of the area as a function of the horizon radius for the 5d asymptotically flat Schwarzschild solution (in red) and the 4d asymptotically flat Schwarzschild solution times one AdS radius. As one can see from this plot, the geometry of the braneworld black holes smoothly interpolates between the 5d behaviour for small black holes $(R{_{4}\ell}^{2}\ell)$ and the 4d behaviour for large black holes $(R_{4} \gg \ell)$. Therefore, we confirm that standard 4d gravity on the brane is recovered for large black holes and that the latter can indeed be seen as small deformations of the 4d asymptotically flat Schwarzschild solution.

5 Summary and Conclusions

In Sect. 2 we have briefly reviewed a new method for casting the Einstein equations into a manifestly elliptic form which is amenable for numerics. We have also reviewed two standard algorithms for solving the equations numerically, namely the Ricci–DeTurck flow and Newton’s method.

Using this machinery, in Sect. 3 we have numerically constructed a static black hole solution in (the Poincare patch of) AdS whose boundary metric is conformal to the 4d asymptotically flat Schwarzschild solution. Using AdS/CFT we have identified this solution as the gravitational dual of $\mathcal{N} = 4$ SYM in the background of Schwarzschild in the Unruh vacuum. Interestingly, for this solution the Lichnerowicz operator Δ _L is positive definite which implies that it is a stable fixed point of Ricci flow [16].

Naive arguments [11] would have suggested that such a black hole cannot be static. However, our construction shows that this is not the case, and the leading O(N _c ²) solution is both smooth and static. We have also argued that one can perturb this black hole by deforming the boundary metric and construct an arbitrarily large braneworld black hole.

In Sect. 4 we have numerically constructed braneworld black holes of various sizes. Rather surprisingly, we have found that, at least in our gauge, the solutions do not appear to be very smooth. It would be interesting to understand in detail why this is so. Using our numerical solutions we have checked that 4d gravity on the brane is recovered for braneworld black holes which are large compared to the radius of AdS. Therefore, the RSII model can be in agreement with astrophysical observations.

One can check that for all braneworld black holes that we have constructed Δ _L has one, and only one, negative mode. Moreover, for large black holes, the negative mode that we find approaches the celebrated negative mode of 4d Schwarzschild. These results suggest that braneworld black holes should be stable under gravitational perturbations. Further evidence for this has been noted recently by Abdolrahimi et al. [18, 19], who have shown that braneworld black holes have greater entropy than a 4d Schwarzschild black hole with the same mass.