Keywords

1 Introduction

In the context of developing recycling and low-carbon economy, the important of closed-loop supply chain managements has been widely recognized by governments, researchers, and practitioners. As a big manufacturing country, many used products have been produced in China every year, which provide plenty of materials for developing closed-loop supply chains. Unfortunately, due to the low efficiency of operation, the enterprises that implement closed-loop supply chain managements cannot get sufficient and stable used products, and then not obtain profits. The low efficiency of operation is a serious impediment to the application and development of closed-loop supply chains in China.

The pricing is one of the important decisions, which is closely related to the efficiency of closed-loop supply chains. Therefore, many research efforts have been made to study pricing decisions facing closed-loop supply chain problems [1–9]. For example, Savaskan et al. studied the pricing decisions in bilateral monopoly closed-loop supply chains based on noncooperative game [1]. Savaskan et al. further studied pricing decisions in closed-loop supply chains with one monopoly manufacturer and two competing retailers [2]. Ferrer and Jayashankar studied pricing decisions in multicycle closed-loop supply chains with two different markets [3]. Based on above studies, Ferrer and Jayashankar continued to discuss the pricing decisions of new and remanufactured products with considering the less recycling numbers contracts [4]. Atasu et al. studied pricing decisions with considering the influence of manufacturer’s competition, green consumer groups, and market growth [5]. Bao et al. investigated pricing decisions in bilateral monopoly closed-loop supply chains with the restricted number of recycling products and difference between new and used products [6].

Although many advances have been made on pricing decision in closed-loop supply chains, the researches on pricing decisions with disrupted situations are rarely found in literature. However, decision makers often face unstable situations in the closed-loop supply chains. Generally, disruptive events will significantly influence the performance of supply chains. Moreover, there are plenty of evidences to suggest that production costs are relatively easier to disrupt in closed-loop supply chains.

Disruption management of supply chains has gained much attention among researchers and practitioners [10–19]. For instance, Qi et al. studied pricing and coordination decisions in a one-supplier–one-retailer supply chain with demand disruptions [10]. Xiao et al. then extended disruption management of the supply chain with multiple competing retailers [11]. Xiao and Yu developed an indirect evolutionary game model to study evolutionarily stable strategies of retailers on market target selection with demand and raw material supply disruptions [12]. Yu et al. studied how to handle disruptions in the supply chain under wholesale price contract [13]. Xiao and Qi investigated how to coordinate a supply chain with multiple competing retailers using game theory when the production cost was disrupted [14]. Chen and Xiao designed linear quantity discount and wholesale price contracts in a supply chain with production cost and demand disruptions [15]. Zhang et al. investigated how to coordinate the supply chain with demand disruptions by revenue-sharing contracts [16]. Huang et al. studied pricing and production decisions in dual-channel supply chains when production costs are disrupted [17].

The above literatures have found many important insights in disruption management of supply chains. However, most of them only concerned about decisions in open-loop supply chains, but closed-loop supply chains. Closed-loop supply chains are more complex, which have characteristics of not only forward logistics but also reverse logistics. Consequently, manufacturing costs and other related parameters are more easily disrupted in closed-loop supply chains.

In this research, we analyze decisions in bilateral monopoly closed-loop supply chains with manufacturing cost disruptions. We find the optimal decisions in stable contexts have some robustness. The optimal decisions are revised only when manufacturing cost disruptions exceeds some thresholds. The centralized decision maker and manufacturer in decentralized decision making always prefer to change their decisions when the absolute value of disruptions are larger than the threshold. However, the retailer in decentralized decision making prefer to change his decision only when manufacturing cost disruptions are negative.

The rest of this paper is organized as follows. After introducing the model assumptions and notations in Sect. 2, the decision models without disruptions are described in Sect. 3. Decision models with disruptions are developed in Sect. 4. Section 5 presents some numerical examples. Conclusions and extensions are provided in Sect. 6.

2 Model Assumptions and Notations

We mainly discuss decisions in a closed-loop supply chain with one dominant manufacturer and one retailer. The manufacturer is in charge of re/manufacturing new products and collecting used products, and the retailer is responsible to distribute new products.

Before presenting models we introduce the following notation. Cm, unit cost of manufacturing a new product; Cr, unit cost of remanufacturing a new product; Δ, unit cost savings from remanufacturing a product, that is Δ = C m  − C r ; u 1, marginal disposal cost; u 2, the marginal underage cost; q(p) = ϕ − βp, market demand with p represents the retailer’s price, and ϕ and β are positive parameters; τ, return rate of used products, and \( \tau =\sqrt{I/B} \), where I stands for fixed investments in collection activities and B a scaling parameter; Π, profit function; ( )C, results from centralized decisions; ( )M, results from the manufacturer; ( )R, results from the retailer; ( )U, results from unchanged decisions with disruptions; ( )*, results from the optimal solutions.

In order to simplify research process, we make the following assumptions based on existing research.

Assumption 1

Manufacturing and remanufacturing products are identical to customers and can be sold in the same market with the same price.

Assumption 2

We let the sum of used product’s collection price and transportation cost is zero since it is exogenous and does not affect the results.

Assumption 3

Manufacturers and retailers make decisions in the game of complete information.

Assumption 4

We study the pricing decisions in a two-period closed-loop supply chain. In the first period, the manufacturer purchases some raw materials due to a long lead time, and then products new products in the second period. The preliminary production plan is made based on the estimated manufacturing cost Cm in the first period, and the actual production plan is made based on real production cost Cm + δ, where the manufacturing cost disruption is δ in the second period.

3 Decision Models Without Disruptions

In this section we present the centralized and decentralized decision models as baseline, which are used to study the impact of manufacturing cost disruptions on decisions.

3.1 Centralized Decision Model

In a centralized closed-loop supply chain, the decision maker makes her decision based on maximizing the total profits of closed-loop supply chain. Based on our assumptions, the centralized pricing model is determined by

$$ \underset{p,\tau }{ \max }\ {\displaystyle {\Pi}_{\mathrm{C}}}=\left(\phi -\beta p\right)\left(p-{\mathrm{C}}_{\mathrm{m}}+\Delta \tau \right)-\mathrm{B}{\tau}^2 $$

According to the first-order optimal conditions, the optimal solutions of the above model are given by

$$ {p_{\mathrm{C}}}^{*}=\frac{2\mathrm{B}\left(\phi +\beta {\mathrm{C}}_{\mathrm{m}}\right)-\beta \phi {\Delta}^2}{\beta \left(4\mathrm{B}-\beta {\Delta}^2\right)} $$
(1)
$$ {\tau_{\mathrm{C}}}^{*}=\frac{\Delta \left(\phi -\beta {\mathrm{C}}_{\mathrm{m}}\right)}{4\mathrm{B}-\beta {\Delta}^2} $$
(2)
$$ {q_{\mathrm{C}}}^{*}=\frac{2\mathrm{B}\left(\phi -\beta {\mathrm{C}}_{\mathrm{m}}\right)}{4\mathrm{B}-\beta {\Delta}^2} $$
(3)
$$ {{\prod}_{\mathrm{C}}}^{*}=\frac{\mathrm{B}{\left(\phi -\beta {\mathrm{C}}_{\mathrm{m}}\right)}^2}{\beta \left(4\mathrm{B}-\beta {\Delta}^2\right)} $$
(4)

3.2 Decentralized Decision Model

As a Stackelberg leader, the manufacturer first decides ϖ, τ, and the retailer then decides p. Thus, the decentralized pricing model can be given by

$$ \begin{aligned}\underset{\varpi, \tau }{ \max }{\displaystyle {\Pi}_{\mathrm{M}}}&=\left(\phi -\beta p\right)\left(\varpi -{\mathrm{C}}_{\mathrm{m}}+\Delta \tau \right)-\mathrm{B}{\tau}^2\\ \mathrm{s}.\mathrm{t}.p&\in {\mathrm{argmax}\Pi}_{\mathrm{R}}=\left(\phi -\beta p\right)\left(p-\varpi \right)\end{aligned} $$

By using backward induction and the first order condition, the optimal solutions are given by

$$ {\varpi}^{*}=\frac{\left(4\mathrm{B}-\beta {\Delta}^2\right)\phi +4\mathrm{B}\beta {\mathrm{C}}_{\mathrm{m}}}{\beta \left(8\mathrm{B}-\beta {\Delta}^2\right)} $$
(5)
$$ {p}^{*}=\frac{\left(6\mathrm{B}-\beta {\Delta}^2\right)\phi +2\beta {\mathrm{BC}}_{\mathrm{m}}}{\beta \left(8\mathrm{B}-\beta {\Delta}^2\right)} $$
(6)
$$ {\tau}^{*}=\frac{\Delta \left(\phi -\beta {\mathrm{C}}_{\mathrm{m}}\right)}{8\mathrm{B}-\beta {\Delta}^2} $$
(7)
$$ {q}^{*}=\frac{2\mathrm{B}\left(\phi -\beta {\mathrm{C}}_{\mathrm{m}}\right)}{8\mathrm{B}-\beta {\Delta}^2} $$
(8)
$$ {\Pi_{\mathrm{M}}}^{*}=\frac{\mathrm{B}{\left(\phi -\beta {\mathrm{C}}_{\mathrm{m}}\right)}^2}{\beta \left(8\mathrm{B}-\beta {\Delta}^2\right)} $$
(9)
$$ {\Pi_{\mathrm{R}}}^{*}=\frac{4{\mathrm{B}}^2{\left(\phi -\beta {\mathrm{C}}_{\mathrm{m}}\right)}^2}{\beta {\left(8\mathrm{B}-\beta {\Delta}^2\right)}^2} $$
(10)

4 Decision Models with Cost Disruptions

In this section, we discuss the decision models with manufacturing cost disruptions. If the manufacturing cost disruption δ > 0, the actual manufacturing cost is larger than estimated. In this context, the decision maker will increase his pricing, and there will be disposal costs for unsold products. If the manufacturing cost disruption δ < 0, the actual manufacturing cost is smaller than estimated. In this context, the decision maker will decrease his pricing, and there will be underage costs for unmet demand.

4.1 Centralized Decision Model with Disruptions

The centralized decision model with disruptions δ > 0 is given by

$$ \begin{aligned}\underset{\tilde{p},\tilde{\tau}}{ \max }\ {\displaystyle {\tilde{\Pi}}_{\mathrm{C}}}&=\left(\phi -\beta \tilde{p}\right)\left(\tilde{p}-\right({\mathrm{C}}_{\mathrm{m}}+\delta \left)+\Delta \tilde{\tau}\right)\\ {}& \quad\ -\mathrm{B}{\tilde{\tau}}^2-{\mu}_1\left(\frac{2\mathrm{B}\left(\phi -\beta {\mathrm{C}}_{\mathrm{m}}\right)}{4\mathrm{B}-\beta {\Delta}^2}-\left(\phi -\beta \tilde{p}\right)\right)\end{aligned} $$

The centralized decision model with disruptions δ < 0 is given by

$$ \begin{aligned}\underset{\tilde{p},\tilde{\tau}}{ \max }\ {\displaystyle {\tilde{\Pi}}^{\mathrm{C}}}&=\left(\phi -\beta \tilde{p}\right)\left(\tilde{p}-\right({\mathrm{C}}_{\mathrm{m}}+\delta \left)+\Delta \tilde{\tau}\right)-\mathrm{B}{\tilde{\tau}}^2\\ {}& \quad\ -{\mu}_2\left(\left(\phi -\beta \tilde{p}\right)-\frac{2\mathrm{B}\left(\phi -\beta {\mathrm{C}}_{\mathrm{m}}\right)}{4\mathrm{B}-\beta {\Delta}^2}\right)\end{aligned} $$

We can derive the optimal solutions by the first-order optimal conditions. The optimal solutions are given by

$$ {{\tilde{p}}_{\mathrm{C}}}^{*}=\left\{\begin{array}{l}\dfrac{2\mathrm{B}\left(\phi +\beta {\mathrm{C}}_{\mathrm{m}}+\beta \delta -\beta {\mu}_1\right)-\beta \phi {\Delta}^2}{\beta \left(4\mathrm{B}-\beta {\Delta}^2\right)}\begin{array}{cc}\hfill \hfill & \hfill \delta >{\mu}_1\hfill \end{array}\\[1pc] {}\dfrac{2\mathrm{B}\left(\phi +\beta \left({\mathrm{C}}_{\mathrm{m}}+\delta +{\mu}_2\right)\right)-\beta \phi {\Delta}^2}{\beta \left(4\mathrm{B}-\beta {\Delta}^2\right)}\begin{array}{cc}\hfill \hfill & \hfill \delta <-{\mu}_2\hfill \end{array}\end{array}\right. $$
(11)
$$ {{\tilde{\tau}}_{\mathrm{C}}}^{*}=\left\{\begin{array}{l}\dfrac{\Delta \left(\phi -\beta {\mathrm{C}}_{\mathrm{m}}+\beta {\mu}_1-\beta \delta \right)}{4\mathrm{B}-\beta {\Delta}^2}\begin{array}{cc}\hfill \hfill & \hfill \delta >{\mu}_1\hfill \end{array}\\[1pc] {}\dfrac{\Delta \left(\phi -\beta \left({\mathrm{C}}_{\mathrm{m}}+{\mu}_2+\delta \right)\right)}{4\mathrm{B}-\beta {\Delta}^2}\begin{array}{cc}\hfill \hfill & \hfill \delta <-{\mu}_2\hfill \end{array}\end{array}\right. $$
(12)
$$ {{\tilde{q}}_{\mathrm{C}}}^{*}=\left\{\begin{array}{l}\dfrac{2\mathrm{B}\left(\phi -\beta {\mathrm{C}}_{\mathrm{m}}+\beta {\mu}_1-\beta \delta \right)}{4\mathrm{B}-\beta {\Delta}^2}\begin{array}{cc}\hfill \hfill & \hfill \delta >{\mu}_1\hfill \end{array}\\[1pc] {}\dfrac{2\mathrm{B}\left(\phi -\beta \left({\mathrm{C}}_{\mathrm{m}}+{\mu}_2+\delta \right)\right)}{4\mathrm{B}-\beta {\Delta}^2}\begin{array}{cc}\hfill \hfill & \hfill \delta <-{\mu}_2\hfill \end{array}\end{array}\right. $$
(13)
$$ {{\tilde{\Pi}}_{\mathrm{C}}}^{*}=\left\{\begin{array}{l}\dfrac{\mathrm{B}\left({\left(\phi -\beta {\mathrm{C}}_{\mathrm{m}}-\beta \delta \right)}^2-2{\beta}^2\delta {\mu}_1+{\beta}^2{\mu_1}^2\right)}{\beta \left(4\mathrm{B}-\beta {\Delta}^2\right)}\begin{array}{cc}\hfill \hfill & \hfill \delta >{\mu}_1\hfill \end{array}\\[1pc] {}{\prod}_{\mathrm{C}}^{\mathrm{U}}=\dfrac{\mathrm{B}\left(\phi -\beta {\mathrm{C}}_{\mathrm{m}}\right)\left(\phi -\beta {\mathrm{C}}_{\mathrm{m}}-2\beta \delta \right)}{\beta \left(4\mathrm{B}-\beta {\Delta}^2\right)}\begin{array}{cc}\hfill \hfill & \hfill -{\mu}_2\le \delta \le {\mu}_1\hfill \end{array}\\[1pc] {}\dfrac{\mathrm{B}\Big({\left(\phi -\beta {\mathrm{C}}_{\mathrm{m}}-\beta \delta \right)}^2+{\beta}^2{\mu}_2\left(2\delta +{\mu}_2\right)}{\beta \left(4\mathrm{B}-\beta {\Delta}^2\right)}\begin{array}{cc}\hfill \hfill & \hfill \kern1em \delta <-{\mu}_2\hfill \end{array}\end{array}\right. $$
(14)

If − u 2 ≤ δ ≤ u 1, the optimal solutions are same with the optimal in centralized model without disruption except the profits.

4.2 Decentralized Pricing Model with Disruptions

The decentralized decision model with disruptions δ > 0 can be given by

$$ \begin{aligned}\underset{\tilde{\varpi},\tilde{\tau}}{ \max }{\displaystyle {\tilde{\Pi}}_{\mathrm{M}}}&=\left(\phi -\beta \tilde{p}\right)\left(\tilde{\varpi}-\right({\mathrm{C}}_{\mathrm{m}}+\delta \left)+\Delta \tilde{\tau}\right)-\mathrm{B}{\tilde{\tau}}^2\\ &\quad\ -{\mu}_1\left(\frac{2\mathrm{B}\left(\phi -\beta {\mathrm{C}}_{\mathrm{m}}\right)}{8\mathrm{B}-\beta {\Delta}^2}-\left(\phi -\beta \tilde{p}\right)\right)\\ {}\mathrm{s}.\mathrm{t}.\tilde{p}&\in \mathrm{argmax}{\tilde{\Pi}}_{\mathrm{R}}=\left(\phi -\beta \tilde{p}\right)\left(\tilde{p}-\tilde{\varpi}\right)\end{aligned} $$

The decentralized decision model with disruptions δ < 0 can be given by

$$ \begin{aligned}\underset{\tilde{\varpi},\tilde{\tau}}{ \max }{\displaystyle {\tilde{\Pi}}_{\mathrm{M}}}&=\left(\phi -\beta \tilde{p}\right)\left(\tilde{\varpi}-\right({\mathrm{C}}_{\mathrm{m}}+\delta \left)+\Delta \tilde{\tau}\right)-\mathrm{B}{\tilde{\tau}}^2\\ {}& \quad\ -{\mu}_2\left(\left(\phi -\beta \tilde{p}\right)-\frac{2\mathrm{B}\left(\phi -\beta {\mathrm{C}}_{\mathrm{m}}\right)}{8\mathrm{B}-\beta {\Delta}^2}\right)\\ {}\mathrm{s}.\mathrm{t}.\tilde{p}&\in \mathrm{argmax}{\tilde{\Pi}}_{\mathrm{R}}=\left(\phi -\beta \tilde{p}\right)\left(\tilde{p}-\tilde{\varpi}\right)\end{aligned} $$

We can get the optimal solutions by using backward induction and the first order condition. The optimal solutions can be given by

$$ {\tilde{\varpi}}^{*}=\left\{\begin{array}{l}\dfrac{\left(4\mathrm{B}-\beta {\Delta}^2\right)\phi +4\mathrm{B}\beta \left({\mathrm{C}}_{\mathrm{m}}+\delta -{\mu}_1\right)}{\beta \left(8\mathrm{B}-\beta {\Delta}^2\right)}\begin{array}{cc}\hfill \hfill & \hfill \delta >{\mu}_1\hfill \end{array}\\[1pc] {}\dfrac{\left(4\mathrm{B}-\beta {\Delta}^2\right)\phi +4\mathrm{B}\beta \left({\mathrm{C}}_{\mathrm{m}}+\delta +{\mu}_2\right)}{\beta \left(8\mathrm{B}-\beta {\Delta}^2\right)}\begin{array}{cc}\hfill \hfill & \hfill \delta <-{\mu}_2\hfill \end{array}\end{array}\right. $$
(15)
$$ {\tilde{p}}^{*}=\left\{\begin{array}{l}\dfrac{\left(6\mathrm{B}-\beta {\Delta}^2\right)\phi +2\beta \mathrm{B}\left({\mathrm{C}}_{\mathrm{m}}+\delta -{\mu}_1\right)}{\beta \left(8\mathrm{B}-\beta {\Delta}^2\right)}\begin{array}{cc}\hfill \hfill & \hfill \delta >{\mu}_1\hfill \end{array}\\[1pc] {}\dfrac{\left(6\mathrm{B}-\beta {\Delta}^2\right)\phi +2\beta \mathrm{B}\left({\mathrm{C}}_{\mathrm{m}}+\delta +{\mu}_2\right)}{\beta \left(8\mathrm{B}-\beta {\Delta}^2\right)}\begin{array}{cc}\hfill \hfill & \hfill \delta <-{\mu}_2\hfill \end{array}\end{array}\right. $$
(16)
$$ {\tilde{\tau}}^{*}=\left\{\begin{array}{l}\dfrac{\Delta \left(\phi -\beta \left({\mathrm{C}}_{\mathrm{m}}+\delta -{\mu}_1\right)\right)}{8\mathrm{B}-\beta {\Delta}^2}\begin{array}{cc}\hfill \hfill & \hfill \delta >{\mu}_1\hfill \end{array}\\[1pc] {}\dfrac{\Delta \left(\phi -\beta \left({\mathrm{C}}_{\mathrm{m}}+\delta +{\mu}_2\right)\right)}{8\mathrm{B}-\beta {\Delta}^2}\begin{array}{cc}\hfill \hfill & \hfill \delta <-{\mu}_2\hfill \end{array}\end{array}\right. $$
(17)
$$ {\tilde{q}}^{*}=\left\{\begin{array}{l}\dfrac{2\mathrm{B}\left(\phi -\beta \left({\mathrm{C}}_{\mathrm{m}}+\delta -{\mu}_1\right)\right)}{8\mathrm{B}-\beta {\Delta}^2}\begin{array}{cc}\hfill \hfill & \hfill \delta >{\mu}_1\hfill \end{array}\\[1pc] {}\dfrac{2\mathrm{B}\left(\phi -\beta \left({\mathrm{C}}_{\mathrm{m}}+\delta +{\mu}_2\right)\right)}{8\mathrm{B}-\beta {\Delta}^2}\begin{array}{cc}\hfill \hfill & \hfill \delta <-{\mu}_2\hfill \end{array}\end{array}\right. $$
(18)
$$ {{\tilde{\Pi}}_{\mathrm{M}}}^{*}=\left\{\begin{array}{l}\dfrac{\mathrm{B}{\left(\phi -\beta \left({\mathrm{C}}_{\mathrm{m}}+\delta \right)\right)}^2-{\beta}^2{\mu}_1\left(2\delta -{\mu}_1\right)\Big)}{\beta \left(8\mathrm{B}-\beta {\Delta}^2\right)}\begin{array}{cc}\hfill \hfill & \hfill \delta >{\mu}_1\hfill \end{array}\\[10pt] {}\dfrac{\mathrm{B}\left(\phi -\beta {\mathrm{C}}_{\mathrm{m}}\right)\left(\phi -\beta {\mathrm{C}}_{\mathrm{m}}-2\beta \delta \right)}{\beta \left(8\mathrm{B}-\beta {\Delta}^2\right)}\begin{array}{cc}\hfill \hfill & \hfill -{\mu}_2\le \delta \le {\mu}_1\hfill \end{array}\\[10pt] {}\dfrac{\mathrm{B}\left({\left(\phi -\beta \left({\mathrm{C}}_{\mathrm{m}}+\delta \right)\right)}^2+{\beta}^2{\mu}_2\left(2\delta +{\mu}_2\right)\right)}{\beta \left(8\mathrm{B}-\beta {\Delta}^2\right)}\begin{array}{cc}\hfill \hfill & \hfill \delta <-{\mu}_2\hfill \end{array}\end{array}\right. $$
(19)
$$ {{\tilde{\Pi}}_{\mathrm{R}}}^{*}=\left\{\begin{array}{l}\dfrac{4{\mathrm{B}}^2{\left(\phi -\beta \left({\mathrm{C}}_{\mathrm{m}}+\delta -{\mu}_1\right)\right)}^2}{\beta {\left(8\mathrm{B}-\beta {\Delta}^2\right)}^2}\begin{array}{cc}\hfill \hfill & \hfill \delta >{\mu}_1\hfill \end{array}\\[10pt] {}\dfrac{4{\mathrm{B}}^2{\left(\phi -\beta {\mathrm{C}}_{\mathrm{m}}\right)}^2}{\beta {\left(8\mathrm{B}-\beta {\Delta}^2\right)}^2}\begin{array}{cc}\hfill \hfill & \hfill -{\mu}_2\le \delta \le {\mu}_1\hfill \end{array}\\[10pt] {}\dfrac{4{\mathrm{B}}^2{\left(\phi -\beta \left({\mathrm{C}}_{\mathrm{m}}+\delta +{\mu}_2\right)\right)}^2}{\beta {\left(8\mathrm{B}-\beta {\Delta}^2\right)}^2}\begin{array}{cc}\hfill \hfill & \hfill \delta <-{\mu}_2\hfill \end{array}\end{array}\right. $$
(20)

If − u 2 ≤ δ ≤ u 1 the optimal solutions are same with the optimal in decentralized model without disruption except the profits.

We can get the following propositions form comparing those solutions in different contexts.

Proposition 1

The decisions in closed-loop supply chains have some robustness (− u 2 ≤ δ ≤ u 1) with manufacturing cost disruptions in the both centralized and decentralized situations.

That is, decision makers will retain their optimal solutions of decision models without disruptions when the manufacturing cost disruption is small (− u 2 ≤ δ ≤ u 1).

Proposition 2

When δ > μ 1, the market pricing is increased, while return ratio and quantity are decreased with disruptions; when δ ≤ − μ 2, the market pricing is decreased, while return ratio and quantity are increased with disruptions.

Proposition 3

The decision maker in centralized closed-loop supply chain prefers to change her decisions when manufacturing cost is disrupted.

Proposition 4

The manufacturer in decentralized closed-loop supply chain prefers to change her decisions, while the retailer only prefer to change his decisions when δ ≤ − μ 2.

5 Numerical Analysis

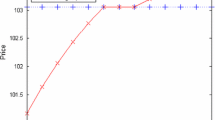
In order to depict solutions more clearly, we make some numerical analyses in this section. We let B = 100, ϕ = 150 β = 4, Cm = 10, Δ = 2, μ 1 = μ 2 = 2, − 8 ≤ δ ≤ 8. The detailed decisions solutions are provided in Figs. 1, 2, 3, 4, and 5.

Fig. 1
figure 1

Pricing in centralized model with disruptions

Full size image
Fig. 2
figure 2

Return rates in centralized model with disruptions

Full size image
Fig. 3
figure 3

Profits in centralized model with disruptions

Full size image
Fig. 4
figure 4

Manufacturer profits in decentralized model with disruptions

Full size image
Fig. 5
figure 5

Retailer profits in decentralized model with disruptions

Full size image

From Figs. 1, 2, 3, 4, and 5, we find that decisions have some robustness with manufacturing cost disruptions in the both centralized and decentralized situations. The market pricing is increased, while return ratio and quantity are decreased with disruptions when δ > u 1; market pricing is decreased, while return ratio and quantity are increased with the absolute value of disruptions when δ < − u 2. For the larger profits, decision maker in centralized context prefer to change her decisions with disruptions. The manufacturer in decentralized context also prefer to change her decisions, while the retailer only prefer to change his decisions when δ < − u 2. Those are consistent with Proposition 1–4.

6 Conclusion

In this paper, we study decision models of closed-loop supply chains with manufacturing cost disruptions. We find the optimal decisions in stable contexts have some robustness. The optimal decisions are revised only when manufacturing cost disruptions exceeds the thresholds. The centralized decision maker and manufacturer in decentralized decision making always prefer to change their decisions when disruptions exceed the threshold. However, the retailer in decentralized decision making change his decision only when manufacturing cost disruptions are negative. This paper makes some contributions to the literature. However, we just consider very simple channel structure. How about decision models when there are multiple manufacturers or retailers? Those questions are our further research.