Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

As dense granular materials are sheared, they finally yield under stress and start flowing. The resulting flow is not necessarily homogeneous like in normal fluids. At low shear rates, grains form solid like regions separated by narrow regions between them, called shear bands [1–3]. The rigid blocks move relative to each other in such a way that the strain is localized in shear bands, i.e. along the narrow interfaces between the unstrained parts. Understanding the mechanism of material failure is of great importance in industry and geophysics, and hence shear band formation is widely investigated experimentally [4–14] and numerically [15–18].

The shear bands are dependent on size and shape of the grains [5, 8] and, most of the time, are narrow (of the order of a few grain diameters) and localized near the boundaries [1, 7, 13], which makes the theoretical description more difficult. For example, in a Couette cell geometry one always observes that a narrow shear band forms near the inner cylinder [4–6]. However, using a modified Couette geometry, Fenistein and co-workers managed to generate wide shear zones in the bulk of the material away from the confining cylinders [2, 8]. The experimental setup was a Couette cell (two co-axial cylinders) modified by splitting the bottom into two rings which were attached to the cylinders. The cell was filled with grains up to height H and one of the cylinders together with its co-moving bottom ring were rotated. In this way, they drove the system from the split bottom, which initiates a shear band with cylindrical symmetry. The shear band is pinned to the split bottom and its width W grows with height. The angular velocity profile at the surface follows an error function characterized by the width and center position of the shear zone at the surface. The center of shear zone shifts towards the inner cylinder with increasing the filling height H independent of the particle properties. The width W, however, depends on the shape and size of the grains. Using a theory based on the principle of minimum dissipation, Unger et al. described the position of the shear band with the assumption of negligible width of the shear band [15]. The model produced results in excellent agreement with the experiments with no fitting parameter. Later, a generalized version of this method proposed which was capable of reproducing the width of the shear bands [18].

In the present work, we introduce a new geometry which initiates a wide shear band in bulk and narrow ones near the confining walls simultaneously. The effective friction coefficient is different in bulk and near the rough boundaries. This difference, together with the possibility of choosing different grain size and filling height, leads to different scenarios for shear band formation. We use the least dissipation principle to describe the behavior and compare the results with experimental data.

2 Shear Band Formation as a Variational Problem

According to the experimental findings (from Refs. [2, 8]), the width of shear band W depends on the grain properties. One can make W arbitrarily small, by using a suitable choice of the size and shape of the grains. This justifies the narrow band approximation used in Ref. [15] to calculate the center position of the shear band. Applying the idea of the principle of least dissipation, they required a time-independent (steady) flow which leads to the minimum rate of energy dissipation and fulfils the external constraint conditions. Assuming a narrow shear band, the dissipation occurs throughout the interface between the two sliding rigid blocks which leads to the following variational problem

$$\displaystyle{ \int v\,p\,\mu _{\text{eff}}\,\mathit{dS} = \text{min}, }$$
(1)

where v, p, and dS are the relative velocity of the blocks, the pressure, and the sliding surface at height h, respectively, and the dissipation is integrated over the whole sliding surface. The effective coarse-grained friction coefficient \(\mu _{ \text{eff}}\) can be assumed to remain constant in the bulk of the material. Then, assuming hydrostatic pressure, Eq. (1) for the modified Couette geometry leads to

$$\displaystyle{ \int {r}^{2}\,(H - h)\,{\left [1 + {(\mathit{dr}/\mathit{dh})}^{2}\right ]}^{1/2}\,\mathit{dh} = \text{min}. }$$
(2)

Equation (2) provides a unique path for the shear band inside the bulk of the material, which is in agreement with the center position obtained from experiments [15].

In practice, the path of the shear band is not frozen due to the presence of disorder and inhomogeneities. Because of the relative displacements in the shear band, the spatial distribution of the inhomogeneities changes with time, which may change the global minimum path and produce instantaneous shear bands. If a random potential is replaced (in order to take into account the disordered nature of the system), then an ensemble average over the instantaneous shear bands, obtained via the principle of least dissipation, reproduces a wide shear band [18]. The width W obtained this way matches remarkably with the experimental data.

Fig. 1
figure 1

(left) Schematic view of our modified Couette cell. (right) Side view

Full size image

3 Experimental Setup

Our experimental setup is basically a modified Couette geometry with a split bottom near the outer cylinder (see Fig. 1). The gap between the bottom plate and the outer cylinder is around 400 μm. The space between the two cylinders is filled with spherical glass beads up to a height H, and the inner cylinder rotates together with the attached bottom plate. The diameter of the grains ranges from 1 to 3 mm, thus no particle can escape from the split bottom. The side walls and bottom disk made rough by gluing a layer of grains. The system is driven from the bottom by a motor. The resulting flow at the free surface is monitored from above by a fast CCD camera at a rate of 60 frames/s with pixel resolution of 100 μm. The flow rapidly reaches to a stationary state (of the order of few seconds) where the angular velocity profile is symmetric with respect to the cylinder axis.

Fig. 2
figure 2

(left) Angular velocity (ω) profile as a function of the distance r−R 1 from the inner cylinder for different filling heights. R 1 is the radius of the inner cylinder. (right) The derivative of ω with respect to r. The ratio between the effective friction coefficients in bulk and wall \(\mu _{ \text{bulk}}/\mu _{\text{wall}}\) is set to 1. 0

Full size image

4 Numerical Results

We first apply the numerical method of Sect. 2 to the geometry of our experimental setup. We use a random potential field and find the path which minimizes the rate of energy dissipation and fulfils the constraints. As the local structure is changed along the shear path, we change the randomness in the neighborhood of the shear band and search for the optimal path anew. This process is repeated many times, and the shear band is finally determined as the ensemble average over all realizations.

Fig. 3
figure 3

The same plots as in Fig. 2 but for \(\mu _{ \text{wall}}/\mu _{\text{bulk}}\,=\,0.7\). The arrows show the center position of the shear bands for intermediate filling heights

Full size image
Fig. 4
figure 4

Numerical results for the phase diagram of the possible shear bands in the (\(\mu _{\text{wall}}\), \(\mu _{ \text{bulk}}\)) space for different ratios between the filling height H and the width of the system L: \(H/L=\) (a) 0. 5, (b) 1. 0, (c) 2. 0, and (d) 3. 0. The blue square, green cross, and red plus denote, respectively, a shear band near the outer cylinder, a wide shear band in the middle, and a shear band near the inner cylinder

Full size image

We fix the ratio R 1∕R 2 between the radius of the inner and outer cylinders and vary the ratio H∕L (aspect ratio, \(L = R_{2} - R_{1}\)), the lattice size (larger than the grain diameter d), and the ratio between the effective friction coefficient in the bulk and near the rough walls \(\mu _{\text{bulk}}/\mu _{\text{wall}}\). Most of the time, the numerical results produce an angular velocity profile at the surface which can be well fitted by an error function, i.e. a wide shear band exists in the bulk of the system (see Fig. 2). However, for relatively large grains (d∕L ≥ 0. 04) and in the intermediate filling heights we find different types of velocity profile, which imply the existence of simultaneous shear bands: relatively narrow shear bands near the confining walls, and a wide shear zone in the middle (Fig. 3).

The phase behavior for different values of \(\mu _{ \text{bulk}}\) and \(\mu _{ \text{wall}}\) is shown in Fig. 4. Since the walls are made rough with the same grains as those used in the bulk, one expects that \(\mu _{\text{wall}} <\mu _{\text{bulk}}\) in our setup. Therefore, Fig. 4b reveals that the chance of multiple shear band formation is remarkably larger for intermediate filling heights (L < = H).

Fig. 5
figure 5

Experimental data for the angular velocity profile (top) and its derivative (bottom) as a function of the distance from the inner cylinder for different shear rates

Full size image

5 Experimental Evidence

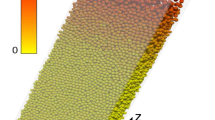
The experimental data show two different situations depending on the particle size. For small grains, there is always a single shear band which starts at the split bottom and reaches the surface. It is located near the outer cylinder for small filling heights, but it becomes wider and shifts towards the inner cylinder with increasing H, a behavior reported previously in the literature. Interestingly, for larger grains, there can be more than one shear band on the surface in agreement with numerical results. An example is shown in Fig. 5 belonging to 2 mm glass beads and H∕L ∼ 1. 2. Besides the wide middle shear band, a narrow one also forms near the inner cylinder. The behavior is robust with respect to the choice of shear velocity. By varying the grain size and filling height, we are currently looking for cases where two shear bands form near the rough walls or all three types of shear band coexist simultaneously.