Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Sebastian Sager (in 2006, [56]) and Christian Kirches (in 2010, [39]) received their Ph.D.s from Heidelberg University under the supervision of Gerhard Reinelt, thus becoming grand-sons of Martin Grötschel. Michael Jung is a Ph.D. student at Heidelberg University supervised by Reinelt and Sager, and expects to become both a grandson and a grand-grandson of Grötschel in 2013. Another interesting link is the scientific and personal socialization of all three authors in the realm of Hans Georg Bock, who, like Grötschel, is a protagonist of the University of Augsburg’s golden age of applied mathematics in the late eighties.

Mixed-integer optimal control problems (MIOCPs) have been gaining significantly increased interest over the last years. This is due to the fact that the underlying processes have a high potential for optimization, while at the same time they are hard to assess manually due to their combinatorial, nonlinear, and dynamic nature. Typical examples are the choice of gears in automotive control [26, 40], water or gas networks [14, 49], traffic flow [23, 32], supply chain networks [29], distributed autonomous systems [1], and processes in chemical engineering that involve valves [38, 65]. The truck benchmark problem we present in this article is motivated by work of [35, 39, 68] on heavy duty trucks. See [59] for an open benchmark library for MIOCPs. In this article, we are especially interested in switching decisions that imply constraints. In the interest of readability we focus on the specific problem class of MIOCPs in ordinary differential equations (ODEs) of the following form.

Definition 1

(MIOCP)

In this contribution a mixed-integer optimal control problem (MIOCP) refers to the switched system on a fixed time horizon [0,t f] given by

(1)

The logical operator \(\bigvee_{i \in\{1, \ldots, {n_{\omega }}\}}\) implies that at all times t∈[0,t f] exactly one of the n ω possible modes is chosen and is represented here by time-dependent logical literals Y i (⋅), 1≤i≤n ω . The optimal control \(u: [0, t_{\mathrm {f}}] \rightarrow \mathbb {R}^{n_{u}}\) is assumed to be measurable and of bounded variation, the differential states \(x: [0, t_{\mathrm {f}}] \rightarrow \mathbb {R}^{n_{x}}\) to be uniquely determined once a switching regime Y(⋅) and the controls u(⋅) are fixed. The vectors \(v^{i} \in \mathbb {R}^{n_{v}}\) comprise constant values that are specific for the given mode. We write \(\varOmega := \{v^{1}, v^{2}, \ldots, v^{{n_{\omega }}}\}\). The objective function \(e: \mathbb {R}^{n_{x}} \rightarrow \mathbb {R}\) of Mayer type and the constraint functions \(c: \mathbb {R}^{n_{x}} \times \mathbb {R}^{n_{u}} \times \mathbb {R}^{n_{v}} \rightarrow \mathbb {R}^{n_{c}} \) and \(d: \mathbb {R}^{n_{x}} \times \mathbb {R}^{n_{u}}\rightarrow \mathbb {R}^{d}\) are assumed to be sufficiently often continuously differentiable.

For example, in Sect. 2 the vectors v i will denote degrees of efficiency and engine speed bounds for a particular choice i of the gear. Note that problem class (1) can be generalized in many directions to include different objective functionals, multi-point constraints, algebraic variables, more general hybrid systems, and the likes, compare [57] for further details and references.

Although the first MIOCPs, namely the optimization of subway trains that are equipped with discrete acceleration stages, were already solved in the early eighties for the city of New York [12], the so-called indirect methods used there do not seem appropriate for generic optimal control problems with underlying nonlinear dynamic systems and mixed path-control constraints. The discussion of advantages and disadvantages of indirect approaches is ongoing since the 1980s and beyond the scope of this paper. See [57] for a discussion of the applicability of dynamic programming and global maximum principles to MIOCP and further references.

Direct and all-at-once methods, such as Bock’s direct multiple shooting [13, 44] and direct collocation [5, 9, 10] have emerged as the methods of choice for the computational solution of many purely continuous optimal control problems. They are also at the heart of our approach to MIOCP. These approaches have in common that they result in highly structured nonlinear programs (NLPs). As the focus of this article is on properties of relaxed MIOCPs, we do not go into details on how these transformations are carried out, but rather refer the interested reader to [11, 44]. Nevertheless, we need some NLP definitions to illustrate and transfer important concepts.

Definition 2

(NLP)

A nonlinear programming problem (NLP) is given by

$$ \min_{y\in \mathbb {R}^{n_y}} E(y) \quad\mbox{s.t.}\quad C(y)=0, \qquad D(y)\geq0 $$
(2)

with twice continuously differentiable functions \(E: \mathbb {R}^{n_{y}} \rightarrow \mathbb {R}\), \(C: \mathbb {R}^{n_{y}} \rightarrow \mathbb {R}^{n_{C}}\), and \(D: \mathbb {R}^{n_{y}} \rightarrow \mathbb {R}^{n_{D}}\).

Note that we distinguish between control problems and nonlinear programs by using lower and upper case letters respectively, and make use of the unusual E for the objective function to avoid confusion with the right hand side function f(⋅).

Definition 3

(LICQ)

A nonlinear programming problem is said to satisfy the linear independence constraint qualification (LICQ) in a feasible point \(\bar{y}\in \mathbb {R}^{n_{y}}\) if for all \(d\neq0 \in \mathbb {R}^{n_{y}}\) it holds that

$$ \begin{aligned} \nabla C_i(\bar{y})^Td& \neq0,\quad 1 \leq i \leq n_{C}, \\\nabla D_i(\bar{y})^Td&\neq0, \quad i \in\bigl\{ 1 \leq j \leq n_{D}: D_j(\bar{y})=0\bigr\}. \end{aligned} $$
(3)

In Sect. 4 we will see that certain constraint formulations do not enjoy the LICQ property. Thus, we discuss mathematical programs with complementarity structure.

Definition 4

(MPCC, MPVC)

A nonlinear programming problem

$$ \begin{aligned} &\min_{y\in \mathbb {R}^{n_y}} E(y) \\&\mbox{s.t.}\quad G(y) \geq0,\qquad H(y)\geq0,\qquad G_i(y)\cdot H_i(y)=0,\quad 1 \leq i \leq n_{GH}, \end{aligned} $$
(4)

with twice continuously differentiable functions E, G, and H is called a Mathematical Program with Complementarity Constraints, e.g., [7]. An NLP

$$ \min_{y\in \mathbb {R}^{n_y}} E(y) \quad\mbox{s.t.}\quad H(y) \geq0,\qquad G_i(y)\cdot H_i(y)\leq0, \quad 1 \leq i \leq n_{GH}, $$
(5)

with twice continuously differentiable functions F, G, and H is called a Mathematical Program with Vanishing Constraints, see e.g., [2].

MPCCs and MPVCs are known to possess critical points that violate LICQ. Their computational solution with standard NLP software is prone to numerical difficulties and will often terminate in suboptimal points that possess trivial descent directions and are not local minimizers of (4) or (5).

Remark 1

(MINLP view of MPVCs)

One way to see the difficulty is a look at the mixed-integer nonlinear program given by

$$ \min_{y\in \mathbb {R}^{n_y}, z \in\{0,1\}} E(y) \quad\mbox{s.t.}\quad G(y) \leq zb $$
(6)

with G such that \(\{y\in \mathbb {R}^{n_{y}} | G(y)\leq0\}=\{0\}\). It is closely related to problem (5) as H i (y) toggles the constraint on H i (y)⋅G i (y) in (5) like z does for the constraint on G(y)−b in (6):

$$\begin{aligned} z=1, G(y)-b \leq0 \quad \Longleftrightarrow&\quad H_i(y)>0, H_i(y)\cdot G_i(y)\leq0, \\z=0, G(y)=0 \quad \Longleftrightarrow&\quad H_i(y)=0, H_i(y)\cdot G_i(y)=0. \end{aligned}$$

In this article, we investigate different approaches to reformulate problem (1). Here, reformulations are optimal control problems that have the same feasible set and hence the same optimal solution if integrality is required, but have a possibly different and larger feasible set if the discrete decisions are relaxed. In Sect. 3 we discuss formulations of the dynamic equations with further references to the literature. With respect to formulations of the inequalities in the logical disjunctions in (1), not only tightness of the relaxation is crucial. Also, constraint qualifications may or may not hold and homotopies might be needed to obtain convergence to local solutions. We refer to this as “well-behavedness” of a relaxation for our benchmark problem.

There are several reformulations of logical relationships in the literature. Generalized Disjunctive Programming results directly from a logical modeling paradigm. It generalizes the disjunctive programming approach of [4]. Logical variables are usually either incorporated by means of big-M constraints or via a convex hull formulation, see [31, 50, 51, 67]. From a different point of view, disjunctive programming formulations can be interpreted as the result of reformulation-linearization technique (RLT) steps [64]. For both, the convex hull relaxation uses perspective functions. Based on this, the use of perspective cuts to strengthen convex MINLP relaxations has been proposed in various articles, for example [15, 22, 33]. We refer the reader to [8] for a recent survey on MINLP techniques.

Complementarity ( 4 ) and Vanishing Constraints (5) are another way to look at logical implications. The general concept of nonlinear optimization over nonconvex structures is discussed in [62, 63]. For the comparatively young problem class of MPVCs we refer to [2, 36]. Due to the lack of constraint qualification, various approaches for the computational solution of MPCCs and MPVCs have been devised and include regularizations [36, 54, 66], smoothing [16, 36], and combinations thereof; see [24] for an overview. Nonlinear programming for MPCCs is addressed in [3, 21, 45, 47]. Active set methods tailored to the nonconvex structure are discussed in [17, 39, 43]. Formulations of MPCCs and MPVCs in optimal control can be found in [7, 39, 43, 52, 53].

The remainder of this article is organized as follows. In Sect. 2 we describe a heavy-duty truck cruise control problem based on a dynamic vehicle model that includes gear shift decisions. This is a prototypical MIOCP with constraints based on logical implications. In Sect. 3 we explain the partial outer convexification approach for MIOCPs. We discuss extensions of this approach and different reformulations arising for the heavy-duty truck model, and numerically assess the advantage of partial outer convexification over an inner convexification. In Sect. 4 we investigate reformulations for logical implication constraints. We discuss merits and drawbacks as well as the consequences arising for underlying NLP solvers. Numerical results for the heavy-duty truck control problem are presented in Sect. 5.

2 A Cruise Control Problem for a Heavy-Duty Truck

In this section we describe a cruise control problem for a heavy-duty truck, and model it as a mixed-integer tracking control problem on a prediction horizon.

Typical heavy-duty trucks feature from n μ =8 to n μ =24 gears with different transmission ratios and efficiencies. The decision on energy-optimal gear shift strategies under real-time constraints usually requires extensive training on the driver’s side, is a subject of intense scientific research, and bears considerable potential for savings especially in view of future hybrid engines, e.g., [35, 39, 68].

Controls and Dynamic System

We describe a basic ODE truck model as introduced in [68] that is used for all computations. The ODE system of the truck model comprises three input controls: the indicated engine torque M ind, the engine brakes torque M EB, and the integer gear choice μ.

The vehicle model involves two differential states, velocity v and accumulated fuel consumption Q. Traveled distance s is chosen as the independent variable and we consider the interval [0,s f]. The first state v(s) denotes velocity (in m/s) and is determined from the sum of directed torques,

$$ m v(s) \dot{v}(s) = \bigl(M_\mathrm{acc}(s)- M_\mathrm{brk}(s) \bigr)i_\mathrm{A}/r_\mathrm{stat}-M_\mathrm {air}(s)-M_\mathrm{road}(s), $$
(7)

depending on the effective accelerating and braking torques M acc, M brk as well as on turbulent and static friction torques M air, M road (all in Nm). Further, i A is the fixed axle transmission ratio and r stat (in m) is the static tire radius. The second state, fuel consumption Q(s) (in l/s), is computed from integration over a consumption map

$$ v(s) \dot{Q}(s) = Q_\mathrm{fuel}\bigl(n_\mathrm{eng} \bigl(s, \mu(s)\bigr), M_\mathrm{ind}(s)\bigr), $$
(8)

depending on engine speed n eng and torque M ind. Several terms are computed from algebraic formulas. The transmitted engine speed n eng (in 1/min) depends on the selected gear μ and is obtained from velocity,

$$ n_\mathrm{eng}\bigl(s, \mu(s)\bigr) := v(s) i_\mathrm{A} i_\mathrm{T}\bigl(\mu(s)\bigr) 60/(2\pi r_\mathrm{stat}). $$

The accelerating torque M acc is computed from the ratio i T(μ) and efficiency η T(μ) associated with the selected gear μ. Braking torques M brk are due to controlled engine brake torque M EB and internal engine friction torque M fric,

$$\begin{aligned} M_\mathrm{acc}(s) :=& i_\mathrm{T}\bigl(\mu(s)\bigr) \eta_\mathrm{T}\bigl(\mu(s)\bigr) M_\mathrm{ind}(s), \\M_\mathrm{brk}(s) :=& M_\mathrm{EB}(s) + i_\mathrm{T} \bigl(\mu(s)\bigr) M_\mathrm {fric}\bigl(n_\mathrm{eng}\bigl(s, \mu(s)\bigr)\bigr). \end{aligned}$$

Additional braking torques due to turbulent friction M air, and due to static road conditions M road, are taken into account,

$$ M_\mathrm{air}(s) := \frac{1}{2} c_\mathrm{w} A \rho_\mathrm {air} v^2(s),\qquad M_\mathrm{road}(s) := m g \bigl(\sin\gamma(s)+f_\mathrm{r}\cos\gamma(s)\bigr). $$

Here c w is the shape coefficient, A denotes the flow surface (in m2), and ρ air the air density (in kg/m3). Further, m is the vehicle’s mass (in kg), gravity is denoted by g (in m/s2), γ(s) denotes the road’s slope, and f r is a rolling friction coefficient.

Objective

The cost criterion to be minimized on the prediction horizon [0,s f] is composed of a weighted sum of three different objectives. To simplify notation we transform the Lagrange terms into a Mayer term by introducing artificial differential states. First, the deviation of the truck’s velocity from the desired one is penalized,

$$ v(s) \dot{\varPhi }_\mathrm{dev}(s) := \bigl(v(s)-v_\mathrm {des}(s) \bigr)^2 $$
(9)

Second, the fuel consumption is found from a fuel consumption rate map Q, see [39], and depends on the integer gear choice μ(s),

$$ v(s) \dot{\varPhi }_\mathrm{fuel} := Q \bigl(n_\mathrm{eng}\bigl(s, \mu(s)\bigr), M_\mathrm{ind}(s) \bigr). $$
(10)

Third, rapid changes of the engine and brake torques degrade driving comfort,

$$ v(s) \dot{\varPhi }_\mathrm{comf} := \dot{M}_\mathrm{ind}^2(s) + \dot {M}_\mathrm{brk}^2(s), $$
(11)

where we approximate the torque derivatives by one-sided finite differences.

Constraints

On the prediction horizon mechanical constraints and velocity limits need to be respected. Beside the bounds on the truck input controls and on the system’s states for s∈[0,s f],

$$ 0 \leq M_\mathrm{ind}(s),\qquad 0 \leq M_\mathrm{brk}(s) \leq M_{\mathrm{brk},\mathrm{max}}, $$
(12)

the truck’s velocity v(s) is subject to velocity limits imposed by law,

$$ v(s) \leq v_\mathrm{law}(s),\quad s \in[0,s_{\mathrm {f}}]. $$
(13)

The indicated torque must respect state-dependent upper limits as specified by the engine characteristics for s∈[0,s f]:

$$ M_\mathrm{ind}(s) \leq M_{\mathrm{ind},\mathrm{max}} \bigl(n_\mathrm{eng}\bigl(s, \mu (s)\bigr) \bigr). $$
(14)

In addition, the transmitted engine speed n eng(s,μ(s)) must stay within prescribed limits according to the engine’s specification,

$$ n_{\mathrm{eng},\mathrm{min}} \leq n_\mathrm{eng}\bigl(s, \mu(s) \bigr) \leq n_{\mathrm{eng},\mathrm{max}},\quad s \in[0,s_{\mathrm {f}}]. $$
(15)

Problem Formulation

The MIOC problem formulation for the heavy-duty truck control problem on the prediction horizon s∈[0,s f] reads

(16)

with state vector x(s)=(v,Q,Φ dev,Φ fuel,Φ comf)(s), continuous control vector u(s)=(M ind,M brk)(s), integer controls μ(s), and initial state information x 0. Note that problem (16) is a MIOCP of form (1), with the gear choice μ(s) that causes switches in the right hand side as well as in the constraints and the associated vectors v i=(i T(i),η T(i)) that contain gear-specific values for transmission ratio and efficiency.

Logical Implications

The modeling and optimization with logical variables has gained increasing interest, [31, 50]. The main reason is that it provides a modeling paradigm that is both generic and intuitive, and allows for tailored relaxations and algorithms.

Logical literals Y∈{false,true} can of course be identified with binary variables z i ∈{0,1}, or can be used implicitly, as we did in formulation (16),

$$ Y_i(t) = \mathrm{true} \quad\Leftrightarrow\quad\mu(t) = i. $$

It is well known that logical relations and Boolean expressions can be represented as linear (in)equalities. For example, the implication is represented by

$$Y_1 \Rightarrow Y_2 \quad\Longleftrightarrow\quad\lnot Y_1 \vee Y_2 \quad\Longleftrightarrow\quad1 - z_1 + z_2 \ge1. $$

For time-dependent logical literals Y(⋅), systems of differential equations, and implied constraints the representation is, however, neither straightforward nor unique.

In Sect. 3 we discuss two different formulations for the ODE system and review recent results. Constraints (14) and (15) are of particular interest in the context of this article. They represent the logical implication

When gear i is active, gear-specific constraints must hold.

In Sect. 4, we address different mathematical reformulations of this implication and investigate the tightness of the induced relaxations.

3 Inner and Outer Convexification in MIOC

In this section we investigate two different approaches to reformulate problem (1) when n c =0, i.e., when no mode-specific constraints are present and only the right hand side function of the dynamic system depends on the logical mode choice at time t. We denote the two approaches by inner convexification and (partial) outer convexification, depending on how the variables that represent the logical choice enter the right hand side.

The goal in both cases is identical: a formulation that allows the relaxation of discrete decisions. The relaxed MIOCPs are purely continuous control problems that can be solved using, for example, Bock’s direct multiple shooting method or direct collocation.

Using the truck control problem from Sect. 2, we compare both approaches numerically and explain qualitatively why the outer convexification formulation performs so much better than the inner convexification. We close this section by referring to related work and extensions.

Inner Convexification

For some control problems of type (1) it is possible to reformulate the time-dependent disjunctions by means of a function \(g: [1, {n_{\omega }}] \rightarrow \mathbb {R}^{n_{v}}\) that can be inserted into the right hand side function f(⋅) and has the property g(i)=v i for i∈{1,…,n ω }. Possibilities are a piecewise linear representation of the form

$$ g(i + \xi_{i+1}) = \xi_i v^i + \xi_{i+1} v^{i+1} $$
(17)

with special ordered set type 2 (SOS-2) variables

$$\xi_i \in[0,1],\qquad \sum_i \xi_i = 1,\qquad \xi_i \neq0 \quad\Rightarrow\quad \xi_j = 0 \quad\forall j \neq i, i+1, $$

a convex combination

$$ g \Biggl(\sum _{i=1}^{n_{\omega }}\xi_i i \Biggr) = \sum _{i=1}^{n_{\omega }}\xi_i v^i $$
(18)

with special ordered set type 1 (SOS-1) variables ξ i ∈[0,1], ∑ i ξ i =1, or fitted smooth convex functions g(⋅) as suggested in [25]. Either way, this approach allows a reformulation of (1) into

Definition 5

(MIOCP after IC Reformulation)

$$\begin{aligned} & \min _{x(\cdot), u(\cdot), \psi(\cdot)} e\bigl(x(t_{\mathrm {f}})\bigr) \\& \mbox{s.t.}\quad \dot{x}(t) = f\bigl(x(t), u(t), g(\psi)\bigr) \quad \forall t \in[0,t_{\mathrm {f}}], \\& \phantom{\mbox{s.t.}\quad} 0 \le d\bigl(x(t),u(t)\bigr) \quad \forall t \in[0, t_{\mathrm {f}}], \\& \phantom{\mbox{s.t.}\quad} x(0) = x_0, \\& \phantom{\mbox{s.t.}\quad} \psi(t) \in\{1, \ldots, {n_{\omega }}\} \quad \forall t \in[0,t_{\mathrm {f}}]. \end{aligned}$$
(19)

By construction, problem (19) can be relaxed toward ψ(t)∈[1,n ω ].

Outer Convexification

The outer convexification approach (or partial outer convexification, because the convexification applies to the integer controls only, and not to the rest of the control problem) has been investigated in the context of optimal control in [56, 60, 61]. It consists of an evaluation of all possible right hand sides, their multiplication with convex multipliers, and the summation of the products. We introduce control functions \(\omega: [0,t_{\mathrm {f}}] \rightarrow\{0,1\}^{{n_{\omega }}}\) as convex multipliers and obtain:

Definition 6

(MIOCP after OC Reformulation)

$$\begin{aligned} & \min _{{x(\cdot), u(\cdot), \omega(\cdot)}} e\bigl(x(t_{\mathrm {f}})\bigr) \\& \mbox{s.t.}\quad \dot{x}(t) = \sum_{i=1}^{{n_{\omega }}} \omega_i(t) f\bigl(x(t), u(t), v^i\bigr) \quad \forall t \in[0,t_{\mathrm {f}}], \\&\phantom{\mbox{s.t.}\quad} 0 \le d\bigl(x(t),u(t)\bigr) \quad \forall t \in[0, t_{\mathrm {f}}], \\& \phantom{\mbox{s.t.}\quad} x(0) = x_0 \\& \phantom{\mbox{s.t.}\quad} 1 = \sum_{i=1}^{{n_{\omega }}} \omega_i(t),\quad \omega(t) \in\{0,1\} ^{{n_{\omega }}}\ \forall t \in[0,t_{\mathrm {f}}]. \end{aligned}$$
(20)

Problem (20) can be relaxed toward \(\omega(t) \in [0,1]^{{n_{\omega }}}\). We use the notation \(\alpha(t) \in[0,1]^{{n_{\omega }}}\) to highlight the difference between the original problem and its continuous relaxation. In the following we need the notation of

Definition 7

(Fractionality of solutions)

The fractionality of binary control functions ω(⋅) on a time horizon [0,t f] is given by

$$\frac{1}{{n_{\omega }}}\sum_{i=1}^{{n_{\omega }}} \int _{0}^{t_{\mathrm {f}}} \bigl(0.5 - \bigl \Vert \omega_i(\tau) - 0.5\bigr \Vert \bigr) \mathrm{d} \tau. $$

Discussion of Inner Versus Outer Convexification

Relaxations of reformulation (19) may be faster to solve, as we only have one control function ψ:[0,t f]→[1,n ω ] that enters the control problem instead of n ω functions ω i :[0,t f]→[0,1] in (20). Hence, there are less derivatives to be computed and the subproblems arising in iterations of an interior point or SQP approach are cheaper to solve. Moreover in (20), the aggregated right hand side function ∑ i f(⋅,v i) may become more expensive to evaluate. As n ω reflects the number of possible combinations and switches, this number may get large. Note that the linear equality constraint may be used for elimination of one function at the cost of losing some sparsity.

However, depending on the separability properties of f(⋅), integer controls often decouple, leading to a reduced number n ω of admissible choices, e.g., [30].

Example 1

(Outer Convexification and Separability)

Assume we have

$$ \dot{x}(t) = f_1\bigl(\cdot, v_1(t)\bigr) + f_2\bigl(\cdot, v_2(t)\bigr),\quad v_1(t) \in \varOmega _1, v_2(t) \in \varOmega _2. $$

Then an equivalent reformulation leading to \({n_{\omega }}= n_{\omega_{1}} + n_{\omega_{2}}\) controls instead of \({n_{\omega }}= n_{\omega_{1}} n_{\omega_{2}}\) is given for t∈[t 0,t f ] by

$$\begin{aligned} \dot{x}(t) =& \sum_{i=1}^{n_{\omega_1}} f_1\bigl(\cdot, v_1^i\bigr) \omega _{1,i}(t) + \sum_{i=1}^{n_{\omega_2}} f_2\bigl(\cdot, v_2^i\bigr) \omega _{2,i}(t), \\\sum_{i=1}^{n_{\omega_1}} \omega_{1,i}(t) =& 1,\quad \omega_1 \in\{0,1\} ^{n_{\omega_1}},\qquad \sum _{i=1}^{n_{\omega_2}} \omega_{2,i}(t) = 1,\quad \omega_2 \in\{0,1\} ^{n_{\omega_2}}. \end{aligned}$$

In most practical applications the binary control functions enter linearly (such as valve controls that indicate whether a certain flow term is present or not), or n ω increases linearly with the number of choices (e.g., the gears), or integer controls decouple. Hence, one can expect a modest (linear) increase in the number of control functions. This increase is usually more than outweighed by important advantages of (20) over (19):

  • Not in all cases can a meaningful inner convexification g(⋅) be found. An example are black-box simulators that can only be evaluated for certain modes (integer values), but not in between. In general, using g(⋅) for a relaxation may lead to problems such as divisions by zero, or index changes in the DAE case [6]. Evaluating the model only for vectors v i avoids these problems;

  • The integer gap between the optimal solutions of (19) and its relaxation may become arbitrarily large [56], whereas the integer gap between the optimal solutions of (20) and its relaxation is bounded by a multiple of the control discretization grid size Δt [61].

Finding a tight relaxation of (20) is vitally important for the computational solution of (1). It allows a decoupling of the MIOCP into a continuous OCP and a mixed-integer linear programming problem with a huge potential for computational savings and a posteriori bounds on the gap to the best possible MIOCP solution [37, 61]. Moreover, the relaxed control problems often have optimal integer solutions, which implies almost arbitrary computational savings when compared to an OCP-based branch&bound approach to solve (19) to optimality. This has first been compared in [40] for a benchmark problem posed in [25]. While identical solutions were obtained, a speedup of several orders of magnitude was observed for the outer convexification approach. Similar behavior can be observed when comparing to MINLP-based branch&bound. We use the truck control example from Sect. 2 to reproduce and explain this qualitative result.

Inner and Outer Convexification for Truck Control

Optimal solutions by their very nature tend to exploit constraints as much as possible. In the special case of vehicle operation and for a fixed acceleration, it is natural that the gear is chosen that provides the largest torque when compared to all other gears.

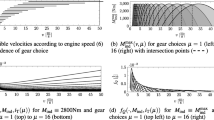
In Fig. 1 we show the maximum indicated engine torque M ind,max depending on the velocity v for two adjacent gear choices μ(⋅)=i and μ(⋅)=i+1. Figure 1 (left) shows

$$ M_{\mathrm{ind},\mathrm{max}}^\mathrm{IC}(v) = M_{\mathrm{ind},\mathrm{max}} \bigl(n_\mathrm{eng} \bigl(v(s), \xi i + (1-\xi) (i+1)\bigr)\bigr) $$
(21)

for ξ=0.0,0.1,…,1.0, while Fig. 1 (right) shows

$$ M_{\mathrm{ind},\mathrm{max}}^\mathrm{OC}(v) = \alpha M_{\mathrm{ind},\mathrm{max}} \bigl(n_\mathrm{eng}\bigl(v(s),i\bigr)\bigr) + (1-\alpha) M_{\mathrm{ind},\mathrm{max}} \bigl(n_\mathrm{eng}\bigl(v(s),i+1\bigr)\bigr) $$
(22)

for α=0.0,0.1,…,1.0. Apparently, in the particular case of truck control, the relaxation of (19) comprises combinations of the state variable v(⋅) and non-integral ξ∈(0,1) that yield an unphysical, larger value of \(M_{\mathrm{ind},\mathrm{max}}^{\mathrm{IC}}\). Conversely, the relaxation of (20) is by construction maximal only for α∈{0,1}. Thus, one can expect that optimal solutions of the relaxed version of (20) are integral, whereas solutions of the relaxation of (19) may have non-integral solutions ξ∈(0,1). The two approaches would only coincide if both n eng and M ind,max were linear functions of v i. The special case of truck control is prototypical for many (in particular time-optimal) MIOCPs, as often bang-bang solutions are optimal. However, this is not guaranteed in the general case.

Fig. 1
figure 1

Maximum indicated engine torque M ind,max depending on the velocity v for two adjacent gear choices μ(⋅)=i and μ(⋅)=i+1. Left: inner convexification (19). Right: outer convexification (20). Observe the maximal indicated engine torques for non-integral values of ξ (gray) on the left hand side, while non-integral values for α (gray) on the right hand side are never better than integral values (black)

Full size image

To evaluate this effect, we apply both inner and outer convexification to the truck control problem (16), however for the time being without the constraints (14)–(15). For convenience, we use formulation (18) in the following. The effect is strongest for time- and energy-optimal driving, hence we consider the case where λ fuel=1, λ dev=λ comf=0 in the uphill setting of Fig. 2.

Table 1 shows numerical results for the cruise control of the heavy-duty truck. Both the inner and the outer convexification formulations have been relaxed and solved to local optimality with the active-set solver SNOpt [28] and the interior point solver Ipopt [69]. The most important findings can be summarized as follows:

  • For inner convexification, the fractionality of the optimal relaxed gear choices α j (⋅) does not improve for finer discretizations. For the outer convexification however, it goes to zero as the control discretization grid is equidistantly refined. The reason is that the optimal control α(⋅) of (20) is of bang-bang type;

  • There is a gap between the lower bound from the relaxed IC solutions and the best possible integer solution, which is almost attained by the OC formulation;

  • The interior point code Ipopt seems to perform better on inner convexification, the SQP code SNOpt performs better on outer convexification;

  • Both codes run into problems with inner convexification instances.

Table 1 Fractionality as in Definition 7, objective function value, and CPU time obtained with SNOpt/Ipopt for the solution of relaxations of (19) and (20) with different control grids
Full size table

Although on single instances it may be faster to compute the relaxation of the inner convexification formulation, it is clear that outer convexification is the method of choice within a branch and bound framework. This is due to the tighter relaxation (better bound) in combination with the feature that relaxed solutions are usually already almost integer feasible if the control discretization grid is chosen adequately.

Extending the Outer Convexification Approach

The advantages of outer convexification over inner convexification have stimulated additional research into the formulation (20). Here, we briefly review significant developments for the reader’s convenience. First, to fully exploit the beneficial integrality property that has been exemplified above and that is related to bang–bang solutions in optimal control, direct methods need to be equipped with adaptivity in the control grid discretization and follow-up transformations into a switching time optimization, [56, 60]. Second, so-called sensitivity-seeking or path-constrained arcs (i.e., time periods during which α(⋅) is not binary) can be treated with tailored sum up rounding strategies. This rounding strategy is a constructive part in the proof for the dependence of the integer gap on the control discretization grid size Δt. Furthermore, it is the optimal solution to a MILP that minimizes the deviation of a binary control ω(⋅) from a relaxed one α(⋅) with respect to

$$\max_{t \in[0,t_{\mathrm {f}}]}\biggl \| \int_0^t \omega(\tau) - \alpha(\tau ) \mathrm{d} \tau \biggr\|. $$

If additional constraints like a maximum number of switches need to be fulfilled, tailored branching algorithms can be applied to efficiently solve the constrained MILP [37]. Third, the numerical algebra to cope with the specific structures induced by the control functions α(⋅) can be exploited in the context of SQP approaches [41, 42]. Finally, an extension to more general MIOCPs is possible, e.g., to multi-objective problems [48], to differential-algebraic systems [27], and to certain partial differential equations [34]. For an overview see [57, 58].

4 Constraint Formulations

In this section, we study reformulations for logically implied constraints c(⋅), i.e., n c >0 in (1). Again, we consider reformulations that are equivalent for integer control functions and discuss properties of their relaxations. We do this both in general and for the special case of the constraints (14)–(15) of the heavy-duty truck model from Sect. 2 that result in

$$ c^\mathrm{truck}(v, M_\mathrm{ind}, \mu) = \begin{pmatrix} M_{\mathrm{ind},\mathrm{max}} (n_\mathrm{eng}(v,\mu) ) - M_\mathrm {ind} \\n_{\mathrm{eng},\mathrm{max}} - n_\mathrm{eng} (v,\mu ) \\n_\mathrm{eng} (v,\mu ) - n_{{\mathrm{eng},\mathrm{min}}} \end{pmatrix} . $$
(23)

In the interest of notational simplicity we omit the lower linear engine speed bound n eng(v,μ)−n eng,min in the rest of this section. We note that the function c truck(⋅) has components that are quadratic and linear in i T(μ),

$$ c^\mathrm{truck}(v, M_\mathrm{ind}, \mu) = \begin{pmatrix} 3000 - (3 i_\mathrm{A} i_\mathrm{T}(\mu) v/(\pi r_\mathrm {stat}) - 125 )^2 - M_\mathrm{ind} \\\pi r_\mathrm{stat} n_{\mathrm{eng},\mathrm{max}}/(30 i_\mathrm{A} i_\mathrm {T}(\mu )) - v \end{pmatrix} . $$
(24)

4.1 Inner Convexification of the Constraints

The inner convexification formulation (19) can be augmented in a straightforward way with constraints

$$0 \le c\bigl(x(t), u(t), g(\psi)\bigr) $$

that guarantee that integer feasible solutions ψ∈{1,…,n ω } of (19) are feasible solutions of (1). Using (18) for g(⋅) we obtain the following reformulation of the constraints (14), (15),

$$\begin{aligned} 0 \le& 3000 - \Biggl(3 i_\mathrm{A} \Biggl(\sum _{i=1}^{n_{\omega }}\alpha_i i_\mathrm{T}(i) \Biggr) v/(\pi r_\mathrm{stat}) - 125 \Biggr)^2 - M_\mathrm {ind}, \end{aligned}$$
(25a)
$$\begin{aligned} 0 \le& \pi r_\mathrm{stat} n_{\mathrm{eng},\mathrm{max}}\Big/ \Biggl(30 i_\mathrm{A} \Biggl(\sum_{i=1}^{n_{\omega }}\alpha_i i_\mathrm{T}(i) \Biggr) \Biggr) - v. \end{aligned}$$
(25b)

Just as in Sect. 3, the evaluation of convex combinations within a nonlinear function may give rise to optimality of feasible fractional values, while neighboring integer values may not be optimal. Hence, the inner convexification approach can be expected to potentially yield weak relaxations.

4.2 Outer Convexification/One Row Formulation of the Constraints

The outer convexification reformulation (20) can be applied to the constraint expression as well. Residuals are evaluated for all possible choices, and the constraint is imposed on the convex combination of residuals resulting in

$$ 0 \le \sum_{i=1}^{{n_{\omega }}} \alpha_i(t) c\bigl(x(t), u(t), v^i\bigr). $$
(26)

This reformulation avoids the problem of evaluation in fractional choices, and ensures that all feasible integer points are feasible points of the original MIOCP.

Remark 2

(LICQ for Outer Convexification)

Let \((\bar{x},\bar{u},\bar{\alpha})\) be a feasible solution of the relaxation of problem (20), (26) and let the matrix

of active constraints have full row rank. Drop the upper bounds α i (⋅)≤1, which are implicitly implied by α i (⋅)≥0 and ∑ i α i (⋅)=1. Then LICQ is satisfied for the relaxation of problem (20), (26).

Proof

We look at the constraint matrix of all (active) constraints in \((\cdot , \bar{\alpha})\), given by

Due to feasibility of \(\bar{\alpha}\) and the SOS-1 constraint there exists at least one index 1≤i≤n ω for which α i (t)≥0 is not active. Hence, the bottom n ω rows are linearly independent. The first block of rows may contribute an entry in column i, but by assumption is linearly independent from the other rows due to the right-most block of columns, which concludes the proof. □

The same holds true if we eliminate one of the multipliers α i using the SOS-1 constraint, which becomes an inequality constraint. For the heavy-duty truck model, the torque constraint (14) and the engine speed constraint (15) are reformulated to read

$$\begin{aligned} 0 \leq&\sum_{i=1}^{n_{\mu}} \alpha_i(t) M_{\mathrm{ind},\mathrm{max}} \bigl(n_\mathrm{eng}\bigl(v(s),i \bigr) \bigr) - M_\mathrm{ind}(s), \end{aligned}$$
(27a)
$$\begin{aligned} 0 \leq& n_{\mathrm{eng},\mathrm{max}} - \sum _{i=1}^{n_{\mu}}\alpha_i(t) n_\mathrm {eng} \bigl(v(s),i \bigr). \end{aligned}$$
(27b)

Note that (25b) and (27b) are identical, as i T(μ) enters linearly.

As the constraints are summed up, compensatory effects may lead to feasible residuals for fractional values of the convex multipliers in both cases, as observed in [39]. For example, a first gear choice leading to an engine speed violating the upper bound n eng,max and a second gear choice in violation of the lower bound n eng,min may form a feasible convex combination in (27b).

4.3 Complementarity Formulation

To address the problem of compensatory effects, [39] proposes to enforce feasibility individually for each possible choice of the integer control via

$$ 0 \leq\alpha_i(t) c\bigl(x(t), u(t), v^i\bigr),\quad 1 \leq i \leq n_{{n_{\omega }}}. $$
(28)

For the heavy-duty truck model, torque and engine speed constraints are

$$\begin{aligned} 0 \leq&\alpha_i(t) \bigl(M_{\mathrm{ind},\mathrm{max}} \bigl(n_\mathrm {eng}\bigl(v(s),i\bigr) \bigr) - M_\mathrm{ind}(s) \bigr), \end{aligned}$$
(29a)
$$\begin{aligned} 0 \leq&\alpha_i(t) \bigl(n_{\mathrm{eng},\mathrm{max}} - n_\mathrm{eng} \bigl(v(s),i \bigr) \bigr) \end{aligned}$$
(29b)

for 1≤i≤n μ . It is obvious that optimal solutions with nonzero convex multiplier α i (t)>0 are now feasible for α i (t)=1 as well. Compared to the outer convexification formulation, the number of constraints has increased from 4 to 4n μ , though. More important, due to the structure of the constraints (29a)–(29b), the NLP obtained from discretization of the relaxed convexified MIOCP now is a MPVC in the form of (5). In the case of equality constraints, we obtain a MPCC, see (4).

4.4 Addressing the Complementarity Formulation

As mentioned in the introduction, MPCCs and MPVCs lose constraint qualification. This can also be seen directly.

Remark 3

(No LICQ for Complementarity)

Let \((\bar{x},\bar{u},\bar{\alpha})\) be a feasible solution of the relaxation of problem (20), (28) with

$$\bar{\alpha_i}(t) = 0,\qquad c\bigl(\bar{x}, \bar{u}, v^i\bigr) = 0 $$

for at least one 1≤i≤n ω . Then LICQ is not satisfied.

Proof

We look at the constraint matrix of all constraints in \((\cdot, \bar {\alpha})\), given by

and note that the rows that correspond to \(\bar{\alpha}_{i}(t) c(\cdot , v^{i}) \ge0\) contain only zeros, leading to a trivially linear dependent constraint system. □

The constraint system also violates the weaker Mangasarian-Fromovitz constraint qualification. However, some cone-based constraint qualifications are satisfied, e.g., [2]. Thus, local minimizers are still KKT points.

Complementarity Pivoting Techniques

Computational approaches for solving MPCCs and MPVCs directly are mentioned in the introduction, but generally rely on dedicated implementations of complementarity solvers. If one intends to use existing numerical software, then the complementarity reformulation (28) needs to be addressed by regularization or smoothing techniques that recover LICQ.

Regularization and Smoothing Techniques

These techniques follow the principle of reformulation of the MPCC or MPVC in violation of LICQ using a parameter ε>0 in a way that recovers constraint qualification for \(\varepsilon\in(0,\overline{\varepsilon})\). Then, convergence of the sequence of local minimizers to a limit point is established for ε→0. The assessment of the type of stationarity obtained for the limit point is crucial. For MIOCP, we find it essential to ask for Bouligand stationarity. Lesser stationarity concepts allow for termination in spurious stationary points that possess trivial descent directions, thus giving rise to “missed” switches of the integer control.

In the following, an overview over different possible reformulations is given, and their general form is presented and applied to the particular truck problem.

Regularization Reformulations

Conversely, regularization formulations relax the feasible set using ε>0 by requiring

$$ - \varepsilon\leq\alpha_i(t)\cdot c\bigl(x(t), u(t), v^i \bigr),\quad 1 \leq i \leq n_{{n_{\omega }}} \quad\mbox{(MPVC)}, $$

or, in what is sometimes referred to as the lumped formulation,

$$ -\varepsilon\leq\sum_{i=1}^{n_{{n_{\omega }}}} \alpha_i(t)\cdot c\bigl(x(t), u(t), v^i\bigr). $$
(30)

For MIOC and in particular for the truck model, the lumped formulation will satisfy LICQ but amounts to applying outer convexification to the original constraint, see Sect. 4.2. For the truck model, the first formulation reads

$$\begin{aligned} -\varepsilon \leq&\alpha_i(t)\cdot \bigl(M_{\mathrm{ind},\mathrm{max}} \bigl(n_\mathrm{eng}\bigl(v(s),i\bigr) \bigr)- M_\mathrm{ind}(s) \bigr) \end{aligned}$$
(31a)
$$\begin{aligned} -\varepsilon \leq&\alpha_i(t)\cdot \bigl(n_{\mathrm{eng},\mathrm{max}}-n_\mathrm {eng} \bigl(v(s),i \bigr) \bigr) \end{aligned}$$
(31b)

NCP Function Reformulations

A function \(\phi:\mathbb {R}^{2}\rightarrow \mathbb {R}\) is called NCP-function if

$$\begin{aligned} \phi(a,b)=0 \quad \Rightarrow&\quad a \geq0, b \geq0, ab=0,\quad \mbox{(MPCC)}, \\\phi(a,b)=0 \quad \Rightarrow&\quad b \geq0, ab\leq0, \quad\mbox{(MPVC)}, \end{aligned}$$

see, e.g., [18] for a survey. For MPCCs the Fischer-Burmeister function

$$\phi^\mathrm{FB}(a,b):=a+b-\sqrt{a^2+b^2} $$

may be used, [19]. For MPVC, [36] uses the NCP function

$$ \phi^\mathrm{VC}(a,b)=\frac{1}{2} \bigl(ab + \sqrt{a^2b^2} +\sqrt{b^2}-b \bigr). $$
(32)

Piecewise smooth complementarity functions to replace the complementarity constraint in a MPCC are developed in [46], and a one-to-one correspondence between strongly stationary points and KKT points of the reformulated MPCC is established. The non-smoothness is shown to not impede the convergence of SQP methods. The approach however cannot avoid convergence of SQP solvers to spurious stationary points in the degenerate case. The NCP formulation for the truck model is

$$\begin{aligned} 0 \geq&\phi^\mathrm{VC} \bigl(M_\mathrm{ind}(s)-M_{\mathrm{ind},\mathrm{max}} \bigl(n_\mathrm{eng}\bigl(v(s),i\bigr) \bigr), \alpha_i(t) \bigr), \end{aligned}$$
(33a)
$$\begin{aligned} 0 \geq&\phi^\mathrm{VC} \bigl(n_\mathrm{eng} \bigl(v(s),i \bigr)-n_{\mathrm{eng},\mathrm{max}}, \alpha_i(t) \bigr). \end{aligned}$$
(33b)

Smoothing Reformulations

Smoothing reformulations have first been developed for MPCCs and work by appropriately including a smoothing parameter ε>0:

$$ 0 \geq\phi_\varepsilon \bigl(- c\bigl(x(t), u(t), v^i\bigr), \alpha_i(t) \bigr),\quad 1 \leq i \leq n_{{n_{\omega }}} \quad \mbox{(MPVC)}, $$
(34)

with NCP function ϕ, e.g., \(\phi_{\varepsilon}^{\mathrm{FB}}(a,b):=a+b-\sqrt{a^{2}+b^{2}+\varepsilon}\) for MPCC and

$$ 0 \geq\phi_\varepsilon^\mathrm{VC}(a,b) := \frac {1}{2} \bigl(ab + \sqrt{a^2b^2 + \varepsilon^2} +\sqrt {b^2+\varepsilon^2}-b \bigr) $$
(35)

for MPVC. For MPCC, smoothing under an LICQ-type assumption and a second order condition has been shown to yield B-stationarity of the limit point. For MPVC, smoothing is shown in [36] to not yield a satisfactory framework for solving MPVCs. For the truck model, the smoothing reformulation reads

$$\begin{aligned} 0 \geq&\phi_\varepsilon^\mathrm{VC} \bigl(M_\mathrm {ind}(s)-M_{\mathrm{ind},\mathrm{max}} \bigl(n_\mathrm{eng} \bigl(v(s),i\bigr) \bigr), \alpha_i(t) \bigr), \end{aligned}$$
(36a)
$$\begin{aligned} 0 \geq&\phi_\varepsilon^\mathrm{VC} \bigl(n_\mathrm{eng} \bigl(v(s),i \bigr)-n_{\mathrm{eng},\mathrm{max}}, \alpha_i(t) \bigr). \end{aligned}$$
(36b)

Smoothing-Regularization Reformulations

Smoothing-regularization approaches combine the concepts of smoothing and regularization to form

$$ \varepsilon\geq\phi_\varepsilon \bigl(- c\bigl(x(t), u(t), v^i \bigr), \alpha _i(t) \bigr),\quad 1 \leq i \leq n_{{n_{\omega }}}\quad \mbox{(MPVC)}. $$
(37)

For MPVC, using (32), the smoothing-relaxation formulation reads \(\varepsilon\geq\phi^{\mathrm{VC}}_{\varepsilon}(a,b)\). Convergence for ε→0 to a B-stationary limit point is established under a weak LICQ-type constraint qualification, assuming existence and asymptotic nondegeneracy of a sequence {x ε } ε→0 of feasible points for the sequence NLP(ε). LICQ is shown to be satisfied for all NLP(ε) with \(\varepsilon\in(0,\overline{\varepsilon})\).

For the truck problem, the smoothing-regularization formulation reads

$$\begin{aligned} \varepsilon \geq&\phi_\varepsilon^\mathrm{VC} \bigl(M_\mathrm {ind}(s)-M_{\mathrm{ind},\mathrm{max}} \bigl(n_\mathrm{eng} \bigl(v(s),i\bigr) \bigr), \alpha _i(t) \bigr), \end{aligned}$$
(38a)
$$\begin{aligned} \varepsilon \geq&\phi_\varepsilon^\mathrm{VC} \bigl(n_\mathrm {eng} \bigl(v(s),i \bigr)-n_{\mathrm{eng},\mathrm{max}}, \alpha_i(t) \bigr). \end{aligned}$$
(38b)

4.5 Generalized Disjunctive Programming

Based on the work of Balas for integer linear programs, Grossmann and coworkers developed Generalized Disjunctive Programming (GDP) for mixed-integer nonlinear programs [31]. The problem formulation (1) uses disjunctive notation, hence it is natural to take the GDP point of view. It is motivated by disjunctions of the form

(39)

with application in process synthesis where Y i represents presence or absence of units and y a vector of continuous variables. If a corresponding unit is not used, the equation B i y=0 eliminates variables and e i =0 sets the costs to zero.

As stated above, logical relations Φ(Y)=true can be translated into constraints with binary variables z∈{0,1}|I|. An interesting question, however, is how the disjunctions are formulated. We consider two approaches.

Big-M

Using large enough constants M is a well-known technique to model logical relations in combinatorial optimization. For (39), this yields

$$ g_i(y) \le M (1 - z_i),\qquad - M z_i \le B_i y \le M z_i,\qquad e_i = z_i \gamma_i. $$

Convex Hull Reformulation

A possibly tighter relaxation can be obtained from the nonlinear convex hull reformulation. It makes use of the perspective of a function.

Definition 8

(Perspective function)

The perspective of a function \(f: \mathbb {R}^{n} \rightarrow \mathbb {R}\) is the function \(\hat{f}: \mathbb {R}^{n+1} \rightarrow \mathbb {R}\) defined by

$$\hat{f}(\lambda, y) = \begin{cases} \lambda f(y / \lambda) & \mbox{if } \lambda> 0, \\0 & \mbox{if } \lambda= 0, y = 0, \\\infty& \mbox{otherwise}. \end{cases} $$

An important property is that if f(⋅) is convex, then \(\hat {f}(\cdot)\) is also convex. Perspectives have been used for strong formulations of MINLPs [15] and have been gaining increasing interest lately also for the derivation of perspective cuts, e.g., [33]. Perspectives can be used to obtain the nonlinear convex hull of a feasible set as follows:

Definition 9

(Nonlinear Convex Hull)

Problem (6) can be equivalently restated as minimization over all (y,λ) of the nonconvex function

$$ \varPhi (y,\lambda):= \begin{cases} 0 & \mbox{if } \lambda=0, y=0, \\F(y) & \mbox{if } \lambda=1, G(y)\leq b, \\\infty& \mbox{else}. \end{cases} $$
(40)

wherein we have assumed w.l.o.g. that Φ(0,λ)=0. The closure \(\overline{\mathit{co}} \varPhi (y,\lambda)\) of the convex hull of Φ is given by

$$ \overline{\mathit{co}} \varPhi (y,\lambda)= \begin{cases} 0 & \mbox{if } \lambda=0, y=0, \\\lambda F(y/\lambda) & \mbox{if } \lambda\in(0,1], G(y)\leq\lambda b, \\\infty& \mbox{else}. \end{cases} $$
(41)

The convex hull representation of the GDP (39) is then obtained by introduction of additional variables 0≤λ ij ≤1, λ i1+λ i0=1 and 0≤v ij ≤λ ij U, y=v i1+v i0 and constraints 0≥λ i1 g i (v i1/λ i1), B i v i0=0, f i =λ i1 γ i .

Numerical Difficulties

For constraint formulations using perspectives usually LICQ holds. The reason is that unlike in Remark 3, the derivative λ∇ v g(v/λ)≠0 for λ=0. E.g., for linear constraints g(v)=av+b we have λ∇ v g(v/λ)=a.

However, for nonlinear g(⋅) there are computational challenges due to division by zero or near-zero values. For ε>0 sufficiently small λf(y/λ) can be approximated by (λ+ε)f(y/(λ+ε)), [31], or by (λ)f(y/(λ+ε)), [50], or as proposed in the Ph.D. thesis of Nicolas Sawaya by ((1−ε)λ+ε)f(y/((1−ε)λ+ε)). The results may depend heavily on the choice of ε and be computationally challenging.

4.6 Generalized Disjunctive Programming for MIOCP

First, we consider the Big-M formulation for GDP. For general constraints c(⋅) and SOS-1 variables α(⋅) we obtain for \(1 \leq i \leq n_{{n_{\omega }}}\)

$$ M \bigl(\alpha_i(t)-1\bigr) \leq c\bigl(x(t), u(t), v^i\bigr) $$
(42)

and thus for the truck constraints (23) for 1≤i≤n μ

$$\begin{aligned} M \bigl(\alpha_i(t)-1\bigr) \leq& \bigl(M_{\mathrm{ind},\mathrm{max}} \bigl(n_\mathrm {eng}\bigl(v(s),i\bigr) \bigr) - M_\mathrm{ind}(s) \bigr), \end{aligned}$$
(43a)
$$\begin{aligned} M \bigl(\alpha_i(t)-1\bigr) \leq& \bigl(n_{\mathrm{eng},\mathrm{max}} - n_\mathrm {eng} \bigl(v(s),i \bigr) \bigr). \end{aligned}$$
(43b)

This formulation does not cause LICQ problems and good values for M can be determined from bounds on v(⋅). Still, it is expected to give weak relaxations.

Second, we apply the GDP convex hull technique to the MIOCP (1). [50] proposed to lift all variables (controls, differential states, horizon lengths). We describe one of the many possibilities that stem from a modeler’s freedom to lift only some of the variables and to use different formulations for the disjunctive constraints.

One first observation is that we can use the convex multiplier functions α i (⋅) from outer convexification in place of λ, and let y(⋅):=(x(⋅),u(⋅)). The perspective formulation for the constraints c(⋅) then yields

$$ 0 \leq\alpha_i(t) c \bigl( x(t) / \alpha_i(t), u(t) / \alpha _i(t), v^i \bigr),\quad t \in[0,t_{\mathrm {f}}], i = 1, \ldots, {n_{\omega }}. $$
(44)

To properly obtain the convex hull, we also apply this procedure to the dynamic constraint for t∈[0,t f], i=1,…,n ω :

$$\begin{aligned} 0 =& \alpha_i(t) \bigl(\dot{x}(t)/ \alpha_i(t) - f \bigl(x(t)/ \alpha _i(t),u(t)/ \alpha_i(t),v^i \bigr)\bigr) \end{aligned}$$
(45a)
$$\begin{aligned} =& \dot{x}(t) - \alpha_i(t) f\bigl(x(t)/ \alpha_i(t),u(t)/ \alpha_i(t),v^i\bigr). \end{aligned}$$
(45b)

We introduce disaggregated state derivatives \(\dot{x}^{i}(\cdot)\), resulting states x i(⋅), and disaggregated control decision variables u i(⋅) for all nonlinearly entering controls:

$$ \dot{x}(t)=\sum_{i=1}^{n_\omega} \dot{x}^i(t),\qquad x(t)=\sum_{i=1}^{n_\omega}x^i(t), \qquad u(t)=\sum_{i=1}^{n_\omega}u^i(t). $$

We consider a time discretization of the states of problem (1),

$$\begin{aligned} x(t_k) :=&s_k,\qquad \dot{x}(t)=f\bigl(x(t),u(t),v(t) \bigr),\quad t \in[t_k,t_{k+1}], \end{aligned}$$
(46a)
$$\begin{aligned} s_{k+1} =&x\bigl(t_{k+1}; t_k,s_k,u( \cdot),v(\cdot)\bigr),\quad 0 \leq k \leq N-1, \end{aligned}$$
(46b)

which yields the MIOCP

(47)

with k=0,…,N−1, for which the convex hull formulation is, with piecewise constant controls α i (t)=α ik and t∈[t k ,t k+1] for k=0,…,N−1,

$$\begin{aligned} & \min_{{s, u, \alpha}}e(s_N) \\& \mbox{s.t.}\quad \dot{x}^i(t) =\alpha_{ik} f \bigl(x^i(t)/\alpha_{ik}, u^i(t)/\alpha _{ik}, v^i\bigr) \\&\phantom{\mbox{s.t.}\quad} x^i(t_k) = \alpha_{ik} s_k \\&\phantom{\mbox{s.t.}\quad} s_{k+1} =\sum_{i=1}^{n_\omega}x^i \bigl(t_{k+1}; t_k, s_k, u^i(\cdot )/\alpha_{ik}, v^i\bigr) \\&\phantom{\mbox{s.t.}\quad} 0 \le\alpha_{ik} c\bigl(x^i(t)/ \alpha_{ik}, u^i(t)/\alpha_{ik}, v^i \bigr) \\&\phantom{\mbox{s.t.}\quad} 0 \le d \Biggl(\sum_{i=1}^{n_\omega}x^i(t), \sum_{i=1}^{n_\omega}u^i(t) \Biggr) \\&\phantom{\mbox{s.t.}\quad} \sum_{i=1}^{n_\omega} \alpha_{ik} =1,\qquad 0 \leq x^i(t) \leq\alpha _{ik}M^\mathrm{s},\qquad 0 \leq u^i(t) \leq \alpha_{ik}M^\mathrm{u}. \end{aligned}$$
(48)

Note that for the purpose of the disjunctive term controlled by Y ik , s k is a constant when forming the perspective of the initial value constraint. Moreover, as the s k+1 enter linearly, we do not disaggregate them but instead aggregate the IVP results. Next, we enforce path constraints 0≤x i(⋅)≤α ik M s, c(⋅) and d(⋅) in the discretization points t=t k only, as is customary in direct optimal control. The respective constraints of (48) are replaced by

$$\begin{aligned} 0 \leq& s_k \leq M^\mathrm{s} \end{aligned}$$
(49a)
$$\begin{aligned} 0 \leq&\alpha_{ik} c\bigl(s_k, u^i(t_k)/ \alpha_{ik}, v^i\bigr) \end{aligned}$$
(49b)
$$\begin{aligned} 0 \leq& d \Biggl(s_k,\sum_{i=1}^{n_\omega} u^i(t_k) \Biggr). \end{aligned}$$
(49c)

We further substitute u by \(\bar{u}_{i}(t) = u_{i}(t) / \alpha_{ik}\). This poses no problem for α ik =0 due to the bound \(u_{i}(t) \le\alpha_{ik} M^{\mathrm{u}}_{k}\), and yields lifted controls \(\bar{u}_{i}(t)\) with \(0 \leq\bar{u}^{i}(t_{k}) \leq M^{\mathrm{u}}\):

$$\begin{aligned} \dot{x}^i(t) =& \alpha_{ik} f\bigl(x^i(t)/ \alpha_{ik}, \bar{u}^i(t_k), v^i \bigr) \end{aligned}$$
(50a)
$$\begin{aligned} 0 \leq&\alpha_{ik} c\bigl(s_k, \bar{u}^i(t_k), v^i\bigr) \end{aligned}$$
(50b)
$$\begin{aligned} 0 \leq& d \Biggl(s_k,\sum_{i=1}^{n_\omega} \alpha_{ik} \bar {u}^i(t_k) \Biggr) \end{aligned}$$
(50c)

Since this formulation still poses numerical difficulties, we go one step further and modify the problem by aggregating the states over all time steps and not only during the shooting intervals. This idea comes from the observation that, except for the ODE constraint, the x i(⋅) enter only via their convex combination. Hence, we replace x i(t) by α ik x(t) and obtain \(\sum_{i=1}^{n_{\omega}} x^{i}(t_{k+1}) = \sum_{i=1}^{n_{\omega}} \alpha_{ik} x(t_{k+1}) = x(t_{k+1})\) and thus (51)

$$\begin{aligned} & \min_{{s, \bar{u}, \alpha}} e(s_N) \\&\mbox{s.t.}\quad \dot{x}(t) =\sum_{i=1}^{n_\omega} \alpha_{ik} f\bigl(x(t), \bar {u}^i(t), v^i \bigr) \\&\phantom{\mbox{s.t.}\quad} x(t_k) =s_k \\& \phantom{\mbox{s.t.}\quad} s_{k+1} =x\bigl(t_{k+1}; t_k, s_k, \bar{u}(\cdot)\bigr) \\&\phantom{\mbox{s.t.}\quad} 0 \le\alpha_{ik} c\bigl(s_k, \bar{u}^i(t_k), v^i\bigr) \\&\phantom{\mbox{s.t.}\quad} 0 \le d \Biggl(s_k,\sum _{i=1}^{n_\omega} \alpha_{ik} \bar {u}^i(t) \Biggr) \\& \phantom{\mbox{s.t.}\quad} \sum_{i=1}^{n_\omega} \alpha_{ik} =1,\qquad 0 \leq s_k \leq M^\mathrm {s},\qquad 0 \leq\bar{u}^i(t) \leq M^\mathrm{u} \end{aligned}$$
(51)

is partial outer convexification of the ODE, uses the vanishing constraint formulation for the constraints, but differs in the disaggregation of the controls \(\bar{u}^{i}(\cdot)\), which gives the system more freedom to potentially find a better solution. Note that this particular way of making use of a GDP formulation needs to be smoothened again, e.g., using (38a)–(38b). For the application at hand this approach was superior to a full lifting and the difficult numerical treatment of the constraints that are quadratic in 1/α i (⋅).

Table 2 summarizes the reformulations for constraints directly depending on an integer control that have been discussed in this section.

Table 2 Comparison of constraint reformulations for α i =1⇒γ i ≤v≤Γ i and their properties
Full size table

5 Numerical Results

In this section we illustrate above concepts by applying the different formulations to the engine speed constraints of the heavy duty truck.

Reproducible Benchmark Implementations

We aim to make the heavy-duty truck cruise control problem available to the community as a MIOCP benchmark problem. A complete description comprises scenario data for γ(s) and v law(s) that characterizes the route to be traveled, with positioning information s assumed to be available. It also comprises M ind,max:=3000−(n eng(s,μ(s))−1250)2/100, M fric, Q fuel, n eng,min, and n eng,max as vehicle- and engine-specific nonlinear data sets. This data as well as other parameter values, functions, and initial values is available on the web page [55] and in the thesis [39]. Moreover, this web page includes AMPL models for all reformulations we use throughout this article.

In the following calculations, we discretize all control problems using an implicit Euler method with 40 equidistant steps on the horizon [0,1000].

Computational Setup

All results were computed on a single core of an Intel Core i7-2600 CPU with 3.40 GHz and 8 GB memory. Ipopt 3.10.0 and SNOpt 7.2-8 were run with the standard solver options, invoked from AMPL version 20120505. For the homotopy methods, Ipopt warm start options were added. The homotopy method starts with a big value for ε to find a solution for the control problem without vanishing constraints. The last solution σ ∗ is stored together with the corresponding ε ∗. ε ∗ is then adjusted by a factor δ to obtain a new ε as in Algorithm 1.

Algorithm 1
figure 2

Homotopy method for problems presented in Sect. 4.4 and Sect. 4.6

Full size image

Note that also δ>1 is allowed, since sometimes the last solution cannot be restored even with the same ε due to numerical difficulties.

Discussion of Scenarios

We present numerical results for two selected scenarios in Fig. 2 and Fig. 3. The track’s height profile is shown on top, followed by eight plots of the relaxed (local) optimal solutions identified by Ipopt for the formulations listed in Table 2. From both scenarios, a clear picture emerges. Inner convexification solutions suffer from significant infeasibility. Outer convexification is computationally the fastest formulation, and yields reasonable approximations that in parts suffer from compensatory effects. In contrast, the three vanishing constraint formulations succeed in yielding feasible solutions for both scenarios. For scenario 2, these solutions are even integer feasible, while for scenario 1 there are at most two control intervals with fractional gear choices. For the feasible vanishing constraint solutions, we can also compare the resulting objective functions. Here, the simple regularized formulations performs best, with the smoothing-regularization and the plain vanishing constraint formulation tied in second place. The GDP Big-M formulation does not yield feasible solutions, while our convex hull variant of GDP performs slightly better than outer convexification also in terms of integer feasibility. It suffers from a high computational runtime, though. The combination of integer control functions, nonlinear constraints, and nonlinear differential equations allows for a variety of different GDP implementations within a direct multiple shooting or direct collocation framework and may allow for significant better performance.

Fig. 2
figure 3

Relaxed gear choices α j (reflected by the intensity of gray) and corresponding velocities

Full size image
Fig. 3
figure 4

Relaxed gear choices α j (reflected by the intensity of gray) and corresponding velocities

Full size image

6 Future Developments

From the computational results, some evidence can be read in favor of vanishing constraint formulations. For the case of equality constraints depending on the integer control, complementarity constraints are obtained. In view of the computational inefficiency and the remaining infeasibility of homotopy based approaches, it will be desirable to treat MPCCs and MPVCs in their rigorous formulation of Sect. 4.3, Eqs. (29a)–(29b) in the future. SLP-EQP methods, first described by [20], can do so efficiently when the LP subproblem is replaced by the corresponding LPCC [17] or LPVC. Moreover, they can be shown to identify B-stationary points of such problems [47]. The efficiency improvements one would gain from such a computational setup would also make the application to closed-loop mixed-integer control [39] viable.

It will be interesting to study all constraints in the context of a Branch&Cut framework. Furthermore a comparison of global solutions would be helpful. As generic global solvers like Couenne cannot yet solve the benchmark, a specific dynamic programming approach seems the best choice.

Overcoming the numerical problems associated with perspective functions and a better exploitation of the numerical features of the resulting optimal control problems are yet other challenges.