Abstract
Steiner trees are constructed to connect a set of terminal nodes in a graph. This basic version of the Steiner tree problem is idealized, but it can effectively guide the search for successful approaches to many relevant variants, from both a theoretical and a computational point of view. This article illustrates the theoretical and algorithmic progress on Steiner tree type problems on two examples, the Steiner connectivity and the Steiner tree packing problem.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
The Steiner tree problem (stp) is one of the showcases of combinatorial optimization. It deals with finding a best connection of a number of vertices in a network and can formally be stated as follows:
Given a weighted graph G=(V,E,c) and a non-empty set of vertices T⊆V called terminals, find an edge set S ∗ such that (V(S ∗),S ∗) is a tree of minimal weight that spans T.
The stp is extensively covered in the literature, see [33, 35] for an introduction and [32] for a state-of-the-art survey on models and solution techniques. Many papers claim real-world applications, especially in vlsi -design and wire-routing, but also in telecommunication and traffic network design. Such applications usually refer to generalizations of the stp, which still require to connect a number of terminals, but by more than one tree, by something that is not precisely a tree, a constrained tree, etc. Such stipulations have always made Steiner trees a lively and exciting research topic for theoreticians and practitioners alike. Theoretical progress on the stp will typically serve as a blueprint to approach a particular Steiner tree problem; this knowledge is supplemented by specific developments, which in turn can advance the general theory. This is the Martin Grötschel way of optimization.
We illustrate (t)his approach in this article using two examples, the Steiner connectivity problem (scp) and the Steiner tree packing problem (stpp). The scp, discussed in Sect. 2, generalizes the stp by connecting the terminals using a set of paths instead of edges; this is motivated by line planning problems in public and rail transit, see [3]. The Steiner connectivity problem serves as an example that often results can be transferred from the basic Steiner tree problem to a more general setting, however, not all results and not always in a completely straightforward way. The stpp, studied in Sect. 3, deals with connecting several sets of terminals by several trees that cannot share edges; this models the internal wiring in a chip. The Steiner tree packing problem is difficult because it integrates a connection and a packing aspect; it is particularly well suited to illustrate the algorithmic progress of the last 20 years. However, chips are much larger now and the challenge has also grown. Steiner trees will therefore remain an exciting topic, at least until Martin Grötschel’s 100th birthday—can there be a better message?
2 The Steiner Connectivity Problem
Transportation and networks have always been two of Martin Grötschel’s favorite topics and it was therefore inevitable that at some point he would get involved in a research project on designing the line system of a public transportation system. Identifying origin-destination demand points with terminals, and lines with hyperedges, this leads directly to a hypergraph version of the Steiner tree problem, which we denote the Steiner connectivity problem, see [4, 23]. How difficult is this? In such a case, Martin Grötschel will always advocate a thorough investigation with a careful look at details, which can or cannot make a big difference. In particular, when it comes to graphs, digraphs, and hypergraphs, he becomes furious about “sloppy notation” that doesn’t distinguish between uv, (u,v), and {u,v}, because results do not automatically carry over between these cases. Martin Grötschel is correct, and the ability to seamlessly shift his attention from little details to the grand picture is without doubt one of his greatest strengths.
A formal description of the Steiner connectivity problem (scp) is as follows. We are given an undirected graph G=(V,E), a set of terminal nodes
T⊆V, and a set of elementary paths
 in G. The paths have nonnegative costs
in G. The paths have nonnegative costs  . The problem is to find a set of paths
. The problem is to find a set of paths  of minimal cost
of minimal cost  that connect the terminals, i.e., such that for each pair of distinct terminal nodes t
1,t
2∈T there exists a path q from t
1 to t
2 in G such that each edge of q is covered by at least one path of
that connect the terminals, i.e., such that for each pair of distinct terminal nodes t
1,t
2∈T there exists a path q from t
1 to t
2 in G such that each edge of q is covered by at least one path of  . We can assume w.l.o.g. that every edge is covered by a path, i.e., for every e∈E there is a
. We can assume w.l.o.g. that every edge is covered by a path, i.e., for every e∈E there is a  such that e∈p; in particular, G has no loops. Figure 1 gives an example of a Steiner connectivity problem and a feasible solution. Identifying the paths
such that e∈p; in particular, G has no loops. Figure 1 gives an example of a Steiner connectivity problem and a feasible solution. Identifying the paths  with hyperedges in the hypergraph
with hyperedges in the hypergraph  leads to an equivalent statement in terms of hypergraphs, in which the terminals have to be connected by a minimum cost set of hyperedges.
leads to an equivalent statement in terms of hypergraphs, in which the terminals have to be connected by a minimum cost set of hyperedges.
The Steiner connectivity problem is a good example for an extension study. Indeed, many results on Steiner trees can be generalized to the hypergraph setting, but not all, and not all directly. We illustrate this for two cases, namely, the 2-terminal case, and the “all-terminal case”, where all nodes are terminals. The latter generalizes spanning trees to “spanning sets”, but, in contrast to the graphical case, is \(\mathcal {NP}\)-hard. The first deals with finding a shortest hyperpath; we will see that structural properties of shortest paths carry over to this situation by proving the companion theorem to Menger’s theorem for hypergraphs. A further polyhedral and computational investigation of the Steiner connectivity problem can be found in [4].
2.1 The All-Terminal Case and the Greedy Algorithm
The all-terminal case T=V of the Steiner tree problem is a simple minimum spanning tree problem. In the Steiner connectivity setting, however, this case is hard. This is because of a strong relation between the scp and the set covering problem that will be discussed now.
Proposition 1
The Steiner connectivity problem is \(\mathcal {NP}\)-hard for T=V, even for unit costs.
Proof
We reduce the set covering problem to the all-terminal Steiner connectivity problem. In a set covering problem we are given a finite set S and a set \(\mathcal{M}\subseteq2^{S}\). The problem is to find a subset \(\mathcal{M}'\subseteq\mathcal{M}\) of minimal cardinality \(|\mathcal{M}'|\) such that for all s∈S there exists an \(M\in\mathcal{M}'\) with s∈M.
Given a set covering instance, we define an all-terminal Steiner connectivity instance in a graph G=(V,E) as follows: The nodes are V=S∪{v}=T with v being one extra node. Let us write V={s 0,s 1,s 2,…}, where v=s 0. All nodes are terminal nodes. We first assume that G is a complete graph and later remove all edges that are not covered by paths after their construction. For each set \(M\in\mathcal{M}\) order the elements in M arbitrarily and construct a path beginning in node v and passing through all nodes of M in the given order, compare with Fig. 2. The cost of each such path is 1.
Top: A Steiner connectivity instance corresponding to a set covering instance with S={a,b,c,d,e} and \(\mathcal{M}=(\{a,c\}, \{b,d\},\{b,c\}, \{c,e\},\{a,d,e\})\). Bottom: A minimal solution for the Steiner connectivity problem corresponding to the minimal cover \({\mathcal{M}'}=(\{b,c\},\{a,d,e\})\)
It is easy to see that a cover \(\mathcal{M}'\) with at most k elements exists if and only if a set of paths exists that connects V with cost at most k, k≥0. □
Corollary 1
SCP is strongly \(\mathcal {NP}\)-hard for |T|=|V|−k, k constant.
Proof
We add k isolated nodes to the graph G in the proof of Proposition 1. □
Proposition 2
There is no polynomial time α-approximation algorithm for SCP with α=γ⋅log|V|, γ≤1, unless \(\mathcal {P}=\mathcal {NP}\).
Proof
The transformation in Proposition 1 is approximation preserving, since there exists a cost preserving bijection between the solutions of the set covering instance and its corresponding Steiner connectivity instance. It has been shown that the set covering problem is not approximable in the sense that there exists no polynomial time approximation algorithm with approximation factor smaller than logarithmic (in the number of nodes) unless \(\mathcal {P}=\mathcal {NP}\), see Feige [10]. □
The proof of Proposition 1 shows that the set covering problem can be transformed to the all-terminal Steiner connectivity problem. On the other hand, the all-terminal Steiner connectivity problem can be interpreted as a submodular set covering problem. Recall that a function \(z:2^{N}\rightarrow \mathbb {R}\) from a set N={1,…,n} to the reals is submodular if the following inequalities hold:
The problem
is called the submodular set covering problem if z is a nondecreasing submodular function. We call this problem integer-valued if \(z:2^{N}\rightarrow \mathbb {Z}\). Let  and define for
and define for 

where  denotes the set of edges covered by the paths in
denotes the set of edges covered by the paths in  ;
;  can be interpreted as the maximum number of edges in
can be interpreted as the maximum number of edges in  containing no cycle. Note that this definition corresponds to the rank function for an edge set in a graphical matroid, i.e.,
containing no cycle. Note that this definition corresponds to the rank function for an edge set in a graphical matroid, i.e.,  , see, e.g., Oxley [31]. The function z is, therefore, a nondecreasing, integer-valued, submodular set function; this follows since
, see, e.g., Oxley [31]. The function z is, therefore, a nondecreasing, integer-valued, submodular set function; this follows since  for
for  . Note that
. Note that  means that
means that  connects V. Hence, the Steiner connectivity problem can be seen as an integer-valued submodular set covering problem. We have z(p)=|p| for
connects V. Hence, the Steiner connectivity problem can be seen as an integer-valued submodular set covering problem. We have z(p)=|p| for  and z(∅)=0. For such problems, there exists a greedy algorithm that works fairly well:
and z(∅)=0. For such problems, there exists a greedy algorithm that works fairly well:
Theorem 1
(Wolsey [37], 1982)
There is a greedy heuristic that gives an \(H(k)=\sum_{i=1}^{k}\frac{1}{i}\) approximation guarantee for integer-valued submodular set covering problems, where k=max j∈N z({j})−z(∅).
Such a greedy algorithm therefore also gives an approximation guarantee of \(H(k)=\sum_{i=1}^{k} \frac{1}{i}\) for the all-terminal Steiner connectivity problem if all paths contain at most k edges. This bound is asymptotically optimal, see Feige [10] and compare with Proposition 2.
Wolsey’s result generalizes an earlier one of Chvátal [8] who showed that a greedy algorithm gives an \(H(k)=\sum_{i=1}^{k} \frac{1}{i}\) approximation guarantee for the set covering problem, where k is the largest column sum. Chvátal’s reasoning can be extended to an elementary proof involving combinatorial counting arguments that are interesting in their own right. It goes as follows.
The proof analyzes the greedy heuristic in Algorithm 1. This procedure starts in an initial state in which each single node forms a smallest possible (connected) component. The algorithm then chooses in each iteration a path that minimizes the ratio of cost over the number of components that are connected by the path minus one. These connected components are merged into a new connected component. The algorithm terminates when everything has been merged into a single connected component.
We use the following notation. Let B
i be the set of connected components and  the set of chosen paths after iteration i of Algorithm 1. Note that in each iteration at least two connected components are merged, i.e., |B
i| decreases strictly with increasing i. Let us further denote by
the set of chosen paths after iteration i of Algorithm 1. Note that in each iteration at least two connected components are merged, i.e., |B
i| decreases strictly with increasing i. Let us further denote by

the component reduction number of path p and iteration i, i.e., if p were chosen in iteration i, the total number of connected components would reduce by N(p,i). Note that N(p,i) is nonincreasing for increasing i, i.e., N(p,1)≥…≥N(p,n) where n is the last iteration of Algorithm 1. Let  . Algorithm 1 then computes a solution of cost
. Algorithm 1 then computes a solution of cost  . Let, further,
. Let, further,  be an optimal V-connecting set. Finally, we denote by \(H(k)=\sum_{i=1}^{k}\tfrac{1}{i}\) the sum of the first k terms of the harmonic series.
be an optimal V-connecting set. Finally, we denote by \(H(k)=\sum_{i=1}^{k}\tfrac{1}{i}\) the sum of the first k terms of the harmonic series.
In order to analyze the greedy algorithm, we derive a lemma concerning the sum of the component reduction numbers of the optimal paths in iteration i∈{1,…,n}. This number is always greater than or equal to the sum of the component reduction numbers of the paths that are chosen by the greedy algorithm.
Lemma 1
In Algorithm 1 holds

Proof
Consider the right hand side of inequality (1). We get

The claim then follows since each V-connecting set has to connect all connected components in  . □
. □
Proposition 3
The greedy Algorithm
1
gives an
H(k) approximation guarantee for Steiner connectivity problems, where
 is the maximum path length, i.e.,
is the maximum path length, i.e.,

Proof
The idea of the proof is as follows. In a first step (assignment), we assign the path  (added to
(added to  in iteration i=1,…,n in Algorithm 1) to a subset of optimal paths
in iteration i=1,…,n in Algorithm 1) to a subset of optimal paths  . In a second step (bounding), we show that the cost of path p(i) can be bounded from above by the cost of the paths in O(i). In a third step (summation), we show that the cost of each path of the optimal solution
. In a second step (bounding), we show that the cost of path p(i) can be bounded from above by the cost of the paths in O(i). In a third step (summation), we show that the cost of each path of the optimal solution  is used at most H(k) times in the bounding step.
is used at most H(k) times in the bounding step.
-
1.
Step: Assignment. Consider Algorithm 2. It assigns to each path p(i), i=1,…,n, of the greedy algorithm (passed in reverse order), a set
 of optimal paths. The component reduction value N(p(i),i) for each path p(i), i=1,…,n, is distributed to the paths o∈O(i). To this purpose values υ(o,i) are computed such that υ(o,i)>0⇔o∈O(i). More precisely, in each iteration i a set
of optimal paths. The component reduction value N(p(i),i) for each path p(i), i=1,…,n, is distributed to the paths o∈O(i). To this purpose values υ(o,i) are computed such that υ(o,i)>0⇔o∈O(i). More precisely, in each iteration i a set 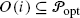 is chosen such that
$$ \sum_{o\in O(i)}\upsilon (o,i)=N\bigl(p(i),i\bigr) \quad\forall i=1,\ldots, n. $$(2)
is chosen such that
$$ \sum_{o\in O(i)}\upsilon (o,i)=N\bigl(p(i),i\bigr) \quad\forall i=1,\ldots, n. $$(2)Here, the values υ(o,i), o∈O, i=1,…,n, satisfy the following condition
$$ \sum_{j=i}^n \upsilon (o,j) \leq N(o,i)\quad\forall o\in O(i), i=1,\ldots, n. $$(3)Lemma 1 ensures that these values υ(o,i), i=1,…,n, exist.
-
2.
Step: Bounding. Consider the path p(i), i∈{1,…,n}, in iteration i of Algorithm 1 and the corresponding set O(i)={o 1,…,o h } defined in Algorithm 2. Path p(i) achieves the minimum in the ratio test in Step 3 of Algorithm 1. Using this fact and equation (2), the cost of p(i) can be bounded as follows
$$ \left. \begin{array}{c} \left. \begin{array}{lcl} \frac{c_{p(i)}}{N(p(i),i)}&\leq&\frac{c_{o_1}}{N(o_1,i)}\\&\vdots&\\\frac{c_{p(i)}}{N(p(i),i)}&\leq&\frac{c_{o_1}}{N(o_1,i)}\\\end{array} \right\}\upsilon (o_1,i)\mbox{ times}\\\vdots\\\left. \begin{array}{lcl} \frac{c_{p(i)}}{N(p(i),i)}&\leq&\frac{c_{o_h}}{N(o_h,i)}\\&\vdots&\\\frac{c_{p(i)}}{N(p(i),i)}&\leq&\frac{c_{o_h}}{N(o_h,i)}\\\end{array} \right\}\upsilon (o_h,i)\mbox{ times}\\\end{array} \right\}N\bigl(p(i),i\bigr) \mbox{ times}. $$Hence, we have \(c_{p(i)}\leq\sum_{o\in O(i)} \frac{c_{o}}{N(o,i)}\upsilon (o,i)\).
-
3.
Step: Summation. We finally consider how often the costs of a path
 are used in the bounding step. We have N(p,i)∈{0,1,2,…,|p|},
are used in the bounding step. We have N(p,i)∈{0,1,2,…,|p|}, 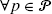 , i=1,…,n, hence, the total cost for a path
, i=1,…,n, hence, the total cost for a path  in the bounding step can be rewritten as
$$ \sum_{i=1}^{n}\frac{c_o}{N(o,i)}\upsilon (o,i)= \frac{c_o}{1}a_1 + \frac{c_o}{2}a_2 + \ldots+ \frac{c_o}{|o|}a_{|o|}. $$(4)
in the bounding step can be rewritten as
$$ \sum_{i=1}^{n}\frac{c_o}{N(o,i)}\upsilon (o,i)= \frac{c_o}{1}a_1 + \frac{c_o}{2}a_2 + \ldots+ \frac{c_o}{|o|}a_{|o|}. $$(4)Here, the coefficients
$$a_k=\mathop{\sum_{i=1}}_{N(o,i)=k} ^n \upsilon (o,i),\quad k=1,\ldots, |o|, $$are sums of the values υ(o,i). Note that N(o,i) is increasing for decreasing i. Let s k ∈{1,…,n} be the smallest iteration index of Algorithm 1 such that N(o,s k )=k, k=1,…,|o| (for k=|o| we have s k =1), if such an index exists. Then equation (3) implies
$$ a_k \leq\sum_{j=1}^{k}a_j\leq k, \quad k=1,\ldots,|o|. $$(5)This follows immediately if a k =0, i.e., if N(o,i)≠k for all i=1,…,n. Otherwise
$$\sum_{j=1}^{k}a_j=\sum_{j=1}^{k}\mathop{\sum_{i=1}}_{N(o,i)=j} ^n \upsilon (o,i) =\sum_{i=s_k}^n \upsilon (o,i)\leq N(o,s_k)=k. $$The term \(\tfrac{c_{o}}{k}\) decreases with increasing k and is maximal for k=1, and (5) implies a 1≤1. This means that the sum (4) is maximal for a 1=1. Repeating this argument for a 2, etc., the sum (4) is maximal if all coefficients a k , k=1,…,|o|, are 1. We then get
$$\sum_{i=1}^{n}\frac{c_o}{N(o,i)}\upsilon (o,i)\leq\frac{c_o}{1} + \frac{c_o}{2} + \ldots+ \frac{c_o}{|o|}\leq c_oH\bigl(|o|\bigr). $$Putting everything together, we get

□
Figure 3 shows a worst-case example for the greedy heuristic. We have k paths p i consisting of one edge with cost \(c_{p_{i}}=\frac{1}{i}\), i=1,…,k, and one path consisting of k edges with cost \(c_{p_{k+1}}= 1+\varepsilon\), ε>0. The greedy algorithm takes the paths p 1,…,p k in reverse order at a total cost of H(k). The optimal solution contains only path p k+1 with a cost of 1+ε.
2.2 The 2-Terminal Case and the Companion Theorem to Menger’s Theorem
The 2-terminal case of the Steiner connectivity problem is to find a shortest set of paths connecting two given nodes. This is equivalent to finding a shortest hyperpath in a hypergraph that arises by interpreting paths as hyperedges. This problem can in turn be transformed into an ordinary shortest path problem in a graph replacing each path by a clique with edge weights equal to the path weight. In other words, shortest hyperpaths behave just like shortest paths. Turning to several st-paths, it is also known that Menger’s theorem, stating that the maximum number of edge disjoint st-paths equals the minimum number of edges in an st-cut, generalizes to hypergraphs, see Frank [11]. In the graph case, a further result is known, the companion theorem to Menger’s theorem, that is obtained by interchanging the roles of st-paths and st-cuts, see Robacker [36]. Both results together establish paths and cuts in graphs as a blocking pair, see Fulkerson [12]. We show in this section that the companion to Menger’s theorem also holds for hypergraphs. More precisely, we prove the following theorem.
Theorem 2
The minimum cardinality of an st-hyperpath is equal to the maximum number of hyperedge-disjoint st-hypercuts.
This result does not follow from the above mentioned shortest path transformation. In fact, we show a stronger result, namely, that the inequality system of the cut formulation to find a shortest st-hyperpath (or 2-terminal Steiner connecting set) is totally dual integral. This extends the blocking property of paths and cuts to hypergraphs and establishes a complete structural similarity between paths and 2-terminal Steiner connecting sets.
We use the following notation. Let  be a connected undirected hypergraph with costs \(c_{e}\in \mathbb {R}\) for all hyperedges
be a connected undirected hypergraph with costs \(c_{e}\in \mathbb {R}\) for all hyperedges  , and s and t be two different nodes of H. Consider the following linear program
, and s and t be two different nodes of H. Consider the following linear program

Here, we have a variable x
e
for each hyperedge  . For W⊆V∖{t}, s∈W, an st-hypercut
. For W⊆V∖{t}, s∈W, an st-hypercut
 is the set of all hyperedges having at least one node in each shore. The inequality (6) guarantees for each st-hypercut that the sum of the x-values over all edges in this hypercut is at least 1. We will see that for nonnegative costs the program (SH) always has an optimal solution that is an st-hyperpath, i.e., a minimum cost set of hyperedges that connects s and t.
is the set of all hyperedges having at least one node in each shore. The inequality (6) guarantees for each st-hypercut that the sum of the x-values over all edges in this hypercut is at least 1. We will see that for nonnegative costs the program (SH) always has an optimal solution that is an st-hyperpath, i.e., a minimum cost set of hyperedges that connects s and t.
For nonnegative costs, the primal-dual Algorithm 3 computes an optimal integral solution for program (SH) with x
e
≤1,  . It generalizes Dijkstra’s algorithm to the hypergraph setting and has a better complexity than the “clique transformation method” mentioned at the beginning of the section. Its main purpose, however, is to show that the inequality system of program (SH) is totally dual integral (TDI).
. It generalizes Dijkstra’s algorithm to the hypergraph setting and has a better complexity than the “clique transformation method” mentioned at the beginning of the section. Its main purpose, however, is to show that the inequality system of program (SH) is totally dual integral (TDI).
Theorem 3
The inequality system of program (SH) is TDI.
Proof
Program (SH) has the following dual

where  . If c
e
<0 for an
. If c
e
<0 for an  then (SH) has no finite solution since x is not bounded from above; with x
e
→∞ we can improve the objective arbitrarily. This means that we can assume a nonnegative integer cost vector in the following. We prove the claim for this case by showing that the primal-dual shortest hyperpath Algorithm 3 constructs optimal integral solutions x for (SH) and y for (7) with the same objective value.
then (SH) has no finite solution since x is not bounded from above; with x
e
→∞ we can improve the objective arbitrarily. This means that we can assume a nonnegative integer cost vector in the following. We prove the claim for this case by showing that the primal-dual shortest hyperpath Algorithm 3 constructs optimal integral solutions x for (SH) and y for (7) with the same objective value.
The algorithm adds nodes v i to sets W i−1={v 1,…,v i−1} in the order of increasing distance d(v i ) from s=v 0 (=v 1), i.e., d(v i−1)≤d(v i )<∞, i=1,…,h, with h being the last iteration of the while loop 3. This produces a sequence of nested st-hypercuts δ(W i ), i=1,…,h−1.
We first show that y is a solution of program (7). Lines 2 and 13 imply y≥0. In fact, the variables y W can take positive values only for W∈{W 1,…,W h−1}.
It remains to show that

Let  . If v
i
∉e for all i=1,…,h−1, then e∉δ(W
i
), i=1,…,h−1, i.e.,
. If v
i
∉e for all i=1,…,h−1, then e∉δ(W
i
), i=1,…,h−1, i.e.,  . Otherwise, let 1≤i<h be the minimal index smaller than h such that v
i
∈e, i.e., e∉δ(W
j
) for 1≤j<i<h but e∈δ(W
i
), and let i≤ℓ≤h−1 be the maximal index such that e∈δ(W
j
) for i≤j≤ℓ. Then inequality (8) becomes
. Otherwise, let 1≤i<h be the minimal index smaller than h such that v
i
∈e, i.e., e∉δ(W
j
) for 1≤j<i<h but e∈δ(W
i
), and let i≤ℓ≤h−1 be the maximal index such that e∈δ(W
j
) for i≤j≤ℓ. Then inequality (8) becomes

For the last inequality we distinguish the cases v ℓ+1∈e and v ℓ+1∉e. The first case follows since v i ∈e. In the second case, ℓ+1=h, i.e., v ℓ+1=v h =t and there exists a node w∈e with w∉W h−1. Since d(v ℓ+1)=d(t)≤d(w) and w,v i ∈e, the second case follows analogously.
Now we show that x is a solution of program (SH). Due to the definition of x we have x≥0. We have to show that
Consider the nodes t=u 1,…,u k =s computed in the while loop starting in line 18 and an st-hypercut δ(W). Let i be the largest index with u i ∉W and u i+1∈W. This index exists since u 1=t∉W and u k =s∈W. Then we have \(x_{e(u_{i})}=1\), e(u i )∈δ(W), and inequality (9) is satisfied.
The objective value of program (7) is
We, finally, get for the objective value of program (SH)

i.e., x and y have the same objective value and are therefore optimal for (SH) and (7). Since c
e
is integral, it follows that d(v
i
) is integral for i=0,…,h. Therefore, \(y_{W_{i}}\), i=1,…,h−1, is also integral (line 13). This shows the claim for c
e
≥0,  . □
. □
Setting c≡1 yields Theorem 2, a combinatorial result on hypergraph connectivity which has, to the best of our knowledge, not been considered before. Denote the maximum number of hyperedge-disjoint st-hypercuts the Grötschel st-index of a hypergraph. We can then restate Theorem 2 as follows:
Theorem 4
(Grötschel st-index Theorem)
The minimum cardinality of an st-hyperpath is equal to the Grötschel st-index.
Figure 4 gives an illustration. As this result is derived from a careful analysis of the hypergraph vs. the graph case, we feel that it fits very well to dedicate this Theorem to Martin Grötschel on the occasion of his 65th birthday.
Interchanging the roles of st-hyperpaths and st-hypercuts yields Menger’s theorem for hypergraphs, see [11].
Theorem 5
The minimum cardinality of an st-hypercut is equal to the maximum number of hyperedge-disjoint st-hyperpaths.
Grötschel’s and Menger’s Theorems 4 and 5 are therefore companion theorems indeed.
3 The Steiner Tree Packing Problem
When Martin Grötschel came in 1989 to Alexander Martin and suggested the topic of packing Steiner trees in graphs as a Ph.D. thesis, he became immediately very curious about it. Martin Grötschel further supported it by saying that this is a topic for the next decades. He claimed that very few is known when it comes to packing problems in general, one reason among others is that it is open on how to integrate and exploit dual information. And he seems to be right until today. We all know that some progress has been made when it comes to classical packing problems such as the set packing or the bin packing problem. But for the stpp, when the objects to be packed have no fixed shape and are flexible in size and structure in dependence on the other objects to be packed, the problem seems to be harder by orders of magnitudes. None of the successful techniques like preprocessing or heuristics for the single Steiner tree problem work anymore, and new ideas must be developed. With very few exceptions, cf. [14–19], the stpp is still open for wonderful discoveries, supporting once more the great ability of Martin Grötschel to identify future trends and challenging problems.
The Steiner tree packing problem (stpp) looks at the following situation. Instead of having one set of terminals, we have N non-empty disjoint sets T 1,…,T N , called Nets, that have to be “packed” into the graph simultaneously, i.e., the resulting edge sets S 1,…,S N have to be pairwise disjoint. In these applications, G is usually some sort of 3D grid graph. [19, 20, 27] give detailed explanations of the modeling requirements in vlsi-design. From a theoretical point of view, much less is known, see [7, 26].
Three routing models for 2D or 3D grid graphs are of particular interest:
- Channel routing::
-
Here, a complete rectangular grid graph is used. The terminals of the nets are exclusively located on two opposing borders. The size of the routing area is not fixed in advance. All nets have only two terminals, i.e., |T i |=2.
- Switchbox routing::
-
We are given a complete rectangular grid graph. The terminals may be located on all four sides of the graph. Thus, the size of the routing area is fixed.
- General routing::
-
In this case the grid graph may contain holes or have a non-rectangular shape. The size of the routing area is fixed and the terminals may be located arbitrarily.
The intersection of the nets is an important issue in Steiner tree packing. Again three different models are possible:
- Manhattan:
-
(Fig. 5(a)) Consider some (planar) grid graph. The nets must be routed in an edge disjoint fashion with the additional restriction that nets that meet at some node are not allowed to bend at this node, i.e., so-called Knock-knees are not allowed. This restriction guarantees that the resulting routing can be laid out on two layers at the possible expense of causing long detours.
- Knock-knee:
-
(Fig. 5(b)) Again, some (planar) grid graph is given and the task is to find an edge disjoint routing of the nets. In this model Knock-knees are possible. Very frequently, the wiring length of a solution is smaller than in the Manhattan model. The main drawback is that the assignment to layers is neglected.
- Node disjoint:
-
(Fig. 5(c)) The nets have to be routed in a node disjoint fashion. Since no crossing of nets is possible in a planar grid graph, this requires a multi-layer model, i.e., a 3D grid graph.
While channel routing usually involves only a single layer, switchbox and general routing problems are typically multi-layer problems. Using the Manhattan and Knock-knee intersection is a way to reduce the problems to a single layer. Accordingly, the multi-layer models typically use the node disjoint intersection. While the multi-layer model is well suited to reflect reality, the resulting graphs become quite large. We consider two possibilities to model multiple layers; a third possibility is to use a single-layer model with edge capacities greater than one:
- k-crossed layers:
-
(Fig. 6(a)) A k-dimensional grid graph (i.e., k copies of a grid graph are stacked on top of each other and corresponding nodes are connected by perpendicular lines, so-called vias) is given, where k denotes the number of layers. This is called the k-layer model in [27].
- k-aligned layers:
-
(Fig. 6(b)) This model is similar to the crossed-layer model, but in each layer there are only connections in one direction, either east-to-west or north-to-south. [27] calls this the directional multi-layer model. [26] indicate that for k=2 this model resembles the technology used in vlsi-wiring best. It is mentioned in [2] that current technology can use a much higher number of layers (20 and more).
Note that for switchbox routing there is a one-to-one mapping between feasible solutions for the Manhattan one-layer model (mol) and the node disjoint two-aligned-layer model (tal), assuming that there are never two terminals on top of each other, i.e., connected by a via.
For the general routing model, this mapping might not be possible. If a terminal is within the grid, there is no easy way to decide the correct layer for the terminal in the two-layer model.
Unfortunately, in the seven “classic” instances given by [6, 9, 29] two terminals are connected to a single corner in several cases. This stems from the use of connectors, i.e., the terminal is outside the grid and connected to it by a dedicated edge. In the multi-layer models there has to be an edge from the terminal to all permissible layers (Fig. 6(c)).
The Knock-knee one-layer model can also be seen as an attempt to approximate the node disjoint two-crossed-layer model. But mapping between these two models is not as easy. [5] have designed an algorithm that guarantees that any solution in the Knock-knee one-layer model can be routed in a node disjoint four-crossed-layer model, but deciding whether three layers are enough has been shown to be \(\mathcal {NP}\)-complete by [28].
For our computational investigations we will use a multicommodity flow formulation [25] that was proposed by [38] for the stp. Given a weighted bidirectional grid digraph G=(V,A,c) and sets T 1,…,T N , N>0, |T n |>0 of terminals, we arbitrarily choose a root r n ∈T n for each \(n\in \mathcal {N}:=\{1,\ldots,N\}\). Let \(R=\{r_{n}|n\in \mathcal {N}\}\) be the set of all roots and \(T=\bigcup_{n\in \mathcal {N}} T_{n}\) be the union of all terminals. We introduce binary variables \(x^{n}_{ij}\) for all \(n\in \mathcal {N}\) and (i,j)∈A, where \(x^{n}_{ij}=1\) if and only if arc (i,j)∈S n . Additionally, we introduce binary variables \(y^{t}_{ij}\), for all t∈T∖R. For all i∈V, we define \(\delta^{+}_{i}:=\{(i,j)\in A\}\) and \(\delta^{-}_{i}:=\{(j,i)\in A\}\). For all t∈T n , \(n\in \mathcal {N}\), we define σ(t):=n. The following formulation models all routing choices for any number of layers, crossed and aligned, with Knock-knee intersection:
To use node disjoint intersection we have to add:
3.1 Valid Inequalities
For the node disjoint crossed-layer model there is a class of simple but very effective cuts, which are introduced in [21]. Consider a stpp problem of two nets, each has two terminals as in Fig. 7. The flows shown in the picture correspond to an optimal solution of the lp relaxation. However, it can be seen that if none of the two flows (r 1,t 1) and (r 2,t 2) leaves the upper layer, they have to cross each other, i.e., the node disjoint intersection condition is violated. In the following we construct cuts, which cut off the fractional solution in Fig. 7.
lp relaxation solution violates (17)
A pair (s 1,t 1),(s 2,t 2)∈T×(T∖R) are called crossed if these four terminals lie on the boundary and in the same layer, σ(s 1)=σ(t 1), σ(s 2)=σ(t 2), σ(s 1)≠σ(s 2), and, moreover, the line segments (s 1,t 1) and (s 2,t 2) cross each other. Let \(\mathcal{C}\) be the set of all crossing pairs and for each node v we denote by v z the layer number of node v. Then the following inequality is valid for (10):
where \(\mathcal{C}(R):= \{ ((s_{1},t_{1}), (s_{2},t_{2}) )\in\mathcal{ C} | s_{1}, s_{2}\in R \}\). Equation (17) means that at least one of the two flows (r 1,t 1) and (r 2,t 2) has to leave the layer containing these terminals.
A triple (r 1,t 1),(r 2,t 2),(r 3,t 3)∈R×(T∖R) is called a crossing triple if each two of them are a crossing pair in \(\mathcal{C}(R)\). Let \(\mathcal{C T}\) be the set of all crossing triples then the following inequality is valid for (10):
This is a direct implication from summing up the three corresponding inequalities of type (17) taking into account that the variables have to be integral.
Based on the same principle, we can derive more valid cuts involving both variables x and y. Again, we assume that all terminals lie on the boundary. Let u and v be two terminals in one layer of a net n and the root of this net does not belong to the layer containing u and v. If there exist a root r and a terminal t of another net such that (u,v) and (r,t) cross each other, i.e., \(((u,v),(r,t) )\in\mathcal{C}\), then the following inequality is valid for (10)
The following valid cut is similar to (19) but two terminal pairs and three terminals of a third net are involved. We consider an arbitrary net n with at least three terminals and four terminals r 1, t 1, r 2 and t 2 of two other nets n 1 and n 2, σ(r 1)=σ(t 1)=n 1≠n, σ(r 2)=σ(t 2)=n 2≠n, n 1≠n 2, with r 1,r 2∈R. If there exist three terminals u, v and w of net n lying in the same layer such that
then the following inequality is valid:
Since all terminals lie on the boundary, each line segment between two terminals, which crosses an edge of a “triangle” of three terminals (including the case that they lie in a line), crosses exactly two edges of this triangle. Therefore, condition (20) just ensures that the line segments (r 1,t 1) and (r 2,t 2) cross the triangle (u,v,w) in two different pairs of edges. Inequality (21) means that the total number of vias used by the flows (r 1,t 1) and (r 2,t 2) and the net n to enter the layer containing these terminals is at least two. The proof can be found in [21]. Moreover, one can prove that, if u, v and w satisfy the above condition and u, v and w do not lie in the same layer as the root of net n then the following inequality is valid:
The proof can also be found in [21].
The next type of valid inequality does not require any of the terminals to be the root of the net they belong to. For arbitrary three terminals u 1, v 1 and w 1 of a net n 1, and arbitrary three terminals u 2, v 2 and w 2 of a net n 2≠n 1, if
and
i.e., the two triangles (u 1,v 1,w 1) and (u 2,v 2,w 2) cross each other, then the following inequality is valid for (10):
where δ i is 1 if the root of net n i does not lie in the same layer as u i , v i and w i , and 0 otherwise.
3.2 Heuristics
As we will see in the following the above described model provides very strong lower bounds in practice. Nevertheless, current IP solvers often not only fail to solve the IP model to optimality, it is even very time-consuming to find a feasible solution.
However, based on the special structure of the grid graph we can find optimal solutions for all of our considered instances in reasonable time. The following is an extension to [21] and describes the heuristics we developed to improve the solution of the stpp. The heuristics presented in this section are based on solving the IP of relaxed problems. There are two kinds of relaxed problems. The first one is also the stpp problem using the multicommodity flow formulation (10) but on a subgraph of the original grid graph. The second one is the original multicommodity flow IP where some variables are fixed based on a given feasible solution of the original problem. In the following we call these two kinds of heuristics phase 1 and phase 2, respectively. The solving process of the stpp starts with phase 1 and then executes phase 2. The two phases of the heuristics are presented in detail below.
3.2.1 Heuristics Phase 1
Computational results show that feasible solutions of the multi-aligned layers can be found easily if they exist. This motivates us to consider a heuristic process, where instead of starting solving the original multi-crossed layers model, we solve several stp problems corresponding to some sparser underlying grids, e.g., the multi-aligned layers grid. After each step we obtain a feasible solution. Then we add some edges to the grid and resolve the stp problem which corresponds to the new grid, using the solution from the previous step as a start value for the optimization problem. The question is which edges should be added in each step. There is no optimal strategy at the moment. Algorithm 4 describes our implemented algorithm, where S(l,r,b,t) is the set of all edges lying outside [l,K−r]×[b,L−t], i.e.,
with (i x ,i y ) is the coordinate of the vertex i in the layer which it belongs to, [0,K]×[0,L] is the given grid, and E is the set of edges in the multi-crossed layer model.
Figure 8 demonstrates the grid graphs in the three steps, where the added edges are dotted.
It is still unknown what is the best way to choose the parameters (l 2,r 2,b 2,t 2) and (l 3,r 3,b 3,t 3). For the instances in Sect. 3.3 we choose l 2=r 2=b 2=t 2=3 for pedabox-2 and l 2=r 2=b 2=t 2=5 for the other instances. In step 3, to obtain the parameters l 3, r 3, b 3, t 3, we increase the corresponding parameters l 2, r 2, b 2, t 2 from step 2 by at most 2. For example, we choose l 3=r 3=7 and b 3=t 3=6 for the instances difficult-2 and more-diff-2.
3.2.2 Heuristics Phase 2
Having a feasible solution from heuristics phase 1 we can start the fixing heuristics. Figure 9 shows an example for the procedure of these heuristics. This figure reads from left to right and from top to bottom. Let us start with the picture on top left. We fix the variables corresponding to the edges in the gray region to the values of the given feasible solution for those variables. Then we solve the IP (10) with those fixings and obtain a possibly better feasible solution. With the newly obtained feasible solution we go to the second step described by the second picture in the top of Fig. 9, where again the fixing area is colored by gray, and so on. The given feasible solution from the beginning is improved step by step, where each step uses the best feasible solution obtained in the previous step for fixing. At the moment there is no common rule for the fixing region and the number of steps. Algorithm 5 presents the pseudo code of phase 2 in our implemented code. We execute four steps with the sequence of the fixing regions as the four pictures either on the left side or on the right side of Fig. 9, respectively, as follows. Let K×L be the size of the grid. Without loss of generality, we assume that K≤L. Otherwise we have to modify the following definition accordingly by switching the role of K and L. The four fixing regions are defined as
where 3≤p 1,p 2≤4 and 5≤p 3,p 4≤6 are chosen depending on instances. For our considered instances, this procedure gives us already optimal solutions. However, for larger instances, we may need to execute more steps and/or use more types of fixing regions, e.g., all eight steps in Fig. 9.
3.3 Computational Results
In this section, we present computational results obtained by generating the integer program resulting from the directed multicommodity flow formulation with ZIMPL [24] and then solving it with CPLEX 12.3 for the stpp instances taken from [30]. All computations are done on a 48 GB RAM dual quad-core Intel Xeon X5672 at 3.20 GHz with TurboBoost active and Hyperthreading deactivated. Since the crossed-layer model proved to be much harder to solve, we used all eight cores, while just one core was utilized for the other models. Still, for the crossed-layer models we will use minutes as the unit for reporting time, in contrast to seconds for the other models. As we had expected from earlier experiments, the MCF-Cuts [1, 34] introduced by CPLEX 12 had no impact on solving the instances. The reason is that the models used in this paper are not capacitated. If not noted otherwise, CPLEX was used in default mode with integer optimality gap tolerance set to 0.0.
3.3.1 Results for the Knock-Knee One-Layer Model
Table 1 shows the results for the Knock-knee one-layer model. B&B Nodes denotes the number of Branch-and-Bound nodes including the root node evaluated by CPLEX. The column labeled Time shows the consumed CPU time in seconds. lp relaxation lists the objective function value of the initial lp relaxation of the root node before any cuts applied by CPLEX. Finally, arcs is the total number of arcs used in the optimal solution which for one-layer models is equivalent to the optimal objective value.
As we can see from the table, the lp relaxation of the flow model is rather strong. This is in line with other reported results including [22, 30]. Since for difficult-1, mod-dense-1, more-diff-1, and pedabox-1 the relaxation already provides the optimal value, it is possible to solve these instances without any branching. For termintens-1 the relaxation is one below the optimum, but CPLEX is able to push the lower bound up by generating Gomory rounding and 0–1/2-Chvátal-Gomory cuts. The number of B&B nodes and therefore the computing time depends very much on the branching decisions taken. During our experiments the solutions were always found in the tree and not by heuristics. By using improved settings, like switching off the heuristics and just trying to move the best bound, the number of nodes needed for aug-dense-1 and dense-1 can be at least halved.
3.3.2 Results for the Node Disjoint Multi-aligned-layer Model
Table 2 shows results for the node disjoint multi-aligned-layer model. Since this is a multi-layer model we have to assign costs to the vias. These are given in the column labeled Via-cost. The column labeled LP relaxation gives the objective value of the initial lp relaxation. The next three columns list the numbers of vias, “regular” arcs, and vias+arcs in the optimal solution.
In case of unit via costs, the objective value of the lp relaxation is equal to the objective value of the optimal integer solution for all instances except for more-diff-2. The value of the lp relaxation for more-diff-2 is 518.6 (optimal 522). This is weaker than the value reported in [19], which indicates that some of the strengthening cuts used by [19] to tighten the undirected partitioning formulation can also be used to tighten the directed flow formulation. On the other hand, for pedabox-2 the relaxation is stronger than reported. The instances where the lp relaxation does not reach the optimum are different ones from the Knock-knee-one-layer model.
Via Minimization
Traditionally via minimization is viewed as a separate problem after the routing has taken place [13]. Since we work with multi-layer models, via minimization is part of the routing. As can be seen in Table 2 we tried the “classical” instances with three different cost settings for the vias. First unit costs were used to minimize the total number of arcs, including vias. Next, the number of vias was minimized by setting the cost to 1,000, which dominates the total cost of all “regular” arcs, ensuring that a global minimum is reached. Finally, the cost of each via was set to 0.001, effectively minimizing the number of “regular” arcs. This results in solutions that have the same number of arcs as reported in [19] for the Manhattan one-layer model.
Interestingly, the number of vias is constant for aug-dense-2, pedabox-2, modifieddense-3, and dense-3. For the other instances, a minimization of the number of vias always results in detours, i.e., a higher total number of arcs used.
New Instances
All the instances presented so far are relatively old and can be solved in less than 12 minutes with CPLEX. To get an outlook on how far our approach will take us, we tried some new instances, see Table 3. sb80-80 and sb99-99 are randomly generated switchbox instances. sb80-80 is about 35 times the size of the largest “classical” instance, and the resulting ip has more than six million variables and almost twenty million non-zero entries in the constraint matrix. sb99-99 is again about 2 times larger than sb80-80. As discussed in [21] and [25], for several instances it was faster to solve the lp relaxations from scratch with the barrier algorithm than to reoptimize with the dual simplex algorithm. This setting is used for the new instances with a newer version of CPLEX, namely, CPLEX 12.4.
For sb80-80 the value of the lp relaxation turned out to be equal to the value of the integer optimal solution, namely 6533, and only one branch and bound node is needed. CPLEX takes 94,926 seconds to solve the root relaxation and finishes after 94,232 seconds, i.e., 26.18 hours, with the optimal solution, which has 226 vias and 6307 normal arcs, see Fig. 10.
The time for solving the root relaxation of sb99-99 is 356,664 seconds, i.e., 4.13 days. After more than 2 weeks CPLEX cannot either find a feasible solution or prove that the problem is infeasible. Gurobi 5.0 also experiences the same difficulty with this instance.
These computations show the bottleneck of our approach. The resulting ips are large and solving their lp relaxations is already very hard. Any improvement in solving lp will turn out directly to an improvement in our approach.
3.3.3 Results for the Node Disjoint Multi-crossed-layer Model
Finally, we will have a look at the crossed-layer models. For the instances listed in Table 4, except for dense-3 and mod-dense-3, the heuristics presented in Sect. 3.2 was used to provide CPLEX with a starting solution. For dense-3 and mod-dense-3 CPLEX quickly found solutions. Therefore, employing the heuristics provided no advantage. For all instances the provided solution turned out to be already optimal. The time needed to compute these initial solution is given under Heur.
To solve the instances we used 8 threads in opportunistic mode, the total times needed including the heuristics is reported in column Total as minutes of wall clock time. The optimization emphasis of CPLEX was set to “optimality”, cut generation was set “aggressive” for Gomory-, 0–1/2-, and cover-cuts, all other cuts were set to “moderate”. Furthermore, we explicitly added cuts (17)–(25) presented in Sect. 3.1 to the User-Cut pool of CPLEX.
While it is possible to find reasonable solutions with our heuristics, proving optimality is still a hard task. The table is ordered by an increasing difference between the lp relaxation and the optimum value. As can be seen this is reflected quite well in the number of B&B nodes needed to prove optimality. While the cuts we presented in this paper proved quite helpful, the main reason for the long running time is that solving the node lps is very time consuming. For example, the number of B&B nodes that CPLEX needs to solve the instance termintens-2 is merely 3,453. However, it takes 51.7 hours to solve the problem and 43.3 hours for the first 2,000 nodes.
Figure 11 shows the primal and dual bounds during the solving process of the instance pedabox-2 with CPLEX using default setting and CPLEX using our heuristics, valid cuts, and variables elimination. Clearly, our approach improves both primal and dual bounds. For pedabox-2 with unit via-cost, our heuristics found an optimal solution after 17.8 minutes, while CPLEX alone could not find the optimal value after more than 80 hours. For this problem our approach (using crossing cuts and special heuristics) gives a dual bound of value 358.2311 directly after the root node, while default CPLEX reaches this value only after 46.1 hours and 158,507 nodes. We stop solving with default CPLEX after 83.33 hours and 300,516 nodes, and obtain a dual bound of 358.7628. This value is already reached by our approach after 49.6 minutes and 471 nodes.
4 Conclusion and Outlook
The Steiner connectivity and the Steiner tree packing problem are just two examples of challenging and important questions to find the best possible connection of a set of terminals in a graph. For such problems chances are good that we can derive theoretical insights and come up with quite powerful solution algorithms, guided by our knowledge of the basic case. We are admittedly still working on individual problem variants, far from anything like a universal solution engine, and, in fact, going one step further into the direction of industrial models, e.g., in line planning or chip design, immediately makes things much more difficult, and even more, since problem sizes of real-world problems are growing fast. But such is life, would Martin Grötschel say. And he could still come, 20 years after Alexander Martin finished his thesis, into the office of one of his Ph.D. students and talk enthusiastically about an interesting and open Steiner problem.
References
Achterberg, T., Raack, C.: The MCF-separator—detecting and exploiting multi-commodity flows in MIPs. Math. Program. Comput. 2, 125–165 (2010)
Boit, C.: Personal communication (2004)
Borndörfer, R., Karbstein, M.: A direct connection approach to integrated line planning and passenger routing. In: Delling, D., Liberti, L. (eds.) 12th Workshop on Algorithmic Approaches for Transportation Modelling, Optimization, and Systems. OpenAccess Series in Informatics (OASIcs), vol. 25, pp. 47–57. Schloss Dagstuhl–Leibniz-Zentrum für Informatik, Wadern (2012)
Borndörfer, R., Karbstein, M., Pfetsch, M.E.: The Steiner connectivity problem. Math. Program., Ser. A (2012). doi:10.1007/s10107-012-0564-5
Brady, M.L., Brown, D.J.: VLSI routing: four layers suffice. In: Preparata, F.P. (ed.) Advances in Computing Research: VLSI Theory, vol. 2, pp. 245–258. Jai Press, London (1984)
Burstein, M., Pelavin, R.: Hierarchical wire routing. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2, 223–234 (1983)
Chopra, S.: Comparison of formulations and a heuristic for packing Steiner trees in a graph. Ann. Oper. Res. 50, 143–171 (1994)
Chvátal, V.: A greedy heuristic for the set-covering problem. Math. Oper. Res. 4(3), 233–235 (1979)
Coohoon, J.P., Heck, P.L.: BEAVER: a computational-geometry-based tool for switchbox routing. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 7, 684–697 (1988)
Feige, U.: A threshold of lnn for approximating set-cover. In: Proceedings of the 28th ACM Symposium on Theory of Computing, pp. 314–318 (1996)
Frank, A.: Connections in Combinatorial Optimization. Oxford University Press, Oxford (2011)
Fulkerson, D.R.: Blocking and anti-blocking pairs of polyhedra. Math. Program. 1, 168–194 (1971)
Grötschel, M., Jünger, M., Reinelt, G.: Via minimization with pin preassignments and layer preference. Z. Angew. Math. Mech. 69(11), 393–399 (1989)
Grötschel, M., Martin, A., Weismantel, R.: Optimum path packing on wheels: the consecutive case. Comput. Math. Appl. 31, 23–35 (1996)
Grötschel, M., Martin, A., Weismantel, R.: Packing Steiner trees: a cutting plane algorithm and computational results. Math. Program. 72, 125–145 (1996)
Grötschel, M., Martin, A., Weismantel, R.: Packing Steiner trees: further facets. Eur. J. Comb. 17, 39–52 (1996)
Grötschel, M., Martin, A., Weismantel, R.: Packing Steiner trees: polyhedral investigations. Math. Program. 72, 101–123 (1996)
Grötschel, M., Martin, A., Weismantel, R.: Packing Steiner trees: separation algorithms. SIAM J. Discrete Math. 9, 233–257 (1996)
Grötschel, M., Martin, A., Weismantel, R.: The Steiner tree packing problem in VLSI design. Math. Program. 78(2), 265–281 (1997)
Held, S., Korte, B., Rautenbach, D., Vygen, J.: Combinatorial optimization in VLSI design. In: Chvátal, V. (ed.) Combinatorial Optimization—Methods and Applications. NATO Science for Peace and Security Series—D: Information and Communication Security, vol. 31, pp. 33–96 (2011)
Hoàng, N.D., Koch, T.: Steiner tree packing revisited. Math. Methods Oper. Res. 76(1), 95–123 (2012)
Jørgensen, D.G., Meyling, M.: Application of column generation techniques in VLSI design. Master’s thesis, Department of Computer Science, University of Copenhagen (2000)
Karbstein, M.: Line planning and connectivity. Ph.D. thesis, TU Berlin (2013)
Koch, T.:. ZIMPL. zimpl.zib.de
Koch, T.: Rapid mathematical programming. Ph.D. thesis, Technische Universität Berlin (2004)
Korte, B., Prömel, H.J., Steger, A.: Steiner trees in VLSI-layout. In: Korte, B., Lovász, L., Prömel, H.J., Schrijver, A. (eds.) Paths, Flows, and VLSI-Layout. Springer, Berlin (1990)
Lengauer, T.: Combinatorial Algorithms for Integrated Circuit Layout. Wiley, New York (1990)
Lipski, W.: On the structure of three-layer wireable layouts. In: Preparata, F.P. (ed.) Advances in Computing Research: VLSI Theory, vol. 2, pp. 231–244. Jai Press, London (1984)
Luk, W.K.: A greedy switch-box router. Integration 3, 129–149 (1985)
Martin, A.: Packen von Steinerbäumen: Polyedrische Studien und Anwendungen. Ph.D. thesis, Technische Universität Berlin (1992)
Oxley, J.G.: Matroid Theory. Oxford University Press, Oxford (1992)
Polzin, T.: Algorithms for the Steiner problem in networks. Ph.D. thesis, Universität des Saarlandes (2003)
Prömel, H., Steger, A.: The Steiner Tree Problem. Vieweg, Wiesbaden (2002)
Raack, C., Koster, A.M.C.A., Orlowski, S., Wessäly, R.: On cut-based inequalities for capacitated network design polyhedra. Networks 57(2), 141–156 (2011)
Raghavan, S., Magnanti, T.: Network connectivity. In: Dell’Amico, M., Maffioli, F., Martello, S. (eds.) Annotated Bibliographies in Combinatorial Optimization, pp. 335–354. Wiley, Chichester (1997)
Robacker, J.T.: Min-Max theorems on shortest chains and disjunct cuts of a network. Research Memorandum RM-1660, The RAND Corporation, Santa Monica, CA (1956)
Wolsey, L.A.: An analysis of the greedy algorithm for the submodular set covering problem. Combinatorica 2(4), 385–393 (1982)
Wong, R.T.: A dual ascent approach for Steiner tree problems on a directed graph. Math. Program. 28, 271–287 (1984)
Acknowledgements
We thank an anonymous referee and the editors for helpful comments and suggestions that improved the presentation of this paper. The work of Marika Karbstein was supported by the DFG Research Center Matheon “Mathematics for key technologies”.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer-Verlag Berlin Heidelberg
About this chapter
Cite this chapter
Borndörfer, R., Hoang, ND., Karbstein, M., Koch, T., Martin, A. (2013). How Many Steiner Terminals Can You Connect in 20 Years?. In: Jünger, M., Reinelt, G. (eds) Facets of Combinatorial Optimization. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-38189-8_10
Download citation
DOI: https://doi.org/10.1007/978-3-642-38189-8_10
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-38188-1
Online ISBN: 978-3-642-38189-8
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)






 ). Right: A feasible solution with three paths (
). Right: A feasible solution with three paths ( )
)

 of optimal paths. The component reduction value N(p(i),i) for each path p(i), i=1,…,n, is distributed to the paths o∈O(i). To this purpose values υ(o,i) are computed such that υ(o,i)>0⇔o∈O(i). More precisely, in each iteration i a set
of optimal paths. The component reduction value N(p(i),i) for each path p(i), i=1,…,n, is distributed to the paths o∈O(i). To this purpose values υ(o,i) are computed such that υ(o,i)>0⇔o∈O(i). More precisely, in each iteration i a set 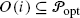 is chosen such that
is chosen such that

 are used in the bounding step. We have N(p,i)∈{0,1,2,…,|p|},
are used in the bounding step. We have N(p,i)∈{0,1,2,…,|p|}, 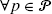 , i=1,…,n, hence, the total cost for a path
, i=1,…,n, hence, the total cost for a path  in the bounding step can be rewritten as
in the bounding step can be rewritten as












