Abstract
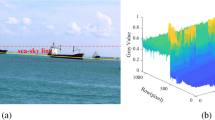
Celestial navigation is one essential means of the marine autonomous navigation, through taking photos of the Water-Sky-Line, natural horizontal plane can be provided for celestial navigation system, and the precision of Water-Sky-Line detection influences the precision of positioning. Traditional edge detection algorithms can only achieve pixel precision, as for more precise position of the Water-Sky-Line, those algorithms can’t achieve. In order to achieve sub-pixel detection, first two processes on the original image are needed, including median filtering and resample, then the pixel sketch coordinates are detected by Kirsch operator, finally an algorithm based on a curve fitting method is introduced, and sub-pixel coordinates are detected. According to experimental analyses, it is effective to half of the pixels; after eliminating outliers, the precision is about 0.5 pixels.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Celestial navigation is a day and night navigation in the world, it only receives radiation of visible light or radio waves from sun, moon, stars and other natural objects. With simple equipments and a characteristic of disguise, it isn’t easily detected and disturbed, and its positioning errors don’t accumulate over time, these are its advantages [1, 2]. Although the development of the satellite navigation system is quicker and the positioning precision is better than celestial navigation, celestial navigation is still one of the indispensable means of navigation technology, especially in the outbreak of war, the satellite signal is vulnerable to enemy’s interferences, and celestial navigation doesn’t exist such drawbacks. Furthermore, the International Maritime Organization (IMO) in “STCW78/95” Convention also explicitly provides that mariners must have the ability to use celestial bodies to determine the ship’s position [3].
Water-Sky-Line is the dividing line to distinguish between the sea and sky, and it determines the natural horizontal plane perpendicular to each other with a plumb line. Based on this characteristic, even at sea, although the instruments swing with the ship and can’t be leveled, the Water-Sky-Line can also determine the water level of ship navigation benchmark [4]. With the rapid development of digital image processing technology and the use of special camera, it allows simultaneous imaging of Water-Sky-Line with stars [5]; image processing to extract the edge of the Water-Sky-Line is a key technology of ship navigation. Traditional pixel-level edge extraction algorithms such as Sobel operator, Kirsch operator, which can only detect the pixel edge of the Water-Sky-Line. In order to achieve more precise celestial navigation at sea, a more precise edge extraction algorithm is needed, which is the sub-pixel Water-Sky-Line detection algorithm. In this paper, a sub-pixel algorithm based on a curve fitting method is introduced [6]; concrete steps are shown in Fig. 55.1.
2 Image Preprocessing
When we capture the image, due to optical system distortion, relative motion or other interferences of the weather conditions, besides the image of the original Water-Sky-Line inevitably contains the influence of noise of the waves, reefs, so the image will present low quality and it is low clear. In order to weaken the influence of the noise and improve the contrast of the sea and sky background, so the image should be preprocessed first, including median filtering and resample (Fig. 55.2).
2.1 Median Filtering
The median filter is a signal processing method based on a kind of statistical theory which can effectively suppress noise nonlinear smoother; the basic principle is replacing one point’s gray value with the point’s surrounding gray values in the digital image, which is \( med(a_{1} ,a_{2} \ldots a_{n} ). \) Take into account the Water-Sky-Line’s salt and pepper noise, 3 × 3 templates can eliminate noise and remain the edge information to some extent [7], so we use 3 × 3 templates.
The result of median filtering is shown in Fig. 55.3; the histogram is shown in Fig. 55.4.
2.2 Resample
According to the Fig. 55.4, the background gray value of the water and sky difference is obvious and concentrates in the two different gray zones. In order to enlarge the gradation differences of the sea and sky background and highlight the degree of gray-scale variation, we use the following methods: according to the gray histogram to set the minimum gradation value \( G_{Min} \) and the maximum gradation value \( G_{Max} \) for re-sampling, then extract the gray value \( G \) of every point, reassignment in accordance with the formula (55.1), the result is shown in Fig. 55.5.
3 Use Kirsch Operator to Detect Pixel Coordinates
Kirsch algorithm use eight templates to operate on every pixel, those eight templates stand for eight different detection directions [8–10], as is shown below.
Suppose the image as \( f, \) template as \( W_{k} , \) and then the gray value at point \( (x,y) \) is
The result of Kirsch operator is shown in Fig. 55.6.
4 Sub-Pixel Algorithm Based on Curve Fitting
4.1 The Gray Value of the Edge
The edge of Water-Sky-Line is step edge, gray value of the step edge is shown in Fig. 55.7a, the equal gray value on both sides respectively symbolize the background and the object, of the gradient portion of the intermediate gray value of the edge is required to detect. Due to the convolution role of optical components and optical diffraction effects, object space’s drastic changes in gray value are gradient changes in the form of optical imaging. The edge difference is shown in Fig. 55.7b, the edge’s differential value is maximum, which is the principle of classical edge extraction. According to the central limit theorem, the edge of the gray value change should be exact position of the Gaussian distribution; the curve in Fig. 55.7b is the sampled value of the Gaussian curve, corresponding to the apex of the curve is the edge’s precise point.
4.2 The Deductive Process
The gray value should obey Gaussian distribution
The difference of the gray value takes logarithm for quadratic curve
So according to the difference of the gray value to fit parabola coefficient
Just taking three pixels’ gray values is enough to solve parabolic coefficient. This can directly acquire vertex position, and has a small amount of calculation, but it doesn’t take advantage of the edge’s information. As for Water-Sky-Line edge, the edge of the gray values’ change may be slow, therefore we can extend to the edge more pixels on both sides, acquire more accurate parabolic coefficient and vertex position by the least square adjustment, five pixels (for example, on both sides and then upward selection is positive, the other side is negative) is suggested in this article, the output gradation value of each pixel can be obtained as follows:
Substitute the gray values of 11 pixels
Use parameter adjustment, error equation is
Solution
Sub-pixel position of the edge is the vertex position
Because the image inevitably contains noise, so that changes in the grayscale value don’t meet the above rules, therefore, there should be two judgments to make.
First, if the difference value is less than or equal to zero, then the difference value’s logarithm of this point is given as 0.
Second, if the absolute value of the sub-pixel correction value is bigger than 5, then the corrected value is not credible, compulsory to be assigned 0.
The result of curve fitting is shown in Fig. 55.8.
According to the result of Fig. 55.8 and Table 55.1, we can conclude that in the original image of 4,288 pixels, as for the Fig. 55.8a, 2,142 pixels succeed in detecting sub-pixel coordinates; then filter 102 outliers and use the quadratic polynomial to fit the sub-pixel edge, and calculate the standard deviation. Analyze the edge without outliers, the precision is 0.5140 pixels. Then about the Fig. 55.8b, 2,156 pixels succeed in detecting sub-pixel coordinates, and the precision is 0.5020 pixels.
5 Conclusion
With the continuous improvement of the accuracy required by maritime celestial navigation, the original pixel-level Water-Sky-line extraction technologies can’t meet the requirements of high-precision positioning and therefore more precise Water-Sky-line edge detection algorithm is needed, which is sub-pixel detection. First this paper describes two steps to extract the pixel-level Water-Sky-line edge from original image, including median filtering, image resample; and then use Kirsch operator to extract coordinates of the pixel level. Finally a curve fitting method is derived, least squares adjustment to solve unknown parameters is used, choose five pixel points near the former pixel coordinates, calculate the sub-pixel coordinates, and realize correction about half of the edge pixels, according to experimental analyses, the precision is about 0.5 pixels, it’s meaningful to realize more precise marine celestial navigation.
References
Bida J, Huilan F (1998) How to develop of astronomical navigation across to the 21st century. Navigation Technology Analecta of the Turn of Century. Chinese Institute of Electronics Navigation Branch, Xi’an, pp 30–38
Anguo W (2007) Modern celestial navigation and its key technologies. J Electron 12:2347–2348
Wencai H, Guanghua Huang L (2002) Research on marine electronics sextant angle sensor system. J Shanghai Maritime Univ 23(3):17–20
Zhao N, Weiting L, Zhiyu Z (2005) Research on digital image processing based on water-sky-line detection. J East China Shipbuilding Inst (Nat Sci) 19(1):54–58
Yulei Y (2012) Research on fish-eye camera stellar calibration technology. Zhengzhou Institute of Surveying and Mapping, p 6
Zhonghai H, Wang B, Yibai L, Lincai C (2004) Subpixel algorithm using a cueve fitting method. Chin J Sci Instrum 24(2):195–197
Kirsch RA (1974) Computer determination of the constituent structure of biological images. Computer boned Res 4:315–318
He B, Ma T, Wang YJ, Honglian Z (2001) VC++ digital image processing. People’s Post and Telecommunication Publishing House, Beijing, pp 459–466
Duan R, Li Q, Li Y (2005) Studies review on edge detecting algorithm of image. J Opt Technol 31(3):415–419
Li J, Tang X, Jiang Y (2007) Research on the comparison of several edge detecting algorithm. J Inf Technol 9:106–108
Acknowledgments
This study is funded by the National Natural Science Fund (41174025, 41174026), Space Navigation and Timing Technology Key Laboratory Open Fund in Shanghai (0901) and Chinese Academy of Sciences Precise Navigation Position and Timing Technology Key Laboratory Open Fund (2012PNTT07).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Li, L., Li, C., Zheng, Y., Zhang, C. (2013). Sub-Pixel Water-Sky-Line Detection Based on a Curve Fitting Method. In: Sun, J., Jiao, W., Wu, H., Shi, C. (eds) China Satellite Navigation Conference (CSNC) 2013 Proceedings. Lecture Notes in Electrical Engineering, vol 245. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-37407-4_55
Download citation
DOI: https://doi.org/10.1007/978-3-642-37407-4_55
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-37406-7
Online ISBN: 978-3-642-37407-4
eBook Packages: EngineeringEngineering (R0)