Keywords

1 Introduction

The new generation of GNSSs all transmit three or more carriers, such as the modernized GPS introduce the L5 signal, besides the previous L1 and L2 signals, the ongoing European Galileo system is designed to transmit L1, E6, E5B, E5A four signals, and the in-operation Chinese COMPASS/Beidou-2 navigation system is transmitting E2, E6, E5B three signals.

Multi-frequency carriers not only introduce more observables, but also form more linear combinations between the observables, which contribute to the AR. The TCAR [1, 2] and CIR [3, 4] are the typical three-carrier ambiguity resolution methods, which are equivalent and both the geometry-free bootstrapping method [5]. TCAR and CIR have the same principle, i.e. first initial with the extra wide-lane (EWL) ambiguity resolution, then resolve the wide-lane (WL) ambiguity based on the unambiguous EWL observable, at last resolve the narrow-lane (NL) ambiguity using the unambiguous EWL and WL observables. Although TCAR/CIR can resolve the EWL ambiguity with high accuracy and efficience, the resolution of WL and NL ambiguity would be biased by the residual ionospheric delay for the shorter wavelengths of WL and NL observables. To dealt with the residual ionospheric delay, Feng Y. proposed a geometry-based TCAR method using the ionosphere-reduced virtual signals [6]. This method firstly generates the virtual observables from linear combinations of the original observables which is biased by a minimum ionospheric error, and then resolve the ambiguity using geometry-based model and searching algorithm. Although the residual ionospheric delay is reduced, it becomes larger when the baseline length increases and the spacial correlation decreases. Thus this method is suit for the short baseline only. Meanwhile, the searching algorithm could reduce the efficience.

The previous three-carrier ambiguity resolution researches focus on the theory and simulation, for there are not enough GNSS satellites transmitting three (or more) signals. The Chinese COMPASS/BeiDou-2 system consists of 5 GEO satellites, 5 IGSO satellites and 4 MEO satellites, and there are more than 10 satellites can transmit B1, B3 and B2 signals, which can be used to form a extra wide-lane and two wide-lane observables. Table 37.1 lists the original and (extra) wide-lane signals of COMPASS/BeiDou-2 satellites. The work in this contribution is based on the COMPASS three-frequency observables.

Table 37.1 Original and (extra) wide-lane signals of COMPASS satellites
Full size table

2 Three-Carrier Ambiguity Resolution

TCAR and CIR are the typical methods for three-carrier ambiguity resolution. We first introduced and analyzed these methods, and then introduced some modifications to accommodate them to the middle and long baseline. In the following introduction, the carrier and code observables are double-differenced in default (omitting the \( \Updelta \nabla \) operator for simplicity), and in meter. The tokens \( f_{1} \), \( f_{2} \) and \( f_{3} \) (\( f_{1} > f_{2} > f_{3} \)) represent the frequencies of B1, B3 and B2 signals, \( L_{1} \), \( L_{2} \) and \( L_{3} \) represent the carrier phase observables, and \( P_{1} \), \( P_{2} \) and \( P_{3} \) represent the code observables, respectively. In the analysis, there is an assumption that the fixed ambiguity in each step is unbiased, which is used as a true value in the following step.

2.1 TCAR/CIR Methods

TCAR/CIR methods firstly generate the extra wide-lane and wide-line observables, which are sorted by the wavelength, then initial with the M-W combination [7, 8] to determine the EWL ambiguity, and then step to the shorter WL ambiguity resolution, and at last the NL ambiguities are resolved. In this procedure, the later step must use the result of the former step.

The double-differenced phase and code observables can be represented as

$$ \left\{ \begin{aligned} L_{i} & = \rho^{\prime} - \eta_{i} I_{1} - \lambda_{i} N_{i} + \varepsilon_{L} \\ P_{i} & = \rho^{\prime} + \eta_{i} I_{1} + \varepsilon_{P} \\ \end{aligned} \right.,\begin{array}{*{20}c} {} \\ \end{array} \eta_{i} = \frac{{f_{1}^{2} }}{{f_{i}^{2} }},\begin{array}{*{20}c} {} \\ \end{array} i = 1,2,3 $$

where \( L_{i} \) and \( P_{i} \) are the double-differenced phase and code observables, \( \rho^{\prime} \) contains the double-differenced geometric distance and non-dispersive errors, \( I_{1} \) is the double-differenced ionospheric delay in \( L_{1} \) and \( P_{1} \), \( \eta_{i} \) is the scale factor of residual ionospheric delay in \( L_{1} \) and \( P_{i} \) with regard to \( L_{1} \) and \( P_{1} \), \( \lambda_{i} \) and \( N_{i} \) are the wavelength and ambiguity of \( L_{i} \), \( \varepsilon_{L} \) and \( \varepsilon_{P} \) are noise in carrier and code observables with the assumption \( \sigma_{{L_{1} }} = \sigma_{{L_{2} }} = \sigma_{{L_{3} }} = \sigma_{L} \) and \( \sigma_{{P_{1} }} = \sigma_{{P_{2} }} = \sigma_{{P_{3} }} = \sigma_{P} \). For the COMPASS/BeiDou-2 system \( \sigma_{L} = 0.005\,{\text{m}} \), \( \sigma_{P} = 0.8\,{\text{m}} \) [9].

There is combination between any two observables:

$$ \left\{ \begin{aligned} L_{ab} & = \frac{{f_{a} L_{a} - f_{b} L_{b} }}{{f_{a} - f_{b} }} = \rho^{\prime} + \eta_{ab} I_{1} - \lambda_{ab} N_{ab} + \varepsilon_{{L_{ab} }} \\ P_{ab} & = \frac{{f_{a} P_{a} + f_{b} P_{b} }}{{f_{a} + f_{b} }} = \rho^{\prime} + \eta_{ab} I_{1} + \varepsilon_{{P_{ab} }} \\ \end{aligned} \right.,\;\eta_{ab} = \frac{{f_{1}^{2} }}{{f_{a} f_{b} }},\;a,b = 1,2,3\;and\;a \ne b $$

where \( \lambda_{ab} \), \( N_{ab} \) and \( \eta_{ab} \) denote the wavelength, ambiguity and residual ionospheric scalar factor of EWL and WL observables \( L_{ab} \). Then the TCAR/CIR express as the following steps:

1. Resolve the EWL ambiguity \( \hat{N}_{23} \)

$$ \begin{aligned} N_{23} & = {{(P_{23} - L_{23} + \varepsilon_{23} )} \mathord{\left/ {\vphantom {{(P_{23} - L_{23} + \varepsilon_{23} )} {\lambda_{23} }}} \right. \kern-0pt} {\lambda_{23} }} \\ \sigma_{23} & = {{\sigma_{P} \sqrt {f_{2}^{2} + f_{3}^{2} } } \mathord{\left/ {\vphantom {{\sigma_{P} \sqrt {f_{2}^{2} + f_{3}^{2} } } {(f_{2} + f_{3} )}}} \right. \kern-0pt} {(f_{2} + f_{3} )}} \\ \hat{N}_{23} & = Int(N_{23} ) \\ \end{aligned} $$

2. Resolve the WL ambiguity \( \hat{N}_{12} \) and \( \hat{N}_{13} \)

$$ \begin{aligned} & N_{12} = {{\left[ {L{}_{23} + \lambda_{23} \hat{N}_{23} - L_{12} - \left( {\eta_{23} - \eta_{12} } \right)I_{1} + \varepsilon_{12} } \right]} \mathord{\left/ {\vphantom {{\left[ {L{}_{23} + \lambda_{23} \hat{N}_{23} - L_{12} - \left( {\eta_{23} - \eta_{12} } \right)I_{1} + \varepsilon_{12} } \right]} {\lambda_{12} }}} \right. \kern-0pt} {\lambda_{12} }} \\ & \eta_{23} - \eta_{12} = \frac{{f_{1} (f_{3} - f_{1} )}}{{f_{2} f_{3} }},\sigma_{12} = \sqrt {\sigma_{{L_{23} }}^{2} + \sigma_{{L_{12} }}^{2} } \\ & \hat{N}_{12} = Int(N_{12} ),\;\hat{N}_{13} = \hat{N}_{12} + \hat{N}_{23} \\ \end{aligned} $$

3. Resolve the NL ambiguity \( \hat{N}_{1} \), \( \hat{N}_{2} \) and \( \hat{N}_{3} \)

$$ \begin{aligned} & N_{3} = {{\left[ {L{}_{13} + \lambda_{13} \hat{N}_{13} - L_{3} - (\eta_{13} + \eta_{3} )I_{1} + \varepsilon_{3} } \right]} \mathord{\left/ {\vphantom {{\left[ {L{}_{13} + \lambda_{13} \hat{N}_{13} - L_{3} - (\eta_{13} + \eta_{3} )I_{1} + \varepsilon_{3} } \right]} {\lambda_{3} }}} \right. \kern-0pt} {\lambda_{3} }} \\ & \eta_{13} + \eta_{3} = - \frac{{f_{1} (f_{1} + f_{3} )}}{{f_{3}^{2} }},\;\sigma_{3} = \sqrt {\sigma_{{L_{13} }}^{2} + \sigma_{{L_{3} }}^{2} } \\ & \hat{N}_{3} = Int(N_{3} ),\;\hat{N}_{2} = \hat{N}_{23} + \hat{N}_{3} ,\;\hat{N}_{1} = \hat{N}_{13} + \hat{N}_{3} \\ \end{aligned} $$

where \( N_{ab} \) and \( N_{i} \) are the float ambiguities, \( \varepsilon_{ab} \) and \( \varepsilon_{i} \) denote the noises of ambiguities \( N_{ab} \) and \( N_{i} \), whose variances are \( \sigma_{ab} \) and \( \sigma_{i} \), \( \hat{N}_{ab} \) and \( \hat{N}_{i} \) are the fixed ambiguities.

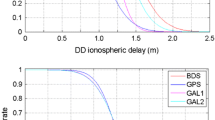
Of the three steps, the EWL ambiguity \( \hat{N}_{23} \) in step (1) is affected by the measurement noise, while the WL ambiguity \( \hat{N}_{12} \) in step (2) and NL ambiguity \( \hat{N}_{3} \) in step (3) are biased by the residual ionospheric error in addition to the measurement noise. It is obvious that TCAR/CIR methods ignore the residual ionospheric error, which limits their application to short baseline. As the baseline length increases, the spacial correlation of ionospheric error decreases and there is larger residual ionospheric delay. Figure 37.1 shows the residual ionospheric delay in Changsha-Guangzhou baseline (563 km) for different satellite pairs. The blue line represent the residual ionospheric delay derived from the unambiguous WL observables \( L_{12} \) and \( L_{13} \), and the red line represent the residual ionospheric delay derived from the unambiguous original observables \( L_{1} \) and \( L_{2} \). As it is shown, the residual ionospheric delay is a few meters and varies sharply, which makes the ambiguity resolution more difficult.

Fig. 37.1
figure 1

The residual ionospheric delay in Changsha-Guangzhou 563 km baseline for satellite pairs C01-C04 and C01-C10

Full size image

Table 37.2 lists the errors in the above procedures. We assume the variance of COMPASS code and phase observables are 0.8 and 0.005 m respectively [9], and the residual ionospheric error in \( L_{1} \) and \( P_{1} \) is 1.5 m. As it is showed in Table 37.2, there is large error in the TCAR/CIR method, i.e. more than 0.5 cycles in step (2) and about 18 cycles in step (3), which hamper the ambiguity resolution.

Table 37.2 Errors in the EWL, WL and NL ambiguities resolution using TCAR/CIR method
Full size table

2.2 Modified TCAR/CIR Method

To deal with the residual ionospheric delay in middle and long baseline, we modified the step (2) and (3) of TCAR/CIR, eliminating the residual ionospheric delay. The key point of the modification is forming the linear combination between code observables or unambiguous EWL and WL observables. The linear combination coefficients should be subject to the conditions: minimal noise, unchanged geometry scale and identical ionospheric delay with that of the observable to be resolved the ambiguity.

Using \( P_{1} \), \( P_{3} \) and the unambiguous \( L_{23} \) in step (1), we can get the combined observable as follow:

$$ \overset{\hbox{$\smash{\scriptscriptstyle\frown}$}}{L}_{12} = \alpha \cdot P_{1} + \beta \cdot P_{2} + \gamma \cdot (L_{23} + \lambda_{23} \hat{N}_{23} ) $$

where the coefficients \( \alpha \), \( \beta \) and \( \gamma \) subject to:

$$ \left\{ \begin{aligned} & \alpha + \beta + \gamma = 1 \\ & \alpha \eta_{1} + \beta \eta_{2} + \gamma \eta_{23} = \eta_{12} \\ & (\alpha^{2} + \beta^{2} )\sigma_{P}^{2} + \gamma^{2} \sigma_{{L_{23} }}^{2} = \hbox{min} \\ \end{aligned} \right. $$

Thus we get \( \alpha = 0. 5 9 9 \), \( \beta = - 0.082 \) and \( \gamma = 0.483 \) for the current COMPASS signals. Then the step (2) can be modified as:

$$ \begin{aligned} N_{12} & = {{\left[ {\overset{\hbox{$\smash{\scriptscriptstyle\frown}$}}{L} {}_{12} - L_{12} + \varepsilon_{12} } \right]} \mathord{\left/ {\vphantom {{\left[ {\overset{\hbox{$\smash{\scriptscriptstyle\frown}$}}{L} {}_{12} - L_{12} + \varepsilon_{12} } \right]} {\lambda_{12} }}} \right. \kern-0pt} {\lambda_{12} }} \\ \sigma_{12} & = \sqrt {\sigma_{{\overset{\hbox{$\smash{\scriptscriptstyle\frown}$}}{L}_{12} }}^{2} + \sigma_{{L_{12} }}^{2} } \\ \hat{N}_{12} & = Int(N_{12} ),\;\hat{N}_{13} = \hat{N}_{12} + \hat{N}_{23} \\ \end{aligned} $$

Similarly, using the unambiguous \( L_{23} \) in step (1), \( L_{12} \) and \( L_{13} \) above, we can get the combined observable as follow:

$$ \overset{\hbox{$\smash{\scriptscriptstyle\frown}$}}{L}_{3} = \alpha \cdot (L_{23} + \lambda_{23} \hat{N}_{23} ) + \beta \cdot (L_{12} + \lambda_{12} \hat{N}_{12} ) + \gamma \cdot (L_{13} + \lambda_{13} \hat{N}_{13} ) $$

where \( \alpha \), \( \beta \) and \( \gamma \) have the similar restriction:

$$ \left\{ \begin{aligned} & \alpha + \beta + \gamma = 1 \\ & \alpha \eta_{23} + \beta \eta_{12} + \gamma \eta_{13} = - \eta_{3} \\ & \alpha^{2} \sigma_{{L_{23} }}^{2} + \beta^{2} \sigma_{{L_{12} }}^{2} + \gamma^{2} \sigma_{{L_{13} }}^{2} = \hbox{min} \\ \end{aligned} \right. $$

Thus, we get \( \alpha = - 8. 6 6 1 \), \( \beta = 6.111 \) and \( \gamma = 3.550 \). The step (3) can be modified as:

$$ \begin{aligned} N_{3} & = {{\left[ {\overset{\hbox{$\smash{\scriptscriptstyle\frown}$}}{L} {}_{3} - L_{3} + \varepsilon_{3} } \right]} \mathord{\left/ {\vphantom {{\left[ {\overset{\hbox{$\smash{\scriptscriptstyle\frown}$}}{L} {}_{3} - L_{3} + \varepsilon_{3} } \right]} {\lambda_{3} }}} \right. \kern-0pt} {\lambda_{3} }} \\ \sigma_{3} & = \sqrt {\sigma_{{\overset{\hbox{$\smash{\scriptscriptstyle\frown}$}}{L}_{3} }}^{2} + \sigma_{{L_{3} }}^{2} } \\ \hat{N}_{3} & = Int(N_{3} ),\;\hat{N}_{2} = \hat{N}_{23} + \hat{N}_{3} ,\;\hat{N}_{1} = \hat{N}_{13} + \hat{N}_{3} \\ \end{aligned} $$

The above modifications eliminate the residual ionospheric delay, geometry distance and the non-dispersive error. As a result, there is only the random noise, which can be reduced by averaging multiple observables, though it is magnified by the modification.

Table 37.3 list the errors in AR procedure using modified TCAR/CIR method.

Table 37.3 Errors in the EWL, WL and NL ambiguities resolution using modified TCAR/CIR method
Full size table

We can find the modified TCAR/CIR method reduces the errors in step (2) slightly from 0.547 to 0.478, and that in step (3) sharply form 17.913 to 5.062.

3 Result

Based on the synchronous COMPASS observables in Changsha-Guangzhou (563 km) baseline from 8:45 (UTC), Nov 23, 2012 to 21:15 (UTC), Nov 23, 2012, we validated the modified TCAR/CIR method.

Adopting the modified TCAR/CIR method proposed by this contribution, we resolved the EWL, WL and NL ambiguities. The ambiguity residuals (the difference between each float ambiguities and the fixed ambiguity) are display in Fig. 37.2. The ambiguity residuals of EWL are less than 0.5 cycle, which means the EWL ambiguity can be resolved at a single epoch. The WL ambiguity residuals are less than 1 cycle, so the WL ambiguity can be resolved by averaging a few epochs. As the NL ambiguity residuals exceed to a few cycles, the NL ambiguity should be resolved by averaging much more observables in a long period.

Fig. 37.2
figure 2

EWL, WL and NL ambiguity residuals in Changsha-Guangzhou 563 km baseline for different satellite pairs C01-C04 and C01-C10

Full size image

4 Conclusion and Discussion

The TCAR and CIR methods both ignore the double-differenced residual ionospheric delay, which restricts their application to short baseline (less than 10 km). For the middle and long baseline, residual ionospheric delay could introduce large systematic error, which biases the ambiguity resolution. To deal with this problem, this contribution modified the TCAR/CIR method, resulting in a ionosphere- and geometry-free three-carrier ambiguity resolution method. The modified TCAR/CIR method reduces the errors in step (2) slightly and that in step (3) sharply. For the 563 km long baseline, the proposed method can resolve the EWL ambiguity at a single epoch, and the WL ambiguity by averaging a few observables, while the NL should be resolved by averaging much more observables in a long period.