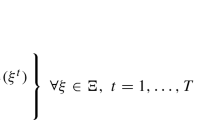The Bayesian Search Game

Abstract

The aim of this chapter is to draw links between (1) No Free Lunch (NFL) theorems which, interpreted inversely, lay the foundation of how to design search heuristics that exploit prior knowledge about the function, (2) partially observable Markov decision processes (POMDP) and their approach to the problem of sequentially and optimally choosing search points, and (3) the use of Gaussian processes as a representation of belief, i.e., knowledge about the problem. On the one hand, this joint discussion of NFL, POMDPs and Gaussian processes will give a broader view on the problem of search heuristics. On the other hand this will naturally introduce us to efficient global optimization algorithms that are well known in operations research and geology (Gutmann, J Glob Optim 19:201–227, 2001; Jones et al., J Glob Optim 13:455–492, 1998; Jones, J Glob Optim 21:345–383, 2001) and which, in our view, naturally arise from a discussion of NFL and POMDPs.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

7.1 Introduction

We consider the problem of optimization, where an objective function $f:\ X \rightarrow \mathbb{R}$ is fixed but unknown and an algorithm has to find points in the domain X which maximize f(x). In this paper we take the view that search is a problem of navigating through belief space. With “belief” we denote our current knowledge about the objective function represented in terms of a probability distribution over problems (functions). In principle, Bayes’ rule tells us how to update this belief state when we explore a new search point and thereby gain new knowledge about the objective function. In that sense, repeatedly querying search points generates a trajectory through belief space—and efficient search means to “navigate” through belief space in a goal-directed manner. For instance, navigating with the goal to gain information about the objective function, or with the goal to reach a belief that implies certainty about the location of the optimum of the objective function.

In this view, the problem of optimization can be framed as a partially observable Markov decision process problem just in the same way as standard navigation problems. The POMDP formulation naturally ties in with an alternative formulation of the No Free Lunch (NFL) theorem: In the next section we present such a formulation which is equivalent to the one in [5] but, instead of relying on classical notions like “closed under permutation”, is formulated in terms of the structure of the function prior P(f). In a sequential search process, this prior is updated to become a new posterior P(f | observations) after each exploration of a search point and observation of the corresponding function value. This posterior is the belief state in the corresponding POMDPs. Therefore, the POMDP framework directly implies the optimal policy in the case that NFL conditions do not hold.

Clearly, for most relevant cases the optimal search policy is infeasible to compute. However, when making strong assumptions about the prior belief—that is, our initial knowledge about the objective function—and approximating optimal planning with optimal 1- or 2-step look-ahead planning, then such algorithms become tractable. An example is search in continuous spaces when the prior belief is a Gaussian process. The resulting approximate optimal search algorithms are of high practical relevance and have a long history in operations research and geology (e.g., under the name of kriging) [2, 6, 7].

The material covered in this chapter is complementary to the survey on (approximately) optimal search algorithms in Chap. 6. In particular, Chap. 6 gives an explicit introduction to kriging, while the focus of this chapter is on the alternative formulation of NFL, how this ties in with the POMDP approach to optimal search policies, and a basic demonstration of a truly planning (2-step look-ahead) search policy in the case of Gaussian processes.

In the following section we present an alternative formulation of a general NFL result that is equivalent to the one presented in [5]. Section 7.3 briefly introduces the most relevant notions of POMDPs. Section 7.4 then draws the relation between POMDPs and optimization. We interpret optimization as a “Bayesian search game” and discuss the belief update when we acquire new observations during search. In Sect. 7.5 we define some simple heuristic policies to choose new search points based on the current belief, including one that would be optimal for a two-step horizon problem. Finally, in Sect. 7.6 we discuss the use of Gaussian processes as belief representation, as was done before in the context of kriging [2, 6, 7], and illustrate the resulting optimization algorithms on some examples. The reader may experience the idea of search using Gaussian processes by literally playing the Bayesian search game (competing with a Gaussian processes-based search policy), using the implementation given at the author’s webpage.¹

7.2 Yet Another Formulation of NFL

Let us begin with a simple formulation of No Free Lunch (NFL) [16]. Roughly speaking, NFL theorems specify conditions under which “informed search”—that is, picking search points better than random—is impossible. These issues are intimately linked to the conditions under which generalization in learning theory is possible—which we discuss briefly below. The point in specifying such conditions is that (1) one should never try to write an efficient search algorithm when NFL conditions hold, and (2) the NFL theorems should give a hint on how to design a search algorithm when these conditions do not hold.

There are many alternative formulations of NFL theorems; a standard one for optimization is [16]. In [5] we presented a general formulation which specifies conditions on the probability distribution over the objective function. The formulation we present here is equivalent to the one in [5] but more naturally leads to the notion of beliefs, POMDPs and Bayesian search. The specific formulation and proof we give here are, to our knowledge, novel—but only a minor variant of the existing formulations; see [5] for a more extensive discussion of existing NFL formulations.

Let X be a finite or continuous search space. We call elements in X sites. Assume a search algorithm is applied on a function f:  X → Y sampled from P(f). We write f _x for the function value of f at site x. A non-revisiting algorithm iteratively samples a new site x _t and gets in return an observation $y_{t} = f_{x_{t}}$. We formalize an algorithm $\mathcal{A}$ as a search distribution $P(x_{t}\,\vert \,x_{0:t-1},y_{0:t-1};\mathcal{A})$ conditioned on previous samples and their observed values, and the initial search distribution $P(x_{0};\mathcal{A})$, with zero probability of revisitation, $x_{t} \in x_{0:t-1} \Rightarrow P(x_{t}\,\vert \,x_{0:t-1},y_{0:t-1};\mathcal{A}) = 0$. All this defines a stochastic process of the search algorithm interacting with the objective function, as summarized by the joint distribution

$$\displaystyle\begin{array}{rcl} & & P(f,x_{0:T},y_{0:T};\mathcal{A}) \\ & & = P(f)\ P(y_{0}\,\vert \,x_{0},f)\ P(x_{0};\mathcal{A})\ \prod _{t=1}^{T}P(y_{ t}\,\vert \,x_{t},f)\ P(x_{t}\,\vert \,x_{0:t-1},y_{0:t-1};\mathcal{A}).{}\end{array}$$

(7.1)

Theorem 7.1.

In this setting, a basic NFL theorem reads

$$\displaystyle\begin{array}{rcl} & & \exists h: Y \rightarrow \mathbb{R}\ \ \text{s.t.} \\ & & \forall \text{ finite subsets }\{x_{1},..,x_{K}\} \subset X:\ P(f_{x_{1}},..,f_{x_{K}}) =\prod _{ k=1}^{K}h(f_{ x_{k}}){}\end{array}$$

(7.2)

$$\displaystyle\begin{array}{rcl} & & \qquad \Longleftrightarrow\qquad \forall _{\mathcal{A}},\forall _{T}:\ P(y_{0:T};\mathcal{A}) =\prod _{ i=0}^{T}h(y_{ i})\quad \mbox{ (independent of $\mathcal{A}$) }{}\end{array}$$

(7.3)

The condition (7.2) on the left simply says that P(f) factorizes identically,² which means that every f _x is mutually independent from every other f _x′—nothing can be learnt about f _x′ from f _x . The “for-all-finite-subsets” formulation we used is typical for continuous X and in analogy to the definition of Gaussian processes (see below). Additionally, the condition (7.2) says that every marginal distribution $h(f_{x_{k}})$ (we called $h: Y \rightarrow \mathbb{R}$ histogram of function values in [5]) is identical, independent of the site x _k . In other terms, the function values are identically independently distributed (independently refers to different sites x). Hence, no algorithm can predict the observation at a new site based on previous samples better than with a constant marginal that ignores previous samples and the location of the site. The inevitable result is that the function values an algorithm observes are a random sequence independent of the algorithm itself.

Proof.

We first show Eq. (7.2) ⇒ Eq. (7.3): Up to some total time t we have the random variables f, x _0: t , y _0: t . Their joint is given by Eq. (7.1). Here, $P(y_{t}\,\vert \,x_{t},f)$ is the probability of observing a value y _t when sampling at point x _t , given the function is f. This could account for noisy function evaluations, but for simplicity here we simply assume $P(y_{t}\,\vert \,x_{t},f) =\delta _{y_{t},f_{x_{ t}}}$. Given this joint, we find

$$\displaystyle\begin{array}{rcl} & & P(y_{t}\,\vert \,x_{0:t-1},y_{0:t-1};\mathcal{A}) \\ & =& \sum _{x_{t}\in X}\Big[\sum _{f}P(y_{t}\,\vert \,x_{t},f)\ P(f\,\vert \,x_{0:t-1},y_{0:t-1})\Big]\ P(x_{t}\,\vert \,x_{0:t-1},y_{0:t-1};\mathcal{A}) \\ & =& \sum _{x_{t}\in X}P(f_{x_{t}}\! =\! y_{t}\,\vert \,x_{0:t-1},y_{0:t-1})\ P(x_{t}\,\vert \,x_{0:t-1},y_{0:t-1};\mathcal{A}) \\ & =& \sum _{x_{t}\in X}h(y_{t})\ P(x_{t}\,\vert \,x_{0:t-1},y_{0:t-1};\mathcal{A}) = h(y_{t}). {}\end{array}$$

(7.4)

The last line used the fact that the algorithm is non-revisiting and that P(f) factorized, such that $P(f_{x_{t}}\! =\! y_{t}\,\vert \,x_{0:t-1},y_{0:t-1}) = P(f_{x_{t}}\! =\! y_{t}) = h(y_{t})$. (For X continuous we need to replace summations by integrals.) This means that a newly sampled function value y _t is independent of the algorithm $\mathcal{A}$ and of the history $x_{0:t-1},y_{0:t-1}$. By induction over t = 0, 1, … we get the right-hand side (RHS), Eq. (7.3).

We now show the inverse Eq. (7.2) ⇐ Eq. (7.3): To show ¬(7.2) ⇒ ¬(7.3) let $\{x_{1},..,x_{K}\}$ for which $P(f_{x_{1}},..,f_{x_{K}})$ does not identically factorize. We distinguish two cases: (i) In the case that the marginals are not identical (h depends on the site) it is clear that two algorithms that pick two different sites (with different marginals h) as the first search point will have a different P(y ₀)—and the RHS (7.3) is violated. (ii) If all marginals $P(f_{x_{1}}) = h(f_{x_{1}})$ are the same but $P(f_{x_{1}},..,f_{x_{K}})$ does not factorize, then at least one conditional $P(f_{x_{1}}\,\vert \,f_{x_{2}},..,f_{x_{K}})\not =h(f_{x_{1}})$ is different from the marginal. Two algorithms that deterministically first pick $x_{2},..,x_{K}$ and then, depending on the conditional $P(f_{x_{1}}\,\vert \,f_{x_{2}},..,f_{x_{K}})$ will pick either x ₁ or an outside point in $X\setminus \{x_{1},..,x_{K}\}$ (here we need the real subset $\{x_{1},..,x_{K}\} \subset X$ rather than the ⊆ X) will have a different P(y _K ) than random search—and the RHS (7.3) is violated.

To link to more traditional presentations: The left-hand side, LHS (7.2), is related to sets of functions which are closed under permutation. In particular, associating equal probability to functions in a set closed under permutation leads to independent and identically distributed function values at different points. The LHS (7.2) is equivalent to the so-called strong NFL conditions in [5]. Further, one usually assumes some criterion $\mathcal{C}$ that evaluates the quality of an algorithm $\mathcal{A}$ by mapping the sequence y _0: t of observed values to a real number. Obviously, if P(y _0: t ) is independent of the algorithm, then so is $\sum _{y_{0:t}}P(y_{0:t})\ C(y_{0:t})$. In traditional terms this means, averaged over all functions (in terms of P(f)), the quality of an algorithm is independent of the algorithm. For instance, every algorithm is as good as random search.

A note on continuous spaces: The LHS condition (7.2) is interesting in the case of continuous search spaces, which touches deeply into the notion of well-defined measures over functions in continuous space. Naively, the LHS condition (7.2) describes something like a Gaussian process with a zero covariance function, C(x, x′) = 0 for any x ≠ x′. At first sight there seems to be no problem in defining such a distribution over functions also in continuous space, in particular because the definition of a Gaussian process only makes reference to function value distributions over finite subsets of the domain. However, [1] make the point that this “zero-covariance” Gaussian process is actually not a proper Lebesgue measure over the space of function. This means any P(f) which fulfils the LHS (7.2) is not a Lebesgue measure. Inversely, if we assume that P(f) is a Lebesgue measure—and [1] imply that this is the only sensible definition of measure over functions in continuous space—then it follows that NFL does not hold in continuous domains.

A note on generalization in statistical learning theory: The NFL theorem, as we formulated it, is closely related to the issue of generalization: Can the algorithm generalize knowledge gained from sites x _1: T−1 to a new site? NFL says that this is not possible without assumptions on the underlying function. On the surface this seems to contradict the classical foundation of statistical learning theory, stating that generalization to “new” data is possible without making assumptions about the underlying function. The origin of this seeming contradiction is simply the use of the word “new data” in both contexts. The prototypical setup in statistical learning theory considers a joint distribution P(X, Y ) = P(Y | X) P(X) from which data $\{(x_{i},y_{i})\}_{i=0}^{N}$ was sampled i.i.d. In that context, a “new” data point x ^∗ is one that is equally sampled from the same source P(X) as the previous data—without ruling out revisitation of the same site. Statements on generalization roughly state that, in the limit of large N, generalization to new data is possible. If the domain X is finite, the limit of large N implies that new data points are likely to coincide with previously observed sites and the possibility of generalization is obvious. If the domain is continuous, the chance to revisit exactly the same site is zero and it seems that revisitation is not an issue and NFL holds—however, as we discussed in the previous section, w.r.t. standard Lebesgue measures over functions, NFL does not hold in continuous spaces.

7.3 Some Background on POMDPs

Our formulation of NFL states that, assuming a fully factored distribution over functions, any search algorithm will have the same expected performance. Inversely this implies that when we assume a non-factored distribution over functions—which we call function prior—then the algorithm has at least a chance to exploit previous observations $x_{0:t},y_{0:t}$ to decide “intelligently” (better than random search) about the next sample x _t+1.

Partial observable Markov decision processes (POMDP) give us a clear description of how an optimal (fully Bayes-rational) algorithm would choose the next sample point based on previous observations. The point in referring to POMDPs will not be that we will in practice be able to design fully Bayes-optimal search algorithms—this is in any realistic case computationally infeasible. However, the POMDP framework provides us with two important aspects: First the notion of a belief, which can be shown to subsume all the information from the history of observations $x_{0:t},y_{0:t}$ that is necessary to make optimal decisions. And second, the POMDP framework provides us with promising approximate decision heuristics, for instance, iteratively using the optimal two-step look-ahead strategy as an approximation to the optimal T-step look-ahead for a problem of horizon T, as is discussed in detail in Sect. 7.5.

We briefly introduce POMDPs and the notion of beliefs in POMDPs here. For more details see [9]. A POMDP is a stochastic model of the interaction of an agent with an environment where the agent does not fully observe the state s _t of the environment but only has access to (“partial”) observations y _t . For every time step t the environment is in state s _t , the agent chooses an action a _t+1, the world transitions into a new state according to a conditional probability $P(s_{t+1}\,\vert \,a_{t+1},s_{t})$, and the agent gets a new observation according to $P(y_{t+1}\,\vert \,s_{t+1},a_{t+1})$.

Since each single observation y _t gives only partial information about the state, it is in general suboptimal for the agent to use only y _t to decide on an action a _t+1. A better alternative for the agent would be to take the full history $(y_{0:t},a_{0:t})$ as input to choose an action—since this provides all the information accessible to the agent at the time this, in principle, supports choosing optimal actions. However, it can be shown [9] that a sufficient alternative input to choose optimal actions is the posterior distribution $P(s_{t}\,\vert \,y_{0:t},a_{0:t})$. This should not be a surprise: given the Markovian structure of the world itself, if the agent would have access to the state s _t then optimal policy would map s _t directly to a _t+1. If, as in POMDPs, the agent does not have access to s _t , then the state posterior $P(s_{t}\,\vert \,y_{0:t},a_{0:t})$ provides all the information about s _t accessible to the agent, i.e., that can be inferred from previous observations and actions.

Fig. 7.1

Dynamic Bayesian network for the stochastic process of a (belief-based) agent interacting within a POMDP—for simplify in the case of finite horizon and final reward only

The state posterior is also called the belief $b_{t} = P(s_{t}\,\vert \,y_{0:t},a_{0:t})$. To summarize, Fig. 7.1 illustrates the stochastic process of a (belief-based) agent interacting within a POMDP as a dynamic Bayesian network. The environment is described by the state transition probabilities $P(s_{t+1}\,\vert \,a_{t+1},s_{t})$, the observation probabilities $P(y_{t}\,\vert \,s_{t},a_{t})$, and the initial state distribution P(s ₀). The agent is described (in the belief-based case³) by the policy $\pi: b_{t}\mapsto a_{t+1}$ that maps the current belief state to the action. In each step, after executing action a _t+1 and observing y _t+1, the agent updates the belief using Bayes’ rule:

$$\displaystyle\begin{array}{rcl} b_{t+1}(s_{t+1})& =& P(s_{t+1}\,\vert \,y_{0:t+1},a_{0:t+1}) \\ & & \propto P(y_{t+1}\,\vert \,s_{t+1},y_{0:t},a_{0:t})\ P(s_{t+1}\,\vert \,y_{0:t},a_{0:t}) \\ & =& P(y_{t+1}\,\vert \,s_{t+1},a_{t})\ \Big[\sum _{s_{t}}P(s_{t+1},s_{t}\,\vert \,y_{0:t},a_{0:t})\Big] \\ & =& P(y_{t+1}\,\vert \,s_{t+1},a_{t})\ \sum _{s_{t}}P(s_{t+1}\,\vert \,s_{t},a_{t})\ b_{t}(s_{t}) {}\end{array}$$

(7.5)

This equation is called belief update. The prior belief $b_{0}(s_{0})$ is initialized with the initial state distribution P(s ₀).

7.4 From NFL to Beliefs and the Bayesian Search Game

Table 7.1 summarizes how one can draw a relation between the problem of optimization and POMDPs. The action a _t of the agent/algorithm correspond to the next site x _t that the algorithm explores. The state s _t of the environment corresponds to the unknown underlying function f—a difference here is that in POMDPs the environment state is manipulated by actions, whereas in search exploring a site x _t does not change the function f of the environment. But as in a POMDP, the environment state f is not fully observable. Only a partial observation $P(y_{t}\,\vert \,f,x_{t})$ is accessible to the agent/algorithm depending on the site it explores.

Table 7.1 Translation of the search game as a partially observable Markov decision process

As in POMDPs, the belief b _t (f) captures all information about the state f that is accessible to the algorithm. The P(f) defined in the previous section provides the prior belief b ₀(f): = P(f); in Eq. (7.4) we also referred to the posterior belief at time t,

$$\displaystyle\begin{array}{rcl} b_{t}(f):= P(f\,\vert \,x_{0:t},y_{0:t}).& &{}\end{array}$$

(7.6)

NFL says that if the prior belief factorizes in identical marginals, then there is no way to derive a smart sampling heuristic from this belief. The reason is that in the NFL case the belief cannot be updated in a useful way. Why is this? Given a new observation y _t at x _t we can update the belief in the sense that now we explicitly know the function value at x _t —but we cannot update the belief about function values at yet unexplored sites because the NFL conditions do not allow us to generalize to unexplored sites. Hence the belief over yet unexplored sites always remains i.i.d. with marginals h(y).

Inversely, the belief is a generic and exhaustive way to capture all of what we can possibly know about the underlying function given the observations made so far. In particular, when NFL condition (7.2) does not hold, then an observation y _t at some site x _t tells us something about the function at other sites. The belief state is an exact description of this information about yet unexplored sites.

The stochastic search processes of a belief-based algorithm, which pick new search points based on a policy $\pi _{t}: b_{t-1}\mapsto x_{t}$, can be depicted as the dynamic Bayesian network (DBN) as in Fig. 7.2. This process can be viewed as a (single-player) game: The game starts with the player picking a specific prior belief b ₀ over the space of functions, and with the environment choosing a specific function f from some function prior P(f). For simplification, we assume that the player is informed on P(f) such that his prior belief coincides with the function prior, b ₀(f) = P(f). This initialization of the game corresponds to the first two nodes on the left in the DBN.

In the first time step, it will use the policy $\pi _{t}: b_{t-1}\mapsto x_{t}$ to pick a first site at time $x_{1} =\pi _{1}(b_{0})$. The environment responds by returning the function evaluation $y_{1} = f(x_{1})$. The player updates its belief as in Eq. (7.5). Since in our case the function f is not influenced by the action x _t the belief update simplifies to

$$\displaystyle\begin{array}{rcl} b_{t}(f)& =& P(f\,\vert \,x_{0:t},y_{0:t}) \\ & & \propto P(y_{t}\,\vert \,f,x_{0:t},y_{0:t-1})\ P(f\,\vert \,x_{0:t},y_{0:t-1}) \\ & =& P(y_{t}\,\vert \,x_{t},f)\ b_{t-1}(f) {}\end{array}$$

(7.7)

The game continues like that until, at some final deadline T, a reward R is emitted depending only on the last sample.

Fig. 7.2

The dynamic Bayesian network describing the search game. f is a function sampled from P(f). b _t is a belief over functions that the player maintains; it is initialized deterministically to b ₀ = P(f). $x_{t} \sim \pi _{t}(b_{t})$ is the player’s sample action at time t, and $y_{t} = f(x_{t})$ the evaluation feedback

Drawing the connection to POMDPs does not directly lead to new efficient solution methods. However, some simple facts from POMDPs also help us understand the problem of search better: (1) We know that the optimal policy in POMDPs is a deterministic function from beliefs to actions. This notion of optimality in POMDPs is very general and implies optimal solutions to the so-called exploration-exploitation problem [12] or strategies to gain information for later payoff. Clearly, such strategies are also relevant in the context of search. (2) A POMDP can be reformulated as a Markov decision process (MDP) with world state $\tilde{s}_{t} = (s_{t},b_{t})$—that is, when we think of the tuple $(s_{t},b_{t})$ as the new (embedding) world state. This also implies that optimal policies can be found by computing a value function $V (s_{t},b_{t})$ over this embedding space. Note that this value function is a function over the space of distributions—and thereby of extremely high complexity. Point-based value iteration methods follow this approach by exploiting a sparse structure of the value function [9].

7.5 Belief-Based Search Policies

In this section we consider some basic heuristic policies to choose the next search point based on the current belief. For simplicity we consider a finite horizon T where the reward is exactly the function value $f(x_{T}) \in \mathbb{R}$ of the last site. The objective is then: Find a policy $\pi _{t}:\ b_{t}\mapsto x_{t+1}$ (different for each t) that maximizes the expectation of f(x _T ).

The problem the player is faced with is obviously a problem of planning ahead, i.e., taking samples that allow him to learn as much as possible about f (shaping its belief favorably) such that at the deadline T he is as well informed as possible to pick the final sample. But what are computationally feasible policies in practice? Let us define some basic policies here:

The k-step look-ahead policy: ${\pi }^{k}:\ b_{t}\mapsto x_{t+1}$ is defined as the optimal policy for picking x _t+1 based on b _t , assuming that the horizon $T = t + k$ is k steps ahead. For large k, computing this policy is infeasible. For k = 1 or k = 2 approximations may be feasible.

The greedy policy: π ^k = 1 is the one-step lookahead policy which picks the point x _t+1 that maximizes the predictive mean $\hat{f}_{t}(x) =\int _{f}f(x)\ b_{t}(f)\ \mathit{df }$, that is, the mean function given the current belief b _t ,

$$\displaystyle\begin{array}{rcl} {\pi }^{k=1}(b_{ t}) = \text{argmax}_{x}\hat{f}_{t}(x).& &{}\end{array}$$

(7.8)

Thereby, the greedy policy is the optimal policy for the final pick of x _T based on b _T−1.

The two-step look-ahead: This policy π ^k = 2 is

$$\displaystyle\begin{array}{rcl} {\pi }^{k=2}(b_{ t})& =& \text{argmax}_{x_{t+1}}\int _{y_{t+1}}\max _{x_{t+2}}\hat{f}_{t+1}(x_{t+2})\ P(y_{t+1}\,\vert \,x_{t+1},b_{t}){}\end{array}$$

(7.9)

$$\displaystyle\begin{array}{rcl} \hat{f}_{t+1}& =& \int _{f}f(x)b(f;y_{t+1},x_{t+1},b_{t})df{}\end{array}$$

(7.10)

where $b(f;y_{t+1},x_{t+1},b_{t})$ is the belief when updating b _t with the new observations according to Eq. (7.7). The term $\max _{x_{t+2}}\hat{f}_{t+1}(x_{t+2})$ is the expected reward when the greedy policy is applied in the next step. The integral over y _t+1 accounts for all possible outcomes (and corresponding belief updates) for the sample x _t+1. In that sense, the two-step look-ahead policy can imply explorative strategies: One might want to pick x _t+1 such that the outcome y _t+1 contains crucial information for the belief update such that the final (greedy) pick has maximal expected reward.

A simple exploration policy π ^explore is to always pick the site x _t+1 that maximizes the predictive variance $\hat{\sigma }_{t}{(x)}^{2} =\int _{f}{[f(x) -\hat{ f}_{t}(x)]}^{2}b_{t}(f)df$ of the belief. This strategy aims at learning as much as possible about the function, but neglects that we are interested in high function values and should thus learn as much as possible about regions where we hope to find high function values.

A simple exploit-explore policy π ^EE is to pick the site x _t+1 that maximizes $g_{t}(x) =\hat{ f}_{t}(x) +\alpha \sigma _{t}(x)$, that is, a combination of the predictive mean and variance. g _t (x) can be interpreted as an optimistic function value estimate: The value could potentially be α standard deviations above the current mean estimation.

Another heuristic combining exploration and exploitation is the expected improvement policy π ^EI. Let $Y _{t} =\max \{ y_{1:T}\}$ be the maximum value observed so far. We can compute for each site x the expected improvement $q_{t}(x) =\int _{f}f(x)\delta _{f(x)>Y _{t}}b_{t}(f)df$, where δ is the indicator function. This expected improvement computes a mean value, as with $\hat{f}_{t}$, but only over function values greater than Y _t .

7.6 Experiments with Gaussian Processes as Belief Representation

The belief update in Eq. (7.7) is a simple equation, but for a concrete algorithm it requires to represent a distribution over function space and be able to multiply the likelihood term $P(y_{t}\,\vert \,x_{t},f)$ to the belief to become a new belief. What is a family of distributions over functions which we can be represented in computers and which is conjugate (that is, if the old belief is an element of this family, then the updated belief is also an element of this family)?

Gaussian processes [13] are such a family of distributions over continuous functions. They can be defined as follows. Let f ∼ GP(μ, C) be a random function sampled from a Gaussian process with mean function μ(x) and covariance function C(x, x′). Then, for any finite set of points $\{x_{1},\ldots,x_{N}\}$, the vector $(f(x_{1}),\ldots,f(x_{N}))$ is distributed joint Gaussian with mean vector $(\mu (x_{1}),\ldots,\mu (x_{N}))$ and covariance matrix $C(x_{i},x_{j})$, i, j = 1… N. Since this definition describes the behavior of random functions on finite subsets it fits nicely with our formulation of NFL.

The covariance function C(x, x′) is typically decaying with the distance | x − x′ | such that points close to each other are strongly correlated. This leads to smooth functions. Often C(x, x′) is chosen squared exponential $C(x,x\prime) {=\nu }^{2}\exp \{ - {(x - x\prime)}^{2}/{2\nu }^{2}\} +\delta { _{x=x\prime}\varrho }^{2}$ with correlation bandwidth ν (and observation standard deviation $\varrho$). Figure 7.3 displays a number of functions sampled independently from a GP prior with constant mean μ(x) = 0 and bandwidth $\nu = \frac{1} {2}$. This should illustrate what it means to assume such a prior: We believe a priori that functions typically look like those in Fig. 7.3, in particular w.r.t. the type of smoothness. (GPs are related to cubic splines, see [13].)

It is a common approach to use GPs as a representation of the belief b for search and optimization problems; in geology this method is also called kriging [2, 6, 7]. One often assumes that a single function evaluation is expensive (e.g., drilling a hole to get a geological probe) and therefore extensive computational cost to evaluate a policy is acceptable.

To demonstrate the use of Gaussian processes to represent beliefs we implemented a Bayesian search game, which can be downloaded from the author’s webpage.⁴ Here we report on some quantitative experiments. We implemented the policies π ^k = 1, π ^k = 2, π ^EE, π ^EI, π ^explore simply by evaluating the respective integrals over a grid. This becomes expensive already for k = 2.

Fig. 7.3

Ten sample functions from a Gaussian process prior with bandwidth $\nu = \frac{1} {2}$

We performed some experiments with Gaussian process beliefs to illustrate and evaluate the different policies defined in the previous section. The objective is to find the optimum of a function sampled from a Gaussian process with bandwidth $\nu = \frac{1} {2}$. The search is constrained to the interval [−1, 1].

Table 7.2 Performance for different policies for finding the optimum of a function sampled from a GP prior with bandwidth $\nu = \frac{1} {2}$, constrained to the search interval [−1, 1]. We measure the loss as the difference between the last sampled value f(x _T ) and the true optimum of the function. The algorithm is only allowed to take T = 10 (respectively, T = 5) samples. Mean and standard deviation are given for 10,000 random functions

Table 7.2 displays the results when we allow the algorithms to take only T = 10 or T = 5 samples to find the optimum. The objective is the final loss: the difference between the last sampled value f(x _T ) and the true optimum of the function. We also report on the average loss during the T samples. Although this is not the objective it indicates whether the algorithm tends to sample good points also in intermediate steps.

For T = 10 we find that the expected improvement policy π ^EI and the simple exploration policy π ^explore perform best. Both of them are rather exploratory, which is evident also from the high average loss. In contrast, π ^EE with α = 1 is less exploratory, focuses on a (local) optimum earlier, leading to higher final loss but lower average loss. For comparison we also tested for only T = 5, where the greedier π ^EE with α = 1 performs slightly better than the other policies.

Finally, we also want to demonstrate the effect of two-step look-ahead planning. It is not easy to find a problem class for which this policy performs better than the others. Here is a slightly contrived example: We sampled random functions from a GP prior with large bandwidth ν = 1 (very smooth functions) which were additionally conditioned on f(x) = 0 at the sites $x = -0.9,0,0.9$. Figure 7.4 displays 10 random samples from this prior.

Fig. 7.4

Ten sample functions from a Gaussian process prior with bandwidth ν = 1 conditioned on f(x) = 0 for $x = -0.9,0,0.9$

Table 7.3 Performance for different policies for finding the optimum of a function sampled from a GP prior illustrated in Fig. 7.4. The algorithm is only allowed to take T = 2 samples. Mean and standard deviation are given for 10,000 random functions

Table 7.3 displays the results for all policies with only T = 2—that is, the algorithm only has one sample to learn as much as possible about the function before placing the final sample, which decides on the final loss. First, we find that all algorithms π ^EE, π ^EI, π ^explore have the same performance. This is because they all first sample the site $x = -0.45$ or x = 0. 45, which have maximal entropy, and then sample the last point using the greedy policy. Hence, they are all equivalent for T = 2.

The two-step look-ahead policy behaves differently: It first samples a point very near by x = 0 (approximately x = 0. 05). The observation at this point implicitly allows the algorithm to infer the slope of the true function around x = 0. This implies a “better informed” GP posterior of the function, which has more certainty about the function on both sides rather than only on one side of x = 0. As a consequence, the final (greedy) pick of x _T is better than with the other algorithms.

This rather contrived example demonstrates, on the one hand, the intricate implications of lookahead strategies—how they pick points based on how their knowledge for future picks is improved. On the other hand, the minimal differences in performance and given that we had to construct such complicated scenarios to demonstrate the advantage of a two-step look-ahead strategy argues against such strategies. Note that π ^k = 2 is computationally orders of magnitude slower than the other policies.

7.7 Discussion

In this chapter we presented a discussion of three seemingly unconnected topics: No Free Lunch, POMDPs, and Gaussian processes. However, we hope it became clear that these topics are closely related.

NFL & Gaussian processes: In our formulation, the NFL condition (7.2) is that the function prior identically factorizes on any finite subset $\{x_{1},..,x_{K}\} \subset X$. Only if this condition is violated can we hope for an efficient search algorithm. Violation of this constraint implies that function values on finite subsets are dependent—a Gaussian process by definition describes exactly this correlation of values on finite subsets. Therefore, in our view, a Gaussian process is a very natural and simple model of the violation of NFL conditions. At this point one should note that, although Gaussian processes are typically formulated for continuous X with continuous covariance function, they can of course also be applied on discrete spaces, e.g., with a covariance function depending on the Hamming distance or other similarity measures.

NFL & POMDPs: The reason we discussed POMDPs in the context of NFL is that the POMDP framework explicitly states what the optimal search algorithm would be. In particular, the POMDP framework clarifies that the notion of a belief is a sufficient representation of all the knowledge gained from previous explorations, in the sense that the optimal algorithm can be viewed as a policy mapping from the belief to a new search point. Generally, we do not want to over-stress the discussion of truly optimal search algorithms. The POMDP framework formulated here leads to optimal search (given the assumption of the prior belief). Hutter [4] has discussed universal optimality, where the role of the prior is replaced by a complexity measure over algorithms (Solomonoff complexity). In both cases the computational complexity of evaluating the optimal policy is exponential and the key is to have good approximate policies. However, the notion of the belief leads naturally to the existing literature on optimization using heuristics like the expected improvement policy.

Let us also mention estimation of distribution algorithms (EDAs) [8]. It has been argued before that EDAs implicitly learn about the problem by shaping the search distribution [14]. From our perspective, EDAs (and also genetic algorithms) try to perform two tasks at once with the search distribution: They use it to accumulate information about the problem (representing where optima might be), and they use it to describe the next sample point. The belief framework suggests to disentangle these two issues: The belief is used to represent all knowledge and a separate policy maps it to a new samples. From a Bayesian perspective the benefit is that there is no loss in information in the belief update.

Finally, let us discuss related literature. Gutmann [2], Jones [7], and Jones et al. [6] discuss global optimization using response surfaces (also called surrogates, or kriging). Our Gaussian process search algorithm is an instance of such global response surface modelling. However, this work has not made the connection to POMDPs, NFL and look-ahead planning. Only the maximizing immediate measures (figures of merit) like the expected improvement has been discussed in this context.

Another branch of research focuses on local models of the fitness function [3, 10, 15]. These methods are very effective when many samples can be taken (where a global model would become infeasible). However, look-ahead heuristic or a well-defined Bayesian belief update has not been discussed in this context.