Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

3.1 Introduction

The concept of a fitness landscape originated in the 1930s in theoretical biology [75, 76] as a means of conceptualizing evolutionary adaptation: A fitness landscape is a kind of potential function on which a population moves uphill due to the combined effects of mutation and selection. Thus, natural selection acts like hill climbing on the topography implied by the fitness function.

From a mathematical point of view, a landscape landscape consists of three ingredients: a set X of configurations that are to be searched, a topological structure \(\mathcal{T}\) on X that describes how X can be traversed, and a fitness or cost function \(f: X \rightarrow \mathbb{R}\) that evaluates the individual points x ∈ X. This generic structure is common to many formal models, from evolutionary biology to statistical physics and operations research [5, 26, 40, 41]. The topological structure \(\mathcal{T}\) is often specified as a move set, move set that is, as a function \(N: X \rightarrow \mathfrak{P}(X)\) specifying for each configuration x ∈ X the subset N(x) ⊆ X of configurations that are reachable from x. Usually, the move set is constructed in a symmetric way, satisfying x ∈ N(y) ⇔ y ∈ N(x). The configuration space or search space \((X,\mathcal{T} )\) becomes an undirected finite graph G in this case. Then for each x ∈ X, the degree of x is given by deg(x) =  | N(x) | . We say that G is d-regular for non-negative integer d if deg(x) = d for all x ∈ X.

Without losing generality we assume that optimization strives to find those x ∈ X for which f(x) is small. Thus, f is interpreted as energy (or fitness with negative sign), and we are particularly interested in the minima of f. local minimum A configuration x ∈ X is a local minimum if f(x) ≤ f(y) for all y ∈ N(x). By M we denote the set of all local minima of the landscape. A local minimum \(\hat{x} \in M\) is global if, for all y ∈ X, \(f(\hat{x}) \leq f(y)\).

Fig. 3.1
figure 1

A small instance (a) of the Traveling Salesman Problem with illustration of three different move types (b)–(d) described in the main text

Full size image

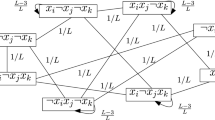
The Traveling Salesman Problem (TSP) [22], traveling salesman see Fig. 3.1, may serve as an example. Given a set of n vertices (cities, locations) \(\{1,\ldots,n\}\) and a (not necessarily symmetric) matrix of distances or travel costs d ij , the task is to find the permutation (tour) π that minimizes the total travel cost

$$\displaystyle\begin{array}{rcl} f(\pi ) =\sum _{ i=1}^{n}d_{\pi (i),\pi (i+1)}& &{}\end{array}$$
(3.1)

where indices are interpreted modulo n. A landscape arises by imposing a topological structure on the set S n of permutations, i.e., by specifying a move set that determines which tours are adjacent. Often the structure of the problem suggests one particular move set as natural, while others might look quite far-fetched. In principle, however, the choice of the move set is independent of the function f. For the TSP, for instance, three choices come to mind:

  1. 1.

    Exchange (Displacement) moves relocate a single city to another position in the tour

    $$\displaystyle\begin{array}{rcl} & & (1,\ldots,i,i + 1,i + 2,\ldots j,j + 1,\ldots,n) {}\\ & & \quad \mapsto (1,\ldots,i,i + 2,\ldots j,i + 1,j + 1,\ldots,n). {}\\ \end{array}$$

    See Fig. 3.1b.

  2. 2.

    Reversals cut the tour in two pieces and invert the order in which one half is transversed.

    $$\displaystyle\begin{array}{rcl} & & (1,\ldots,i,i + 1,i + 2,\ldots,k - 2,k - 1,k,\ldots n) {}\\ & & \quad \mapsto (1,\ldots,i,k - 1,k - 2,\ldots,i + 2,i + 1,k,\ldots n). {}\\ \end{array}$$

    See Fig. 3.1c.

  3. 3.

    Transpositions exchange the location of a single city

    $$\displaystyle\begin{array}{rcl} & & (1,\ldots,i - 1,i,i + 1,\ldots,k - 1,k,k + 1\ldots n) {}\\ & & \quad \mapsto (1,\ldots,i - 1,k,i + 1,\ldots,k - 1,i,k + 1,\ldots n). {}\\ \end{array}$$

    See Fig. 3.1d.

3.2 Ruggedness

landscape!rugged

The notion of rugged landscapes dates back to the 1980s, when Stuart Kauffman began to investigate these structures in some detail [32]. The intuition is simple. Once the landscape is fixed by virtue of the move set, optimization algorithms making local moves w.r.t. this move set will “see” a complex topography of mountain ranges, local optima, and saddles that influences their behavior. The more “rugged” this topography, the harder it becomes for an optimization algorithm based on local search to find the global optimum or even a good solution. Ruggedness can be quantified in many ways, however [29]:

  1. 1.

    The length distribution of down-hill walks, either gradient descent or so-called adaptive walks, is easily measured in computer simulations but is hard to deal with rigorously, see, e.g., [37].

  2. 2.

    Richard Palmer [45] proposed to call a landscape f rugged if the number of local optima scales exponentially with some measure of system size, e.g., the number of cities of a TSP. The distribution of local optima is in several cases accessible by the toolkit of statistical mechanics, see e.g. [50].

  3. 3.

    Barrier trees give a much more detailed view compared to local optima alone. Gradient walks are implicitly included in barrier tree computations. Section 3.3 of this chapter reviews barrier trees and other concise representations of landscapes.

  4. 4.

    Correlation measures capture landscape structure in terms of the time scales on which the cost varies under a random walk. These involve algebraic approaches with spectral decomposition, which are the topic of Sects. 3.4 and 3.5.

3.3 Barriers

barrier

Optimization by local search or gradient walks is guaranteed to be successful in a landscape with a unique cost minimum. In all other cases, variations of local search are more suitable [14, 33] when they accept inferior solutions to some extent. Then the walk eventually overcomes a barrier to pass over a saddle and enters the basin of an adjacent – possibly lower – local minimum. In this section we formalize the notions of walks, barriers, saddles, basins, and their adjacency. They form the basis of coarse-grained representations of landscapes. These representations “live” on the set of local minima M which is typically much smaller than the set of configurations X.

We review four such representations. Inherent structure networks contain complete information about adjacency of the gradient walk basins of the local minima. Barrier trees describe for each pair of local minima the barrier, i.e., the increase in cost to be overcome in order to travel between the minima. The funnel digraph displays the paths taken by an idealized search dynamics that takes the exit at lowest cost from each basin. Valleys were recently introduced to formalize the landscape structure implied by adaptive walks. Figure 3.2 serves as a comprehensive illustration throughout this section.

Fig. 3.2
figure 2

Graphical representations of local minima and saddles for the TSP instance of Fig. 3.1 under transpositions. (a) Local minima (circles) and direct saddles between their basins (y-axis not drawn to scale). The inherent structure network is the complete graph because a direct saddle exists for each pair of minima. In the illustration, however, saddles at a cost above 1,400 have been omitted. (b) The barrier tree for the same landscape. An inner node (vertical line) of the barrier tree indicates the minimal cost to be overcome in order to travel between all minima in the subtrees of that node. In (a), the direct saddles relevant for the construction of the barrier tree are drawn as filled rectangles. (c) Local minima are those TSP tours without neighboring tours (configurations) of lower cost. Note that this depends on the move set: Under reversals rather than transpositions, the two rightmost configuration are adjacent. (d) In the funnel digraph, an arc a → b indicates that the lowest direct saddle from minimum a leads to minimum b

Full size image

3.3.1 Walk and Accessibility

For configurations x, y ∈ X, a walk from x to y is a finite sequence of configurations \(\mathbf{w} = (w_{0},w_{1},,\ldots,w_{l})\) with w 0 = x, w l  = y, and \(w_{i} \in N(w_{i-1})\) for all \(i \in \{ 1,2,\ldots,l\}\). By \(\mathbb{P}_{\mathit{xy}}\) we denote the set of all walks from x to y. We say that x and y are mutually accessible at level \(\eta \in \mathbb{R}\), in symbols

$$\displaystyle{ x\,\mbox{ $ {\looparrowleft \!\!\!\!\underline{\,\,\,\,}^{\eta }\,\,\,\,}\!\!\!\!\looparrowright $}\,y\,, }$$
(3.2)

if there is a walk \(\mathbf{w} \in \mathbb{P}_{\mathit{xy}}\) such that f(z) ≤ η for all z ∈ w. The saddle height or fitness barrier between two configurations x, y ∈ X is the smallest level at which x and y are mutually accessible,

$$\displaystyle{ f[x,y] =\min \{\eta \in \mathbb{R}\vert x\,\mbox{ $ {\looparrowleft \!\!\!\!\underline{\,\,\,\,}^{\eta }\,\,\,\,}\!\!\!\!\looparrowright $}\,y\,\}. }$$
(3.3)

The saddle height saddle fulfills the ultrametric ultrametric (strong triangle) inequality. Namely, for all configurations x, y, z ∈ X

$$\displaystyle{ f[x,z] \leq \max \{ f[x,y],f[y,z]\}. }$$
(3.4)

because the set of walks from x to z passing through y is a subset of P xz .

3.3.2 Barrier Tree

Equipped with these concepts, let us return to the consideration of local minima. When restricting arguments to elements of M, the saddle height \(f: M \times M \rightarrow \mathbb{R}\) still fulfills the ultrametric inequality and thereby induces a hierarchical structure on M [47]. To see this, we use the maximum saddle height

$$\displaystyle{ m =\max \{ f[\hat{x},\hat{y}]\vert \hat{x},\hat{y} \in M\} }$$
(3.5)

of the whole landscape to define a relation on M by

$$\displaystyle{ \hat{x} \sim \hat{y}:\Leftrightarrow f[\hat{x},\hat{y}] < m. }$$
(3.6)

If all local minima are pairwise non-adjacent, ∼ is an equivalence relation on M. Its transitivity follows directly from the ultrametric inequality for the saddle height. Unless | M |  = 1, there is at least one pair of minima that are not related. Therefore the relation ∼ generates a partitioning of M into at least two equivalence classes. The argument may then be applied again to each class containing more than one element. This recursion of the partitioning into equivalence classes generates the barrier tree. Its leaves are the singleton classes, i.e., the minima themselves. Each inner node stands for a (sub-)partitioning at a given saddle height.

Fig. 3.3
figure 3

Barrier trees of two fitness landscapes of the same size. Left tree: an instance of the number partitioning number partitioning problem of size N = 10. Right tree: an instance of the truncated random energy model. The trees obtained for the two types of landscapes are distinguishable by measures of tree imbalance [63]

Full size image

Barrier trees serve to reveal geometric differences between landscapes, e.g., by measuring tree balance [63]. Figure 3.3 shows an example for the number partitioning problem [22]. Standard “flooding” algorithms algorithm!flooding construct the barrier tree by agglomeration rather than division because the minima and saddle heights are not known a priori. By scanning the configurations of the landscape in the order of increasing fitness, local minima are detected and joined by an inner tree node when connecting walks are observed [52, 73]. Barrier trees can be defined also for degenerate landscapes landscape!degenerate where the assumption of non-adjacent local minima is not fulfilled [17].

3.3.3 Basins and Inherent Structure Network

More detailed information about the geometry in terms of local minima is captured by basins basin and their adjacency relation. A walk \((w_{0},w_{1},\ldots,w_{l})\) is a gradient walk gradient walk (or steepest descent) steepest descent if each visited configuration w i is the one with lowest fitness in the closed neighborhood of its predecessor,

$$\displaystyle{ f(w_{i}) =\min \{ f(x)\vert x \in N(w_{i-1}) \cup w_{i-1}\},\;1 \leq i \leq l. }$$
(3.7)

From each starting configuration w 0, a sufficiently long gradient walk encounters a local minimum w l  ∈ M. If the encountered minimum g(x) is unique given a starting configuration x ∈ X of a gradient walk, this defines a mapping g: X → M. In the case that neighbors with lowest fitness are not unique, ambiguity of gradient walks is resolved by an additional, e.g., lexicographic ordering on X. The basin or gradient basin of a local minimum \(\hat{x}\) is the set \(B(\hat{x}) = {g}^{-1}(\hat{x})\) of configurations from which a gradient walk leads to \(\hat{x}\). Each basin is non-empty because it contains the local minimum itself. Since each configuration x ∈ X is in the basin of exactly one local minimum g(x), basins are a partitioning of the set X of configurations.

The interface between two local minima \(\hat{x},\hat{y} \in M\) is the set

$$\displaystyle{ I(\hat{x},\hat{y}) =\{ (x,y)\vert x \in B(\hat{x}),y \in B(\hat{y}),x \in N(y)\} }$$
(3.8)

containing all pairs of adjacent configurations shared between the basins. The direct saddle height saddle!direct between \(\hat{x}\) and \(\hat{y}\) is

$$\displaystyle{ h[\hat{x},\hat{y}] =\min \left \{\max \{f(x),f(y)\}\vert (x,y) \in I(\hat{x},\hat{y})\right \}. }$$
(3.9)

Direct saddle height is lower bounded by saddle height,

$$\displaystyle{ h[\hat{x},\hat{y}] \geq f[\hat{x},\hat{y}] }$$
(3.10)

for all \(\hat{x},\hat{y} \in M\) with non-empty interface. A member of the interface \((x,y) \in I(\hat{x},\hat{y})\) is a direct saddle (between \(\hat{x}\) and \(\hat{y}\)) if its cost is the direct saddle height \(\max \{f(x),f(y)\} = h(\hat{x},\hat{y})\).

The inherent structure network inherent structure network (M, H) [13] is defined as a graph with node set M and edge set \(H =\{\{\hat{ x},\hat{y}\}\vert I(\hat{x},\hat{y})\neq \varnothing \}\). An edge thus connects the local minima \(\hat{x}\) and \(\hat{y}\) if and only if there is a path from \(\hat{x}\) to \(\hat{y}\) that lies in the union of basins \(B(\hat{x}) \cup B(\hat{y})\). The saddle heights \(f[\hat{x},\hat{y}]\) can be recovered from the inherent structure network by minimizing the maximum values of the direct saddle height \(h[\hat{p},\hat{q}]\) encountered along a path in (M, H) that connects \(\hat{x}\) and \(\hat{y}\). We remark, finally, that some studies use the term “direct saddle” to denote only the subset of direct saddles for which \(h[\hat{x},\hat{y}] = f[\hat{x},\hat{y}]\), i.e., which cannot be circumvented by a longer but lower path in (M, H) [17, 61]. Exact computation of inherent structure networks requires detection of all direct saddles and is thus restricted to small instances [66]. Efficient sampling methods exist for larger landscapes, e.g. by [38].

For the example in Fig. 3.2, the inherent structure network is the complete graph: All basins are mutually adjacent. Remarkable graph properties, however, have been revealed when studying the inherent structure networks of larger energy landscapes of chemical clusters [13], spin-glass spin-glass models [7], and NK landscapes NK landscape [66]. Compared to random graphs, the inherent structure networks have a large number of closed triangles (“clustering”), modular structure, and broad degree distributions, often with power law tails.

3.3.4 Funnel

Besides barrier tree and inherent structure network, another useful graph representation is the funnel digraph (M, A) [34]. Here, a directed arc runs from \(\hat{x}\) to \(\hat{y}\) if the basins of \(\hat{x}\) and \(\hat{y}\) have a non-empty interface and

$$\displaystyle{ h(\hat{x},\hat{y}) =\min \{ h(\hat{x},\hat{z})\vert \{\hat{x},\hat{z}\} \in E\}. }$$
(3.11)

Thus from each local minimum \(\hat{x}\) an arc points to that neighboring local minimum \(\hat{y}\) that is reached by the smallest direct saddle height. The node \(\hat{x}\) has more than one outgoing arc if more than one neighboring basin is reached over the same minimal directed saddle height.

The definition is motivated by stochastic variants of local search such as Metropolis sampling [39] and simulated annealing [33]. Under the assumption that the search exits a basin via its lowest saddle with the largest probability, the most likely sequences of visits to basins are the directed paths of the funnel digraph. It serves to make precise the concept of a funnel funnel [23, 43, 74]. A local minimum \(\hat{x}\) is in the funnel \(F(\hat{z}) \subseteq M\) of a global minimum \(\hat{z}\) if there is a directed path from \(\hat{x}\) to \(\hat{z}\) on the funnel digraph. Thus the funnel contains all those local minima from which iterative exits over the lowest barrier eventually lead to the ground state [34].

In the funnel digraph for the small TSP instance in Fig. 3.2c,d, we see that the funnel consists of the basins of the global minimum itself (cost 1294) and of the highest local minimum (cost 1389) while the basins of the other three minima are outside the funnel. Numerical studies with the number partitioning problem [22] indicate that funnel size tends to zero for large random instances [34].

3.3.5 Valleys

Adaptive walks generalize gradient walks by accepting any fitness-improving steps. We say that x ∈ X is reachable from y ∈ X if there is an adaptive walk from y to x. A valley [61] is a maximal connected subgraph of X such that no point y∉W is reachable from any starting point x ∈ W. In contrast to basins, valleys do not form a hierarchy but rather can be regarded as a community structure of X, see, e.g., [20]. Instead, they overlap in the upper, high-energy, parts of the landscape, where adaptive walks are not yet committed to a unique local minimum. The parts of gradient basins below the saddle points linking them to other basins therefore are valleys. Conversely, entire gradient basins are always contained in valleys.

The exact mutual relationships among the barrier trees, basins, inherent structure networks, valleys, etc., are still not completely understood, in particular in the context of degenerate landscapes.

3.4 Elementary Landscapes

3.4.1 Graph Laplacian

In the previous section we have taken a geometric or topological approach to analyzing and representing a landscape. The alternative is to adopt an algebraic point of view, interpreting the landscape as a vector of fitness values. The neighborhood structure N on the set X of configurations, which index the fitness vector, also needs an algebraic interpretation. In this contribution we only deal with graphs whose edges are defined by the (symmetric) move set \(N: X \rightarrow \mathfrak{P}(X)\). The most natural choice thus are the adjacency matrix A (with entries A xy  = 1 if x and y are adjacent, i.e., y ∈ N(x), and A xy  = 0 otherwise) and the incidence matrix H. The latter has entries \(\mathbf{H}_{\mathit{ex}} = +1\) if x is the “head end” of the edge e, \(\mathbf{H}_{\mathit{ex}} = -1\) if x is the “tail end” of e, and H ex  = 0 otherwise. (The assignment of head and tail to each edge is arbitrary.) The basic idea of algebraic landscape theory is to explore the connections between the fitness function f and these matrix representations of the search space, and to use combinations the these algebraic object to derive numerical descriptors of landscape structure [49].

A convenient starting point is to consider the local variation of the fitness, e.g., in the form of fitness differences f(x) − f(y) between adjacent vertices y ∈ N(x). The sum of the local changes

$$\displaystyle{ (\mathbf{L}f)(x):=\sum _{y\in N(x)}(f(x) - f(y)) }$$
(3.12)

defines the Laplacian L as a linear operator associated with the graph on (X, N) that can be applied to any function f on the nodes of the graph. When we imagine a spatially extended landscape, e.g., the underlying graph being a lattice, (L f)(x) can be interpreted as the local “curvature” of f at configuration x. In particular, the x-th entry of L f is negative if x is a local minimum and (L f)(x) > 0 for a local maximum.

Since L is a linear operator, it may also be seen as a matrix. In fact, L is intimately related to both the adjacency and the incidence matrix: \(\mathbf{L} = \mathbf{D} -\mathbf{A}\), where D is the diagonal matrix of vertex degrees \(\mathrm{deg}(x):=\sum _{y\in X}\mathbf{A}_{\mathit{xy}}\), and \(\mathbf{L} ={ \mathbf{H}}^{+}\mathbf{H}\). The Laplacian is thus simply a representation of the topological structure of the search space.

3.4.2 Elementary Landscapes

Since L is a symmetric operator (on a finite-dimensional vector space), it can be diagonalized by finding its eigenfunctions. Let us perform the diagonalization for the simple and useful case that the graph is an n-dimensional hypercube with node set \(X =\{ -1,+{1\}}^{n}\) and x ∈ N(y) if and only if x and y differ at exactly one coordinate. For each set of indices \(I \subseteq \{ 1,\ldots,n\}\), the Walsh functions Walsh function are defined as

$$\displaystyle{ w_{I}(x) =\prod _{i\in I}x_{i}. }$$
(3.13)

Figure 3.4 gives an illustration for the three-dimensional case. The Walsh functions form an orthogonal basis of \({\mathbb{R}}^{{2}^{n} }\). With a Walsh function of order | I | , each node of the hypercube has n − | I | neighbors with the opposite value and I neighbors with the same value. This amounts to

$$\displaystyle{ \mathbf{L}w_{I} = 2\vert I\vert w_{I}. }$$
(3.14)

Each Walsh function w I is an eigenvector of \(\mathbb{L}\) for eigenvalue 2 | I | . Now consider a 2-spin glass as a landscape on the hypercube with the cost function

$$\displaystyle{ f(x) = -\sum _{i,j}J_{\mathit{ij}}x_{i}x_{j} }$$
(3.15)

with arbitrary real coefficients J ij . Since \(x_{i}x_{j} = w_{i,j}(x)\) for all x ∈ X, we see that f is a weighted sum of Walsh functions of order 2. Therefore f is an eigenvector of the Laplacian with eigenvalue 2 | I |  = 4. This observation generalizes to p-spin glasses and many other landscapes of interest.

Fig. 3.4
figure 4

The eight Walsh functions of the hypercube in dimension n = 3. Dark and light color of nodes distinguishes the values + 1 and − 1

Full size image
Table 3.1 Examples of elementary landscapes
Full size table

It is convenient to consider landscapes with vanishing average fitness, i.e., instead of f, we use \(\tilde{f}(x) = f(x) -\bar{ f}\), where \(\bar{f} = \frac{1} {\vert X\vert }\sum _{x\in X}f(x)\) is the average cost of an arbitrary configuration. A landscape is elementary landscape!elementary if the zero-mean cost function \(\tilde{f}\) is an eigenfunction of the Laplacian of the underlying graph, i.e.,

$$\displaystyle{ (\mathbf{L}f)(x) =\sum _{y\in N(x)}\left [\tilde{f}(x) -\tilde{ f}(y)\right ] =\lambda _{k}\tilde{f}(x) }$$
(3.16)

Since \(\mathbf{L} ={ \mathbf{H}}^{+}\mathbf{H}\), all eigenvalues are non-negative. In the following, they will be indexed in non-decreasing order

$$\displaystyle\begin{array}{rcl} 0 =\lambda _{0} \leq \lambda _{1} \leq \lambda _{2} \leq \ldots \leq \lambda _{\vert X\vert -1}.& &{}\end{array}$$
(3.17)

First examples of elementary landscapes were identified by Grover and others [9, 24, 55]. Table 3.1 lists some of them. Additional examples are discussed, e.g., by [36, 53, 54, 70]. In most cases, k is small: \(\tilde{f}\) lies in the eigenspace of one of the first few eigenvalues of the Laplacian.

Lov Grover [24] showed that, if f is an elementary landscape, then

$$\displaystyle{ f(\hat{x}_{\min }) \leq \bar{ f} \leq f(\hat{x}_{\max }) }$$
(3.18)

for every local minimum \(\hat{x}_{\min }\) and every local maximum \(\hat{x}_{\max }\). This maximum principle shows that elementary landscapes are in a sense well-behaved: There are no local optima with worse than average fitness \(\bar{f}\). A bound on the global maxima in terms of the maximal local fitness differences can be obtained using a similar argument [12]:

$$\displaystyle{ \lambda \left \vert f(\hat{x}) -\bar{ f}\right \vert \leq \mathrm{ deg}{(\hat{x})\varepsilon }^{{\ast}}\,, }$$
(3.19)

where \({\varepsilon }^{{\ast}} =\max _{\{x,y\}\in E}\vert f(x) - f(y)\vert \) is the “information stability” introduced by [67].

The eigenvalues, λ i , convey information about the underlying graph [42]. For instance, G is connected if and only if λ 1 > 0. The value of λ 1 is often called the algebraic connectivity of the graph G [16]. The corresponding eigenfunctions have a particularly simple form: The vertices with non-negative (non-positive) values of f are connected. More generally, a nodal domain of a function g on G is a maximal connected vertex set on which g does not change sign. A strong nodal domain is a maximal connected vertex set on which g has the same strict sign, + or −. The discrete version of Courant’s nodal domain theorem [6, 10, 15, 46] asserts that an eigenfunction f to eigenvalue λ k (counting multiplicities) has no more than k + 1 weak and k + m k strong nodal domains, where m k is the multiplicity of λ k . The theorem restricts ruggedness in terms of the eigenvalue. Intuitively, the nodal domain theorem ascertains that the number of big mountain ranges (and deep sea valleys) is small for the small eigenvalues of L.

There is, furthermore, a simple quantitative relationship between λ and the autocorrelation function of f of \((X,\mathcal{X})\) [55]. For a D-regular graph G, we have

$$\displaystyle\begin{array}{rcl} r(s) ={ \left (1 -\lambda /D\right )}^{s}& &{}\end{array}$$
(3.20)

r(s) is the autocorrelation function of f along a uniform random walk on G [19, 68]. Similar equations can be derived for correlation measures defined in terms of distances on G [55] and for non-regular graphs [3, 11, 62].

Whitley et al. [71] interpret the eigenvalue equation (3.16) as a statement on the average fitness of the neighbors of a point,

$$\displaystyle\begin{array}{rcl} \langle f\rangle _{x} = \frac{1} {\mathrm{deg}(x)}\sum _{y\in N(x)}f(x)& &{}\end{array}$$
(3.21)

and discuss some implications for local search processes. Local conditions for the existence of improving moves are considered by [70].

3.4.3 Fourier Decomposition

Of course, in most cases, a natural move set \(\mathcal{T}\) does not make f an elementary landscape. In case of the TSP landscape, for example, transpositions and reversals lead to elementary landscapes. One easily checks, on the other hand,

$$\displaystyle\begin{array}{rcl} (\mathbf{L}f)(\pi )& =& \sum _{i,j}\bigg\{d_{\pi (i)\pi (i+1)} + d_{\pi (i+1),\pi (i+2)} + d_{\pi (j)\pi (j+1)} \\ & & \qquad \qquad - d_{\pi (i)\pi (i+2)} - d_{\pi (j)\pi (i+1)} - d_{\pi (i+1)\pi (j+1)}\bigg\} \\ & & = 2n(f(\pi ) -\bar{ f}) + nf(\pi ) -\sum _{i=1}^{n}d_{\pi (i)\pi (i+2)}{}\end{array}$$
(3.22)

which is clearly not of the form \(a_{1}f(\pi ) + a_{0}\) due to the explicit dependence of the last term on the next-nearest neighbors w.r.t. π. Exchange moves therefore do not make the TSP an elementary landscape.

A Fourier-decomposition-like formalism can be employed to decompose arbitrary landscapes into their elementary components [28, 51, 69]:

$$\displaystyle{ f = a_{0} +\sum _{ k>0}^{n-1}a_{ k}f_{k} }$$
(3.23)

where the f k form an orthonormal system of eigenfunctions of the graph Laplacian (\(\mathbf{L}f_{k} =\lambda _{k}f_{k}\), and \(a_{0} =\bar{ f}\) is the average value of the function f). Let us denote the distinct eigenvalues of L by \(\bar{\lambda }_{p}\), sorted in increasing order starting with \(\bar{\lambda }_{0} =\lambda _{0} = 0\). We call p theorder of eigenvalue order of the eigenvalue \(\bar{\lambda }_{p}\). The amplitude spectrum amplitude spectrum of \(f: X \rightarrow \mathbb{R}\) is defined by

$$\displaystyle{ B_{p} =\sum _{k: \lambda _{k}=\bar{\lambda }_{p}}\vert a_{k}{\vert }^{2}\bigg/\sum _{ k>0}\vert a_{k}{\vert }^{2}\;. }$$
(3.24)

By definition, B p  ≥ 0 and \(\sum _{p}B_{p} = 1\). The amplitude measures the relative contribution of the eigenspace of the eigenvalue with order p to the function f. Of course, a landscape is elementary if and only if B p  = 1 for a single order and 0 for all others. For Ising spin-glass modelsspin-glass, for example, the order equals the number of interacting spins, Table 3.1.

In some cases, landscapes are not elementary but at least exhibit a highly localized spectrum. The landscape of the “Low-Autocorrelated Binary String Problem”, for instance, satisfies B p  = 0 for p > 4 [44]. Quadratic assignment problems are also superpositions of eigenfunctions of quasi-abelian Cayleygraphs of the symmetric group with the few lowest eigenvalues [51]. A similar result holds for K-SAT K-SAT problems. An instance of K-SAT consists of n Boolean variables x i , and a set of m clauses each involving exactly K variables in disjunction. The cost function f(x) measures the number of clauses that are satisfied. [64] showed that B p  = 0 for p > K. Similar results are available for frequency assignment problems [72], the subset sum problem [8], or genetic programming parity problems [35]. Numerical studies of the amplitude spectra of several complex real-world landscapes are reported in [4, 25, 51, 65]. A practical procedure for algebraically computing the decomposition of a landscape into its elementary constituents is discussed in [8]. This approach assumes that f(x) is available as an algebraic equation and that an orthonormal basis {f k } is computable.

A block-model block model [70, 71] is a landscape of the form

$$\displaystyle{ f(x) =\sum _{q\in \mathcal{Q}(x)}w_{q} }$$
(3.25)

where \(\mathcal{Q}\) is a set of “building blocks” with weights w q . The subset \(\mathcal{Q}(x) \subseteq \mathcal{Q}\) consists of the blocks that contribute to a particular state x. For instance, the TSP is of this type: \(\mathcal{Q}\) is the collection of intercity connections, and w q is their length. Necessary conditions for block models to be elementary are discussed, e.g., by [70]. Equation (3.25) can be rewritten in the form

$$\displaystyle{ f(x) =\sum _{q\in \mathcal{Q}}w_{q}\vartheta _{q}(x) }$$
(3.26)

where \(\vartheta _{q}(x) = 1\) if \(q \in \mathcal{Q}(x)\), and \(\vartheta _{q}(x) = 0\) otherwise. They form a special case of the additive landscapes considered in the next section.

3.5 Additive Random Landscapes

landscape!additive

Many models of landscapes contain a random component. In spin-glass Hamiltonians of the general form

$$\displaystyle{ f(\boldsymbol{\sigma }) =\sum _{i_{1}<i_{2}<\ldots <i_{p}}a_{i_{1},i_{2},\ldots,i_{p}}\sigma _{1}\sigma _{2}\ldots \sigma _{i_{p}} }$$
(3.27)

with n Ising spin variables σ i  = ±1, the coefficients \(a_{i_{1},i_{2},\ldots,i_{p}}\) are usually considered as random variables drawn from some probability distribution. Similarly, the “thermodynamics” of TSPs can be studied with the distances w q in Eq. (3.25) interpreted as random variables. [48, 58] studied this type of model in a more general setting motivated by Eq. (3.26).

Let \(\vartheta _{q}: X \rightarrow \mathbb{R}\), q ∈ I, be a family of fitness functions on X, where I is some index set, and let c q , q ∈ I, be independent, real-valued, random variables. We consider additive random fitness functions of the form

$$\displaystyle{ f(x) =\sum _{q\in I}c_{q}\vartheta _{q}(x) }$$
(3.28)

on \(G = (X,\mathcal{T} )\). The associated probability space is referred to additive random landscape (a.r.l.) additive random landscape a.r.l. [48]. An a.r.l. is uniform if (1) the c q , q ∈ I, are independently and identically distributed (i.i.d.) and (2) there are constants b 0 and b 1 such that \(\sum _{x\in V }\vartheta _{q}(x) =\vert V \vert b_{0}\) and \(\sum _{x\in V }\vartheta _{q}{(x)}^{2} =\vert V \vert b_{1}\) independent of q. An a.r.l. is strictly uniform if, in addition, \(\sum _{q}\vartheta _{q}(x) = b_{2}\) and \(\sum _{q}\vartheta _{q}{(x)}^{2} = b_{3}\) independently of x ∈ X.

For block models, \(\vartheta _{q}(x) =\vartheta _{q}{(x)}^{2}\). Hence a block model is uniform if each block is contained in the same number configurations and is strictly uniform if in addition, \(\vert \mathcal{Q}(x)\vert \) is independent of x. Furthermore, every a.r.l. with Gaussian measure is additive. This follows immediately by the Karhunen-Loève theorem [30], using the fact that uncorrelated jointly normal distributed variables are already independent. Random versions of elementary landscapes, i.e., those with i.i.d. Fourier coefficients, are of course also a.r.l.s.

Maybe the most famous a.r.l.s are Kauffman’s NK landscape NK landscape models. Consider a binary “genome” x of length n. Each site is associated with a site fitness that is determined from a set of K sequence positions to which position i is epistatically linked. These state-dependent contributions are usually taken as independent uniform random variables [31]. In order to see that an NK model is an a.r.l., we introduce the functions

$$\displaystyle\begin{array}{rcl} \vartheta _{i,y(i)}(x) =\prod _{ k=0}^{\vert y(i)\vert }\delta _{ y(i)_{k},x_{k}}& &{}\end{array}$$
(3.29)

where y(i) k denotes a particular (binary) state of position k in the epistatic neighborhood y(i) of i. In other words, \(\vartheta _{i,y(i)}(x) = 1\) if the argument x coincides on the K epistatic neighbors of i with a particular binary pattern y(i). It is not hard to check that NK models are strictly uniform [48].

An important observation in this context is that short-range spin-glass models can be understood as a.r.l.s for which the p-spin eigenfunctions (of the Laplacian of the Boolean hypercube)

$$\displaystyle\begin{array}{rcl} \vartheta _{i_{1}i_{2}\ldots i_{p}}(\boldsymbol{\sigma }) =\prod _{ k=1}^{p}\sigma _{ i_{k}}& &{}\end{array}$$
(3.30)

take on the role of the characteristic functions \(\{\vartheta _{j}\}\). The coefficients are then taken from a mixed distribution of the form \(\rho (c) = (1-\mu )\mathrm{Gauss}_{(0,s)}(c) +\mu \delta (c)\). Thus there is a finite probability p that a coefficient c j vanishes. In this setting one can easily evaluate the degree of neutrality,neutrality i.e., the expected fraction of neutral neighbors

$$\displaystyle\begin{array}{rcl} \nu (x) = \frac{1} {\vert N(x)\vert }\mathbb{E}\left [\big\vert \{y \in N(x): f(x) = f(y)\}\big\vert \right ]& &{}\end{array}$$
(3.31)

One finds

$$\displaystyle{ \nu (x) = \frac{1} {D}\sum {_{y\in N(x)}\mu }^{c_{y}(x)}\qquad c_{ y}(x):= \vert \{q \in I\vert \vartheta _{q}(x)\neq \vartheta _{q}(y)\}\vert }$$
(3.32)

which, for the case of the p-spin models can be evaluated explicitly as \(\nu (x) {=\mu }^{{n-1\choose p-1}}\) [48]. The value of ν can thus be tuned by μ, the fraction of vanishing coefficients. On the other hand, the Laplacian eigenvalue and hence the algebraic measures of ruggedness depend only on the interaction order p. Hence, ruggedness and neutrality are independent properties of landscapes.

Elementary landscapes have restrictions on “plateaus”, that is, on connected subgraphs on which the landscape is flat. In particular, Sutton et al. [64] show for 3-SAT that plateaus cannot contain large balls in G unless their fitness is close to average. A more general understanding of neutrality in elementary landscapes is still missing, however.

There is a close connection between the Fourier decomposition of a (random) landscape and a “symmetry” property of random fields: Stadler and Happel [58] call a random field *-isotropic *-isotropy if its covariance matrix C is a polynomial of the adjacency matrix A of the underlying graph. The interest in this symmetry property arises from the observation that *-isotropy is equivalent to three regularity conditions on the distributions of the Fourier coefficients:

  1. 1.

    \(\mathbb{E}[a_{k}] = 0\) for k ≠ 0.

  2. 2.

    \(\mathbb{C}\rtimes \succapprox [a_{k},a_{j}]:= \mathbb{E}[a_{k}a_{j}] - \mathbb{E}[a_{k}]\mathbb{E}[a_{j}] =\mathrm{ Var}[a_{k}]\delta _{kj}\).

  3. 3.

    \(\mathrm{Var}[a_{k}] =\mathrm{ Var}[a_{j}]\) if \(\varphi _{k}(x)\) and \(\varphi _{j}(x)\) are eigenfunctions to the same eigenvalue of the graph Laplacian.

In Gaussian case, *-isotropy also has an interpretation as a maximum entropy condition: Gaussian random fields satisfying these three conditions maximize entropy subject to the constraint of a given amplitude spectrum [56].

Fig. 3.5
figure 5

Empirically, the number \(\mathcal{N}\) of local optima in many landscape scales exponentially with system size n. The values of \(\mu:=\lim _{n\rightarrow \infty }\frac{1} {n}\log \mathcal{N}(n)\) can be estimated surprisingly accurately by the correlation length conjecture for *-isotropic landscapes (•) and nearly *-isotropic landscapes (▴) (Data are taken from [58])

Full size image

An interesting empirical observation in this context is the correlation length conjecture [59]. It states that we should expect about one local optimum within a ball B in G whose radius r is given by the distance covered by random walk of length ℓ on G, where

$$\displaystyle{ \ell=\sum _{ s=0}^{\infty }r(s) }$$
(3.33)

is the correlation length of the landscape. This simple rule yields surprisingly accurate estimates of the number of local optima in isotropic and nearly isotropic landscapes, see Fig. 3.5. The accuracy of the estimate seems to decline with increasing deviations from *-isotropy [21, 44, 58].

3.6 Outlook

Most of the theoretical results for fitness landscapes have been obtained for very simple search processes, i.e., for landscapes on simple graphs. In the field of genetic algorithms, on the other hand, the search operators themselves are typically much more complex, involving recombination of pairs of individuals drawn from a population. A few attempts have been made to elucidate the mathematical structure of landscapes on more general topologies [18, 60, 61], considering generalized versions of barrier trees and basins. A generalization of the Fourier decomposition and a notion of elementary landscapes under recombination was explored in [62], introducing a Markov chain on X that in a certain sense mimics the action of crossover. In this formalism, a close connection between elementary landscapes and Holland’s schemata [27] becomes apparent. It remains a topic for future research, however, if and how spectral properties of landscapes can be formulated in general for population-based search operators in which offsprings are created from more than one parent.

Despite the tentative computational results that suggest a tight connection between spectral properties of a landscape, statistical features of the Fourier coefficients, and geometric properties such as the distribution of local minima, there is at present no coherent theory that captures these connections. We suspect that a deeper understanding of relations between these different aspects of landscapes will be a prerequisite for any predictive theory of the performance of optimization algorithms on particular landscape problems.