Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Nanoelectronic devices—and to their extreme-end single-molecule electronics—always require coupling the active units characterized by nanoscale dimensions to contacts, wires, and packaging, characterized by much larger scales. However, the behavior of the whole device is determined by the interplay of different transport mechanisms occurring at different length scales. The typical approach in charge transport is to concentrate on the nanoscale devices with accurate simulations and then treat the contacts and the environment as effective circuit components within a SPICE-like approach. There are problems, however, that cannot be easily decoupled in such a simple way. In molecular electronics, small changes of local potentials can have large effects on the electronic and transport properties of the system, and for this reason, accurate density-functional tools have been developed in the last decade in order to describe charge-transport mechanisms in molecules when transport is dominated by quantum coherence. However, computational limitations prevent treating substantial parts of the contacting leads at the same level of accuracy. The only practical solution is to tackle the problem in a pragmatic cutting-and-sewing approach in which the molecular transport is treated using quantum-transport methods and the contacting leads and surrounding environment is described as a continuous medium using semiclassical models.

Heat dissipation, and more in general energy transport, is another important example of nonlinear coupling between the nano-world and its environment. Miniaturization obviously increases the power density of heat generation, making heat management one of the key issues that needs to be addressed in order to improve the stability and reliability of nanodevices. Heat dissipation depends on the transport property at all scales, and careful simulations are crucial in order to predict and control the working temperatures reached in the device.

The wide span of length scales and transport phenomena requires the development of new tools of multiscale character. A general a priori methodology for such a multiscale coupling has not been established to date, especially when quantum- and classical-charge-transport models are sewed together. Most of the solutions must be guided by physical intuition, requirement of consistency, and continuity equations. The situation is similar to the practical needs that have guided the developments of sophisticated QM/MM coupling schemes and have proven quite useful in molecular dynamics simulations in order to understand a wide range of physical phenomena, from structural properties to excitation dynamics and mass transport.

In this work an example towards the development of quantum-classical multiscale coupling for charge and heat transport is presented and applied to the problem of heating of a benzo-di-pyridine molecule adsorbed on a Cu substrate when current is driven across by an STM measurement.

2 Coupling Quantum with Semiclassical Transport Models

Nonequilibrium Green’s functions (NEGF) have become a standard tool to analyze transport in nanodevices [1] when quantum coherence plays a relevant role. Yet, the evaluation of NEGF is numerically very expensive, especially when scattering is included. In general the microscopic domain in which quantum effects need to be fully taken into account is restricted to the molecular scale and/or its close surroundings. The molecular region is embedded within a macroscopic domain, where simpler phenomenological transport equations can be solved. A multiscale/multiphysics approach is therefore necessary in order to efficiently compute transport in the whole system. To this end we have developed a coupling scheme between drift-diffusion (DD) and NEGF transport models which are solved on different subdomains. These are coupled via boundary conditions: the macroscale models providing boundary conditions in terms of electrochemical potentials, whereas the microscale models provide flux boundary conditions to the macro domains. In order to ensure continuity conditions on current, the two models are coupled self-consistently with an iteration scheme that starts with a guess solution. This method goes under the name of bridge multiscale approach [2, 3]. In the same way, heat dissipation at the molecular scale is coupled to a Fourier heat-transport model at larger scales by imposing temperature boundary conditions and heat flux. A problem in this coupling scheme is that molecular transport needs to be simulated using atomistic approaches, whereas macroscopic scales are treated as effective continuous media and the differential equations are discretized on meshes. Sewing the two models requires appropriate interpolations and embracing schemes of the electronic charge density and currents at the interfaces between atoms and finite elements.

3 FEM and Atomistic Model of the Tip/Molecule/Substrate

The first step is to build a realistic model of the STM tip, which is typically tungsten-made ultrasharp objects fabricated using electromigration processes [4].

Figure 1 shows a micrograph of one of such tips [5]. Based on available SEM/TEM images, a model comprising 2 μm of the tip ending has been built. This is considered sufficient for the purposes of the subsequent computations, especially heat transport along the tip. The tip is still reduced to an idealized model having a conical shape with a termination assumed as an ideal hemisphere of 3 nm in diameter, as shown in Fig. 2. A flat substrate is also included in the model.

Fig. 1
figure 1

SEM image of an electrochemically etched ultrasharp STM tip made of tungsten

Full size image
Fig. 2
figure 2

(Right) FEM model of tip apex including 2 μm of tip and substrate. (Center) Zoom in of the tip/molecule/substrate mesh before atoms are added and (left) atomistic model

Full size image

The next step is to introduce an adequate atomistic description of the tip/molecule/Cu substrate. This is obtained in a three-step procedure. The first step consists in filling with atoms the mesh regions at the tip apex and substrate, which is done assuming a [111]Cu orientation and imposing the same atomistic Cu geometry within the tip. The reason for doing this is justified by the fact that in most STM/STS experiments, the tip is dipped on the substrate before imaging, and after this procedure, it is likely to pick up a substantial fraction of substrate atoms.

The following step is to insert a pre-relaxed benzene-di-pyridine molecule within the tip/substrate gap, including two extra Cu atoms which are bonded to the nitrogen atoms of the molecule and to the tip and substrate, respectively. This is done following the indication that these kinds of molecules tend to bind to Cu adatoms [6]. Finally the geometry is relaxed, including the two Cu atoms, keeping fixed the substrate and tip. A relaxed geometry for tip-substrate distance of 1.2 nm is shown in Fig. 3. All DFT calculations in this work have been performed using the density-functional tight-binding (DFTB) approach and its extensions to transport. For an extended review of the method, see [7, 8].

Fig. 3
figure 3

(Left) A view of the relaxed geometry of the tip/molecule/substrate system and (right) potential profile computed at a bias of 1.0 V

Full size image

4 Electron–Phonon Coupling and IETS Spectrum

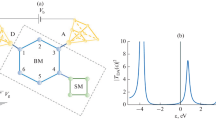
Once the final geometry has been obtained, the vibrational modes of the molecule and the electron–vibron (localized phonon) coupling matrices are computed at the bias V = 0 [9, 10]. A good insight of the electron–phonon scattering can be obtained looking at the inelastic electron tunneling spectroscopy (IETS) [11], which is proportional to \({\mathrm{d}}^{2}I/\mathrm{d}{V }^{2}\) in order to enhance the onset of inelastic vibronic excitations by the tunneling electrons.

The simulated IETS spectrum is shown in Fig. 4 and reveals few dominant peaks corresponding to specific vibrational modes of the pyridine and benzene cages. The most important peak, at 1, 810 cm − 1, actually originates from a combination of two modes with even and odd symmetry with respect to the molecular reflection plane. In Fig. 4, only the mode with odd symmetry is shown. The IETS signal is computed and measured at low temperatures (T = 4. 2 K) and low bias \((V \sim 400\,\mathrm{mV})\) in order to reduce noise. When large biases are applied, the molecule heats up and the vibronic population becomes strongly a nonequilibrium distribution, and it is not obvious that these modes are still dominating.

Fig. 4
figure 4

Simulated IETS signal of the molecule and vibrational modes giving the largest signal

Full size image

5 Nonequilibrium Phonon Distributions and Molecular Heating

The nonequilibrium phonon population can be computed by setting a self-consistent calculation in which the average occupation of each vibrational mode is computed following a simple rate equation whose linearized solution is [12]

$${N}_{q} = \frac{{n}_{q}({T}_{0}){J}_{q} + {E}_{q}} {{J}_{q} + {A}_{q} - {E}_{q}}$$
(1)

where J q is the rate of phonon dissipated in the contacts, A q and E q are the rates of phonon absorbed and emitted in the molecule, and \({n}_{q}({T}_{0})\) is the equilibrium Bose–Einstein phonon distribution in the reservoirs. Expressions for A q and E q can be derived from the NEGF theory and can be found in [9]. Figure 5 shows the nonequilibrium distribution of quanta in all vibrational modes for different applied bias voltages. Solid lines are best distribution estimators assuming a Bose–Einstein form and give an effective molecular temperature. The estimator is defined such that the total energy stored in the vibrational modes is conserved, namely,

$$U ={ \sum }_{q}\hslash {\omega }_{q}{N}_{q} ={ \sum }_{q}\hslash {\omega }_{q}{n}_{q}({T}_{\mathit{mol}})$$
(2)

It is possible to observe that low-energy modes tend to be less populated with respect to the equilibrium distribution, whereas high-energy modes are much more populated. This effect is due to the fact that the electron–phonon coupling occurs mainly with the high-energy modes which couple very weakly to the reservoirs due to a strong band mismatch. It should be noted, however, that these calculations neglect anharmonicity eventually responsible for phonon decays from high to low energies. This redistribution is expected to give a final population that is much closer to an equilibrium distribution, characterized by an effective temperature, especially when internal relaxations are much faster than dissipation into the reservoirs. The equilibrium distribution that conserves total energy, as computed and shown in Fig. 5, is therefore realistic. It is also worth to observe that in these calculations it is not simply possible to just retain those few modes giving the largest IETS signal, but to the contrary, all vibrational modes must be included. This is because the actual equilibrium population depends on the delicate ratio between emission and absorption given by Eq. (1) in which the denominator can be small or the ratio can approach unity.

Fig. 5
figure 5

Average number of vibrational quanta in each molecular mode and temperature fit using a Bose–Einstein distribution

Full size image

The calculation of the coherent and incoherent current across the molecule includes a self-consistent calculation of the potential profile. In order to properly consider the tip shape, a large portion of the latter is included in the calculation at the level of an effective medium drift-diffusion model. This is necessary since a complete atomistic simulation of the tip would be computationally too demanding. An example of potential profile is shown in the right panel of Fig. 3, obtained by coupling the DFTB-NEGF charge density and potential solution [8] to the drift-diffusion solution, as explained in Sect. 1. The metallic contacts efficiently screen the applied bias and, as expected, the potential drops almost entirely across the tip/molecule/substrate junction due to its large resistance.

6 Coupling to Fourier Thermal Transport and Tip Heating

The knowledge of the temperature profile of the STM tip under bias is a relevant problem in order to understand tip-induced excitations and tip degradation and helps to disentangle the tip signal from molecular electroluminescence. In order to study this problem, the molecular heat dissipation is coupled to the tip and substrate where a simpler Fourier thermal transport model is used. This is done because the size of the contact makes rapidly intractable the problem of electron–phonon coupling and thermal transport at the atomistic level.

It turns out that the heat released in the molecule is only a small fraction of the total available power, \(P = I \cdot V\), from the applied bias. For instance, at the applied bias of 1.0 V, only about 1 nW is released in the molecule, whereas for a typical tunneling current of 1 μA, the power supplied is 1 μW, i.e., about three orders of magnitude larger. This does not immediately imply that electron–phonon scattering events are rare. In fact comparing the tunneling rate of \(\sim 1{0}^{13}\ e/s\) with the total absorption and emission rates of \(\sim 1{0}^{12}1/s\), we conclude that one electron in ten suffers an incoherent scattering. The net rate of phonon emitted is the result of the close balance between absorption and emission rates which tend to cancel each other.

Ultimately the electric power has to be released somewhere as heat. We assume that the hot electrons release their energy within a mean free path in the tip and the substrate that can be estimated to be about 5–10 nm. Consequently we assume that all the electronic energy is converted into heat within this distance.

In order to simulate how this energy is transported away along the tip and in the substrate, we couple the microscopic heat dissipation to a Fourier heat-transport equation. This phenomenological model requires as input the thermal conductivity of the materials, a quantity taken from database values that also depends on temperature. Thermal conductance is also strongly affected by size effects due to surface roughness scattering at the boundaries. Typically, the thermal conductance shows a Fuchs-Sondheimer behavior that scales with the inverse of the wire cross section. Metallic nanowires with 10-nm cross section can exhibit an increase of thermal resistance up to one order of magnitude with respect to bulk values. This is expected to play a crucial role near the tip apex, where the diameter can reach few nanometers. The size effect has been included in a phenomenological way, using the results of [13]. The thermal conductance of the vacuum gap between tip and substrate is assumed to be zero, although this may lead to a small error since it neglects radiative effects. The simulation is performed assuming an environment temperature of liquid Helium of 4.2 K as in low temperature STM [6]. In our simulations, however, we cannot simply assume fixed temperature boundary conditions since we are still simulating only a subpart of the whole system (2 μm of tip length rather than the whole tip of Fig. 1). Consequently a fixed thermal surface conductance is imposed on the outer boundaries of the tip and substrate cross sections, simulating an effective heat flux with bulk thermal conductivities. This is the same as assuming that the system is embedded in a material with constant thermal resistance and reaches the equilibrium thermostat temperature only far away from the tunneling junction.

The results of the nonequilibrium temperature profiles computed at a substrate bias of 1 V are shown in Fig. 6. The right and left diagrams show the temperature map in the tip and substrate, respectively. It is possible to appreciate how the size effect strongly influences the tip thermal conductance, hence the temperature map. Temperatures as high as 145 K can be found near the tip apex, where the hot tunneling electrons release their extra energy. On the other hand, the substrate that does not suffer size effects does not show noticeable heating.

Fig. 6
figure 6

Temperature profiles of the STM tip (right) and substrate (left)

Full size image

The temperature map depends on the heat-transport properties in the nanoscale tip which are lumped here into an effective thermal conductivity. A Fourier heat-transport model taking into account for size effects in a phenomenological way can be seen as a first approximation to the problem. Simulations based on the Boltzmann transport equation or atomistic phonon transport models including surface roughness and phonon–phonon scattering may be necessary in order to account for realistic density of states and nonequilibrium phonon transport, improving the accuracy of these predictions.

7 Conclusions

Density-functional tight-binding calculations and NEGF have been applied to the electron–phonon scattering and heat dissipation problem in a molecular junction. The calculations performed at atomistic scales serve as boundary condition to a drift-diffusion/Fourier model of charge and heat transport in the mesoscopic STM tip. The method can be seen as a first step towards a multiscale/multiphysics modeling of electrothermal coupling between molecular transport and heat dissipation in mesoscale continuum media. The calculations show that even at moderate applied biases, the STM tip apex can reach temperatures much larger than the environment. The model can be useful in future applications of molecular electronics devices.