Keywords

Introduction

The formation of perched water tables in the upper soil layers, during an infiltration process at low infiltration rate, is an important shallow-landslide triggering mechanism. In fact, when the soil approaches the saturation of the upper layers, the apparent cohesion reduces and, when the saturation is reached, also the effective strengths reduce. Soil failures can therefore be triggered not only by a positive pore pressure, but also by the presence of soil layers close to saturated conditions (e.g. van Asch et al. 2009). An accurate description of the subsurface soil-water dynamics, also accounting for the effect of the unhomogeneities of the soil hydraulic properties, can therefore lead to important information on soil safety. In this paper we will focus on the effect of the layering of the hydraulic conductivity at saturation on the soil-water dynamics. As a consequence of the genetic layering, in fact, the conductivity at saturation tends to decrease across the upper soil horizons, being higher in the A horizons, rich in macropores, and – due to intrasolum leakage – lower in the B ones (Kirkby 1969). On mountains, where strong erosive processes act and the mass movement is a key soil forming factor, the soil horizonation cannot fully develop and a smooth decrease of the conductivity at saturation typically occurs in the upper soil layers. Two limit cases can then describe the soil characteristics below the upper soil layers: one can find either an impervious bedrock, or a highly permeable layer of regolith or fractured and fissured rock. During our field measurement campaigns in two Alpine catchments, a gradual decrease, on average, was observed for the vertical conductivity at saturation through the upper soil layers (Barontini et al. 2005). Consistent with literature data (e.g. Beven 1984), the pattern was found to be reasonably approximated by an exponential decay. By means of an analytical solution of the 1D Richards equation in a layered soil, Barontini et al. (2007) proved that, during an imbibition at constant water content at the soil surface, a gradual decrease of the hydraulic conductivity can lead to non-monotonic profiles of water content. The profiles show a peak which onsets at the soil surface. It is then enveloped as the position of the maximum moves downward and its magnitude increases. Therefore, after some time since the beginning of the imbibition, a subsurface layer is characterized by a closer to saturation water content than the surface one. As the soil saturation is reached at one point, there a perched water table is expected to onset.

With the aim of better understanding these phenomena the case of infiltration at constant rate in a 2D sloping soil layer of finite thickness, with exponentially decreasing hydraulic conductivity at saturation with depth, was numerically investigated by means of Hydrus-2D/3D (Simunek et al. 1999) and the results are here presented. In order to extend the validity of the analyses to different soils and to guide further investigations, the problem was led to a dimensionless form based on an application of the Buckingham π-theorem and the results were compared with theoretical ones for the 1D (Barontini and Ranzi 2010) and 2D case (Barontini et al. 2011). Since a description of the pressure field in case of a perched water table formation is provided, the obtained results can contribute to better define the hydrological loads of hillslope stability analyses, particularly in the framework of the undefined-length slope. After a theoretical recall, the adopted dimensionless approach is presented. Then the set up of the numerical simulations and the results are introduced and discussed.

Theory

Perched Water Tables Formation and Properties

In a classical work, Zaslavsky (1964) stated that, in case of a horizontal pervious soil with conductivity K s,1 laying on an impervious one with conductivity K s,2  < K s,1 , the condition for a perched water table to onset in the upper layer is that the Darcian flux downward q, due to infiltration from the soil surface, is q > K s,2 . When a steady condition is reached in this case, the flux in the upper soil layer takes place in the direction of the increasing tensiometer-pressure potential, whose maximum is reached at the bottom of the saturated layer, at the interface with the impervious horizon. In a sharply layered soil, therefore, a perched water will onset within a layer (the layer 1 in the example) due to external causes, viz the conductivity reduction at the interface between the layer 1 and the underlying layer 2.

Barontini and Ranzi (2010) recently showed that in a horizontal and gradually layered soil, with decreasing hydraulic conductivity at saturation with depth K s (x*), being x* the vertical coordinate positive downward, a perched water table can onset also due to internal causes to the soil layer. Let us consider, in fact, a soil layer with finite thickness x f * characterized by monotonically decreasing K s (x*):

$$ {K_s}\left( {{x^{ * }}} \right) = {K_{{s,o}}}f\left( {{x^{ * }}} \right), $$
(1)

in which K s,o is the conductivity at saturation at the soil surface x* = 0 and f(x*) is a monotonically decreasing function such that f(0) = 1. Let us assume besides that the underlying soil layer is characterized by higher conductivity K s,2  > K s (x f *) and it is not able to exercise any retention. For the sake of continuity of the total hydraulic head Φ = η − x*, the tensiometer-pressure potential η of the soil at x f * should be null. We recall that the tensiometer-pressure potential is defined as η = ψ, i.e. the matric potential, if it is non-positive, while η = h, i.e. the pressure potential, if it is positive. A perched water table onsets if at x f *, being η = 0, the gradient of η is negative, i.e.:

$$ {\left. {\frac{{\rm d\eta }}{{\rm d{x^{ * }}}}} \right|_{{x_f^{ * }}}} < 0. $$
(2)

The infiltration threshold i f above which a perched water table onsets in the upper layer is given by:

$$ {i_f} = {K_s}\left( {x_f^{ * }} \right), $$
(3)

i.e. the value of K s (x f *) is the upper boundary for the infiltration rate in order not to onset a perched water table. At i f , in fact, the downward flux in x f *, expressed by the Darcy law, is sustained by a purely gravitational gradient. With the same hypotheses the infiltration rate i* leading the soil layer to waterlogging is given by the value of the equivalent hydraulic conductivity at saturation over the interval [0, x f ], i.e.:

$$ i^* = K_{{s,eq}}^{{\left[ {0,x_f^{ * }} \right]}} \equiv {K_{{s,o}}}\frac{{x_f^{ * }}}{{\int_0^{{x_f^{ * }}} {\frac{{\rm dx^{\prime}}}{{f\left( {x^{\prime}} \right)}}} }}. $$
(4)

As the perched water table is bounded by two surfaces at η = 0, it is also characterized by a maximum of η inside, in the position x* max such that:

$$ \begin{array}{lll} {i = {K_s}\left( {x_{{\max }}^{ * }} \right)} &, & {{i_f} < i \leqslant {i^{ * }}} \\\end{array}. $$
(5)

The corresponding η max = h max is directly given by an integration of the Darcy law within the saturated layer:

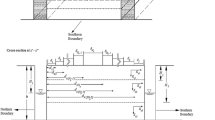
$$ {h_{{\max }}} = - \left( {x_f^{ * } - x_{{\max }}^{ * }} \right) + \int_{{x_{{\max }}^{ * }}}^{{x_f^{ * }}} {\frac{i}{{{K_x}\left( {x^{\prime}} \right)}}dx^{\prime}}. $$
(6)

Let us consider now a finite thickness soil layer laying on a hillslope, tilted of an angle β with the horizontal as represented in Fig. 1. Let x* be the transverse coordinate, such that x* = 0 at the soil surface and x* is positive as entering within the soil. Conversely let x be a vertical coordinate, with same origin as x*, positive downward. From Fig. 1 one gets that:

$$ {x^{ * }} = x\cos \beta. $$
(7)

Let the soil conductivity be eventually anisotropic, with principal directions x* and y*. The ratio r between the lateral and transverse conductivity at saturation is usually higher than 1. Now let i be the rainfall component normal to the soil surface. With the same condition at the lower boundary, i.e. η (x f *) = 0, but accounting for the 2D domain, a perched water is now considered to onset if:

$$ {\left. {\frac{{\partial \eta }}{{\partial {x^{ * }}}}} \right|_{{x_f^{ * }}}} < 0. $$
(8)

Consistent conditions at the lateral boundary at the domain are a no flux entering the domain at the upstream boundary, as for the presence of a watershed, and a seepage condition at the downstream boundary.

Fig. 1
figure 00201

Sketch of the investigated soil domain with details on the boundary conditions

Full size image

Barontini et al. (2011) showed that, under the hypothesis of undefined length of the slope, the infiltration threshold for condition (8) to hold is given by:

$$ {i_f}\left( \beta \right) = {K_s}\left( {x_f^{ * }} \right)\cos \beta, $$
(9)

which is less than the case of horizontal soil given by (3). This is due to the fact that the gravitational gradient sustaining the flux transversely to the soil layer is less effective as the slope increases. Therefore, the maximum infiltration, which can be sustained without gaining any negative pressure gradient at the lower soil interface, will be reduced accordingly. In the case of the soil of Fig. 1, one can also get the infiltration rate leading to waterlogging by means of the following equation:

$$ {i^{ * }}\left( \beta \right) = K_{{s,eq}}^{{\left[ {0;x_f^{ * }} \right]}}\cos \left( \beta \right), $$
(10)

which substitutes (4). The authors proved also that the position x* max, of the maximum pressure head within the perched water table, given by (5) does not depend, at fixed thickness of the perched water table, on the soil slope β. The value of the maximum h at waterlogging is given, from (6), by:

$$ {h_{{\max }}}\left( \beta \right) = {h_{{\max }}}\cos \beta. $$
(11)

In the investigated case the conductivity at saturation was assumed to exponentially decrease with depth with a scale of exponential decrease L. Equation 1 takes the form:

$$ {K_s}\left( {{x^{ * }}} \right) = {K_{{s,o}}}{e^{{ - \frac{{{x^{ * }}}}{L}}}}. $$
(12)

If referred to x, (12) takes the form:

$$ \begin{array}{lll} {{K_s}(x) = {K_{{s,o}}}{e^{{ - \frac{x}{{L^{\prime}}}}}}} &, & {L^{\prime} = \frac{L}{{\cos \beta }}} \\\end{array}. $$
(13)

Equations 12 and 13 allow to determine the numerical values given by (3, 4, 5 and 6) and (9, 10 and 11) for a horizontal and a sloping soil, respectively.

Dimensionless Approach

According to Corey et al. (1965) the firsts to describe the displacement of immiscible fluids in a porous medium by means of a dimensionless approach were Leverett and Coauthors in their 1942 paper (Leverett et al. 1942). Since then various approaches were attempted in this direction, both at the microscale, typically in view of petrologic applications, and at a continuum scale, for hydraulic and hydrological applications. A dimensionless approach can prove to be very powerful both in order to design hydraulic models and in order to lead the parameters choices for numerical applications. One of the key aspects of a dimensionless approach to the flow of immiscible fluids in a porous medium is the capability of properly representing, in dynamically coherent dimensionless form, the interfacial pressure of the fluids, viz the capillary curve in the case of the water flow in a granular porous medium. Leverett et al. (1942) suggested that, if expressed in a particular dimensionless form, the capillary curves of unconsolidated sands coalesce on a single curve, the so called j function. In the case, instead, of an organic soil, for which the relationship between the water content and its energetic state should account also for the effect of the organic matter content, the coalescence of the retention relationship on the same curve is much more difficult. Corey et al. (1965) therefore stated that a model of flow in an unsaturated soil will be effective only if the soil-water constitutive laws have the same structure and the same values for some parameters.

In this work we propose a parameters choice, based on an application of the Buckingham π-theorem in the framework of a continuum approach, in order to describe the effect of the soil anisotropy and steepness on the following steady properties of the perched water tables: (a) the infiltration threshold for a perched water table to onset, (b) the infiltration rate to lead the soil to waterlogging, (c) the position and magnitude of the maximum positive pressure head at waterlogging. Even if the problem is characterized by a transition from unsaturated to saturated soil, the proposed dimensionless approach is focused on steady and saturated flow conditions, which are not sensitively affected by the soil-water retention relationship. The obtained results can be therefore reliable also for different soils with different soil-water constitutive laws.

Considering the case of a steady infiltration in an exponentially K s -decreasing soil, inferiorly bounded by a surface at ψ(x f *) = ψ(x f ) = 0 and for defined initial conditions, we can write, for any generic state property S of the soil, the formal dependency:

$$ S = f(\phi, {\theta_s},{\theta_r},{\psi_1},m,n,\ell, {K_{{s,o}}},L^{\prime},r,{x_f},{y_v},\beta, i). $$
(14)

In (14), besides the parameters already introduced, φ, θ s, θ r [−] are respectively the porosity, the volumetric water content at saturation, and the volumetric residual water content; ψ 1 [L], m [−], n [−] are the parameters of the soil-water retention relationship described by van Genuchten’s function, with the usual constraint that m = 1 − 1/n; ℓ is the relative-conductivity function parameter, according to Mualem’s framework; y v is the horizontal projection of the slope length.

Before analysing (14) three important remarks need to be added. Firstly, as a continuum approach was chosen, the dependency on the water mechanical properties, viz its density, its dynamic viscosity and its capillary tension at the air–water interface, are not explicitly represented but they are implicitly accounted for in the definition of the hydraulic conductivity at saturation and of the soil–water retention relationship parameters. Then, focusing on the description of the soil–water dynamics, it is not needed to explicit any dependency of S on soil mechanical properties, e.g. the soil particle density, its cohesion or its angle of internal friction. Finally as the unique mass force involved in the problem is the gravitational field, it is not explicitly represented in the formulation but it is implicitly included in the definition of the hydraulic conductivity at saturation.

In (14) there are on the whole 14 parameters which can be roughly grouped as in the followings. The parameters φ, θ s, θ r, ψ 1, m, n, ℓ, K s,o (8 parameters) describe the soil–water constitutive laws. Among these, the porosity φ does not play here an important role as the control role on the soil capacity of storing water is played by the effective porosity θ s − θ r; φ will be therefore neglected in the further analysis. Moreover Mualem’s ℓ parameter is usually set at 0.5. Its dependency in the dimensional analysis will be neglected as well. The characterising parameters of the soil-water constitutive laws are therefore reduced to the 6 parameters of the van Genuchten-Mualem framework. L′ and r (2 parameters) describe the conductivity unhomogeneity and anisotropy (L′ being introduced in [13]); x f , y v , β (3 parameters) describe the problem geometry. Finally i, only 1 parameter, describes the boundary conditions as the other boundary conditions are structural for the problem and will not be explicitly introduced in the dimensional analysis. By a dimensional point of view the parameters can be grouped into three groups. φ, θ s, θ r, m, n, ℓ, r, β (8 parameters) are dimensionless and are presented in their basic form, i.e. they have not been normalized yet; ψ 1, L′, x f , y v (4 parameters) are lengths [L]; K s,o , i (2 parameters) are velocities [LT−1].

As observed e.g. by Corey et al. (1965, p.7), the effective soil porosity θ s − θ r characterises the non-steady soil dynamics. Here, as steady conditions are focused on, it is dropped from the dimensional analysis. Moreover as it appears from (5, 9, 10 and 11), which hold for a sloping soil, also the other parameters characterizing the unsaturated soil flow, i.e. m, n, ℓ and ψ 1, do not explicitly emerge from the theoretical framework. This fact is mainly due to the focus on properties of saturated conditions flow. Therefore also these parameters are dropped from the dimensional analysis. Equation 14 is rewritten as:

$$ S = f({K_{{s,o}}},L^{\prime},r,{x_f},{y_v},\beta, i). $$
(15)

According to the Buckingham π-theorem, only two dimensional scales are required in this case to fully express the problem in a dimensionless form. The set of dimensional variables we propose is given by a scaling-length L s  = x f and a scaling-velocity U s  = K s,o . In dimensionless form, and with the usual symbol π for the dimensionless variables, (15) is rewritten as:

$$ {\pi_S} = F({\pi_{{L^{\prime}}}},{\pi_y},{\pi_i},r,\beta ). $$
(16)

The effect of π i , r, β on the formation, the thickness and the maximum pressure head of a perched water table will be explored. The theoretical values previously presented are rewritten in dimensionless form. One gets for i f :

$$ {\pi_{{{i_f}}}} = {e^{{ - \frac{1}{{{\pi_{{L^{\prime}}}}}}}}}\cos \beta, $$
(17)

and for i*:

$$ {\pi_{{i*}}} = \frac{1}{{{\pi_{{L^{\prime}}}}\left( {{e^{{\frac{1}{{{\pi_{{L^{\prime}}}}}}}}} - 1} \right)}}\cos \beta. $$
(18)

Numerical Experiments

The numerical experiments were designed in order to simulate a steady process at constant infiltration rate by means of the software Hydrus-2D/3D, which numerically solves the Richards equation. The dimensions of the mesh are given in Fig. 1. In order to represent a gradually decreasing conductivity with depth, the 0.5 m-thick soil layer was subdivided into five layers of 0.1 m, each of them with uniform conductivity at saturation, equivalent to that of the gradually varying layer over the same thickness (e.g. Barontini et al. 2007). K s,o was assumed to be 8.14E-04 m/s and L′ = 0.19 m. A coupled van Genuchten-Mualem constitutive laws model applied to describe the unsaturated soil-water properties. ψ 1 = 0.16 m, m = 0.34, n = 1.51, measured for a sand, were chosen as retention curve parameters. As initial conditions were required in order to perform the simulations, aiming at defining steady and almost uniform conditions along the slope, a 12 h preliminary simulation at low infiltration rate (1.4E-06 m/s) was performed. The obtained initial conditions are represented in Fig. 2. Referring to (16) two dimensionless parameters were fixed (π L′  = 0.38, π y  = 20); the maximum value of π i was chosen bigger than π i* , enough to observe waterlogging; r was chosen equal to 1, 5, 10, and β spanning from 5° to 30° each 5°.

Fig. 2
figure 00202

Initial conditions of the flow domain after 12 h infiltration at low infiltration rate, β = 15°, r = 5

Full size image

As an example of the results, in Fig. 3 the pressure potential field of a 15° sloping soil with anisotropy factor r = 5 is represented for i*. As it can be seen an area of positive pressure head, up to a pressure potential of 0.15 m, is observed in the central part of the mesh. This area is above and below bounded by surfaces at null or negative matric potential ψ and, even if there is a long central branch at almost uniform characteristics, upstream and downstream boundary effects are observed. The length of the branches affected by boundary effects increases as the anisotropy factor increases, so that at r = 10 it was not recognizable, for the investigated slope, a central branch with uniform-flow pattern. On the other hand, at r = 1, i.e. in the absence of anisotropy, the central branch with almost uniform pressure distribution is much longer and there the hypothesis of uniform flow is realistic.

Fig. 3
figure 00203

Steady state conditions after 6 h simulation with soil at waterlogging, β = 15°, r = 5

Full size image

Discussion

In Figs. 4 and 5 the steady profiles of ψ and h in the middle section of the mesh are plotted, as a function of β and at r = 5, for the two limit cases of infiltration rate i f and i*. In the unsaturated range a flow takes place in the direction of the increasing ψ. The ψ-profiles are weakly sensitive to β and close to saturation, thus playing an important role for the soil stability. At the bottom an almost vertical slope of the profile is observed. The corresponding dimensionless i f (β) given by (17) are represented in Fig. 6. It can be seen that i f (β) is less than that estimated for the case of β = 0°, coherently with the theory. It is moreover well interpreted by the theoretical model both for the magnitude and for the independence on the soil anisotropy.

Fig. 4
figure 00204

Tensiometer-pressure profiles in the middle section of the flow domain, in steady conditions, at i = i f

Full size image
Fig. 5
figure 00205

Pressure profiles in the middle section of the flow domain, in steady conditions, at i = i*

Full size image
Fig. 6
figure 00206

Dimensionless infiltration rates π if  = i f /K s,o and π i*  = i*/K s,o as a function of the slope β and of the anisotropy factor r, compared with the corresponding estimates for the 1D case (dashed black lines) and for the 2D case (dashed red lines)

Full size image

In Fig. 5 the pressure profiles at waterlogging are represented for the same case at r = 5. The non-monotonic patterns of h are observed. Moreover the maximum of h is reached almost in the same position for all the curves, accordingly with the theoretical analyses, and it is quite sensitive at β, since it decreases as β increases. The corresponding dimensionless i*(β) given by (18) are represented in Fig. 6 and compared with the theoretical 1D and 2D estimate. Also in this case i*(β) is less than that estimated for the case of β = 0° and it is sensitive to the soil slope. The agreement with theoretical values is worse than for i f (β) as the anisotropy factor r increases. This behavior is attributed to the fact that, at increasing r the branch, where an almost uniform flux takes place, reduces and the boundary effects gain importance.

The maximum pressure head π h,max = h max //x f is represented in Fig. 7 depending on β and r and compared with theoretical 1D and 2D estimates (the latter is reported as quasi-1D in the Figure). It is not sensitively dependent on r and the agreement between the 2D theoretical and numerical results is fair.

Fig. 7
figure 00207

Dimensionless maximum pressure head π h,max = h max /x f in the middle section at waterlogging infiltration rate as a function of the slope β and of the anisotropy factor r, compared with the corresponding estimates for the 1D case (dashed black line) and for the 2D case (“quasi-1D”, dashed red line)

Full size image

Conclusions

The conditions for perched water table formation and for waterlogging were numerically investigated for a sloping soil layer characterized by exponentially decreasing conductivity with depth. The numerical results were compared with theoretical analyses. In order to lead the numerical experiments and to define a methodology to generalize the results, a preliminary dimensional analysis was performed. The vertical soil depth x f and the upper soil hydraulic conductivity at saturation K s,o were proposed as a set of independent variables in order to transform the problem in dimensionless form. Five dimensionless groups, including the anisotropy coefficient r and the soil slope β, were addressed to describe the steady properties of the perched water table. The numerical results and the theoretical 2D analyses provided by Barontini et al. (2011) were found to be in good agreement for the infiltration rate at the perched water table onset, for the maximum pressure head at waterlogging, and for the infiltration rate at waterlogging for low values of the anisotropy factor. The agreement is worse as the anisotropy factor increases because the uniform flow hypotheses underlying to the theoretical framework require longer slopes in order to properly apply.