Abstract
General and effective methods are required for providing good automation strategies to prove properties of sequent systems. Structural properties such as admissibility, invertibility, and permutability of rules are crucial in proof theory, and they can be used for proving other key properties such as cut-elimination. However, finding proofs for these properties requires inductive reasoning over the provability relation, which is often quite elaborated, exponentially exhaustive, and error prone. This paper aims at developing automatic techniques for proving structural properties of sequent systems. The proposed techniques are presented in the rewriting logic metalogical framework, and use rewrite- and narrowing-based reasoning. They have been fully mechanized in Maude and achieve a great degree of automation when used on several sequent systems, including intuitionistic and classical logics, linear logic, and normal modal logics.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Contemporary proof theory started with Gentzen’s natural deduction and sequent calculus in the 1930’s [7], and it has had a continuous development with the proposal of several proof systems for many logics. Proof systems are important tools for formalizing, reasoning, and analyzing structural properties of proofs, as well as determining computational and metalogical consequences of logical systems. As a matter of fact, proposing good calculi is one of the main research topics in proof theory.
It is more or less consensus that a good proof system should support the notion of analytic proof [5], where every formula that appears in a proof must be a sub-formula of the formulas to be proved. This restriction can be exploited to prove important metalogical properties of sequent systems such as consistency. In sequent systems, analyticity is often guaranteed by the cut-elimination property: if B follows from A and C follows from B, then C follows from A. That is, intermediate lemmas (e.g., B) can be “cut” from the proof system. It turns out that the proof of cut-elimination for a given system is often quite elaborated, exponentially exhaustive, and error prone. Hence the need for general and effective methods for providing good automation strategies. In the case of cut-elimination, some of such methods strongly depend on the ability of showing permutability of rules that may depend on additional properties such as admissibility and invertibility of rules, which – in turn – may require induction-based reasoning.
Rewriting logic [6, 15] is a metalogical framework that can be used to represent other logics and to reason about their metalogical properties [14]. When compared to a logical framework, a metalogical framework is more powerful because it includes the ability to reason about a logic’s entailment relation as opposed to just being sound to simulate it. Moreover, important computational aspects of the logical system under study need to be encoded in flexible ways, so that such a system can become data, and be subject to transformations and efficient execution in a computational engine. Thanks to its reflective capabilities and initial reachability semantics, important inductive aspects of rewriting logic theories can be encoded in its own metalanguage so that theories, proofs, and provability can be mechanically analyzed with the help of rewriting logic systems such as Maude [6].
This paper develops new techniques, using rewriting logic as a metalogical framework, for reasoning about properties of sequent systems. Relying on rewrite- and narrowing-based reasoning, these techniques are introduced as procedures for proving admissibility, invertibility, and permutability of inference rules. Such procedures have been fully implemented in Maude. The case study analyses included in this paper comprise the following sequent systems: propositional intuitionistic logic (\(\mathsf {G3ip}\)), multi-conclusion propositional intuitionistic logic (\(\mathsf {mLJ}\)), propositional classical logic (\(\mathsf {G3cp}\)), propositional linear logic (\(\mathsf {LL}\)), and normal modal logics (\(\mathsf {K}\) and \(\mathsf {S4}\)). Beyond advocating for the use of rewriting logic as a metalogical framework, the novel algorithms presented here are able to automatically discharge many proof obligations and ultimately obtain the expected results.
The approach can be summarized as follows. The inference rules of a sequent system \(\mathcal {S}\) are specified as (backward) rewrite rules modulo structural axioms (e.g., associativity, commutativity, and identity) in \(\mathcal {R}_\mathcal {S}\), inducing a rewrite relation \(\rightarrow _\mathcal {S}\) on multisets of sequents. From the rewriting logic viewpoint, the main results presented here are metatheorems about inductive reachability properties of \(\rightarrow _\mathcal {S}\). These metatheorems entail sufficient conditions for proving inductive properties that can be generated and checked with the help of term rewriting and narrowing. More precisely, given an inductive property \(\phi \) about \(\mathcal {S}\), several subgoals \(\phi _i\) are generated by unification modulo axioms. The system \(\mathcal {S}\) is extended to \(\mathcal {S}'\) by adding inductive lemmas as axioms and, if each \(\phi _i\) can be \(\rightarrow _{\mathcal {S}'}\)-rewritten to the empty multiset, then \(\phi \) holds in the initial reachability model of \(\mathcal {S}\). In such a process, the original rewrite theory \(\mathcal {R}_\mathcal {S}\) is extended and transformed in several ways: a painless task to implement thanks to the off-the-shelf reflective capabilities of rewriting logic supported by Maude. Ultimately, the resulting metatheorems can be seen as tactics for automating reasoning of sequent systems in rewriting logic. This approach is generic in the sense that only mild restrictions are imposed on the formulas of the sequent system \(\mathcal {S}\) and modular since properties can be proved incrementally.
Outline. The rest of the paper is organized as follows. Section 2 introduces the structural properties of sequent systems that are considered in this work and Sect. 3 presents order-sorted rewriting logic and its main features as a logical framework. Then, Sect. 4 establishes how to prove the structural properties based on a rewriting approach and Sect. 5 shows how to automate the process of proving these properties. Section 6 presents different sequent systems and properties that can be proved with the approach. Finally, Sect. 7 concludes the paper and presents some future research directions.
2 Three Structural Properties of Sequent-Based Logics
This section presents and illustrates three structural properties of sequent systems, namely, permutability, admissibility, and invertibility of rules. Notation and standard definitions are presented, which are illustrated with detailed examples.
Definition 1
(Sequent). Let \(\mathcal {L}\) be a formal language consisting of well-formed formulas. A sequent is an expression of the form \(\varGamma \vdash \varDelta \) where \(\varGamma \) (the antecedent) and \(\varDelta \) (the succedent) are finite multisets of formulas in \(\mathcal {L}\), and \(\vdash \) is the meta-level symbol of consequence. If the succedent of a sequent contains at most one formula, it is called single-conclusion, and multiple-conclusion, otherwise.
Definition 2
(Sequent System). A sequent system \(\mathcal {S}\) is a set of rules of the form

where the sequent S is the conclusion inferred from the premise sequents \(S_1,\ldots ,S_n\) in the rule r. If the set of premises is empty, then r is an axiom. In a rule introducing a connective, the formula with that connective in the conclusion sequent is the principal formula, and its sub-formulas in the premises are the auxiliary formulas. Systems with empty antecedents are called one-sided; otherwise they are called two-sided.
As an example, Fig. 1 presents the two-sided single-conclusion propositional intuitionistic sequent system \(\mathsf {G3ip}\) [21], with formulas built from the grammar:
where p is an atomic proposition. In this system, for instance, the conclusion \(F\vee G\) of \(\vee _L\) is the principal formula, while the formulas F and G are auxiliary formulas.
Definition 3
(Derivation). A derivation in a sequent system \(\mathcal {S}\) (called \(\mathcal {S}\)-derivation) is a finite labeled tree with nodes labeled by sequents and a single root, axioms at the top nodes, and where each node is connected with the (immediate) successor nodes (if any) according to the inference rules. A sequent S is derivable in the sequent system \(\mathcal {S}\), denoted  , iff there is a derivation of S in \(\mathcal {S}\). The system \(\mathcal {S}\) is usually omitted when it can be inferred from the context.
, iff there is a derivation of S in \(\mathcal {S}\). The system \(\mathcal {S}\) is usually omitted when it can be inferred from the context.
It is important to clearly distinguish the two different notions associated to the symbols  and
and  namely: the former is used to build sequents, while the latter (introduced in Definition 3) denotes derivability in a sequent system.
namely: the former is used to build sequents, while the latter (introduced in Definition 3) denotes derivability in a sequent system.
Definition 4
(Height of derivation). The height of a derivation is the greatest number of successive applications of rules in it, where an axiom has height 0.
The structural property of rule permutability [17, 19] is stated next.
Definition 5
(Permutability). Let \(r_1\) and \(r_2\) be inference rules in a sequent system \(\mathcal {S}\). The rule \(r_2\) permutes down \(r_1\), notation \(r_2 \downarrow r_1\), if for every \(\mathcal {S}\)-derivation of a sequent S in which \(r_1\) operates on S and \(r_2\) operates on one or more of \(r_1\)’s premises (but not on auxiliary formulas of \(r_1\)), there exists another \(\mathcal {S}\)-derivation of S in which \(r_2\) operates on S and \(r_1\) operates on zero or more of \(r_2\)’s premises (but not on auxiliary formulas of \(r_2\)).
For instance, consider the left \(\vee _L\) and right \(\vee _{R_i}\) rules for disjunction in \(\mathsf {G3ip}\). First, it can be observed that \(\vee _L\downarrow \vee _{R_i}\) by using the following transformation:

The inverse permutation, however, does not hold, i.e.,  . In fact, in the following derivation,
. In fact, in the following derivation,

derivability of  does not imply derivability of
does not imply derivability of  ; hence, such a derivation cannot start by applying the rule \(\vee _{R_i}\).
; hence, such a derivation cannot start by applying the rule \(\vee _{R_i}\).
Other two important structural properties are admissibility and invertibility.
Definition 6
(Admissibility and Invertibility). Let \(\mathcal {S}\) be a sequent system. An inference rule

is called:
-
i.
admissible in \(\mathcal {S}\) if S is derivable in \(\mathcal {S}\) whenever \(S_1,\ldots , S_n\) are derivable in \(\mathcal {S}\).
-
ii.
invertible in \(\mathcal {S}\) if the rules \(\frac{S}{S_1}, \ldots , \frac{S}{S_n}\) are admissible in \(\mathcal {S}\).
Proving invertibility often requires induction on the height of derivations, where all the possible rule applications have to be considered. For example, for proving that \(\vee _L\) is invertible in \(\mathsf {G3ip}\), the goal is to show that both  and
and  are derivable whenever
are derivable whenever  is derivable. The result follows by a case analysis on the shape of the derivation of
is derivable. The result follows by a case analysis on the shape of the derivation of  . Consider, e.g., the case when \(C=A\supset B\) and the last rule applied is \(\supset _{R}\), i.e., consider the following derivation:
. Consider, e.g., the case when \(C=A\supset B\) and the last rule applied is \(\supset _{R}\), i.e., consider the following derivation:

Then, by the inductive hypothesis,  and
and  are derivable and, by using \(\supset _R\), the following holds:
are derivable and, by using \(\supset _R\), the following holds:

as needed. On the other hand, \(\vee _{R_i}\) is not invertible: if \(p_1,p_2\) are different atomic propositions, then  is derivable for \(i=1,2\), but
is derivable for \(i=1,2\), but  is not for \(i\not = j\).
is not for \(i\not = j\).
In general, proving invertibility may involve some subtle details, as it will be seen in Sect. 6. A common one is the need for admissibility of the weakening structural rule. A structural rule does not introduce logical connectives, but instead changes the structure of the sequent. Since sequents are built from multisets, such changes are related to the cardinality of a formula or its presence/absence in a context. For example, the structural rules for weakening and contraction in the intuitionistic setting are:

These rules are admissible in \(\mathsf {G3ip}\). The proof of admissibility of weakening is independent of any other results and it is also by induction on the height of derivations (and considering all possible rule applications).
Admissibility of contraction is more involved and often it depends on invertibility results. As an example, suppose that

Observe that the inductive hypothesis cannot be applied since the premises do not have duplicated copies of auxiliary formulas. In order to obtain a proof, invertibility of \(\vee _L\) is needed: the derivability of  and
and  implies the derivability of
implies the derivability of  and
and  ; moreover, by the inductive hypothesis,
; moreover, by the inductive hypothesis,  and
and  are derivable, and the result follows.
are derivable, and the result follows.
3 Rewriting Logic Preliminaries
This section briefly explains order-sorted rewriting logic [15] and its main features as a logical framework. Maude [6] is a language and tool supporting the formal specification and analysis of rewrite theories.
An order-sorted signature \(\varSigma \) is a tuple \(\varSigma = (S,\le ,F)\) with a finite poset of sorts \((S,\le )\) and a set of function symbols F typed with sorts in S, which can be subsort-overloaded. For \(X = \{X_s\}_{s\in S}\) an S-indexed family of disjoint variable sets with each \(X_s\) countably infinite, the set of terms of sort s and the set of ground terms of sort s are denoted, respectively, by \(T_\varSigma (X)_s\) and \(T_{\varSigma ,s}\); similarly, \(T_\varSigma (X)\) and \(T_\varSigma \) denote the set of terms and the set of ground terms. A substitution is an S-indexed mapping \(\theta : X \longrightarrow T_\varSigma (X)\) that is different from the identity only for a finite subset of X and such that \(\theta (x) \in T_\varSigma (X)_s\) if \(x \in X_s\), for any \(x \in X\) and \(s\in S\). A substitution \(\theta \) is called ground iff \(\theta (x) \in T_\varSigma \) or \(\theta (x) = x\) for any \(x \in X\). The application of a substitution \(\theta \) to a term t is denoted by \(t\theta \).
A rewrite theory is a tuple \(\mathcal {R}= (\varSigma , E \uplus B, R)\) with: (i) \((\varSigma , E \uplus B)\) an order-sorted equational theory with signature \(\varSigma \), E a set of (possibly conditional) equations over \(T_\varSigma \), and B a set of structural axioms – disjoint from the set of equations E – over \(T_\varSigma \) for which there is a finitary matching algorithm (e.g., associativity, commutativity, and identity, or combinations of them); and (ii) R a finite set of (possibly with equational conditions) rewrite rules over \(T_\varSigma \). A rewrite theory \(\mathcal {R}\) induces a rewrite relation \(\rightarrow _{\mathcal {R}}\) on \(T_{\varSigma }(X)\) defined for every \(t,u \in T_\varSigma (X)\) by \(t \rightarrow _\mathcal {R}u\) if and only if there is a rule \((l \rightarrow r\; \mathbf{if} \; {\phi }) \in R\) and a substitution \(\theta : X \longrightarrow T_\varSigma (X)\) satisfying \(t =_{E \uplus B} l\theta \), \(u =_{E \uplus B} r\theta \), and \(\phi \theta \) is (equationally) provable from \(E\uplus B\) [2].
Appropriate requirements are needed to make an equational theory \(\mathcal {R}\) executable in Maude. It is assumed that the equations E can be oriented into a set of (possibly conditional) sort-decreasing, operationally terminating, and confluent rewrite rules \(\overrightarrow{E}\) modulo B [6]. For a rewrite theory \(\mathcal {R}\), the rewrite relation \(\rightarrow _\mathcal {R}\) is undecidable in general, even if its underlying equational theory is executable, unless conditions such as coherence [22] are given (i.e., rewriting with \(\rightarrow _{R/E \uplus B}\) can be decomposed into rewriting with \(\rightarrow _{E/B}\) and \(\rightarrow _{R/B}\)). The executability of a rewrite theory \(\mathcal {R}\) ultimately means that its mathematical and execution semantics coincide.
The rewriting logic specification of a sequent system \(\mathcal {S}\) is a rewrite theory \(\mathcal {R}_\mathcal {S}= (\varSigma _\mathcal {S}, E_\mathcal {S}\uplus B_\mathcal {S}, R_\mathcal {S})\) where: \(\varSigma _\mathcal {S}\) is an order-sorted signature describing the syntax of the logic \(\mathcal {S}\); \(E_\mathcal {S}\) is a set of executable equations modulo \(B_\mathcal {S}\) corresponding to those parts of the deduction process that, being deterministic, can be safely automated as computation rules without any proof search; and \(R_\mathcal {S}\) is a set of executable rewrite rules modulo \(B_\mathcal {S}\) capturing those non-deterministic aspects of logical inference in \(\mathcal {S}\) that require proof search. The point is that although both the computation rules \(E_\mathcal {S}\) and the deduction rules \(R_\mathcal {S}\) are executed by rewriting modulo the set of structural axioms \(B_\mathcal {S}\), by the executability assumptions on \(\mathcal {R}_\mathcal {S}\), the rewrite relation \(\rightarrow _{E_\mathcal {S}/ B_\mathcal {S}}\) has a single outcome in the form of a canonical form and thus can be executed blindly with “don’t care” non-determinism and without any proof search. Furthermore, \(B_\mathcal {S}\) provides yet one more level of computational automation in the form of \(B_\mathcal {S}\)-matching and \(B_\mathcal {S}\)-unification algorithms. This interplay between axioms, equations, and rewrite rules can ultimately make the specification \(\mathcal {R}_\mathcal {S}\) very efficient with modest memory requirements.
4 Checking Admissibility, Invertibility, and Permutability
This section presents rewrite- and narrowing-based techniques for proving admissibility, invertibility, and permutability in sequent systems. They are presented as metatheorems about sequent systems – with the help of rewrite-based scaffolding such as terms and substitutions – and provide sufficient conditions for proving the desired properties.
The techniques introduced in this section assume that a sequent system \(\mathcal {S}\) is a set of inference rules with sequents in the set \(T_{\varSigma _\mathcal {S}}(X)\), where \(\varSigma _\mathcal {S}\) is an order-sorted signature (see Section 3). The expression \(\mathcal {S}_1 \cup \mathcal {S}_2\) denotes the extension of the sequent system \(\mathcal {S}_1\) by adding the inference rules of \(\mathcal {S}_2\) (and vice versa); in this case, the sequents in the resulting sequent system \(\mathcal {S}_1 \cup \mathcal {S}_2\) are terms in the signature \(\varSigma _{\mathcal {S}_1} \cup \varSigma _{\mathcal {S}_2}\). By an abuse of notation, for \(\mathcal {S}\) a sequent system and S a sequent, the expression \(\mathcal {S}\cup \{S\}\) denotes the sequent system obtained from \(\mathcal {S}\) by adding the sequent S as an axiom, understood as a zero-premise rule. This convention is extensively used in the main results of this section. Finally, given a term \(t \in T_{\varSigma _\mathcal {S}}(X)\), with \(\varSigma _\mathcal {S}= (S,\le ,F)\), \(\overline{t} \in T_{(S,\le , F\cup C_{\overline{t}})}(X)\) is the term obtained from t by turning each variable \(x \in \textit{vars}(t)\) of sort \(s\in S\) into the fresh constant \(\overline{x}\) of sort s and where \(C_{\overline{t}} = \{\overline{x} \mid x \in \textit{vars}(t) \}\)
It is assumed the existence of a unification algorithm for multisets (or sets) of sequents. Given two sequent terms S and T built from a signature \(\varSigma _\mathcal {S}\) and structural axioms \(B_\mathcal {S}\), the expression \(\textit{CSU}_{B_\mathcal {S}}(S, T)\) denotes the complete set of unifiers of S and T modulo \(B_\mathcal {S}\). Recall that \(\textit{CSU}_{B_\mathcal {S}}(S, T)\) satisfies that, for each substitution \(\sigma : X \longrightarrow T_\varSigma (X)\), there are substitutions \(\theta \in \textit{CSU}_{B_\mathcal {S}}(S, T)\) and \(\gamma : X \longrightarrow T_\varSigma (X)\) such that \(\sigma =_{B_\mathcal {S}} \theta \gamma \). Note that for a combination of free and associative and/or commutative and/or identity axioms \(B_\mathcal {S}\), except for symbols that are associative but not commutative, such a finitary unification algorithm exists. In the development of this section, the expression \(\textit{CSU}\) is used as an abbreviation for \(\textit{CSU}_{B_\mathcal {S}}\), where \(B_\mathcal {S}\) are the structural axioms for sets/multisets of sequents.
Definition 7 introduces a notion of admissibility of a rule relative to another rule.
Definition 7
(Local admissibility). Let  be a rule, \(\mathcal {S}\) be a sequent system and
be a rule, \(\mathcal {S}\) be a sequent system and  be an inference rule in \(\mathcal {S}\). The rule \(r_s\) is admissible relative to \(r_t\) in \(\mathcal {S}\) iff for each \(\theta \in \textit{CSU}(S_1,T)\):
be an inference rule in \(\mathcal {S}\). The rule \(r_s\) is admissible relative to \(r_t\) in \(\mathcal {S}\) iff for each \(\theta \in \textit{CSU}(S_1,T)\):

where the variables in S and T are assumed disjoint.
For proving admissibility of the rule \(r_s\), the goal is to prove that if \(S_1\) is derivable, then S is derivable. The proof follows by induction on the height of a derivation \(\pi \) of \(S_1\) (see Sect. 2). Suppose that the last rule applied in \(\pi \) is \(r_t\). This is only possible if \(S_1\) and T “are the same”, up to substitutions. Hence, the idea is that each unifier \(\theta \) of \(S_1\) and T covers the cases where the rule \(r_t\) can be applied on the sequent \(S_1\); different proof obligations are generated for each unifier. Consider, for instance, the proof obligation of the ground sequent \(\overline{S\theta }\) for a given \(\theta \in \textit{CSU}(S_1, T)\). Namely, assume as hypothesis that the derivation below is valid in order to show that the sequent \(\overline{S\theta }\) is provable:

This means that all the premises in (1) should be assumed derivable. This is the purpose of extending the sequent system with the set of ground sequents \(\left\{ \overline{T_j\theta } \mid j \in 1 .. n \right\} \), interpreted here as axioms, in Definition 7. Moreover, by induction, it can be assumed that the theorem (i.e., \(S_1\) implies S) is valid for the premises of (1) (note that such premises have a shorter derivation compared to the derivation of \(S_1\theta \)). Therefore, the following set of sequents can also be assumed as derivable and, thus, are added as axioms:
If, from the extended sequent system it is possible to show that the ground sequent \(\overline{S\theta }\) is derivable, then the theorem will work for the particular case when \(r_t\) is the last applied rule in the derivation \(\pi \) of \(S_1\). Since a complete set of unifiers is finite for sequents (as assumed in this section for any sequent system \(\mathcal {S}\)), then there are finitely many proof obligations to discharge in order to check if a rule is admissible relative to a rule in a sequent system. Observe that the set \(\textit{CSU}(S,T)\) may be empty. In this case, the set of proof obligations is empty and the property vacuously holds.
Theorem 1 presents sufficient conditions for the admissibility of a rule in a sequent system based on the notion of admissibility relative to a rule.
Theorem 1
Let \(\mathcal {S}\) be a sequent system and  be an inference rule. If \(r_s\) is admissible relative to each \(r_t\) in \(\mathcal {S}\), then \(r_s\) is admissible in \(\mathcal {S}\).
be an inference rule. If \(r_s\) is admissible relative to each \(r_t\) in \(\mathcal {S}\), then \(r_s\) is admissible in \(\mathcal {S}\).
Proof
Assume that \(S_1\) is derivable in the system \(\mathcal {S}\). The proof proceeds by induction on the height of such a derivation with case analysis on the last rule applied. Assume that the last applied rule is \(r_t\). By hypothesis (using Definition 7), it can be concluded that S is derivable and the result follows.
The following definition introduces a notion of invertibility of a rule relative to another rule.
Definition 8
(Local invertibility). Let \(\mathcal {S}\) be a sequent system, and let  and
and  be inference rules in \(\mathcal {S}\). The rule \(r_s\) is invertible relative to \(r_t\) iff for each \(\theta \in \textit{CSU}(S,T)\) and \(1\le l\le m \):
be inference rules in \(\mathcal {S}\). The rule \(r_s\) is invertible relative to \(r_t\) iff for each \(\theta \in \textit{CSU}(S,T)\) and \(1\le l\le m \):

where the variables in S and T are assumed disjoint.
For checking invertibility of a rule \(r_s\), the goal is to check that derivability is not lost when moving from the conclusion S to the premises \(S_l\). The proof is by induction on the derivation \(\pi \) of S. Suppose that the last rule applied in \(\pi \) is \(r_t\). For this to happen at the first place, S and T must unify. Then, for each \(\theta \in \textit{CSU}(S,T)\), the premise sequents \(\overline{T_j\theta }\) of \(r_t\) are assumed to be derivable (and used to extend \(\mathcal {S}\) with new axioms). Moreover, each ground term \(\overline{S_i\gamma }\) can also be used as an inductive hypothesis since any application of \(r_s\) on \(\overline{T_j\theta }\) has a shorter derivation than that of \(\overline{T\theta }\). If, from all this in addition to the rules in \(\mathcal {S}\), it is possible to prove derivable the premises \(S_l\) for all \(1 \le l \le m\), then the theorem will work for the particular case where \(r_t\) was the last applied rule in the derivation \(\pi \) of S.
If the set \(\textit{CSU}(S,T)\) is empty, this means that the rules \(r_t\) and \(r_s\) cannot be applied on the same sequent and the property vacuously holds. For instance, consider the system \(\mathsf {G3ip}\) in Fig. 1: the proof of invertibility of \(\wedge _R\) does not need to consider the case of invertibility relative to \(\vee _R\) since it is not possible to have, at the same time, a conjunction and a disjunction on the succedent of the sequent. In other logics as, e.g., \(\mathsf {G3cp}\) (see Sect. 6.3), this proof obligation is certainly not vacuously discarded.
Theorem 2 presents sufficient conditions for checking the invertibility of a rule in a sequent system. The proof is similar to the one given for Theorem 1.
Theorem 2
Let \(\mathcal {S}\) be a sequent system and \(r_s\) an inference rule in \(\mathcal {S}\). If \(r_s\) is invertible relative to each \(r_t\) in \(\mathcal {S}\), then \(r_s\) is invertible in \(\mathcal {S}\).
This section is concluded by establishing conditions to prove permutability of rules.
Theorem 3
Let \(\mathcal {S}\) be a sequent system and  ,
,  be inference rules in \(\mathcal {S}\). Then \(r_s\downarrow r_t\) iff for each \(\theta \in \textit{CSU}(S,T)\), \(1 \le i \le m\), \(\gamma \in \textit{CSU}(T,\overline{S_i\theta })\), and \(1 \le l \le n\):
be inference rules in \(\mathcal {S}\). Then \(r_s\downarrow r_t\) iff for each \(\theta \in \textit{CSU}(S,T)\), \(1 \le i \le m\), \(\gamma \in \textit{CSU}(T,\overline{S_i\theta })\), and \(1 \le l \le n\):

where the variables in S and T are assumed disjoint.
Proof
Checking permutability does not require induction but a proof transformation. First of all, \(r_s,r_t\) should be applied to the conclusion sequent, hence all unifiers between the conclusions S and T are considered. Second, different cases need to be considered when \(r_t\) can be applied to one of the premises of \(r_s\). Thus there is a proof obligation for each premise \(S_i\theta \) where \(r_t\) can be applied. In each of such proof obligations the goal is to show that the premises of \(r_t\) are derivable (\(T_l\theta \) on the right). For that, it can be assumed that the premises of \(r_t\) applied to the given premise of \(r_s\) are derivable (\(T_j\gamma \) expression). Moreover, all the other premises of \(r_s\) are also assumed as derivable (\(S_k\theta \) expression). If, from all these ground sequents and the rules in \(\mathcal {S}\) it can be proved that \(T_l\) is derivable, for each \(l=1..n\), then \(r_s\downarrow r_t\).
5 Reflective Implementation
The design and implementation of a prototype that offers support for the narrowing procedures introduced in Sect. 4 is discussed. The reader is referred to http://subsell.logic.at/theorem-maude for the implementation and the experiments summarized in Sect. 6.
5.1 Sequent System Specification
The reflective implementation relies on the following functional module that needs to be realized by the object-logic (i.e., the system to be analyzed):

The sort Sequent is used to represent sequent terms and the sort SSequent for representing multisets of sequent terms separated by comma. The constant proved is the identity of the multiset constructor and represents the empty sequent (i.e., no goals need to be discharged).
When formalizing a sequent system \(\mathcal {S}\) as a rewrite theory \(\mathcal {R}_\mathcal {S}\) there are two options (backwards or forwards) for expressing an inference rule as rewrite rule. In this paper, the backwards reasoning option is adopted, which rewrites the target goal of an inference system to its premises. Hence, for instance, the rule \(\wedge _L\) in \(\mathsf {G3ip}\) will be expressed as a rewrite rule of the form \(\varGamma , F \wedge G \vdash C \rightarrow \varGamma , F , G \vdash C.\) The implementation assumes also a specific encoding for the inference rules as follows.
Definition 9
(Encoding logical rules). A sequent rule  is encoded in the reflective implementation as:
is encoded in the reflective implementation as:
 if \(m=0\); and
if \(m=0\); and
 if \(m>0\).
if \(m>0\).
The first case in the encoding of logical rules corresponds to the case of an axiom, i.e., an inference rule without premises. The constant proved denotes the fact that an instance of an axiom is derivable by definition. The second case corresponds to those rules that have premises that need to be proved derivable.
The implementation requires a module with any (reasonable) concrete syntax for formulas and sequents, and adhering to the encoding of inference rules above. For instance, the following snippet of code specifies the syntax for the system \(\mathsf {G3ip}\):

The following module extends the module OBJ-LOGIC and specifies the inference rules of \(\mathsf {G3ip}\).

The constant  is used to deal with extra-variables on the right-hand side of the rules, as it will be shown in an example below.
is used to deal with extra-variables on the right-hand side of the rules, as it will be shown in an example below.
5.2 Property Specification
The reflective implementation uses the following theory to specify the input to the analysis task, i.e., the sequents to be proved derivable:

Such a theory specifies the name of the module to be analyzed, the already proved theorems (e.g., admissibility of a given structural rule) and the rules that have been already proved to be invertible. As an example, the following snippet of code shows the implementation of the theory  for the module
for the module  :
:

As noted in Sect. 4, the properties of interest are specified by a sequent system \(\mathcal {S}\) and an inference rule r. Given a rewrite theory \(\mathcal {R}_\mathcal {S}\) representing \(\mathcal {S}\), the inference rule r to be checked admissible, invertible, or permutable in \(\mathcal {S}\) is represented by a rewrite rule, expressed as a meta-term, in the syntax of \(\mathcal {S}\). For instance, the statement of the theorem for invertibility of \(\wedge _R\) is generated with the aid of the auxiliary definition

that given the identifier of the rule ( , in this case) returns the following rule:
, in this case) returns the following rule:

 is the meta-representation of the rule
is the meta-representation of the rule

This is a very flexible way of encoding the theorems to be proved. For instance, in order to use the inductive hypothesis on a sequent \(T_j\), it suffices to rewrite  on \(T_j\), thus resulting in the needed (derivable) sequents/axioms (see e.g., the term \(\{\overline{S_i\gamma } \mid \gamma \in \textit{CSU}(S,\overline{T_j\theta })\}\) in Definition 8).
on \(T_j\), thus resulting in the needed (derivable) sequents/axioms (see e.g., the term \(\{\overline{S_i\gamma } \mid \gamma \in \textit{CSU}(S,\overline{T_j\theta })\}\) in Definition 8).
Special care needs to be taken when the inference rule to check has extra variables in the premises. In general, the rewrite rule associated to such an inference rule would have extra variables in the right-hand side and could not be used for execution (unless a strategy is provided). Nevertheless, these extra variables can be encoded as fresh constants, yielding a rewrite rule that is executable. This is exemplified in the theorem for admissibility of Weakening in module  that uses the constant
that uses the constant  defined in the module
defined in the module  . Note that
. Note that  is just the meta-representation of
is just the meta-representation of

It is worth noticing that this rewriting rule is written from the premise to the conclusion (see rule \(\mathsf {W}\) in Sect. 2). The reason is that the proof of admissibility requires to show that assuming the premise of the rule, the conclusion is valid (see Definition 7).
5.3 The Algorithms
The reflective implementation follows closely the definitions of the previous section. It offers functions that implement algorithms for each one of the theorems in Sect. 4; for sequent system \(\mathcal {R}_\mathcal {S}\) and rule r:
-
admissible? checks if r is admissible in \(\mathcal {S}\) by validating the conditions in Theorem 1.
-
invertible? checks if r is invertible in \(\mathcal {S}\) by validating the conditions in Theorem 2.
-
permutes? checks if r permutes in \(\mathcal {S}\) by validating the conditions in Theorem 3.
The output of each one of these algorithms is a list of tests, one per rule in \(\mathcal {S}\). The test for a rule \(r_t\) indicates whether r has the desired property relative to \(r_t\). Take for instance the procedure:

Given the identifier of a rule Q, it first builds the invertibility theorem, generates and executes all the needed proof obligations ( ) and returns
) and returns  only if all the proof obligations succeed (
only if all the proof obligations succeed ( ).
).
The procedure  tests the given rule Q against all the rules defined in the module. It uses the auxiliary function:
tests the given rule Q against all the rules defined in the module. It uses the auxiliary function:

that computes the set of unifiers by using the Maude function  and checks the conditions described in Sect. 4. For that, operations on the
and checks the conditions described in Sect. 4. For that, operations on the  are used to, e.g., extend the module with the needed axioms (rewriting rules when \(m=0\) in Definition 9) and transform variables into constants. Moreover, the
are used to, e.g., extend the module with the needed axioms (rewriting rules when \(m=0\) in Definition 9) and transform variables into constants. Moreover, the  procedure is used to check the entailment in, e.g., Definition 7.
procedure is used to check the entailment in, e.g., Definition 7.
Since the entailment relation is, in general, undecidable, all the tests are performed up to a given search depth and, when it is reached, the procedure returns  . Hence the procedures are sound (in the sense of the theorems in Sect. 4) but not complete (due to the undecidability of the logic and the fact that the goals are inductive properties).
. Hence the procedures are sound (in the sense of the theorems in Sect. 4) but not complete (due to the undecidability of the logic and the fact that the goals are inductive properties).
Finally, the implementation also includes macros based on these algorithms, e.g., analyzePermutation for checking the permutation status of all rules.
6 Case Studies
This section presents properties of several sequent systems that can be automatically checked with the algorithms presented in Sect. 5. The general idea is that, given a sequent system \(\mathcal {S}\) and a sequent S representing an admissibility, invertibility, or permutability problem instance, the experiments in this section use the encoding for \(\mathcal {S}\) and S (Sect. 5) – and the rewriting logic framework – to check if S is derivable in \(\mathcal {S}\), as follows:

where \(\textit{enc}(\mathcal {S})\) and \(\textit{enc}(S)\) denote, respectively, the encoding of \(\mathcal {S}\) and S.
For each calculi, the results about invertibility and admissibility of the structural rules \(\mathsf {W}\) (weakening) and \(\mathsf {C}\) (contraction), and permutability are summarized in a table using the following conventions:
- \(\checkmark _\texttt {\!\!T}\) :
-
means that the property holds for the given system and the tool is able to prove it (thus returning true).
- \(\checkmark _\texttt {\!\!F}\) :
-
means that the property does not hold for the given system and the tool returns false.
- \(\sim _{\texttt {DN}}\) :
-
means that the property holds but the tool was not able to prove it (then returning false).
6.1 System \(\mathsf {G3ip}\)
An important remark is that propositional intuitionistic logic is decidable. However, since the rule \(\supset _L\) replicates the principal formula in the left premise, a careless specification of this rule can result in infinite computations. For instance, the sequent  is not provable. However, a proof search trying to rewrite that sequent into proved will generate the infinite chain of goals
is not provable. However, a proof search trying to rewrite that sequent into proved will generate the infinite chain of goals  .
.
One solution for this problem is to consider sets instead of multisets of sequents (i.e., by adding an equation for idempotency in the module SEQUENT). This solution is akin to the procedure of detecting whether a sequent in a derivation tree is equal to one of its predecessors. In this way a complete decision procedure for propositional intuitionistic logic can be obtained.
The results for invertibility of rules and admissibility of structural rules for \(\mathsf {G3ip}\) are summarized below.
Invertibilities | Structural | \(\mathsf {G3ip}_\mathsf {W}\) | \(\mathsf {G3ip}_{+inv}\) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
I | \(\vee _L\) | \(\vee _{R_i}\) | \(\wedge _L\) | \(\wedge _R\) | \(\top _R\) | \(\top _L\) | \(\bot _L\) | \(\supset _L\) | \(\supset _R\) | \(\supset _L^{pR}\) | \(\mathsf {W}\) | \(\mathsf {C}\) | \(\supset _R\) | \(\mathsf {C}\) |
\(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!F}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!F}\) | \(\sim _{\texttt {DN}}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\sim _{\texttt {DN}}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) |
The non-invertible rules in this system are \(\vee _{R_i}\) and \(\supset _L\). Note that \(\supset _R\) is invertible but the implementation failed to prove it. The reason is that the proof for this case requires admissibility of \(\mathsf {W}\). More precisely, consider a derivation of the sequent  and suppose that the last applied rule was
and suppose that the last applied rule was

By inductive hypothesis on the right premise,  is derivable. Considering the left premise, since
is derivable. Considering the left premise, since  is derivable, admissibility of weakening implies that
is derivable, admissibility of weakening implies that  is also derivable, hence
is also derivable, hence  is derivable and the result follows. It turns out that the admissibility of \(\mathsf {W}\) is automatically proved by the algorithms. Let \(\mathsf {G3ip}_\mathsf {W}\) denote the system \(\mathsf {G3ip}\) with the admissible rule \(\mathsf {W}\) added: in this system, the invertibility of \(\supset _R\) can be automatically proved.
is derivable and the result follows. It turns out that the admissibility of \(\mathsf {W}\) is automatically proved by the algorithms. Let \(\mathsf {G3ip}_\mathsf {W}\) denote the system \(\mathsf {G3ip}\) with the admissible rule \(\mathsf {W}\) added: in this system, the invertibility of \(\supset _R\) can be automatically proved.
Although the rule \(\supset _L\) is not invertible, it is invertible in its right premise. That is, if  is derivable, then so is
is derivable, then so is  . This result can also be proved by induction on the height of the derivation and the implementation returns a positive answer (this corresponds to the entry \(\supset _L^{pR}\) in the table above).
. This result can also be proved by induction on the height of the derivation and the implementation returns a positive answer (this corresponds to the entry \(\supset _L^{pR}\) in the table above).
Finally, as mentioned in Sect. 2, the proof of admissibility of contraction often requires the invertibility of rules. As an example, consider the derivation

By inductive hypothesis on the left premise,  is derivable and by invertibility of \(\supset _L\) on the right premise,
is derivable and by invertibility of \(\supset _L\) on the right premise,  is derivable and the result follows. Hence, by adding all the invertibilities already proved (system \(\mathsf {G3ip}_{+inv}\) in the table), the tool was able to prove admissibility of the rule \(\mathsf {C}\).
is derivable and the result follows. Hence, by adding all the invertibilities already proved (system \(\mathsf {G3ip}_{+inv}\) in the table), the tool was able to prove admissibility of the rule \(\mathsf {C}\).
As shown in Sect. 2, the proof of permutability of rules requires the invertibility lemmas and admissibility of weakening (already proved). Using the system \(\mathsf {G3ip}_{+inv}\), the tool was able to prove all the permutability lemmas for propositional intuitionistic logic. The following table summarizes some of these results.
\(\wedge _R \downarrow \wedge _L\) | \(\wedge _L \downarrow \wedge _R\) | \(\vee _i \downarrow \wedge _L\) | \(\wedge _L\downarrow \vee _i \) | \(\vee _{R_i} \downarrow \vee _L\) | \(\vee _L \downarrow \vee _{R_i}\) | \(\vee _{R_i} \downarrow \supset _L\) | \(\supset _L \downarrow \vee _{R_i}\) | \(\supset _L \downarrow \supset _L\) | \(\wedge _L \downarrow \supset _R\) | \(\supset _R\downarrow \wedge _L \) |
|---|---|---|---|---|---|---|---|---|---|---|
\(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!F}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) |
Note that the approach followed for \(\mathsf {G3ip}\), \(\mathsf {G3ip}_\mathsf {W}\) and \(\mathsf {G3ip}_{+inv}\) in this section provides an example of a modular proof, where theorems are added as hypothesis to the system. In this way, more involved properties can be discarded.
6.2 Multi-conclusion Propositional Intuitionistic Logic (\(\mathsf {mLJ}\))
Maehara’s \(\mathsf {mLJ}\) [13] is a multiple conclusion system for intuitionistic logic. The rules are exactly the same as in \(\mathsf {G3ip}\), except for the \(\vee _R\) and implication (see Fig. 2). While the left rule copies the implication in the left premise, the right implication forces all formulas in the succedent of the conclusion sequent to be weakened (when viewed bottom-up). This guarantees that, when the \(\supset _R\) rule is applied on \(A\supset B\), the formula B should be proved assuming only the pre-existent antecedent context extended with the formula A. This creates an interdependency between A and B.
The introduction rules in \(\mathsf {mLJ}\) are invertible, with the exception of \(\supset _R\). In particular, two different applications of \(\supset _R\) (on the same sequent) do not permute. For instance, from the premise of

the sequent  is not derivable. The results for this system are summarized in the table below:
is not derivable. The results for this system are summarized in the table below:
Invertibilities | Structural | \(\mathsf {mLJ}_{+inv}\) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
I | \(\vee _L\) | \(\vee _{R}\) | \(\wedge _L\) | \(\wedge _R\) | \(\top _R\) | \(\top _L\) | \(\bot _L\) | \(\supset _L\) | \(\supset _R\) | \(\mathsf {W}\) | \(\mathsf {C}\) | \(\mathsf {C}\) |
\(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!F}\) | \(\checkmark _\texttt {\!\!T}\) | \(\sim _{\texttt {DN}}\) | \(\checkmark _\texttt {\!\!T}\) |
6.3 Propositional Classical Logic (\(\mathsf {G3cp}\))
\(\mathsf {G3cp}\) [21] is a well known two-sided sequent system for classical logic, where the structural rules are implicit and all the rules are invertible. Differently from \(\mathsf {G3ip}\), weakening is not needed for the proof of invertibility of \(\supset _R\). However, contraction still depends on invertibility results. The results are summarized below:
Invertibilities | Structural | \(\mathsf {G3cp}{+inv}\) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
I | \(\vee _L\) | \(\vee _{R}\) | \(\wedge _L\) | \(\wedge _R\) | \(\top _R\) | \(\top _L\) | \(\bot _L\) | \(\supset _L\) | \(\supset _R\) | \(\mathsf {W}\) | \(\mathsf {C}\) | \(\mathsf {C}\) |
\(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\sim _{\texttt {DN}}\) | \(\checkmark _\texttt {\!\!T}\) |
Assuming the already proved invertibility lemmas, the prover is able to show that, for all pair of rules \(r_1, r_2\) in the system, \(r_1 \downarrow r_2\).
6.4 Linear Logic (\(\mathsf {LL}\))
Linear logic [8] is a resource-conscious logic, in the sense that formulas are consumed when used during proofs, unless they are marked with the exponential \(\mathord {?}\) (whose dual is \(\mathop {!}\)), in which case, they behave classically. Propositional \(\mathsf {LL}\) connectives include the additive conjunction \( \mathbin { \& }\) and disjunction \(\oplus \) and their multiplicative versions \(\otimes \) and  . The proof system for one-sided (classical) propositional linear logic is depicted in Fig. 3.
. The proof system for one-sided (classical) propositional linear logic is depicted in Fig. 3.
Since formulas of the form \(\mathord {?}F\) can be contracted and weakened, such formulas can be treated as in classical logic, while the remaining formulas are treated linearly. This is reflected into the syntax of the so called dyadic sequents (Fig. 4) which have two contexts: \(\varTheta \) is a set of formulas and \(\varGamma \) a multiset of formulas. The sequent  is interpreted as the linear logic sequent
is interpreted as the linear logic sequent  where \(\mathord {?}\varTheta = \{\mathord {?}A \mid A \in \varTheta \}\). It is then possible to define a proof system without explicit weakening and contraction (system \(\mathsf {D\!-\!LL}\) in Fig. 4). The complete dyadic proof system can be found in [1].
where \(\mathord {?}\varTheta = \{\mathord {?}A \mid A \in \varTheta \}\). It is then possible to define a proof system without explicit weakening and contraction (system \(\mathsf {D\!-\!LL}\) in Fig. 4). The complete dyadic proof system can be found in [1].
Since propositional LL is undecidable [12], infinite computations are possible. In this case study, a search bound is used to force termination of the implementation. Since all the theorems include a very controlled number of connectives (usually the 2 connectives involved in the application of the rules), this seems to be a fair solution.
For the monadic (\(\mathsf {LL}\)) and the dyadic (\(\mathsf {D\!-\!LL}\)) systems, the results of invertibility of rules are summarized in the next table.
\(\mathsf {LL}\) and \(\mathsf {D\!-\!LL}\) | \(\mathsf {LL}\) | \(\mathsf {D\!-\!LL}\) | \(\mathsf {D\!-\!LL}_{+\mathsf {W}_c}\) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
1 | \(\bot \) | \(\top \) | \(\otimes \) | \( \mathbin { \& }\) |
| \(\oplus _i\) | ! | ? | \(?_\mathsf {C}\) | \(?_\mathsf {W}\) | ? | copy | ? |
\(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!F}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!F}\) | \(\checkmark _\texttt {\!\!F}\) | \(\checkmark _\texttt {\!\!F}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!F}\) | \(\sim _{\texttt {DN}}\) | \(\checkmark _\texttt {\!\!F}\) | \(\checkmark _\texttt {\!\!T}\) |
In \(\mathsf {LL}\), the rules ? (dereliction) and \(?_\mathsf {W}\) (weakening) are not invertible, while \(?_\mathsf {C}\) (contraction) is invertible. In \(\mathsf {D\!-\!LL}\), the rule ? is invertible. However, the proof of this theorem fails for the case \(\otimes \). To obtain a proof, first admissibility of weakening for the classical context is proved: if  is derivable, then
is derivable, then  is derivable (rule \(\mathsf {W}_c\)). ? is proved invertible in \(\mathsf {D\!-\!LL}_{+\mathsf {W}_c}\).
is derivable (rule \(\mathsf {W}_c\)). ? is proved invertible in \(\mathsf {D\!-\!LL}_{+\mathsf {W}_c}\).
Finally, the prover was able to discharge the following theorems:
-
(\(\mathsf {LL}\)) If
 is derivable then
is derivable then  is derivable.
is derivable. -
(\(\mathsf {D\!-\!LL}\)) If
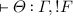 is derivable then
is derivable then  is derivable.
is derivable.
6.5 Normal Modal Logics: \(\mathsf {K}\) and \(\mathsf {S4}\)
A modal is an expression (like necessarily or possibly) that is used to qualify the truth of a judgment, e.g., \(\Box A\) can be read as “the formula A is necessarily true”. The most familiar modal logics are constructed from the modal logic \(\mathsf {K}\) and its extensions are called normal modal logics. The system \(\mathsf {S4}\) is an extension of \(\mathsf {K}\) where \(\Box \Box A\equiv \Box A\) holds. Figure 5 presents the modal sequent rules for \(\mathsf {K}\) and \(\mathsf {S4}\).
All the propositional rules are invertible in both \(\mathsf {K}\) and \(\mathsf {S4}\), \(\mathsf {k}\) and \(\mathsf {4}\) are not invertible (due to the implicit weakening) while \(\mathsf {T}\) is invertible. Similar to the previous systems, the admissibility of \(\mathsf {W}\) follows immediately and the proof of admissibility of \(\mathsf {C}\) requires as hypotheses the already proved invertibility lemmas:
Invertibilities | Structural | Modal Rules | \(\mathsf {K}_{+inv}\) | \(\mathsf {S4}_{+inv}\) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
I | \(\vee _L\) | \(\vee _{R}\) | \(\wedge _L\) | \(\wedge _R\) | \(\top _R\) | \(\top _L\) | \(\bot _L\) | \(\supset _L\) | \(\supset _R\) | \(\mathsf {W}\) | \(\mathsf {C}\) | \(\mathsf {k}\) | \(\mathsf {4}\) | \(\mathsf {T}\) | \(\mathsf {C}\) | \(\mathsf {C}\) |
\(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\sim _{\texttt {DN}}\) | \(\checkmark _\texttt {\!\!F}\) | \(\checkmark _\texttt {\!\!F}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) | \(\checkmark _\texttt {\!\!T}\) |
7 Related Work and Concluding Remarks
The proposal of many proof systems for many logics demanded trustful methods for determining good properties. In general, the checking was normally done via a case-by-case analysis, by trying exhaustively all the possible combinations of application of rules in a system. The advent of automated reasoning changed completely the scenery, since theorems started being proved automatically in meta-level frameworks. This has brought a whole new perspective to the field of proof theory: useless proof search steps, usually singular to a specific logic, have been disregarded in favor of developing general and universal methods for providing good automation strategies. These developments have ultimately helped in determining general conceptual characteristics of logical systems, as well as in identifying effective meta-level frameworks that can capture (and reason about) them in a natural way.
This work moves forward towards this direction: it proposes a general, natural, and uniform way of proving key properties of sequent systems using the rewriting logic framework, enabling modular proofs of meta-level properties of logical systems. Permutability of rules is a nice start case study since it is heavily used in cut-elimination proofs. Moreover, permutability has a rewriting counterpart: showing that applying a rule \(r_1\) followed by a rule \(r_2\) is the same as applying \(r_2\) then \(r_1\) can be interpreted as having the diamond property on the application of these two rules. The proof of permutability itself does not need inductive methods explicitly: they are hidden in other needed results like admissibility of weakening and invertibility of rules. The approach adopted in this work profits, as much as possible, from modularity. First permutability is tested without any other assumptions; then, if possible, prove admissibility of weakening and invertibility theorems; finally, add the proven theorems modularly to the system and re-run the permutability test: some cases for which the tool previously failed can now be proved. The same core algorithm can be used for proving admissibility of contraction, for example, which also depends on invertibility results.
The choice of rewriting logic as a meta-level framework brought advantages over some other options in the literature. Indeed, while approaches using logical frameworks depend heavily on the specification method and/or the implicit properties of the meta and object logics, rewriting logic enables the specification of the rules as they are actually written in text and figures. Consider for example the LF framework [20], based on intuitionistic logic, where the left context is handled by the framework as a set. Specifying sequent systems based on multisets requires elaborated mechanisms, which makes the encoding far from being natural. Moving from intuitionistic to linear logic solves this problem [4, 16], but still several sequent systems cannot be naturally specified in the \(\mathsf {LL}\) framework, as it is the case of \(\mathsf {mLJ}\). This latter situation can be partially fixed by adding subexponentials to linear logic (\(\mathsf {SELL}\)) [18, 19], but then the resulting encoding although natural, is often non-trivial and it cannot be fully automated. Moreover, several logical systems cannot be naturally specified in \(\mathsf {SELL}\), such as \(\mathsf {K}\). All in all, this paper is yet another proof that rewriting logic is an innovative and elegant framework for reasoning about logical systems, since results and systems themselves can be modularly extended. In fact, the approach here can be extended to reason about a large class of systems, including normal (multi)-modal [11] and paraconsistent [9] sequent systems. The authors conjecture that the same approach can be used for extensions of sequent systems themselves, like nested [3] or linear nested [10] systems. This is an interesting future research path worth pursuing.
Finally, a word about cut-elimination. The usual cut-elimination proof strategy can be summarized by the following steps: (i) transforming a proof with cuts into a proof with principal cuts; (ii) transforming a proof with principal cuts into a proof with atomic cuts; (iii) transforming a proof with atomic cuts into a cut-free proof. While step (ii) is not difficult to solve (see e.g., [16]), steps (i) and (iii) strongly depend on the ability of showing permutability of rules. With the results presented in this work, it seems reasonable to envisage the use of the approach – both the techniques and their implementation – in order to fully automate cut-elimination proofs for various proof systems. It is worth noticing, though, that the aim of this paper is more general: proving results in a modular way permits maximizing their subsequent use in other applications as well. For example, it would be interesting to investigate further the role of invertible rules as equational rules in rewriting systems. While this idea sounds more than reasonable, it is necessary to check whether promoting invertible rules to equations preserves completeness of the system (e.g., the resulting equational theory needs to be, at least, ground confluent and terminating). If the answer to this question is in the affirmative for a large class of systems, then the approach presented here also opens the possibility, e.g., to automatically access focused systems [1].
References
Andreoli, J.-M.: Logic programming with focusing proofs in linear logic. J. Logic Comput. 2(3), 297–347 (1992)
Bruni, R., Meseguer, J.: Semantic foundations for generalized rewrite theories. Theoret. Comput. Sci. 360(1–3), 386–414 (2006)
Brünnler, K.: Deep sequent systems for modal logic. Arch. Math. Logic 48, 551–577 (2009)
Cervesato, I., Pfenning, F.: A linear logical framework. Inf. Comput. 179(1), 19–75 (2002)
Ciabattoni, A., Galatos, N., Terui, K.: From axioms to analytic rules in nonclassical logics. In: LICS, pp. 229–240. IEEE Computer Society Press (2008)
Clavel, M., et al.: All About Maude - A High-Performance Logical Framework. LNCS, vol. 4350. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-71999-1
Gentzen, G.: Investigations into logical deduction. In: Szabo, M.E. (ed.) The Collected Papers of Gerhard Gentzen, North-Holland, pp. 68–131 (1969)
Girard, J.-Y.: Linear logic. Theoret. Comput. Sci. 50, 1–102 (1987)
Lahav, O., Marcos, J., Zohar, Y.: Sequent systems for negative modalities. Logica Universalis 11(3), 345–382 (2017)
Lellmann, B.: Linear nested sequents, 2-sequents and hypersequents. In: De Nivelle, H. (ed.) TABLEAUX 2015. LNCS (LNAI), vol. 9323, pp. 135–150. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-24312-2_10
Lellmann, B., Pimentel, E.: Proof search in nested sequent calculi. In: Davis, M., Fehnker, A., McIver, A., Voronkov, A. (eds.) LPAR 2015. LNCS, vol. 9450, pp. 558–574. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48899-7_39
Lincoln, P., Mitchell, J., Scedrov, A., Shankar, N.: Decision problems for propositional linear logic. Ann. Pure Appl. Logic 56, 239–311 (1992)
Maehara, S.: Eine darstellung der intuitionistischen logik in der klassischen. Nagoya Math. J. 7, 45–64 (1954)
Martí-Oliet, N., Meseguer, J.: Rewriting logic as a logical and semantic framework. In: Gabbay, D.M., Guenthner, F. (eds.) Handbook of Philosophical Logic, pp. 1–87. Springer, Dordrecht (2002)
Meseguer, J.: Conditional rewriting logic as a unified model of concurrency. Theoret. Comput. Sci. 96(1), 73–155 (1992)
Miller, D., Pimentel, E.: A formal framework for specifying sequent calculus proof systems. Theoret. Comput. Sci. 474, 98–116 (2013)
Miller, D., Saurin, A.: From proofs to focused proofs: a modular proof of focalization in linear logic. In: Duparc, J., Henzinger, T.A. (eds.) CSL 2007. LNCS, vol. 4646, pp. 405–419. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74915-8_31
Nigam, V., Pimentel, E., Reis, G.: An extended framework for specifying and reasoning about proof systems. J. Logic Comput. 26(2), 539–576 (2016)
Nigam, V., Reis, G., Lima, L.: Quati: an automated tool for proving permutation lemmas. In: Demri, S., Kapur, D., Weidenbach, C. (eds.) IJCAR 2014. LNCS (LNAI), vol. 8562, pp. 255–261. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08587-6_18
Pfenning, F.: Structural cut elimination I. Intuitionistic and classical logic. Inf. Comput. 157(1/2), 84–141 (2000)
Troelstra, A.S., Schwichtenberg, H.: Basic Proof Theory. Cambridge University Press, New York (1996)
Viry, P.: Equational rules for rewriting logic. Theoret. Comput. Sci. 285(2), 487–517 (2002)
Acknowledgements
The authors would like to thank the anonymous reviewers for their valuable comments on an earlier draft of this paper. The work of the three authors was supported by CAPES, Colciencias, and INRIA via the STIC AmSud project “EPIC: EPistemic Interactive Concurrency” (Proc. No 88881.117603/2016-01). The work of Pimentel and Olarte was also supported by CNPq and the project FWF START Y544-N23.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this paper
Cite this paper
Olarte, C., Pimentel, E., Rocha, C. (2018). Proving Structural Properties of Sequent Systems in Rewriting Logic. In: Rusu, V. (eds) Rewriting Logic and Its Applications. WRLA 2018. Lecture Notes in Computer Science(), vol 11152. Springer, Cham. https://doi.org/10.1007/978-3-319-99840-4_7
Download citation
DOI: https://doi.org/10.1007/978-3-319-99840-4_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-99839-8
Online ISBN: 978-3-319-99840-4
eBook Packages: Computer ScienceComputer Science (R0)



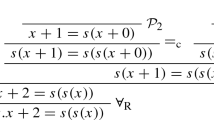
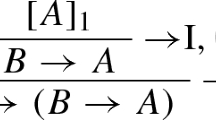





 is derivable then
is derivable then  is derivable.
is derivable.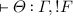 is derivable then
is derivable then  is derivable.
is derivable.