Robust Reliable $H_{\infty }$ Control and Input-to-State Stabilization for Uncertain Hybrid Systems

Abstract

The main objective of this paper to design a robust reliable $H_{\infty }$ control and a switching law for a class of uncertain switched systems under an average dwell time switching signal that guarantees ISS not only when all the actuators are operational, but also when some of them experience failure. The faulty actuator output is assumed to be nonzero, which is treated as a disturbance signal that is augmented with the system disturbance input. The input-to-state stability (ISS) property is analyzed by the multiple Lyapunov functions and comparison principle approach. A numerical example is introduced to illustrate the validity of the theoretical results.

1 Introduction

There has been a growing interest in studying switched systems in the last three decades due to their widespread applications in different fields such as aircraft, automotive industry, robotics, control systems, biological, epidemic disease models; see [7, 8, 10] and the references therein. By a switched system we mean a special class of hybrid systems that consist of a family of continuous- or discrete-time dynamical subsystems (or modes), and a switching rule (or signal). The role of the switching signal is to govern the jump among the subsystems. The stability of switched systems has received much attention and has been studied using either the common Lyapunov function method [11], or the multiple Lyapunov function method [2]. It has been realized that it is more convenient to use multiple Lyapunov functions than the common Lyapunov function since having only one Lyapunov function for all the modes under study is not practical and is difficult to construct.

The reliable control is the controller that tolerates actuator and/or sensor failures. In reality, the failure of control components is frequently encountered, yet the immediate repair may not be feasible, such as in the case of aerospace or submarine system, etc. Therefore, designing a reliable controller to guarantee an acceptable level of performance becomes crucial. The trend to design reliable controllers has been increased; see for instance [4, 12, 15, 16, 18]. In most of the available results about reliable control, the faulty actuators are modelled as outages i.e., the output is assumed to be zero. In [1, 9, 12, 16], the output signal is considered as a disturbance signal with bounded magnitude that is augmented with the system disturbance signal.

The $H_\infty$ control has received a great deal of attention in control theory [3, 17]. It is a useful measure used to guarantee the performance of the plant when dealing with control problems that involve robust design. However, in the event of control component failures, the stability or performance of the plant may not be achieved by such designs. Therefore, it would be advantageous if it is associated with a reliable control design to handle such failures when they occur. One may refer to [1, 9, 12, 18].

In practice, most of the real control systems are subject to some disturbance inputs. ISS notion, introduced in [13] which addresses the system response to a bounded disturbance when the unforced system is asymptotically stable, is an efficient tool to deal with these disturbances. As a result, it becomes important in the modern nonlinear control theory and design [1, 13, 14].

This paper is organized as follows. Section 2 involves the problem description, definitions, and a useful lemma. The main results and proofs are stated in Sect. 3. A numerical example with simulations is presented in Sect. 4. The conclusion is given in Sect. 5.

2 Problem Formulation and Preliminaries

Throughout this paper, $\mathbb {R}^n$ denotes the n-dimensional Euclidean space; $\mathbb {R}_{+}$ refers to the nonnegative real numbers; $\mathbb {R}^{n\times m}$ is the class of all $n\times m$ real matrices. A symmetric matrix P is said to be positive definite if all its eigenvalues are positive. Moreover, If $P \in \mathbb {R}^{n\times n}$, denote by $\lambda _{max}(P)$($\lambda _{min}(P)$) the maximum (minimum) eigenvalue of P. If $V(x)=x^{T}Px$, the following inequalities are always true

$$\begin{aligned} c_{1}||x||^{2}\le V(x)\le c_{2}||x||^{2}, \end{aligned}$$

(1)

where $c_{1}=\lambda _{min}(P), \, c_{2}=\lambda _{max}(P)$. If $x\in \mathbb {R}^{n}$, then ||x|| refers to the Euclidean vector norm of x. $L_{2}[t_0, \infty )$ is the space of square integrable vector-valued functions on $[t_0, \infty )$ and $||\cdot ||_{2}$ denotes $L_{2}[t_0, \infty )$-norm (i.e., $w \in L_{2}[t_0, \infty )$ means $||w||_{2}^{2}=\int _{t_0}^{\infty }||w(t)||^{2} \, dt \, < \infty$). Consider a class of uncertain switched systems given by

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{x} = (A_{\rho (t)}+ \varDelta A_{\rho (t)}) x + B_{\rho (t)} u+G_{\rho (t)}w+f_{\rho (t)}(x) , \\ z=C_{\rho (t)}x+F_{\rho (t)}u, ~~~~ x(t_0)=x_0, \end{array} \right. \end{aligned}$$

(2)

where $x\in \mathbb {R}^{n}$ is the system state, $u\in \mathbb {R}^{q}$ is the control input, $w\in \mathbb {R}^p$ is an input disturbance, which is assumed to be bounded, and $z\in \mathbb {R}^{r}$ is the controlled output. $\rho$ is the switching law which is a piecewise constant function defined by $\rho : [t_{0}, \infty ) \rightarrow \mathscr {S}=\{1,2,\cdots , N\}$. The role of $\rho$ is to switch among the system modes. For each $i\in \mathscr {S}, ~ A_{i}$ is a non Hurwitz matrix, $K_{i}\in \mathbb {R}^{q\times n}$ is the control gain matrix such that $u=K_{i}x$, where $(A_{i},B_{i})$ is assumed to be stabilizable, $f_{i}(x)\in \mathbb {R}^{n}$ is some nonlinearity, $A_{i}, \, B_{i}, \,G_{i}, \, C_{i}$ and $F_{i}$ are known real constant matrices, and $\varDelta A_{i}$ is a deterministic piecewise continuous function of time t which represents parameter uncertainty with bounded norm and it also gives the structure of the system uncertainty. For any $i\in \mathscr {S}$, the closed-loop system is

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{x} = (A_{i} + \varDelta A_{i}+B_{i}K_{i}) x+G_{i}w+f_{i}(x), \\ z=C_{ic}x, ~~~~ x(t_0)=x_0, \qquad \text{ where } C_{ic}=C_{i}+F_{i}K_{i}. \end{array} \right. \end{aligned}$$

(3)

To analyze the reliable stabilization with respect to actuator failures, the q control actuators are divided into two sets. $\Sigma \subseteq \{1,2, \ldots ,q\}$ the set of actuators that are susceptible to failure, i.e., they may occasionally fail, and $\overline{\Sigma }\subseteq \{1,2, \ldots ,q\} -\Sigma$ the other set of actuators which are robust to failures and essential to stabilize the given system. The elements of $\Sigma$ are redundant in terms of the stabilization but necessary to improve the system performance, while the elements of $\overline{\Sigma }$ are required to stabilize the system and assumed that they never fail, i.e., the pair $(A_{i},B_{i\overline{\Sigma }})$ is assumed to be stabilizable.

For $i \in \mathscr {S}$, consider the decomposition of the control matrix $B_{i}=B_{i\Sigma }+B_{i\overline{\Sigma }},$ where $B_{i\Sigma }, \, B_{i\overline{\Sigma }}$ are the control matrices associated with $\Sigma , \, \overline{\Sigma }$ respectively, and $B_{i\Sigma }, \, B_{i\overline{\Sigma }}$ are generated by zeroing out the columns corresponding to $\overline{\Sigma }$ and $\Sigma$, respectively. For a fixed $i\in \mathscr {S}$, let $\sigma \subseteq \Sigma$ corresponds to some of the actuators that experience failure, and assume that the output of faulty actuators is any arbitrary energy-bounded signal (or disturbance input) which belongs to $L_{2}[t_0,\infty )$. Then, the decomposition becomes $B_{i}=B_{i\sigma }+B_{i\overline{\sigma }},$ where $B_{i\sigma }$ and $B_{i\overline{\sigma }}$ have the same definition of $B_{i\Sigma }$ and $B_{i\overline{\Sigma }}$, respectively. Furthermore, the augmented disturbance input to the system becomes

$$ w_{\sigma }^{F}=(w^{T} ~~ (u_{\sigma }^{F})^{T} )^{T}, $$

where $u_{\sigma }^{F}\in \mathbb {R}^{q}$ is the failure vector whose elements corresponding to the set of faulty actuators $\sigma$, and F here stands for “failure”. Since the control input u is applied to the system through the normal actuators, and the outputs of the faulty actuators are assumed to be arbitrary signals, the closed-loop system becomes

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{x} = (A_{i} + \varDelta A_{i}+B_{i\overline{\sigma }}K_{i}) x+G_{ic}w_{\sigma }^{F}+f_{i}(x) , ~~ i \in \mathscr {S}=\{1,2, \ldots ,N\}, \\ z=C_{ic}x, ~~~~ x(t_0)=x_0,, \qquad \text{ where } G_{ic}=(G_{i} ~~ B_{i\sigma }). \end{array} \right. \end{aligned}$$

(4)

Definition 2.1

[6] (Class-K function) A function $\rho :[0,r)\rightarrow [0, \infty )$ is said to belong to class $\mathscr {K}$ (i.e., $\rho \in \mathscr {K}$) if it is continuous, strictly increasing, and $\rho (0)=0$.

Definition 2.2

(Input-to-State Stability) System (3) is said to be robustly globally exponentially ISS if there exist positive constants $\lambda , \, \overline{\lambda }$ and a function $\rho \in \mathscr {K}$ such that, for any solution $x(t)=x(t,t_{0},x_0)$,

$$ ||x|| \le \overline{\lambda }||x_{0}||e^{-\lambda (t-t_{0})}+\rho \left( \sup _{t_{0}\le \tau \le t}||w(\tau )||\right) , ~~ \forall \, t\ge t_{0}. $$

Definition 2.3

(input-to-state stability with an $H_{\infty }$-norm (ISS-$H_{\infty }$)) Given a constant $\gamma >0$, system (3) is said to be ISS-$H_{\infty }$ if there exists a state feedback law $u(t)=K_{i}x(t),$ such that, for any admissible parameter uncertainties $\varDelta A_{i}$, the closed loop system (3) is globally exponentially ISS, and the controlled output z satisfies

$$ ||z||^{2}_{2}=\int _{t_{0}}^{\infty }||z||^{2} \, dt \le \gamma ^{2} ||w||^{2}_{2} +m_{0}, $$

for some positive constant $m_0$.

Assumption A

For $i\in \mathscr {S}$, the admissible parameter uncertainties are defined by

$$ \varDelta A_{i}(t)=D_{i} \mathscr {U}_{i}(t) H_{i}, ~~ \forall \, t\in \mathbb {R}_{+}, $$

with $D_{i}, \, H_{i}$ being known real matrices with appropriate dimensions that give the structure of the uncertainty, and $\mathscr {U}_{i}(t)$ being unknown real time-varying matrix representing the uncertain parameter and satisfying $||\mathscr {U}_{i}(t)|| \le 1$.

Lemma 2.4

For any arbitrary positive constants $\xi _{1}$, $\xi _{2}$ and $\xi _{3}$, and a positive definite matrix P, we have

• (i) $2x^{T}P\left( \varDelta A\right) x \le x^{T}\left( \xi _{1} { {PDD}}^{T}P+ \frac{1}{\xi _{1}}H^{T}H\right) x$.

• (ii) $2x^{T}{} { {PG}}w \le x^{T}\left( \xi _{2} { {PGG}}^{T}P\right) x+ \frac{1}{\xi _{2}}w^{T}w$.

• (iii) $2x^{T}{} { {Pf}}(x)\le x^{T}\left( \xi _{3}P^{2}+\frac{1}{\xi _{3}}\delta I\right) x$ such that $||f(x)||^{2}\le \delta ||x||^{2}$ with $\delta >0$.

Proof

For (i), we have

$$\begin{aligned} 0\le & {} (\sqrt{\xi _{1}}x^{T}({ {PD}}\mathscr {U})-\frac{1}{\sqrt{\xi _{1}}}x^{T}H^{T})(\sqrt{\xi _{1}}x^{T}({ {PD}}\mathscr {U})-\frac{1}{\sqrt{\xi _{1}}}x^{T}H^{T})^{T}\\= & {} \xi _{1}x^{T}{} { {PDD}}^{T}Px+\frac{1}{\xi _{1}}x^{T}H^{T}Hx-2x^{T}({ {PD}}\mathscr {U}H)x, \end{aligned}$$

which leads to $2x^{T}(PD\mathscr {U}H)x \le x^{T}\left( \xi _{1}{} { {PDD}}^{T}P+\frac{1}{\xi _{1}}H^{T}H\right) x$, which yields the desired result. The inequalities in $({ {ii}})$ and $({ {iii}})$ can be proved similarly.    $\square$

Average Dwell Time Condition (ADTC) [5]. The number of switches $N(t_0,t)$ in the interval $(t_{0},t)$ for a finite t satisfies $N(t_{0},t) \le N_{0}+ \frac{t-t_{0}}{\tau _{a}},$ where $N_{0}>0$ is the chatter bound, and $\tau _{a}$ is the average dwell time.

Here, by dwell time we mean the time between two consecutive switches, while the chatter bound is an upper bound for the number of switches in an interval of length smaller than $\tau _a$.

3 Main Results

Theorem 3.1

Let the controller gain $K_{i}$ and the constant $\gamma _{i}>0$ be given, and assume that Assumption A holds. Then, the switched control system (3) is robustly globally exponentially ISS with an $H_{\infty }$-norm bound $\gamma$ if the ADTC holds, and there exist positive constants $\xi _{1i}, \, \xi _{2i}, \, \xi _{3i}$, and a positive definite matrix $P_{i}$ satisfying the Riccati-like equation

$$\begin{aligned} (&A_{i}+B_{i}K_{i})^{T}P_{i}+P_{i}(A_{i}+B_{i}K_{i})+\xi _{1i}P_{i}D_{i}D_{i}^{T}P_{i}+\frac{1}{\xi _{1i}}H_{i}^{T}H_{i}+C_{ic}^{T}C_{ic} \nonumber \\&\quad +\xi _{2i}P_{i}G_{i}G_{i}^{T}P_{i}+\xi _{3i}P_{i}^{2}+\frac{1}{\xi _{3i}}\delta _{i}I+\alpha _{i}P_{i}=0, \end{aligned}$$

(5)

where $\delta _{i}>0$ such that $||f_{i}(x)||^{2}\le \delta _{i}||x||^{2}$, and $\alpha _i>0$ is the decay rate of mode i.

Proof

Let $x(t)=x(t,t_{0},x_{0})$ be the solution of system (3). For any $i\in \mathscr {S}$, define $V_{i}(x)= x^{T}P_{i} x$ as a Lyapunov function candidate for the ith mode. Then,

$$\begin{aligned} \dot{V}_{i}(x)&= x^{T} [(A_{i} + B_{i}K_{i})^{T} P_{i}+ P_{i} (A_{i} + B_{i}K_{i})] x+2x^{T}P_{i}(\varDelta A_{i})x \\&\quad +2x^{T}P_{i}G_{i}w+2x^{T}P_{i}f_{i}(x)\\&\quad \le x^{T} [(A_{i} + B_{i}K_{i})^{T} P_{i}+ P_{i} (A_{i} + B_{i}K_{i})+\xi _{1i}P_{i}D_{i}D_{i}^{T}P_{i} \\&\quad +\xi _{2i}P_{i}G_{i}G_{i}^{T}P_{i}+\frac{1}{\xi _{1i}}H_{i}^{T}H_{i}\\&\quad +\xi _{3i}P_{i}^{2}+\frac{1}{\xi _{3i}}\delta _{i}I] x+ \frac{1}{\xi _{2i}}w^{T}w=\; -\alpha _{i}V_{i}(x)+\frac{1}{\xi _{2i}}w^{T}w, \end{aligned}$$

where we used $||f_{i}(x)||^{2}\le \delta _{i}||x||^{2}$ and Lemma 2.4 in the second bottom line, and condition (5) in the last line. Hence, for each subinterval $[t_{k-1},t_{k})$ we have, after adding-subtracting the term $\theta _iV_i(x)$,

$$\begin{aligned} \dot{V}_{i}(x)\le & {} -(\alpha _{i}-\theta _{i})V_{i}(x)-\theta _{i}V_{i}(x)+w^{T}w/\xi _{2i} ~~~\\\le & {} -\overline{\alpha }_{i}V_{i}(x)-\theta _{i}V_{i}(x)+w^{T}w/\xi _{2i}, \end{aligned}$$

where $\overline{\alpha }_{i}=\alpha _{i}-\theta _{i}$ for some $0<\theta _{i}<\alpha _{i}$. The foregoing inequality implies that

$$ \dot{V}_{i}(x) \le -\overline{\alpha }_{i}V_{i}(x), ~~~ \text{ for } \text{ all } \; t\in [t_{k-1},t_{k}), $$

provided that the sum $-\theta _{i}V_{i}(x)+w^{T}w/\xi _{2i}<0$ or $V_{i}(x)>\frac{1}{\theta _{i}\xi _{2i}}||w||^{2}$. By (1), $||x||>\frac{||w||}{\sqrt{\theta _{i}c_{2}\xi _{2i}}}=:\rho _{i}(||w||).$ Then, for all $t \in [t_{k-1},t_{k})$, $V_{i}(x(t)) \le V_{i} (x(t_{k-1})) e^{-\overline{\alpha }_{i}(t-t_{k-1})}$ provided that $||x||>\rho (||w||)$, where $\rho (||w||)=\max _{i\in \mathscr {S}} \{ \rho _{i}(||w||) \}$. From (1), we have for any $i,j \in \mathscr {S}$

$$\begin{aligned} V_{j}(x(t)) \le \mu V_{i}(x(t)), \; ~ \mu =c_{2}/c_{1}, \end{aligned}$$

(6)

where $c_{1}=\min _{i\in \mathscr {S}}\{\lambda _{min}(P_{i})\}$ and $c_{2}=\max _{i\in \mathscr {S}}\{\lambda _{max}(P_{i})\}$. Then, for $i\in \mathscr {S}$ and $t\in [t_{k-1},t_{k})$, we have $V_{i}(x(t)) \le \mu ^{k-1} e^{-\overline{\alpha }_{i}(t-t_{k-1})} e^{-\overline{\alpha }_{i-1}(t_{k-1}-t_{k-2})} \cdots e^{-\overline{\alpha }_{1}(t_{1}-t_{0})}V_{1}(x_{0})$ provided that $||x||>\rho (||w||)$. Letting $\alpha ^{*}=\min \{ \overline{\alpha }_{i} ; \, i\in \mathscr {S} \}$, one may get

$$\begin{aligned} {V}_{i}(x(t))\le & {} \mu ^{k-1} e^{-\alpha ^{*} (t-t_{0})} V_{1}(x_{0})=e^{(k-1)\ln \mu -\alpha ^{*} (t-t_{0})} V_{1}(x_{0}) \end{aligned}$$

provided that $||x||>\rho (||w||)$. Using the ADTC with $N_{0}=\frac{\eta }{\ln \mu }, \, \tau _{a}=\frac{\ln \mu }{\alpha ^{*}-\nu }, \; (\nu <\alpha ^{*}),$ for some arbitrary positive constant $\eta$, we get

$$ V_{i}(x(t)) \le e^{\eta -\nu (t-t_{0})} V_{1}(x_{0}) \qquad \text{ provided } \text{ that } ~ ||x||>\rho (||w||). $$

This implies that [6] $||x||\le b||x_{0}||e^{-\nu (t-t_{0})/2}+\gamma (\sup _{t_{0}\le \tau \le t}||w(\tau )||), ~~ t \ge t_{0},$ where $b=\sqrt{e^{\eta }c_{2}/c_{1}}$, and $\gamma (s)=\sqrt{\frac{c_{2}}{c_{1}}}\rho (s),$ which completes the proof of exponential ISS.

To prove the upper bound on the output magnitude ||z||, for any $i\in \mathscr {S}$, we introduce the performance function $J_{i}=\int _{t_{0}}^{\infty }(z^{T}z-\gamma _{i}^{2}w^{T}w)dt.$ Then,

$$\begin{aligned} J_{i} \le&\int _{t_{0}}^{\infty }(z^{T}z-\gamma _{i}^{2}w^{T}w)\;dt+\int _{t_0}^{\infty }\dot{V}_{i} \, dt+V_{i}(x_{0})\\ \le&\int _{t_{0}}^{\infty }(z^{T}z-\gamma _{i}^{2}w^{T}w)\;dt+V_{i}(x_{0})+\int _{t_{0}}^{\infty } \{x^{T} [(A_{i} + B_{i}K_{i})^{T} P_{i}+ P_{i} (A_{i} + B_{i}K_{i}) \\&+\xi _{1i}P_{i}D_{i}D_{i}^{T}P_{i}+\frac{1}{\xi _{1i}}H_{i}^{T}H_{i}+\xi _{3i}P_{i}^{2}+\frac{1}{\xi _{3i}}\delta _{i}I-\gamma _{i}^{-2}P_{i}G_{i}G_{i}^{T}P_{i}\\&+\gamma _{i}^{-2}P_{i}G_{i}G_{i}^{T}P_{i}]x + 2x^{T}P_{i}G_{i}w \} \; dt\\ =&\;V_{i}(x_{0})+\int _{t_{0}}^{\infty }\{x^{T} [(A_{i} + B_{i}K_{i})^{T} P_{i}+ P_{i} (A_{i} + B_{i}K_{i})+\xi _{1i}P_{i}D_{i}D_{i}^{T}P_{i}+\frac{1}{\xi _{1i}}H_{i}^{T}H_{i}\\&+\xi _{3i}P_{i}^{2}+\frac{1}{\xi _{3i}}\delta _{i}I+\,\gamma _{i}^{-2}P_{i}G_{i}G_{i}^{T}P_{i}+C_{ic}^{T}C_{ic}]x\}\; dt\\&-\int _{t_{0}}^{\infty }\gamma _{i}^{2}(w-\gamma _{i}^{-2}G_{i}^{T}P_{i}x)^{T}(w-\gamma _{i}^{-2}G_{i}^{T}P_{i}x) \; dt.\\ \end{aligned}$$

The last term is strictly negative, so, using condition (5) with $\gamma _{i}^{-2}=\xi _{2i}$, we get $J_{i} \le V_{i}(x_{0})$. Recalling the definition of $J_i$, we see that $||z||_{2}^{2}\le \gamma ^{2}||w||_{2}^{2}+m_{0},$ where $m_{0}=\max _{i\in \mathscr {S}}\{V_{i}(x_{0})\}$, and $\gamma = \max _{i\in \mathscr {S}}\{\gamma _{i}\}$. This completes the proof.    $\square$

Theorem 3.2

(Reliability) Let the constant $\gamma _{i}>0$ be given. Assume that Assumption A holds, the switched control system (4) is robustly globally exponentially ISS-$H_{\infty }$ if the ADTC holds, the controller gain $K_{i}=-\frac{1}{2} \varepsilon _{i}B_{i\overline{\sigma }}^{T}P_{i}$, for some constants $\varepsilon _{i}>0$, and positive definite matrix $P_{i}$, and there exist positive constants $\xi _{1i}, \, \xi _{2i}, \, \xi _{3i}, \, \varepsilon _{i}$, and a positive definite matrix $P_{i}$ satisfying the Riccati-like equation

$$\begin{aligned}&A_{i}^{T}P_{i}+P_{i}A_{i}+P_{i}(\xi _{1i}D_{i}D_{i}^{T}+\xi _{2i}G_{ic}G_{ic}^{T}-\varepsilon _{i}B_{i\overline{\Sigma }}B_{i\overline{\Sigma }}^{T}+\xi _{3i}I)P_{i}\nonumber \\&\quad +\frac{1}{\xi _{1i}}H_{i}^{T}H_{i}+C_{ic}^{T}C_{ic}+\frac{1}{\xi _{3i}}\delta _{i}I+\alpha _{i}P_{i}=0, \end{aligned}$$

(7)

where $\delta _{i}$ is a positive constant such that $||f_{i}(x)||^{2}\le \delta _{i}||x||^{2}$ holds.

Proof

Let $x(t)=x(t,t_{0},x_{0})$ be the solution of system (4). For any $i\in \mathscr {S}$, define $V_{i}(x)= x^{T}P_{i} x$ as a Lyapunov function candidate for the ith mode. Then,

$$\begin{aligned} \dot{V}_{i}(x)\\&= x^{T} [A_{i}^{T} P_{i}+ P_{i} A_{i}+2P_{i}(\varDelta A_{i})+(B_{i\overline{\sigma }}K_{i})^{T}P_{i}+P_{i}B_{i\overline{\sigma }}K_{i}]x\\&\quad +2x^{T}P_{i}G_{ic}w_{\sigma }^{F}+2x^{T}P_{i}f_{i}(x)\\ {}&= x^{T} [A_{i}^{T} P_{i}+ P_{i} A_{i}+2P_{i}(\varDelta A_{i})-\varepsilon _{i}P_{i}(B_{i\overline{\sigma }})(B_{i\overline{\sigma }})^{T}P_{i}]x \\&\quad +2x^{T}P_{i}G_{ic}w_{\sigma }^{F}+2x^{T}P_{i}f_{i}(x)\\&\le x^{T} [A_{i}^{T} P_{i}+ P_{i} A_{i}+\xi _{1i}P_{i}D_{i}D_{i}^{T}P_{i}+\xi _{2i}P_{i}G_{ic}G_{ic}^{T}P_{i}\\&\quad +\frac{1}{\xi _{1i}}H_{i}^{T}H_{i}+\xi _{3i}P_{i}^{2}+\frac{1}{\xi _{3i}}\delta _{i}I -\varepsilon _{i}P_{i}(B_{i\overline{\sigma }})(B_{i\overline{\sigma }})^{T}P_{i}]x+ \frac{1}{\xi _{2i}}(w_{\sigma }^{F})^{T}w_{\sigma }^{F}\\&\le x^{T}[A_{i}^{T}P_{i}+P_{i}A_{i}+P_{i}(\xi _{1i}D_{i}D_{i}^{T}+\xi _{2i}G_{ic}G_{ic}^{T}-\varepsilon _{i}B_{i\overline{\Sigma }}B_{i\overline{\Sigma }}^{T}\\&\quad +\xi _{3i}I)P_{i}+\frac{1}{\xi _{1i}}H_{i}^{T}H_{i}\\&+\frac{1}{\xi _{3i}}\delta _{i}I]x+\frac{1}{\xi _{2i}}(w_{\sigma }^{F})^{T}w_{\sigma }^{F}=-\alpha _{i}V_{i}(x)+\frac{1}{\xi _{2i}}(w_{\sigma }^{F})^{T}w_{\sigma }^{F}, \end{aligned}$$

where we used $||f_{i}(x)||^{2}\le \delta _{i}||x||^{2}$ and Lemma 2.4 in the third bottom line, the fact that [12] $B_{i\overline{\Sigma }} (B_{i\overline{\Sigma }})^{T} \le B_{i\overline{\sigma }} (B_{i\overline{\sigma }})^{T},$ and condition (5) in the last line. Then, for all $t\in [t_{k-1},t_{k})$, we have

$$\begin{aligned} \dot{V}_{i}(x)\le & {} -\overline{\alpha }_{i}V_{i}(x)-\theta _{i}V_{i}(x)+(w_{\sigma }^{F})^{T}w_{\sigma }^{F}/\xi _{2i}, \end{aligned}$$

where $\overline{\alpha }_{i}=\alpha _{i}-\theta _{i}$ and $0<\theta _{i}<\alpha _{i}$. This implies that $\dot{V}_{i}(x) \le -\overline{\alpha }_{i}V_{i}(x), ~~~ \text{ for } \text{ all } ~ t\in [t_{k-1}, t_{k})$ provided that $||x||>\frac{||w_{\sigma }^{F}||}{\sqrt{\theta _{i}c_{2}\xi _{2i}}}=:\rho _{i}(||w_{\sigma }^{F}||).$ As done in Theorem 3.1, one may get $V_{i}(x(t)) \le e^{\eta -\nu (t-t_{0})} V_{1}(x_{0})$ provided that $||x||>\rho (||w||)$, where $\rho (||w||)=\max _{i\in \mathscr {S}} \{ \rho _{i}(||w||) \}$. This also implies that [6]

$$ ||x||\le b||x_{0}||e^{-\nu (t-t_{0})}+\gamma (\sup _{t_0 \le \tau \le t}||w_{\sigma }^{F}(\tau )||), ~~ t \ge t_{0}, $$

where $b=\sqrt{e^{\eta }c_{2}/c_{1}}$, $\gamma (s)=\sqrt{\frac{c_{2}}{c_{1}}}\rho (s).$ As for the upper bound on ||z||, we follow the same steps in Theorem 3.1, where $J_{i}=\int _{t_{0}}^{\infty }(z^{T}z-\gamma _{i}^{2}(w_{\sigma }^{F})^{T}w_{\sigma }^{F})dt,$ to obtain $||z||_{2}^{2}\le \gamma ^{2}||w_{\sigma }^{F}||_{2}^{2}+m_{0},$ where $m_{0}=\max _{i\in \mathscr {S}}\{V_{i}(x_{0})\},$ and $\gamma = \max _{i\in \mathscr {S}}\{\gamma _{i}\}$.    $\square$

4 Numerical Example

Example 1

Consider system (3) where $\mathscr {S}=\{1,2\}$,

$$ A_1=\left[ \begin{array}{cc} 0.2 &{} 0 .1\\ 0 &{} -6 \end{array} \right] , B_1=\left[ \begin{array}{cc} -7 &{} 1 \\ 0.1 &{} 0.2 \end{array} \right] , C_1=\left[ \begin{array}{cc} 2 &{} 0.1 \\ 0 &{} 2 \end{array} \right] , F_1=\left[ \begin{array}{cc} 0.1 &{} -2 \\ 0.1 &{} 0 \end{array} \right] , $$

$$ D_1=\left[ \begin{array}{cc} 1\\ 0 \end{array} \right] , H_1=\left[ \begin{array}{cc} 0 &{} 1 \\ \end{array} \right] , G_1=\left[ \begin{array}{cc} 1 &{} 0 \\ 0 &{} 1 \end{array} \right] , f_{1}=0.01\left[ \begin{array}{cc} \sin (x_{1}) \\ \sin (x_{2}) \end{array} \right] , \mathscr {U}_1=\sin (t), $$

$\varepsilon _1=2, \; \xi _{11}=0.2, \; \gamma _1=0.1, \; \alpha _1=2, \; \xi _{21}=\gamma _1^{-2}, \; \xi _{31}=1,$ and $\theta _1=1$ with $t_0=0$. From $||f_{i}(x)||^{2}\le \delta _{i}||x||^{2}$, one may get $\delta _{1}=0.01$. As for the second mode, we take

$$ A_2=\left[ \begin{array}{cc} -9 &{} 0 .2\\ 0 &{} 0.1 \end{array} \right] , B_2=\left[ \begin{array}{cc} 0.1 &{} 0.5 \\ 0.1 &{} -8 \end{array} \right] , C_2=\left[ \begin{array}{cc} 1 &{} 0 \\ 0 &{} 0.5 \end{array} \right] , F_2=\left[ \begin{array}{cc} 0.1 &{} 0 \\ -3 &{} 0.1 \end{array} \right] , $$

$$ D_2=\left[ \begin{array}{cc} 0\\ 1 \end{array} \right] , H_2=\left[ \begin{array}{cc} 1 &{} 0 \\ \end{array} \right] , G_2=\left[ \begin{array}{cc} 1 &{} 0 \\ 0 &{} 1 \end{array} \right] , f_{2}=0.01\left[ \begin{array}{cc} \sin (x_{1}) \\ \sin (x_{2}) \end{array} \right] , \mathscr {U}_{2}=\sin (t), $$

$\varepsilon _2=0.5, \; \xi _{12}=0.3, \; \gamma _2=0.15, \; \alpha _2=2.5, \; \xi _{22}=\gamma _2^{-2}, \; \xi _{32}=1,$ and $\theta _2=1.5.$ From $||f_{i}(x)||^{2}\le \delta _{i}||x||^{2}$, one may get that $\delta _{2}=0.01.$ Let the system input disturbance be defined by $w(t)= \left[ \sin (t) ~ \sin (t) \right] ^T$.

Case 1

(All the actuators are operational) When all the control actuators are operational, from Riccati-like equation,

$$ P_1=\left[ \begin{array}{cc} 1.6437 &{} 0.0149\\ 0.0149 &{} 0.2499 \end{array} \right] , P_2=\left[ \begin{array}{cc} 0.1633 &{} 0.0859\\ 0.0859 &{} 0.2724 \end{array} \right] , $$

with $c_{11}\,{=}\,\lambda _{\min }{(P_1)}\,{=}\,0.2498, c_{12}=\lambda _{\max }{(P_1)}=1.6439, c_{21}=\lambda _{\min }{(P_2)}=0.1161$, $c_{22}=\lambda _{\max }{(P_2)}=0.3197$, so, $c_1=0.1161, \; c_{2}=1.6439$, and

$$ K_1=\left[ \begin{array}{cc} 11.5047 &{} 0.0796\\ -1.6467 &{} -0.0649 \end{array} \right] , K_2=\left[ \begin{array}{cc} -0.0062 &{} -0.0090\\ 0.1514 &{} 0.5342 \end{array} \right] . $$

Thus, the matrices $A_{1}+B_{1}K_{1}$ and $A_{2}+B_{2}K_{2}$ are Hurwitz. The average dwell time is $\tau _{a}= \frac{\ln \mu }{\alpha ^{*}-\nu }=2.7898$, with $\nu =0.05$.

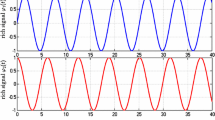
Figure 1a shows the simulation results of ||x|| (top) and $\gamma (||w||)=\sqrt{c_2/c_1} \rho (||w||)$ (bottom), where $\rho (s)=\max \{\rho _{1}(s), \, \rho _{2}(s)\}$ and $\rho _{i}(s)=s/ \sqrt{c_{2} \theta _{i} \xi _{2i}}$, and $\tau _{a}=3.$

Case 2

(Failure in the second actuator in the first mode and first actuator in the second mode) When there is a failure in the second actuator, i.e., $B_{1\Sigma }=\{2\}$ and $B_{1\overline{\Sigma }}=\left[ \begin{array}{cc} -7 &{} 0 \\ 0.1 &{} 0 \end{array} \right] ,$ and $B_{2\Sigma }=\{1\}$ and $B_{2\overline{\Sigma }}=\left[ \begin{array}{cc} 0 &{} 0.5 \\ 0 &{} -8 \end{array} \right] ,$ we have from Riccati-like equation,

$$ P_1=\left[ \begin{array}{cc} 1.1265 &{} -0.1913\\ -0.1913 &{} 0.3110 \end{array} \right] , ~ P_2=\left[ \begin{array}{cc} 0.1676 &{} 0.0980\\ 0.0980 &{} 0.2436 \end{array} \right] , $$

with $c_{11}=\lambda _{\min }{(P_1)}=0.2683, \; c_{12}=\lambda _{\max }{(P_1)}=1.1691, \; c_{21}=0.1005, \; c_{22}=0.3107$, so $c_1=0.1005, \; c_{2}=1.1691$, and the control gain matrices

$$ K_1=\left[ \begin{array}{cc} 7.9046 &{} -1.3703\\ 0 &{} 0 \end{array} \right] , K_2=\left[ \begin{array}{cc} 0 &{} 0\\ 0.1751 &{} 0.4750 \end{array} \right] . $$

Thus, the matrices $A_{1}+B_{1}K_{1}$ and $A_{2}+B_{2}K_{2}$ are Hurwitz, and $\tau _{a}=2.5834$. Figure 1b shows the simulation results of ||x|| (top) and $\gamma (||w||)=\sqrt{c_2/c_1} \rho (||w||)$ (bottom), where $\rho (s)=\max \{\rho _{1}(s), \, \rho _{2}(s)\}$ and $\rho _{i}(s)=s/ \sqrt{c_{2} \theta _{i} \xi _{2i}}$, $\tau _{a}=3$.

Fig. 1

Input-to-state stabilization

5 Conclusion

We have considered a time-varying parameter uncertainty in the system state, an $L_2$ norm-bounded input disturbance, and a linearly bounded nonlinear term. The output of the faulty actuators has been treated as a disturbing signal that has been augmented with the system disturbance. We have shown that, using the average dwell time with multiple Lyapunov functions, the switched system is exponentially input-to-state stabilizable, when every individual mode is exponentially input-to-state stabilized by a reliable feedback controller.