Hydrodynamic Analysis of Sound Wave Propagation in a Reactive Mixture Confined Between Two Parallel Plates

Abstract

The aim of this work is to study the problem of sound wave propagation through a binary mixture undergoing a reversible chemical reaction of type A $+$ A $\rightleftharpoons$ B $+$ B, when the mixture is confined between two flat, infinite and parallel plates. One plate is stationary, whereas the other oscillates harmonically in time and constitutes an emanating source of sound waves that propagate in the mixture. The boundary conditions imposed in our problem correspond to assume that the plates are impenetrable and that the mixture chemically react at the surface plates, reaching the chemical equilibrium instantaneously. The reactive mixture is described by the Navier-Stokes equations derived from the Boltzmann equation in a chemical regime for which the chemical reaction is in its final stage. Explicit expressions for transport coefficients and chemically production rates are supplemented by the kinetic theory. Starting from this setting, we study the dynamics of the sound waves in the reactive mixture in the low frequency regime and investigate the influence of the chemical reaction on the properties of interest in the considered problem. We then compute the amplitude and phase profiles of the relevant macroscopic quantities, showing how they vary in the reactive flow between the plates in dependence on several factors, as the chemical activation energy, concentration of products and reactants, as well as oscillation speed parameter.

1 Introduction

The mathematical modelling of sound wave propagation in a rarefied medium and the correct description of the properties of interest in terms of both the rarefaction degree of the medium and the sound frequency of the wave is a topic of great relevance in several fields. This subject appears in many applied situations of modern engineering, associated with porous nanomaterials, vibrating micro-devices, near-vacuum systems, acoustic measurements, propagation of noise and many other problems.

These facts have motivated many scientific contributions, both theoretical and numerical [1,2,3,4,5,6,7,8,9,10,11]. In particular, theoretical works and numerical simulations can provide some guidance in experimental studies and design of many devices, and can help to predict the acoustic behaviour in many systems.

From the mathematical point of view, the modelling of sound wave propagation is based on the Navier-Stokes equations when a regime of continuum flow and low oscillation frequencies is considered. However, when the systems approach the micro scale or when high oscillation frequencies are taken into account, other regimes should be considered for which the Navier-Stokes equations become not valid and the Boltzmann equation is used to capture the rarefaction effects or to treat the boundary Knudsen layer [5, 11].

Various problems have been studied in several regimes of propagation, considering a one-component gas or a mixture of inert gases, either occupying a semi-infinite space [11,12,13] or confined between two parallel plates [1, 5, 9, 10]. In particular, Ref. [5] addresses the problem of sound propagation in a monoatomic gas confined between source and receptor of sound waves over a wide range of gas rarefaction and sound frequency regimes. The results presented in Ref. [5] show many interesting features concerning, in particular, how the sound waves reflected from the receptor influence the solution of the problem when the distance between both plates is varying.

On the other hand, some problems associated to sound wave propagation have also been investigated in the context of chemically reactive mixtures [3, 6, 14,15,16,17,18]. The results indicate that the sound propagation can be considerably influenced by the chemical reaction.

However, the presence of the chemical reaction introduces additional complexities and, in general, one considers some simplifications in order to solve the sound wave problem. For instance, in Refs. [3, 14, 15] the problem is formulated in an unbounded domain, so that no boundary conditions are involved, assuming that the mixture fields are the sum of an equilibrium value plus an harmonic wave of small amplitude. In Refs. [14, 15, 17, 18], an Eulerian mixture is considered and the transport effects are absent, so that only the effects of chemical reactions on sound propagation are considered. In Ref. [6], a binary mixture confined between two parallel plates is considered and the gaseous particles can react chemically at one wall only, with infinitely fast chemical reaction so that the gaseous particles reach the equilibrium instantaneously and the flow between the boundaries is non-reactive.

The problems described in the latter reference have motivated the study developed in the present paper, and we give here a further contribution for the sound wave propagation problem within a chemically reactive mixture.

We consider a binary mixture confined between source and receptor, in the presence of a chemical reaction of type $A + A \rightleftharpoons B + B$, which is typical of isomers [19]. Our approach is based on the Navier-Stokes equations with temperature jump and velocity impenetrable conditions at both source and receptor of sound waves. A chemical regime for which the chemical reaction is in its final stage is assumed.

Since there are no papers regarding the temperature jump in reactive gas mixtures, the temperature jump coefficient for a single gas is used here. This choice is motivated by two facts. First, both constituents have the same molecular mass, as a consequence of the mass conservation during the chemical reaction, so that they are identical in mechanical sense. Second, the chemical reaction is in its final stage, so that chemical transformations become less frequent and the deviations from the chemical equilibrium are small. Therefore, in the context of the present problem, this simplification does not seem to be so restrictive. In fact, it is well known that for a mixture with a small ratio of molecular masses, the temperature jump coefficient does not differ significantly from that for a single gas, see paper [12]. However, it is our future research plan to determine the temperature jump coefficient for a more general reactive gas mixture, resorting to an appropriate model in kinetic theory for the description of the reactive mixture.

Starting from this setting, we study the sound wave propagation in the reactive mixture in the low frequency regime and investigate both the influence of the chemical reaction and the effects of the reflected waves from the receptor on the relevant macroscopic quantities. We perform some numerical computations to investigate how the amplitudes and phases vary in dependence of several parameters, as the chemical activation energy, concentration of products and reactants (exothermic or endothermic dominant reaction), distance between source and receptor and oscillation speed parameter.

2 Description of the Mixture

We consider a binary mixture of monoatomic gases whose constituents, denoted by A and B, undergo a reversible chemical reaction of symmetric type represented by

$$\begin{aligned} A + A \rightleftharpoons B + B . \end{aligned}$$

(1)

Both constituents have the same molecular mass m and the same molecular diameter d. The molar fraction of each species in the mixture is defined as

$$\begin{aligned} x_A = \frac{n_A}{n_A + n_B}, \qquad x_B = 1 - x_A, \end{aligned}$$

(2)

where $n_{\alpha }$ ($\alpha$ = A, B) denotes the number density of species $\alpha$ in the mixture, with $n=n_A+n_B$ the total number density of the mixture.

The constituents have different binding energies $\varepsilon _A$ and $\varepsilon _B$, so that we introduce the heat of the chemical reaction defined as the binding energy difference between reactants and products of the forward reaction,

$$\begin{aligned} E=2(\varepsilon _A-\varepsilon _B) . \end{aligned}$$

(3)

Observe that the forward reaction in (1) is exothermic when $E>0$, whereas it is endothermic when $E<0$.

The hydrodynamic model describing the considered mixture is that of the reactive Navier-Stokes equations [3, 19] formed by the balance equations for the number densities $n_A$ of the reactants and $n_B$ of the products, together with the conservation equations for the momentum and total energy of the whole mixture. The transport coefficients involved in the description of the mixture are the shear viscosity $\mu$, diffusion D, thermal diffusion ratio $\kappa _T$ and thermal conductivity $\lambda$.

The interaction among the constituents due to the chemical reaction (1) is specified by the chemical production rate $\mathscr {T}$, which plays an important role in the model. In the present analysis, the reaction rate is explicitly obtained from the kinetic theory of reactive mixtures, as it will be explained in Sect. 4. The concentration of each constituent in the reactive mixture is measured by the corresponding number density $n_\alpha$ ($\alpha =A, B$).

For sake of brevity, we omit here the full system of reactive Navier-Stokes equations, since they will be introduced in its one-dimensional form in Sect. 4.

3 Statement of the Problem

We assume that the mixture is quiescent in equilibrium conditions, confined between two flat, infinite and parallel plates, located at $x'\!=\!0$ and $x'\!=\!L'$, where $x'$ is the first space coordinate of a 3-dimensional orthogonal reference frame $Ox'y'z'$.

Both plates are kept at the same uniform temperature, which is the equilibrium temperature $T_0$ of the mixture. The plate located at $x'\!=\!L'$ is at rest, whereas the one located at $x'\!=\!0$ oscillates harmonically in time, in the $x'$-direction, i.e. in the direction orthogonal to its own plane, with angular frequency $\omega$ and velocity

$$\begin{aligned} U_p(t) = \mathfrak {R}\left( U e^{- {i} \omega t} \right) , \end{aligned}$$

(4)

where $\mathfrak {R}$ denotes the real part of a complex number, i is the imaginary unit and $U \!\in \! \mathbb {R}$ represents the constant amplitude of the oscillating velocity. We assume that U is very small when compared to the characteristic molecular speed $v_m$ of the mixture, that is

$$\begin{aligned} U \ll v_m , \qquad v_m = \sqrt{\frac{2k_BT_0}{m}}, \end{aligned}$$

(5)

where $k_B$ is the Boltzmann constant, $T_0$ is the equilibrium temperature of the mixture and m is the molecular mass of the species.

Perturbations. According to this description, the oscillating plate ($x'\!=\!0$) constitutes an emanating source of sound waves that propagate in the $x'$-direction and slightly deviate the properties of the reactive mixture from the equilibrium state. On the other hand, the stationary plate ($x'\!=\!L'$) behaves as a receptor of sound waves and can significantly change the flow due to the influence of the reflected waves from the plate. The sound waves generated by the oscillating plate disturb the number densities $n_\alpha$ and mean velocities $v_\alpha$ of the constituents ($\alpha =A,B$), as well as the mass density $\rho$, temperature T, pressure p and heat flux q of the mixture. We assume that all mixture properties depend harmonically on time and introduce the following expansions of the state variables around an equilibrium state,

$$\begin{aligned} \begin{aligned}&n_\alpha (t,x') = n_{\alpha 0} + \mathfrak {R}{[\overline{n}_\alpha (x') \, e^{- {i} \omega t}]} , \\&v_\alpha (t,x') = \mathfrak {R}{[ \overline{v}_\alpha (x') \, e^{- {i} \omega t}]} , \\&\rho (t,x') = \rho _0 + \mathfrak {R}{[\overline{\rho }(x') \, e^{- {i} \omega t}]} , \\&v (t,x') = \mathfrak {R}{[ \overline{v}(x') \, e^{- {i} \omega t} ]}, \\&T (t,x') = T_0 +\mathfrak {R}{[\overline{T}(x') \, e^{- {i} \omega t}]} . \end{aligned} \end{aligned}$$

(6)

Here, the quantities $n_{\alpha 0}$, $\rho _0$, $T_0$ are constant and refer to the thermodynamical equilibrium state of the reactive mixture, so that the number densities $n_{A0}$, $n_{B0}$ of the constituents and the temperature $T_0$ of the mixture are constrained to the mass action law of the model, see [19], that is

$$\begin{aligned} \exp \left( \! - \frac{E}{k_BT_0} \right) = \left( \frac{n_{A0}}{n_{B0}} \right) ^{\!2} , \end{aligned}$$

(7)

where E is the reaction heat defined in (3). Furthermore, the quantities $\overline{n}_\alpha (x')$, $\overline{v}_\alpha (x')$, $\overline{\rho }(x')$, $\overline{v}(x')$, $\overline{T}(x')$ appearing in expansions (6) represent the complex spatial perturbations of the corresponding state variables.

Under these conditions, a linearized theory based on the reactive Navier-Stokes equations is appropriate to describe the dynamics and the chemical kinetics of the perturbed variables (6), in particular to describe the spatial evolution of the perturbation amplitudes.

Relevant parameters. The relevant parameters in this description are the rarefaction parameter, $\delta$, which is inversely proportional to the well known Knudsen number [20], and the oscillation parameter, $\theta$, defined by

$$\begin{aligned} \delta = \frac{L' p_0}{\eta v_m}, \qquad \theta = \omega \tau , \end{aligned}$$

(8)

where $L'$ is the distance between the plates, already introduced, $v_m$ is given in (5), $p_0$ is the equilibrium pressure of the mixture, $\eta$ the shear viscosity of the mixture and $\tau$ represents the effective mean free time between successive molecular collisions.

Note that the oscillation parameter $\theta$ is defined as in [3] and corresponds to the ratio of the oscillation frequency to the collision frequency.

For convenience, the dimensionless x-coordinate is introduced as

$$\begin{aligned} x=\frac{x'\omega }{v_m}, \end{aligned}$$

(9)

and, as a consequence, the dimensionless distance between the plates is written as $L=\delta \theta$. Since our mathematical setting corresponds to the hydrodynamic regime, large values for $\delta$ and small values for $\theta$ are considered, i.e. $\delta \gg 1$ and $\theta \ll 1$.

Boundary conditions. The interaction of the reactive mixture with the surface plates is described by the boundary conditions to be imposed to our differential equations. We assume that both plates are impenetrable, so that the mixture accommodates its bulk velocity to the velocity of the plates. In fact, at the stationary plate ($x\!=\!L$), the mixture instantaneously relax to a resting state and its bulk velocity vanishes at this boundary. At the oscillatory plate ($x\!=\!0$), the mixture instantaneously accommodates its bulk velocity to the velocity of the plate, as a consequence of the oscillatory movement of the plate itself. Therefore, from (4) and (6), the boundary conditions for the spatial part of the mixture bulk velocity are given as

$$\begin{aligned} \overline{v}(x) \vert _{_{x=0}} = U, \qquad \overline{v}(x) \vert _{_{x=L}} = 0 . \end{aligned}$$

(10)

Concerning the temperature, jump conditions at source and receptor are employed, so that from (6) we have

$$\begin{aligned} \overline{T}\vert _{_{x=0}} = T_0 + {\zeta _T} \theta \; \frac{\partial \overline{T}}{\partial x}\bigg \vert _{x=0} \;, \qquad \overline{T}\vert _{_{x=L}} = T_0 - {\zeta _T} \theta \, \frac{\partial \overline{T}}{\partial x}\bigg \vert _{x=L} \;, \end{aligned}$$

(11)

where $\zeta _T$ is the temperature jump coefficient, see papers [8, 12, 21,22,23].

As explained and motivated in the Introduction, we will use, in this work, the temperature jump coefficient for a single gas, namely $\zeta _T = 1.954$, see [5, 12], as an approximation of the corresponding coefficient in the considered binary reactive mixture.

4 Hydrodynamic Equations for the Reactive Mixture

Starting from a kinetic description in terms of a Boltzmann equation for the considered binary reactive mixture, the macroscopic field equations of the reactive flow can be derived in the hydrodynamic limit at Navier-Stokes level. This derivation has been addressed in paper [24] for the reactive mixture considered in our work.

Basic fields and macroscopic equations. The basic fields of the mixture are the particle number densities $n_A$ of the reactants and $n_B$ of products, the velocity v and temperature T of the mixture. For the problem under consideration, the balance equations for these fields can be written in the following form (see paper [3])

$$\begin{aligned}&\frac{\partial n_\alpha }{\partial t}+\frac{\partial }{\partial x'} {\left( n_\alpha v_\alpha \right) } = \lambda _\alpha \mathscr {T}, \quad \alpha = A,B , \end{aligned}$$

(12)

$$\begin{aligned}&\rho \frac{\partial v}{\partial t} \!+\! \rho v \frac{\partial v}{\partial x'} + \frac{\partial P_{xx}}{\partial x'}=0, \end{aligned}$$

(13)

$$\begin{aligned}&\frac{3}{2} \frac{p}{T} \! \left( \frac{\partial T}{\partial t} + v \frac{\partial T}{\partial x'} \right) + \frac{\partial q}{\partial x'} - \frac{E}{2} \frac{\partial }{\partial x'} \Big [n_A (v_A - v) \Big ] + P_{xx} \frac{\partial v}{\partial x'} = \frac{E}{2} \mathscr {T}, \end{aligned}$$

(14)

where $\mathscr {T}$ represents the reaction production term due to the chemical reaction, $\lambda _\alpha$ is the stoichiometric coefficient of each constituent, with $\lambda _A = - \lambda _B = -1$. Moreover, the symbol E stands for the chemical reaction heat introduced in (3). Finally, plain symbols refer to the whole mixture and have the usual meaning in kinetic theory and fluid mechanics [19], in particular $p=nk_BT$ is the mixture pressure, q the heat flux and $P_{xx}$ the first component of the pressure tensor.

The constitutive relations for the field equations (12–14) have been derived in paper [24] in the form

$$\begin{aligned}&{Fick\,law}&v_A \!-\! v = - \frac{D}{n_A} \left( \frac{n_B}{n} \frac{\partial n_A}{\partial x'} \!-\! \frac{n_A}{n} \frac{\partial n_B}{\partial x'} \!+\! \frac{n}{T} \, \kappa _T \frac{\partial T}{\partial x'} \right) \end{aligned}$$

(15)

$$\begin{aligned}&{Newton\,law}&P_{xx} = p - \frac{4}{3} \eta \frac{\partial v}{\partial x'} \end{aligned}$$

(16)

$$\begin{aligned}&{Fourier\,law}&q = - \lambda \, \frac{\partial T}{\partial x'} + \left( \frac{E}{2} + \frac{n}{n_A n_B} \, p \, \kappa _T \right) \! n_A (v_A - v) \end{aligned}$$

(17)

$$\begin{aligned}&{Reaction\,rate\,law}&\mathscr {T}= \ell \, \frac{{\mathscr {A}}}{k_BT} \end{aligned}$$

(18)

where D, $\eta$ and $\lambda$ are the coefficients of diffusion, shear viscosity and thermal conductivity, respectively, $\kappa _T$ is the thermal diffusion ratio, $\ell$ the coefficient of the forward reaction rate and $\mathscr {A}$ the chemical affinity of the forward reaction given by

$$\begin{aligned} {\mathscr {A}} = E + 2k_BT \ln \left( \frac{n_A}{n_B} \right) . \end{aligned}$$

(19)

Equations (12–14) with their constitutive conditions (15–18) represent the closed set of Navier-Stokes equations for the binary reactive mixture considered here. Such equations have been derived in paper [24] from a kinetic theory dynamics and therefore explicit expressions have been obtained in the quoted paper for the transport coefficients $D, \eta , \lambda , \kappa _T$ and reaction rate coefficient $\ell$.

5 Analysis of Sound Propagation in the Reactive Mixture

The linearized equations for the problem in question are obtained by inserting the representation (6) into both the balance equations (12)–(14) and the constitutive relations (15)–(18), keeping only linear terms of the field deviations. The resulting set of equations describes the spatial evolution of the complex perturbation of the state variables, and is written as follows.

$$\begin{aligned}&- i \omega \, \overline{n}_A + x_A n_{0} \frac{d\overline{v}}{dx'} -D x_B \frac{d^2\overline{n}_A}{dx'^2} +D x_A \frac{d^2\overline{n}_B}{dx'^2} -D \frac{n_0}{T_0} \kappa _T \frac{d^2\overline{T}}{dx'^2} \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad = - \frac{2\ell _0}{n_0} \left( \frac{\overline{n}_A}{x_A} - \frac{\overline{n}_B}{x_B} \right) \! , \end{aligned}$$

(20)

$$\begin{aligned}&- i \omega \, \overline{n}_B + x_B n_{0} \frac{d\overline{v}}{dx'} -D x_A \frac{d^2\overline{n}_B}{dx'^2} +D x_B\frac{d^2\overline{n}_A}{dx'^2} +D \frac{n_0}{T_0} \kappa _T \frac{d^2\overline{T}}{dx'^2} \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad = \frac{2\ell _0}{n_0} \left( \frac{\overline{n}_A}{x_A} - \frac{\overline{n}_B}{x_B} \right) \! , \end{aligned}$$

(21)

$$\begin{aligned}&- i \omega m n_0 \overline{v} + k_B T_0 \frac{d\overline{n}}{dx'} + k_B n_0 \frac{d\overline{T}}{dx'} - \frac{4}{3} \eta \frac{d^2\overline{v}}{dx'^2} = 0, \end{aligned}$$

(22)

$$\begin{aligned}&- \frac{3}{2} i \omega k_B n_0 \overline{T} - \lambda \frac{d^2\overline{T}}{dx'^2} - \frac{k_B T_0}{x_A} \kappa _T D \frac{d^2 \overline{n}_A}{dx'^2} + \frac{k_B T_0}{x_B} \kappa _T D \frac{d^2 \overline{n}_B}{dx'^2} + n_0 k_B T_0 \frac{d\overline{v}}{dx'} \\&\qquad \qquad \qquad - \frac{n_0 k_B}{x_A x_B} D \kappa _T^2 \frac{d^2 \overline{T}}{dx'^2} = \frac{E \ell _0}{n_0} \left( \frac{\overline{n}_A}{x_A} - \frac{\overline{n}_B}{x_B} \right) , \nonumber \end{aligned}$$

(23)

where $\ell _0$ is the dimensionless coefficient of the forward reaction rate, given by

$$\begin{aligned} \ell _0 = - 4 x_A n_0^2 d^2 s^2 \sqrt{\frac{\pi k_B T_0}{m}} \exp \left( - \frac{\varepsilon _f}{k_B T_0}\right) , \end{aligned}$$

(24)

with s being the steric factor and $\varepsilon _f$ the activation energy of the forward chemical reaction. Moreover, we use here the notation $x_\alpha$ for the equilibrium molar fraction of species $\alpha$ in the mixture, $x_\alpha = n_{\alpha 0} / n_0$ ($\alpha \!=\!A,B$), and $x_A, x_B$ are related to the reaction heat through the mass action law (7). Accordingly, the forward chemical reaction reaction is exothermic if $x_A<0.5$, whereas it is endothermic if $x_A>0.5$.

After some algebraic manipulation, the system of equations (20–23) is reduced to two differential equations for the bulk velocity of species A and B as

$$\begin{aligned} A_1 \frac{d^4\overline{v}_A}{dx'^4} + B_1 \frac{d^2\overline{v}_A}{dx'^2} + C_1 \overline{v}_A = 0, \qquad A_2 \frac{d^4\overline{v}_B}{dx'^4} + B_2 \frac{d^2\overline{v}_B}{dx'^2} + C_2 \overline{v}_B = 0 \end{aligned}$$

(25)

where $A_i, \, B_i, \, C_i$, for $i=1,2$, are known coefficients depending on the transport coefficients and equilibrium quantities as follows

$$\begin{aligned}&A_1 \!=\! -\lambda \left( \frac{i T_0}{\omega } + \frac{4 \eta }{3k_Bn_0} \right) , \nonumber \\&B_1 \!=\! \frac{5}{2} k_B n_0 T_0 \!-\! 2 i \eta \omega \!-\! \frac{\rho _0}{k_B n_0} i \lambda \omega + \frac{k_B n_0 T_0}{x_A} \kappa _T \!+\! \frac{E\ell _0}{x_A x_B T_0} \! \left( \! \frac{i T_0}{\omega } + \frac{4 \eta }{3k_Bn_0} \! \right) \! \kappa _T, \\&C_1 \!=\! \frac{3}{2} \rho _0 \omega ^2 + \frac{E\ell _0}{x_A D} + \frac{E\ell _0}{x_A x_B T_0} \frac{\rho _0}{k_B n_0} \; i \omega \kappa _T, \nonumber \end{aligned}$$

(26)

and

$$\begin{aligned} A_2&\!=\! A_1 , \nonumber \\ B_2&\!=\! \frac{5}{2} k_B n_0 T_0 \!-\! 2 i \eta \omega \!-\! \frac{\rho _0}{k_B n_0} i \lambda \omega - \frac{k_B n_0 T_0}{x_B} \kappa _T \!+\! \frac{E\ell _0}{x_A x_B T_0} \! \left( \! \frac{i T_0}{\omega } + \frac{4 \eta }{3k_Bn_0} \! \right) \! \kappa _T , \\ C_2&\!=\! \frac{3}{2} \rho _0 \omega ^2 - \frac{E\ell _0 }{x_B D} + \frac{E\ell _0}{x_A x_B T_0} \frac{\rho _0}{k_B n_0} \; i \omega \kappa _T . \nonumber \end{aligned}$$

(27)

For convenience, the equations given by (25) are written in a dimensionless form by referring them to the dimensionless x-coordinate (9) and by introducing the following dimensionless macroscopic fields

$$\begin{aligned}&n^* = \frac{\overline{n}}{n_0} \frac{v_m}{U} \, ,&n^*_\alpha = \frac{\overline{n}_\alpha }{n_0} \frac{v_m}{U} \, ,&v^* = \frac{\overline{v}}{U} \, , \end{aligned}$$

(28)

$$\begin{aligned}&v^*_\alpha = \frac{\overline{v}_\alpha }{U} \, ,&T^* = \frac{\overline{T}}{T_0} \frac{v_m}{U} \, ,&P_{xx}^* = \frac{\overline{P}_{xx}}{P_0} \frac{v_m}{U}. \end{aligned}$$

(29)

Such fields measure the deviation of the macroscopic fields introduced in (6) with respect to corresponding equilibrium values. Furthermore, the dimensionless transport coefficients are introduced as

$$\begin{aligned} \eta ^* = \frac{\eta }{\eta _I} \,, \quad \lambda ^* = \frac{\lambda }{\lambda _I} \,, \quad D^* = \frac{D}{D_I} \;, \end{aligned}$$

(30)

where $\eta _I, \, \lambda _I, \,D_I$ are the first-order approximation to the coefficients of shear viscosity, thermal conductivity and diffusion of an inert gas of hard-spheres with diameter d, given by (see, again, paper [24])

$$\begin{aligned} \eta _I = \frac{5}{16} \frac{1}{d^2} \sqrt{\frac{mk_BT_0}{\pi }} \;, \quad \lambda _I = \frac{75}{64} \frac{k_B}{d^2} \sqrt{\frac{k_BT_0}{\pi m}} \;, \quad D_I = \frac{177}{464} \frac{1}{n_0 d^2} \sqrt{\frac{k_BT_0}{\pi m}} \; . \end{aligned}$$

(31)

Table 1 shows the values of the transport coefficients in the reactive mixture, for different values of the dimensionless activation energy $\varepsilon ^*$=$\,{\varepsilon _f}/{k_BT_0}$ and molar fraction $x_A$ specifying the exothermic ($x_A<0.5$) or endothermic ($x_A>0.5$) character of the forward reaction. Observe that high values of the activation energy mean that the energy barrier that the particles must overcome in order to react chemically is to high, so that only few particles react chemically. In particular, the case $\varepsilon ^*=20$ represents a limiting situation of this type in which the effects of the chemical reaction becomes almost negligible and the values of the dimensionless transport coefficients $D^*$, $\eta ^*$, $\lambda ^*$ approach the unity and $\kappa _T$ vanishes, as shown in Table 1.

Table 1 Dimensionless transport coefficients for different values of the forward activation energy $\varepsilon ^*$ and reactants molar fraction $x_A$. The data is obtained with the results derived in paper [24]

We also specify the effective mean free time $\tau$ between successive molecular collisions and introduce both the exponential factor $\varDelta$ of the Arrhenius law and the dimensionless reaction heat $\mathscr {E}$, given by

$$\begin{aligned} \tau = \frac{4}{5} \frac{\eta _I}{k_B n_0 T_0} , \qquad \varDelta = x_A^2 s^2 \exp \left( - \frac{\varepsilon _f}{k_B T_0}\right) , \qquad \mathscr {E}= \frac{E}{k_B T_0}. \end{aligned}$$

(32)

Therefore, the dimensionless equations read

$$\begin{aligned} A'_1 \frac{d^4 v_A^*}{dx^4} + B'_1 \frac{d^2 v_A^*}{dx^2} + C'_1 v_A^* = 0, \qquad A'_2 \frac{d^4 v_B^*}{dx^4} + B'_2 \frac{d^2 v_B^*}{dx^2} + C'_2 v_B^* = 0 \end{aligned}$$

(33)

where

$$\begin{aligned} A'_1&= - \frac{25}{32} i \theta \lambda ^* - \frac{125}{96} \theta ^2 \lambda ^* \eta ^*, \nonumber \\ B'_1&= \frac{5}{6} - \frac{5}{6} i \theta \eta ^* - \frac{25}{16} i \theta \lambda ^* + \frac{1}{3x_A} \kappa _T - \frac{\mathscr {E}^*\varDelta }{3 x_A x_B} \left( \frac{i}{\theta } + \frac{5}{3} \eta ^* \right) , \\ C'_1&= 1 - \frac{232}{531} \frac{\mathscr {E}\varDelta }{x_A \theta ^2 D^*} - \frac{2}{3} i \frac{\mathscr {E}\varDelta }{x_A x_ B \theta } \kappa _T, \nonumber \end{aligned}$$

(34)

and

$$\begin{aligned} A'_2&= A'_1, \nonumber \\ B'_2&= \frac{5}{6} - \frac{5}{6} i \theta \eta ^* - \frac{25}{16} i \theta \lambda ^* - \frac{1}{3x_B} \kappa _T - \frac{\mathscr {E}^*\varDelta }{3 x_A x_B} \left( \frac{i}{\theta } + \frac{5}{3} \eta ^* \right) , \\ C'_2&= 1 + \frac{232}{531} \frac{\mathscr {E}\varDelta }{x_B \theta ^2 D^*} - \frac{2}{3} i \frac{\mathscr {E}\varDelta }{x_A x_ B \theta } \kappa _T. \nonumber \end{aligned}$$

(35)

The analytic solutions of the equations given by (33) are

$$\begin{aligned} \begin{aligned}&v_A^*(x)=a_1\text{ e }^{ik_{1A}x}+b_1\text{ e }^{-ik_{1A}x}+c_1\text{ e }^{ik_{2A}x}+d_1\text{ e }^{-ik_{2A}x},\\&v_B^*(x)=a_2\text{ e }^{ik_{1B}x}+b_2\text{ e }^{-ik_{1B}x}+c_2\text{ e }^{ik_{2B}x}+d_2\text{ e }^{-ik_{2B}x}, \end{aligned} \end{aligned}$$

(36)

where the complex wave numbers $k_{1A}$, $k_{2A}$, $k_{1B}$ and $k_{2B}$ read

$$\begin{aligned} k_{1A}=\sqrt{\frac{B_1'-\sqrt{B_1'^2-4A_1'C_1'}}{2A_1'}} \;\; , \qquad k_{2A}=\sqrt{\frac{B_1'+\sqrt{B_1'^2-4A_1'C_1'}}{2A_1'}} \;\; , \end{aligned}$$

(37)

$$\begin{aligned} k_{1B}=\sqrt{\frac{B_2'-\sqrt{B_2'^2-4A_2'C_2'}}{2A_2'}} \;\; ,\qquad k_{2B}=\sqrt{\frac{B_2'+\sqrt{B_2'^2-4A_2'C_2'}}{2A_2'}} \;\;. \end{aligned}$$

(38)

The constants $a_j$, $b_j$, $c_j$ and $d_j$ ($j=1, 2$) are determined via the set of algebraic equations obtained from the boundary conditions (10) and (11). Note that, since $v_A^*$ and $v_B^*$ are known from (36), (37 and 38), all the other moments (28–29) of the mixture can be obtained from the set of linearized balance equations (20–23). In particular, the temperatures $T_A^*$ and $T_B^*$, whose expressions are used in the boundary condition (11), are written as follows

$$\begin{aligned} T_A^*= t_{11} \frac{dv_A^*}{dx} + t_{12} \frac{d^3 v_A^*}{dx^3} \;, \qquad T_B^*= t_{21} \frac{dv_B^*}{dx} + t_{22} \frac{d^3 v_B^*}{dx^3} \;, \end{aligned}$$

(39)

where

$$\begin{aligned} \begin{aligned} t_{11}&= -\frac{2}{3} \, \frac{i \mathscr {E}\varDelta }{x_A x_B \theta \xi } \left( 1 - \frac{2i\varDelta }{x_B \theta } \right) + \frac{2}{3} \frac{\mathscr {E}\varDelta }{x_B \theta } -\frac{25}{8} \lambda ^* \theta -\frac{59}{58} \frac{D^* \kappa ^2_T \theta }{x_A x_B} -\frac{2}{3} \, i \,, \\ t_{12}&= \frac{59}{116} \frac{i D^* \! \kappa _T \theta }{x_A x_B} \! \left( \! \frac{1}{\xi }\!-\! \frac{2i\varDelta }{x_B \theta \xi } \!+\! ix_A \!+\! i \kappa _T \!+\! \frac{5}{3} \! \kappa _T \eta ^* \theta \!\right) \!-\! \frac{25}{16} \lambda ^*\! \theta \! \left( \!1 \!-\! \frac{5}{3} \, i \eta ^*\theta \!\right) \!\! , \\ t_{21}&= -\frac{4}{3} \, \frac{i \mathscr {E}\varDelta ^2}{x_A x_B^2 \theta ^2 \xi } + \frac{2}{3} \frac{\mathscr {E}\varDelta }{x_B \theta } -\frac{25}{8} \lambda ^* \theta -\frac{59}{58} \frac{D^* \kappa ^2_T \theta }{x_A x_B} -\frac{2}{3} \, i \,, \\ t_{22}&= \frac{59}{116} \frac{i D^* \! \kappa _T \theta }{x_A x_B} \left( \! \frac{1}{\xi }\!-\! \frac{2i\varDelta }{x_B \theta \xi } \!+\! ix_A \!+\! i \kappa _T \!+\! \frac{5}{3} \kappa _T \eta ^* \theta \right) \!-\! \frac{25}{16} \lambda ^* \theta \! \left( \! 1 \!-\! \frac{5}{3} \, i \eta ^*\theta \! \right) \! . \end{aligned} \end{aligned}$$

Here, we have introduced the notation $\displaystyle \xi = i + \frac{2\varDelta }{x_A x_B \theta }$.

6 Results and Discussion

Usually, in acoustics, the quantity measured in experiments is the pressure difference in the direction of sound propagation, $P_{xx}^*$ in our notation. The attenuation coefficient and phase speed are then determined by using the experimental data measured at the receptor. In the context of a chemically reactive mixture, the temperature deviation from equilibrium, $T^*$ in our notation, is another important indicator of the effects induced by the chemical reaction.

Therefore, we use the solution obtained in the previous section to determine the amplitudes and phases of the macroscopic fields and focus our attention on the pressure difference $P_{xx}^*$ and temperature deviation $T^*$.

Since such quantities are complex, they can be represented in the form

$$\begin{aligned} P_{xx}^*(x) = A_P(x) \exp \big [ i \varphi _P(x) \big ] , \qquad T^*(x) = A_T(x) \exp \big [ i \varphi _T(x) \big ] , \end{aligned}$$

(40)

where $A_P(x) , \, A_T(x)$ are the amplitudes and $\varphi _P(x) , \, \varphi _T(x)$ are the corresponding phases. These amplitudes and phases give a measure of the deviation of the macroscopic properties of the gas mixture from the corresponding values in equilibrium. They were calculated as functions of the rarefaction $\delta$ and oscillation $\theta$ parameters, the molar fraction $x_A$ of the reactants and activation energy $\epsilon _f$ of the chemical reaction.

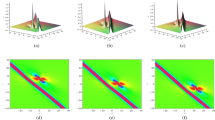
Figures 1 and 2 show the profiles of the amplitude and phase of the pressure difference $P_{xx}^*$ when $x_A=0.3$ (exothermic reaction), $\delta =10$ and $\theta =0.1$, $\theta =0.01$. Figures 3 and 4 show the profiles of the amplitude and phase of the temperature deviation $T^*$ when $x_A=0.3$ (exothermic reaction), $\delta =10$ and $\theta =0.1$, $\theta =0.01$.

Figures 5, 6, 7 and 8 show the same quantities $P_{xx}^*$ and $T^*$ for the endothermic reaction corresponding to $x_A=0.7$.

Note that, since $L=\delta \theta$ is the distance between the source and receptor, the situations considered in the figures correspond to a variation in the distance between the plates. Therefore, to analyse how the distance between the plates influence the amplitude and phase of $P_{xx}^*$ and $T^*$, we can compare the plots given in Figs. 1 and 2, 3 and 4, 5 and 6, 7 and 8, respectively. As one can see from the figures, the closer the receptor, the larger the influence of the reflected waves from the receptor on the properties of the gas flow, as expected, since the sound waves are less attenuated when the distance between the plates is smaller. This feature is observed for both exothermic (Figs. 1, 2, 3 and 4) and endothermic (Figs. 5, 6, 7 and 8) reactions.

Moreover, in the limit of high activation energy, $\epsilon ^*=10$, the mixture tends to a non-reactive configuration, so that the effects of the chemical reaction on the macroscopic properties of the mixture can be inferred by comparing the profiles for $\epsilon ^*=2$, $\epsilon ^*=5$ with those for $\epsilon ^*=10$. We can see that only in the situation $\epsilon ^*=2$, the profiles of the plotted quantities are significantly different from those corresponding to a non-reactive gas. These results should be analysed together with the values of the transport coefficients presented in Table 1. Accordingly, we can see that, regarding the influence of the chemical reaction on the solution of the problem, such influence is rather significant when also the transport coefficients show a larger deviation from the corresponding values in the inert mixture, that is, when the dimensionless values shown in Table 1 are not so close to the unity.

Another aspect that can be recognizable from the figures is that the amplitudes and phases of $P_{xx}^*$ and $T^*$ are larger when the reaction is endothermic (Figs. 5, 6, 7 and 8). This behaviour is in agreement with the results obtained in Refs. [3, 15], in the sense that, in Refs. [3, 15], it is shown that, for low oscillation frequencies, the attenuation of the sound waves are smaller for the endothermic reaction than for the exothermic one.

Observe that, combining the results shown in Figs. 1, 2, 3, 4, 5, 6, 7 and 8 with the values of the transport coefficients presented in Table 1, we can infer that the transport coefficients also contribute to increase the amplitudes and phases of $P_{xx}^*$ and $T^*$ when the reaction is endothermic, since Table 1 shows that the deviation of the reactive transport coefficients from the corresponding inert values is larger for the endothermic reaction than for the exothermic one.

Fig. 1

Amplitude (left) and phase (right) of the pressure difference $P_{xx}^*$ when the exothermic reaction dominates ($x_A=0.3$), for $\delta =10$ and $\theta =0.1$

Fig. 2

Amplitude (left) and phase (right) of the pressure difference $P_{xx}^*$ when the exothermic reaction dominates ($x_A=0.3$), for $\delta =10$ and $\theta =0.01$

Fig. 3

Amplitude (left) and phase (right) of the pressure difference $T^*$ when the exothermic reaction dominates ($x_A=0.3$), for $\delta =10$ and $\theta =0.1$

Fig. 4

Amplitude (left) and phase (right) of the temperature deviation difference $T^*$ when the exothermic reaction dominates ($x_A=0.3$), for $\delta =10$ and $\theta =0.01$

Fig. 5

Amplitude (left) and phase (right) of the pressure difference $P_{xx}^*$ when the endothermic reaction dominates ($x_A=0.7$), for $\delta =10$ and $\theta =0.1$

Fig. 6

Amplitude (left) and phase (right) of the pressure difference $P_{xx}^*$ when the endothermic reaction dominates ($x_A=0.7$), for $\delta =10$ and $\theta =0.01$

Fig. 7

Amplitude (left) and phase (right) of the pressure difference $T^*$ when the endothermic reaction dominates ($x_A=0.7$), for $\delta =10$ and $\theta =0.1$

Fig. 8

Amplitude (left) and phase (right) of the temperature deviation difference $T^*$ when the endothermic reaction dominates ($x_A=0.7$), for $\delta =10$ and $\theta =0.01$

7 Final Remarks and Future Plans

In this paper we have analysed the sound wave propagation through a binary mixture undergoing a reversible chemical reaction of symmetric type. The mixture is confined between two flat, infinite and parallel plates, one of them is stationary whereas the other one oscillates harmonically in time and constitutes an emanating source of sound waves that propagate in the mixture. The mathematical problem was studied in the low frequency regime, using the Navier-Stokes equations with chemically reaction rate derived from the kinetic theory of reactive mixtures, assuming temperature jump and velocity impenetrable conditions at both plates.

The main objective of our study was to investigate the influence of the chemical reaction on the properties of interest in the considered problem and how the sound waves reflected from the receptor influence the solution of the problem when the distance between both plates is varying and when the dominant chemical reaction is of exothermic or endothermic type.

To the best of our knowledge, similar sound wave propagation problems have been studied only in the context of non-reactive systems, and no results are known for chemically reactive mixtures and, thus, our analysis in this paper gives the first contribution in this direction. However, the presence of the chemical reaction, combined with the type of boundary conditions, brings additional complexities in the sound wave propagation problem, and we have introduced a simplified assumption for what concerns the temperature jump coefficient appearing in the boundary conditions, as it was explained and motivated in the Introduction.

In our opinion, this simplification is not so restrictive in the context of the present problem, however, if we consider a general mixture with a more complex chemical reaction, the temperature jump coefficient should be determined resorting to an appropriate model of the kinetic theory for chemically reactive mixtures. This development is the subject of a future work.