Keywords

1 Introduction

The current trend in the field of power generation is the reduction of rotor-to-seal clearances to match the requirements of power output, efficiency and operational life. Conversely, this design approach leads to stability issues [1]. Therefore, the prediction of labyrinth seals dynamics needs much more attention.

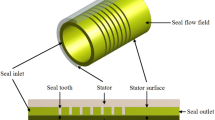
Labyrinth seal is a non-contact seal, composed of two or more teeth arranged in a manner able to impose a tortuous passage to the fluid. The working principle is based on reducing the fluid leakage by dissipating the kinetic energy of the fluid via sequential cavities that are defined by position of the teeth. The teeth can be located on the rotor, stator or both. Depending on the teeth location, various configurations can be defined: straight-through, staggered, slanted and stepped labyrinth seals. Straight-through configuration is the most common labyrinth seal used in real applications because it is the easiest to be manufactured. However, staggered seals are becoming popular because they can reduce the leakage on equal radial clearance with respect to the straight-through ones. Generally, staggered seals are widely used in steam turbines whereas straight-through seals are used in high-pressure compressors that historically show instability issues and this is the reason why academic research are mainly focused on this configuration. For staggered seals, there are few analytical models and experimental data for the prediction of their stability or instability contribution [2, 3].

The fluid-dynamics within the cavities of labyrinth seals is definitively influenced by the teeth location. Furthermore, the angle at which the flow approaches each tooth is correlated to the coefficients of discharge and to the kinetic energy carry-over coefficient, which strongly influence the leakage.

The dynamic force, produced by the non-uniform pressure distribution within the seal, in the direction of the rotor displacement (direct force) can change the natural frequencies of the machine, whereas the force in the orthogonal direction of the rotor displacement (cross-coupled force) can influence the stability.

The influence of labyrinth seals on the machine stability is typically investigated by using the standard finite beam-element rotordynamic model [16]. The dynamic behavior of labyrinth seals is modeled by the linearized coefficients [4], the so-called rotordynamic coefficients, using stiffness and damping matrices as,

$$ - \left( {\begin{array}{*{20}c} {F_{x} \left( t \right)} \\ {F_{y} \left( t \right)} \\ \end{array} } \right) = \left[ {\begin{array}{*{20}c} {k_{xx} \left( \omega \right)} & {k_{xy} \left( \omega \right)} \\ {k_{yx} \left( \omega \right)} & {k_{yy} \left( \omega \right)} \\ \end{array} } \right]\left( {\begin{array}{*{20}c} {x\left( t \right)} \\ {y\left( t \right)} \\ \end{array} } \right) + \left[ {\begin{array}{*{20}c} {c_{xx} \left( \omega \right)} & {c_{xy} \left( \omega \right)} \\ {c_{yx} \left( \omega \right)} & {c_{yy} \left( \omega \right)} \\ \end{array} } \right]\left( {\begin{array}{*{20}c} {\dot{x}\left( t \right)} \\ {\dot{y}\left( t \right)} \\ \end{array} } \right) $$
(1)

The inertia contribution in gas labyrinth seals is negligible; hence, the mass matrix is generally not considered. Due to the axisymmetric geometry of labyrinth seals, the eight linearized rotordynamics coefficients can be reduced to four. The stiffness and damping matrices are re-arranged as,

$$ - \left( {\begin{array}{*{20}c} {F_{x} \left( t \right)} \\ {F_{y} \left( t \right)} \\ \end{array} } \right) = \left[ {\begin{array}{*{20}c} {K\left( \omega \right)} & {k\left( \omega \right)} \\ { - k\left( \omega \right)} & {K\left( \omega \right)} \\ \end{array} } \right]\left( {\begin{array}{*{20}c} {x\left( t \right)} \\ {y\left( t \right)} \\ \end{array} } \right) + \left[ {\begin{array}{*{20}c} {C\left( \omega \right)} & {c\left( \omega \right)} \\ { - c\left( \omega \right)} & {C\left( \omega \right)} \\ \end{array} } \right]\left( {\begin{array}{*{20}c} {\dot{x}\left( t \right)} \\ {\dot{y}\left( t \right)} \\ \end{array} } \right) $$
(2)

In the following, the dependence of stiffness and damping coefficients from the whirling speed \( \omega \) will be omitted for simplicity. The cross coupled stiffness coefficient \( k \) and direct damping coefficient \( C \) are responsible of destabilizing forces. The resulting cross-coupled force is given by,

$$ F_{t} = \left( {C\omega - k} \right)r_{0} $$
(3)

where \( r_{0} \) is the radius of the orbit. The effective damping can be defined as,

$$ C_{eff} = C - \frac{k}{\omega } $$
(4)

Labyrinth seals contribute with destabilizing effects on the machine dynamics when the effective damping is negative. The effective stiffness is defined as:

$$ K_{eff} = K + c\, \omega $$
(5)

and it is related to the machine natural frequency. Usually, the effective stiffness of labyrinth seals is not considered for the dynamic behavior for the machine because its value is one order of magnitude lower than that of journal bearings [5, 6].

The first analytical model of labyrinth seals, containing the fundamental physical elements for a dynamic characterization was given by Iwatsubo [7]. The model, well known as the bulk-flow model, is based on one-control volume (1CV) for each cavity of the labyrinth seal. Bulk-flow quantities can be defined in each CV. The continuity and circumferential momentum equations are solved for each cavity. The leakage mass-flow rate can be estimated via empirical correlations. The turbulence is considered by estimating the friction factor between the fluid and wall boundaries. The governing equations are solved using the perturbation method. Initially, the steady-state problem (rotor centered with the seal) must be solved. Then, the solution of the perturbed problem (by imposing an orbit to the rotor) that is also truncated at the first order, can be estimated by imposing an analytical form solution. Finally, the dynamic forces can be estimated by integrating the pressure along the circumferential direction. The rotordynamic coefficients are calculated by knowing the radius of the rotor orbit.

The bulk-flow model (BFM) represents the most used calculation method applied for industrial design to calculate the seal rotordynamic coefficients because it is time efficient compared to Computational Fluid Dynamics (CFD) approaches. Moreover, the accuracy of CFD predictions is comparable to BFM predictions [8].

A new BFM has been introduced starting from the considerations made from the authors in [9] and the results shown by Moore in [10]. New boundary conditions (BCs) can be defined in the BFM. The authors’ assumption has been also validated by dedicated CFD analysis.

In this paper, the authors present the experimental results for a staggered labyrinth seal tested using the high-pressure seal test-rig (HPSTR) owned by the authors’ company. The test rig allows the characterization of labyrinth seals in high-pressure conditions. The main capabilities and the identification procedures of the test-rig are described in a previous paper of the same authors [11]. The results of an experimental campaign on a 14 tooth-on-stator straight-through labyrinth seal have been reported in [9, 12]. The comparison with the experimental data shows improvement in the prediction of the rotordynamic coefficients.

2 Bulk-Flow Model

The baseline structure of the BFM developed by the authors for staggered labyrinth seals is here described. The model is based on the 1CV BFM developed by the same authors in [9, 13, 14]. The substantial differences with respect to the BFM for straight-through labyrinth seals are given by the geometry of the CVs, the leakage correlation used to estimate the axial velocity and by the impact of the inlet and outlet regions on the calculation of the rotordynamic coefficients.

The most innovative contribution, with respect to the models available in the literature, is the perturbation of the pressure and circumferential velocity in the inlet and outlet regions, where, usually, they are considered equal to zero in common BFMs [4, 9].

Moore observed in [10] that the contribution of the upstream and downstream sections on the calculation of the rotordynamic coefficients is not negligible. He proposed a 3D-CFD model to predict the flow conditions and rotordynamic coefficients. By considering the inlet and outlet regions for the estimation of the fluid forces on the rotor, the predictions become more accurate compared to experimental results. Because the seal force is generated by the perturbation of the pressure, the assumption of null perturbation of the pressure in the inlet and outlet regions is not correct.

In the model proposed in this paper, two additional CVs have been added at the inlet and outlet regions with a proper mathematical treatment of the governing equations.

2.1 Governing Equations

The governing equations are represented by the continuity, circumferential momentum and energy equations. The energy equation is evaluated only in the zeroth-order problem as described in [13]. 1CV for each cavity has been considered as shown in Fig. 1.

Fig. 1.
figure 1

CVs and bulk-flow quantities.

Full size image

Because long teeth alternate with the rotor steps, two different CVs can be defined. The control volume labelled as CVa in Fig. 1, presents the long tooth on the upstream side and the short tooth combined with the rotor step on the downstream side. The control volume labelled as CVb in Fig. 1, presents the short tooth combined with the rotor step on the upstream side and the long tooth on the downstream side. Because the enthalpy is assumed to be independent on the orbit motion of the rotor as explained in [9], the derivatives of the enthalpy with respect to the time and to the angular coordinate are null. The governing equations can be stated as,

  • Continuity equation:

    $$ \frac{\partial }{\partial t}\left( {\rho_{i} A_{i} } \right) + \frac{\partial }{\partial \vartheta }\left( {\frac{{\rho_{i} A_{i} V_{i} }}{R}} \right) + \dot{m}_{i + 1} - \dot{m}_{i} = 0 $$
    (6)

  • Circumferential momentum equation:

    $$ \frac{\partial }{\partial t}\left( {\rho_{i} A_{i} V_{i} } \right) + \frac{\partial }{\partial \vartheta }\left( {\frac{{\rho_{i} A_{i} V_{i}^{2} }}{R}} \right) + \dot{m}_{i + 1} V_{i} - \dot{m}_{i} V_{i - 1} = - \frac{{A_{i} }}{R}\frac{{\partial P_{i} }}{\partial \vartheta } + \tau_{ri} a_{ri} - \tau_{si} a_{si} $$
    (7)

  • Energy equation:

    $$ \dot{m}_{i} \left( {h_{i} + \frac{{V_{i}^{2} }}{2}} \right) - \dot{m}_{i + 1} \left( {h_{i - 1} + \frac{{V_{i - 1}^{2} }}{2}} \right) = \tau_{ri} a_{ri} R\varOmega $$
    (8)

where \( P_{i} \), \( V_{i} \), \( \rho_{i} \) and \( h_{i} \) are the bulk-flow pressure, the circumferential velocity, the density and the enthalpy in the \( i \)-th cavity of the seal respectively.

The geometrical quantities \( A_{i} \), \( a_{ri} \) and \( a_{si} \) represent the tangential area and the dimensional lengths where the shear stresses are applied. The tangential area has different expressions depending on the type of CV considered.

Using the nomenclature given in Fig. 2, the tangential area for CVa and CVb, is defined, respectively, as

$$ A_{i} = \left( {\frac{T}{2} - W} \right)\left( {B + G} \right) - \left( {\frac{T}{2} - W - C} \right)B $$
(9)

and

$$ A_{i} = \left( {\frac{T}{2} - W} \right)\left( {B + G} \right) - \left( {C + F - \frac{T}{2}} \right)B $$
(10)

whereas, \( a_{ri} \) and \( a_{si} \) are defined for both the CVs as,

Fig. 2.
figure 2

Scheme and nomenclature used to describe staggered labyrinth seals.

Full size image
$$ a_{ri} = \frac{T}{2} - W + B $$
(11)
$$ a_{si} = \frac{T}{2} - W + 2\left( {G - s} \right) + B $$
(12)

The leakage correlation replaces the axial momentum equation in defining the axial velocity and pressure distributions along the seal cavities. The leakage correlation employed in the model is the generalized Neumann correlation for real gases [15]:

$$ \dot{m}_{i} = \frac{{R_{i} }}{R}C_{fi} H_{i} \sqrt {P_{i - 1} \rho_{i - 1} - P_{i} \rho_{i} } $$
(13)

where \( C_{fi} \) is the discharge coefficients and \( H_{i} \) is the dynamic radial clearance. The leakage is per unit circumferential length because the governing equations are divided by \( 2\pi R \). The axial cross-sectional area for the leakage (annulus area) is equal, for the CVa, to \( \pi \left( {R + H_{i} } \right)^{2} - \pi R^{2} \) that can be approximated to \( 2\pi RH_{i} \). Thus, dividing the leakage by \( 2\pi R \), only the term \( H_{i} \) remains in the leakage equation. Thus, for the CVa control volume, \( \frac{{R_{i} }}{R} = 1 \) and \( \frac{{R_{i} }}{R} = 1 + \frac{{H_{i} }}{R} \) for the CVb control volume.

In staggered labyrinth seals, the kinetic energy carry-over coefficient is equal to the unity for all the teeth as suggested by Childs [5]. The discharge coefficient has been estimated by the Chaplygin correlation as,

$$ \begin{aligned} C_{fi} & = \frac{\pi }{{\pi + 2 - 5s_{0i} + 2s_{0i}^{2} }} \\ s_{0i} & = \left( {\frac{{P_{i - 1} }}{{P_{i} }}} \right)^{{\frac{\gamma - 1}{\gamma }}} - 1 \\ \end{aligned} $$
(14)

If the flow sonic condition is reached under the last tooth (choked flow), the leakage mass flow-rate becomes independent by the downstream pressure. To check if the flow is subsonic or choked, the axial velocity is compared with the speed of sound \( (\varsigma ) \) of the fluid. The speed of sound is evaluated using the fluid properties database and it is a function of the pressure and density of the previous cavity (\( \varsigma_{i} = f\left( {P_{i - 1} ,\rho_{i - 1} } \right) \)).

The axial velocity is estimated using the definition of the leakage mass flow-rate, which is:

$$ U_{i} = \frac{{\dot{m}_{i} }}{{C_{fi} H_{i} \rho_{i - 1} }} $$
(15)

If the axial velocity is equal or larger than the speed of sound, the leakage mass-flow rate equation becomes:

$$ \dot{m}_{i} = C_{fi} H_{i} \rho_{i - 1} \varsigma_{i} $$
(16)

For the calculations of the circumferential shear stresses (\( \tau_{si} \) on the stator and \( \tau_{ri} \) on the rotor), it is necessary to use a correlation explicit formula to estimate the Darcy friction factor (\( f_{si} \) and \( f_{ri} \)). The shear stresses are defined as:

$$ \tau_{si} = \frac{{\rho_{i} }}{2}f_{si} V_{i} V_{Si} $$
(17)
$$ \tau_{ri} = \frac{{\rho_{i} }}{2}f_{ri} \left( {R\varOmega - V_{i} } \right)V_{Ri} $$
(18)

where \( V_{Si} \) and \( V_{Ri} \) are the modulus of the fluid velocity, on the stator and rotor surfaces respectively, considering the axial and circumferential components of the velocity. They can be defined as:

$$ V_{Si} = \sqrt {U_{i}^{2} + V_{i}^{2} } $$
(19)
$$ V_{Ri} = \sqrt {U_{i}^{2} + \left( {R\varOmega - V_{i} } \right)^{2} } $$
(20)

For the calculation of the circumferential shear stresses, the Swamee-Jain correlation is used to estimate the friction factor between the fluid and the rotor/stator wall, as described in [13].

2.2 Perturbation Analysis

The perturbation analysis is used to solve the continuity and circumferential momentum equations. The rotor position is perturbed with respect to the centred position, and a circular orbit is assumed.

$$ P_{i} = P_{0i} + \varepsilon P_{1i} \left( {t,\vartheta } \right) $$
(21)
$$ \rho_{i} = \rho_{0i} + \varepsilon \rho_{1i} \left( {t,\vartheta } \right) $$
(22)
$$ h_{i} = h_{0i} $$
(23)
$$ V_{i} = V_{0i} + \varepsilon V_{1i} \left( {t,\vartheta } \right) $$
(24)
$$ H_{i} = s_{i} + \varepsilon H_{1} \left( {t,\vartheta } \right) $$
(25)

The perturbation theory comprises mathematical methods for finding an approximate solution of the problem, by starting from the steady-state solution (centred rotor within the seal). The solutions of the problem are expanded and truncated at the first-order, hence the thermodynamic and kinematic variables of the model (generally indicated with the symbol \( \square \)) are separated in the steady-state terms \( \square_{0i} \) and in the perturbed terms \( \square_{1i} \left( {t,\vartheta } \right) \).

2.3 Zeroth-Order Problem

The continuity, circumferential momentum and energy zeroth-order equations, for each CV in the seal cavities, are iteratively solved using the multi-variate Newton-Raphson algorithm to find the solution in terms of pressure, density, enthalpy and circumferential velocity in each cavity. The boundary conditions (BCs) used in the zeroth-order problem are the Dirichlet BCs in the inlet and outlet sides. The inlet pressure, circumferential velocity and enthalpy are imposed at the inlet, whereas the outlet pressure, circumferential velocity and enthalpy are imposed at the outlet side. These quantities are calculated by using the seal operating conditions: inlet/static pressure, inlet temperature, pre-swirl and rotor rotational speed. The solution of the zeroth-order problem must satisfy the following equations:

$$ \dot{m}_{01} \equiv \cdots \equiv \dot{m}_{0i} \equiv \cdots \equiv \dot{m}_{0NT} \equiv \dot{m}_{0} $$
(26)
$$ \dot{m}_{0} V_{0i} - \dot{m}_{0} V_{0i - 1} = \tau_{0ri} a_{ri} - \tau_{0si} a_{ri} $$
(27)
$$ \dot{m}_{0} \left( {h_{0i} + \frac{{V_{0i}^{2} }}{2}} \right) - \dot{m}_{0} \left( {h_{0i - 1} + \frac{{V_{0i - 1}^{2} }}{2}} \right) = \tau_{0ri} a_{ri} R\varOmega $$
(28)

The main contribution of the energy equation is the coupling of the continuity equation with the circumferential momentum equation in the zeroth-order problem. Considering an isenthalpic process, these equations are independent one from each other, and the estimation of the mass flow-rate and thermodynamic properties of the fluid (steady pressure and density) does not depend on the circumferential velocity. In the model developed in this paper, the equations are linked because the density depends on the enthalpy that is calculated (in the energy equation) based on the circumferential velocity and rotor shear stress.

2.4 First-Order Problem

The first-order problem is governed by the continuity and circumferential momentum equations. By imposing a circular orbit to the rotor and linearizing the governing equations, the only solutions admitted for the perturbed pressure and circumferential velocity have the same mathematical expression of the perturbed clearance.

By imposing them, the first-order equations result as,

  • Continuity first-order equation:

    $$ \begin{array}{*{20}c} {\frac{{A_{0i} \frac{{\partial \rho_{i} }}{{\partial P_{1i} }}V_{0i} }}{R}\frac{{\partial P_{1i} }}{\partial \vartheta } + A_{0i} \frac{{\partial \rho_{i} }}{{\partial P_{1i} }}\frac{{\partial P_{1i} }}{\partial t} + \frac{{A_{0i} \rho_{i} }}{R}\frac{{\partial V_{1i} }}{\partial \vartheta }} \\ { + \,\left( {\frac{{\partial \dot{m}_{i + 1} }}{{\partial P_{1i} }} - \frac{{\partial \dot{m}_{i} }}{{\partial P_{1i} }}} \right)P_{1i} - \frac{{\partial \dot{m}_{i} }}{{\partial P_{1i - 1} }}P_{1i - 1} } \\ { + \,\frac{{\partial \dot{m}_{i + 1} }}{{\partial P_{1i + 1} }}P_{1i + 1} = - \frac{{\left( {\frac{T}{2} - W} \right)\rho_{i} V_{0i} }}{R}\frac{{\partial H_{1} }}{\partial \vartheta }} \\ { - \,\left( {\frac{T}{2} - W} \right)\rho_{i} \frac{{\partial H_{1} }}{\partial t} - \left( {\frac{{\partial \dot{m}_{i + 1} }}{{\partial H_{1} }} - \frac{{\partial \dot{m}_{i} }}{{\partial H_{1} }}} \right)H_{1} } \\ \end{array} $$
    (29)

  • Circumferential momentum first-order equation:

    $$ \begin{array}{*{20}c} {\frac{{\left( {\frac{T}{2} - W} \right)\rho_{i} V_{0i}^{2} }}{R}\frac{{\partial H_{1} }}{\partial \vartheta } + \left( {\frac{{A_{0i} }}{R} + \frac{{A_{0i} V_{0i}^{2} }}{R}\frac{{\partial \rho_{i} }}{{\partial P_{1i} }}} \right)\frac{{\partial P_{1i} }}{\partial \vartheta } + \frac{{2A_{0i} \rho_{i} V_{0i} }}{R}\frac{{\partial V_{1i} }}{\partial \vartheta }} \\ { + \,A_{0i} \rho_{i} \frac{{\partial V_{1i} }}{\partial t} + \left( {\frac{T}{2} - W} \right)\rho_{i} V_{0i} \frac{{\partial H_{1} }}{\partial t}} \\ { + \,H_{1} \left( { - a_{ri} \frac{{\partial \tau_{r1i} }}{{\partial H_{1} }} + a_{si} \frac{{\partial \tau_{s1i} }}{{\partial H_{1} }} + \frac{{\partial \dot{m}_{i} }}{{\partial H_{1} }}\left( {V_{0i} - V_{0i - 1} } \right)} \right)} \\ { + \,V_{1i} \left( { - a_{ri} \frac{{\partial \tau_{r1i} }}{{\partial V_{1i} }} + a_{si} \frac{{\partial \tau_{s1i} }}{{\partial V_{1i} }} + \dot{m}_{0} } \right)} \\ { + \,P_{1i - 1} \left( {\frac{{\partial \tau_{r1i} }}{{\partial P_{1i - 1} }}\left( {a_{si} - a_{ri} } \right) + \frac{{\partial \dot{m}_{i} }}{{\partial P_{1i - 1} }}\left( {V_{0i} - V_{0i - 1} } \right)} \right)} \\ { + \,P_{1i} \left( {\frac{{\partial \tau_{r1i} }}{{\partial P_{1i} }}\left( {a_{si} - a_{ri} } \right) + \frac{{\partial \dot{m}_{i} }}{{\partial P_{1i} }}V_{0i - 1} - \frac{{\partial \dot{m}_{i - 1} }}{{\partial P_{1i} }}V_{0i} } \right) + A_{0i} V_{0i} \frac{{\partial \rho_{i} }}{{\partial P_{1i} }}\frac{{\partial P_{1i} }}{\partial t}} \\ { + \,\frac{{\partial \dot{m}_{i + 1} }}{{\partial P_{1i + 1} }}V_{0i} P_{1i + 1} - \dot{m}_{0} V_{1i - 1} - \dot{m}_{0} V_{1i - 1} + \frac{{\partial \dot{m}_{i} }}{{\partial P_{1i - 1} }}\left( {V_{0i} - V_{0i - 1} } \right)P_{1i - 1} = 0} \\ \end{array} $$
    (30)

Generally, the perturbation of the pressure and circumferential velocity at the inlet and outlet regions are assumed to be equal to zero.

As already said, a novelty has been introduced in the model proposed in this paper by considering the perturbation of the pressure and circumferential velocity in the inlet and outlet regions. Two additional CVs, one in the inlet and one in the outlet region, have been introduced in the seal model. Consequently, the first-order continuity and circumferential momentum equations are solved also in the additional CVs. Nevertheless, the zeroth-order solution for these CVs is required, as well as the BCs for the zeroth-order problem. It is reasonable to assume that the zeroth-order upstream pressure with respect to the inlet region (\( P_{0ui} \)) is the same of the inlet (\( P_{0in} \)).

The same assumption is made for the zeroth-order downstream pressure with respect to the outlet region (\( P_{0do} \)) that is equal to the outlet pressure (\( P_{out} \)). The zeroth-order circumferential velocities (\( V_{0ui} \), \( V_{0do} \)) and enthalpies (\( h_{0ui} \), \( h_{0do} \)) can be calculated using the zeroth-order circumferential momentum and energy equations.

Regarding the BCs for the first-order problem, it can be reasonably assumed that the perturbed pressures (\( P_{1ui} \), \( P_{1do} \)) and circumferential velocities (\( V_{1ui} \), \( V_{1do} \)) at the seal CVs boundaries can be considered null sufficiently far from the seal cavities. The scheme of the BCs is reported in Fig. 3. Because the perturbed pressure in the upstream inlet region is null and the steady-state pressure is equal to that of the inlet region (\( P_{ui} = P_{0in} \)), the mass-flow rate between these two CVs cannot be expressed using the Neumann correlation (see Eq. (13)). However, a leakage exists, and it is assumed to be equal to the steady-state mass-flow (\( \dot{m}_{0} \)) and independent on the perturbation of the inlet region. Therefore, by considering the continuity and circumferential momentum equations for the Inlet CV, the derivatives of the incoming mass-flow with respect to the perturbed pressures \( P_{1in} \) and \( P_{1ui} \) are equal to zero. Consequently, the following terms are null in the first-order equations:

Fig. 3.
figure 3

Control volumes used in the BFM proposed by the authors.

Full size image
$$ \frac{{\partial \dot{m}_{in} }}{{\partial P_{1in} }} = 0 $$
(31)
$$ \frac{{\partial \dot{m}_{i} }}{{\partial P_{1ui} }} = 0 $$
(32)

For the same reasons, by considering the continuity and circumferential momentum equations in the Outlet CV, the derivatives of the outgoing mass-flow with respect to the perturbed pressure are equal to zero. Consequently, the following the terms are null in the first-order equations:

$$ \frac{{\partial \dot{m}_{out + 1} }}{{\partial P_{1out} }} = 0 $$
(33)
$$ \frac{{\partial \dot{m}_{out + 1} }}{{\partial P_{1do} }} = 0 $$
(34)

As previously stated, Moore in [10] demonstrated that the upstream and downstream sections contribute to the rotordynamic coefficients. By comparing the CFD results with experimental measurements, the introduction of inlet and outlet regions, improved the CFD predictions [17]. In this paper, the authors performed a CFD analysis based on the Integral Perturbation Method (IPM) aimed at estimating the perturbation of the pressure in the inlet region and to prove the assumptions made in the BFM. The IPM considers the full unsteady simulation with the mesh motion to directly consider rotor oscillatory movements. The CFD analysis clearly shows that the contribution of the inlet and outlet regions to the dynamic forces, generated by the surrounding fluid, is not negligible. This fact conflicts with the assumption in the original BFM in which the perturbation of the pressure is considered null at the inlet and outlet regions.

2.5 Calculation of the Rotordynamic Coefficients

The dynamic force acting on the rotor [9] surrounded by the labyrinth seal is given by:

$$ F = F_{x} + {\text{j}}F_{y} = - \varepsilon R_{s} \mathop \sum \limits_{i = 1}^{N - 1} L_{i} \left[ {\int\limits_{0}^{2\pi } {\left( {P_{1i} {\text{e}}^{{{\text{j}}\vartheta }} - {\text{j}}a_{ri} \tau_{r1i} P_{1i} {\text{e}}^{{{\text{j}}\vartheta }} } \right)} } \right] $$
(35)

The solution of the two equations obtained by considering the real and imaginary parts of Eq. (35) allows the rotordynamic coefficients to be defined as:

$$ \begin{array}{*{20}c} {K = \frac{1}{2}{\text{Re}}\left( {Z^{ + } + Z^{ - } } \right)} & {k = - \frac{1}{2}{\text{Im}}\left( {Z^{ + } + Z^{ - } } \right)} \\ \end{array} $$
(36)
$$ \begin{array}{*{20}c} {C = - \frac{1}{2\varOmega }{\text{Im}}\left( {Z^{ + } - Z^{ - } } \right)} & {c = - \frac{1}{2\varOmega }{\text{Re}}\left( {Z^{ + } - Z^{ - } } \right)} \\ \end{array} $$
(37)

where,

$$ Z^{ + } = \pi R_{s} \sum\limits_{i = 1}^{N - 1} {\left( {\frac{T}{2} - W} \right)} \int\limits_{0}^{2\pi } {\left[ {P_{1i}^{ + } \left( {1 - {\text{j}}a_{ri} \frac{{\partial \tau_{ri} }}{{\partial P_{1i} }}} \right)} \right.} \left. { - {\text{j}}a_{ri} \frac{{\partial \tau_{ri} }}{{\partial V_{1i} }}V_{1i}^{ + } + {\text{j}}a_{ri} \frac{{\partial \tau_{ri} }}{{\partial H_{1} }}} \right] $$
(38)
$$ Z^{ - } = \pi R_{s} \sum\limits_{i = 1}^{N - 1} {\left( {\frac{T}{2} - W} \right)} \int\limits_{0}^{2\pi } {\left[ {P_{1i}^{ - } \left( {1 - {\text{j}}a_{ri} \frac{{\partial \tau_{ri} }}{{\partial P_{1i} }}} \right)} \right.} \left. { - {\text{j}}a_{ri} \frac{{\partial \tau_{ri} }}{{\partial V_{1i} }}V_{1i}^{ - } + {\text{j}}a_{ri} \frac{{\partial \tau_{ri} }}{{\partial H_{1} }}} \right] $$
(39)

Each cavity contributes to the overall rotordynamic coefficients. The sum of the rotordynamic coefficient of each cavity allows the coefficients of the seal to be obtained.

3 Experimental Campaign

The main features of the HPSTR are [11]:

  • inlet pressure up to 500 bar;

  • pressure ratio up to 2.5;

  • rotational speed up to 15000 rpm;

  • control of the rotor orbit by active magnetic bearings (AMBs) with an excitation frequency up to 250 Hz;

  • multiple excitation frequencies;

  • interchangeable swirler device to set the desired pre-swirl ratio (also negative pre-swirl ratio by inverting the rotational speed);

  • possibility to test off-center rotor position.

Figure 4 shows the external casing of the HPSTR that is very similar to an actual industrial plant because it is equipped with a high-pressure compressor, a gearbox and an electric motor connected to a complex high-pressure gas loop. All these details are not provided here because already illustrated in [11].

Fig. 4.
figure 4

High-pressure seal test-rig.

Full size image

The HPSTR working principle consists of injecting the nitrogen into the casing at controlled pressure. The gas flows through the swirler device which sets the circumferential velocity of the fluid and the pre-swirl at the seal entrance. Then, the nitrogen flows into the two test seals that are the object of the test. Their back-to-back configuration is used to balance the axial load. The orbit motion of the rotor is controlled by AMBs, which apply the needed dynamic forces to shake the rotor. These forces are measured through current measurements and dedicated calibrations, see [11].

The rotordynamic coefficients associated to the labyrinth seals are finally computed applying an identification algorithm which is based on simple rotor equations of motion. All relevant forces and displacements are measured and equations are inverted solving for the unknown coefficients. With respect to the experimental activity described in [12], the instrumentation has been improved by introducing a specific probe to measure more precisely the pre-swirl at the seal entrance. An accurate measurement of process parameters is critical to compare the experimental tests data to predictions.

The staggered labyrinth seal tested in the HPSTR is representative of a balancing drum seal mounted in a medium steam turbine (see Fig. 5). The final layout of the staggered labyrinth seals is shown in Fig. 6. The geometrical parameters of the labyrinth seal and operating conditions are listed in Table 1.

Fig. 5.
figure 5

Scheme of the staggered labyrinth seal used in the experimental tests.

Full size image
Fig. 6.
figure 6

Final layout of the staggered labyrinth seal installed in the HPSTR.

Full size image
Table 1. Seal geometry and operating conditions.
Full size table

The radial clearance listed in Table 1 is the nominal one, therefore it doesn’t consider the radial growth caused by the centrifugal force. For confidential reasons, only two experiments are shown in the paper.

The experimental data in terms of rotordynamic coefficients and leakage mass-flow are shown, compared to the numerical predictions, in the body of the paper and in the Appendix A.

4 Comparison with Experimental Data and Numerical Results

The numerical results, in terms of rotordynamic coefficients and leakage mass-flow, have been compared with the experimental measurements.

The direct damping and cross-coupled stiffness are shown in Figs. 7 and 8, where the numerical results of the original BFM and those considering also the inlet and outlet regions are also plotted. The BFM with the inlet and outlet regions takes into account for the rotordynamic coefficients generated in the two “new” CVs. By considering only the CVs in the cavities of the seal, and taking into account the perturbation of the pressure and circumferential velocity at the seal boundaries, a new BFM can be introduced. The new BFM considers different BCs with respect to the original one. Thus, three different models are shown in the following paper.

Fig. 7.
figure 7

Comparison of predictions and measurements of direct damping and cross-coupled stiffness coefficients as a function of the whirling speed for the experiment A.

Full size image
Fig. 8.
figure 8

Comparison of predictions and measurements of direct damping and cross-coupled stiffness coefficients as a function of the whirling speed for the experiment B.

Full size image

It can be noticed in Figs. 7 and 8 that both the BFM with the inlet and outlet regions and the BFM with new BCs are more accurate in the estimation of the rotordynamic coefficients than the original BFM. Slight differences can be observed between the two new BFMs. It can be deduced that the assumption of considering the perturbation of the pressure and circumferential velocity at the seal boundaries equal to zero is not correct if compared to CFD result as already noticed by Moore. Moreover, the predictions of the rotordynamic coefficients is strongly improved.

The uncertainty range for each measured point is also reported. The uncertainties are larger with the increase in the whirling speed. The trends of the two experiments are very similar. As expected, the coefficients are frequency dependent as already shown for a teeth-on-stator straight-through labyrinth seal in [12]. The experimental coefficients of the experiment B are higher than those of the experiment A because of the higher pressure drop condition.

Generally, the trend of the coefficients as a function of the whirling speed is well reproduced by the three BFMs. The direct damping is slightly underestimated with respect to the experimental one. Thus, BFMs result to be conservative in the rotordynamic design phase.

The comparison of the mass-flow measured during the experiments with those predicted by the bulk-flow model for both experiments is shown in Fig. 9. The uncertainty range is almost 10% of the average value. The predictions are very accurate compared to the experimental measurements. The mass-flow is the same for the BFMs considered in the paper.

Fig. 9.
figure 9

Comparison of the mass-flow measured and predicted.

Full size image

The contribution of each cavity of the seal to the rotordynamic coefficients is shown in Fig. 10. The solid lines are the results of the original BFM, whereas the dotted lines are the results of the model by considering the perturbation in the inlet and outlet regions. Five lines for each model are represented in the Fig. 10, consistently with the five whirling frequencies.

Fig. 10.
figure 10

Trend of the predicted direct damping and cross-coupled stiffness as a function of the seal’s cavity for the experiment B.

Full size image

It can be observed that the new BFMs show a different trend of the coefficients. In the original BFM seems that the coefficients in the first and last cavities are constrained to be close to zero by the fact that the perturbations are null at the boundaries.

Despite the perturbations are considered both in the inlet and outlet in the new BFM, the coefficients at the seal end are equal to the coefficients calculated with the original BFM. Trying to figure out a correlation between the coefficients and the zeroth-order quantities, the trend of the coefficients of the new BFM is similar to that of the zeroth-order pressure and density along the seal cavity. Whereas, the coefficients calculated with the original BFM are uncorrelated with all the zeroth-order quantities.

By considering the results in Figs. 7 and 8 for the experiment B, the BFM with the inlet and outlet regions consider the coefficients contribution of the inlet and outlet cavities as shown in Fig. 10.

The BFM with new BCs considers the coefficients of the model with the inlet and outlet regions but the overall seal coefficients do not take into account the coefficient contributions of the inlet and outlet regions, but only those corresponding to the cavities from 1 to 19 (see Fig. 10), such as for the original BFM.

This approach is finally making the BFM physically more consistent and improves the match with experimental data by an average factor 2 which is not negligible at all.

5 Conclusion

In the paper, the experimental results obtained from an experimental campaign on a staggered labyrinth seal have been presented and a new BFM has been introduced by considering the perturbation of the pressure and circumferential velocity in the inlet and outlet regions.

Actual BFMs consider the perturbations null despite perturbations are captured by Moore comparing CFD analysis with experimental measurements. The new BFMs improve the predictions of the rotordynamic coefficients compared to experiments by an average factor 2. The predicted mass-flow are very accurate for both the tests. he baseline structure of the BFM developed by the authors for staggered labyrinth seals is here described. The model is based on the 1CV BFM developed by the same authors in [9, 13, 14]. The substantial differences with respect to the BFM for straight-through labyrinth.