Abstract
This glossary contains an annotated listing of some 300 parameters of graphs, together with their definitions, and, for most of these, a reference to the authors who introduced them. Let G = (V, E) be an undirected graph having order n = |V | vertices and size m = |E| edges. Two graphs G and H are isomorphic, denoted G ≃ H, if there exists a bijection ϕ : V (G) → V (H) such that two vertices u and v are adjacent in G if and only if the two vertices ϕ(u) and ϕ(v) are adjacent in H. For the purposes of this paper, we shall say that a parameter of a graph G is any integer-valued function \(f: \mathcal {G} \rightarrow \mathcal {Z}\) from the class of all finite graphs \(\mathcal {G}\) to the integers \(\mathcal {Z}\), such that for any two graphs G and H, if G is isomorphic to H then f(G) = f(H). This glossary also contains a listing of some 70 conjectures related to these parameters, more than 26 new parameters and open problem areas for study, and some 600 references to papers in which these parameters were introduced and then studied.
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
1 Introduction
Keeping with the theme of this series of monographs, which is to provide extensive discussions of favorite conjectures and open problems in graph theory, in this chapter we present an annotated glossary of graph theory parameters along with conjectures involving many of them. We also list several suggested new parameters and open problems. Although this chapter deviates from the “story-telling style” adopted in the other chapters, we hope that this glossary with its conjectures and open problems serves as a useful tool for researchers, fitting in its own way within the theme of this series.
Let G = (V, E) be a finite undirected graph with vertex set V = {v 1, v 2, …, v n} of order n = |V |, and edge set E with size m = |E|, consisting of unordered pairs of distinct vertices in V . By a partition of the vertex set V we mean a family π = {V 1, V 2, …, V k} of pairwise disjoint sets whose union equals V , that is, for all 1 ≤ i < j ≤ k, V i ∩ V j = ∅ and \(\displaystyle {\bigcup \limits _{i=1}^k V_i = V}\); for such a partition π, we will say that π has order k. Two graphs G and H are isomorphic, denoted G ≃ H, if there exists a bijection ϕ : V (G) → V (H) such that two vertices u and v are adjacent in G if and only if the two vertices ϕ(u) and ϕ(v) are adjacent in H. Identifying when two graphs are isomorphic is both practical and theoretically interesting, while the decision problem is hard to categorize [28, 501, 505, 538]. A parameter of a graph G is a numerical value (usually a non-negative integer) that can be associated with any graph such that whenever two graphs are isomorphic, they have the same associated parameter value. A finite set \(\mathcal {I}\) of parameters is said to be complete if whenever two graphs have the same values for every parameter in the set \(\mathcal {I}\), then the two graphs are isomorphic. We know of no finite complete set of parameters for the class of all finite, undirected graphs. Indeed, one could easily conjecture that a finite complete set of parameters does not exist for the family of all graphs.
However, complete sets of parameters do exist for some limited families of graphs. For example, the one parameter n, the order of a graph, is a complete set of parameters for the family of all complete graphs K n, the family of paths P n, and the family of cycles C n. The two parameters {n, m}, the order and the size of a graph, form a complete set for the family of all graphs of order n ≤ 3, that is, the value of these two parameters uniquely identifies any graph of order n ≤ 3. It seems likely, therefore, that complete sets of parameters can be discovered for various families of graphs. But if complete sets of parameters for limited families of graphs exist, then from what list of parameters can they be chosen?
This brings us to the first motivation for presenting a glossary of more than 300 parameters of graphs. From this listing, complete sets of parameters for limited families of graphs can be chosen.
A second motivation for creating this glossary of parameters is the study of graphical parameters themselves. What types of parameters have been defined and studied? Indeed, what other types of parameters have not been defined? Merely reading through this listing of parameters and understanding how they are defined will surely suggest even more parameters that can be studied.
A third motivation for creating this glossary has to do with results of the form: a(G) + b(G) ≤ n + c, or a(G) + b(G) ≥ n + c, where a(G) and b(G) are two parameters, n is the order of a graph G, and c is some, usually small, constant. In 1969, Geller and Hedetniemi [282] showed that for many pairs of parameters, inequalities like these exist, provided that the parameters are well-behaved under either of the following two operations: (1) identifying two non-adjacent vertices u and v in a graph G, called an elementary homomorphism, where Gε denotes the resulting graph, or (2) contracting two adjacent vertices u and v to a single vertex, called an elementary contraction, where Gθ denotes the resulting graph. By well-behaved we mean that the value of a parameter does not change by more than, say, 1; for example, if for any graph G, a(G) ≥ a(Gε) ± 1, or a(G) ≤ a(Gθ) ± 1. Often one can prove that such inequalities as a(G) + b(G) ≤ n + c or a(G) + b(G) ≥ n + c exist if one of the parameters remains unchanged while the second parameter changes by at most 1 under either of these two elementary operations. The question then is: for which pairs of parameters are such theorems possible? All that remains is to study how any of the following parameters can change under either of these two elementary operations.
A fourth motivation for creating this listing of parameters is to provide a partial answer to the general question: has a proposed new parameter already been defined? Or, has a parameter similar to a proposed parameter been defined?
A fifth, and final, motivation for creating this glossary is simply to have in one place, a reasonably comprehensive list of most of the generally recognized graph parameters, together with their definitions and a couple of references where more information about them can be found. Of course, it is recommended that one should consult a good search engine, like MathSciNet or GoogleScholar, in order to thoroughly search what is known about any of these parameters. This listing of parameters is not intended to be complete. While it may be reasonably comprehensive, the number of graph theory parameters that have been studied in the literature is much greater than the number presented here. We apologize in advance if we have omitted anyone’s favorite parameters.
One might well say that many of the graph parameters that have appeared in the literature are obscure and uninteresting. This is, of course, always a matter of personal choice. But it is too easy to make small changes in any of these definitions and thereby create a seemingly “new” parameter. Indeed, one of the criticisms of graph theory is that it has too many uninteresting parameters. One should always ask, is this “new” parameter worth studying? Is it interesting? What is the motivation for studying this new parameter? Is there some real-world application for this parameter? Is there some theoretical justification for studying it? Is it related in some interesting or important ways to existing parameters? Does this parameter help us understand better some other parameters? Just because it is “new” doesn’t mean that it is worth studying.
Thus, having a glossary of parameters provides both a reference tool for researchers and a source for open problems. In keeping with the theme of conjectures and open problems, following our glossary of parameters, we present a sample of some 70 conjectures involving them.
This glossary is certainly not the first of its kind. A discussion of many of these parameters can be found in the book Handbook of Graph Theory, Second Edition edited by Gross et al. [314], the two books Fundamentals of Domination in Graphs, [361] and Domination in Graphs, Advanced Topics [360] written and edited by Haynes, Hedetniemi and Slater, and the two books on graph coloring, Chromatic Graph Theory by Chartrand and Zhang [118], and Graph Coloring Problems by Jensen and Toft [434].
Along the direction we are taking by listing conjectures in this glossary, similar work has been conducted since 1968 by Vizing [627], Gallian’s survey of conjectures in 1989 [277], Bollobás in 2004 [60], Broersma et al. in 2012 [85], Bonato and Nowakoski in 2012 [65], and more recently by Bondy in 2014 [66]. While still a survey of conjectures, in 2010 Aouchiche and Hansen [18] wrote an expository work of conjectures in spectral graph theory conjectured by computers. In addition, lists of open problems and conjectures can be found on West’s homepage http://faculty.math.illinois.edu/~west/openp/ and the Graffiti website http://cms.dt.uh.edu/faculty/delavinae/research/wowII maintained by DeLaviña.
This glossary, however, differs in several important respects from existing glossaries and surveys. First, it is by far the most comprehensive in listing fairly well-studied graph theory parameters. Second, it is more than a listing of definitions of parameters in that it provides historical information about the origins and authors of these parameters. Third, more than a glossary, we provide annotations to many of these parameters. And fourth, we provide an extensive listing of conjectures about many of these parameters, which provides depth to simple definitions, as well as a collection of some two dozen new parameters and problems to study. In addition, this glossary provides an overview of the nature of graph theory parameters, with an eye toward the creation of new ideas in graph theory. The remainder of this glossary contains some 300 graph parameters, some 70 conjectures, and around 600 references.
2 Categories of Parameters of Graphs
In this section we discuss the mathematical nature of different types of parameters of graphs. A quick overview of these parameters shows that they naturally fall into a few general categories, the most common being the following:
-
1.
Basic structural characteristics of a graph, like the order (number of vertices), the size (number of edges), the degrees of the vertices, the lengths of shortest paths between pairs of vertices (geodesics), the maximum length of a path (detour number), the minimum length of a chordless cycle (girth), the maximum length of a cycle (circumference), or the maximum order of a complete subgraph (clique number).
-
2.
The minimum or maximum cardinality of a set of vertices or edges, and in a few cases a set of vertices and edges, having some given property \(\mathcal {P}\). If the property \(\mathcal {P}\) in question is hereditary, meaning that every subset of a set of this type, called a \(\mathcal {P}\)-set, is also a \(\mathcal {P}\)-set, then one is generally interested in sets of maximum cardinality. A common example of a hereditary property is that a set is independent, meaning no two vertices in the set are adjacent. But there is also interest in finding maximal \(\mathcal {P}\)-sets having minimum cardinality. Similarly, some properties \(\mathcal {P}\) are super-hereditary, meaning that every superset of a \(\mathcal {P}\)-set is also a \(\mathcal {P}\)-set. A common example of a super-hereditary property is that of being a dominating set, meaning that every vertex not in the set is adjacent to at least one vertex in the set. In this case, one is interested in finding \(\mathcal {P}\)-sets having minimum cardinality, or minimal \(\mathcal {P}\)-sets of maximum cardinality.
-
3.
The minimum number of vertices or edges whose removal results in a graph having some property \(\mathcal {P}\), such as being disconnected, planar or bipartite, or the minimum number of vertices or edges which added to a graph results in a graph having some property \(\mathcal {P}\).
-
4.
The minimum or maximum order k of a partition π = {V 1, V 2, …, V k} of the vertex set V , or π = {E 1, E 2, …, E k} of the edge set E, such that each set V i or E j of the partition has some property \(\mathcal {P}\). Most commonly these include a wide variety of chromatic numbers. Occasionally, a condition is placed on pairs V i, V j of sets, for example, that the subgraph G[V i ∪ V j] induced by two independent sets V i and V j is acyclic, these being called acyclic colorings. Again, if the property \(\mathcal {P}\) is hereditary, e.g. being an independent set, then one is interested in minimum order partitions, as in the chromatic number, but if the property is super-hereditary, as is a dominating set, then one is interested in maximum order partitions, like the domatic number.
-
5.
An optimal linear arrangement of the vertices or edges of a graph which minimizes or maximizes some number, as in the bandwidth of a graph, or in the bipartite crossing number.
-
6.
The dimension of a certain type of vector space associated a graph, such as the rank of the adjacency matrix, incidence matrix, neighborhood matrix or the Laplacian matrix, that is, the dimension of the row space of a matrix associated with a graph.
-
7.
The amount of time, or steps, necessary to accomplish some objective in a connected graph, such as broadcasting, that is, disseminating a message from one vertex in a graph to all other vertices, or in pebbling, whereby you must move pebbles in a sequence of pebbling moves so that any vertex can receive a pebble.
3 Parameters of Graphs
Before we proceed with our compendium of parameters, we need to define a few basic terms, which are used in the definitions in the following subsections.
Let G = (V, E) be a graph with vertex set V = {v 1, v 2, …, v n}. The open neighborhood of a vertex v ∈ V is the set N(v) = {u | uv ∈ E} of vertices u that are adjacent to v; these vertices are called neighbors of v. The degree of a vertex v is deg(v) = |N(v)|. The closed neighborhood of a vertex v is the set N[v] = N(v) ∪{v}. A vertex v with deg(v) = 0 is called an isolated vertex, and a vertex v with deg(v) = 1 is called a leaf.
The open neighborhood of a set S ⊆ V of vertices is the set N(S) =⋃v ∈ S N(v), and the closed neighborhood of S is the set N[S] =⋃v ∈ S N[v].
A walk in a graph G from a vertex u to a vertex v is an alternating sequence of vertices u i and edges e i of the form W : u = u 0, e 1, u 1, e 2, u 2, …, u k−1, e k, u k = v, where for 1 ≤ i ≤ k, e i = u i−1 u i. A walk W containing no repeated edges, i.e. for 1 ≤ i < j ≤ k, e i ≠ e j, is called a trail. A walk W containing no repeated vertices is called a path. A cycle is a path whose first and last vertices are the same. A chord is an edge between two nonconsecutive vertices of a cycle. The length of a walk equals the number of edges in the walk. The distance d(u, v) between two vertices u and v, in a connected graph G, equals the minimum length of a path from u to v. A shortest, or minimum length, path between two vertices u and v is called a u − v geodesic; a v-geodesic is any shortest path from v to another vertex; a geodesic is any shortest path in a graph.
A graph G is connected if there is a path between every pair of vertices of G. A component of a graph is a maximal connected subgraph. A vertex v ∈ V is a cutvertex if the graph G − v obtained by deleting v and all edges containing v has more components than G. An edge e = uv is a bridge if the graph G − e obtained by deleting e has more components than G.
A graph G of order n is called k-vertex-connected (or simply, k-connected) if n ≥ k + 1 and the deletion of any k − 1 or fewer vertices leaves a connected graph.
If G = (V, E) and S ⊆ V , then the subgraph of G induced by S is the graph G[S], whose vertex set is S and whose edges are all the edges in E both of whose vertices are in S. A subgraph G′ = (V ′, E′) of a graph G is called complete if for every u, v ∈ V ′, uv ∈ E′, that is every pair of vertices in G′ are adjacent.
Let F be an arbitrary graph. A graph G is said to be F-free if G does not contain F as an induced subgraph. A graph is bipartite if its vertex set V (G) can be partitioned into two sets X and Y such that every edge in G joins a vertex in X and a vertex in Y ; it is K 3-free.
3.1 Basic Numbers
In this subsection we list the most basic numbers that are used in defining the parameters in the following subsections.
-
1.
order n = |V |, number of vertices.
-
2.
size m = |E|, number of edges.
-
3.
minimum degree δ(G) = min{deg(u) : u ∈ V }, minimum degree of a vertex in G.
-
4.
maximum degree Δ(G) = max{deg(u) : u ∈ V }, maximum degree of a vertex in G.
-
5.
degree sequence of a graph, d 1 ≥ d 2 ≥… ≥ d n, where d i = deg(v i) equals the degree of vertex v i.
-
6.
average degree of a graph, \({\frac {\sum _{v \in V} deg(v)}{n}} = \frac {2m}{n}\).
3.2 Connectivity and Subgraph Numbers
In this subsection we present parameters related to connectivity in graphs.
-
1.
binding number bind(G), min{|N(X)|∕|X| : ∅ ≠ X ⊆ V (G) and N(X) ≠ V (G)}, defined by Katerinis and Woodall [445]. See also Lyle and Goddard [492], and Nam [511].
-
2.
blocks bl(G), number of blocks in G. A block of a graph G is a maximal nonseparable subgraph of G, that is, a maximal subgraph having no cutvertices.
-
3.
bridges br(G), number of bridges in G.
-
4.
circumference cir(G), maximum length or order of a cycle in G.
-
5.
induced circumference, maximum length of an induced cycle in G, or equivalently, maximum length of a chordless cycle in G.
-
6.
clique number ω(G), maximum order of a complete subgraph of G.
-
7.
components c(G), number of maximal connected subgraphs.
-
8.
vertex connectivity κ(G), minimum number of vertices in a cutset. A vertex cutset is a set S ⊂ V in a connected graph whose removal results in a graph which is either not connected or consists of a single vertex. A graph is said to be k-connected if κ(G) = k.
-
9.
upper vertex connectivity κ +(G), maximum number of vertices in a minimal vertex cutset.
-
10.
edge connectivity λ(G), minimum number of edges in a cutset. An edge cutset is a set S ⊆ E in a connected graph whose removal results in a graph which is not connected. We assume that λ(K 1) = 0.
-
11.
upper edge connectivity λ +(G), maximum number of edges in a minimal edge cutset.
-
12.
cutvertices cut(G), number of cutvertices in G.
-
13.
cycle number cycle(v), number of distinct cycles containing vertex v.
-
14.
girth(G), minimum length of a cycle in G.
-
15.
intersection number Ω(G). Let \(\mathcal {F} = \{S_1, S_2, \ldots , S_k\}\) be a family of subsets of a set S. The intersection graph of \(\mathcal {F}\) is the graph \(G(\mathcal {F}) = (\mathcal {F}, E(\mathcal {F}))\), where two vertices S i and S j are adjacent in \(G(\mathcal {F})\) if and only if S i ∩ S j ≠ ∅. The intersection number Ω(G) equals the minimum number of elements in a set S such that G is isomorphic to an intersection graph \(G(\mathcal {F})\) on some family \(\mathcal {F}\) of subsets of S; introduced by Erdös, Goodman, and Pósa in 1966 [226]; see also Harary [337] and [338].
-
16.
edge clique cover number θ cc(G), minimum order k of an edge clique cover, that is, a set \(\mathcal {E} = \{C_1, C_2, \ldots , C_k\}\) such that (1) for 1 ≤ i ≤ k, C i is a complete subgraph of G, and (2) for every edge uv ∈ E(G), there exists a j, 1 ≤ j ≤ k, such that uv ∈ C j. This number equals the intersection number Ω(G), defined above; cf. Erdös, Goodman and Pósa in 1966 [226] and Harary [337].
Theorem 1 For any graph G, Ω(G) = θ cc(G).
-
17.
toughness t(G), maximum value of t for which G is t-tough. A graph G is called t-tough if each subset S ⊆ V with c(G − S) > 1 satisfies |S|∕c(G − S) ≥ t; defined by Chvátal in 1973 [156]. We refer the reader to the survey by Bauer [37] and also the chapter on toughness and related conjectures by Lesniak [481] in Volume 1 of this series [287].
3.3 Degree and Distance Numbers
This subsection contains the definitions of parameters which are defined in terms of the degrees of the vertices in a graph or the distances d(u, v) between vertices in a graph.
-
1.
convex number cvx(G). For two vertices u, v ∈ V , let I(u, v) denote the set of all vertices lying on a u-v geodesic in G. For a set S, let I(S) = ∪u,v ∈ S I(u, v). A set S is convex if I(S) = S. The convex number cvx(G) is the maximum cardinality of a proper convex set of G; introduced by Chartrand and Zhang in 1999 [115].
-
2.
detour length τ′(G),Footnote 1 maximum length of a path in G, and detour number τ(G), maximum number of vertices in a path in G; introduced by Kapoor, Kronk and Lick in 1968 [442]. See also Broere et al. [83].
-
3.
induced detour number idn(G), maximum length of an induced path in G; introduced by Buckley and Harary in 1988 [87].
-
4.
detour number dn(G). For two vertices u, v ∈ V , the detour distance D(u, v) is the length of a longest u − v path in G. A u − v path of length D(u, v) is called a u − v detour. The closed detour interval ID[u, v] consists of u, v, and all vertices in some u − v detour in G. For S ⊆ V , ID[S] =⋃u,v ∈ S ID[u, v]. A set S of vertices is a detour set if ID[S] = V , and the detour number dn(G) is the minimum cardinality of a detour set in G; cf. Chartrand et al. [128].
-
5.
diameter, diam(G), maximum length of a geodesic in G, or equivalently, diam(G) = max{ecc(v) : v ∈ V }.
-
6.
eccentricity ecc(v), maximum length d(v, w) of a v-geodesic, or equivalently, ecc(v) = max{d(v, w) : w ∈ V }.
-
7.
geodetic number gn(G). The closed interval I[u, v] consists of vertices u and v and all vertices that lie on some u − v geodesic in G. For a set S ⊆ V , let I[S] =⋃u,v ∈ S I[u, v]. A set S of vertices is a geodetic set if I[S] = V , and the minimum cardinality of a geodetic set is the geodetic number gn(G); introduced by Harary et al. [347]; see also Chartrand et al. [127] and Chartrand et al. [130].
-
8.
Hamiltonian number h(G). Let c = v 1, v 2, …, v n, v n+1 = v 1 be a cyclic ordering of the vertices of a graph G. Let \(d(c) = \sum _{i=1}^n d(v_i, v_{i+1})\). The Hamiltonian number h(G) = min{d(c) : c a cyclic ordering of V }; introduced by Chartrand, Thomas, Saenpholphat, and Zhang in 2004 [131].
-
9.
upper Hamiltonian number h +(G) = max{d(c) : c a cyclic ordering of V }; introduced by Chartrand et al. [131].
-
10.
Hamiltonian completion number hc(G), minimum number of edges not in E(G), which when added to G create a graph G′ having a Hamiltonian cycle, defined by Goodman and Hedetniemi in 1974 [309] and later expanded on by Goodman et al. in 1975 [310] and by Slater et al. in 1976 [590].
-
11.
Harary index.
$$\displaystyle \begin{aligned}H(G) = \sum_{u,v \in V} d(u, v)^{-1}\end{aligned}$$Introduced independently in 1993 by Plavšić et al. [523] and Ivanciuc et al.[431].
-
12.
Hosoya index. One plus the number of matchings in a graph G, or equivalently, one plus the number of independent sets of edges, including the empty set; introduced by Hosoya in 1971 [423], used in the study of organic compounds, shown to be positively correlated with the boiling points of alkane isomers; also called the Z index.
-
13.
weak hub-integrity WHI(G) = min{|S| + m e(G − S)}, where S is a hub set and m e(G − S) denotes the number of edges in a largest component of G − S; introduced by Mahde and Mathad in 2017 [494].
-
14.
periphery per(G), number of vertices v with ecc(v) = diam(G). The periphery of a graph refers to either the set of all vertices having eccentricity equal to diam(G) or the subgraph induced by this set of vertices.
-
15.
radius rad(G), minimum eccentricity of a vertex in G, i.e. rad(G) = min{ecc(v) : v ∈ V }. The center of a graph C(G) refers either to the set of vertices having minimum eccentricity or the subgraph induced by this set of vertices. A vertex v ∈ C(G) is called a central vertex.
-
16.
status s(v) =∑u ∈ V d(u, v). The median M(G) of a graph G equals the set of vertices having minimum status, or the subgraph induced by this set of vertices, defined by Harary in 1959 [336], and by Buckley and Harary in 1990 [88].
-
17.
average distance \(\mu (G) = \frac {1}{n(n-1)}\sigma (G)\) defined by Dankelmann in 1997 [181], where
$$\displaystyle \begin{aligned}\sigma(G) = \sum_{u,v \in V} d(u, v)\end{aligned}$$is the Weiner index of G ; see below in this subsection for the definition of Weiner index.
-
18.
rank r(G), the rank of the adjacency matrix A(G) of a graph G, that is, the dimension of the vector space spanned by either the columns or the rows of the adjacency matrix A(G). Let r′(G) denote the rank of the closed neighborhood matrix N(G) = A(G) + I; as discussed by Hedetniemi, Jacobs and Laskar in [386].
-
19.
minimum rank mr(G), minimum rank of any generalized matrix of G. A generalized adjacency matrix of an adjacency matrix A(G) is any matrix of real numbers with the same pattern of non-zeroes as that of A(G); cf. Fallat and Hogben [240], who show that (1) mr(G) ≤ n − 1, (2) for connected G, mr(G) = 1 if and only if G = K n, (3) mr(P n) = n − 1, and (4) mr(C n) = n − 2.
-
20.
orthogonal rank ε(G). An orthogonal representation of a graph G is function \(\phi : V \rightarrow \mathcal {C}\) from V to the non-zero vectors of some vector space \(\mathcal {C}\), such that for every uv ∈ E, ϕ(u) is orthogonal to ϕ(v). The orthogonality graph of ϕ is the graph ϕ(G) = (ϕ(V ), E(ϕ)), where ϕ(u) is adjacent to ϕ(v) if and only if ϕ(u) and ϕ(v) are orthogonal. The orthogonal rank ε(G) equals the smallest integer c such that G has an orthogonal representation in the vector space \(\mathcal {C}^c.\) Let ε 1(G) equal the smallest integer c such that G has an orthogonal representation in the vector space \(\mathcal {C}^c\), such that every vector ϕ(v) has modulus one. Let χ(G) denote the chromatic number of a graph G. In [96] Cameron et al. show that for every graph G,
$$\displaystyle \begin{aligned}\omega(G) \leq \varepsilon(G) \leq \varepsilon_1(G) \leq \chi(G).\end{aligned}$$ -
21.
Randić connectivity index.
$$\displaystyle \begin{aligned}R(G) = \sum_{uv \in E} (deg(u)deg(v))^{-1/2}.\end{aligned}$$Introduced by Randić in 1975 [535].
-
22.
metric dimension dim(G). Let S = {v 1, v 2, …, v k} be an ordered set of k vertices in a graph G = (V, E), and let w ∈ V be an arbitrary vertex. The metric representation of w with respect to the set S is the k-vector
$$\displaystyle \begin{aligned}r(w|S) = (d(w, v_1), d(w, v_2), \ldots, d(w, v_k)).\end{aligned}$$A set S is said to be a resolving set for G if distinct vertices in V have distinct metric representations with respect to S. The minimum cardinality of a resolving set for G is called its metric dimension and is denoted dim(G).
This concept was introduced by Slater in 1975 [584], who called the metric dimension the location number loc(G). This concept was independently introduced by Harary and Melter [343] in 1976, who used the term metric dimension.
-
23.
upper metric dimension dim +(G). A resolving set S for a graph G is said to be minimal if no proper subset of S is a resolving set for G. The maximum cardinality of a minimal resolving set for a graph G is called the upper metric dimension of G and is denoted dim +(G); introduced by Chartrand, Poisson, and Zhang in 2000 [125], see also Chartrand and Zhang [117].
-
24.
total influence number η t(G). Given a set S ⊆ V , and a vertex v ∈ S, the total influence of v is \(\eta _t(v) = \sum _{u \in V - S} \frac {1}{2^{d(u,v)}}\). The total influence of set S is η t(S) =∑v ∈ S η t(v). The total influence of a graph G is η t(G) = max S⊆V{η t(S)}; defined by Daugherty, Lyle and Laskar in 2005 [183]; cf. also Aytac and Kartal [27].
-
25.
traceable number t(G). Let l = v 1, v 2, …, v n be a linear ordering of the vertices of a graph G. Let \(d(l) = \sum _{i=1}^{n-1} d(v_i, v_{i+1})\). The traceable number t(G) = min{d(l) : l a linear ordering of V }; introduced by Saenpholphat, Okamoto, and Zhang in 2006 [550]. The upper traceable number t +(G) can also be defined as t +(G) = max{d(l) : l is a linear ordering of V }. The authors also define the traceable number of a vertex v, as t(v) = min{d(l) : l is a linear ordering of V in which v 1 = v}. Thus, the traceable center TC(G) of G can be said to consist of the set of vertices having minimum t(v), or the subgraph induced by this set of vertices; this does not appear to have been studied.
-
26.
trail number tr(G), maximum length of a trail in G; cf. Bollobás and Harary [61], who determine tr(G) over all graphs of order n and size m. Note that the trail number of a graph G equals its maximum m = |E| if and only if G has at most two vertices of odd degree, that is, G has an Eulerian walk.
-
27.
Wiener index.
$$\displaystyle \begin{aligned}\sigma(G) = \sum_{u,v \in V} d(u, v)\end{aligned}$$Introduced by Wiener in 1947 [638], it is the oldest topological index of the graph of a chemical compound related to molecular branching. Also studied graph theoretically by Harary as gross status [336], by Entringer, Jackson and Snyder as distance [222] and by Šoltés as the transmission number [594].
-
28.
first Zagreb index, sum of the squares of the vertex degrees,
$$\displaystyle \begin{aligned}M_1(G) = \sum_{v \in V} deg(v)^2\end{aligned}$$Introduced by Gutman and Trinajstić in 1972 [319]; cf. Zhou and Gutman [659].
-
29.
second Zagreb index, sum of the products of the vertex degrees of adjacent vertices,
$$\displaystyle \begin{aligned}M_2(G) = \sum_{uv \in E} deg(u)deg(v)\end{aligned}$$Introduced by Gutman and Trinajstić in 1972 [319]; cf. Došic et al. [203].
-
30.
modified Zagreb indices. First modified Zagreb index:
$$\displaystyle \begin{aligned}\sum_{v \in V} (deg(v)^2)^{-1}.\end{aligned}$$Second modified Zagreb index:
$$\displaystyle \begin{aligned}\sum_{uv \in E} (deg(u)deg(v))^{-1}.\end{aligned}$$Introduced by Nicolić et al. [515].
3.4 Bandwidth and other Labeling Numbers
All of the parameters in this subsection consider proper numberings of a graph G of order n, that is, is a bijection f : V →{1, 2, …, n}, or a labeling of the vertices of G with distinct integers from 1 to n. The parameters are defined in terms of a minimum or maximum of some objective function over all possible proper numberings.
-
1.
bandsize bs(G). For a proper numbering f, let bs f(G) = |{|f(u) − f(v)| : uv ∈ E}| that is, the number of distinct differences |f(u) − f(v)| over all edges uv ∈ E. The bandsize bs(G) = min{bs f(G) : f is a proper numbering of G}; introduced by Heinrich and Hell in 1987 [401] and Erdös, Hell and Winkler in 1989 [229].
-
2.
bandwidth B(G). For a proper numbering f, B f(G) = max{|f(u) − f(v)| : uv ∈ E}. The bandwidth B(G) = min{B f(G) : f is a proper numbering of G}; introduced by Harper in 1964 [349]. See surveys by Chinn et al. in 1982 [152] and Lai and Williams in 1999 [475].
-
3.
additive bandwidth, B +(G). For a proper numbering f, \(B^+_f(G) = max \{|f(u) + f(v) - (n+1)| : uv \in E\}\). The additive bandwidth \(B^+(G) = min \{B^+_f(G) : f\) is a proper numbering of G}; introduced by Bascuñán, Ruiz and Slater in 1992 [34] and further developed by Bascunan et al. in 1995 [35].
-
4.
edge bandwidth B′(G). For a proper edge numbering f : E →{1, 2, …, m} of G, define \(B^{\prime }_f(G) = max \{|f(e_i) - f(e_j)| : e_i\) adjacent to e j}. The edge bandwidth is defined as \(B'(G) = min \{B^{\prime }_f(G) : f\) is a proper edge numbering of G}; see Jiang et al. [435].
-
5.
edge sum or bandwidth sum s(G). For a proper numbering f, define s f =∑uv ∈ E|f(u) − f(v)|. The edge sum of G is defined as s(G) = min{s f(G) : f is a proper numbering of G}; introduced by Harper in 1964 [349].
-
6.
cutwidth cutw(G). For a proper numbering f and for every 1 ≤ i < n, define E i = {uv ∈ E : f(u) ≤ i < f(v)}. The cutwidth of f is cutw(f) = max{|E i| : 1 ≤ i < n}. The cutwidth of G is cutw(G) = min{cutw(f) : f is a proper numbering of G}; cf. Korach and Solel [460]. One can also define the minimum cutwidth of a proper numbering f to be mincutw(f) = min{|E i| : 1 ≤ i < n}. The maximinimal cutwidth, maxmincutw(G) = max{mincutw(f) : f is a proper numbering of G}.
-
7.
MAX CUT, or maxcut(G), the maximum number of edges between V 1 and V 2 in a bipartition of V . Equivalently, maxcut(G) equals the maximum number of bicolored edges in a 2 coloring of the vertices of G. This is a standard NP-complete problem, found in Garey and Johnson, as problem ND17, on p.210 of [281]. See also the upper edge connectivity λ +(G) in Section 3.2.
-
8.
(vertex) irregularity strength vs(G). An edge k-labeling of a graph G is a function λ : E →{1, 2, …, k}. An edge k-labeling λ is called vertex irregular if for every v ∈ V , wt(v) =∑uv ∈ E λ(uv) is unique, that is, for no two vertices u and v is wt(u) = wt(v). The vertex irregularity strength vs(G) equals the minimum k such that G has a vertex irregular k-labeling; introduced by Chartrand, Jacobson, Lehel, Oellermann, Ruiz, and Saba in 1988 [119]. See also Ebert et al. [216].
-
9.
(edge) irregularity strength es(G). A vertex k-labeling λ : V →{1, 2, …, k} is called edge irregular if for every edge uv ∈ E, wt(uv) = λ(u) + λ(v) is unique, that is, for no two edges e, e′∈ E is wt(e) = wt(e′). The edge irregularity strength es(G) equals the minimum integer k such that G has an edge irregular k-labeling; introduced by Chartrand et al. in 1988 [119]: see also Al-Mushayt [7].
-
10.
total vertex irregularity strength tvs(G). A total k-labeling of a graph G is a function λ : V ∪ E →{1, 2, …, k}. A total k-labeling λ is called vertex irregular if for every v ∈ V , wt(v) = λ(v) +∑uv ∈ E λ(uv) is unique, that is, for no two vertices u and v is wt(u) = wt(v). The total vertex irregularity strength tvs(G) equals the minimum k such that G has a total vertex irregular k-labeling; introduced by Bača, Jendrol, Miller and Ryan in 2007 [29]; see also Nurdin et al. [516].
-
11.
total edge irregularity strength tes(G). A total k-labeling of a graph G is a function λ : V ∪ E →{1, 2, …, k}. A total k-labeling λ is called edge irregular if for every uv ∈ E, wt(uv) = λ(u) + λ(uv) + λ(v) is unique, that is, for no two edges e, e′∈ E is wt(e) = wt(e′). The total edge irregularity strength tes(G) equals the minimum k such that G has a total edge irregular k-labeling; introduced by Bača, Jendrol, Miller, and Ryan in 2007 [29].
-
12.
profile P(G). For a proper numbering f and for every v ∈ V , define the profile of a vertex v ∈ V to be p f(v) = max{{0}∪{f(v) − f(x)| : x ∈ N(v)}}. Define P f(G) =∑v ∈ V p f(v). The profile P(G) = min{P f(G) : f a proper numbering of G}; see Lin and Yuan [487] and Lai and Williams [475].
-
13.
topological bandwidth B ∗(G). We say that a graph G′ is a refinement of a graph G if G′ can be obtained from G by subdividing some subset of the edges E(G). The topological bandwidth B ∗(G) = min{B(G′) : G′ is a refinement of G}; introduced by Makedon, Papadimitriou, and Sudborough in 1983 [495], see also Kloks and Tan [456].
3.5 Decomposition and Partition Numbers
Most of the parameters in this subsection involve either a (vertex) partition π = {V 1, V 2, …, V k} or an (edge) partition π′ = {E 1, E 2, …, E k} so that each set V i or E i has some given property. The remaining parameters involve a family of not necessarily disjoint subsets of a graph whose union is the entire set, and which has some given property.
-
1.
(vertex) arboricity va(G), minimum order of a partition π = {V 1, V 2, …, V k} into forests, that is, the subgraph G[V i] induced by each set V i is a disjoint union of trees; introduced and studied by Nash-Williams in 1964 [512],and Raspaud and Wang in 2008 [537].
-
2.
tree vertex covering number or tree arboricity ta(G), minimum order of a partition π = {V 1, V 2, …, V k} into trees, that is, the subgraph G[V i] induced by each set V i is a tree. See Foregger and Foregger [268].
-
3.
tree edge covering number or tree edge arboricity ta′(G), minimum order of a partition π = {E 1, E 2, …, E k} into trees, that is, the subgraph G[E i] induced by each set E i is a tree. See Chung [438].
-
4.
linear arboricity la(G), minimum order of a partition π′ = {E 1, E 2, …, E k} into linear forests, that is, each component in each edge-induced subgraph G[E i] is a path; introduced and studied by Akiyama, Exoo, and Harary in 1981 [6], and Alon in 1988 [13].
-
5.
star arboricity st(G), minimum order of a partition π′ = {E 1, E 2, …, E k} into star forests. A star forest or galaxy is a forest (acyclic graph) whose components are stars; introduced by Algor and Alon in 1989 [12]; see also Hakimi, Mitchem, and Schmeichel [328], who show that every planar graph has star arboricity at most 5.
-
6.
star partition number γ ∗(G), minimum order of a partition π = {V 1, V 2, …, V k}, such that the subgraph induced by every set V i is a star; introduced by Walikar [633].
-
7.
clique edge partition number cep(G) or clique edge covering number cc(G), minimum order k of an edge partition π = {E 1, E 2, …, E k} such that for 1 ≤ i ≤ k, the induced graph G[E i] is a complete subgraph, or clique, or equivalently, the minimum number of pairwise-disjoint cliques which contain every edge. See surveys by Pullman in 1983 [527] and Monson, Pullman, and Rees in 1995 [509], the latter of which contains a bibliography of 131 publications on the topic and over 30 open problems.
-
8.
clique vertex partition number cvp(G) or clique vertex covering number, minimum order k of an vertex partition π = {V 1, V 2, …, V k} such that for 1 ≤ i ≤ k, the induced graph G[V i] is a complete subgraph, or clique. Note that a clique vertex partition of a graph G is a proper coloring in the complement \(\overline {G}\) of G. See surveys by Pullman [527] and Monson et al. [509].
-
9.
k-defective colorings. A graph G has a k-defective coloring of order m if it has a vertex partition π = {V 1, V 2, …, V m} such that for all 1 ≤ i ≤ m, Δ(G[V i]) ≤ k. The k-defective coloring number D k(G) equals the minimum integer m such that G has a k-defective coloring of order m; introduced by Cowen, Cowen, and Woodall in 1986 [174]; see also Archdeacon [19]. It follows, therefore, that for 0 ≤ k ≤ Δ(G), 1 = D Δ(G)(G) ≤ D k(G) ≤ D 0(G) = χ(G), where χ(G) is the chromatic number of G.
-
10.
tree width. A tree decomposition of a graph G = (V, E) is a tree T(G) with vertices in order V (T(G)) = {V 1, V 2, …, V p} having the following three properties: (i) \(\bigcup _{1}^{p} V_i = V(G)\), (ii) for every edge uv ∈ E(G), there is an i such that u, v ∈ V i, and (iii) for every 1 ≤ i ≤ j ≤ k ≤ p, V i ∩ V k ⊆ V j. It is important to point out that the significance of Condition (iii) is that for every vertex v ∈ V (G), the set of vertices V i ∈ E(T(G)) which contain vertex v forms a subtree of T(G). The width of a tree decomposition \(tw(T(G)) = \max \{|V_i| - 1 : 1 \leq i \leq p \}\). The tree width tw(G) = min{tw(T(G)) : T(G) is a tree decomposition of G}.
Earliest references to the concept of tree width include the following by Bertele and Brioshi [48], Halin noticed in 1976 that tree width has properties in common with the Hadwiger number in [330]. But Seymour and Thomas developed a min-max theorem for tree-width in 1993 [568], Robertson and Seymour developed algorithms in 1996 [543] and re-discovered tree width in developing their theory of graph minors in 1984 [542]. More details can be found in the 1994 work of Bodlaender [57]; see also Korach and Solel [460].
-
11.
path (decomposition) number, pn(G). A path decomposition is a family of paths such that every edge e ∈ E lies on precisely one path. The path number pn(G) equals the minimum number of paths in a path decomposition of G; perhaps first discussed for directed graphs by Alspach and Pullman in 1974 [15], see also Arumugam et al. [22].
-
12.
path width, pw(G) = min{pw(P(G)) : P(G) a path decomposition of G}. The width of a path decomposition \(pw(P) = \max \{|V_i| - 1 : 1\leq i \leq p \}\); cf. Korach and Solel [460].
-
13.
path length, pl(G) = min{pl(P) : P a path decomposition of G}. The path length of a path decomposition P of G is \(pl(P) = max_{1 \leq i \leq p} \{ max_{u,v \in V_i} d(u,v) \}\}\). The reader is referred to Dragan et al. [204].
-
14.
path partition number π p(G), minimum order of a partition π = {V 1, V 2, …, V k} such that each induced subgraph G[V i] contains a spanning, or Hamiltonian, path; cf. Vu Dinh [631].
-
15.
induced path partition number π ip(G), minimum order of a vertex partition π = {V 1, V 2, …, V k} such that each induced subgraph G[V i] is a path; cf. Broere et al. [84].
3.6 Covering, Packing, Independence, and Matching Numbers
A set S ⊆ V of vertices is independent if no two vertices in S are adjacent, and a set M ⊆ E of edges is independent or a matching if no two edges in M are adjacent, that is, have a vertex in common. Given a matching M, V [M] is the set of vertices incident with an edge in M, and G[V (M)] is the subgraph induced by the vertices in V (M). A graph G of even order n = 2k has a perfect matching if it has a matching M of cardinality k.
A set S of vertices or edges is said to cover another set T if every element of T either contains an element of S or is adjacent or incident to an element of S.
All of the parameters in this subsection have to do with sets that are independent or cover other sets. These include some of the most basic of all parameters in graph theory.
-
1.
vertex independence numbers i(G) and α(G), minimum and maximum cardinality of a maximal independent set. While the notation i(G) is fairly standard for the independent domination number, many papers denote the vertex independence number by β 0(G).
-
2.
k-dependence number α k(G), maximum cardinality of a set S such that for every vertex u ∈ S, |N(u) ∩ S|≤ k; introduced by Fink and Jacobson in 1985 [264], whose conjecture, that the k-domination number γ k(G) [defined below] is a lower bound for the k-dependence number, was proved by Favaron in 1985 [248]. Improved lower bounds for α k(G) were obtained by Favaron in 1988 [249] and Caro and Tuza in 1991 [99]. It is worth mentioning that today most authors refer to sets S ⊆ V that are k-independent, for positive integers k, meaning that the maximum degree of the induced subgraph G[S] is at most k − 1. Thus, k-independent sets are precisely (k − 1)-dependent. The reader is referred to the 2012 survey by Chellali et al. [138].
-
3.
vertex covering numbers β(G) and β +(G), minimum and maximum cardinality of a minimal vertex cover, that is, a set of vertices S such that for every edge uv ∈ E, {u, v}∩ S ≠ ∅. We note that in many papers the vertex covering number is denoted by α(G). It should be noted that by a well-known theorem of Gallai, for any graph G of order n, α(G) + β(G) = n.
-
4.
edge covering numbers β′(G) and β ′+(G), minimum and maximum cardinality of a minimal edge cover, that is, a set M of edges such that every vertex v ∈ V is incident with at least one edge in M.
-
5.
triangle cover number τ 3(G), minimum cardinality of triangle cover, that is, a set F ⊂ E of edges such that every triangle in G contains an edge in F. See Tuza [616] and Yuster [647].
-
6.
triangle packing number ν 3(G), maximum cardinality of a set of pairwise edge-disjoint triangles. See Tuza [616], who conjectured that for every graph G, τ 3(G) ≤ 2ν 3(G). See also Yuster [647].
-
7.
clique covering number cc(G). A clique covering is a set of cliques containing every edge at least once.
See Orlin [518].
-
8.
clique packing number cp(G). A clique packing is a collection of cliques containing every edge at most once.
-
9.
2-packing numbers p 2(G) and P 2(G), minimum and maximum cardinality of a maximal 2-packing in G, that is, a set S such that for every vertex v ∈ V , |N[v] ∩ S|≤ 1. Equivalently, a 2-packing can be defined as a set S having the property that for any two vertices u, v ∈ S, d(u, v) > 2. From this, one can naturally define a k-packing to be a set S having the property that for any two vertices u, v ∈ S, d(u, v) > k.
-
10.
matching numbers α ′−(G) and α′(G), minimum and maximum cardinality of a maximal matching in G. It should be noted that by a well-known theorem of Gallai, for any graph G of order n with no isolated vertices, α′(G) + β′(G) = n. In many papers, the matching number is denoted by β 1(G). As far as we know, the parameter α ′−(G), called the lower matching number has not been studied very much.
-
11.
induced, or strong, matching number, α ∗(G), maximum cardinality of a matching M such that the subgraph G[V (M)] consists of disjoint K 2’s, or equivalently, no edge in E − M connects two edges in M. This was introduced by Cameron in 1989 [95], and further studied by Horák et al. in 1993 [422], by Golumbic and Laskar in 1993 [307], and by Brandstädt and Mosca in 2011 [73].
-
12.
disconnected matching number \(\alpha ^{\prime }_{dc}(G)\), maximum number of edges in a matching M such that the subgraph G[V (M)] is disconnected; cf. Goddard et al. [298].
-
13.
forcing matching number. Let G be a graph that admits a perfect matching. The forcing number of a perfect matching M of G is defined as the smallest number of edges in a subset S ⊆ M, such that S is in no other perfect matching; introduced by Harary, Klein, and Zívković in 1991 [346], and further studied by Pachter and Kim in 1998 [519].
-
14.
anti-forcing matching number of a perfect matching M in a graph G is defined as the minimum number of edges not in M, whose deletion results in a graph G′ having only M as a perfect matching. The minimum (resp. maximum) anti-forcing number of G is the minimum (resp. maximum) anti-forcing number of all perfect matchings M in G. It is shown by Deng and Zhang that the maximum anti-forcing number of a graph is at most its cyclomatic number, and the graphs with maximum anti-forcing number achieving the upper bound are characterized;introduced by Deng and Zhang in 2017 [192].
-
15.
isolate-free matching number \(\alpha ^{\prime }_{if}(G)\), maximum number of edges in a matching M such that either |M| = 1 or the subgraph G[V (M)] contains no K 2 component; cf. Goddard et al. [298].
-
16.
acyclic matching number, \(\alpha ^{\prime }_{ac}(G)\), maximum cardinality of an acyclic matching M, that is, a matching M such that the subgraph G[V (M)] is acyclic; introduced by Goddard et al. in 2005 [298].
-
17.
matchability number μ(G), minimum cardinality of a maximal matchable set of vertices in G. A set S of vertices is called matchable if there exists an injection ϕ : S → V − S such that for every vertex u ∈ S, u is adjacent to ϕ(u); introduced by Cockayne, Hedetniemi and Laskar in 1998 [164], and further studied by Dean et al. [186].
-
18.
uniquely restricted matching number \(\alpha ^{\prime }_{ur}(G)\), maximum cardinality of a matching M such that G[V (M)] has exactly one maximum matching, or equivalently, G[V (M)] does not contain a cycle, the edges of which alternate between edges in M and edges not in M. This was introduced by Golumbic, Hirst, and Lewenstein in 2001, see also Mishra [506].
3.7 Coloring Numbers
In this subsection, a vertex k-coloring is simply a vertex partition π = {V 1, V 2, …, V k} into k color classes V i, for 1 ≤ i ≤ k. We say that a vertex v ∈ V i is colored i or assigned the color i. Virtually all of the vertex coloring numbers in this subsection have in common that they equal the minimum or maximum order k of a coloring such that each color class V i has some property \(\mathcal {P}\). A coloring is called proper if every V i is an independent set.
An edge k-coloring is defined similarly, namely an edge partition
π′ = {E 1, E 2, …, E k} into k color classes E i.
-
1.
chromatic number χ(G), minimum order k of a proper vertex coloring π = {V 1, V 2, …, V k} of G. If π is a proper coloring of G with χ(G) = k colors, then the same partition is a partition of the complement \(\overline {G}\) of G into complete subgraphs, called a clique partition, as defined and discussed in Section 3.6. The reader is referred to the book on graph coloring by Chartrand and Zhang [118] and the large collection of 200 graph coloring problems in the 1995 book by Jensen and Toft [434].
-
2.
Grundy number Γr(G), maximum order of a proper coloring π = {V 1, V 2, …, V k}, such that for every i, 2 ≤ i ≤ k, every vertex in V i is adjacent to at least one vertex in every V j, for all 1 ≤ j < i; named after a paper by P. M. Grundy in 1939 [316], and introduced by Christen and Selkow in 1979 [153]; see also Hedetniemi et al. [382] and Zaker [648]. Grundy colorings are also called greedy colorings, which result from the process of arbitrarily ordering the vertices v 1, v 2, …, v n, coloring vertex v 1 with color 1, and then for i = 2 to n, coloring vertex v i with the smallest color not used to color a vertex adjacent to v i. The Grundy number is the maximum number of colors that can be used in any greedy coloring of G.
-
3.
partial Grundy number ∂Γr(G), maximum order of a proper coloring π = {V 1, V 2, …, V k}, such that for every i, 2 ≤ i ≤ k, there exists at least one vertex in V i, called a Grundy vertex, that is adjacent to at least one vertex in every V j, for all 1 ≤ j < i ≤ k; introduced by Erdös, Hedetniemi, Laskar, and Prins in 2003 [233]. See also Shi et al. [579], Effantin and Kheddouci [220], and Balakrishnan and Kavaskar [31]. Note that in a Grundy coloring, all vertices are Grundy vertices, but in a partial Grundy coloring, each color class is required to have only one Grundy vertex.
-
4.
achromatic number ψ(G), maximum order of a complete proper coloring of G. A partition π = {V 1, V 2, …, V k} is called complete if for every pair of distinct color classes V i and V j, 1 ≤ i < j ≤ k, there is a vertex in V i that is adjacent to a vertex in V j; introduced by Harary and Hedetniemi in 1970 [342]. See also Cairnie and Edwards [94], and Hughes and MacGillivray [428].
-
5.
pseudo-achromatic number ψ s(G), maximum order of a complete coloring of G; introduced by Gupta in 1969 [318]. See also Bhave [49], Edwards [218] and Hedetniemi [379]. Note than all proper colorings of a graph with χ(G) colors, all Grundy colorings, and all partial Grundy colorings are complete colorings. Therefore, for any graph G,
$$\displaystyle \begin{aligned}\chi(G) \leq \varGamma r(G) \leq \partial \varGamma r(G) \leq \psi(G) \leq \psi_s(G).\end{aligned}$$ -
6.
acyclic chromatic number a(G), minimum number of colors in a proper coloring π = {V 1, V 2, …, V k} such that for any two color classes V i and V j, the bipartite subgraph induced by V i ∪ V j is acyclic; introduced by Grunbaum in 1973 [315]. See also Borodin [67] and Goddard [293]. In his original paper Grünbaum conjectured that for any planar graph G, a(G) ≤ 5; this was later proved correct by Borodin in 1979 [67].
-
7.
acyclic chromatic index a′(G), minimum order of a proper edge coloring π′ = {E 1, E 2, …, E k} such that for every 1 ≤ i < j ≤ k, the induced subgraph G[E i ∪ E j] is acyclic, or equivalently, such that every cycle contains edges with at least three different colors; introduced in 1978 and 1980 by Fiamčík [259, 260].
-
8.
b-chromatic number χ b(G), maximum order of a proper coloring
π = {V 1, V 2, …, V k} such that every set V i contains at least one colorful vertex. A vertex v ∈ V i is colorful if it is adjacent to at least one vertex in every color class V j, j ≠ i; introduced by Irving and Manlove in 1999 [430]. See also Kouider and Mahéo [463].
-
9.
broadcast chromatic number χ b(G), minimum order of a proper vertex coloring π = {V 1, V 2, …, V k}, such that for 1 ≤ i ≤ k, the set V i is an i-packing, that is, for any two vertices u, v ∈ V i, d(u, v) > i. It can be seen that for any graph G, χ b(G) ≤ β(G) + 1, where β(G) is the vertex covering number of G. This was introduced by Goddard et al. [299], who showed that for any infinite grid graph G, χ b(G) ≤ 23. This has subsequently been improved by several authors, the most recent, by Martin et al. [498] who show that
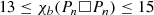 . The most recent papers on this parameter call this the packing chromatic number χ
ρ(G).
. The most recent papers on this parameter call this the packing chromatic number χ
ρ(G). -
10.
chromatic sum χ σ(G), minimum sum of all of the colors used in a proper vertex coloring of G with positive integers; introduced by Erdös, Kubicka and Schwenk in 1990 [231] and further studied by Kubicka in 2004 [468] and in 2005 [469].
-
11.
cd-chromatic number χ cd(G), minimum order k of a proper coloring π = {V 1, V 2, …, V k} such that for every 1 ≤ i ≤ k, there exists a vertex u i ∈ V such that u i dominates V i, that is, u i is adjacent to every vertex in V i. These are called cd-colorings; introduced by Venkatakrishnan and Swaminathan in 2014 [620]. See also Shalu et al. in 2017 [574] and Krithika et al. in 2017 [465].
-
12.
chromatic dimension dim(G). Let S = {v 1, v 2, …, v k} be a vertex set in a connected graph G. For each vertex v ∈ V , define the code
$$\displaystyle \begin{aligned}c(v,S) = (d(v,v_1), d(v, v_2), \ldots, d(v, v_k)).\end{aligned}$$The set S is a proper S-coloring of G if distinct vertices have distinct codes. A proper S-coloring of minimum cardinality k is called a color basis for G and the number of vertices in a color basis is called the chromatic dimension dim(G); introduced by Chartrand and Zhang in 2000 [116].
-
13.
circular chromatic number χ c(G). Let \(\mathcal {A}_r\) denote the set of open, unit length arcs of a circle C of Euclidean length r. An r-circular coloring of a graph G is a function \(c : V \rightarrow \mathcal {A}_r\) such that for every uv ∈ E, c(u) ∩ c(v) = ∅. A graph G is r-circular colorable if it has an r-circular coloring. The circular chromatic number χ c(G) = inf{r : G is r-circular colorable }; introduced by Vince in 1988 [623]. It can be seen that for any finite graph, the circular chromatic number is always rational and χ(G) − 1 ≤ χ c(G) ≤ χ(G). The reader is referred to an extensive survey by Zhu [662] which contains, among other things, many conjectures and some 28 open problems about the circular chromatic number; see also Junosza-Szaniawski [437] and Zhu [660].
-
14.
co-chromatic number z(G), minimum order k of a coloring π = {V 1, V 2, …, V k} such that for every 1 ≤ i ≤ k, the induced subgraph G[V i] is either a complete graph or an empty graph (that is, V i is an independent set); introduced by Lesniak-Foster and Straight in 1977 [482], who showed that if G is triangle-free, then z(G) = χ(G). See also PhD thesis by Gimbel [290], Erdös et al. [230], and Chudnovsky [154].
-
15.
degree-bounded chromatic number. A degree-bounded coloring is a proper coloring db : V →{1, 2, …, Δ(G)} having the property that for every vertex v ∈ V , db(v) ≤ deg(v). The db-chromatic number χ db(G) equals the minimum integer k such that G is db-colorable using only the colors 1, 2, …, k. Note, not every graph is db-colorable; introduced by Hakimi, Mitchem, and Schmeichel in 1995 [327]. The authors show that if a connected graph G has a block, that is neither a complete graph nor an odd cycle, then G is db-colorable.
-
16.
distance-s chromatic number χ s(G). An L s -coloring is a proper coloring c : V →{1, 2, …, n} such that for all u, v ∈ V , c(u) = c(v) implies d(u, v) ≥ s + 1. The s-chromatic number χ s(G) equals the minimum integer s such that G has an s-coloring; introduced by Speranza in 1975 [595]. See also Gionfriddo [292] and Marino and Puccio [497].
-
17.
distinguishing chromatic number χ D(G). A proper vertex k-coloring c : V →{1, 2, …, k} is said to be k-distinguishing if the only automorphism of G that preserves all vertex colors is the identity. The distinguishing chromatic number χ D(G) equals the minimum k such that G has a distinguishing proper k-coloring; introduced by Collins and Trenk in 2006 [173].
-
18.
distinguishing number D(G). A labeling h : V →{1, 2, …, k} is said to be k-distinguishing if the only automorphism of G that preserves all vertex labels is the identity. The distinguishing number D(G) equals the minimum k such that G has a k-distinguishing labeling; introduced by Albertson and Collins in 1996 [10].
-
19.
dominator chromatic number χ d(G). A dominator coloring of a graph G is a proper coloring π = {V 1, V 2, …, V k} such that for every vertex v ∈ V , there exists a set V i such that v is adjacent to, or dominates, every vertex in V i. The dominator chromatic number χ d(G) equals the minimum order of a dominator coloring of G; suggested by Hedetniemi, Hedetniemi, McRae and Blair in [393] but introduced by Gera, Rasmussen, and Horton in 2006 [286], and further studied by Gera in 2007 [284, 285], Chellali and Maffray in 2012 [136], and Arumugam et al. in [24, 25].
-
20.
edge chromatic number or chromatic index χ′(G), minimum order of an edge partition π′ = {E 1, E 2, …, E k}, such that every set E i is an independent set of edges, i.e. a matching; perhaps first studied by Vizing in 1965 [626], who showed that for every nonempty graph G, χ′(G) ≤ 1 + Δ(G). See also Fiamčík and Jucović [261] and Alavi and Behzad [8].
-
21.
fall chromatic number χ f(G). A vertex v ∈ V i in a proper k-coloring π = {V 1, V 2, …, V k} is called colorful if it is adjacent to at least one vertex in every color class V j, i ≠ j. A fall coloring is a coloring in which every vertex is colorful. The fall chromatic number χ f(G) and fall achromatic number ψ f(G) equal the minimum and maximum integer k for which G has a fall coloring; introduced by Dunbar, Hedetniemi, Hedetniemi, Jacobs, Knisely, Laskar, and Rall in 2000 [213]. It should be noted that not every graph has a fall coloring. See also Shaebani [569].
-
22.
fractional chromatic number χ f(G). Let \(\mathcal {I}\) denote the family of all independent sets in a graph G. A fractional coloring of G is a function \(c : \mathcal {I} \rightarrow [0, 1]\) such that for every v ∈ V , \(\sum _{S \in \mathcal {I} x \in S} c(S) = 1\). The value of a fractional coloring c is \(\sum (c) = \sum _{S \in \mathcal {I}} c(S)\). The fractional chromatic number \(\chi _f(G) = inf \{\sum (c) : c \mbox{ is a fractional coloring of G} \}\); introduced as the multicoloring number by Hilton, Rado, and Scott in 1973 [417] and as the set chromatic number by Bollobás and Thomassen in 1979 [63]. See also the book by Scheinerman and Ullman [562].
-
23.
forcing chromatic number F χ(G), minimum integer k such that there is a set of k vertices in G and a coloring of those k vertices that extends uniquely to a proper s-coloring of G, where χ(G) = s; introduced by Harary in [340]. See also Pachter and Kim in [519].
-
24.
harmonious chromatic number h(G). A harmonious k-coloring is a proper coloring π = {V 1, V 2, …, V k} with the added property that between any two color classes V i and V j there can be at most one edge. The harmonious chromatic number h(G) equals the minimum integer k for which G has a harmonious coloring. This concept appears to have been independently discovered by Harary and Plantholt in 1982 [345] and Hopcroft and Krishnamoorthy in 1983 [420]. Lee and Mitchem [478] have shown that for any graph G, \(1 + \varDelta (G) \leq h(G) \leq (1 + \varDelta (G)^2) \lceil \sqrt {n} \rceil \); see also Edwards [217] and Edwards and McDiarmid [219].
-
25.
upper harmonious chromatic number H(G). A harmonious k-coloring π = {V 1, V 2, …, V k} is called minimal if the partition which results by combining any two color classes into one, V i ∪ V j, is no longer a harmonious coloring. The upper harmonious chromatic number H(G) equals the maximum integer k for which G has a minimal harmonious k-coloring. This was introduced by Chen, Domke, Hattingh, and Laskar in 1999 [148]; see also Hattingh et al. [353].
-
26.
line-distinguishing chromatic number or harmonic (chromatic) number h′(G), the minimum number of colors which can be assigned to the vertices of a graph G such that no two edges receive the same color pair. A line-distinguishing coloring need not be a proper coloring, but if not, then for each color, at most one edge can receive an identical color pair with that color. Stated, equivalently, a line-distinguishing coloring is a vertex partition π = {V 1, V 2, …, V k} such that for every 1 ≤ i ≤ k, the induced subgraph G[V i] can contain at most one edge, and between any two color classes V i and V j there can be at most one edge. Thus, a line-distinguishing coloring which is also a proper coloring is called a harmonious coloring. This idea and name was introduced by Harary and Plantholt in 1982 [345] but the same idea was independently discovered by Hopcroft and Krishnamoorthy in 1983 [420]. One can show that for any graph G, Δ(G) ≤ h′(G) ≤ h(G). See also Salvi [551].
-
27.
upper line-distinguishing chromatic number H′(G). A line-distinguishing k-coloring π = {V 1, V 2, …, V k} is called minimal if the partition which results by combining any two color classes into one, V i ∪ V j, is no longer a line-distinguishing coloring. The upper line-distinguishing chromatic number H′(G) equals the maximum integer k for which G has a minimal line-distinguishing k-coloring. This was introduced by Chen, Domke, Hattingh, and Laskar in 1999 [148]; see also Hattingh et al. [353].
-
28.
incidence chromatic number χ i(G). An incidence in a graph G is a pair (v, e) where vertex v is incident to edge e. Two incidences (u, e) and (v, f) are adjacent if either (1) u = v, (2) e = f, (3) uv = e or (4) uv = f. An incidence coloring is an assignment of colors to the incidences such that adjacent incidences are assigned different colors. The incidence chromatic number χ i(G) equals the minimum number of colors required to color the incidences of G; introduced by Brualdi and Massey in 1993 [86]. See also Gregor et al. [312]. It is complex to see, but it appears that χ i(G) = χ(L(S(G))2), where L(G) is the line graph of G, S(G) is the subdivision graph of G, and G 2 denotes the square of a graph G.
-
29.
interval chromatic number. Let G = (V, E) be a graph with a nonnegative weight function wt defined on the vertices in V . An interval coloring assigns to each vertex v ∈ V an open interval of size wt(v), such that if two vertices u, v are adjacent, then the corresponding intervals do not intersect. The size of an interval coloring is the total size of the union of all assigned intervals. The minimum possible size of an interval coloring is the interval chromatic number. Stockmeyer (cf. Golumbic [306]) proved that determining the interval chromatic number of NP-complete even if G is an interval graph and wt is restricted to the values 1 and 2; see also Shalom [573].
-
30.
irregular chromatic number χ ir(G). Let c : V (G) →{1, 2, …, k} be a proper vertex k-coloring of a graph G. Let code(v) = (a 0, a 1, …, a k), where a 0 = c(v) and for 1 ≤ i ≤ k, a i equals the number of neighbors of v colored i. The coloring c is called irregular if distinct vertices have distinct codes, that is, u ≠ v implies code(u) ≠ code(v). The irregular chromatic number χ ir(G) equals the minimum k such that G has an irregular k-coloring; introduced by Radcliffe and Zhang in 2006 [531].
-
31.
irredundant chromatic number χ irr(G). A set S is an irredundant set if for every vertex v ∈ S, pn[v] = N[v] − N[S −{v}] ≠ ∅. An irredundant k-coloring of a graph G is a vertex partition π = {V 1, V 2, …, V k} such that for all 1 ≤ i ≤ k, V i is an irredundant set. The irredundant chromatic number χ irr(G) equals the minimum order k of an irredundant k-coloring; introduced by Haynes, Hedetniemi, Hedetniemi, McRae, and Slater in 2008 [369]. Notice that every proper coloring is an irredundant coloring, since every independent set is irredundant. Thus,it follows that for any graph G, χ irr(G) ≤ χ(G).
-
32.
open irredundant chromatic number χ oir(G). A set S is an open irredundant set if for every vertex v ∈ S, pn(v) = N(v) − N[S −{v}] ≠ ∅. An open irredundant k-coloring of a graph G is a vertex partition π = {V 1, V 2, …, V k} such that for all 1 ≤ i ≤ k, V i is an open irredundant set. The open irredundant chromatic number χ oir(G) equals the minimum order k of an open irredundant k-coloring, or the minimum order of a vertex partition into open irredundant sets; cf. Arumugam et al. [23].
-
33.
L(2, 1)-labeling number or L(2, 1)-coloring number λ(G), minimum value k of a proper k-coloring f : V →{0, 1, 2, …, k}, such that if any two vertices u and v are adjacent then |f(u) − f(v)|≥ 2, and if d(u, v) = 2, then f(u) ≠ f(v). The basic ideas for L(2, 1)-colorings originated with Hale in 1980 [329]; but was introduced for study by Yeh in 1990 [643] and Griggs and Yeh in 1992 [313]. See also Klavzar and Spacapan [454].
-
34.
list chromatic number χ l(G), minimum integer k such that if every vertex v ∈ V is assigned a list L(v) of at least k distinct colors, then G has a proper vertex coloring, where the color chosen for every vertex v is an element of L(v); introduced by Vizing in 1976 [628] and independently by Erdös, Rubin and Taylor in 1979 [227].
-
35.
list edge chromatic number, or list chromatic index \(\chi ^{\prime }_l(G)\), minimum integer k such that if every edge e ∈ E is assigned a list L(e) of at least k distinct colors, then G has a proper edge coloring, where the color chosen for every edge e is an element of L(e); cf. Bollobás and Harris in 1985 [62], cf. also Galvin [279] and Slivnik [592].
-
36.
neighborhood-restricted achromatic number or [≤ k]-achromatic number ψ [≤k](G). Given a vertex partition π = {V 1, V 2, …, V k}, let deg π[v] = |{i : N[v] ∩ V i ≠ ∅}|. A partition π is said to be a [≤ k]-coloring if for every v ∈ V , deg π[v] ≤ k, that is, no vertex is adjacent to more than k distinctly colored vertices. The [≤ k]-achromatic number ψ [≤k](G) is the maximum order of a [≤ k]-coloring of G; introduced by Chandler, Desormeaux, Haynes, and Hedetniemi in 2016 [107].
-
37.
packing chromatic number. This is the same parameter as the broadcast chromatic number χ b(G), defined above, but called this by Korže and Vesel [461].
-
38.
proper connection number pc(G) and strong proper connection number spc(G). Let G be a connected, arbitrarily edge-colored graph. A path P in G is called a proper path if no two adjacent edges of P are colored the same. A proper u − v geodesic is a proper path of length d(u, v). An edge coloring c is called a proper-path coloring if every pair of vertices u, v ∈ V are connected by a proper path, and is called a strong proper-path coloring if every pair u, v of vertices are connected by a proper u − v geodesic. The minimum number of colors in a proper-path coloring is called the proper connection number pc(G) and the minimum number of colors in a strong proper-path coloring is called the strong proper connection number spc(G). These coloring numbers are related to the rainbow connection number rc(G), and strong rainbow connection number src(G); cf. Andrews et al. [17] and Lumduanhom et al. [491].
-
39.
quorum coloring number ψ q(G), maximum order k of a partition π = {V 1, V 2, …, V k} such that for every vertex 1 ≤ i ≤ k, every vertex v ∈ V i satisfies |N[v] ∩ V i|≥|N[v]|∕2, that is, at least half of the vertices in the closed neighborhood of every vertex v have the same color as v; introduced by Hedetniemi, Hedetniemi, Laskar, and Mulder in 2013 [398]. Quorum colorings are very similar to satisfactory partitions due to Shafique and Dutton [570] in which the condition is that at least half of the vertices in the open neighborhood of every vertex v have the same color as v. Since not all graphs have a satisfactory partition, for example complete graphs, the primary focus of research on satisfactory partitions is to decide if an arbitrary graph G has a satisfactory partition and to find classes of graphs that do or do not have them. On the other hand, since all graphs have quorum colorings, the primary focus of quorum colorings is on determining the maximum order of a quorum coloring of a given graph.
-
40.
radio number rn(G). A radio labeling c of a connected graph G is an assignment of distinct positive integers to the vertices v ∈ V such that d(u, v) + |c(u) − c(v)|≥ 1 + diam(G), for every two distinct vertices u, v ∈ V . The radio number rn(c) of a radio labeling c is the maximum integer assigned to a vertex v ∈ V . The radio number rn(G) = min{rn(c) : c a radio labeling of G}. This concept was introduced by Chartrand, Erwin, Zhang, and Harary in 2001 [126].
-
41.
rainbow connection number rc(G) or strong rainbow connection number src(G), minimum number of colors required to color the edges of a connected graph G so that between any pair of vertices u and v, there is a u − v path, or u − v geodesic, no two edges of which are colored the same; introduced by Chartrand, Johns, McKeon and Zhang in 2008 [132]. See also Li et al. [486], Hao [335], Caro et al. [101], and Schiermeyer [563].
-
42.
rank number and arank number χ r(G) and ψ r(G). A proper coloring c : V →{1, 2, …, k} is a k-ranking if c(u) = c(v) implies that every u − v path contains a vertex w such that c(w) > c(u). A k-ranking is minimal if decreasing the value c(u) assigned to any vertex u ∈ V produces a coloring that is not a k-ranking. The rank number χ r(G) and the arank number ψ r(G) equal the minimum and maximum k, respectively, such that G has a minimal k-ranking; cf. Iyer et al. [432], de la Torre et al. [184] and Ghoshal et al. [289].
-
43.
strong chromatic index \(\chi _s^{\prime }(G)\), minimum number of colors that can be used in a proper edge coloring of G so that for every vertex v ∈ V , the set C(v) of colors incident to vertex v is unique; introduced by Burris and Schelp in 1997 [92]. See also Togni [612].
-
44.
strong chromatic number χ s(G), minimum order of a proper coloring π = {V 1, V 2, …, V k} having the property that for every 1 ≤ i ≤ k, no vertex v ∈ V has two neighbors in V i; this is equivalent to saying that no vertex has two neighbors with the same color, or that every set V i is a 2-packing; introduced by Sampathkumar and Pushpa Latha in 1995 [555]. See also Narahari et al. [593].
-
45.
strong chromatic index \(\chi _s^{\prime }(G)\). A strong edge coloring of a graph G is a proper edge coloring such that every color class is an induced, or strong, matching in G, or equivalently, if no edge is adjacent to two edges with the same color. The strong chromatic index \(\chi ^{\prime }_s(G)\) equals the minimum number of colors in a strong edge coloring of G; introduced by Fouquet and Jolivet in 1983 [269]. This parameter was introduced independently by Faudree et al. [247] and by Horák in 1990 [421]. See also Yang and Zhu [641] and Bensmail et al. [43].
-
46.
subchromatic number χ K(G), minimum order of a partition π = {V 1, V 2, …, V k}, such that the subgraph induced by every set V i is a disjoint union of complete subgraphs of G; introduced by Albertson, Jamison, Hedetniemi, and Locke in 1989 [11]. See also Gimbel and Hartman [291]. Note the similarity of the subchromatic number and the co-chromatic number, z(G), also defined in this subsection, where each color class is either a complete graph or an independent set. Note that for any graph G:
$$\displaystyle \begin{aligned}\chi_K(G) \leq z(G) \leq \chi(G) \leq \varGamma r(G) \leq \partial \varGamma r(G) \leq \psi(G) \leq \psi_s(G).\end{aligned}$$ -
47.
t-tone chromatic number χ tt(G). For a positive integer t, a t-tone coloring c of a graph G is an assignment of t-element subsets of [k] = {1, 2, …, k} for some integer k > t to the vertices v ∈ V such that for every two vertices u, v ∈ V , if d(u, v) = d, then |c(u) ∩ c(v)| < d. The t-tone chromatic number χ tt(G) equals the minimum number of colors in a t-tone coloring of G. The concept of t-tone colorings was introduced by Chartrand in 2009 and first studied by Fonger, Goss, Phillips, and Segroves in [267]. Note that every t-tone coloring is a proper coloring.
-
48.
total chromatic number χ ′′(G), minimum order of a partition of the vertices and edges, Π = {S 1, S 2, …, S k}, such that each set S i, consisting of a collection of vertices and edges, contains no pair of adjacent vertices, no pair of adjacent edges, and no vertex incident with an edge. Clearly, χ ′′(G) ≥ Δ(G) + 1. It remains an open conjecture, due independently to Behzad [39] and Vizing [625], that for any graph G, χ ′′(G) ≤ Δ(G) + 2. See also Campos and de Mello [97], Vijayaditya [622] and Chartrand et al. [133].
-
49.
adjacent vertex distinguishing total chromatic number \(\chi ^{\prime \prime }_a(G)\). A total coloring c : E ∪ V →{1, 2, …, k} is called adjacent vertex distinguishing if for every edge uv ∈ E, c(u) ∪ c(E(u)) ≠ c(v) ∪ c(E(v)), where E(u) denotes the set of edges incident with vertex u. This concept has been attributed to Zhang, Chen, Li, Yao, Lu and Wang in 2005 [657], but a paper by Chen precedes this by one year [144]. Since then, many papers have been written on these colorings, cf. two recent papers by Hu et al. [426] and by Huang et al. [427].
-
50.
vector chromatic number χ V(G). For t ≥ 2, a vector t-coloring of a graph G with vertex set V = {v 1, v 2, …, v n} consists of an assignment p = (p 1, p 2, …, p n) of real unit vectors to the vertices of V such that v i v j ∈ E if \(p_i^T p_j \leq \frac {-1}{t - 1}\). The vector chromatic number χ V(G) equals the minimum real number t ≥ 2 for which G has a vector t-coloring; introduced by Karger, Motwani, and Sudan in 1994 [443]. See also Godsil et al. [303, 304].
3.8 Domination Numbers
A set S ⊆ V of vertices is a dominating set if N[S] = V , that is, every vertex in V − S is adjacent to, or equivalently is at distance one from, at least one vertex in S. Thus, if every vertex in S has some desired resource, then every vertex in V − S has easy, one edge access to a vertex in their neighborhood having this resource. From the perspective of vertices in S they have the property that they can ‘observe’ over one edge, every vertex in V − S. The many variations of dominating sets are based on (1) conditions which are placed on the subgraph G[S] induced by a dominating set S, (2) conditions which are placed on the vertices in V − S, or (3) conditions which are placed on the edges between vertices in S and vertices in V − S.
-
1.
domination numbers γ(G) and Γ(G), minimum and maximum cardinalities of a minimal dominating set. The reader is referred to the two books on domination in graphs by Haynes, Hedetniemi and Slater in 1998 [361] and in [360].
-
2.
enclaveless numbers ψ(G) and Ψ(G), minimum and maximum number of vertices in a maximal enclaveless set. A set S is enclaveless if it does not contain a vertex u ∈ S such that N[u] ⊆ S. It can be seen that for any graph G of order n, γ(G) + Ψ(G) = n, and Γ(G) + ψ(G) = n. It can also be seen that the enclaveless number Ψ(G) also equals the maximum number of pendant edges in a spanning forest of G. The concept of enclaveless sets was introduced by Slater in 1977 [586].
3.8.1 Conditions on S
-
1.
independent domination i(G), minimum cardinality of a dominating set that is also independent. Independent domination was introduced by Berge in 1962 [44].
-
2.
total domination γ t(G) and Γ t(G), minimum and maximum cardinalities of a minimal total dominating set. A set S ⊆ V of vertices is a total dominating set if N(S) = V , that is, every vertex in V is adjacent to at least one vertex in S. These parameters were introduced by Cockayne, Dawes, and Hedetniemi in 1980 in [163]. The definitive and most comprehensive treatment of total domination is the book on this subject by Henning and Yeo in 2013 [411].
-
3.
connected domination γ c(G), minimum cardinality of a dominating set S such that the induced subgraph G[S] is connected. This was introduced by Sampathkumar and Walikar in 1979 [558]. One can also consider the k-connected domination number γ kc(G), the minimum cardinality of a dominating set S such that the induced subgraph G[S] is k-connected; cf. Shang et al. [575].
-
4.
acyclic domination γ a(G), minimum cardinality of a dominating set S such that the induced subgraph G[S] is acyclic. This was introduced by Hedetniemi, Hedetniemi, and Rall in 2000 [390], see also Goddard, Haynes and Knisley in 2004 [296].
-
5.
capacity-k domination \(\gamma _{cap_k}(G)\), minimum order of a vertex partition
π = {V 1, V 2, …, V k}, such that the subgraph induced by every set V i has a spanning star of order at most k + 1, or equivalently, a dominating set S in which no vertex in S has to dominate more than k vertices in V − S; introduced by Goddard, Hedetniemi, Huff, and McRae in 2010 [300].
-
6.
clique domination γ K(G), minimum cardinality k of a dominating set S ⊆ V such that G[S] ≃ K k. Of course, such a dominating set might not exist for all graphs G, cf. Labendia and Canoy [473].
-
7.
convex domination γ conv(G). A set S ⊆ V is called convex if for any two vertices u, v ∈ S, the vertices contained in all u − v geodesics belong to S. A set S is a convex dominating set if it is convex and dominating. The convex domination number γ conv(G) equals the minimum cardinality of a convex dominating set in G. This was introduced by Lemańska in 2004 [479].
-
8.
weakly convex domination γ wcon(G). A set S ⊆ V is called weakly convex if for any two vertices u, v ∈ S, there exists at least one u − v geodesic, all of whose vertices belong to S. A set S is a weakly convex dominating set if it is weakly convex and dominating. The weakly convex domination number γ wcon(G) equals the minimum cardinality of a weakly convex dominating set in G; first appeared in a paper by Lemańska in 2004 [479].
-
9.
cycle domination γ cy(G), minimum cardinality of a dominating set S ⊆ V such that G[S] has a Hamiltonian cycle. Such a dominating set might not exist for all graphs G. Harary and Nash-Williams have shown that the line graph L(G) of a graph G is Hamiltonian if and only if G contains a dominating cycle or G ≃ K 1,n, for n ≥ 3 [344].
-
10.
equivalence domination γ e(G), minimum cardinality of an equivalence dominating set. A set S is called an equivalence set if G[S] is a disjoint union of complete subgraphs; introduced by Arumugam and Sundarakannan in 2015 [21]. It is easy to see that equivalence domination generalizes 1-dependent domination, and therefore, for any graph G,
$$\displaystyle \begin{aligned}\gamma(G) \leq \gamma_e(G) \leq \gamma_{[1]}(G) \leq i(G).\end{aligned}$$ -
11.
forcing domination number F γ(G). A subset T of a minimum dominating set S is a forcing subset for S if S is the unique minimum dominating set containing T. The forcing domination number F γ(S) of S is the minimum cardinality among the forcing subsets of S, and the forcing domination number F γ(G) of G is the minimum forcing domination number among the minimum dominating sets S of G. It follows from the definition that F γ(G) ≤ γ(G). Chartrand et al. [123] show that for all integers 0 ≤ a ≤ b, with b positive, there exists a graph G with F γ(G) = a and γ(G) = b.
-
12.
geodetic domination γ g(G). A geodetic set S is a set such that I[S] = ∪x,y ∈ S I[x, y] = V , where the closed interval I[x, y] consists of x, y and all vertices lying on some x − y geodesic. A geodetic dominating set is both a geodetic set and a dominating set. In other words, S is a geodetic dominating set if every vertex in V − S lies on a shortest path between two vertices in S. The minimum cardinality of a geodetic dominating set of G is its geodetic domination number; introduced by Chartrand, Harary, and Zhang in 1999 [124]. See also Hansberg and Volkmann in [333] and Escuadro et al. in [237].
-
13.
global domination γ g(G), minimum cardinality of a set S such that S is a dominating set in G and S is also a dominating set in the complement \(\overline {G}\) of G; introduced by Sampathkumar in 1989 [553]. The reader is referred to a chapter on global domination by Brigham and Carrington in 1998 [79], and a paper by Rall [533].
-
14.
k-dependent domination γ [k](G), minimum cardinality of a dominating set S such that for every vertex u ∈ S, |N(u) ∩ S|≤ k, that is, each vertex in S has at most k neighbors in S; first defined by Favaron et al. in 2002 [254]; see also Fink and Jacobson [263] and Samodivkin [552]. Notice that if S is a 1-dependent dominating set then the induced subgraph G[S] is a disjoint union of isolated vertices and K 2s. Thus, for any graph G, γ(G) ≤ γ [1](G) ≤ i(G).
-
15.
paired domination γ pr(G), minimum cardinality of a dominating set S such that the induced subgraph G[S] has a perfect matching; introduced by Haynes and Slater in 1995 [358] and [359]. We refer the reader to Desormeaux and Henning’s [193] survey on paired domination. See also Henning [407] for several conjectures related to paired and other variants of domination.
-
16.
semipaired domination γ pr(G), minimum cardinality of a semipaired dominating set, that is, a dominating set S for which the vertices in S can be partitioned into |S|∕2 pairs {u, v} such that d(u, v) ≤ 2; introduced by Haynes and Henning in 2018 [376].
-
17.
semitotal domination γ t2(G), minimum cardinality of a semitotal dominating set, that is, a dominating set such that every vertex u ∈ S is within distance 2 of a second vertex in S; introduced by Goddard, Henning, and McPillan in 2014 [302], but also defined in part by Hedetniemi et al. [395] in 2008.
3.8.2 Conditions on V (G) − S
-
1.
α-domination γ α(G), for 0 < α < 1, minimum cardinality of a set S such that for every vertex v ∈ V − S, |N(v) ∩ S|∕|N[v]|≥ α; introduced by Dunbar et al. in 2000 [214]. See also Gagarin et al. [275].
-
2.
outer-connected domination \(\gamma _{\overline {c}}(G)\), minimum cardinality of dominating set S such that the induced subgraph G[V − S] is connected; cf. Akhbari et al. [5].
-
3.
b-disjunctive domination \(\gamma ^d_b(G)\), minimum cardinality of a set S having the property that for every vertex u ∈ V − S, either u is adjacent to a vertex in S or there exist b vertices in S such that u is at distance 2 from each of these b vertices; introduced by Goddard, Henning, and McPillan in 2014 [301]. See also Henning and Marcon [410].
-
4.
distance domination γ ≤k(G), minimum cardinality of a set S having the property that for every vertex u ∈ V − S there exists a vertex v ∈ S such that d(u, v) ≤ k; introduced by Slater in 1976 [585]. See Henning [403] for a comprehensive chapter of results on distance domination.
-
5.
upper distance-k domination Γ ≤k(G), maximum cardinality of a minimal distance-k dominating set in G, that is, a dominating set S such that every vertex u ∈ V − S is within distance k of at least one vertex in S. The reader is referred to a chapter on distance domination by Henning in [403].
-
6.
edge-cut domination \(\gamma ^{\prime }_{ct}(G)\). An edge dominating set F ⊆ E of a graph G = (V, E) is an edge cut dominating set if the subgraph G[E − F] is disconnected. The edge cut domination number \(\gamma ^{\prime }_{ct}(G)\) equals the minimum cardinality of an edge cut dominating set in G, cf. Fenstermacher et al. [258].
-
7.
step domination γ step(G). The k-neighborhood of a vertex v ∈ V is the set N =k(v) = {u ∈ V |d(u, v) = k}, of vertices whose distance from v is exactly k. A set S = {v 1, v 2, …, v k} is called a step dominating set if there exists a set of k nonnegative integers i 1, i 2, …, i k, such that \(\pi = \{N_{=i_1}(v_1), N_{=i_2}(v_2), \ldots , N_{=i_k}(v_k)\}\) is a partition of V (G). The step domination number γ step(G) equals the minimum cardinality of a step dominating set in G; introduced by Chartrand, Jacobson, Kubicka, and Kubicki in 1998 [120].
-
8.
exact 2-step domination γ =2(G). A set S ⊆ V is called an exact 2-step dominating set if for every vertex v ∈ V , there exists a unique u ∈ S, such that d(u, v) = 2. The exact 2-step domination number γ =2(G) equals the minimum cardinality of an exact 2-step dominating set in G; introduced by Chartrand, Harary, Hossain, and Schultz in 1995 [122]. See also Williams [639]. Note that exact 2-step dominating sets do not exist for all graphs.
-
9.
downhill domination γ dn(G), minimum cardinality of a downhill dominating set. A set S ⊆ V is a downhill dominating set if every vertex v ∈ V lies on some downhill path from a vertex in S. A path P = v 1, v 2, …, v k is a downhill path if for every 1 ≤ i ≤ k − 1, deg(v i) ≥ deg(v i+1); introduced by Haynes, Hedetniemi, Jamieson, and Jamieson in 2014 [373]. See also Chen and Fujita [145].
-
10.
edge domination γ′(G) and Γ′(G), minimum and maximum cardinalities of a minimal edge dominating set. The edge domination number and the independent edge domination number i′(G) were perhaps first discussed by Mitchell and Hedetniemi in 1977 [381], who showed that for trees T, γ′(T) = i′(T). It is clear that for any graph G, and its line graph L(G), γ′(G) = γ(L(G)). Since 1977, relatively little research has been done on the various types of edge domination in graphs. See, for example, Yannakakis and Gavril [642] and Chaemchen [105].
-
11.
edge-vertex domination γ ev(G), minimum cardinality of an ev-dominating set. A set M ⊆ E is an ev-dominating set if every vertex v ∈ V is either incident to an edge in M or is adjacent to a vertex that is incident to an edge in M. This was introduced by Laskar and Peters in 1985 [477] and developed by Peters in his PhD thesis in 1986 [522]. See also the PhD thesis of Lewis [483]. This is closely related to vertex-edge domination γ ve(G) defined below.
-
12.
exponential domination γ e(G), minimum cardinality of a set S having the property that for every vertex v ∈ V − S, w s(v) ≥ 1, where
\(w_s(v) = \sum _{u \in S} \frac {1}{2^{\overline {d}(u,v) -1}}.\)
and \(\overline {d}(u, v)\) equals the length of a shortest path in V − (S −{u}) if such a path exists, and ∞ otherwise; introduced by Dankelmann, Day, Erwin, Mukwembi, and Swart in 2009 [182].
-
13.
inverse domination γ −1(G), minimum cardinality of a dominating set S ∗ that is contained in the complement of a minimum dominating set of G; introduced by Kulli and Sigarkanti in 1991 [471]; cf. Domke et al. [200].
-
14.
fair domination fd(G). A fair dominating set in a graph (or FD-set) is a dominating set S such that all vertices not in S are dominated by the same number of vertices in S; that is, every two vertices not in S have the same number of neighbors in S. The fair domination number fd(G) is the minimum cardinality of an FD-set; introduced by Caro, Hansberg, and Henning in 2012 [102].
-
15.
k-domination γ k(G), minimum cardinality of a dominating set S having the property that for every vertex v ∈ V − S, |N(v) ∩ S|≥ k; introduced by Fink and Jacobson in 1985 [263]. See also DaLaVina et al.[190] and Chellali et al. [138].
-
16.
[1, k]-domination γ [1,k](G). A subset S ⊆ V is a [1, k]-(dominating) set if for every vertex v ∈ V − S, 1 ≤|N(v) ∩ S|≤ k; introduced by Chellali et al. in 2014 [140].
-
17.
liars domination. Liar’s domination is about the detection of intruders in a graph G. We assume that an intruder can be located at any vertex v ∈ V . Intruders are detected by devices placed at various vertices, say u ∈ V , which can detect the presence and location of an intruder at any vertex in N[u]. A dominating set S can therefore detect and locate any intruder in a graph G. Liar’s domination considers the case of a single intruder in a graph, when a single detection device in S can fail, or lie. In this case, at least a double dominating set is required, but any triple dominating set will suffice. The reader is referred to the PhD Thesis of Roden Bowie in 2008 [72] and the papers by Roden and Slater [546] and Slater [588].
-
18.
location domination γ L(G), minimum cardinality of a dominating set S having the property that for no two vertices v, w ∈ V − S is N(v) ∩ S = N(w) ∩ S; introduced by Slater in 1975 [584]. See also Rall and Slater [534], Slater [587] and Exoo et al. [238]. The reader is also referred to a bibliography maintained by A. Lobstein, of more than 370 papers concerned with locating domination and its variations at: https://www.lri.fr/~lobstein/debutBIBidetlocdom.pdf.
-
19.
mixed domination γ m(G), minimum cardinality of a set S of vertices and edges such that every edge not in S is either adjacent to an edge in S or incident to a vertex in S, and every vertex not in S is either adjacent to a vertex in S or incident to an edge in S; introduced by Alavi, Behzad, Lesniak-Foster, and Nordhaus in 1977 [9], and later called mixed domination by Sampathkumar and Kamath in 1992 [554]. See also Zhao et al. [658].
-
20.
P 3 -domination \(\gamma _{P_3}(G)\), minimum cardinality of P 3-dominating set. A set S is P 3 -dominating if every vertex v ∈ V − S forms a P 3 with two vertices in S. This can happen in one of two ways: either v is dominated by two vertices in S, or v is dominated by a vertex u ∈ S that is adjacent to another vertex w ∈ S. Introduced by Haynes, Hedetniemi, Henning, and Slater in 2003 [366], who showed that for any graph G, \(\gamma _{P_3}(G) \leq \{\gamma _t(G), \gamma _2(G) \}\), and that equality holds for any tree. This equality was later shown to hold for chordal graphs by Chellali and Favaron in [135].
-
21.
power domination γ P(G), minimum cardinality of power dominating set. A set S is a power dominating set if all vertices in V are observed by vertices in S. A vertex observes itself and all of its neighbors, and if an observed vertex has all but one of its neighbors observed, then the remaining neighbor becomes observed; introduced by Haynes, Hedetniemi, Hedetniemi, and Henning in 2002 [364]. See also Guo, Niedermeier, and Raible [317] and generalizations to k-power domination, in which a vertex is observed if all but k of its neighbors have been observed. This was introduced by Chang et al. [111] and studied later by Dorbec and Klavžar [202].
-
22.
restrained domination γ r(G), minimum cardinality of a dominating set S such that every vertex in V − S has a neighbor in V − S; introduced by Domke, Hattingh, Hedetniemi, Laskar, and Markus in 1999 [198]. See also Henning [404] and Domke et al. [199]. See outer-connected domination.
-
23.
secondary domination, γ 1,2(G) and γ 1,3(G), minimum cardinalities of a (1, 2) − and (1, 3)-dominating set, respectively. A set S is a (1, k)-dominating set if |S|≥ 2 and for every vertex v ∈ V − S there exists two vertices u 1, u 2 ∈ S such that d(v, u 1) = 1 and d(v, u 2) ≤ k. The following inequality chain exists for these parameters:
$$\displaystyle \begin{aligned}\gamma(G) = \gamma_{1,4}(G) \leq \gamma_{1,3}(G) \leq \gamma_{1,2}(G) \leq \gamma_{1,1}(G) = \gamma_2(G).\end{aligned}$$This was introduced by Hedetniemi, Hedetniemi, Knisely, and Rall in 2008 [395]; see also Jamieson and Jamieson [433].
-
24.
[1, 2]-domination γ [1,2](G), minimum cardinality of a dominating set such that no vertex in V − S has more than two neighbors in S; introduced by Chellali, Haynes, Hedetniemi, and McRae in 2013 [139].
-
25.
split domination γ splt(G), minimum cardinality of a split dominating set in G. A dominating set S of vertices is called split dominating if the induced subgraph G[V − S] is either disconnected or K 1; introduced by Kulli and Janakiram in 1997 [470].
-
26.
vertex-edge domination γ ve(G), minimum cardinality of a ve-dominating set. A set S ⊆ V is a ve-dominating set if for every edge e = uv ∈ E, either u ∈ S, v ∈ S or there exists a vertex w ∈ S such that either uw ∈ E or vw ∈ E. This concept was first suggested by Alavi, Behzad, Lesniak-Foster and Nordhaus in 1977 [9], but was clarified and developed by Peters in his PhD thesis in 1986 [522], by Laskar and Peters in [477], and later by Lewis in his PhD thesis in 2007 [483]. In Lewis et al. [484] the following inequality chain is established.
$$\displaystyle \begin{aligned}ir_{ve}(G) \leq \gamma_{ve}(G) \leq i_{ve}(G) \leq \alpha_{ve}(G) \leq \varGamma_{ve}(G) \leq IR_{ve}(G).\end{aligned}$$See also Boutrig et al. [69].
3.8.3 Conditions on (V (G), S)
-
1.
cost effective domination γ ce(G) and Γ ce(G), minimum and maximum cardinalities of a dominating set that is cost effective. A vertex v ∈ S in a graph G = (V, E) is said to be cost effective if it is adjacent to at least as many vertices in V − S as it is in S. A dominating set S is cost effective if every vertex in S is cost effective. This idea originates in a paper by Aharoni, Milner, and Prikry in 1990 [4], and was later given the name cost effective domination by Haynes, Hedetniemi, Hedetniemi, McCoy, and Vasylieva in 2012 [372]; see also Haynes et al. [375].
-
2.
very cost effective domination γ vce(G) and Γ vce(G), minimum and maximum cardinalities of a dominating set that is very cost effective. A vertex v ∈ S in a graph G = (V, E) is said to be very cost effective if it is adjacent to more vertices in V − S than it is in S. A dominating set S is very cost effective if every vertex in S is very cost effective; cf. Haynes et al. in 2012 [372] and [375].
-
3.
detour domination γ D(G). For a vertex v ∈ V , define D −(v) = min{D(u, v) : u ∈ V −{v}}, where D(u, v) equals the maximum length of a u − v path in G. A vertex u is called a detour neighbor of v if D(u, v) = D −(v). A vertex v is said to detour dominate a vertex u if u = v or u is a detour neighbor of v. A set S ⊂ V is called a detour dominating set if every vertex in V is detour dominated by some vertex in S. The detour domination number γ D(G) of G equals the minimum cardinality of a detour dominating set in G; introduced by Chartrand, Haynes, Henning and Zhang in 2004 [128].
-
4.
independent distance-k domination numbers i ≤k(G) and α ≤k(G), minimum and maximum cardinalities of a minimal independent distance-k dominating set in G; cf. Fricke, Hedetniemi, and Henning [270].
-
5.
total distance domination \(\gamma ^k_t(G)\). A set S of vertices is called a total distance-k dominating set if every vertex in V is within distance k of a vertex in S. The total distance-k domination number \(\gamma ^k_t(G)\) equals the minimum cardinality of a total distance-k dominating set; introducted by Henning, Oellermann, and Swart in 1995 [414].
-
6.
weakly connected domination γ w(G), minimum cardinality of a dominating set that is weakly connected. A set S is weakly connected if the graph with vertex set N[S] and all edges having at least one vertex in S is connected. This was introduced by Dunbar, Grossman, Hattingh, Hedetniemi, and McRae in 1995 [210]; see also Domke et al. [201] and Hattingh and Henning [352].
-
7.
secure domination γ s(G), minimum cardinality of a secure dominating set. A set S is a secure dominating set if for every vertex v ∈ V − S, there is an adjacent vertex u ∈ S such that the set S −{u}∪{v} is a dominating set; introduced by Cockayne, Favaron, and Mynhardt in 2003 [169]. See also Burger et al. [91].
-
8.
eternal domination γ ∞(G), minimum cardinality of an eternally secure set in G. A set S of vertices is an eternal dominating set or eternally secure set if for all possible sequences of vertices u 1, u 2, …, there exists a sequence of dominating sets S = S 1, S 2, … and a sequence v 1, v 2, … such that for all i, S i+1 = S i −{v i}∪{u i}, where v i ∈ S i ∩ N[u i]; introduced by Burger, Cockayne, Gründlingh, Mynhardt, van Vuuren, and Winterbach in 2004 [90], and further developed by Goddard, Hedetniemi and Hedetniemi in 2005 [297].
-
9.
Hamiltonian domination γ H(G). For vertices u, v ∈ V , let D(u, v) denote the length of a longest u − v path in G. For a vertex v, let D +(v) = max{D(u, v) : u ∈ V −{v}}. A vertex u is called a Hamiltonian neighbor of v if D(u, v) = D +(v). A vertex v is said to Hamiltonian dominate a vertex u if u = v or u is a Hamiltonian neighbor of v. A set S ⊆ V is called a Hamiltonian dominating set if every vertex in V is Hamiltonian dominated by some vertex in S. The Hamiltonian domination number γ H(G) equals the minimum cardinality of a Hamiltonian dominating set in G; introduced by Chartrand et al. [129].
-
10.
injective domination γ in(G). The common neighborhood of two vertices u and v is the set N(u, v) = N(u) ∩ N(v). A set S ⊆ V is called an injective dominating set if for every vertex v ∈ V − S there exists a vertex u ∈ S such that N(u, v) ≠ ∅. The injective domination number γ in(G) equals the minimum cardinality of an injective dominating set in G; introduced by Alqesmah, Alwardi, and Rangarajan in 2018 [14].
-
11.
k-tuple domination γ ×k(G), minimum cardinality of a dominating set S having the property that for every vertex v ∈ V , |N[v] ∩ S|≥ k; introduced by Harary and Haynes in 2000 [341].
-
12.
k-emergency response number R k(G), minimum cardinality of a k-emergency response set. A set S is a k-emergency response set if a set of responders stationed at the vertices in S can respond, by staying put or moving to a neighbor, to simultaneous emergencies at each vertex of any set A ⊆ V of size at most k; introduced by Blair et al. in 2009 [55].
-
13.
movable domination number \(\gamma _m^1(G)\). A 1-movable dominating set is a dominating set S ⊂ V (G), having the property that for every v ∈ S, there exists a vertex u ∈ N(v) such that S −{v}∪{u} is a dominating set, capturing the idea that every vertex v in the dominating set can be replaced by a neighbor in N(v) and create another dominating set. The cardinality of a smallest movable dominating set of G is the 1-movable domination number \(\gamma _m^1(G)\); introduced by Blair, Gera, and Horton in 2011 [56].
-
14.
odd domination γ odd(G), minimum cardinality of a dominating set having the property that for every vertex v ∈ V , |N[v] ∩ S| is an odd number. Odd domination and the fact that every graph G has an odd dominating set was introduced and proved by Sutner in 1989 [598]. See also Caro et al. [100] and Caro and Klostermeyer [98].
-
15.
partial domination γ p(G). Let p ∈ [0, 1]. A set S ⊆ V is a p-dominating set if \(\frac {|N[S]|}{|V|} \geq p\), that is, the set S dominates the fraction p of all vertices in G. The partial domination number γ p(G) equals the minimum cardinality of a p-dominating set in G; introduced by Case et al. [103].
-
16.
private domination Γ pvt(G), maximum cardinality of a dominating set, every vertex in which has an external private neighbor, that is, for every vertex v ∈ S there exists a vertex w ∈ V − S for which N(w) ∩ S = {v}; equivalently, the maximum cardinality of an open irredundant dominating set. Notice that by definition, for any graph G, Γ pvt(G) ≤{Γ(G), OIR(G)}; introduced by Hedetniemi, Hedetniemi, and Jacobs in 1990 [387]. See also Prasad et al. [524]. It should be noted that the minimum cardinality of a private dominating set of any isolate-free graph always equals the domination number γ(G).
-
17.
stratified domination. A graph F is called 2-stratified if its vertices are partitioned into two non-empty sets, colored red and blue, but rooted at a given blue vertex v. A graph G is said to be F-colored if it is two-colored red and blue and every blue vertex v belongs to a copy of F rooted at v. The F-domination number of G is the minimum number of red vertices in an F-coloring of G. It can be seen that if F = K 2 then F-domination is equal to normal domination in graphs. This concept was suggested by Rashidi in his PhD thesis in 1994 [536], and later developed by Chartrand et al. in 1995 [121], studied in Gera’s PhD thesis in 2005 [283], and by Haynes, Henning and Zhang in 2009 [370].
-
18.
strong domination γ s(G), minimum cardinality of a dominating set S having the property that for every vertex w ∈ V − S there exists a vertex v ∈ S such that v is adjacent to w and deg(v) ≥ deg(w), that is, every vertex w ∈ V − S is dominated by a vertex v ∈ S whose degree is greater than or equal to the degree of w; introduced by Sampathkumar and Pushpa Latha in 1996 [556].
-
19.
weak domination γ w(G), minimum cardinality of a dominating set S having the property that for every vertex w ∈ V − S there exists a vertex v ∈ S such that v is adjacent to w and deg(v) ≤ deg(w), that is, every vertex w ∈ V − S is dominated by a vertex v ∈ S whose degree is less than or equal to the degree of w; introduced by Sampathkumar and Pushpa Latha in 1996 [556].
3.9 Dominating Function Numbers
All of the parameters in this subsection consider vertex labelings of the form f : V → X where X is a finite set of integers, and the function satisfies the general condition that for every vertex v ∈ V , ∑u ∈ N[v] f(u) ≥ 1. Unless otherwise stated, the weight of a function f is Σ v ∈ V f(v).
-
1.
broadcast domination γ b(G) and Γ b(G), minimum and maximum weights, respectively, of a minimal function f : V →{0, 1, 2, …, diam(G)}, such that for every vertex v ∈ V , with f(v) = 0, there exists a vertex u ∈ V such that f(u) ≥ d(u, v). In this case, we say that vertex v hears a broadcast from vertex u, or in general, a vertex v hears a broadcast from a vertex u if f(u) ≥ d(u, v). Such a function is called a dominating broadcast.
$$\displaystyle \begin{aligned}\gamma_b(G) \leq min\{\gamma(G), rad(G)\} \leq max\{\varGamma(G), diam(G)\} \leq \varGamma_b(G).\end{aligned}$$This was introduced by Erwin in 2004 [236]. See Dunbar et al. [215], Bresar and Spacapan [75], and Dabney et al. [179].
Also defined in these papers are: p b(G) and P b(G), the broadcast packing numbers [in a packing broadcast no vertex in the set hears two or more broadcasts], the broadcast independence numbers i b(G) and α b(G) [in an independent broadcast no vertex with f(v) > 0 hears another broadcast], and Γ ib(G) and Γ eb(G), the maximum weights of a minimal independent and dominating broadcast [every vertex hears at least one broadcast] and an efficient dominating broadcast [every vertex hears exactly one broadcast]. It is noteworthy that a minimum weight dominating broadcast can always be achieved with an efficient broadcast, and consequently the problem of computing the broadcast domination number γ b(G) of any graph can be computed in polynomial time, cf. Heggernes and Lokshtanov [400].
-
2.
fractional domination γ f(G), minimum weight of a function f : V → [0, 1] such that for every vertex v ∈ V , ∑u ∈ N[v] f(u) ≥ 1; introduced by Hedetniemi, Hedetniemi, and Wimer in 1987 [384]. See also the PhD thesis by Rubalcaba in 2005 [548].
-
3.
{k}-domination γ {k}(G), minimum weight of a function f : V →{0, 1, 2, …, k} such that for every vertex v ∈ V , Σ u ∈ N[v] f(u) ≥ k; introduced by Domke et al. in 1991 [197]. See also Hou and Lu [424].
-
4.
majority domination γ maj(G), minimum weight of a function f : V →{−1, 0, 1} such that for at least half of the vertices v ∈ V , f(N[v]) ≥ 1; introduced by Broere, Hattingh, Henning, and McRae in 1995 [82]. See also a chapter on majority domination by Hattingh in 1998 [351], and papers by Yeh and Chang [644] and Holm [418].
-
5.
minus domination γ −(G), minimum weight of a function f : V →{−1, 0, 1} such that for every vertex v ∈ V , f(N[v]) ≥ 1; introduced by Dunbar, Hedetniemi, Henning, and McRae in 1999 [212]. See also Dunbar et al. [209] and [208] and Zelinka [655].
-
6.
k-rainbow domination γ rk(G), minimum weight of a function that assigns to each vertex a subset of colors chosen from the set {1, 2, …, k}, that is, \(f:V(G)\rightarrow \mathcal {P(}\{1,2, \ldots , k\})\), such that for every vertex v ∈ V with f(v) = ∅, ⋃u ∈ N(v) f(u) = {1, 2, …, k}. Such a function f is called a k-rainbow dominating function (kRDF) of G; introduced by Brešar and Kraner in 2007 [76] and in 2008 by Brešar, Henning and Rall in 2008 [77].
-
7.
signed domination γ ±(G), minimum weight of a function f : V →{−1, 1} such that for every vertex v ∈ V , f(N[v]) ≥ 1; introduced by Dunbar, Hedetniemi, Henning, and Slater in 1995 [207]. See also Haas and Wexler [323], Chen and Song [146] and Hosseini Moghaddam, Khodkar, and Samadi [508].
-
8.
Roman domination γ R(G), minimum weight of a function f : V →{0, 1, 2} such that every vertex u ∈ V , with f(u) = 0 is adjacent to a vertex v ∈ V with f(v) = 2; introduced by Cockayne, Dreyer, Hedetniemi, and Hedetniemi in 2004 [170]. Since its introduction in 2004, many varieties of Roman domination (RD) have appeared, too numerous to define all here. We define a few varieties below.
-
9.
weak Roman domination γ r(G), minimum weight of a function f : V →{0, 1, 2} such that every vertex u with f(u) = 0 is adjacent to a vertex v with f(v) > 0, and the function f′ obtained from f by setting f′(u) = 1, f′(v) = f(v) − 1, and f′(w) = f(w), for all w ∈ V −{u, v} has no vertex x with f′(x) = 0 and all neighbors y ∈ N(x) have f′(y) = 0; introduced by Henning and Hedetniemi in 2001 [408].
-
10.
Roman {2}-domination γ R2(G), minimum weight of a function f : V →{0, 1, 2} such that for every vertex v ∈ V with f(v) = 0, either v is adjacent to a vertex w with f(w) = 2 or v is adjacent to two vertices x, y with f(x) = f(y) = 1; introduced by Chellali, Haynes, Hedetniemi, and McRae in 2016 [141], but is called Italian domination in [409].
-
11.
double Roman domination γ dR(G), minimum weight of a function f : V (G) →{0, 1, 2, 3} satisfying the following conditions. For i ∈{0, 1, 2, 3}, let V i = {v ∈ V (G)|f(v) = i}. (1) if f(v) = 0, then vertex v must have at least two neighbors in V 2 or one neighbor in V 3. (2) if f(v) = 1, then v must have at least one neighbor in V 2 ∪ V 3; introduced by Beeler, Haynes, and Hedetniemi in 2016 [38].
-
12.
Roman k-domination γ kR(G), minimum weight of a function f : V →{0, 1, 2} such that every vertex v for which f(v) = 0 is adjacent to at least k vertices v 1, v 2, …, v k, where f(v i) = 2 for 1 ≤ i ≤ k; defined by Hansberg and Volkmann in 2009 [332].
-
13.
independent Roman domination i R(G), minimum weight of a Roman dominating function f for which the set of vertices assigned positive values under f is independent; defined by Cockayne, Dreyer, Hedetniemi and Hedetniemi in 2004 [170].
-
14.
edge Roman domination \(\gamma ^{\prime }_R(G)\), minimum weight of a function f : E(G) →{0, 1, 2} such that every edge e with f(e) = 0 is adjacent to some edge e′ with f(e′) = 2; introduced by Pushpam and Mai in 2009 [528]. See also Chang et al. [112].
-
15.
signed Roman domination γ sR(G), minimum weight of a function f : V →{−1, 1, 2} such that for every vertex v ∈ V , (1) f(N[v]) ≥ 1, and (2) if f(v) = −1 then v must have a neighbor w with f(w) = 2; introduced by Ahangar, Henning, Löwenstein, Zhao, and Samodivkin in 2014 [2]. See also Haas and Wexler [323], Chen and Song [146] and Hosseini Maghaddam et al. [508].
-
16.
total Roman domination γ tR(G), minimum weight of a Roman dominating function with the additional property that the subgraph of G induced by the set of all vertices assigned positive values under f has no isolated vertices; introduced by Liu and Chang in 2013 [488]. See also Ahangar, Henning, Samodivkin, and Yero in 2016 [3].
3.10 Domatic Numbers
In its most general form, a domatic number is the maximum order k of a vertex partition π = {V 1, V 2, …, V k}, such that each set V i is a given type of dominating set. Thus, there are as many types of domatic numbers as there are types of dominating sets. In this subsection, we define only nine of the many types of domatic numbers that have been studied. For more on domatic numbers, see the chapter by Zelinka in [654].
-
1.
domatic number d(G), maximum order of a partition of V (G) into dominating sets; introduced by Cockayne and Hedetniemi in 1975 [161].
-
2.
total domatic number d t(G), maximum order of a partition of V (G) into total dominating sets; introduced by Zelinka in 1989 [653].
-
3.
connected domatic number d c(G), maximum order of a partition of V (G) into connected dominating sets; introduced by Zelinka in 1986 [652].
-
4.
paired domatic number d pr(G), maximum order of a partition of V (G) into paired dominating sets; introduced by Haynes and Slater in 1995 [358].
-
5.
k-domatic number d k(G), maximum order of a partition of V (G) into distance-k dominating sets; introduced by Zelinka in 1983 [651].
-
6.
edge-domatic number ed(G), maximum order of a partition of E(G) into edge dominating sets; introduced by Zelinka in 1983 [650]. The edge-domatic number of G is the domatic number of the line graph of G.
-
7.
signed domatic number d S(G), maximum number of functions in a signed dominating family (of functions) of G; introduced by Volkmann and Zelinka in 2005 [629]. A set {f 1, f 2, …, f d} of signed dominating functions on G with the property that \(\displaystyle \sum _{i=1}^d f_i(v) \le 1\) for each v ∈ V (G) is called a signed dominating family (of functions) on G.
-
8.
Roman domatic number d R(G), maximum number of functions in a Roman dominating family (of functions) of G; introduced by Sheikholeslami and Volkmann in 2010 [578]. A set {f 1, f 2, …, f d} of Roman dominating functions on G with the property that \(\displaystyle \sum _{i=1}^d f_i(v) \le 2\) for each v ∈ V (G) is called a Roman dominating family (of functions) on G.
-
9.
fractional domatic number FD(G). A thoroughly distributed dominating family \({\mathcal {F}}_{\mathrm {dom}}\) of a graph G is a family of (not necessarily distinct) dominating sets of G. Let \(d_{\mathcal {F}}\) denote the maximum times any vertex of G appears in \({\mathcal {F}}_{\mathrm {dom}}\), and define the effective ratio of the family \({\mathcal {F}}_{\mathrm {dom}}\) as the ratio of the number of sets in \({\mathcal {F}}_{\mathrm {dom}}\) to \(d_{\mathcal {F}}\). The fractional domatic number FD(G) is defined as the supremum of the effective ratio taken over all thoroughly distributed dominating families. That is,
$$\displaystyle \begin{aligned} FD(G) = \sup_{{\mathcal{F}}_{\mathrm{dom}}} \, \frac{ |{\mathcal{F}}_{\mathrm{dom}}| }{ d_{\mathcal{F}} }. \end{aligned}$$The fractional domatic number was introduced in 1990 by Rall [532].
The fractional total domatic number is defined analogously. The fractional total domatic number was introduced by Goddard and Henning [295], and studied further, for example, by Abbas et al. [1] and Henning and Yeo [412].
3.11 Domination and Coloring Related Numbers
In this subsection we list a variety of parameters having some relationships with coloring or domination in graphs.
-
1.
annihilation number a(G), maximum integer k such that the sum of the first k terms of the non-decreasing degree sequence of G is at most the size m = |E| of G. This was introduced and studied by Pepper in 2009 [521]. Desormeaux, Haynes, and Henning in 2013 [194] showed that for the total domination number of any tree T, γ t(T) ≤ a(T) + 1; Dehgardi, Norouzian, and Sheikholeslami in 2013 [187] showed that for the domination number, γ(T) ≤ (3a(T) + 2)∕4; Dehgardi, Sheikholeslami and Khodkar in 2014 [188], showed that for the paired domination number, \(\gamma _{pr}(T) \leq \frac {4a(T)+2}{3}\); Desormeaux, Henning, Rall and Yeo in 2014 [195] showed that for the 2-domination number of trees T, γ 2(T) ≤ a(T) + 1; and Amjadi in 2015 [16], showed that for the double domination number, \(\gamma _{\times 2}(T) \leq \frac {3a(T)+1}{2}\).
-
2.
acquisition number a(G). To a connected graph G, assign the value 1 to all vertices, that is, let f(v) = 1 for all v ∈ V . An acquisition is the process of selecting two adjacent vertices u and v where f(u) ≥ f(v) > 0, and redefining f(u) = f(u) + f(v) and f(v) = 0. This process continues until no more acquisitions are possible. The acquisition number a(G) is the minimum possible number of vertices having a nonzero value at the end of an acquisition sequence. Note that if S is the set of vertices having nonzero value at the end of an acquisition sequences, then S is an independent set. This parameter was introduced in 1995 by Lampert and Slater [476] and further studied by Slater and Wang [589].
-
3.
R-annihilated number ra(G). For a vertex u ∈ S, whose set of private neighbors pn[u, S] with respect to S is nonempty, a vertex v ∈ V − S is said to annihilate u if v is adjacent to every vertex in pn[u, S]. This means that u has a private neighbor with respect to the set S but does not have a private neighbor with respect to the set S ∪{v}. Let R = V − N[S] denote the subset of V not dominated by S. Then S is said to be R-annihilated, or an Ra-set, if every vertex in R annihilates some vertex in S. This is the property satisfied by every maximal irredundant set. The minimum cardinality of an Ra-set is denoted by ra(G); introduced by Cockayne, Favaron, Puech and Mynhardt in 1998 [167], and further studied by Puech in 2000 [525].
-
4.
bondage number b(G), minimum number of edges that can be deleted from G in order to increase the domination number. This parameter was introduced by Fink, Jacobson, Kinch, and Roberts in 1990 [265], and further studied by Hartnell and Rall in 1994 [350], and Wang in 1996 [636].
-
5.
cost effective numbers ce(G) and CE(G), minimum and maximum cardinalities of a maximal cost effective set. A set S is cost effective if for every vertex u ∈ S, |N(u) ∩ (V − S)|≥|N(u) ∩ S|, introduced by Chellali, Haynes, and Hedetniemi in 2017 [142].
-
6.
very cost effective numbers vce(G) and V CE(G), minimum and maximum cardinalities of a maximal very cost effective set. A set S is very cost effective if for every vertex u ∈ S, |N(u) ∩ (V − S)| > |N(u) ∩ S|; introduced by Chellali et al. in 2017 [142].
-
7.
differential number ∂(G), maximum value of |B(S)|−|S|, for a set S ⊆ V , where B(S) = N[S] − S. Note that for any isolate-free graph G,
$$\displaystyle \begin{aligned}n - 2\gamma(G) \leq \partial(G) \leq n - \gamma(G) -1 = \varPsi(G) - 1.\end{aligned}$$This was introduced by Mashburn, Haynes, Hedetniemi, Hedetniemi, and Slater in 2006 [499]; see also Haynes et al. [374].
-
8.
domination equivalence numbers de(G) and DE(G), minimum and maximum number of vertices in a domination equivalent pair. A set S of vertices has a domination equivalent if there exists a set R ⊆ V − S such that N[S] = N[R]. Similarly, one can define the open domination equivalence numbers, ode(G) and ODE(G), in terms of two disjoint sets S and R such that N(S) = N(R). Note that it is easy to see that for any graph G of order n, de(G) ≤ γ(G), and DE(G) = n − γ(G); introduced by Blair, Goddard, Hedetniemi, Hedetniemi, and Horton in 2005 [53].
-
9.
domination subdivision number sd γ(G), minimum number of edges which when subdivided once increase the domination number. This concept is due to Arumugam, but was first defined and studied by Haynes, Hedetniemi and Hedetniemi in 2000 [362]. See also Haynes et al. in 2001 [363] where it is shown that for any connected graph of order n ≥ 3, sd γ(G) ≤ γ(G) + 1.
A large number of variants of the domination subdivision number have been studied since this parameter was introduced, including connected domination, double domination, independent domination, convex domination, weakly convex domination, rainbow domination, game total domination, restrained domination, doubly connected, and Roman domination subdivision numbers, which are too numerous to discuss here. We mention only the following two variants.
-
10.
total domination subdivision number \(sd_{\gamma _t}(G)\), minimum number of edges which when subdivided once increase the total domination number; introduced by Haynes, Hedetniemi, and van der Merwe in 2003 [367]. See also Haynes et al. [368].
-
11.
paired domination subdivision number \(sd_{\gamma _{pr}}(G)\), minimum number of edges which when subdivided once increase the paired domination number; introduced by Favaron, Karami, and Sheikholeslami in 2009 [256].
-
12.
efficiency of a graph ε(G). The efficiency of a set S ⊆ V is defined as ε(S) = |{v ∈ V − S : |N(v) ∩ S| = 1}|, that is, the efficiency of a set S equals the number of vertices in V − S that are adjacent to exactly one vertex in S. The efficiency of a graph ε(G) equals the maximum efficiency of a set S ⊆ V , that is, the maximum number of vertices that can be dominated exactly once by a set S; introduced by Bernhard, Hedetniemi, and Jacobs in 1993 [47]. See also Blair [52], Telle and Proskurowski [603] and Hedetniemi et al. [396].
-
13.
hub number hub(G). A vertex set S having the property that for every u, v ∈ V − S, there exists a u − v path, every internal vertex of which belongs to S is called a hub set. The hub number of a graph G equals the minimum cardinality of a hub set in G; introduced as the hub number by Walsh in 2006 [634], and later studied by Grauman et al. [311], who showed that
$$\displaystyle \begin{aligned}h(G) \leq h_c(G) \leq \gamma_c(G) \leq h(G) + 1,\end{aligned}$$where h c(G), the connected hub number, equals the minimum cardinality of a hub set S for which the induced subgraph G[S] is connected, and γ c(G) equals the connected domination number of G.
However, the original idea seems to be due to Newman-Wolfe, Dutton, and Brigham in 1988 [514], who gave the following definitions. A subset S is a strong connecting set (SCS) if every pair of vertices not in S has a connecting path through S. Similarly, S is a weak connecting set (WCS) if every pair of nonadjacent vertices not in S has a connecting path through S. The minimum cardinality of an SCS (resp. WCS) equals the strong connection number γ s(G) (resp.weak connection number γ w(G)). They show that for any connected graph G,
$$\displaystyle \begin{aligned}\gamma_w(G) \leq \gamma_s(G) \leq \gamma_c(G)_ \leq \gamma_w(G) + 1.\end{aligned}$$See also Johnson, Slater, and Walsh [436].
-
14.
iterated independence numbers i ∗(G) and α ∗(G), minimum and maximum number of iterations possible in a process of iteratively removing from G a maximal independent set. It can be seen that i ∗(G) = χ(G) and α ∗(G) = Γr(G), the Grundy number of G.
-
15.
iterated domination numbers γ ∗(G) and Γ ∗(G), minimum and maximum number of iterations possible in a process of iteratively removing from G a minimal dominating set.
-
16.
iterated irredundance numbers ir ∗(G) and IR ∗(G), minimum and maximum number of iterations possible in a process of iteratively removing from G a maximal irredundant set.
All of these iterated numbers were introduced by Hedetniemi, Hedetniemi, McRae, Parks, and Telle in 2004 [392], who observed that for any graph G,
$$\displaystyle \begin{aligned}ir^*(G) \leq \gamma^*(G) \leq i^*(G) = \chi(G) \leq \alpha^*(G) \leq \varGamma^*(G) \leq IR^*(G).\end{aligned}$$It remains an open problem to show, without appealing to the Four Color Theorem, that for any planar graph G, ir ∗(G) ≤ 4 and γ ∗(G) ≤ 4.
-
17.
neighborhood numbers n(G) and N(G), minimum and maximum cardinalities of a minimal neighborhood set, that is, a set S such that ⋃u ∈ S G[N[u]] = G; introduced by Sampathkumar and Neeralagi in 1986 [557]. See also Brigham and Dutton [80] and Chang et al. [109].
-
18.
reinforcement number r(G), minimum number of edges that have to be added to G so that in the resulting graph G′, γ(G′) < γ(G); introduced by Kok and Mynhardt in 1990 [459]. See also Blair et al. [54].
3.12 Alliance Numbers
The concepts related to an alliance in a graph G were introduced by Kristiansen, Hedetniemi, and Hedetniemi in 2004 [391]. Since then more than 100 papers have been written about these types of sets of vertices in a graph. The reader is referred to a recent, extensive survey on alliances in graphs by González Yero and Ridríguez-Velázquez [646].
-
1.
defensive alliance number a(G), minimum cardinality of a set S having the property that for every vertex u ∈ S, |N[u] ∩ S|≥|N(u) ∩ (V − S)|; introduced by Kristiansen, Hedetniemi, and Hedetniemi in 2004 [391]. See also Fricke et al. [272] and Sigarreta and Rodriguez [580].
-
2.
offensive alliance number a 0(G), minimum cardinality of a set S having the property that for every vertex v ∈ (V − S) ∩ N(S), |N(v) ∩ S|≥|N[v] ∩ (V − S)|; introduced by Kristiansen et al. [391]. See also Chellali [134] and Rodriguez and Sigarreta [547].
-
3.
powerful alliance number a p(G), minimum cardinality of a set S that is both a defensive alliance and an offensive alliance; introduced by Brigham, Dutton, Haynes, and Hedetniemi in 2009 [81].
-
4.
global defensive alliance number γ a(G), minimum cardinality of a defensive alliance S that is also a dominating set, that is, every vertex v ∈ V − S is adjacent to at least one vertex in the defensive alliance S; introduced by Haynes, Hedetniemi, and Henning in 2003 [365]. See also Favaron in [250] and Bouzefrane, Chellali, and Haynes in [71].
-
5.
global offensive alliance number \(\gamma _{a_o}(G)\), minimum cardinality of an offensive alliance that is also a dominating set, that is, every vertex v ∈ V − S is adjacent to at least one vertex in the offensive alliance S; introduced by Sigarreta and Rodriguez in 2009 [581] and Bouzefrane and Chellali [70]. See also Chellali and Volkmann [137].
-
6.
global powerful alliance number \(\gamma _{a_p}(G)\), minimum cardinality of a powerful alliance that is also a dominating set, that is, every vertex v ∈ V − S is adjacent to at least one vertex in the powerful alliance S.
-
7.
defensive alliance partition number ψ a(G), maximum order k of a partition π = {V 1, V 2, …, V k}, such that each set V i is a defensive alliance. This idea seems to have originated in a paper by Gerber and Kobler in 2000 [288], was studied by Shafique and Dutton in 2002 [570], and further studied by Haynes and Lachniet in [357], and Eroh and Gera in [234, 235].
-
8.
distribution center number dc(G), minimum cardinality of a distribution center of a graph G. A non-empty set of vertices S ⊆ V is a distribution center if every vertex v ∈ (V − S) ∩ N(S) is adjacent to a vertex u ∈ S with |N[u] ∩ S|≥|N[v] ∩ (V ∖ S)|; introduced by Desormeaux et al in 2018 [196].
3.13 Irredundance Numbers
The concept of an irredundant set in a graph is a natural consequence of the property of being a minimal dominating set. If S is a minimal dominating set, then for every vertex v ∈ S, the subset S −{v} is no longer a dominating set. This means that every vertex v ∈ S must either (i) dominate some vertex in V − S that no vertex in S −{v} dominates, or (ii) no vertex in S −{v} dominates v. Any set S in which every vertex v satisfies condition (i) or (ii) is an irredundant set; note that the set S itself need not be a dominating set. From this one observation, all of the types of irredundant sets defined in this subsection naturally arise. A very comprehensive and in-depth study of the concept of irredundance in graphs can be found in the Ph.D. thesis of Finbow [262].
-
1.
irredundance numbers ir(G) and IR(G), minimum and maximum cardinalities of a maximal irredundant set. A set S is an irredundant set if for every vertex v ∈ S, pn[v] = N[v] − N[S −{v}] ≠ ∅. The set pn[v] is called the set of private neighbors of v with respect to the set S. If v ∈ pn[v], then v is not adjacent to any vertex in S −{v} and v is said to be its own private neighbor. Every vertex w ∈ V − S for which w ∈ pn[v] is called an external private neighbor of v. It is worth noting that every minimal dominating set is an irredundant set. Irredundant sets were first defined and studied by Cockayne, Hedetniemi and Miller in 1978 [162]. See also early survey paper by Hedetniemi et al. [383], and a comprehensive paper showing the full generality of irredundance in graphs by Cockayne and Finbow [160]. In [386], Hedetniemi, Jacobs and Laskar show that IR(G) = p′(G) ≤ r(N(G)), where p′(G) equals the maximum integer k such that the closed neighborhood matrix contains a k × k permutation submatrix, and r(N(G)) equals the rank of the neighborhood matrix.
-
2.
open irredundance oir(G) and OIR(G), minimum and maximum cardinalities of a maximal open irredundant set in G. A set S is open irredundant if every vertex u ∈ S has an external private neighbor; first studied by Farley and Schacham in 1983 [245]; see also Farley and Proskurowski [244], Cockayne et al. [171], and Cockayne [159].
-
3.
open irredundance ooir(G) and OOIR(G), minimum and maximum cardinalities of a maximal open irredundant set in G. A set S is open irredundant if every vertex u ∈ S has an external or internal private neighbor. An internal private neighbor of a vertex u ∈ S is a vertex v ∈ S whose only neighbor in S is u; introduced by Cockayne, Finbow, and Swarts in 2010 [172]. In [386] Hedetniemi, Jacobs and Laskar show that OOIR(G) = p(G) ≤ r(G), where p(G) equals the maximum integer k such that the adjacency matrix contains a k × k permutation submatrix and r(G) denotes the rank of G, i.e. dimension of the row space of the adjacency matrix A(G) of G.
-
4.
closed open irredundance coir(G) and COIR(G), minimum and maximum cardinalities of a maximal closed open irredundant set in G. A set S is closed open irredundant if every vertex u ∈ S has either itself as a private neighbor, an external private neighbor or an internal private neighbor.
-
5.
total irredundance ir t(G) and IR t(G), minimum and maximum cardinalities of a maximal total irredundant set. A set S is a total irredundant if and only if for every vertex v ∈ V , N[v] − N[S −{v}] ≠ ∅; introduced by Favaron, Haynes, Hedetniemi, Henning, and Knisley in 2002 [253]. See also Hedetniemi, Hedetniemi, and Jacobs [388].
-
6.
co-irredundance, cir(G) and CIR(G), the minimum and maximum cardinalities of a minimal co-irredundant set. A set S is a co-irredundant set if and only if the complement V − S is an irredundant set; introduced by Arumugam, Hedetniemi, Hedetniemi, Sathikala, and Sudha in 2015 [26], who showed the following:
$$\displaystyle \begin{aligned}ir(G) \leq \gamma(G) \leq cir(G) \leq \psi(G) \leq \beta(G) \leq \beta^+(G) \leq \varPsi(G) \leq CIR(G).\end{aligned}$$$$\displaystyle \begin{aligned}CIR(G) \geq \varPsi(G) \geq IR(G) \geq \varGamma(G) \geq \alpha(G) \geq i(G) \geq \gamma(G) \geq ir(G).\end{aligned}$$ -
7.
external redundance er(G) and ER(G), minimum and maximum cardinalities of a minimal external redundant set. A set S is external redundant if for all vertices v ∈ V − S, there exists a vertex w ∈ S ∪{v} such that pn[w, S ∪{v}] = ∅, and if w ∈ S then pn[w, S] ≠ ∅. An equivalent definition of external redundance is the following. For any set S of vertices, define the private neighbor count pnc(S) to equal the number of vertices in S that have a private neighbor. A set S is pnc-maximal if for every vertex v ∈ V − S, pnc(S ∪{v}) ≤ pnc(S). It can be seen that er(G) and ER(G) equal the minimum and maximum cardinalities of a pnc-maximal set in G. Note that:
$$\displaystyle \begin{aligned}er(G) \leq ir(G) \leq \gamma(G) \leq i(G) \leq \alpha(G) \leq \varGamma(G) \leq IR(G) \leq ER(G).\end{aligned}$$External redundance was introduced by Cockayne, Hattingh, Hedetniemi, Hedetniemi, and McRae in 1997 [166]; see also Goddard and Hedetniemi [294].
Arumugam et al. [26] have combined many of the domination and irredundance parameters into the following inequalities and equalities, which they have called the Extended Domination Chain, and the Extended Covering Chain, respectively.
$$\displaystyle \begin{aligned} \begin{array}{cccccccc} ir(G)&\leq\gamma(G)&\leq i(G)&\leq\alpha(G)&\leq\varGamma(G)&\leq IR(G)&\leq\varPsi(G)&\leq\ CIR(G) \\ + & + & + & + & + & + & + & + \\ CIR(G)& \geq \varPsi(G) & \geq \varLambda(G) & \geq \beta(G) & \geq \psi(G) & \geq \ cir(G) & \geq \gamma(G) & \geq ir(G) \\ = & = & = & = & = & = & = & = \\ n & n & n & n & n & n & n & n \\ \end{array} \end{aligned}$$They also added the following interesting comparison of two inequality chains:
$$\displaystyle \begin{aligned} \begin{array}{cccccc} \gamma(G) & \leq \ i(G) & \leq \alpha(G) & \leq \varGamma(G) & \leq \ IR(G) & \leq \varPsi(G) \\ \gamma(G) & \leq \ cir(G) & \leq \psi(G) & \leq \beta(G) & \leq \varLambda(G) & \leq \varPsi(G) \\ \end{array} \end{aligned}$$
3.14 Perfect, Nearly Perfect, and Almost Perfect Numbers
A vertex v in a set S ⊆ V is called S-perfect if |N[v] ∩ S| = 1, that is, the closed neighborhood N[v] contains exactly one vertex in S.
A vertex v in a set S ⊆ V is called almost S-perfect if it is either S-perfect or is adjacent to an S-perfect vertex.
When we say more simply that a vertex is perfect or almost perfect it is always with reference to some given set S.
-
1.
perfect set numbers θ p(G) and Θ p(G). A set S ⊆ V is perfect if every vertex v ∈ S is perfect. It is easy to show that a set S is perfect if and only if it is independent. Thus, the minimum cardinality of a maximally perfect set θ p(G) = i(G), the independent domination number i(G), while the maximum cardinality of a perfect set Θ p(G) = α(G), the vertex independence number.
-
2.
semi-perfect code, perfect domination,or externally perfect sets γ p(G) and Γ p(G), minimum and maximum cardinalities of a perfect dominating set. A (dominating) set S is perfect if every vertex v ∈ V − S is adjacent to exactly one vertex in S. Note that for the 2 × 3 grid graph
 , γ
p(G) = 2 while Γ
p(G) = 3; introduced by Fellows and Hoover in 1991 [257]. See also Cockayne et al. [165], Chang et al. [110] and Yen and Lee [645].
, γ
p(G) = 2 while Γ
p(G) = 3; introduced by Fellows and Hoover in 1991 [257]. See also Cockayne et al. [165], Chang et al. [110] and Yen and Lee [645]. -
3.
almost perfect set numbers θ ap(G) and Θ ap(G). A set S is almost perfect if every vertex v ∈ S is almost perfect; for brevity, we say that an almost perfect set is an ap set. The minimum cardinality of a maximal ap set is θ ap(G), and the maximum cardinality of an ap set is Θ ap(G); introduced by Hedetniemi, Hedetniemi, and Hedetniemi in 2004 [397], where it is shown that for any graph G, θ ap(G) = ir(G) and Θ ap(G) = IR(G).
-
4.
externally almost perfect set numbers θ eap(G) and Θ eap(G), minimum and maximum cardinalities of a minimal eap set in G. A set S is externally almost perfect if every vertex u ∈ V − S is either perfect or adjacent to a perfect vertex; for brevity, we say that an externally almost perfect set is an eap set; cf. [397].
-
5.
completely almost perfect set numbers or perfect neighborhood numbers θ(G) and Θ(G). A set S is completely almost perfect if every vertex v ∈ V is either perfect or is adjacent to a perfect vertex. Completely almost perfect sets are called perfect neighborhood sets in the literature. Let θ(G) and Θ(G) equal the minimum and maximum cardinalities of a perfect neighborhood set in G. This concept was introduced by Fricke, Haynes, Hedetniemi, Hedetniemi, and Henning in 1999 [271], who showed that for any graph G, Θ(G) = Γ(G); see also Cockayne et al. [168], Favaron and Puech [252], Fricke et al. [271] and Hedetniemi et al. [389].
-
6.
perfect codes, efficient domination, completely perfect sets or perfect total domination γ P(G), minimum cardinality of a set S ⊆ V having the property that for every vertex v ∈ V , |S ∩ N[v]| = 1. Equivalently, a perfect code consists of a set S = {v 1, v 2, …, v k}⊆ V having the property that V = {N[v 1], N[v 2], …, N[v k]} is a partition of V (G). It is important to point out that not every graph has a perfect code or efficient dominating set, for example, the cycle C 5; introduced by Biggs in 1973 [51]. See also the survey of varieties of perfect codes by Klostermeyer [457].
-
7.
nearly perfect numbers n p(G) and N p(G). A set S is perfect if every vertex in V − S is adjacent to exactly one vertex in S. A set S of vertices is nearly perfect if every vertex in V − S is adjacent to at most one vertex in S. Nearly perfect sets are closely related to 2-packings of graphs, strongly stable sets, dominating sets and efficient dominating sets. A nearly perfect set S is 1-minimal if for every vertex u ∈ S, the set S −{u} is not nearly perfect. Similarly, a nearly perfect set S is 1-maximal if for every vertex u ∈ V − S, S ∪{u} is not nearly perfect. Let n p(G) equal the minimum cardinality of a 1-maximal nearly perfect set, and N p(G) equal the maximum cardinality of a 1-minimal nearly perfect set; introduced by Dunbar et al. in 1995 [206]. See also Kwaśnik and Perl [472].
3.15 Broadcast Numbers
-
1.
broadcast time bt(G), minimum time for a vertex in G to complete a broadcast to every other vertex in V , by a series of phone calls, subject to (1) each call involves only two vertices, (2) each call requires one unit of time, (3) a vertex can participate in only one call per unit of time, and (4) a vertex can only call a vertex to which it is adjacent. Broadcasting can also be described in terms of matchings, as follows: Given V 0 ⊆ V , we seek to broadcast to all vertices from V 0 by a broadcast sequence V 0, E 1, V 1, E 2, V 2, …E k, V k = V , where E i is a matching (not necessarily a perfect matching) between V i−1 and V i and V i = V i−1 ∪{v : uv ∈ E i, u ∈ V i−1}. The broadcast time bt(G) equals the minimum k for which there is a broadcast sequence in G from some vertex V 0 = {v}; among the first to introduce this were Baker and Shostak in 1972 [30]. There are many different and diverse models of broadcasting in graphs, too numerous to define here, quite a few of which are discussed in the 1988 survey by Hedetniemi et al. [385] and the 1995 survey by Hromkovic et al. [425].
-
2.
gossip time gt(G). In broadcasting, one vertex in a graph G has an item of information and needs to communicate it to every other vertex. In gossiping, every vertex in V has an item of information and needs to communicate it to every other vertex. Thus, broadcasting is a one-to-all process, while gossiping is an all-to-all process. The gossip time is the minimum time for all vertices in a graph to complete a gossip; introduced by Tijdeman in 1971 [611].
-
3.
polling time pt(G), minimum time for a vertex in G to poll all of the vertices in a graph, subject to (1) each call involves only two vertices, (2) each call requires one unit of time, (3) a vertex can participate in only one call per unit of time, and (4) a vertex can only call a vertex to which it is adjacent. Polling is the process of completing a broadcast to all vertices and then receiving a response from all vertices. This was introduced by Cheston and Hedetniemi in 1984 [150].
3.16 Pebbling Numbers
Let G = (V, E) be a graph. Let \(f: V \rightarrow \mathcal {N}\) be a pebbling function that assigns to each vertex v ∈ V a nonnegative integer \(f(v) \in \mathcal {N}\). We say that v has been assigned f(v) pebbles and that f is a pebbling configuration. Let w(f) =∑v ∈ V f(v) equal the total number of pebbles assigned by the function f. A pebbling move consists of removing two pebbles from a vertex u ∈ V and then adding one pebble to an adjacent vertex v ∈ N(u). A pebbling configuration f is said to be solvable if for every vertex v ∈ V , there exists a sequence (possibly empty) of pebbling moves that results in a pebble on v.
The concept of pebbling was introduced in 1989 by Chung [155], where she proved that the pebbling number of the n-cube equals 2n. As with many graph theory parameters, since the introduction of pebbling by Chung, many different variations of pebbling have been studied; the reader is referred to a general discussion of these by Hurlbert [429]. In this subsection we review only a few of the many variants of pebbling.
-
1.
pebbling number π(G), minimum number k such that every pebbling configuration \(f: V \rightarrow \mathcal {N}\) with w(f) = k is solvable. Thus, the central focus of graph pebbling is to determine a minimum number of pebbles so that no matter how they are placed on the vertices of a graph G, there will always be a sequence of pebbling moves that can move at least one pebble to any specified vertex of G. Consider a path P n of order n ≥ 1. It is easy to see that if all pebbles are initially placed on one of the two endvertices of P n, then 2n−1 pebbles will be required. Thus, pebbling numbers can be exponential in the order n of a graph G.
-
2.
optimal pebbling number π ∗(G). In 1995, Pachtor et al. [520] defined the optimal pebbling number π ∗(G) to be the minimum weight of a solvable pebbling configuration of G.
-
3.
cover pebbling number π c(G). In cover pebbling the goal is to eventually place pebbles on all vertices of the graph simultaneously. If that can be achieved starting with some particular initial configuration of pebbles, the configuration is called solvable. The cover pebbling number π c(G) is the minimum integer k such that every configuration containing k pebbles is solvable; cf. Sjöstrand [582] and Crull et al. [175].
-
4.
domination cover pebbling number ψ(G). In domination cover pebbling the goal is to eventually place at least one pebble on all the vertices of a dominating set of G. If that can be achieved starting with some particular initial configuration of pebbles, the configuration is called solvable. The domination cover pebbling number ψ(G) is the minimum integer k such that every configuration containing k pebbles is solvable; cf. Gardner et al. [280].
-
5.
t-pebbling number π t(G), minimum weight such that every pebbling configuration weight π t(G) is t-fold solvable. A pebbling configuration f is said to be t-fold solvable if for every vertex v ∈ V , there exists a sequence (possibly empty) of pebbling moves that results in t pebbles on v; cf. Lourdusamy and Somasundaram [489].
-
6.
optimal t-pebbling number \(\pi _t^*(G)\), minimum weight of a t-fold solvable pebbling configuration of G: see Herscovici et al. [415].
-
7.
t-restricted optimal pebbling number \(\pi ^*_t(G)\). A pebbling configuration f is a t-restricted pebbling configuration (abbreviated tRPC) if f(v) ≤ t for all v ∈ V . The t-restricted optimal pebbling number \(\pi ^*_t(G)\) is the minimum weight of a solvable tRPC on G; introduced by Chellali et al. [143].
-
8.
rubbling number ρ(G). In graph pebbling, only the pebbling move is allowed; while in graph rubbling both pebbling and rubbling moves are available. A rubbling move adds a pebble on a vertex v while removing a pebble from each of two vertices adjacent to v. A rubbling configuration f is said to be solvable if for every vertex v ∈ V , there exists a sequence (possibly empty) of pebbling and rubbling moves that results in a pebble on v. The rubbling number of a graph G, denoted ρ(G), is the minimum number k such that every rubbling configuration of k is solvable.
-
9.
optimal rubbling number ρ ∗(G), minimum weight of a solvable rubbling configuration of G. Rubbling and optimal rubbling were introduced by Belford and Sieben in 2009 [42] and studied by Katona and Papp in [446] and Katona and Sieben in [447].
3.17 Topological Numbers
In integrated circuit design the objective is to place the components of an electrical circuit, such as resistors, capacitors, transistors and inductors, on a plane surface and then connect them with wires in such a way that two wires do not overlap, or cross. This gives rise to the problem of minimizing the number of crossings in a graph drawn on a surface, such as the plane. All of the parameters in this subsection are concerned with embedding graphs on surfaces or decomposing graphs into subgraphs which can be embedded on specific surfaces.
-
1.
crossing number ν(G), minimum number of pairwise edge crossings in a plane embedding of G. A plane embedding of a graph G is defined by a function f which assigns to each vertex v ∈ V a unique point in the plane, and for every edge uv ∈ E, a line is drawn in the plane connecting the two points f(u) and f(v), in such a way that the line connecting u and v does not pass through any points f(w), for any w ∈ V not equal to u or v. If the line connecting two vertices u and v crosses the line connecting two other vertices w and x, this counts as one pairwise edge crossing. A comprehensive, 113-page survey of many types of crossing numbers has been written by M. Schaefer in 2017 [561]. The interested reader is also referred to the 2016 survey paper by Székely [599].
-
2.
bipartite crossing number. A two-layer drawing of a bipartite graph G = (X, Y, E) places vertices in X on one line and those in Y on another line parallel to the first, and draws edges as straight line segments between the vertices on these two parallel lines. A crossing in a two-layer drawing is a pair of edges that intersect each other at a point not representing a vertex. The bipartite crossing number cr XY(G) equals the smallest number of crossings possible in a 2-layer drawing of G; cf. Shahrokhi et al. [571], and Kobayashi et al. [458].
-
3.
circular crossing number. A circular k-partite drawing of a k-partite graph G is obtained by partitioning a circle into k arc segments, placing the vertices of the i th partite set into the ith arc segment, and then drawing the edges as chords of the circle, so that no more than two chords meet at the same crossing. The circular crossing number cpr k(G) is the minimum number of crossings taken over all circular k-partite drawings, all possible assignments of vertices to arc segments, and all numberings of the parts. This crossing number generalizes both the bipartite crossing number and the outerplanar crossing number; cf. Riskin [541].
-
4.
outerplanar crossing number ν 1(G). An outerplanar or convex drawing of a graph places the vertices on a circle and draws the edges as line segments. The outerplanar crossing number ν 1(G) is the minimum number of pairs of crossing edges among all such drawings. See Shahrokhi et al. [572], and Czabarka et al. [178].
-
5.
rectilinear crossing number. A rectilinear drawing of a graph is one where each edge is drawn as a straight-line segment, and the rectilinear crossing number of a graph is the minimum number of crossings over all rectilinear drawings; cf., for example, Bienstock and Dean [50].
-
6.
point-coarseness and point-outercoarseness ξ(G) and ξ 0, maximum number of subsets into which V(G) can be partitioned so that each subset induces a graph that is homeomorphic from K 5 or K 3,3, K 4 or K 2,3, respectively. Two graphs G and H are homeomorphic if they become isomorphic after smoothing all vertices of degree 2, that is removing a vertex v of degree two with neighbors u and w and then adding the edge uw. Point-coarseness was introduced by Mitchem in 1973 [507]. See also Michalak in 1985 [504].
-
7.
genus g(G), minimum integer g such that G can be embedded on the orientable surface S g without any edge crossings/intersections; cf. Walsh et al. [635].
-
8.
Hadwiger number had(G), maximum integer k such that the complete graph K k is a minor of G. A graph H is a minor of a graph G if H can be formed from G by a finite sequence of edge deletions and edge contractions. The famous Hadwiger Conjecture is that for any graph G, χ(G) ≤ had(G). Hadwiger’s Conjecture has been shown to be true for k ≤ 6, and remains open for k > 6; cf. Duchet and Meyniel [205], Robertson and Song [544], Böhme et al. [58], and Chandran and Sivadason [108].
-
9.
thickness θ(G), minimum number of planar subgraphs whose union is G; cf. Tutte [614], Beineke [41], Kainen [439], Halton [331], Mutzel et al. [510], and Kawano and Yamazaki [448].
-
10.
outerthickness θ 0(G). A graph is outerplanar if it can be embedded in the plane so that every vertex lies on the outer face, or equivalently, if the graph contains no subdivision of K 4 or K 2,3. The outerthickness of a graph G is the minimum number of outerplanar graphs whose union is G; cf. Guy and Nowakowski [321] and [322].
-
11.
page number pn(G). A book embedding of a graph G consists of an ordering of the vertices V along the spine of a book and an embedding of each edge uv ∈ E on one page of the book so that no two edges embedded on the same page intersect. The minimum number of pages in a book embedding of G is its page number pn(G); cf. Malitz [496].
4 Conjectures
In this section, we give a sampling of conjectures involving the graph parameters presented in this glossary.
4.1 Basic Structural
We begin with four easy-to-state conjectures.
Conjecture 1 (Erdös and Sós [223])
If G is a graph with average degree at least k − 2 for a positive integer k, then every tree of order k is contained in G as a subgraph.
There are many partial results on this conjecture. For example, McLennon [503] proved that a graph with average degree at least k − 2 contains every tree of order k whose diameter does not exceed 4 as a subgraph.
We now consider the maximum number of edges that must be removed to make a triangle-free graph bipartite.
Conjecture 2 (Erdös et al. [228])
Every triangle-free graph on n vertices can be made bipartite by deleting at most n 2∕25 edges.
This bound, if true, is best possible. Consider a blow-up of a cycle C 5, that is, replacing each vertex of the C 5 with k ≥ 1 independent vertices and replacing each edge uv of C 5 with the complete bipartite graph K k,k. This conjecture was proved for graphs with at least n 2∕5 edges by Erdös, Gyori and Simonovits in 1991 [232], but the general conjecture remains open.
Given a graph G = (V, E), a vertex-deleted subgraph of G, denoted G v, is a subgraph formed by deleting exactly one vertex v from G together with all edges containing vertex v. Clearly, G v is an induced subgraph of G. For a graph G, the deck of G is the multiset of all vertex-deleted subgraphs of G. Each graph in the deck is called a card. Two graphs that have the same deck are said to be hypomorphic. A graphical parameter is recognizable if, for each graph G of order at least 3, it is possible to determine it from the graph’s deck. It is easy to see that all of the basic structural parameters in Section 3.1, e.g. order, size, δ(G), Δ(G), degree sequence, the isolated vertices and leaves are recognizable. This leads to the 1957 conjecture of Kelly [452] and the 1960 conjecture of Ulam [617]:
Conjecture 3 (Reconstruction Conjecture [452, 617])
Any two hypomorphic graphs on at least three vertices are isomorphic.
Note that the requirement that the graphs have at least three vertices is necessary because both graphs on two vertices have the same decks. In 1974, Harary suggested a stronger version of the conjecture [339]:
Conjecture 4 (Set Reconstruction Conjecture [339])
Any two graphs on at least four vertices with the same sets of vertex-deleted subgraphs are isomorphic.
Both the Reconstruction and Set Reconstruction Conjectures have been verified for all graphs with at most 11 vertices by McKay, in 1997 [502]. In a probabilistic sense, it was shown by Bollobás [59] in 1990 that almost all graphs are reconstructible. This means that the probability that a randomly chosen graph on n vertices is not reconstructible goes to 0 as n goes to infinity. In fact, it was shown that not only are almost all graphs reconstructible, but in fact, the entire deck is not necessary to reconstruct them as almost all graphs have the property that there exist three cards in their deck that uniquely determine the graph. Conjecture 3 has been verified for a number of infinite classes of graphs, including regular graphs, trees, disconnected graphs, unit interval graphs, and maximal planar graphs.
4.2 Connectivity and Subgraphs
In 1989 Thomassen [608] conjectured that any graph with high enough connectivity should contain a k-connected spanning, bipartite subgraph.
Conjecture 5 (Thomassen [608])
For all k, there exists a function f(k) such that for all graphs G, if κ(G) ≥ f(k), then G contains a spanning, bipartite H with κ(H) ≥ k.
In 2015 Delcourt and Ferber [191] showed that Conjecture 5 is true up to a log n factor.
In 2003 Kriesell [464] posted the following conjecture related to the connectivity of a graph.
Conjecture 6 (Kriesell [464])
If G is a graph and S a subset of vertices of G such that for any pair u, v ∈ S there are 2k edge-disjoint paths from u to v in G, then G contains k edge-disjoint trees, each of which contains S.
It follows from Mader’s splitting-off theorem (see [493]) that Kriesell’s Conjecture holds if the degree of every vertex in V − S is even. Kriesell’s Conjecture is true if |S|≤ 5.
The concept of toughness was introduced by Chvàtal [156] as a parameter related to the hamiltonicity of a graph. The following conjecture by Chvátal [156] is still open.
Conjecture 7 (The t 0-Tough Conjecture [156])
There exists a constant t 0 such that every t 0-tough graph is Hamiltonian.
For a long time, it was believed that t 0 = 2 was sufficient for Conjecture 7. However, Bauer et al. [36] showed that if such a constant exists, it must be greater than 2. In fact, they showed that t 0 ≥ 9∕4 if the conjecture is true.
Conjecture 8 (Thomassen [607])
Every 4-connected line graph is Hamiltonian.
In 1991, Zhan [656] proved that every 7-connected line graph is Hamiltonian. In 1994, Lai [474] proved that every 4-connected line graph of a planar graph is Hamiltonian.
Conjecture 9 (Matthews-Sumner [500])
Every 4-connected claw-free graph is Hamiltonian.
We remark that line graphs are claw-free, so the Matthews-Sumner Conjecture implies the Thomassen conjecture. Fleischner conjectured that the two conjectures were equivalent. This was verified by Ryjáček [549] and the result appeared in 1997.
Conjecture 10 (Sheehan [577])
Every Hamiltonian 4-regular graph has a second Hamiltonian cycle.
Combined with earlier results, Sheehan’s Conjecture would imply that every Hamiltonian r-regular graph (r ≥ 3) has a second Hamiltonian cycle. Thomassen [610] verified this for r ≥ 300.
A graph is called uniquely Hamiltonian if it contains precisely one Hamiltonian cycle. In 2014, Fleischner posed the following conjecture.
Conjecture 11 (Fleischner [266])
Every uniquely Hamiltonian graph has connectivity at most 4.
Fleischner’s Conjecture is true for planar graphs as shown by Tutte in 1956. We remark that Fleischner [266] constructed an infinite family of uniquely Hamiltonian graphs of minimum degree 4 and of arbitrarily high maximum degree. Fleischner [266] also showed that there exist infinitely many uniquely Hamiltonian graphs in which every vertex has degree 4 or 14.
The following conjecture posed by David Barnette originally appeared in [33].
Conjecture 12 (Barnette [33])
Every 3-connected cubic planar bipartite graph is Hamiltonian.
Holton et al. [419] proved Barnette’s conjecture for up to 64 vertices, inclusive. Subsequently, the conjecture has been shown to be true for up to 84 vertices, inclusive.
Thomassen [609] posed the following conjecture about chords of longest cycles. A chord of a cycle C is an edge e so that e∉E(C), but both ends of e are in V (C).
Conjecture 13 (Thomassen [609])
If G is a 3-connected graph, every longest cycle in G has a chord.
A graph G is said to be locally connected if the subgraph induced by the open neighborhood of each vertex of G is connected, and G is locally k-connected if G[N(v)] is k-connected for every v ∈ V (G). Chartrand and Pippert [114] proved that every connected, locally connected graph of order at least 3 with maximum degree at most 4 is either Hamiltonian or the complete tripartite graph K 1,1,3. In 1979, Oberly and Sumner [517] proved the following theorem and made a stronger conjecture.
Theorem 2 ([517])
If G is a connected, locally connected, K 1,3 -free graph of order at least 3, then G is Hamiltonian.
Conjecture 14 (Oberly-Sumner [517])
If G is a connected, locally k-connected, K 1,k+2-free graph of order at least 3, then G is Hamiltonian.
Note that Theorem 2 shows that Conjecture 14 is true for k = 1.
A factor of a graph G is a spanning subgraph of G. A graph G is factorable into factors F 1, F 2, …F t if these factors are (pairwise) edge-disjoint and \(\bigcup _{i=1}^t E(F_i) = E(G)\). If G is factorable into factors F 1, F 2, …F t, then {F 1, F 2, …, F t} is called a factorization of G. Further, if F i = H for 1 ≤ i ≤ t in a factorization of G, then G is said to be H-factorable and G has an isomorphic factorization into copies of H. An k-regular factor of G is called an k-factor, and if G has a factorization into k-factors, then G is k-factorable. In particular, a 1-factor of G is a perfect matching of G.
It is believed that the following conjecture originated in a paper by Chetwynd and Hilton [151].
Conjecture 15 (The 1-Factorization Conjecture)
If G is an r-regular graph of even order n such that (1) r ≥ n∕2 if n ≡ 2(mod 4) or (2) r ≥ (n − 1)∕2 if n ≡ 0(mod 4), then G is 1-factorable.
Nash-Williams [513] conjectured that r-regular graphs can be factored into Hamiltonian cycles and possibly one 1-factor.
Conjecture 16 (Nash-Williams [513])
If G is an r-regular graph of even order n such that r ≥ n∕2, then G can be factored into Hamiltonian cycles and at most one 1-factor.
Csaba et al. [176] showed that both Conjectures 15 and 16 hold for sufficiently large n.
The following conjecture was made independently by Szekeres [600] in 1973 and Seymour [566] in 1979. This conjecture, known as the Cycle Double Cover Conjecture, is now widely considered to be among the most important open problems in graph theory.
Conjecture 17 (Cycle Double Cover Conjecture)
For every graph G with no bridge, there is a list of cycles in G so that every edge appears in exactly two cycles.
We remark that the list may have repeated cycles, as is the case with C n. Fan [242] used Seymour’s 6-flow theorem [567] to prove that G has a list of cycles so that every edge is contained in exactly six cycles. The Cycle Double Cover Conjecture is known to be true for every 4-edge-connected graph.
A k-cycle is a cycle of length k. Next we give a well-known conjecture of Erdös and Gyárfás [225].
Conjecture 18 (Erdös - Gyárfás [225])
For every graph G with minimum degree at least 3, there exists a non-negative integer k such that G contains a cycle of length 2k.
Conjecture 18 is among the many problems for whose solution Erdös offered money. Heckman and Krakovski [377] proved the conjecture is true for 3-connected cubic planar graphs. They actually proved a stronger result by showing that every 3-connected, cubic, planar graph contains a cycle of length 2k for some 2 ≤ k ≤ 7. The conjecture also holds for planar claw-free graphs [180] and for K 1,k-free graphs having minimum degree at least k + 1, or maximum degree at least 2k − 1 [576]. Other partial results have been obtained, but the general conjecture is still open.
It is well-known that every two longest paths in a connected graph have a common vertex. Skupien [583] gave examples of connected graphs where seven longest paths do not share a common vertex.
Conjecture 19 (Gallai [276])
If G is a connected graph, then every three longest paths have a vertex in common.
4.3 Distance and Degree
A graph G is called diameter-2-critical if its diameter is two, and the deletion of any edge increases the diameter. The following conjecture was made independently by Murty and Simon (see [93]).
Conjecture 20 (Murty-Simon Conjecture)
If G is a diameter-2-critical graph with n vertices and m edges, then m ≤⌊n 2∕4⌋, with equality if and only if G is the complete bipartite graph \(K_{\left \lfloor \frac {n}{2} \right \rfloor , \left \lceil \frac {n}{2} \right \rceil }\).
According to Füredi [274], Erdös said that this conjecture goes back to the work of Ore in the 1960s. Fan [241] proved the conjecture for n ≤ 24 and for n = 26. In 1992 Füredi [274] gave an asymptotic result proving the conjecture is true for large n, that is, for n > n 0 where n 0 is a tower of 2’s of height about 1014. The conjecture remains open for general n.
Our next three conjectures involve the indices having applications in chemistry, including the problem of finding a compound with a given Wiener index. A major conjecture in this area is whether every positive integer is the Wiener index of some tree.
Conjecture 21 (Wiener Index Conjecture [147, 305, 480])
For every positive integer k (except for some finite set), there exists a tree T with σ(T) = k.
Conjecture 22 (DeLaViña and Waller [189])
If G is a graph of diameter d ≥ 3 and order 2d + 1, then σ(G) ≤ σ(C 2d+1).
The next conjecture relates the Randić connectivity index R(G) to the average distance μ(G).
Conjecture 23 (Fajtlowicz [239])
For all connected graphs G, R(G) ≥ μ(G).
Li and Shi [485] proved Conjecture 23 for graphs G having order n ≥ 15 and minimum degree δ(G) ≥ n∕5, and Cygan et al. [177] proved it for trees.
4.4 Labeling
A graph with m edges is graceful if the vertices can be assigned distinct numbers from among 0, 1, …, m, so that the differences along the edges are precisely 1, 2, …, m. A dynamic survey, of some 415 pages, on graph labelings has been written by Gallian [278]. The following conjecture, posed by Kotzig, Ringel and Rosa, has attracted much attention.
Conjecture 24 (Graceful Tree Conjecture)
Every tree is graceful.
A graph of order n is called prime if one can bijectively label its vertices with integers 1, …, n so that whenever two vertices are adjacent, their labels are relatively prime. According to Gallian [278], this concept was introduced by Entringer, who made the following conjecture.
Conjecture 25
Every tree is prime.
Haxell et al. [356] proved Conjecture 25 for trees having large enough order. The conjecture is also proven for several families of graphs in [613].
The next conjecture involves the L(2, 1)-labeling number λ(G).
Conjecture 26 (Griggs and Yeh [313])
For any graph G with maximum degree Δ(G) = Δ, λ(G) ≤ Δ 2.
Conjecture 26 is known as the Δ 2-conjecture and considered the most important open problem in L(2, 1)-labeling. In their introductory paper, Griggs and Yeh [313] proved that λ(G) ≤ Δ 2 + 2Δ, and the best bound to date is Δ 2 + Δ − 2 shown by Goncalves [308]. Havet et al. [354] showed that Conjecture 26 holds for sufficiently large Δ. Most of the work on this conjecture deals with particular classes of graphs.
4.5 Decomposition
As we have seen, a path-decomposition of a graph G is a set of paths whose edges partition the edge set of G. Equivalently, a path-decomposition is a vertex partition π = {V 1, V 2, …, V k} such that for 1 ≤ i ≤ k, the subgraph G[V i] induced by V i is a path, and every edge uv ∈ E is contained exactly one such path. Our next conjecture is due to Gallai (see [490]).
Conjecture 27 (Gallai)
If G is a connected graph on n vertices, then G can be decomposed into \(\left \lceil n/2 \right \rceil \) paths.
In 1968 Lovász [490] showed that a relaxed form of Conjecture 27 holds when he proved that every graph on n vertices has a decomposition consisting of \(\left \lceil n/2 \right \rceil \) paths and cycles. Conjecture 27 has also been verified for many families of graphs, for example, see [68, 185, 243, 251, 348, 529].
4.6 Covering and Matching
Recall that ν 3(G) is the maximum number of pairwise edge-disjoint triangles in G. In 1981, Tuza [615, 616] conjectured the following upper bound on the triangle cover number τ 3(G).
Conjecture 28 (Tuza [615, 616])
For any graph G, τ 3(G) ≤ 2ν 3(G).
Conjecture 28 has been well-studied and many partial results obtained. For example, Puleo [526] proved the conjecture for all graphs having no subgraph with average degree at least 7. Fractional relaxations on the bound have been obtained. Haxell [355] provided the best such result by showing that τ(G) ≤ 2.87ν(G) for all graphs G.
The next well-known conjecture is attributed to Berge in [565], but it first appeared in [273].
Conjecture 29 ([273, 565])
Every cubic bridgeless graph G contains six perfect matchings such that each edge of G is contained in precisely two of the matchings.
4.7 Coloring
We now consider several conjectures involving graph coloring. It is well-known that the clique number ω(G) is a sharp lower bound on the chromatic number χ(G) for any graph G. Reed [540] conjectured in 1998 an upper bound on χ(G) also involving ω(G). Recall that Δ(G) denotes the maximum degree of G.
Conjecture 30 (Reed [540])
For every graph G,
If G has χ(G) = k, then G is said to be a k-chromatic graph. A graph H is a subdivision of a graph G is H can be obtained from G by inserting vertices of degree two into some, all, or none of the edges of G. Hajós [326] conjectured that a k-chromatic graph contains a subdivision of the complete graph K k as a subgraph.
Conjecture 31 (Hajós [326])
If G is a k-chromatic graph for k ≥ 2, then G contains a subdivision of K k.
Catlin [104] gave counterexamples to Conjecture 31 showing that the conjecture is false for k ≥ 7. Hence, Conjecture 31 is open only for small values of k.
Erdös, Faber, and Lovász (see [224]) formulated the following graph coloring conjecture in 1972.
Conjecture 32 (Erdös-Faber-Lovász Conjecture)
Every graph which can be decomposed into k complete graphs on k vertices (such that every pair of complete graphs has at most one shared vertex) is k-colorable.
We remark that the Erdös-Faber-Lovász Conjecture can be restated in the language of hypergraphs as follows: In every k-uniform linear hypergraph H with k hyperedges, one may color the vertices of H with k colors in such a way that each hyperedge has one vertex of each color.
Given two graphs G and H, we say H is a minor of G if H can be obtained from G by a series of operations: contracting edges, deleting isolated vertices and deleting edges. The following conjecture, due to Hadwiger [324] in 1943, is a generalization of the four color theorem and is perhaps the most challenging conjecture in graph theory.
Conjecture 33 (Hadwiger’s Conjecture [324])
Every k-chromatic graph G contains the complete graph K k as a minor.
Bollobàs et al. [64] claimed that Conjecture 33 is “one of the deepest unsolved problems in graph theory” and showed it holds for almost every graph. Hadwiger [324] proved the conjecture for k ≤ 4 in 1943 when he introduced his conjecture. Before Hadwiger’s Conjecture was formally posed, Wagner [632] had already shown that the case k = 5 is equivalent to the Four Color Theorem. Hence, Hadwiger’s Conjecture 33 is true for k = 5. Also using the Four Color Theorem, Robertson et al. [545] settled the conjecture for k = 6; their paper with this proof won the 1994 Fulkerson Prize. Hence, Conjecture 33 is true for 1 ≤ k ≤ 6, but it remains unsolved for all k > 6.
The categorical product G × H of two graphs G and H is the graph with vertex set V (G) × V (H) and edges (u, v)(u′, v′) ∈ E(G × H) if and only if uv ∈ E(G) and vv′∈ E(H). In 1966, Hedetniemi [378] made the following conjecture on the chromatic number of categorical products.
Conjecture 34 (Hedetniemi’s Conjecture [378])
For any graphs G and H, χ(G × H) = min{χ(G), χ(H)}.
The interested reader is referred to Hedetniemi’s chapter [380] in Volume 1 of this series [287] and to the following three survey papers on Hedetniemi’s Conjecture by Zhu [661], Sauer [560] and Tardif [601].
A similar conjecture was made for the circular chromatic number in [660].
Conjecture 35 (Zhu [660])
For any graphs G and H, χ c(G × H) = min{χ c(G), χ c(H)}.
In a 2001 survey paper on circular chromatic numbers, Zhu [662] remarks that Conjecture 35 is equivalent to the following conjecture.
Conjecture 36 (Zhu [662])
For any number r, if G and H are not r-circular colorable, then G × H is also not r-circular colorable.
When r is an arbitrary integer, this becomes Hedetniemi’s Conjecture (Conjecture 34). Conjecture 36 is known to be true for r = 1, r = 2, and r = 2 + 1∕k, where k is any positive integer (see [221, 325, 662]). As far as we know, the problem is open for all other values of r.
Vizing’s Theorem [626] is a major result for edge coloring.
Theorem 3 (Vizing’s Theorem [626])
For any non-empty graph G,
A graph is said to belong to Class 1 if χ′(G) = Δ(G) and to Class 2 if χ′(G) = Δ(G) + 1.
For each k where k = Δ(G) ≤ 5, there exists planar graph having Δ(G) = k of Class 1 and a planar graph of Class 2. Vizing [626] showed that every planar graph G with Δ(G) ≥ 8 is of Class 1, and conjectured that every graph with Δ(G) ∈{7, 8} is of Class 1. In 2001, Sanders and Zhao [559] verified the case for Δ(G) = 7. Hence, Vizing’s conjecture is as follows.
Conjecture 37 (Vizing [626])
If G is a planar graph with Δ(G) = 6, then G is of Class 1.
A subgraph H with order n′ and size m′ is called an overfull subgraph of G if n′ is odd and m′ > Δ(G) ⋅ (n − 1)∕2. Chetwynd and Hilton [151] conjectured that for graphs G with order n and Δ(G) > n∕3, G belongs to Class 2 if and only if G contains an overfull subgraph.
Conjecture 38 (Chetwynd and Hilton [151])
Let G be a graph with order n and Δ(G) > n∕3. Then G belongs to Class 2 if and only if G contains an overfull subgraph.
Behzad [40] and Vizing [625] independently conjectured that a bound similar to the upper bound of Vizing’s Theorem on the edge chromatic number holds for the total chromatic number.
Conjecture 39 ([40, 625])
For every graph G, χ ′′(G) ≤ Δ(G) + 2.
The following conjecture involving the edge chromatic number χ′(G) and the list chromatic index \(\chi ^{\prime }_l(G)\) first appeared in [62].
Conjecture 40 ([62])
For every nonempty graph G, \(\chi '(G) = \chi ^{\prime }_l(G)\).
The next conjecture involves the strong chromatic index \(\chi ^{\prime }_s(G)\).
Conjecture 41 (Burris and Schelp [92])
If G is a graph of order n and every component of G has order 3 or more, then \(\chi ^{\prime }_s(G) \le n+1\).
We next consider nonproper edge colorings. Given an edge coloring of a graph, the induced color of a vertex is the sum of the colors of its incident edges. The following conjecture, explored by Chartrand [113] in Volume 1 of this series [287], is due to Karoński et al. [444].
Conjecture 42 (The 1-2-3 Conjecture [444])
For every connected graph G of order 3 or more, each edge of G can be assigned one of the colors 1, 2, 3 in such a way that the induced colors of every two adjacent vertices are different.
Karoński et al. [444] showed that there is an infinite class of graphs for which the 1-2-3 Conjecture holds. They also proved that the conjecture holds for connected graphs of order 3 or more having chromatic number at most 3. We note that if you allow four colors, then the conjecture is true.
Our final conjecture in this subsection involves the achromatic number ψ(T) and the pseudo-achromatic number ψ s(T) of trees T. For more details on this conjecture, the reader is referred to [380] in Volume 1 of this series [287], and to Edwards [218].
Conjecture 43 (Achromatic-Pseudoachromatic Tree Conjecture)
For any tree T, ψ(T) ≤ ψ s(T) ≤ ψ(T) + 1.
4.8 Domination
We next give sampling of conjectures involving domination. Arguably the main open problem in the area of domination in graphs is Vizing’s Conjecture, posed as a problem in [624] and later as a conjecture in [627]. Vizing’s conjecture asserts that the domination number of the Cartesian product of two graphs is at least as large as the Cartesian product of their domination numbers.
Conjecture 44 (Vizing’s Conjecture 1963 [624, 627])
For graphs G and H,

In 2000, Clark and Suen [157] proved the looser result that for all graphs G and H, \(\gamma (G\square H)\geq \frac {1}{2}\gamma (G)\gamma (H)\). Suen and Tarr [597] strengthened Clark and Suen’s result by showng that \(\gamma (G\square H)\geq \frac {1}{2}\gamma (G)\gamma (H)+\frac {1}{2}\min \{\gamma (G),\gamma (H)\}\). Furthermore, Krop [466, 467] proved that for any graphs G and H, \(\gamma (G\square H)\geq \frac {\gamma (G)}{2\gamma (G)-1}\gamma (G)\gamma (H)\), and if G is claw-free or P 4-free, then \(\gamma (G\square H)\geq \frac {2}{3}\gamma (G)\gamma (H)\). Employing the packing number, Brešar [74] also improved the result of Clark and Suen. However, Vizing’s Conjecture still remains open. For a survey on Vizing’s Conjecture in 2012, see [78].
Reed [539] conjectured that the domination number of a connected, cubic graph of order n is at most \(\left \lceil n/3 \right \rceil \). But Kostochka and Stodolsky [462] gave a counterexample to disprove this conjecture. However, Kostochka and Stodolsky [462] and Kelmans [453] independently claim that Reed’s conjecture holds for 3-connected cubic graphs.
Conjecture 45 (Kostochka and Stodolsky [462], Kelmans [453])
If G is a 3-connected cubic graph of order n, then \(\gamma (G) \le \left \lceil \frac {n}{3} \right \rceil \).
In Chapter 15 of the first volume of this series, Henning [407] discusses other families for which Reed’s bound is conjectured to hold and poses the following.
Conjecture 46 (Henning [407])
If G is a cubic, bipartite graph of order n, then \(\gamma (G) \le \frac {n}{3}\).
The next two conjectures claim that given large enough girth, Reed’s bound holds.
Conjecture 47 (Verstraete’s Domination Conjecture [407])
If G is a connected, cubic graph on n vertices with girth at least 6, then \(\gamma (G) \le \frac {1}{3}n\).
Recall that i(G) is the independent domination number of G.
Conjecture 48 (Verstraete’s Independent Domination Conjecture [621])
If G is a connected, cubic graph on n vertices with girth at least 6, then \(i(G) \le \frac {1}{3}n\).
Note that for every graph G, γ(G) ≤ i(G). Thus, Conjecture 48 is a stronger conjecture that Conjecture 47.
We next consider a conjecture involving the ratio of the independent domination and the domination numbers.
Conjecture 49 (Rad and Volkmann [530])
If G is a graph with maximum degree Δ(G) ≥ 6, then i(G)∕γ(G) ≤ Δ(G)∕2.
Wang and Wei [637] proved Conjecture 49 for trees.
Recall that the k-domination number γ k(G) denotes the minimum cardinality of a dominating set S having the property that for every vertex v ∈ V − S, |N(v) ∩ S|≥ k.
Conjecture 50 (Fink and Jacobson [263])
For a graph G with δ(G) ≥ k, there exists function f(k) such that for j ≥ f(k), γ k(G) < γ j(G).
Our next conjectures involve the total domination number γ t(G). Thomasse and Yeo [606] posed the following \(\frac {4}{11}\)-conjecture.
Conjecture 51 (Thomasse, Yeo [606])
If G is a graph of order n with δ(G) ≥ 5, then \(\gamma _t(G) \le \frac {4}{11}n\).
Henning and Yeo believe the 4∕11-bound can be improved to a 1∕3-bound if we forbid 4-cycles. Recall that a graph is quadrilateral-free if it contains no 4-cycles, not necessarily induced.
Conjecture 52 (Henning, Yeo [413])
If G is a quadrilateral-free graph of order n with δ(G) ≥ 5, then \(\gamma _t(G) \le \frac {1}{3}n\).
Conjecture 53 (Henning [405])
If G is a planar graph of diameter 3, then γ t(G) ≤ 6.
A graph G is called total domination edge critical if γ t(G + e) < γ t(G) for every edge \(e \in E(\overline {G})\). Further, if γ t(G) = k, then we say that G is a k t -critical graph. This concept was introduced in [619] and, in the same paper, the authors showed that the addition of an edge to a graph can change the total domination number by at most 2. Total domination edge critical graphs G with the property that γ t(G) = k and γ t(G + e) = k − 2 for every edge \(e \in E(\overline {G})\) are called k t -supercritical graphs.
Hanson and Wang [334] showed that a graph is diameter 2-critical if and only if its complement is 3t-critical or 4t-supercritical, relating this concept to the Murty-Simon Conjecture (Conjecture 20). The 4t-supercritical graphs were characterized in [618] as the disjoint unions of two complete graphs. Since the complement of a 4t-supercritical graph is a complete bipartite graph and the number of edges is minimized when the partite sets are of equal cardinality, Conjecture 20 holds for this case. Therefore, proving Conjecture 20 is equivalent to proving the following conjecture.
Conjecture 54
If G is a 3t-critical graph with order n and size m, then \(m(G) > \frac {n(n-2)}{4}\).
In [619] it was proved that any 3t-critical graph has diameter 2 or 3. After the result of Hanson and Wang in [334], Conjecture 54 was verified in [334, 371] for the 3t-critical graphs of diameter 3. Conjecture 54 remains open for the 3t-critical graphs of diameter 2.
Balbuena et al. [32] posed the following stronger conjecture.
Conjecture 55 (Balbuena, et al. [32])
If G is a 3t-critical graph with order n, size m, and diam(G) = 2, then m ≥⌊(n 2 − 4)∕4⌋.
The following conjecture on paired domination was posed by Henning in [407].
Conjecture 56 (Henning [407])
If G is a bipartite, cubic graph of order n, then \(\gamma _{\mathrm {pr}}(G) \le \frac {1}{2}n\).
Recall that γ −1(G) and α(G) denote the inverse domination number and the vertex independence number, respectively. The following conjecture first appeared in [471] as a “theorem,” but later an error was found in the proof.
Conjecture 57
For any isolate-free graph G, γ −1(G) ≤ α(G).
Although to date Conjecture 57 remains unsettled, several partial results offer support of its validity. For more information on Conjecture 57 and these results, the reader is referred to Hedetniemi’s chapter [380] in Volume 1 of this series [287].
Our next conjecture is an upper bound on the Roman domination number in terms of the order of a graph. It is known that \(\gamma _R(G) \le n - {\frac {\gamma (G)}{2}}\) where n ≥ 3 and the domination number γ(G) ≥ 2 (see Favaron et al. [255]). Also, Chambers et al. [106] proved that \(\gamma _R(G) \le {\frac {8n}{11}}\) for any graph G with order n ≥ 9 and minimum degree at least 2.
Bermudo et al. [46] proved that the Roman domination number and the differential are complementary with respect to the order n of the graph G, that is, ∂(G) + γ R(G) = n. Hence, determining a bound on one of them with respect to n yields a bound on the other. Using this fact, Bermudo [45] proved that for any graph G with order n ≥ 9 and minimum degree at least 2, \(\partial (G) \ge {\frac {3\gamma (G)}{4}}\), and so, \(\gamma _R(G) \le n - {\frac {3\gamma (G)}{4}}\). Furthermore, Bermudo [45] conjectures that these bounds can be improved for graphs with minimum degree at least 3.
Conjecture 58 (Bermudo [45])
If G is a graph with minimum degree at least 3, then ∂(G) ≥ γ(G).
Conjecture 58 can be stated equivalently in terms of Roman domination as follows.
Conjecture 59 (Bermudo [45])
If G is a graph with minimum degree at least 3, then γ R(G) ≤ n − γ(G).
The next two conjectures involve the bondage number b(G) of a graph G.
Conjecture 60 (Teschner [604])
For any graph G, \(b(G) \le {\frac {3}{2}} \varDelta (G)\).
Teschner [604] proved that Conjecture 60 holds for graphs having domination number at most 3. Hartnell and Rall [350] and Teschner [605] showed that the bound of Conjecture 60 is sharp for the Cartesian product  . Dunbar et al. [211] conjecture the following upper bound on the bondage number.
. Dunbar et al. [211] conjecture the following upper bound on the bondage number.
Conjecture 61 (Dunbar et al. [211])
If G is a planar graph with maximum degree Δ(G), then b(G) ≤ Δ(G) + 1.
Kang and Yuan [441] have shown that for any connected planar graph G, b(G) ≤ min{8, Δ(G) + 2}, solving Conjecture 61 for planar graphs with Δ(G) ≥ 7 and Conjecture 60 for planar graphs with Δ(G) ≥ 4.
Next we consider a conjecture involving the paired domination subdivision number.
Conjecture 62 (Favaron et al. [256])
For every connected graph G of order n ≥ 3, \(sd_{\gamma _{pr}}(G) \le n-1\).
A graph G is called irredundance perfect if ir(H) = γ(H), for every induced subgraph H of G. A graph that is not irredundance perfect is called irredundance imperfect. We conclude this subsection with two conjectures involving irredundance perfect graphs.
Conjecture 63 (Volkmann and Zverovich [630])
The number of minimal irredundance imperfect graphs is finite.
In [630], Volkmann and Zverovich modified a conjecture of Henning [402] as follows.
Conjecture 64
A graph G is irredundance perfect if and only if G is 5-irredundance perfect.
4.9 Domatic
Recall that the domatic number d(G) of a graph G is the maximum number of disjoint dominating sets in G. The following conjecture was first posed as a question by Kostochka in 2009: Is it true that the vertex set of every cubic, bipartite graph can be partitioned into three dominating sets? This question was subsequently posed as a conjecture by Henning [407] in Volume 1 of this series [287].
Conjecture 65 (Henning [407])
If G is a cubic, bipartite graph, then d(G) = 3.
Recall that the total domatic number d t(G) of a graph G is the maximum number of disjoint total dominating sets. We remark that this parameter is equivalent to the minimum (not necessarily proper) coloring of the vertices of a graph where every color appears in every open neighborhood. Such a coloring in called the coupon coloring problem by Chen et al. [149].
Goddard and Henning [295] showed that if G is a planar graph, then d t(G) ≤ 4 and this bound is best possible. Further, they showed that if G is a toroidal graph, then d t(G) ≤ 5 and this bound is best possible. By a planar triangulation we mean a maximal planar graph. Goddard and Henning [295] posed the following conjecture about the total domatic number of planar triangulations.
Conjecture 66 (Goddard, Henning [295])
If G is a planar triangulation of order at least 4, then d t(G) ≥ 2.
Conjecture 67 (Goddard, Henning [295])
Every planar triangulation with at least four vertices has a proper 4-coloring (C 1, C 2, C 3, C 4) such that C 1 ∪ C 2 and C 3 ∪ C 4 are total dominating sets.
Equivalently, Conjecture 67 claims that V (G) can be partitioned into two total dominating sets both of which induce a bipartite subgraph of G. The authors in [295] show that if G is a planar triangulation and the dual of G is Hamiltonian, then Conjecture 66 holds. As remarked in [295], to prove Conjecture 66 it would be enough to show that every 3-connected cubic planar graph has a 2-factor that does not include a facial cycle. If one imposes larger minimum degree, it appears that even more can be said.
Conjecture 68 (Goddard, Henning [295])
If G is a planar triangulation with δ(G) ≥ 4, then d t(G) ≥ 3.
It is noted in [295] that if Conjecture 68 is true, then the bound is sharp, and the authors in [295] also posed the following conjecture.
Conjecture 69 (Goddard, Henning [295])
If G is a connected cubic graph, then G has a family of four (not necessarily distinct) total dominating sets such that every vertex is in at most two of these.
4.10 Pebbling
Chung [155] attributed the following conjecture to Graham.
Conjecture 70 (Graham’s Conjecture [155])
For graphs G and H, 
We conclude this subsection with an open question on optimal pebbling.
Question ([89])
Is it true that \(\pi ^{\ast }(G)\leq \left \lceil n/2\right \rceil \) whenever G is a connected n-vertex graph with minimum degree at least 3?
4.11 Topological
Determining the crossing number of the complete bipartite graph, known as Turan’s brick factory problem, is one of the oldest and most famous crossing number problems. Zarankiewicz [649] conjectured an exact value.
Conjecture 71 (Zarankiewicz [649])
For the complete bipartite graph K m,n,
Kleitman [455] proved that Conjecture 71 holds for complete bipartite graphs K m,n for min(m, n) ≤ 6.
Guy [320] posed a similar conjecture for complete graphs.
Conjecture 72 (Guy [320])
For the complete graph K n,
5 New Parameters and Open Problems
It seems only natural that any careful study of graph theory parameters will lead to the discovery of new parameters or parameters which have been defined but little studied. In the course of writing this glossary, quite a number of these parameters have come to mind, which might be worth studying. In this section we present these for your consideration. We cannot vouch 100% for the originality of some of these parameters; it has been joked that “no one ever discovers anything for the first time.” We can only say that as of the publication of this chapter, we are not aware that some of these parameters have been defined or under what name, or if they have been studied. Of course, we are always reminded that just because it hasn’t been defined, it doesn’t mean that it is worth studying; only time will tell.
5.1 β-Packing Number
A β-packing of a graph G is a maximal set S having the property that for all vertices v ∈ V − S, |N(v) ∩ S|∕deg(v) ≤ β.
This is inspired by α-domination, as originally defined and studied by Dunbar et al. [214]. A set S is called an α-dominating set, for some value α, 0 < α ≤ 1, if for every vertex v ∈ V − S, |N(v) ∩ S|∕deg(v) ≥ α. The α-domination number of a graph G equals the minimum cardinality of an α-dominating set in G, and is denoted γ α(G). Similarly, the β-packing number equals the maximum cardinality of a β-packing set in G, which could be denoted by ρ β(G).
5.2 Upper Binding Number
In Section 3.2 we define the binding number, bind(G) = min{|N(X)|∕|X| : X ⊆ V, N(X) ≠ V }. For this parameter, we could just as well ask, what about the maximum? Let the upper binding number be Bind(G) = max{|N(X)|∕|X| : X ⊆ V, N(X) ≠ V }. It follows that bind(G) ≤ δ(G) ≤ Δ(G) ≤ Bind(G). Furthermore, if N(X) = V , then X is a total dominating set, and therefore, bind(G) ≤ n∕γ t(G) ≤ Bind(G).
5.3 Broadcasting in Trees with Multiple Originators
There are several papers that consider the problem of partitioning or decomposing trees into sub-trees of various types:
In [246], Farley, Hedetniemi and Proskurowski give a linear algorithm for partitioning the vertices of a tree into a minimum number of sub-trees of diameter at most k. In [640], Yan, Chang, Hedetniemi and Hedetniemi give a linear algorithm for decomposing a tree into a minimum number of paths each of which has at most k vertices. So consider variations on this theme. Partition the vertices (or edges) of a tree into a minimum number of sub-trees, each of a given type. What types would you choose?
Let us suggest minimum broadcast trees. In fact, let us suggest an even more general problem at the same time. Let S ⊆ V be an arbitrary subset of vertices, which act as originators of some common message. Each vertex in S makes a phone call to one neighbor and relays the information, at time t = 1. At time t ≥ 2, any vertex having this information can make a phone call to one neighbor not having this information. This is repeated every time step until all vertices in the graph have received the information.
Thus, we have two parameters: the number of originators, and the amount of time to complete the broadcast. We can define the following parameters:
Let b t(G) equal the minimum number of originators necessary to complete broadcasting within time t in a graph G. Note that any b t-set is, by definition, a distance t dominating set. But a minimum distance t dominating set in general can be much smaller than b t(G).
Let b k(G) equal the minimum number of time steps necessary to reach all vertices of G from a set of k originators.
In particular, consider these two problems when restricted to trees.
In [591], Slater, Cockayne and Hedetniemi develop an algorithm to find all single vertices from which a broadcast can be completed in minimum time in an arbitrary tree. They show that this broadcast center always consists of a star with two or more vertices. Thus, in this paper they give an algorithm for computing the value b 1(T).
Can you construct polynomial algorithms for computing the values of b k(T) for any tree T?
5.4 Cycle Number Cycle(G)
The definition of the cycle number cycle(v) in Section 3.2, as the number of distinct cycles containing vertex v, suggests that one define the cycle number Cycle(G) = max{cycle(v) : v ∈ V }. Similarly, the cycle center CC(G) of a graph G consists of the set of vertices v for which cycle(v) is a maximum. What can you say about the cycle center of a graph G?
5.5 Concave Number ccv(G) and Weakly Convex Number wcvx(G)
The definition of a convex set in Section 3.3 suggests the following two parameters. A set S is said to be concave if for every pair of vertices u, v ∈ S, no shortest u − v path contains a vertex other than u and v in S. The concave number or the concavity ccv(G) is the maximum cardinality of a concave set in G. Note, for example, that any clique in a graph G is a concave set. Similarly, the set of all leaves in a tree is a concave set. Indeed, we conjecture that for any nontrivial tree T, ccv(T) equals the number of leaves of T.
A set S is said to be weakly convex if for every pair of vertices u, v ∈ S there exists a u − v geodesic, every vertex of which belongs to S. Since, by definition, the entire vertex set V is weakly convex, and convex, we seek either the maximum order of a proper subset of vertices that is weakly convex, or the minimum order of a maximal weakly convex set in a graph G.
5.6 Degree-Defined Sets
Let S ⊆ V be an arbitrary set of vertices and consider the three induced subgraphs G[S], G[V − S] and the bipartite subgraph G[S, V − S] induced by the set of edges between vertices in S and vertices in V − S. Let deg u G[S] denote the degree of a vertex u ∈ S in G[S]; deg v G[V − S] the degree of a vertex v ∈ V − S in G[V − S]; deg u G[S, V − S] the degree of a vertex u ∈ S in G[S, V − S] and deg v G[V − S, S] the degree of a vertex v ∈ V − S in G[V − S, S].
By placing conditions on the various combinations of these degrees one defines a wide variety of sets, many of which have been studied. However, even more have received little or no attention, including those in bold in the table below. The basic framework of the table below is due to Telle [602] in his PhD thesis; parts of this table appear on page 292 of [361]. In the table, X denotes that the degree of the vertex can be anything, i.e. it does not matter. We also assume that the graph G in question is a non-trivial connected graph.
Type of set | deg u G[S] | deg u G[S, V − S] | deg v G[V − S, S] | deg v G[V − S] |
|---|---|---|---|---|
1. dominating | X | X | ≥1 | X |
2. total/open dominating | ≥1 | X | ≥1 | X |
3. maximal induced matching | 1 | X | ≥1 | X |
4. 1-dependent dominating | 0,1 | X | ≥1 | X |
5. independent dominating | 0 | X | ≥1 | X |
6. perfect dominating | X | X | 1 | X |
7. perfect total dominating | ≥1 | X | 1 | X |
8. perfect induced matching | 1 | X | 1 | X |
9. 1-dependent perfect dominating | 0,1 | X | 1 | X |
10. efficient dominating | 0 | X | 1 | X |
11. nearly perfect | X | X | 0, 1 | X |
12. total nearly perfect | ≥1 | X | 0, 1 | X |
13. nearly perfect induced matching | 1 | X | 0, 1 | X |
14. open packing/total nearly perfect | 0,1 | X | 0, 1 | X |
15. packing | 0 | X | 0, 1 | X |
16. restrained dominating | X | X | ≥1 | ≥1 |
17. dominating bipartition | X | ≥1 | ≥1 | X |
18. Nearly perfect bipartition | X | 0, 1 | 0, 1 | X |
19. perfect matching | X | 1 | 1 | X |
5.7 Distance-2 Domination Parameters
Distance-k domination has been fairly well studied; the reader is referred to the chapter on distance domination by Henning in [403]. However, distance-2 domination is particularly interesting in view of the fact that quite a few types of sets that have been studied are distance-2 dominating sets. These include the following:
-
1.
all maximal irredundant sets, and there are some 12 varieties that are hereditary,
-
2.
a perfect neighborhood set (θ(G));
-
3.
a maximal two-packing (ρ(G));
-
4.
a minimal external redundant set (er(G));
-
5.
a maximal matchable set (μ(G));
-
6.
a maximal nearly perfect set;
-
7.
a pnc-maximal set;
-
8.
a maximal total irredundant set (IR t(G));
-
9.
an R-annihilated set (ra(G)), and
-
10.
an R-annihilated and irredundant set (rai(G));
In addition, a variety of types of maximal matchings are also distance-2 edge dominating sets, including:
-
11.
a variety of maximal matchings may not produce edge dominating sets, but produce distance-2 edge dominating sets, including a maximal induced matching; a maximal disconnected matching, a maximal acyclic matching; a maximal total matching. The general problem is: how do these types of sets compare as distance-2 dominating sets?
5.8 k-Domatic Number d k(G)
You are given the problem of assigning to any given vertex v ∈ V a set of at most k different resources, that is, each vertex has a capacity of storing at most k resources. The resources are chosen from a list of r different resources, where k ≤ r. You must do this in such a way that every vertex has access, in its closed neighborhood, to all r resources. For a given integer k, how large can r be? Denote this by d k(G). Note that if k = 1, then d 1(G) = d(G), the domatic number. Thus, we could say that d(G) is the first domatic number, while d 2(G) is the second domatic number, etc. This resource allocation problem appears in an unpublished technical report by Hedetniemi, Hedetniemi and Wimer in 1987 [384] and recently by Abbas et al. in [1].
5.9 Dominator Colorings
A dominator partition of a graph G is a partition of the vertex set into sets {V 1, V 2, …, V k}, such that every vertex v ∈ V dominates all of the vertices in at least one block V i of the partition. The dominator partition number of a graph G equals the smallest order of a dominator partition of G and is denoted Π d(G). This concept was introduced and studied by Hedetniemi et al. [399].
In this paper the authors observed the following interesting result:
Theorem 4
For any graph G, γ(G) ≤ Π d(G) ≤ γ(G) + 1.
At the end of this paper, they observed that if you stipulate that every vertex v ∈ V must dominate all of the vertices in at least one block V i of the partition, other than its own block, then what you get is called a total dominator partition. You also get the following result, where Π td(G) is the total dominator partition number and γ t(G) is the total domination number of a graph G.
Theorem 5
For any graph G, γ t(G) ≤ Π td(G) ≤ γ t(G) + 1.
Total dominator partitions are studied in [406, 449,450,451].
Furthermore, if you stipulate that every block V i of the partition be an independent set, i.e. that the partition is a proper coloring, then you define what is called a dominator coloring of G. The dominator coloring number χ d(G) equals the minimum order of a dominator coloring of G. Gera, Rasmussen and Horton have produced the first paper on dominator colorings [286].
But so far what has eluded us is the hoped-for linear algorithm for determining the dominator coloring number, or dominator chromatic number χ d(T) of any tree T.
5.10 Edge Degree Sequences
We often speak of the vertex degree sequence of a graph G of order n, d 1 ≥ d 2 ≥… ≥ d n. But in this glossary we say nothing about the edge degree sequence, deg(e 1) ≥ deg(e 2) ≥… ≥ deg(e m). These integer sequences are just the vertex degree sequences of line graphs of graphs. But since line graphs form a proper subfamily of the family of all graphs, these edge degree sequences are different. By the edge degree, we mean deg(uv) = deg(u) + deg(v) − 2. What can you say about edge degree sequences of graphs?
5.11 Edge-Vertex Connectivity λ v(G) and Vertex-Edge Connectivity κ e(G)
The definitions of vertex connectivity and edge connectivity in Section 3.2 suggest the following. Let S ⊂ V be a vertex cutset. Recall the definition that a vertex cutset is a set S ⊂ V in a connected graph whose removal results in a graph which is either not connected or consists of a single vertex. Thus, when the vertices in a cutset S are removed, all edges which are incident with a vertex in S are also removed. Let λ v(G) equal the minimum number of edges incident with a vertex in a vertex cutset of G.
If F ⊂ E is an edge cutset of a graph G, then when the edges in F are removed, resulting in a disconnected graph G − F, all vertices incident with an edge in F will have their degrees reduced. Let κ e(G) equal the minimum number of vertices incident with an edge in an edge cutset of G.
5.12 Flower Number flower(G) and Petal Number petal(G)
The definition of the cycle number cycle(v) in Section 3.2, as the number of distinct cycles containing vertex v, suggests that one define the petal number petal(G) of a graph G to be maximum number of cycles k in a set C 1, C 2, …, C k, having the property that for any i ≠ j, C i ∩ C j = {v}, that is, these cycles are pairwise vertex disjoint except for having vertex v in common. Each cycle in such a collection is called a petal, and the union of all such cycles defines a flower, the petals of which are centered at v. These subgraphs have applications in distribution networks, in which the central vertex is called a hub and the cycles represent circular routes taken by vehicles, delivering items from the hub and picking up items to be taken back to the hub. Given this, one can define the flower number flower(G) of a graph G to equal the maximum order of a flower subgraph of G, and the petal number petal(G) to equal the maximum number of petals in a flower of G.
5.13 Spider Number spider(G)
A spider is a tree which consists of a collection of paths which are pairwise vertex disjoint, except for having exactly one vertex v in common. These subgraphs have applications in distribution networks, in which the vertex v is called a hub and the paths represent routes taken by vehicles; each vehicle travels from the hub to all of the vertices along the path, delivering items from the hub, and returns from the end of the path, picking up items to be taken back to the hub along the same path. Given this, one could define the spider number spider(G) to equal the maximum order of a (not necessarily induced) spider subgraph in G.
5.14 Four Color Theorems
Arguably the most famous theorem in all of graph theory is the Four Color Theorem, about which volumes have been written. From the perspective of parameters of graphs, the chromatic number χ(G) is a parameter whose largest value over the infinite class of planar graphs is 4, that is, for any planar graph G, χ(G) ≤ 4.
In Sections 3.5 and 3.7 of this Glossary, we have listed and defined about 65 decomposition, partition and coloring parameters of graphs, where we have assumed that graphs are simple, undirected, and have no loops or multiple edges. Consider doing the following: (1) list all 65 such parameters, (2) for each parameter, say generically ρ(G), ask: does there exist a finite constant k, such that for any planar graph G, ρ(G) ≤ k?
For example, the Grundy number, Γr(G) of a tree can be arbitrarily large, and therefore, so can the partial Grundy number ∂Γr(G), the achromatic number, ψ(G), and the pseudoachromatic number, ψ s(G). Thus, when restricted to planar graphs, none of these coloring parameters can be bounded above by a constant.
As another example, we have seen that for the infinite square grid graphs, which of course are planar, the packing chromatic number is bounded between 13 and 15. Does the packing chromatic number have a constant upper bound for the class of planar graphs? Another interesting example is the b-chromatic number; is this number at most 4 for planar graphs?
In Sections 3.6 and 3.7, we define several numbers that are lower bounds for the chromatic number χ(G). From the Four Color Theorem we know that for any planar graph G, χ(G) ≤ 4, and therefore, each of these numbers is at most 4 for planar graphs. But can you prove directly, without using the Four Color Theorem, that any of the following numbers are at most 4 for planar graphs?
-
1.
the co-chromatic number, z(G) ≤ χ(G), each color class is either a clique or an independent set.
-
2.
the sub-chromatic number, χ s(G) ≤ χ(G), each color class is a union of cliques.
-
3.
the iterated domination number, γ ∗(G) ≤ χ(G), each color class is a minimal dominating set in the graph remaining after removing all previous color classes.
-
4.
the iterated irredundance number, ir ∗(G) ≤ χ(G), each color class is a maximal irredundant set in the graph remaining after removing all previous color classes.
-
5.
the k-dependent chromatic number, for any fixed k, χ ≤k(G) ≤ χ(G), each color class is a k-dependent set.
-
6.
the irredundant chromatic number, χ irr(G) ≤ χ(G), each color class is a, not necessarily maximal, irredundant set.
-
7.
forest arboricity, χ F(G) ≤ χ(G), each color class is an induced forest of trees.
-
8.
path arboricity, χ P(G) ≤ χ(G), each color class is an induced forest of paths.
-
9.
star arboricity, χ ∗(G) ≤ χ(G), each color class is an induced forest of stars.
-
10.
spider arboricity, χ S(G) ≤ χ(G), each color class is an induced forest of spiders.
5.15 Generalized Irredundant Sets
In 1999, Cockayne [158] introduced many new kinds of generalized irredundant sets, but perhaps the most interesting ones are the 12 types of irredundant sets that are hereditary, meaning that every subset of a given type of irredundant set, is also an irredundant set of the same type. Let S denote that a vertex has itself as a private neighbor; let I denote that a vertex has an internal private neighbor, and let E denote that a vertex has an external private neighbor, all with respect to some set S. Consider the following 12 types of irredundant sets, that is let IR i(G) equal the maximum cardinality set S having each of the following properties with regard to private neighbors for the elements of S.
-
1.
IR 1[S ∧ E] ……….independent open irredundant sets
-
2.
IR 3[S] ……………..independent sets
-
3.
IR 5[(S ∨ I) ∧ E]
-
4.
IR 7[S ∨ (I ∧ E)]
-
5.
IR 9[(S ∧ E) ∨ (I ∧¬E)]
-
6.
IR 11[S ∨ (I ∧¬E)]
-
7.
IR 13[(S ∧ E) ∨ I]
-
8.
IR 15[S ∨ I] ………1-dependent sets
-
9.
IR 21[E] ……………open irredundant sets
-
10.
IR 23[S ∨ E] ………irredundant sets
-
11.
IR 29[I ∨ E] ………….open-open irredundant sets
-
12.
IR 31[S ∨ I ∨ E] …….closed-open irredundant sets
Cockayne points out the following inequalities between various of these irredundance parameters.
Theorem 6
For any graph G,
-
1.
IR 1 ≤ IR 5 ≤ IR 21
-
2.
IR 9 ≤ IR 13 ≤ IR 29
-
3.
IR 3 ≤ IR 7 ≤ IR 23
-
4.
IR 11 ≤ IR 15 ≤ IR 31
-
5.
IR 1 ≤ IR 3 ≤ IR 11
-
6.
IR 1 ≤ IR 9 ≤ IR 11
-
7.
IR 5 ≤ IR 7 ≤ IR 15
-
8.
IR 5 ≤ IR 13 ≤ IR 15
-
9.
IR 21 ≤ IR 23 ≤ IR 31
-
10.
IR 21 ≤ IR 29 ≤ IR 31
Taken together, these parameters define a 2 × 3 × 2 cube of inequalities, or in other words, they form the prism consisting of two parallel copies of a 2 × 3 grid.
Irredundant sets of types 5, 7, 9, 11, and 13 have not been studied.
5.16 Hall Ratios
The Hall Ratio of a graph G is defined to equal max{|V (H)|∕α(H) : H a subgraph of G}, where α(G) is the vertex independence number of a graph G. This ratio was first introduced by Hilton and Johnson in 1990 [416], and is related to the study of the chromatic number and list colorings of graphs. But the Hall ratio is really quite generic, and brings to mind other ratios, like the binding number and toughness. This suggests that it might be worthwhile to consider the ratios of any number of parameters to the orders of a graph.
5.17 Hamiltonian Bottleneck Number hbn(G)
The definition of the Hamiltonian number h(G) in Section 3.3 suggests the following. Let c = v 1, v 2, …, v n, v n+1 = v 1 be a cyclic ordering of the vertices of a graph G. Let the Hamiltonian bottleneck number of a cyclic ordering c be hbn(c) = max{d(v i, v i+1) : 1 ≤ i ≤ n}, that is, hbn(c) equals the maximum distance between two consecutive vertices of c. The Hamiltonian bottleneck number is hbn(G) = min{hbn(c) : c a cyclic ordering of V }. It follows immediately that hbn(G) = 1 if and only if G is Hamiltonian. The same parameter can be considered for linear orderings l = v 1, v 2, …, v n of the vertices of graphs of order n, in which case one is considering Hamiltonian paths, and one can define the Hamiltonian path bottleneck number hpbn(G). Obviously, hpbn(G) = 1 if and only if G has a Hamiltonian path. In 1964, Sekanina [564] asked, in effect, for which graphs G is hpbn(G) = 2? The author states: “For trees this problem was solved in a paper of F. Neuman, to appear in Čas. Pěst. Mat.”; however, we have not been able to find such a paper. It appears that the graphs for which hbn(G) = 2 are those graphs G whose square G 2 is Hamiltonian, and these graphs have been studied.
5.18 Minimaximal Path Number mmp(G) and Minimaximal Trail Number mmt(G)
The definition of the trail number in Section 3.3 suggests the following. Recall that a trail is a walk having no repeated edges. A path or a trail is maximal if its length cannot be increased by the addition of an edge at either end. It does not appear that the minimum length of a maximal path mmp(G) or the minimum length of a maximal trail mmt(G) have been studied.
5.19 New Inequality Chains from Hereditary and Super-Hereditary Properties
The well-studied domination chain is the following:
where
-
er(G) and ER(G) denote the lower and upper external redundance numbers,
-
ir(G) and IR(G) denote the lower and upper irredundance numbers,
-
γ(G) and Γ(G) denote the lower and upper domination numbers, and
-
i(G) and α(G) denote the independent domination number and the independence number.
We think we understand why these inequality chains exist. For example, independence is a hereditary property, domination is a superhereditary property, and irredundance is a hereditary property. But we do not understand why external redundance is not a superhereditary property.
Thus, in order to figure this out, we think it would be a good idea to study several other inequality chains. The idea is simple.
Start with any hereditary property P 1. Then define two parameters: the minimum cardinality of a maximal P 1-set and the maximum cardinality of a P 1-set, say β 1(G) and α 1(G), respectively.
Next, use the maximality condition of a P 1-set to define a second property P 2. This property P 2 should be super-hereditary. Use this property to define two new parameters: the minimum cardinality of a P 2-set and the maximum cardinality of a minimal P 2-set, say β 2(G) and α 2(G), respectively.
At this point it should be the case that: β 2(G) ≤ β 1(G) ≤ α 1(G) ≤ α 2(G).
Now, continue in the same way. Use the minimality condition of a P 2-set to define a third property P 3. This property should be hereditary. Use this property to define two new parameters: the minimum cardinality of a maximal P 3-set and the maximum cardinality of a P 3-set, say β 3(G) and α 3(G), respectively.
At this point it should be the case that:
As we said, you can start to build such an inequality chain with any hereditary property. Examples of hereditary properties of sets S ⊆ V include the following, where G[S] denotes the subgraph induced by S:
-
1.
G[S] is acyclic,
-
2.
S is k-dependent, i.e. the maximum degree Δ(G[S]) ≤ k,
-
3.
S is a packing,
-
4.
G[S] is bipartite,
-
5.
S is matchable,
-
6.
S is irredundant, open irredundant, open-open irredundant, etc.,
-
7.
S is a restrained set, i.e. for every u ∈ (V − S), N(u) ∩ (V − S) ≠ ∅, or
-
8.
S is enclaveless, i.e. for every u ∈ S, N(u) ∩ (V − S) ≠ ∅.
We should also point out that one can start an inequality chain with a super-hereditary property just as well. Examples of super-hereditary properties include:
-
1.
G[S] contains a cycle,
-
2.
Δ(G[S]) ≥ k,
-
3.
S is a dominating set,
-
4.
S is a total dominating set,
-
5.
S is a strong dominating set,
-
6.
S is an internally strong dominating set,
-
7.
S is a vertex cover,
-
8.
S is a global offensive alliance,
-
9.
S is a distance-k dominating set,
-
10.
S is a P 3-dominating set,
-
11.
S is a capacity-k dominating set.
5.20 New Max and Min Domination Parameters
Subramanian [596], and later Arumugam and Subramanian [20] introduced an independence idea that spawns a whole host of new parameters.
Define the following for every vertex v ∈ V :
-
ir(v) = min {|S|, v ∈ S and S is a maximal irredundant set}
-
γ(v) = min {|S|, v ∈ S and S is a minimal dominating set}
-
i(v) = min {|S|, v ∈ S and S is a maximal independent dominating set}
-
α(v) = max {|S|, v ∈ S and S is an independent set}
-
Γ(v) =max {|S|, v ∈ S and S is a minimal dominating set}
-
IR(v) = max {|S|, v ∈ S and S is an irredundant set}
Now, over all vertices v ∈ V define the following:
-
irmax(G) = max {ir(v) : v ∈ V }
-
γmax(G) = max {γ(v) : v ∈ V }
-
imax(G) = max {i(v) : v ∈ V }
-
αmin(G) = min {α(v) : v ∈ V }
-
Γmin(G) = min {Γ(v) : v ∈ V }
-
IRmin(G) = min {IR(v) : v ∈ V }
The following inequalities follow from these definitions:
Proposition 1
For any graph G,
-
(i)
ir(G) ≤ irmax(G)
-
(ii)
γ(G) ≤ γmax(G)
-
(iii)
i(G) ≤ imax(G)
-
(iv)
αmin(G) ≤ α(G)
-
(v)
Γmin(G) ≤ Γ(G)
-
(vi)
IRmin(G) ≤ IR(G)
These parameters have received very little study.
5.21 P-Matchings and the Independent Matching Number \(\alpha ^{\prime }_{ind}(G)\)
Let e 1 = x 1 y 1, e 2 = x 2 y 2, …, e k = x k y k be the edges of a matching M, and let X(M) = {x , x 2, …, x k} and Y (M) = {y 1, y 2, …, y k}. We can think of the edges of M as being oriented vertically, with the vertices in X(M) being situated above, or to the north of, the vertices in Y (M) to the south. One can see that V (M) = (X(M), Y (M)) represents one of 2k possible orientations of the edges of M. We say that a matching M is independent if it has an orientation such that the set X(M) is an independent set. Thus, the independent matching number \(\alpha ^{\prime }_{ind}(G)\) equals the maximum cardinality of an independent matching in G. For this parameter, for example, it is not difficult to show that for any nontrivial tree T, \(\alpha '(T) = \alpha ^{\prime }_{ind}(T)\).
This, in turn, suggests a broad new concept. A P-matching is a matching M = {x 1 y 1, x 2 y 2, …, x k y k}, such that the set X = {x 1, x 2, …, x k} is a set having property P. There are many properties P of interest. For example, one can define \(\alpha ^{\prime }_c(G)\) to equal the maximum cardinality of a connected matching; in this case, there exists a matching M having an orientation V (M) = (X(M), Y (M)) such that the induced subgraph G[X(M)] is connected. Another interesting example are matchings M where the set X(M) is a dominating set, in which case M is a dominating matching, or where the set X(M) ∪ Y (M) is a dominating set. In this case, V (M) = X(M) ∪ Y (M) is a paired dominating set, as defined in Section 3.8.1. Still another interesting case occurs where both sets X(M) and Y (M) are dominating sets; these could be called matched dominating sets.
5.22 P, Q-Matchings
Let P and Q be two properties of sets of vertices. A matching M is called a P, Q-matching if it has an orientation V (M) = (X(M), Y (M)) such that X(M) has property P and Y (M) has property Q. For example, if P = Q and P is the property of being an independent set, then a doubly independent matching is a matching M having an orientation V (M) = (X(M), Y (M)) in which both X(M) an Y (M) are independent sets.
5.23 Regular and Uniformly Regular Colorings
A partition π = {V 1, V 2, …, V k} of the vertices V of a graph G = (V, E) is called a regular coloring if the subgraph G[V i] induced by each color class V i is a regular graph. The regular chromatic number χ r(G) of a graph G equals the minimum order of a regular coloring of G.
A partition π = {V 1, V 2, …, V k} of the vertices V of a graph G = (V, E) is called a uniformly regular coloring if the subgraph G[V i] induced by each color class V i is a disjoint union of regular graphs. The uniformly regular chromatic number χ ur(G) of a graph G equals the minimum order of a uniformly regular coloring of G.
Uniformly regular colorings are closely related to what are called sub-chromatic colorings which are defined in Section 3.7. The sub-chromatic number χ K(G) equals the minimum order of a partition π = {V 1, V 2, …, V k} of the vertices V of a graph G = (V, E) such that every color class V i induces a subgraph consisting of a disjoint union of complete subgraphs. Thus, sub-chromatic colorings are uniformly regular colorings, but not conversely.
Proposition 2
For any graph G, χ ur(G) ≤ χ r(G) ≤ χ(G).
Can you prove that either χ ur(G) ≤ 4 or χ K(G) ≤ 4 for planar graphs G, without appealing to the Four Color Theorem?
5.24 Two Disjoint \(\mathcal {P}\)-Sets
Hedetniemi et al. [394] considered the minimum cardinality of two disjoint dominating sets in a graph G, called the dual domination number, denoted by γγ(G). It follows, by definition, that 2γ(G) ≤ γγ(G) ≤ γ(G) + γ −1(G), where γ −1(G) is the inverse domination number.
One can also define the upper dual domination number, ΓΓ(G), to equal the maximum cardinality of two disjoint minimal dominating sets in a graph G. This parameter was not studied. But there is more. One can define iγ(G) and αγ(G) to equal the minimum and maximum cardinality of an independent dominating set and a disjoint minimal dominating set, respectively. It then follows from all of these definitions that:
and, in addition, we have:
None of these parameters, other than γγ(G), appear to have been studied.
5.25 Uniformly Strong Sets
In [440], Kamath and Bhat define a vertex v in a graph G = (V, E) to be strong if deg(v) ≥ deg(u) for every vertex u adjacent to v. Similarly, a vertex is called weak if deg(v) ≤ deg(u) for every vertex u adjacent to v. These two definitions suggest a variety of new things that can be studied.
Let us define a set S ⊆ V to be uniformly strong if every vertex u ∈ S is a strong vertex in the induced subgraph G[S]. The maximum cardinality of a uniformly strong set is called the uniformly strong number of a graph G and is denoted S(G). Similarly, the minimum cardinality of a maximal uniformly strong set S, denoted s(G), is called the lower uniformly strong number of G.
Notice that uniformly strong sets are essentially sets S such that the induced subgraph G[S] consists of a disjoint union of regular graphs. Note that the property of being a strong set is neither hereditary nor super-hereditary. The following results follow immediately from the definitions.
Proposition 3
For any regular graph G of order n, s(G) = S(G) = n.
Recall that α(G), the independence number of G, equals the maximum cardinality of an independent set in G. Similarly, α 1(G) is the 1-dependence number, i.e. the maximum cardinality of a set S such that Δ(G[S]) ≤ 1. Similarly, i(G) equals the minimum cardinality of a maximal independent set in G (also called the independent domination number), while i 1(G), the lower 1-dependence number, equals the minimum cardinality of a maximal 1-dependent set in G.
Notice that the subgraphs induced by maximal 1-dependent sets are just disjoint unions of K 1’s and K 2’s. Thus, they are strong sets.
Proposition 4
For any graph G of order n,
Proposition 5
For any tree T, S(T) = α 1(T).
What can you say about the values of s(G) and S(G)?
6 Conclusions
In this glossary we have enumerated some 300 parameters commonly used in graph theory, and for many of these we have presented related conjectures. We also listed several new suggested parameters and open problems. While many of the numbers listed in the glossary and still other parameters have been discussed in other comprehensive books, we feel this is the most comprehensive glossary ever assembled of graph theory parameters. Within the given time and page limitations for producing this glossary, we have annotated many of these parameters with basic properties, results, and conjectures about them, in order to provide a clearer understanding of these parameters beyond their mere definition.
No attempt has been made in this glossary of parameters and related conjectures to be complete. Indeed, it would be a formidable task to construct a complete listing. Furthermore, no attempt has been made to provide a complete bibliography of the publications in which these parameters first appeared or have been studied.
But with an eye toward the creation of future areas of research in graph theory, and their corresponding new parameters, let us close with this thought. Consider each of the following five combinatorial optimization problems, all found in the classic NP-completeness book by Garey and Johnson [281], which is well-known to researchers in graph algorithms and complexity. Each of these five problems has become a well-known, basic NP-complete decision problem.
[SP3] Set Packing
Given a collection S of finite sets and a positive integer k ≤|S|, does S contain at least k mutually disjoint sets?
[SP4] Set Splitting
Given a collection S of subsets of a finite set S, is there a bipartition S = {S 1, S 2} of S, such that no subset in S is contained entirely in S 1 or S 2?
[SP5] Minimum Cover
Given a collection S of finite subsets of a set S, and a positive integer k ≤|S|, does S contain a cover for S of cardinality at most k? that is, a subset S′⊆S where |S′|≤ k and every element of S belongs to at least one member of S′?
[SP6] Minimum Test Set
Given a collection S of finite subsets of a set S, and a positive integer k ≤|S|, does S contain a subset S′⊆S of cardinality at most k, such that for every u, v ∈ S there is at least one set in S’ that contains exactly one of u and v?
[SP7] Set Basis
Given a collection S of finite subsets of a set S, and a positive integer k ≤|S|, is there a collection B of k subsets of S such that for each set S” ∈S there is a sub-collection of B whose union is precisely S”?
Each of these five general set problems has many instances when applied to graphs G = (V, E). First of all, one can speak of the families of sets of vertices in (1) open neighborhoods, (2) closed neighborhoods, (3) paths, (4) induced paths, (5) cycles, (6) induced cycles, (7) complete subgraphs, (8) independent sets, or maximal independent sets, and (9) dominating sets or minimal dominating sets, and many, many more instances.
Next, one can speak of the families of sets of edges in similar sets, e.g. paths, induced paths, cycles, induced cycles, cliques and independent sets of edges, but including the sets of edges E(v) incident to a given vertex v or the sets of edges defining a spanning tree, and many, many more instances.
With each instance of any one of these five general problem types, there will be corresponding minimum, maximum, mini-maximal or maxi-minimal parameters.
Thus, this glossary not only provides a fairly comprehensive collection of parameters that have been defined and studied, but provides many ideas for the discovery and future study of parameters.
Notes
- 1.
Defined in [83] as the order of the detour path.
References
W. Abbas, M. Egerstedt, C.-H. Liu, R. Thomas, P. Whalen, Deploying robots with two sensors in K 1,6-free graphs. J. Graph Theory 82(3), 236–252 (2016)
H.A. Ahangar, M.A. Henning, C. Löwenstein, Y. Zhao, V. Samodivkin, Signed Roman domination in graphs. J. Comb. Optim. 27(2), 241–255 (2014)
H.A. Ahangar, M.A. Henning, V. Samodivkin, I. G. Yero, Total Roman domination in graphs. Appl. Anal. Discret. Math. 10(2), 501–517 (2016)
R. Aharoni, E.C. Milner, K. Prikry, Unfriendly partitions of a graph. J. Combin. Theory, Ser. B 50(1), 1–10 (1990)
M.H. Akhbari, R. Hasni, O. Favaron, H. Karami, S.M. Sheikholeslami, On the outer-connected domination in graphs. J. Comb. Optim. 26(1), 10–18 (2013)
J. Akiyama, G. Exoo, F. Harary, Covering and packing in graphs iv: linear arboricity. Networks 11(1), 69–72 (1981)
O.S. Al Mushayt, On edge irregularity strength of products of certain families of graphs with path P 2. Ars Combin. 135, 323–334 (2017)
Y. Alavi, M. Behzad, Complementary graphs and edge chromatic numbers. SIAM J. Appl. Math. 20(2), 161–163 (1971)
Y. Alavi, M. Behzad, L.M. Lesniak-Foster, E.A. Nordhaus, Total matchings and total coverings of graphs. J. Graph Theory 1(2), 135–140 (1977)
M.O. Albertson, K.L. Collins, Symmetry breaking in graphs. Electron. J. Comb. 3(1), 17 pp. (1996). Research Paper 18
M.O. Albertson, R.E. Jamison, S.T. Hedetniemi, S.C. Locke, The subchromatic number of a graph. Discret. Math. 74, 33–49 (1989)
I. Algor, N. Alon, The star arboricity of graphs. Ann. Discret. Math. 43, 11–22 (1989)
N. Alon, The linear arboricity of graphs. Isr. J. Math. 62(3), 311–325 (1988)
A. Alqesmah, A. Alwardi, R. Rangarajan, On the injective domination polynomial of graphs. Palest. J. Math. 7(1), 234–242 (2018)
B.R. Alspach, N.J. Pullman. Path decompositions of digraphs. Bull. Aust. Math. Soc. 10(3), 421–427 (1974)
J. Amjadi, An upper bound on the double domination number of trees. Kragujev. J. Math. 39(2), 133–139 (2015)
E. Andrews, C. Lumduanhom, E. Laforge, P. Zhang, On proper-path colorings in graphs. J. Comb. Math. Comb. Comput. 97, 189–207 (2016)
M. Aouchiche, P. Hansen, A survey of automated conjectures in spectral graph theory. Linear Algebra Appl. 432(9), 2293–2322 (2010)
D. Archdeacon, A note on defective colorings of graphs in surfaces. J. Graph Theory 11(4), 517–519 (1987)
S. Arumugam, M. Subramanian, Edge subdivision and independence saturation in a graph. Graph Theory Notes of N. Y. LII, 9–12 (2007)
S. Arumugam, M. Sundarakannan, On equality in an upper bound for the equivalence domination number. Quaest. Math. 38(1), 63–71 (2015)
S. Arumugam, S. Suseela, J. Suresh, Acyclic graphoidal covers and path partitions in a graph. Discret. Math. 190(1–3), 67–77 (1998)
S. Arumugam, K. Chandrasekar, K. Raja, S. Sudha, Irredundant and open irredundant colorings of graphs. Bull. Inst. Combin. Appl. 61, 24–36 (2011)
S. Arumugam, K.R. Chandrasekar, N. Misra, G. Philip, S. Saurabh, Algorithmic aspects of dominator colorings in graphs, in International Workshop on Combinatorial Algorithms (Springer, Berlin, 2011), pp. 19–30
S. Arumugam, J. Bagga, K.R. Chandrasekar, On dominator colorings in graphs. Proc. Math. Sci. 122(4), 561–571 (2012)
S. Arumugam, S.T. Hedetniemi, S.M. Hedetniemi, L. Sathikala, S. Sudha, The covering chain of a graph. Util. Math. 98, 183–196 (2015)
A. Aytac, Z. Kartal, Complement graphs and total influence number. Romanian J. Math. Comput. Sci. 7(1), 41–55 (2017)
L. Babai, P. Erdös, S.M. Selkow, Random graph isomorphism. SIAM J. Comput. 9(3), 628–635 (1980)
M. Bača, S. Jendrol, M. Miller, J. Ryan, On irregular total labellings. Discret. Math. 307(11–12), 1378–1388 (2007)
B. Baker, R. Shostak, Gossips and telephones. Discret. Math. 2, 191–193 (1972)
R. Balakrishnan, T. Kavaskar, Color chain of a graph. Graphs Combin. 27(4), 487–493 (2011)
C. Balbuena, A. Hansberg, T.W. Haynes, M.A. Henning, Total domination edge critical graphs with total domination number three and many dominating pairs. Graphs Combin. 31(5), 1163–1176 (2015)
D. Barnette, Conjecture 5, in Recent Problems in Combinatorics, ed. by W.T. Tutte (Academic Press, New York, 1969)
M.E. Bascunán, S. Ruiz, P.J. Slater, The additive bandwidth of grids and complete bipartite graphs. Congr. Numer. 88, 245–254 (1992)
M.E. Bascunán, R.C. Brigham, R.M. Caron, S. Ruiz, P.J. Slater, R.P. Vitray, On the additive bandwidth of graphs. J. Comb. Math. Comb. Comput., 18, 129–144 (1995)
D. Bauer, H.J. Broersma, H.J. Veldman, Not every 2-tough graph is Hamiltonian, in Proceedings of the 5th Twente Workshop on Graphs and Combinatorial Optimization (Enschede, 1997), vol. 99 (2000), pp. 317–321
D. Bauer, H. Broersma, E. Schmeichel, Toughness in graphs–a survey. Graphs Combin. 22(1), 1–35 (2006)
R.A. Beeler, T.W. Haynes, S.T. Hedetniemi, Double Roman domination. Discret. Appl. Math. 211, 23–29 (2016)
M. Behzad, A criterion for the planarity of the total graph of a graph. Math. Proc. Camb. Philos. Soc. 63(3), 679–681 (1967)
M. Behzad, Graphs and Their Chromatic Numbers, PhD thesis, Michigan State University, 1967
L.W. Beineke, On the Decomposition of Complete Graphs into Planar and Other Subgraphs, PhD thesis, University of Michigan, 1965
C. Belford, N. Sieben, Rubbling and optimal rubbling of graphs. Discret. Math. 309(10), 3436–3446 (2009)
J. Bensmail, A. Lagoutte, P. Valicov, Strong edge-coloring of (3, Δ)-bipartite graphs (2015). ArXiv:1412.2624v2 [cs.DM]
C. Berge, Theory of Graphs and Its Applications (Methuen, London, 1962)
S. Bermudo, On the differential and Roman domination number of a graph with minimum degree two. Discret. Appl. Math. 232, 64–72 (2017)
S. Bermudo, H. Fernau, J.M. Sigarreta, The differential and the Roman domination number of a graph. Appl. Anal. Discret. Math. 8(1), 155–171 (2014)
P.J. Bernhard, S.T. Hedetniemi, D.P. Jacobs, Efficient sets in graphs. Discret. Appl. Math. 44(1–3), 99–108 (1993)
U. Bertele, F. Brioschi, Nonserial Dynamic Programming (Academic Press, New York, 1972)
V.N. Bhave, On the pseudoachromatic number of a graph. Fundam. Math. 102, 159–164 (1979)
D. Bienstock, N. Dean, Bounds for rectilinear crossing numbers. J. Graph Theory 17(3), 333–348 (1993)
N. Biggs, Perfect codes in graphs. J. Combin. Theory, Ser. B 15(3), 289–296 (1973)
J.R.S. Blair, The efficiency of AC graphs. Discret. Appl. Math. 44(1–3), 119–138 (1993)
J.R.S. Blair, W. Goddard, S.M. Hedetniemi, S.T. Hedetniemi, S.B. Horton, Domination equivalence in graphs. AKCE Int. J. Graphs Comb. 2, 123–136 (2005)
J.R.S. Blair, W. Goddard, S.T. Hedetniemi, S. Horton, P. Jones, G. Kubicki, On domination and reinforcement numbers in trees. Discret. Math. 308(7), 1165–1175 (2008)
J. Blair, W. Goddard, S.M. Hedetniemi, S.T. Hedetniemi, F. Manne, D.F. Rall, Emergency response sets in graphs. J. Comb. Math. Comb. Comput. 68, 225–243 (2009)
J. Blair, R. Gera, S. Horton, Movable dominating sensor sets in networks. J. Comb. Math. Comb. Comput. 77, 103–123 (2011)
H.L. Bodlaender, A tourist guide through treewidth. Acta Cybernet. 11(1–2), 1 (1994)
T. Böhme, A. Kostochka, A. Thomason, Hadwiger numbers and over-dominating colourings. Discret. Math. 310(20), 2662–2665 (2010)
B. Bollobás, Almost every graph has reconstruction number three. J. Graph Theory 14(1), 1–4 (1990)
B. Bollobás, Extremal Graph Theory (Dover Publications, Mineola, 2004). Reprint of the 1978 original
B. Bollobás, F. Harary, The trail number of a graph, in Graph Theory. North-Holland Mathematics Studies, vol 62 (Elsevier, New York, 1982), pp. 51–60
B. Bollobás, A.J. Harris, List-colourings of graphs. Graphs Combin. 1(1), 115–127 (1985)
B. Bollobás, A. Thomason. Set colourings of graphs. Discret. Math. 25(1), 21–26 (1979)
B. Bollobás, P.A. Catlin, P. Erdös, Hadwiger’s conjecture is true for almost every graph. Eur. J. Comb. 1(3), 195–199 (1980)
A. Bonato, R.J. Nowakowski, Sketchy tweets: ten minute conjectures in graph theory. Math. Intell. 34(1), 8–15 (2012)
A. Bondy, Beautiful conjectures in graph theory. Eur. J. Comb. 37, 4–23 (2014)
O.V. Borodin, On acyclic colorings of planar graphs. Discret. Math. 25(3), 211–236 (1979)
F. Botler, A. Jiménez, On path decompositions of 2k-regular graphs. Discret. Math. 340(6), 1405–1411 (2017)
R. Boutrig, M. Chellali, T.W. Haynes, S.T. Hedetniemi, Vertex-edge domination in graphs. Quaest. Math. 90(2), 355–366 (2016)
M. Bouzefrane, M. Chellali, On the global offensive alliance number of a tree. Opusc. Math. 29(3), 223–228 (2009)
M. Bouzefrane, M. Chellali, T.W. Haynes, Global defensive alliances in trees. Util. Math. 82, 241–252 (2010)
M.R. Bowie, Liar’s Domination and the Domination Continuum: A Dissertation, PhD thesis, University of Alabama in Huntsville, 2008
A. Brandstädt, R. Mosca, On distance-3 matchings and induced matchings. Discret. Appl. Math. 159(7), 509–520 (2011)
B. Brešar, Improving the Clark-Suen bound on the domination number of the Cartesian product of graphs. Discret. Math. 340(10), 2398–2401 (2017)
B. Brešar, S. Špacapan, Broadcast domination of products of graphs. Ars Combin. 92, 303–320 (2009)
B. Brešar, T.K. Šumenjak, On the 2-rainbow domination in graphs. Discret. Appl. Math. 155(17), 2394–2400 (2007)
B. Brešar, M.A. Henning, D.F. Rall, Rainbow domination in graphs. Taiwan. J. Math. 12(1), 213–225 (2008)
B. Brešar, P. Dorbec, W. Goddard, B.L. Hartnell, M.A. Henning, S. Klavžar, D.F. Rall, Vizing’s conjecture: a survey and recent results. J. Graph Theory 69(1), 46–76 (2012)
R.C. Brigham, J.R. Carrington, Global domination, in Domination in Graphs, Advanced Topics, ed. by T.W. Haynes, S.T. Hedetniemi, P.J. Slater. Pure and Applied Mathematics, vol. 209 (Marcel Dekker, New York, 1998), pp. 301–320
R.C. Brigham, R.D. Dutton, Neighborhood numbers, new invariants of undirected graphs. Congr. Numer. 53, 121–132 (1986)
R.C. Brigham, R.D. Dutton, T.W. Haynes, S.T. Hedetniemi, Powerful alliances in graphs. Discret. Math. 309(8), 2140–2147 (2009)
I. Broere, J.H. Hattingh, M.A. Henning, A.A. McRae, Majority domination in graphs. Discret. Math. 138(1–3), 125–135 (1995)
I. Broere, M. Dorfling, J. Dunbar, M. Frick, A path (ological) partition problem. Discuss. Math. Graph Theory 18(1), 113–125 (1998)
I. Broere, E. Jonck, G.S. Domke, L.R. Markus, The induced path number of the complements of some graphs. Australas. J. Comb. 33, 15–32 (2005)
H.J. Broersma, Z. Ryjáček, P. Vrána, How many conjectures can you stand? A survey. Graphs Combin. 28(1), 57–75 (2012)
R.A. Brualdi, J.J. Quinn Massey, Incidence and strong edge colorings of graphs. Discret. Math. 122(1–3), 51–58 (1993)
F. Buckley, F. Harary, On longest induced path in graphs. Chinese Quart. J. Math 3(3), 61–65 (1988)
F. Buckley, F. Harary, Distance in Graphs (Addison-Wesley, Boston, 1990)
D.P. Bunde, E.W. Chambers, D. Cranston, K. Milans, D.B. West, Pebbling and optimal pebbling in graphs. J. Graph Theory 57(3), 215–238 (2008)
A.P. Burger, E.J. Cockayne, W.R. Grundlingh, C.M. Mynhardt, J.H. Van Vuuren, W. Winterbach, Infinite order domination in graphs. J. Comb. Math. Comb. Comput. 50, 179–194 (2004)
A.P. Burger, M.A. Henning, J.H. Van Vuuren, Vertex covers and secure domination in graphs. Quaest. Math. 31(2), 163–171 (2008)
A.C. Burris, R.H. Schelp, Vertex-distinguishing proper edge-colorings. J. Graph Theory 26(2), 73–82 (1997)
L. Caccetta, R. Häggkvist, On diameter critical graphs. Discret. Math. 28(3), 223–229 (1979)
N. Cairnie, K. Edwards, Some results on the achromatic number. J. Graph Theory 26(3), 129–136 (1997)
K. Cameron, Induced matchings. Discret. Appl. Math. 24(1–3), 97–102 (1989)
P.J. Cameron, A. Montanaro, M.W. Newman, S. Severini, A. Winter, On the quantum chromatic number of a graph. Electron. J. Comb. 14(1), R81 (2007)
C.N. Campos, C.P. de Mello, The total chromatic number of some bipartite graphs. Electron. Notes Discrete Math. 22, 557–561 (2008)
Y. Caro, W.F. Klostermeyer, The odd domination number of a graph. J. Comb. Math. Comb. Comput. 44, 65–84 (2003)
Y. Caro, Z. Tuza, Improved lower bounds on k-independence. J. Graph Theory 15(1), 99–107 (1991)
Y. Caro, W.F. Klostermeyer, J.L. Goldwasser, Odd and residue domination numbers of a graph. Discuss. Math. Graph Theory 21(1), 119–136 (2001)
Y. Caro, A. Lev, Y. Roditty, Z. Tuza, R. Yuster, On rainbow connection. Electron. J. Comb. 15(1), R57 (2008)
Y. Caro, A. Hansberg, M. Henning, Fair domination in graphs. Discret. Math. 312(19), 2905–2914 (2012)
B.M. Case, S.T. Hedetniemi, R.C. Laskar, D.J. Lipman, Partial domination in graphs. Congr. Numer. 228, 85–95 (2017)
P.A. Catlin, Hajós’ graph-coloring conjecture: variations and counterexamples. J. Combin. Theory Ser. B 26(2), 268–274 (1979)
A. Chaemchan, The edge domination number of connected graphs. Australas. J. Comb. 48, 185–189 (2010)
E.W. Chambers, B. Kinnersley, N. Prince, D.B. West, Extremal problems for Roman domination. SIAM J. Discret. Math. 23(3), 1575–1586 (2009)
J.D. Chandler, W.J. Desormeaux, T.W. Haynes, S.T. Hedetniemi, Neighborhood-restricted [≤ 2]-achromatic colorings. Discret. Appl. Math. 207, 39–44 (2016)
L.S. Chandran, N. Sivadasan, On the Hadwiger’s conjecture for graph products. Discret. Math. 307(2), 266–273 (2007)
G.J. Chang, M. Farber, Z. Tuza, Algorithmic aspects of neighborhood numbers. SIAM J. Discret. Math. 6(1), 24–29 (1993)
G.J. Chang, C.P. Rangan, S.R. Coorg, Weighted independent perfect domination on cocomparability graphs. Discret. Appl. Math. 63(3), 215–222 (1995)
G.J. Chang, P. Dorbec, M. Montassier, A. Raspaud, Generalized power domination of graphs. Discret. Appl. Math. 160(12), 1691–1698 (2012)
G.J. Chang, S.-H. Chen, C.-H. Liu, Edge Roman domination on graphs. Graphs and Combin. 32(5), 1731–1747 (2016)
G. Chartrand, Highly irregular, in Graph Theory, Favorite Conjectures and Open Problems, ed. by R. Gera, S.T. Hedetniemi, C. Larson (Springer, Berlin, 2016), pp. 1–16
G. Chartrand, R.E. Pippert, Locally connected graphs. Časopis Pěst. Mat. 99, 158–163 (1974)
G. Chartrand, P. Zhang, Convex sets in graphs. Congr. Numer. 136, 19–32 (1999)
G. Chartrand, P. Zhang, On the chromatic dimension of a graph. Congr. Numer. 145, 97–108 (2000)
G. Chartrand, P. Zhang, The theory and applications of resolvability in graphs: a survey. Congr. Numer. 160, 47–68 (2003)
G. Chartrand, P. Zhang, Chromatic Graph Theory (CRC Press, Boca Raton, 2009)
G. Chartrand, M.S. Jacobson, J. Lehel, O.R. Oellermann, S. Ruiz, F. Saba, Irregular networks. 250th Anniversary Conference on Graph Theory (Fort Wayne, IN, 1986). Congr. Numer. 64, 197–210 (1988)
G. Chartrand, M. Jacobson, E. Kubicka, G. Kubicki, The step domination number of a graph. Sci. Ser. A Math. Sci. (N.S.) 6, 29–39 (1994)
G. Chartrand, L. Eroh, M. Schultz, R. Rashidi, N. Sherwani, Distance, stratified graphs, and greatest stratified subgraphs. Congr. Numer. 107, 81–96 (1995)
G. Chartrand, F. Harary, M. Hossaim, K. Schultz, Exact 2-step domination in graphs. Math. Bohem. 120(2), 125–134 (1995)
G. Chartrand, H. Gavlas, R.C. Vandell, F. Harary, The forcing domination number of a graph. J. Comb. Math. Comb. Comput. 25, 161–174 (1997)
G. Chartrand, F. Harary, P. Zhang, The forcing geodetic number of a graph. Discuss. Math. Graph Theory 19, 45–58 (1999)
G. Chartrand, C. Poisson, P. Zhang, Resolvability and the upper dimension of graphs. Comput. Math. Appl. 39(12), 19–28 (2000)
G. Chartrand, D. Erwin, P. Zhang, F. Harary, Radio labelings of graphs. Bull. Inst. Combin. Appl. 33, 77–85 (2001)
G. Chartrand, F. Harary, P. Zhang, On the geodetic number of a graph. Networks 39(1), 1–6 (2002)
G. Chartrand, T.W. Haynes, M.A. Henning, P. Zhang, Detour domination in graphs. Ars Combin. 71, 149–160 (2004)
G. Chartrand, T.W. Haynes, M.A. Henning, P. Zhang, Hamiltonian domination in graphs. Util. Math. 66, 33–45 (2004)
G. Chartrand, G.L. Johns, P. Zhang, On the detour number and geodetic number of a graph. Ars Combin. 72, 3–15 (2004)
G. Chartrand, T. Thomas, V. Saenpholphat, P. Zhang, A new look at hamiltonian walks. Bull. Inst. Combin. Appl. 42, 37–52 (2004)
G. Chartrand, G.L. Johns, K.A. McKeon, P. Zhang, Rainbow connection in graphs. Math. Bohem. 133(1), 85–98 (2008)
G. Chartrand, S.T. Hedetniemi, F. Okamoto, P. Zhang, A four colorings theorem. J. Comb. Math. Comb. Comput. 77, 75–87 (2011)
M. Chellali, Offensive alliances in bipartite graphs. J. Comb. Math. Comb. Comput. 73, 245–255 (2010)
M. Chellali, O. Favaron, On k-star forming sets in graphs. J. Comb. Math. Comb. Comput. 68, 205–214 (2009)
M. Chellali, F. Maffray, Dominator colorings in some classes of graphs. Graphs Combin. 28(1), 97–107 (2012)
M. Chellali, L. Volkmann, Independence and global offensive alliance in graphs. Australas. J. Comb. 47, 125–131 (2010)
M. Chellali, O. Favaron, A. Hansberg, L. Volkmann, k-domination and k-independence in graphs: a survey. Graphs Combin. 28(1), 1–55 (2012)
M. Chellali, T.W. Haynes, S.T. Hedetniemi, A.A. McRae, [1, 2]-sets in graphs. Discret. Appl. Math. 161(18), 2885–2893 (2013)
M. Chellali, O. Favaron, T.W. Haynes, S.T. Hedetniemi, A.A. McRae, Independent [1, k]-sets in graphs. Australas. J. Comb. 59(1), 144–156 (2014)
M. Chellali, T.W. Haynes, S.T. Hedetniemi, A.A. McRae, Roman {2}-domination. Discret. Appl. Math. 204, 22–28 (2016)
M. Chellali, T.W. Haynes, S.T. Hedetniemi, Client–server and cost effective sets in graphs. AKCE Int. J. Graphs Comb. (2017)
M. Chellali, T.W. Haynes, S.T. Hedetniemi, T.M. Lewis, Restricted optimal pebbling and domination in graphs. Discret. Appl. Math. 221, 46–53 (2017)
X. Chen, Adjacent-vertex-distinguishing total chromatic numbers on K 2n+1 − E(p3). Int. J. Pure Appl. Math. 13(1), 19–27 (2004)
X. Chen, S. Fujita, Downhill domination problem in graphs. Inf. Process. Lett. 115(6–8), 580–581 (2015)
W. Chen, E. Song, Lower bounds on several versions of signed domination number. Discret. Math. 308(10), 1837–1846 (2008)
J. Chen, I. Gutman, Y. Yeh, On the sum of all distances in graphs. Tamkang J. Math. 25, 83–86 (1994)
G. Chen, G.S. Domke, J.H. Hattingh, R.C. Laskar, On the upper line-distinguishing and upper harmonious chromatic numbers of a graph. J. Comb. Math. Comb. Comput. 31, 227–239 (1999)
B. Chen, J.H. Kim, M. Tait, J. Verstraete, On coupon colorings of graphs. Discret. Appl. Math. 193, 94–101 (2015)
G.A. Cheston, S.T. Hedetniemi, Polling in tree networks. Congr. Numer. 41, 7–20 (1984)
A.G. Chetwynd, A.J.W. Hilton, Star multigraphs with three vertices of maximum degree. Math. Proc. Camb. Philos. Soc. 100(2), 303–317 (1986)
P.Z. Chinn, J. Chvátalová, A.K. Dewdney, N.E. Gibbs, The bandwidth problem for graphs and matrices - a survey. J. Graph Theory 6, 223–254 (1982)
C.A. Christen, S.M. Selkow, Some perfect coloring properties of graphs. J. Combin. Theory, Ser. B 27(1), 49–59 (1979)
M. Chudnovsky, Cliques and stable sets in undirected graphs, in Geometry, Structure and Randomness in Combinatorics (Springer, Berlin, 2014), pp. 19–25
F. Chung, Pebbling in hypercubes. SIAM J. Discret. Math. 2(4), 467–472 (1989)
V. Chvátal, Tough graphs and hamiltonian circuits. Discret. Math. 5(3), 215–228 (1973)
W.E. Clark, S. Suen, An inequality related to Vizing’s Conjecture. Electron. J. Comb. 7(1), N4, 3 pp. (2000)
E.J. Cockayne, Generalized irredundance in graphs: hereditary properties and Ramsey numbers. J. Comb. Math. Comb. Comput. 31, 15–31 (1999)
E.J. Cockayne, Nordhaus-Gaddum results for open irredundance. J. Comb. Math. Comb. Comput. 47, 213–224 (2003)
E.J. Cockayne, S. Finbow, Generalised irredundance in graphs: Nordhaus-Gaddum bounds. Discuss. Math. Graph Theory 24(1), 147–160 (2004)
E.J. Cockayne, S.T. Hedetniemi, Optimal domination in graphs. IEEE Trans. Circuits and Systems CAS-22(11), 855–857 (1975)
E.J. Cockayne, S.T. Hedetniemi, D.J. Miller, Properties of hereditary hypergraphs and middle graphs. Can. Math. Bull. 21(4), 461–468 (1978)
E.J. Cockayne, R.M. Dawes, S.T. Hedetniemi, Total domination in graphs. Networks 10(3), 211–219 (1980)
E.J. Cockayne, S.T. Hedetniemi, R. Laskar, Gallai theorems for graphs, hypergraphs, and set systems. Discret. Math. 72(1–3), 35–47 (1988)
E.J. Cockayne, B.L. Hartnell, S.T. Hedetniemi, R. Laskar, Perfect domination in graphs. J. Comb. Inf. Syst. Sci. 18, 136–148 (1993)
E.J. Cockayne, J.H. Hattingh, S.M. Hedetniemi, S.T. Hedetniemi, A.A. McRae, Using maximality and minimality conditions to construct inequality chains. Discret. Math. 176(1–3), 43–61 (1997)
E.J. Cockayne, O. Favaron, J. Puech, C.M. Mynhardt, An inequality chain of domination parameters for trees. Discuss. Math. Graph Theory 18(1), 127–142 (1998)
E.J. Cockayne, S.M. Hedetniemi, S.T. Hedetniemi, C.M. Mynhardt, Irredundant and perfect neighbourhood sets in trees. Discret. Math. 188(1–3), 253–260 (1998)
E.J. Cockayne, O. Favaron, C.M. Mynhardt, Secure domination, weak Roman domination and forbidden subgraphs. Bull. Inst. Combin. Appl. 39, 87–100 (2003)
E.J. Cockayne, P.A. Dreyer Jr., S.M. Hedetniemi, S.T. Hedetniemi, Roman domination in graphs. Discret. Math. 278(1–3), 11–22 (2004)
E.J. Cockayne, O. Favaron, S. Finbow, C.M. Mynhardt, Open irredundance and maximum degree in graphs. Discret. Math. 308(23), 5358–5375 (2008)
E.J. Cockayne, S. Finbow, J.S. Swarts, OO-irredundance and maximum degree in paths and trees. J. Comb. Math. Comb. Comput. 73, 223 (2010)
K.L. Collins, A.N. Trenk, The distinguishing chromatic number. Electron. J. Comb. 13(1), 19 pp. (2006). Research Paper 16
L.J. Cowen, R.H. Cowen, D.R. Woodall, Defective colorings of graphs in surfaces: partitions into subgraphs of bounded valency. J. Graph Theory 10(2), 187–195 (1986)
B. Crull, T. Cundiff, P. Feltman, G.H. Hurlbert, L. Pudwell, Z. Szaniszlo, Z. Tuza, The cover pebbling number of graphs. Discret. Math. 296(1), 15–23 (2005)
B. Csaba, D. Kühn, A. Lo, D. Osthus, A. Treglown, Proof of the 1-factorization and Hamilton decomposition conjectures, in The Seventh European Conference on Combinatorics, Graph Theory and Applications. CRM Series, vol. 16 (Ed. Norm., Pisa, 2013), pp. 477–482
M. Cygan, M. Pilipczuk, R. Škrekovski. Relation between randić index and average distance of trees. MATCH Commun. Math. Comput. Chem. 66(2), 605–612 (2011)
E. Czabarka, O. Sỳkora, L. Székely, I. Vrt’o, Outerplanar crossing numbers, the circular arrangement problem and isoperimetric functions. Electron. J. Comb. 11(1), 20 pp. (2004). Research Paper 81
J. Dabney, B.C. Dean, S.T. Hedetniemi, A linear-time algorithm for broadcast domination in a tree. Networks 53(2), 160–169 (2009)
D. Daniel, S.E. Shauger, A result on the Erdös-Gyarfas conjecture in planar graphs. Congr. Numer. 153, 129–139 (2001)
P. Dankelmann, Average distance and domination number. Discret. Appl. Math. 80(1), 21–35 (1997)
P. Dankelmann, D. Day, D. Erwin, S. Mukwembi, H. Swart, Domination with exponential decay. Discret. Math. 309(19), 5877–5883 (2009)
S. Daugherty, J. Lyle, R. Laskar, On the total influence number of a graph. Congr. Numer. 174, 107–121 (2005)
P. de la Torre, R. Greenlaw, A.A. Schäffer, Optimal edge ranking of trees in polynomial time. Algorithmica 13(6), 592–618 (1995)
N. Dean, M. Kouider, Gallai’s conjecture for disconnected graphs. Discret. Math. 213(1–3), 43–54 (2000). Selected topics in discrete mathematics (Warsaw, 1996)
B.C. Dean, S.M. Hedetniemi, S.T. Hedetniemi, J. Lewis, A.A. McRae, Matchability and k-maximal matchings. Discret. Appl. Math. 159(1), 15–22 (2011)
N. Dehgardi, S. Norouzian, S.M. Sheikholeslami, Bounding the domination number of a tree in terms of its annihilation number. Trans. Comb. 2(1), 9–16 (2013)
N. Dehgardi, S.M. Sheikholeslami, A. Khodkar, Bounding the paired-domination number of a tree in terms of its annihilation number. Filomat 28(3), 523–529 (2014)
E. DeLaVina, B. Waller, Spanning trees with many leaves and average distance. Electron. J. Comb. 15(1), 16 pp. (2008). Research Paper 33
E. DeLaViña, W. Goddard, M.A. Henning, R. Pepper, E.R. Vaughan, Bounds on the k-domination number of a graph. Appl. Math. Lett. 24(6), 996–998 (2011)
M. Delcourt, A. Ferber, On a conjecture of Thomassen. Electron. J. Comb. 22(3), 8 (2015). Paper 3.2
K. Deng, H. Zhang, Extremal anti-forcing numbers of perfect matchings of graphs. Discret. Appl. Math. 224, 69–79 (2017)
W.J. Desormeaux, M.A. Henning, Paired domination in graphs: a survey and recent results. Util. Math. 94, 101–166 (2014)
W.J. Desormeaux, T.W. Haynes, M.A. Henning, Relating the annihilation number and the total domination number of a tree. Discret. Appl. Math. 161(3), 349–354 (2013)
W.J. Desormeaux, M.A. Henning, D.F. Rall, A. Yeo, Relating the annihilation number and the 2-domination number of a tree. Discret. Math. 319, 15–23 (2014)
W.J. Desormeaux, T.W. Haynes, S.T. Hedetniemi, C. Moore, Distribution centers in graphs. Discret. Appl. Math. 243, 186–193 (2018).
G.S. Domke, S.T. Hedetniemi, R.C. Laskar, G.H. Fricke, Relationships between integer and fractional parameters of graphs, in Graph Theory, Combinatorics, and Applications, Proceedings of the Sixth Quadrennial International Conference on the Theory and Applications of Graphs, ed. by Y. Alavi, G. Chartrand, O.R. Oellermann, A.J. Schwenk, vol. 1 (1991), pp. 371–387
G.S. Domke, J.H. Hattingh, S.T. Hedetniemi, R.C. Laskar, L.R. Markus, Restrained domination in graphs. Discret. Math. 203(1–3), 61–69 (1999)
G.S. Domke, J.H. Hattingh, M.A. Henning, L.R. Markus, Restrained domination in trees. Discret. Math. 211(1–3), 1–9 (2000)
G.S. Domke, J.E. Dunbar, L.R. Markus, The inverse domination number of a graph. Ars Combin. 72, 149–160 (2004)
G.S. Domke, J.H. Hattingh, L.R. Markus, On weakly connected domination in graphs II. Discret. Math. 305(1–3), 112–122 (2005)
P. Dorbec, S. Klavžar, Generalized power domination: propagation radius and Sierpiński graphs. Acta Appl. Math. 134(1), 75–86 (2014)
T. Došlic, B. Furtula, A. Graovac, I. Gutman, S. Moradi, Z. Yarahmadi, On vertex–degree–based molecular structure descriptors. MATCH Commun. Math. Comput. Chem. 66(2), 613–626 (2011)
F.F. Dragan, E. Köhler, A. Leitert, Line-distortion, bandwidth and path-length of a graph. Algorithmica 77(3), 686–713 (2017)
P. Duchet, H. Meyniel, On Hadwiger’s number and the stability number, in Graph Theory (Cambridge, 1981). North-Holland Mathematics Studies, vol. 62 (North-Holland, Amsterdam, 1982), pp. 71–73
J.E. Dunbar, F.C. Harris Jr., S.M. Hedetniemi, S.T. Hedetniemi, A.A. McRae, R.C. Laskar, Nearly perfect sets in graphs. Discret. Math. 138(1–3), 229–246 (1995)
J.E. Dunbar, S.T. Hedetniemi, M.A. Henning, P.J. Slater, Signed domination in graphs, in Graph Theory, Combinatorics and Algorithms (Kalamazoo, MI, 1992, ed. by Y. Alavi, A. Schwenk, vol. 1 (Wiley, New York, 1995), pp. 311–322
J. Dunbar, W. Goddard, S. Hedetniemi, A. McRae, M.A. Henning, The algorithmic complexity of minus domination in graphs. Discret. Appl. Math. 68(1–2), 73–84 (1996)
J. Dunbar, S. Hedetniemi, M.A. Henning, A.A. McRae, Minus domination in regular graphs. Discret. Math. 149(1–3), 311–312 (1996)
J.E. Dunbar, J.W. Grossman, J.H. Hattingh, S.T. Hedetniemi, A.A. McRae, On weakly connected domination in graphs. Discret. Math. 167, 261–269 (1997)
J.E. Dunbar, T.W. Haynes, U. Teschner, L. Volkmann, Bondage, insensitivity, and reinforcement, in Domination in Graphs, Advanced Topics, ed. by T. W. Haynes, S.T. Hedetniemi, P.J. Slater, vol. 209 (Marcel Dekker, New York, 1998), pp. 471–489
J. Dunbar, S. Hedetniemi, M.A. Henning, A. McRae, Minus domination in graphs. Discret. Math. 199(1–3), 35–47 (1999)
J.E. Dunbar, S.M. Hedetniemi, S.T. Hedetniemi, D.P. Jacobs, J. Knisely, R.C. Laskar, D.F. Rall, Fall colorings of graphs. J. Comb. Math. Comb. Comput. 33, 257–274 (2000)
J.E. Dunbar, D.G. Hoffman, R.C. Laskar, L.R. Markus, α-domination. Discret. Math. 211(1–3), 11–26 (2000)
J.E. Dunbar, D.J. Erwin, T.W. Haynes, S.M. Hedetniemi, S.T. Hedetniemi, Broadcasts in graphs. Discret. Appl. Math. 154(1), 59–75 (2006)
G. Ebert, J. Hemmeter, F. Lazebnik, A. Woldar, Irregularity strengths for certain graphs. Congr. Numer. 71, 39–52 (1990)
K. Edwards, The harmonious chromatic number and the achromatic number, in Surveys in Combinatorics, ed. by R.A. Bailey (Cambridge University Press, Cambridge, 1997), pp. 13–47
K.J. Edwards, Achromatic number versus pseudoachromatic number: a counterexample to a conjecture of Hedetniemi. Discret. Math. 219(1–3), 271–274 (2000)
K. Edwards, C. McDiarmid, The complexity of harmonious colouring for trees. Discret. Appl. Math. 57(2–3), 133–144 (1995)
B. Effantin, H. Kheddouci, Discussion on the (partial) grundy and b-chromatic numbers of graphs. Util. Math. 80, 65–89 (2008)
M. El-Zahar, N. Sauer, The chromatic number of the product of two 4-chromatic graphs is 4. Combinatorica 5(2), 121–126 (1985)
R.C. Entringer, D.E. Jackson, D.A. Snyder, Distance in graphs. Czechoslov. Math. J. 26(2), 283–296 (1976)
P. Erdös, Extremal problems in graph theory, in Theory of Graphs and Its Applications (Academic Press, New York, 1965), pp. 29–36
P. Erdös, On the combinatorial problems which I would most like to see solved. Combinatorica 1(1), 25–42 (1981)
P. Erdös, Some old and new problems in various branches of combinatorics. Discret. Math. 165/166, 227–231 (1997). Graphs and Combinatorics (Marseille, 1995)
P. Erdös, A.W. Goodman, L. Pósa, The representation of a graph by set intersections. Can. J. Math. 18(106–112), 86 (1966)
P. Erdös, A.L. Rubin, H. Taylor, Choosability in graphs. Congr. Numer. 26, 125–157 (1979). Proceedings of the West Coast Conference on Combinatorics, Graph Theory and Computing
P. Erdös, R. Faudree, J. Pach, J. Spencer, How to make a graph bipartite. J. Combin. Theory, Ser. B 45(1), 86–98 (1988)
P. Erdös, P. Hell, P. Winkler, Bandwidth versus bandsize. Ann. Discret. Math. 41, 117–130 (1989)
P. Erdös, J. Gimbel, H.J. Straight, Chromatic number versus cochromatic number in graphs with bounded clique number. Eur. J. Comb. 11(3), 235–240 (1990)
P. Erdös, E. Kubicka, A.J. Schwenk, Graphs that require many colors to achieve their chromatic sum. Congr. Numer. 71, 17–28 (1990)
P. Erdös, E. Győri, M. Simonovits, How many edges should be deleted to make a triangle-free graph bipartite? in Sets, Graphs and Numbers (Budapest, 1991). Colloquia mathematica Societatis János Bolyai, vol. 60 (North-Holland, Amsterdam, 1992), pp. 239–263
P. Erdös, S.T. Hedetniemi, R.C. Laskar, G. Prins, On the equality of the partial Grundy and upper ochromatic numbers of graphs. Discret. Math. 272(1), 53–64 (2003)
L. Eroh, R. Gera, Global alliance partition in trees. J. Comb. Math. Comb. Comput. 66, 161–169 (2008)
L. Eroh, R. Gera, Alliance partition number in graphs. Ars Combin. 103, 519–529 (2012)
D.J. Erwin, Dominating broadcasts in graphs. Bull. Inst. Comb. Appl. 42, 89–105 (2004)
H. Escuadro, R. Gera, A. Hansberg, N.J. Rad, L. Volkmann, Geodetic domination in graphs. J. Comb. Math. Comb. Comput. 66, 161–169 (2008)
G. Exoo, V. Junnila, T. Laihonen, On location-domination of set of vertices in cycles and paths. Congr. Numer. 202, 97–112 (2010)
S. Fajtlowicz, On conjectures of Graffiti. Discret. Math. 72(1–3), 113–118 (1988)
S.M. Fallat, L. Hogben, The minimum rank of symmetric matrices described by a graph: a survey. Linear Algebra Appl. 426(2–3), 558–582 (2007)
G. Fan, On diameter 2-critical graphs. Discret. Math. 67(3), 235–240 (1987)
G. Fan, Integer flows and cycle covers. J. Combin. Theory, Ser. B 54(1), 113–122 (1992)
G. Fan, Path decompositions and Gallai’s conjecture. J. Combin. Theory Ser. B 93(2), 117–125 (2005)
A.M. Farley, A. Proskurowski, Computing the maximum order of an open irredundant set in a tree. Congr. Numer. 41, 219–228 (1984)
A.M. Farley, N. Schacham, Senders in broadcast networks: open irredundancy in graphs. Congr. Numer. 38, 47–57 (1983)
A.M. Farley, S.T. Hedetniemi, A. Proskurowski, Partitioning trees: matching, domination and maximum diameter. Int. J. Comput. Inform. Sci. 10, 55–61 (1981)
R.J. Faudree, R. H. Schelp, A. Gárfás, Z. Tuza, The strong chromatic index of graphs. Ars Combin. 29B, 205–211 (1990). Twelfth British Combinatorial Conference (Norwich, 1989)
O. Favaron, On a conjecture of Fink and Jacobson concerning k-domination and k-dependence. J. Combin. Theory, Ser. B 39(1), 101–102 (1985)
O. Favaron, k-Domination and k-dependence in graphs. Ars Combin. 25C, 159–167 (1988)
O. Favaron, Global alliances and independent domination in some classes of graphs. Electron. J. Comb. 15(1), 9 pp. (2008). Research Paper 123
O. Favaron, M. Kouider, Path partitions and cycle partitions of Eulerian graphs of maximum degree 4. Stud. Sci. Math. Hung. 23(1–2), 237–244 (1988)
O. Favaron, J. Puech, Irredundant and perfect neighborhood sets in graphs and claw-free graphs. Discret. Math. 197, 269–284 (1999)
O. Favaron, T.W. Haynes, S.T. Hedetniemi, M.A. Henning, D.J. Knisley, Total irredundance in graphs. Discret. Math. 256(1–2), 115–127 (2002)
O. Favaron, S.M. Hedetniemi, S.T. Hedetniemi, D.F. Rall, On k-dependent domination. Discret. Math. 249(1–3), 83–94 (2002)
O. Favaron, H. Karami, R. Khoeilar, S.M. Sheikholeslami, On the Roman domination number of a graph. Discret. Math. 309(10), 3447–3451 (2009)
O. Favaron, H. Karami, S.M. Sheikholeslami, Paired-domination subdivision numbers of graphs. Graphs Combin. 25(4), 503–512 (2009)
M.R. Fellows, M.N. Hoover, Perfect domination. Australas. J. Comb. 3(141–150), 3–3 (1991)
T. Fenstermacher, S. Hedetniemi, R. Laskar, Edge cut domination, irredundance and independence in graphs. Congr. Numer. 226, 319–325 (2016)
J. Fiamcik, The acyclic chromatic class of a graph. Math. Slovaca 28(2), 139–145 (1978)
J. Fiamčík, Acyclic chromatic index of a graph with maximum valency three. Arch. Math., Brno 16(2), 81–87 (1980)
J. Fiamčík, E. Jucovič, Colouring the edges of a multigraph. Arch. Math. 21(1), 446–448 (1970)
S. Finbow, Generalisations of Irredundance in Graphs, PhD thesis, University of Victoria, 2003
J.F. Fink, M.S. Jacobson, n-domination in graphs, in Graph Theory with Applications to Algorithms and Computer Science (Wiley, New York, 1985), pp. 283–300
J.F. Fink, M.S. Jacobson, On n-domination, n-dependence and forbidden subgraphs, in Graph Theory and Its Applications to Algorithms and Computer Science (Wiley, New York, 1985), pp. 301–312
J.F. Fink, M.S. Jacobson, L.F. Kinch, J. Roberts, The bondage number of a graph. Discret. Math. 86(1–3), 47–57 (1990)
H. Fleischner, Uniquely Hamiltonian graphs of minimum degree 4. J. Graph Theory 75(2), 167–177 (2014)
N. Fonger, J. Goss, B. Phillips, C. Segroves, Map and t-tone colorings of graph. Research Report, Western Michigan University, 2009
M.F. Foregger, T.H. Foregger, The tree-covering number of a graph. Czechoslov. Math. J. 30(105), 633–639 (1980)
J.L. Fouquet, J.L. Jolivet, Strong edge-colorings of graphs and applications to multi-k-gons. Ars Combin. A 16, 141–150 (1983)
G.H. Fricke, S.T. Hedetniemi, M.A. Henning, Distance independent domination in graphs. Ars Combin. 41(3995), 33–44 (1995)
G.H. Fricke, T.W. Haynes, S.M. Hedetniemi, S.T. Hedetniemi, M.A. Henning, On perfect neighborhood sets in graphs. Discret. Math. 199(1–3), 221–225 (1999)
G.H. Fricke, L.M. Lawson, T.W. Haynes, S.M. Hedetniemi, S.T. Hedetniemi, A note on defensive alliances in graphs. Bull. Inst. Combin. Appl. 38, 37–41 (2003)
D.R. Fulkerson, Blocking and anti-blocking pairs of polyhedra. Math. Program. 1(1), 168–194 (1971)
Z. Füredi, The maximum number of edges in a minimal graph of diameter 2. J. Graph Theory 16(1), 81–98 (1992)
A. Gagarin, A. Poghosyan, V. Zverovich, Upper bounds for α-domination parameters. Graphs Combin. 25(4), 513 (2009)
T. Gallai, Problem 6, in Proceedings of the Colloquium Held at Tihany (Academic Press, New York, 1966)
J.A. Gallian, A survey: recent results, conjectures, and open problems in labeling graphs. J. Graph Theory 13(4), 491–504 (1989)
J.A. Gallian, A dynamic survey of graph labeling. Electron. J. Comb. 18(DS6), 415 pp. (2017)
F. Galvin, The list chromatic index of a bipartite multigraph. J. Combin. Theory, Ser. B 63(1), 153–158 (1995)
J. Gardner, A.P. Godbole, A.M. Teguia, A.Z. Vuong, N. Watson, C.R. Yerger, Domination cover pebbling: graph families (2005). ArXiv preprint math/0507271
M.R. Garey, D.S. Johnson, Computers and Intractability, A Guide to the Theory of NP-Completeness (W. H. Freeman, New York, 2002)
D. Geller, S.T. Hedetniemi, A proof technique in graph theory, in Proof Techniques in Graph Theory (Proceedings of Second Ann Arbor Graph Theory Conference Ann Arbor, Michigan, 1968) (Academic Press, New York, 1969), pp. 49–59
R. Gera, Stratification and Domination in Graphs and Digraphs, PhD thesis, Western Michigan University, 2005
R. Gera, On dominator colorings in graphs. Graph Theory Notes N. Y. 52, 25–30 (2007)
R. Gera, On the dominator colorings in bipartite graphs, in Information Technology, 2007. ITNG’07. Fourth International Conference on (IEEE, Piscataway, 2007), pp. 947–952
R. Gera, C. Rasmussen, S. Horton, Dominator colorings and safe clique partitions. Congr. Numer. 181, 19 (2006)
R. Gera, S. Hedetniemi, C. Larson (eds.), Graph Theory, Favorite Conjectures and Open Problems, vol. 1 (Springer, Berlin, 2016)
M.U. Gerber, D. Kobler, Algorithmic approach to the satisfactory graph partitioning problem. Eur. J. Oper. Res. 125(2), 283–291 (2000)
J. Ghoshal, R. Laskar, D. Pillone, Further results on minimal rankings. Ars Combin. 52, 181–198 (1999)
J.G. Gimbel, The Chromatic and Cochromatic Number of a Graph, PhD thesis, Western Michigan University, 1984
J. Gimbel, C. Hartman, Subcolorings and the subchromatic number of a graph. Discret. Math. 272(2–3), 139–154 (2003)
M. Gionfriddo, On a problem concerning L2 colorings of a plane graph and Ls colorings (italian). Riv. Mat. Univ. Parma (4) 6, 151–160 (1980/1981).
W. Goddard, Acyclic colorings of planar graphs. Discret. Math. 91(1), 91–94 (1991)
W. Goddard, S.T. Hedetniemi, A note on trees, tables, and algorithms. Networks 53(2), 184–190 (2009)
W. Goddard, M.A. Henning, Thoroughly dispersed colorings. J. Graph Theory 88(1), 174–191 (2018)
W. Goddard, T. Haynes, D. Knisley, Hereditary domination and independence parameters. Discuss. Math. Graph Theory 24(2), 239–248 (2004)
W. Goddard, S.M. Hedetniemi, S.T. Hedetniemi, Eternal security in graphs. J. Comb. Math. Comb. Comput. 52, 169–180 (2005)
W. Goddard, S.M. Hedetniemi, S.T. Hedetniemi, R. Laskar, Generalized subgraph-restricted matchings in graphs. Discret. Math. 293(1), 129–138 (2005)
W. Goddard, S.M. Hedetniemi, S.T. Hedetniemi, J.M. Harris, D.F. Rall, Broadcast chromatic numbers of graphs. Ars Combin. 86, 33–50 (2008)
W. Goddard, S.T. Hedetniemi, J.L. Huff, A.A. McRae, Capacitated domination. Ars Combin. 96, 75–86 (2010)
W. Goddard, M.A. Henning, C.A. McPillan, The disjunctive domination number of a graph. Quaest. Math. 37(4), 547–561 (2014)
W. Goddard, M.A. Henning, C.A. McPillan, Semitotal domination in graphs. Util. Math. 94, 67–81 (2014)
C. Godsil, D.E. Roberson, R. Šámal, S. Severini, Sabidussi versus Hedetniemi for three variations of the chromatic number. Combinatorica 36(4), 395–415 (2016)
C. Godsil, D.E. Roberson, B. Rooney, R. Šámal, A. Varvitsiotis, Universal completability, least eigenvalue frameworks, and vector colorings. Discret. Comput. Geom. 58(2), 265–292 (2017)
D. Goldman, S. Istrail, G. Lancia, A. Piccolboni, B. Walenz, Algorithmic strategies in combinatorial chemistry, in Proceedings of the Eleventh Annual ACM-SIAM Symposium on Discrete Algorithms (San Francisco, CA, 2000) (ACM, New York, 2000), pp. 275–284
M.C. Golumbic, Algorithmic Graph Theory and Perfect Graphs. Annals of Discrete Mathematics, vol. 57 (Elsevier Sciience B. V., Amsterdam, 2004)
M.C. Golumbic, R.C. Laskar, Irredundancy in circular arc graphs. Discret. Appl. Math. 44(1–3), 79–89 (1993)
D. Gonçalves, On the l(p, 1)-labelling of graphs. Discret. Math. 308(8), 1405–1414 (2008)
S. Goodman, S. Hedetniemi, On the hamiltonian completion problem, in Graphs and Combinatorics, ed. by R.A. Bari, F. Harary (Springer, Berlin, 1974), pp. 262–272
S.E. Goodman, S.T. Hedetniemi, P.J. Slater, Advances on the hamiltonian completion problem. J. ACM 22(3), 352–360 (1975)
T. Grauman, S.G. Hartke, A. Jobson, B. Kinnersley, D.B. West, L. Wiglesworth, P. Worah, H. Wu, The hub number of a graph. Inf. Process. Lett. 108(4), 226–228 (2008)
P. Gregor, B. Lužar, R. Soták, On incidence coloring conjecture in cartesian products of graphs. Discret. Appl. Math. 213, 93–100 (2016)
R.J. Griggs, R.K. Yeh, Labeling graphs with a condition at distance 2. SIAM J. Discret. Math. 5(4), 586–595 (1992)
J.L. Gross, J. Yellen, P. Zhang, Handbook of Graph Theory. Discrete Mathematics and Its Applications (Boca Raton), 2nd edn. (CRC Press, Boca Raton, 2014)
B. Grünbaum, Acyclic colorings of planar graphs. Isr. J. Math. 14(4), 390–408 (1973)
P.M. Grundy, Mathematics and games. Eureka 2, 6–9 (1939)
J. Guo, R. Niedermeier, D. Raible, Improved algorithms and complexity results for power domination in graphs. Algorithmica 52(2), 177–202 (2008)
R.P. Gupta, Bounds on the chromatic and achromatic numbers of complementary graphs, in Recent Progress in Combinatorics (Academic Press, New York, 1969).
I. Gutman, N. Trinajstić, Graph theory and molecular orbitals. Total φ-electron energy of alternant hydrocarbons. Chem. Phys. Lett. 17(4), 535–538 (1972)
R.K. Guy, Crossing numbers of graphs, in Graph Theory and Applications (Proceedings of Conference, Western Michigan Univeristy, Kalamazoo, MI, 1972; Dedicated to the Memory of J. W. T. Youngs). Lecture Notes in Mathematics, vol. 303 (Springer, Berlin, 1972), pp. 111–124
R.K. Guy, R.J. Nowakowski, The outerthickness & outercoarseness of graphs I. The complete graph & the n-cube, in Topics in Combinatorics and Graph Theory (Springer, Berlin, 1990), pp. 297–310
R.K. Guy, R.J. Nowakowski, The outerthickness & outercoarseness of graphs II. The complete bipartite graph, in Contemporary Methods in Graph Theory (Bibliographisches Institut, Mannheim, 1990), pp. 313–322
R. Haas, T. B. Wexler, Signed domination numbers of a graph and its complement. Discret. Math. 283(1–3), 87–92 (2004)
H. Hadwiger, Über eine Klassifikation der Streckenkomplexe. Vierteljschr. Naturforsch. Ges. Zürich 88, 133–142 (1943)
R. Häggkvist, P. Hell, D.J. Miller, V. Neumann Lara, On multiplicative graphs and the product conjecture. Combinatorica 8(1), 63–74 (1988)
G. Hajós, Über eine Konstruktion nicht n-färbbarer Graphen. Wiss. Z. Martin-Luther Univ. Halle-Wittenberg. Math.-Nat. Reihe. 10, 116–117 (1961)
S.L. Hakimi, J. Mitchem, E.F. Schmeichel, Degree-bounded coloring of graphs: variations on a theme by brooks. J. Graph Theory 20(2), 177–194 (1995)
S.L. Hakimi, J. Mitchem, E. Schmeichel, Star arboricity of graphs. Discret. Math. 149(1–3), 93–98 (1996)
W.K. Hale, Frequency assignment: theory and applications. Proc. IEEE 68(12), 1497–1514 (1980)
R. Halin, S-functions for graphs. J. Geom. 8(1–2), 171–186 (1976)
J.H. Halton, On the thickness of graphs of given degree. Inf. Sci. 54(3), 219–238 (1991)
A. Hansberg, L. Volkmann, Upper bounds on the k-domination number and the k-Roman domination number. Discret. Appl. Math. 157(7), 1634–1639 (2009)
A. Hansberg, L. Volkmann, On the geodetic and geodetic domination numbers of a graph. Discret. Math. 310(15–16), 2140–2146 (2010)
D. Hanson, P. Wang, A note on extremal total domination edge critical graphs. Util. Math. 63, 89–96 (2003)
G. Hao, Rainbow connection of the join of two paths. Ars Combin. 135, 243–247 (2017)
F. Harary, Status and contrastatus. Sociometry 22(1), 23–43 (1959)
F. Harary, Graph Theory (Addison-Wesley, Reading, 1969)
F. Harary, On the intersection number of a graph, in Proof Techniques in Graph Theory (Academic Press, New York, 1969), pp. 71–72
F. Harary, A survey of the reconstruction conjecture, in Graphs and Combinatorics, ed. by R. Bari, F. Harary (Springer, Berlin, 1974), pp. 18–28
F. Harary, Three new directions in graph theory, in Proceedings of the First Estonian Conference on Graphs and Applications, (Tartu-Kääriku, 1991) (1993), pp. 15–19
F. Harary, T.W. Haynes, Double domination in graphs. Ars Combin. 55, 201–214 (2000)
F. Harary, S. Hedetniemi, The achromatic number of a graph. J. Combin. Theory 8(2), 154–161 (1970)
F. Harary, R.A. Melter, On the metric dimension of a graph. Ars Combin. 2, 191–195 (1976)
F. Harary, C.St.J.A. Nash-Williams, On eulerian and hamiltonian graphs and line graphs. Can. Math. Bull. 8, 701–709 (1965)
F. Harary, M. Plantholt, The line-distinguishing chromatic number of a graph. Ars Combin. 14, 241–267 (1982)
F. Harary, D.J. Klein, T.P. Živkovič, Graphical properties of polyhexes: perfect matching vector and forcing. J. Math. Chem. 6(1), 295–306 (1991)
F. Harary, E. Loukakis, C. Tsouros, The geodetic number of a graph. Math. Comput. Model. 17(11), 89–95 (1993)
P. Harding, S. McGuinness, Gallai’s conjecture for graphs of girth at least four. J. Graph Theory 75(3), 256–274 (2014)
L.H. Harper, Optimal assignment of numbers to vertices. J. SIAM 12, 131–135 (1964)
B.L. Hartnell, D.F. Rall, Bounds on the bondage number of a graph. Discret. Math. 128(1–3), 173–177 (1994)
J.H. Hattingh, Majority domination and its generalizations, in Domination in Graphs, Advanced Topics, ed. by T.W. Haynes, S.T. Hedetniemi, P.J. Slater, vol. 209 (Marcel Dekker, New York, 1998), pp. 91–108
J.H. Hattingh, M.A. Henning, Bounds relating the weakly connected domination number to the total domination number and the matching number. Discrete Appl. Math. 157(14), 3086–3093 (2009)
J.H. Hattingh, M.A. Henning, E. Ungerer, Upper line-distinguishing and upper harmonious chromatic numbers of cycles. J. Comb. Math. Comb. Comput. 45, 137–144 (2003)
F. Havet, B. Reed, J.-S. Sereni, L(2, 1)-labelling of graphs, in Proceedings of the Nineteenth Annual ACM-SIAM Symposium on Discrete Algorithms (Society for Industrial and Applied Mathematics, Philadelphia, 2008), pp. 621–630
P.E. Haxell, Packing and covering triangles in graphs. Discret. Math. 195(1–3), 251–254 (1999)
P. Haxell, O. Pikhurko, A. Taraz, Primality of trees. J. Combin. 2(4), 481–500 (2011)
T.W. Haynes, J.A. Lachniet, The alliance partition number of grid graphs. AKCE Int. J. Graphs Comb. 4(1), 51–59 (2007)
T.W. Haynes, P.J. Slater, Paired-domination and the paired-domatic number. Congr. Numer. 109, 65–72 (1995)
T.W. Haynes, P.J. Slater, Paired-domination in graphs. Networks 32(3), 199–206 (1998)
T.W. Haynes, S.T. Hedetniemi, P.J. Slater (eds), Domination in Graphs: Advanced Topics, vol. 209 (Marcel Dekker, New York, 1998)
T.W. Haynes, S.T. Hedetniemi, P.J. Slater, Fundamentals of Domination in Graphs, vol. 208 (Marcel Dekker, New York, 1998)
T.W. Haynes, S.M. Hedetniemi, S.T. Hedetniemi, Domination and independence subdivision numbers of graphs. Discuss. Math. Graph Theory 20(2), 271–280 (2000)
T.W. Haynes, S.M. Hedetniemi, S.T. Hedetniemi, D.P. Jacobs, J. Knisely, L.C. van der Merwe, Domination subdivision numbers. Discuss. Math. Graph Theory 21(2), 239–253 (2001)
T.W. Haynes, S.M. Hedetniemi, S.T. Hedetniemi, M.A. Henning, Domination in graphs applied to electric power networks. SIAM J. Discret. Math. 15(4), 519–529 (2002)
T.W. Haynes, S.T. Hedetniemi, M.A. Henning, Global defensive alliances, in Proceedings of 17th International Symposium on Computer and Information Sciences , I, ISCIS, vol. 17 (2002), pp. 303–307
T.W. Haynes, S.T. Hedetniemi, M.A. Henning, P.J. Slater, H-forming sets in graphs. Discret. Math. 262(1–3), 159–169 (2003)
T.W. Haynes, S.T. Hedetniemi, L.C. van der Merwe, Total domination subdivision numbers. J. Comb. Math. Comb. Comput. 44, 115–128 (2003)
T.W. Haynes, M.A. Henning, L.S. Hopkins, Total domination subdivision numbers of graphs. Discuss. Math. Graph Theory 24(3), 457–467 (2004)
T.W. Haynes, S.M. Hedetniemi, S.T. Hedetniemi, A.A. McRae, P.J. Slater, Irredundant colorings of graphs. Bull. Inst. Combin. Appl. 54, 103–121 (2008)
T.W. Haynes, M.A. Henning, P. Zhang, A survey of stratified domination in graphs. Discret. Math. 309(19), 5806–5819 (2009)
T.W. Haynes, M.A. Henning, L.C. van der Merwe, A. Yeo, On a conjecture of Murty and Simon on diameter 2-critical graphs. Discret. Math. 311(17), 1918–1924 (2011)
T.W. Haynes, S.M. Hedetniemi, S.T. Hedetniemi, T.L. McCoy, I. Vasylieva, Cost effective domination in graphs. Congr. Numer. 211, 197–209 (2012)
T.W. Haynes, S.T. Hedetniemi, J.D. Jamieson, W.B. Jamieson, Downhill domination in graphs. Discuss. Math. Graph Theory 34(3), 603–612 (2014)
T.W. Haynes, S.T. Hedetniemi, H. Scott, Balanced sets in graphs. Util. Math. 93, 343–356 (2014)
T.W. Haynes, S.T. Hedetniemi, T.L. McCoy, T.K. Rodriguez, Bounds on cost effective domination numbers. Quaest. Math. 39(6), 773–783 (2016)
T.W. Haynes, M.A. Henning, Semipaired domination in graphs. J. Comb. Math. Comb. Comput. 104, 93–109 (2018)
C.C. Heckman, R. Krakovski, Erdös-Gyarfas conjecture for cubic planar graphs. Electron. J. Comb. 20(2), 43 (2013). Paper 7
S.T. Hedetniemi, Homomorphisms of Graphs and Automata, PhD thesis, University of Michigan, 1966
S.T. Hedetniemi, New upper bounds for the pseudoachromatic and upper irredundance numbers of a graph. Util. Math. 94, 83–100 (2014)
S.T. Hedetniemi, My top 10 graph theory conjectures and open problems, in Graph Theory, Favorite Conjectures and Open Problems, ed. by R. Gera, S.T. Hedetneimi, C. Larson, vol. 1 (Springer, Berlin, 2016), pp. 109–134
S.T. Hedetniemi, S. Mitchell, Edge domination in trees. Congr. Numer. 19, 489–509 (1977)
S.M. Hedetniemi, S.T. Hedetniemi, T. Beyer, A linear algorithm for the grundy (coloring) number of a tree. Congr. Numer. 36, 351–363 (1982)
S.T. Hedetniemi, R. Laskar, J. Pfaff, Irredundance in graphs: a survey. Congr. Numer. 48, 183–193 (1985)
S.M. Hedetniemi, S.T. Hedetniemi, T.V. Wimer, Linear time resource allocation algorithms for trees. Technical report URI-014, Department of Mathematical Sciences, Clemson University, 1987
S.M. Hedetniemi, S.T. Hedetniemi, A.L. Liestman, A survey of gossiping and broadcasting in communication networks. Networks 18(4), 319–349 (1988)
S.T. Hedetniemi, D.P. Jacobs, R. Laskar, Inequalities involving the rank of a graph. J. Comb. Math. Comb. Comput. 6, 173–176 (1989)
S.M. Hedetniemi, S.T. Hedetniemi, D.P. Jacobs, Private domination: theory and algorithms. Congr. Numer. 79(147–157), 3–3 (1990)
S.M. Hedetniemi, S.T. Hedetniemi, D.P. Jacobs, Total irredundance in graphs: theory and algorithms. Ars Combin. 35, 271–284 (1993)
S.M. Hedetniemi, S.T. Hedetniemi, M.A. Henning, The algorithmic complexity of perfect neighborhoods in graphs. J. Comb. Math. Comb. Comput. 25, 183–192 (1997)
S.M. Hedetniemi, S.T. Hedetniemi, D.F. Rall, Acyclic domination. Discret. Math. 222(1–3), 151–165 (2000)
S.M. Hedetniemi, S.T. Hedetniemi, P. Kristiansen, Alliances in graphs. J. Comb. Math. Comb. Comput. 48, 157–177 (2004)
S.M. Hedetniemi, S.T. Hedetniemi, A.A. McRae, D. Parks, J.A. Telle, Iterated colorings of graphs. Discret. Math. 278(1–3), 81–108 (2004)
S.M. Hedetniemi, S.T. Hedetniemi, A.A. McRae, J.R.S. Blair, Dominator colorings of graphs (2006). Manuscript
S.M. Hedetniemi, S.T. Hedetniemi, R.C. Laskar, L. Markus, P.J. Slater, Disjoint dominating sets in graphs, in Discrete Mathematics. Ramanujan Mathematical Society Lecture Notes Series, vol. 7 (Ramanujan Mathematical Society, Mysore, 2008), pp. 87–100
S.M. Hedetniemi, S.T. Hedetniemi, D.F. Rall, J. Knisely, Secondary domination in graphs. AKCE Int. J. Graphs Comb. 5(2), 117–125 (2008)
S.M. Hedetniemi, S.T. Hedetniemi, H. Jiang, K.E. Kennedy, A.A. McRae, A self-stabilizing algorithm for optimally efficient sets in graphs. Inf. Process. Lett. 112(16), 621–623 (2012)
J.T. Hedetniemi, S.M. Hedetniemi, S.T. Hedetniemi, Perfection in graphs, a new look at irredundance. J. Comb. Math. Comb. Comput. 85, 129–139 (2013)
S.M. Hedetniemi, S.T. Hedetniemi, R. Laskar, H.M. Mulder, Quorum colorings of graphs. AKCE Int. J. Graphs Comb. 10(1), 97–109 (2013)
S.M. Hedetniemi, S.T. Hedetniemi, R. Laskar, A.A. McRae, C.K. Wallis, Dominator partitions of graphs. J. Combin. Inform. Systems Sci. 34(1–4), 183–192 (2018)
P. Heggernes, D. Lokshtanov, Optimal broadcast domination in polynomial time. Discret. Math. 306(24), 3267–3280 (2006)
K. Heinrich, P. Hell, On the problem of bandsize. Graphs Combin. 3(1), 279–284 (1987)
M.A. Henning, Irredundance perfect graphs. Discret. Math. 142(1–3), 107–120 (1995)
M.A. Henning, Distance domination in graphs, in Domination in Graphs, Advanced Topics, ed. by T.W. Haynes, S.T. Hedetniemi, P.J. Slater. Pure and Applied Mathematics, vol. 209 (Marcel Dekker, New York, 1998), pp. 321–350
M.A. Henning, Graphs with large restrained domination number. Discret. Math. 197, 415–429 (1999)
M.A. Henning, A survey of selected recent results on total domination in graphs. Discret. Math. 309(1), 32–63 (2009)
M.A. Henning, Total dominator colorings and total domination in graphs. Graphs Combin. 31, 953–974 (2015)
M.A. Henning, My favorite domination conjectures in graph theory are bounded, in Graph Theory, Favorite Conjectures and Open Problems, ed. by R. Gera, S. Hedetniemi, C. Larson, vol. 1 (Springer, Berlin, 2016), pp. 253–271
M.A. Henning, S.T. Hedetniemi, Defending the Roman Empire—a new strategy. Discret. Math. 266(1–3), 239–251 (2003). The 18th British Combinatorial Conference (Brighton, 2001)
M.A. Henning, W.F. Klostermeyer, Italian domination in trees. Discret. Appl. Math. 217(P3), 557–564 (2017)
M.A. Henning, S.A. Marcon, A constructive characterization of trees with equal total domination and disjunctive domination numbers. Quaest. Math. 39(4), 531–543 (2016)
M.A. Henning, A. Yeo, Total Domination in Graphs (Springer, Berlin, 2013)
M.A. Henning, A. Yeo, A note on fractional disjoint transversals in hypergraphs. Discret. Math. 340(10), 2349–2354 (2017)
M.A. Henning, A. Yeo, Transversals in uniform linear hypergraphs (2018). ArXiv preprint arXiv:1802.01825
M.A. Henning, O.R. Oellermann, H.C. Swart, Relating pairs of distance domination parameters. J. Comb. Math. Comb. Comput. 18, 233–244 (1995)
D.S. Herscovici, B.D. Hester, G.H. Hurlbert, t-pebbling and extensions. Graphs Combin. 29(4), 955–975 (2013)
A.J.W. Hilton, P.D. Johnson Jr., Extending Hall’s theorem, in Topics in Combinatorics and Graph Theory (Oberwolfach, 1990) (Physica, Heidelberg, 1990), pp. 359–371
A.J.W. Hilton, R. Rado, S.H. Scott, A (< 5)-colour theorem for planar graphs. Bull. Lond. Math. Soc. 5(3), 302–306 (1973)
T.S. Holm, On majority domination in graphs. Discret. Math. 239(1–3), 1–12 (2001)
D.A. Holton, B. Manvel, B.D. McKay, Hamiltonian cycles in cubic 3-connected bipartite planar graphs. J. Combin. Theory, Ser. B 38(3), 279–297 (1985)
J.E. Hopcroft, M.S. Krishnamoorthy, On the harmonious colouring of graphs. SIAM J. Algebraic Discrete Methods 4(3), 306–311 (1983)
P. Horák, The strong chromatic index of graphs with maximum degree four, in Contemporary Methods in Graph Theory, ed. by R. Bodendiek (BI Wissenschaftsverlag, Mannheim, 1990), pp. 399–403
P. Horák, H. Qing, W.T. Trotter, Induced matchings in cubic graphs. J. Graph Theory 17(2), 151–160 (1993)
H. Hosoya, Topological index. a newly proposed quantity characterizing the topological nature of structural isomers of saturated hydrocarbons. Bull. Chem. Soc. Jpn. 44(9), 2332–2339 (1971)
X. Hou, Y. Lu, On the {k}-domination number of cartesian products of graphs. Discret. Math. 309(10), 3413–3419 (2009)
J. Hromkovič, R. Klasing, B. Monien, R. Peine, Dissemination of information in interconnection networks (broadcasting & gossiping), in Combinatorial Network Theory (Springer, Berlin, 1996), pp. 125–212
X. Hu, Y. Zhang, Z. Miao, Upper bounds on adjacent vertex distinguishing total chromatic number of graphs. Discret. Appl. Math. 233, 29–32 (2017)
D. Huang, W. Wang, C. Yan, A note on the adjacent vertex distinguishing total chromatic number of graphs. Discret. Math. 312(24), 3544–3546 (2012)
F. Hughes, G. MacGillivray, The achromatic number of graphs: a survey and some new results. Bull. Inst. Combin. Appl. 19, 27–56 (1997)
G. Hurlbert, General graph pebbling. Discret. Appl. Math. 161(9), 1221–1231 (2013)
R.W. Irving, D.F. Manlove, The b-chromatic number of a graph. Discret. Appl. Math. 91(1–3), 127–141 (1999)
O. Ivanciuc, T.S. Balaban, A.T. Balaban, Design of topological indices. Part 4. Reciprocal distance matrix, related local vertex invariants and topological indices. J. Math. Chem. 12(1), 309–318 (1993)
A.V. Iyer, H.D. Ratliff, G. Vijayan, Optimal node ranking of trees. Inf. Process. Lett. 28(5), 225–229 (1988)
L.H. Jamieson, A.C. Jamieson, Algorithms for secondary domination. Congr. Numer. 198, 119–125 (2009)
T.R. Jensen, B. Toft, Graph Coloring Problems (Wiley, New York, 1995)
T. Jiang, D. Mubayi, A. Shastri, D.B. West, Edge-bandwidth of graphs. SIAM J. Discret. Math. 12, 307–316 (1999)
P. Johnson, P. Slater, M. Walsh, The connected hub number and the connected domination number. Networks 58(3), 232–237 (2011)
K. Junosza-Szaniawski, Upper bound on the circular chromatic number of the plane. Electron. J. Comb. 25(1), Paper P1.53 (2018)
F.R.k. Chung, On partitions of graphs into trees. Discret. Math. 23(1), 23–30 (1978)
P.C. Kainen, Thickness and coarseness of graphs. Abh. Math. Sem. Univ. Hamg. 39(1), 88–95 (1973)
S.S. Kamath, R.S. Bhat, On strong (weak) independent sets and vertex coverings of a graph. Discret. Math. 307(9–10), 1136–1145 (2007)
L. Kang, J. Yuan, Bondage number of planar graphs. Discret. Math. 222(1–3), 191–198 (2000)
S.F. Kapoor, H.V. Kronk, D.R. Lick, On detours in graphs. Can. Math. Bull. 11(2), 195–201 (1968)
D. Karger, R. Motwani, M. Sudan, Approximate graph coloring by semidefinite programming, in Foundations of Computer Science, 1994 Proceedings, 35th Annual Symposium on (IEEE, Piscataway, 1994), pp. 2–13
M. Karoński, T. Łuczak, A. Thomason, Edge weights and vertex colours. J. Combin. Theory, Ser. B 91(1), 151–157 (2004)
P. Katerinis, D.R. Woodall, Binding numbers of graphs and the existence of k-factors. Quart. J. Math. 38(2), 221–228 (1987)
G.Y. Katona, L.F. Papp, The optimal rubbling number of ladders, prisms and möbius-ladders. Discret. Appl. Math. 209, 227–246 (2016)
G.Y. Katona, N. Sieben, Bounds on the rubbling and optimal rubbling numbers of graphs. Graphs Combin. 29(3), 535–551 (2013)
S. Kawano, K. Yamazaki, Worst case analysis of a greedy algorithm for graph thickness. Inf. Process. Lett. 85(6), 333–337 (2003)
A.P. Kazemi, Total dominator coloring in product graphs. Util. Math. 94, 329–345 (2014)
A.P. Kazemi, Total dominator chromatic number of a graph. Trans. Comb. 4, 57–68 (2015)
A.P. Kazemi, Total dominator chromatic number of mycieleskian graphs. Util. Math. 103, 129–137 (2017)
P. Kelly, A congruence theorem for trees. Pac. J. Math. 7(1), 961–968 (1957)
A. Kelmans, Counterexamples to the cubic graph domination conjecture (2006). ArXiv preprint math/0607512
S. Klavzar, S. Spacapan, The/spl δ//sup 2/-conjecture for l (2, 1)-labelings is true for direct and strong products of graphs. IEEE Trans. Circuits Syst. J. II: Express Briefs 53(4), 274–277 (2006)
D.J. Kleitman, The crossing number of K 5,n. J. Combin. Theory 9, 315–323 (1970)
T. Kloks, R.B. Tan, Bandwidth and topological bandwidth of graphs with few P 4’s. Discret. Appl. Math. 115(1–3), 117–133 (2001). 1st Japanese-Hungarian Symposium for Discrete Mathematics and its Applications (Kyoto, 1999)
W.F. Klostermeyer, A taxonomy of perfect domination. J. Discret. Math. Sci. Cryptogr. 18(1–2), 105–116 (2015)
Y. Kobayashi, H. Maruta, Y. Nakae, H. Tamaki, A linear edge kernel for two-layer crossing minimization. Theor. Comput. Sci. 554, 74–81 (2014)
J. Kok, C.M. Mynhardt. Reinforcement in graphs. Congr. Numer. 79, 225–231 (1990)
E. Korach, N. Solel, Tree-width, path-width, and cutwidth. Discret. Appl. Math. 43(1), 97–101 (1993)
D. Korže, A. Vesel, On the packing chromatic number of square and hexagonal lattice. Ars. Math. Contemp. 7(1), 13–22 (2014)
A.V. Kostochka, B.Y. Stodolsky, On domination in connected cubic graphs. Discret. Math. 304(1–3), 45–50 (2005)
M. Kouider, M. Mahéo, Some bounds for the b-chromatic number of a graph. Discret. Math. 256(1–2), 267–277 (2002)
M. Kriesell, Edge-disjoint trees containing some given vertices in a graph. J. Combin. Theory, Ser. B 88(1), 53–65 (2003)
R. Krithika, A. Rai, S. Saurabh, P. Tale, Parameterized and exact algorithms for class domination coloring, in International Conference on Current Trends in Theory and Practice of Informatics (Springer, Berlin, 2017), pp. 336–349
E. Krop, A new bound for Vizing’s conjecture (2016). ArXiv preprint arXiv:1608.02107
E. Krop, Vizing’s conjecture: a two-thirds bound for claw-free graphs. Discret. Appl. Math. 230, 162–165 (2017)
E. Kubicka, The chromatic sum of a graph: History and recent developments. Int. J. Math. Math. Sci. 2004(30), 1563–1573 (2004)
E.M. Kubicka, Polynomial algorithm for finding chromatic sum for unicyclic and outerplanar graphs. Ars Combin. 76, 193–202 (2005)
V.R. Kulli, B. Janakiram, The split domination number of a graph. Graph Theory Notes N. Y. 32(3), 16–19 (1997)
V.R. Kulli, S.C. Sigarkanti, Inverse domination in graphs. Nat. Acad. Sci. Lett 14(12), 473–475 (1991)
M. Kwaśnik, M. Perl, Nearly perfect sets in products of graphs. Opuscula Math. 24(2), 177–180 (2004)
M.A. Labendia, S.R. Canoy, Convex domination in the composition and cartesian product of graphs. Czechoslov. Math. J. 62(4), 1003–1009 (2012)
H.-J. Lai, Every 4-connected line graph of a planar graph is hamiltonian. Graphs Combin. 10(2–4), 249–253 (1994)
Y. Lai, K. Williams, A survey of solved problems and applications on bandwidth, edgesum, and profile of graphs. J. Graph Theory 31, 75–94 (1999)
D.E. Lampert, P.J. Slater, The acquisition number of a graph. Congr. Numer. 109, 203–210 (1995)
R. Laskar, K. Peters, Vertex and edge domination parameters in graphs. Congr. Numer. 48, 291–305 (1985)
S.-M. Lee, J. Mitchem, An upper bound for the harmonious chromatic number of a graph. J. Graph Theory 11(4), 565–567 (1987)
M. Lemańska, Weakly convex and convex domination numbers. Opuscula Math. 24(2), 181–188 (2004)
M. Lepović, I. Gutman, A collective property of trees and chemical trees. J. Chem. Inf. Comput. Sci. 38(5), 823–826 (1998)
L. Lesniak, Chvátal’s t 0-tough conjecture, in Graph Theory, Favorite Conjectures and Open Problems, ed. by R. Gera, S.T. Hedetniemi, C. Larson, vol. 1 (Springer, Berlin, 2016), pp. 135–147
L. Lesniak, H.J. Straight, The cochromatic number of a graph. Ars Combin. 3, 39–46 (1977)
J.R. Lewis, Vertex-edge and Edge-vertex Parameters in Graphs, PhD thesis, Clemson University, 2007
J. Lewis, S.T. Hedetniemi, T.W. Haynes, G.H. Fricke, Vertex-edge domination. Util. Math. 81, 193–213 (2010)
X. Li, Y. Shi, Randić index, diameter and the average distance. MATCH Commun. Math. Comput. Chem. 64(2), 425–431 (2010)
H. Li, X. Li, S. Liu, The (strong) rainbow connection numbers of Cayley graphs on Abelian groups. Comput. Math. Appl. 62(11), 4082–4088 (2011)
Y.X. Lin, J.J. Yuan, Minimum profile of grid networks. Syst. Sci. Math. Sci. 7, 56–66 (1994)
C.-H. Liu, G.J. Chang, Roman domination on strongly chordal graphs. J. Combin. Optim. 26(3), 608–619 (2013)
A. Lourdusamy, S. Somasundaran, The t-pebbling number of graphs. Southeast Asian Bull. Math. 30(5), 907–914 (2006)
L. Lovász, On covering of graphs, in Theory of Graphs (Proceedings of the Colloquium, Tihany, 1966) (Academic Press, New York, 1968), pp. 231–236
C. Lumduanhom, E. Laforge, P. Zhang, Chromatic-connection in graphs. Congr. Numer. 225, 37–54 (2015)
J. Lyle, W. Goddard, The binding number of a graph and its cliques. Discret. Appl. Math. 157(15), 3336–3340 (2009)
W. Mader, A reduction method for edge-connectivity in graphs, in Advances in Graph Theory. Annals of Discrete Mathematics, vol. 3 (Elsevier, New York, 1978), pp. 145–164
S.S. Mahde, V. Mathad, On the weak hub-integrity of graphs. Gulf J. Math. 5(2), 71–86 (2017)
F.S. Makedon, C.H. Papadimitriou, I.H. Sudborough, Topological bandwidth, in CAAP ’83 (L’Aquila, 1983). Lecture Notes in Computer Science, vol. 159 (Springer, Berlin, 1983), pp. 317–331
S.M. Malitz, Graphs with E edges have page number O(\(\sqrt {E}\)). J. Algorithms 17(1), 71–84 (1994)
M.C. Marino, L. Puccio, On some parameters associated with Ls colorings of a finite nonoriented graph (italian). Matematiche (Catania) 35(1–2), 301–310 (1980/1983)
B. Martin, F. Raimondi, T. Chen, J. Martin, The packing chromatic number of the infinite square lattice is between 13 and 15. Discret. Appl. Math. 225, 136–142 (2017)
J.L. Mashburn, T.W. Haynes, S.M. Hedetniemi, S.T. Hedetniemi, P.J. Slater, Differentials in graphs. Util. Math. 69, 43–54 (2006)
M.M. Matthews, D.P. Sumner, Hamiltonian results in K 1,3-free graphs. J. Graph Theory 8(1), 139–146 (1984)
B.D. McKay, Practical graph isomorphism. Congr. Numer. 30, 45–87 (1981)
B.D. McKay, Small graphs are reconstructible. Australas. J. Comb. 15, 123–126 (1997)
A. McLennan, The Erdös-Sós conjecture for trees of diameter four. J. Graph Theory 49(4), 291–301 (2005)
D. Michalak, The point-coarseness of complete n-partite graphs. Discuss. Math. 7, 69–78 (1985)
G.L. Miller, Graph isomorphism, general remarks. J. Comput. Syst. Sci. 18(2), 128–142 (1979)
S. Mishra, On the maximum uniquely restricted matching for bipartite graphs. Electron Notes Discrete Math. 37, 345–350 (2011)
J. Mitchem, The point-outercoarseness of complete n-partite graphs. Compos. Math. 26, 101–110 (1973)
S.M.H. Moghaddam, A. Khodkar, B. Samadi, New bounds on the signed domination numbers of graphs. Australas. J. Comb. 61, 273–280 (2015)
S.D. Monson, N.J. Pullman, R. Rees, A survey of clique and biclique coverings and factorizations of (0,1)-matrices. Bull. Inst. Combin. Appl. 14, 17–86 (1995)
P. Mutzel, T. Odenthal, M. Scharbrodt, The thickness of graphs: a survey. Graphs Combin. 14(1), 59–73 (1998)
Y. Nam, Binding numbers and connected factors. Graphs Combin. 26(6), 805–813 (2010)
C.St.J.A. Nash-Williams, Decomposition of finite graphs into forests. J. Lond. Math. Soc. 1(1), 12–12 (1964)
C.St.J.A. Nash-Williams, Hamiltonian arcs and circuits, in Recent Trends in Graph Theory (Proceedings of Conferene, New York, 1970). Lecture Notes in Mathematics, vol. 186 (Springer, Berlin, 1971), pp. 197–210
R.E. Newman-Wolfe, R.D. Dutton, R.C. Brigham, Connecting sets in graphs–a domination related concept. Congr. Numer. 67, 67–76 (1988)
S. Nikolić, G. Kovačević, A. Miličević, N. Trinajstić, The Zagreb indices 30 years after. Croat. Chem. Acta 76(2), 113–124 (2003)
Nurdin, E.T. Baskoro, A.N.M. Salman, N.N. Gaos. On the total vertex irregularity strength of trees. Discret. Math. 310(21), 3043–3048 (2010)
D.J. Oberly, D.P. Sumner, Every connected, locally connected nontrivial graph with no induced claw is Hamiltonian. J. Graph Theory 3(4), 351–356 (1979)
J. Orlin, Contentment in graph theory: covering graphs with cliques. Nederl. Akad. Wetensch. Proc. Ser. A 80=Indag. Math. 39(5), 406–424 (1977)
L. Pachter, P. Kim, Forcing matchings on square grids. Discret. Math. 190(1–3), 287–294 (1998)
L. Pachter, H.S. Snevily, B. Voxman, On pebbling graphs. Congr. Numer. 107, 65–80 (1995)
R. Pepper, On the annihilation number of a graph, in Recent Advances In Electrical Engineering: Proceedings of the 15th American Conference on Applied Mathematics (2009), pp. 217–220
K.W. Peters, Theoretical and Algorithmic Results on Domination and Connectivity, PhD thesis, Clemson University, 1986
D. Plavšić, S. Nikolić, N. Trinajstić, Z. Mihalić, On the Harary index for the characterization of chemical graphs. J. Math. Chem. 12(1), 235–250 (1993)
A.J. Prasad, T.T. Chelvam, S.R. Chellathurai, Private domination number of a graph. J. Discret. Math. Sci. Cryptogr. 10(5), 661–666 (2007)
J. Puech, R-annihilated and independent perfect neighborhood sets in chordal graphs. Discret. Math. 215(1–3), 181–199 (2000)
G.J. Puleo, Tuza’s conjecture for graphs with maximum average degree less than 7. Eur. J. Comb. 49, 134–152 (2015)
N.J. Pullman, Clique coverings of graphs-a survey, in Combinatorial Mathematics, X (Adelaide, 1982). Lecture Notes in Mathematics, vol. 1036 (Springer, Berlin, 1983), pp. 72–85
P.R.L. Pushpam, T.N.M. Mai, Edge Roman domination in graphs. J. Comb. Math. Comb. Comput. 69, 175–182 (2009)
L. Pyber, Covering the edges of a connected graph by paths. J. Combin. Theory Ser. B 66(1), 152–159 (1996)
N.J. Rad, L. Volkmann, A note on the independent domination number in graphs. Discret. Appl. Math. 161(18), 3087–3089 (2013)
M. Radcliffe, P. Zhang, On irregular colorings of graphs. AKCE Int. J. Graphs Comb. 3, 175–191 (2006)
D.F. Rall, A fractional version of domatic number. Congr. Numer. 74, 100–106 (1990)
D.F. Rall, Dominating a graph and its complement. Congr. Numer. 80, 89–89 (1991)
D.F. Rall, P.J. Slater, On location-domination numbers for certain classes of graphs. Congr. Numer. 45, 97–106 (1984)
M. Randić, Characterization of molecular branching. J. Am. Chem. Soc. 97(23), 6609–6615 (1975)
R. Rashidi, The Theory and Applications of Stratified Graphs, PhD thesis, Western Michigan University, 1994
A. Raspaud, W. Wang, On the vertex-arboricity of planar graphs. Eur. J. Comb. 29(4), 1064–1075 (2008)
R.C. Read, D.G. Corneil, The graph isomorphism disease. J. Graph Theory 1(4), 339–363 (1977)
B. Reed, Paths, stars and the number three. Comb. Probab. Comput. 5(3), 277–295 (1996)
B. Reed, ω, δ, and χ. J. Graph Theory 27(4), 177–212 (1998)
A. Riskin, The circular k-partite crossing number of K_{m, n} (2006). ArXiv preprint math/0605235
N. Robertson, P.D. Seymour, Graph minors. III. Planar tree-width. J. Combin. Theory, Ser. B 36(1), 49–64 (1984)
N. Robertson, P.D. Seymour, Graph minors. II. Algorithmic aspects of tree-width. J. Algorithms 7(3), 309–322 (1986)
N. Robertson, Z.-X. Song, Hadwiger number and chromatic number for near regular degree sequences. J. Graph Theory 64(3), 175–183 (2010)
N. Robertson, P. Seymour, R. Thomas, Hadwiger’s conjecture for K 6-free graphs. Combinatorica 13(3), 279–361 (1993)
M.L. Roden, P.J. Slater, Liar’s domination and the domination continuum. Congr. Numer 190, 77–85 (2008)
J.A. Rodriguez, J.M. Sigarreta, Offensive alliances in cubic graphs. Int. Math. Forum 1, 1773–1782 (2006)
R. Rubalcaba, Fractional Domination, Fractional Packings, and Fractional Isomorphisms of Graphs, PhD thesis, Auburn University, 2005
Z. Ryjáček, On a closure concept in claw-free graphs. J. Combin. Theory, Ser. B 70(2), 217–224 (1997)
V. Saenpholphat, F. Okamoto, P. Zhang, Measures of traceability in graphs. Math. Bohem. 131(1), 63–84 (2006)
N.Z. Salvi, A note on the line-distinguishing chromatic number and the chromatic index of a graph. J. Graph Theory 17(5), 589–591 (1993)
V. Samodivkin, On k-dependent domination in graphs. SUT J. Math. 43(1), 99–106 (2007)
E. Sampathkumar, The global domination number of a graph. J. Math. Phys. Sci. 23(5), 377–385 (1989)
E. Sampathkumar, S.S. Kamath, Mixed domination in graphs. Sankhya 54, 399–402 (1992)
E. Sampathkumar, L. Pushpa Latha, Semi-strong chromatic number of a graph. Indian J. Pure Appl. Math. 26, 35–40 (1995)
E. Sampathkumar, L. Pushpa Latha, Strong weak domination and domination balance in a graph. Discret. Math. 161, 235–242 (1996)
E. Sampathkumar, P.S. Neeralagi, The line neighborhood number of a graph. Indian J. Pure Appl. Math. 17(2), 142–149 (1986)
E. Sampathkumar, H.B. Walikar, The connected domination number of a graph. J. Math. Phys. Sci. 13, 607–613 (1979)
D.P. Sanders, Y. Zhao, Planar graphs of maximum degree seven are class I. J. Combin. Theory, Ser. B 83(2), 201–212 (2001)
N. Sauer, Hedetniemi’s conjecture—a survey. Discret. Math. 229(1–3), 261–292 (2001). Combinatorics, graph theory, algorithms and applications
M. Schaefer, The graph crossing number and its variants: a survey. Electron. J. Comb. DS21, 113 pp. (2017)
E.R. Scheinerman, D.H. Ullman, Fractional Graph Theory: A Rational Approach to the Theory of Graphs (Courier Corporation, North Chelmsford, 2011)
I. Schiermeyer, Bounds for the rainbow connection number of graphs. Discuss. Math. Graph Theory 31(2), 387–395 (2011)
M. Sekanina, Problem 28, in Theory of Graphs and Its Applications, Proceedings of the Symposium Held in Smolenice in June 1963 (Academic Press, New York, 1964), p. 164
P.D. Seymour, On multi-colourings of cubic graphs, and conjectures of Fulkerson and Tutte. Proc. Lond. Math. Soc. 3(3), 423–460 (1979)
P.D. Seymour, Some unsolved problems on one-factorizations of graphs, in Graph Theory and Related Topics: Proceedings of the Conference Held in Honour of Professor W. T. Tutte on the Occasion of His Sixtieth Birthday, University of Waterloo, 5–9 July 1977, ed. by J.A. Bondy, U.S.R. Murty (Academic Press New York, 1979)
P.D. Seymour, Nowhere-zero 6-flows. J. Combin. Theory, Ser. B 30(2), 130–135 (1981)
P.D. Seymour, R. Thomas, Graph searching and a min-max theorem for tree-width. J. Combin. Theory, Ser. B 58(1), 22–33 (1993)
S. Shaebani, On fall colorings of graphs, Ars Combin. 120, 199–212 (2015)
K.H. Shafique, R.D. Dutton, On satisfactory partitioning of graphs. Congr. Numer. 154, 183–194 (2002)
F. Shahrokhi, O. Sỳkora, L. Székely, I. Vrto, On bipartite drawings and the linear arrangement problem. SIAM J. Comput. 30(6), 1773–1789 (2001)
F. Shahrokhi, O. Sykora, L. Szekely, I. Vrto, The gap between the crossing numbers and the convex crossing numbers. Contemp. Math. 342, 249–258 (2004)
M. Shalom, On the interval chromatic number of proper interval graphs. Discret. Math. 338(11), 1907–1916 (2015)
M.A. Shalu, S. Vijayakumar, T.P. Sandhya, A lower bound of the cd-chromatic number and its complexity, in Conference on Algorithms and Discrete Applied Mathematics (Springer, Berlin, 2017), pp. 344–355
W. Shang, P. Wan, F. Yao, X. Hu, Algorithms for minimum m-connected k-tuple dominating set problem. Theor. Comput. Sci. 381(1–3), 241–247 (2007)
S.E. Shauger, Results on the Erdös-Gyarfas conjecture in K 1,m-free graphs. Congr. Numer. 134, 61–65 (1998)
J. Sheehan, The multiplicity of Hamiltonian circuits in a graph, in Recent Advances in Graph Theory, (Proceedings Second Czechoslovak Symposium, Prague, 1974), ed. by M. Fiedler (Academia, Prague, 1975), pp. 477–480
S.M. Sheikholeslami, L. Volkmann, The Roman domatic number of a graph. Appl. Math. Lett. 23(10), 1295–1300 (2010)
Z. Shi, W. Goddard, S.T. Hedetniemi, K. Kennedy, R. Laskar, A. McRae, An algorithm for partial grundy number on trees. Discret. Math. 304(1), 108–116 (2005)
J.M. Sigarreta, J.A. Rodríguez, On defensive alliances and line graphs. Appl. Math. Lett. 19(12), 1345–1350 (2006)
J.M. Sigarreta, J.A. Rodríguez, On the global offensive alliance number of a graph. Discret. Appl. Math. 157(2), 219–226 (2009)
J. Sjöstrand, The cover pebbling theorem. Electron. J. Comb. 12(1), 22 (2005)
Z. Skupień, Smallest sets of longest paths with empty intersection. Comb. Probab. Comput. 5(4), 429–436 (1996)
P.J. Slater, Leaves of trees. Congr. Numer. 14(549–559), 37 (1975)
P.J. Slater, R-domination in graphs. J. Assoc. Comput. Mach. 23(3), 446–450 (1976)
P.J. Slater, Enclaveless sets and MK-systems. J. Res. Natl. Bur. Stand. 82(3), 197–202 (1977)
P.J. Slater, Dominating and reference sets in a graph. J. Math. Phys. Sci. 22(4), 445–455 (1988)
P.J. Slater, Liar’s domination. Networks 54(2), 70–74 (2009)
P.J. Slater, Y. Wang, The competitive-acquisition numbers of paths. Congr. Numer. 167, 33 (2004)
P.J. Slater, S.E. Goodman, S.T. Hedetniemi, On the optional hamiltonian completion problem. Networks 6(1), 35–51 (1976)
P.J. Slater, E.J. Cockayne, S.T. Hedetniemi, Information dissemination in trees. SIAM J. Comput. 10, 692–701 (1981)
T. Slivnik, Short proof of Galvin’s theorem on the list-chromatic index of a bipartite multigraph. Comb. Probab. Comput. 5(1), 91–94 (1996)
N.S. Narahari, B. Sooryanarayana, G.K.N. Swamy, Open neighborhood chromatic number of an antiprism graph. Appl. Math. E-Notes 15, 54–62 (2015)
L. Šoltés, Transmission in graphs: a bound and vertex removing. Math. Slovaca 41(1), 11–16 (1991)
F. Speranza, Colorazioni di specie superiore d’un grafo. Boll. Unione Mat. Ital.(4) 12, 53–62 (1975)
M. Subramanian, Studies in Graph Theory - Independence Saturation in Graphs, PhD thesis, Manonmaniam Sundaranar University, Tirunelveli, 2004
S. Suen, J. Tarr, An improved inequality related to Vizing’s conjecture. Electron. J. Comb. 19(1), 8 (2012)
K. Sutner, Linear cellular automata and the Garden-of-Eden. Math. Intell. 11(2), 49–53 (1989)
L.A. Székely, Turán’s brick factory problem: the status of the conjectures of Zarankiewicz and Hill, in Graph Theory, Favorite Conjectures and Open Problems, ed. by R. Gera, S.T. Hedetniemi, C. Larson (Springer, Berlin, 2016), pp. 211–230
G. Szekeres, Polyhedral decompositions of cubic graphs. Bull. Aust. Math. Soc. 8(3), 367–387 (1973)
C. Tardif, Hedetniemi’s conjecture, 40 years later. Graph Theory Notes N. Y. 54, 46–57 (2008)
J.A. Telle, Vertex Partitioning Problems: Characterization, Complexity and Algorithms on Partial k-trees, PhD thesis, University of Oregon, 1994
J.A. Telle, A. Proskurowski, Efficient sets in partial k-trees. Discret. Appl. Math. 44(1–3), 109–117 (1993)
U. Teschner, A new upper bound for the bondage number of graphs with small domination number. Australas. J. Comb. 12, 27–35 (1995)
U. Teschner, The bondage number of a graph G can be much greater than Δ(G). Ars Combin. 43, 81–87 (1996)
S. Thomassé, A. Yeo, Total domination of graphs and small transversals of hypergraphs. Combinatorica 27(4), 473–487 (2007)
C. Thomassen, Reflections on graph theory. J. Graph Theory 10(3), 309–324 (1986)
C. Thomassen, Configurations in graphs of large minimum degree, connectivity, or chromatic number, in Combinatorial Mathematics: Proceedings of the Third International Conference (New York, 1985). Annals of the New York Academy of Sciences, vol. 555 (The New York Academy of Sciences, New York, 1989), pp. 402–412
C. Thomassen, Chords of longest cycles in cubic graphs, J. Combin. Theory, Ser. B 71(2), 211–214 (1997)
C. Thomassen, Independent dominating sets and a second Hamiltonian cycle in regular graphs. J. Combin. Theory, Ser. B 72(1), 104–109 (1998)
R. Tijdeman, On a telephone problem. Nieuw Arch. Wisk. 3(19), 188–192 (1971)
O. Togni, Strong chromatic index of products of graphs. Discrete Math. Theor. Comput. Sci. 9(1), 47–56 (2007)
R. Tout, A.N. Dabboucy, K. Howalla, Prime labeling of graphs. Natl. Acad. Sci. Lett. - India 5(11), 365–368 (1982)
W.T. Tutte, The thickness of a graph. Nederl. Akad. Wetensch. Proc. Ser. A 66 = Indag. Math. 25, 567–577 (1963)
Zs. Tuza, Infinite and finite sets. Vols. I, II, in Proceedings of the Sixth Hungarian Combinatorial Colloquium Held in Eger, 6–11 July 1981, ed. by A. Hajnal, L. Lovász, V.T. Sós. Colloquia Mathematica Societatis János Bolyai, vol. 37 (North-Holland Publishing, Amsterdam, 1984), p. 888
Z. Tuza, A conjecture on triangles of graphs. Graphs Combin. 6(4), 373–380 (1990)
S.M. Ulam, A Collection of Mathematical Problems, vol. 8 (Interscience Publishers, Geneva, 1960)
L.C. van der Merwe, C.M. Mynhardt, T.W. Haynes, Criticality index of total domination. Congr. Numer. 131, 67–73 (1998)
L. van der Merwe, C.M. Mynhardt, T.W. Haynes, Total domination edge critical graphs with maximum diameter. Discuss. Math. Graph Theory 21(2), 187–205 (2001)
Y. Venkatakrishnan, V. Swaminathan, Colour class domination numbers of some classes of graphs. Algebra Discrete Math. 2(18), 301–305 (2014)
J. Verstraete, Personal communication, August 2010
N. Vijayaditya, On total chromatic number of a graph. J. Lond. Math. Soc. 2(3), 405–408 (1971)
A. Vince, Star chromatic number. J. Graph Theory 12(4), 551–559 (1988)
V.G. Vizing, The cartesian product of graphs. Vychisl. Sistemy 9, 30–43 (1963)
V.G. Vizing, On an estimate of the chromatic class of a p-graph. Diskret. Analiz. 3, 25–30 (1964)
V.G. Vizing, Critical graphs with given chromatic class (in Russian). Diskret. Analiz. 5, 9–17 (1965)
V.G. Vizing, Some unsolved problems in graph theory. Uspehi Mat. Nauk 23(6), 117–144 (1968)
V.G. Vizing, Coloring the vertices of a graph in prescribed colors. Diskret. Analiz 29(3), 10 (1976)
L. Volkmann, B. Zelinka, Signed domatic number of a graph. Discret. Appl. Math. 150(1–3), 261–267 (2005)
L. Volkmann, V.E. Zverovich, A disproof of Henning’s conjecture on irredundance perfect graphs. Discret. Math. 254(1–3), 539–554 (2002)
H. Vu Dinh, Path partition number in tough graphs. Discret. Math. 164(1–3), 291–294 (1997)
K. Wagner, Über eine Eigenschaft der ebenen Komplexe. Math. Ann. 114(1), 570–590 (1937)
H.B. Walikar, On star partition number of a graph (1979). Manuscript
M. Walsh, The hub number of a graph. Int. J. Math. Comput. Sci 1(1), 117–124 (2006)
T.R.S. Walsh, A. Giorgetti, A. Mednykh, Enumeration of unrooted orientable maps of arbitrary genus by number of edges and vertices. Discret. Math. 312(17), 2660–2671 (2012)
Y.-L.Wang, On the bondage number of a graph. Discret. Math. 159(1–3), 291–294 (1996)
S. Wang, B. Wei, The ratio of domination and independent domination numbers on trees. Congr. Numer. 227, 287–292 (2016)
H. Wiener, Structural determination of paraffin boiling points. J. Am. Chem. Soc. 69(1), 17–20 (1947)
L.K. Williams, On exact n-step domination. Ars Combin. 58, 13–22 (2001)
J.H. Yan, G.J. Chang, S.M. Hedetniemi, S.T. Hedetniemi, k-path partitions in trees. Discret. Appl. Math. 78, 227–233 (1997)
D. Yang, X. Zhu, Strong chromatic index of sparse graphs. J. Graph Theory 83(4), 334–339 (2016)
M. Yannakakis, F. Gavril, Edge dominating sets in graphs. SIAM J. Appl. Math. 38(3), 364–372 (1980)
K.-C. Yeh, Labeling Graphs with a Condition at Distance Two, PhD thesis, University of South Carolina, 1990
H.-G. Yeh, G.J. Chang, Algorithmic aspects of majority domination. Taiwan. J. Math. 1(3), 343–350 (1997)
C.-C. Yen, R.C.T. Lee, The weighted perfect domination problem and its variants. Discret. Appl. Math. 66(2), 147–160 (1996)
I.G. Yero, J.A. Rodrıguez-Velázquez, A survey on alliances in graphs: defensive alliances. Util. Math. 105, 141–172 (2017)
R. Yuster, Dense graphs with a large triangle cover have a large triangle packing. Comb. Probab. Comput. 21(6), 952–962 (2012)
M. Zaker, Inequalities for the grundy chromatic number of graphs. Discret. Appl. Math. 155(18), 2567–2572 (2007)
C. Zarankiewicz, On a problem of P. Turán concerning graphs. Fund. Math. 41(1), 137–145 (1954)
B. Zelinka, Edge-domatic number of a graph. Czechoslov. Math. J. 33(108)(1), 107–110 (1983)
B. Zelinka, On k-domatic numbers of graphs. Czechoslov. Math. J. 33(108)(2), 309–313 (1983)
B. Zelinka, Connected domatic number of a graph. Math. Slovaca 36(4), 387–392 (1986)
B. Zelinka, Total domatic number and degrees of vertices of a graph. Math. Slovaca 39(1), 7–11 (1989)
B. Zelinka, Domatic numbers of graphs and their variants: a survey, in Domination in Graphs, Advanced Topics, ed. by T.W. Haynes, S.T. Hedetniemi, P. J. Slater, vol. 209 (Marcel Dekker, New York, 1998), pp. 351–378
B. Zelinka, Signed and minus domination in bipartite graphs. Czechoslov. Math. J. 56(2), 587–590 (2006)
S. Zhan, On Hamiltonian line graphs and connectivity. Discret. Math. 89(1), 89–95 (1991)
Z. Zhang, X. Chen, J. Li, B. Yao, X. Lu, J. Wang, On adjacent-vertex-distinguishing total coloring of graphs. Sci. China Ser. A 48(3), 289–299 (2005)
Y. Zhao, L. Kang, M.Y. Sohn, The algorithmic complexity of mixed domination in graphs. Theor. Comput. Sci. 412(22), 2387–2392 (2011)
B. Zhou, I. Gutman, Further properties of Zagreb indices. MATCH Commun. Math. Comput. Chem. 54, 233–239 (2005)
X. Zhu, Star chromatic numbers and products of graphs. J. Graph Theory 16(6), 557–569 (1992)
X. Zhu, A survey on Hedetniemi’s conjecture. Taiwan. J. Math. 2, 1–24 (1998)
X. Zhu, Circular chromatic number: a survey. Discret. Math. 229(1–3), 371–410 (2001)
Acknowledgements
The authors would like to thank Robert Beeler, Gary Chartrand, Mustapha Chellali, Jean Dunbar, Renu Laskar, C.M. Mynhardt, and Ping Zhang for their constructive criticism of the manuscript, which greatly improved this chapter.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Gera, R., Haynes, T.W., Hedetniemi, S.T., Henning, M.A. (2018). An Annotated Glossary of Graph Theory Parameters, with Conjectures. In: Gera, R., Haynes, T., Hedetniemi, S. (eds) Graph Theory. Problem Books in Mathematics. Springer, Cham. https://doi.org/10.1007/978-3-319-97686-0_14
Download citation
DOI: https://doi.org/10.1007/978-3-319-97686-0_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-97684-6
Online ISBN: 978-3-319-97686-0
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)




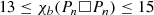 . The most recent papers on this parameter call this the packing chromatic number χ
ρ(G).
. The most recent papers on this parameter call this the packing chromatic number χ
ρ(G). , γ
p(G) = 2 while Γ
p(G) = 3; introduced by Fellows and Hoover in 1991 [
, γ
p(G) = 2 while Γ
p(G) = 3; introduced by Fellows and Hoover in 1991 [