Analytical Modeling and Simulation Study of Homo and Hetero III-V Semiconductor Based Tunnel Field Effect Transistor (TFET)

Abstract

High staggered, Moderate staggered and homo junction III–V semiconductor-based heterojunction TFETs are of interest as they allow a high on–off current ratio and high on current through reduction in the tunneling barrier height. GaAsSb/InGaAs based heterojunction p-n-i-n TFET has shown an increase in the drive current when compared to homojunction due to band engineering. Further engineering can be performed by varying tunneling barrier height (E_beff) from 0.5 to 0.25 eV using differently staggered heterojunction. Thus, the concept of halo doped heterojunction pocket TFET is presented by analytical and simulation study with varying staggered junctions.

1 Introduction

In recent years, prolific research has accounted in incrementing the drain current of TFET and consequently designing a device providing sub threshold slope below the limits with similar performance as that of CMOS technology [1]. Introducing pocket layer in TFET or using hetero materials have shown a considerate improvement in performance than the conventional design. This paper aims at combining some of those techniques.

A p-n junction can be classified on the basis of bandgap, as High staggered hetero, Moderate staggered hetero and Homo junction. The use of these junctions in a TFET as source and channel materials exponents in reducing the tunneling barrier and subsequently increasing drain current [2, 3]. The halo doped pocket hetero junction TFET is the acme of possibility to include in band gap engineering without being utilitarian with materials. Introducing a pocket at the source end and to be able to further reduce the bandgap at the junction using barrier height variation would increment the drain current meteorically. The bandgap engineering performed using tunneling barrier height (E_beff) variation from 0.5 to 0.25 eV is realized by varying the mole fraction of the materials in GaAsSb and InGaAs as source and drain respectively.

An analytical model that would be applicable to all the three structures as mentioned earlier, with halo doped pocket layer is developed and evaluated. The general approach developed objectively is utilized to generate potential, electric field and energy band profile respectively. The results are then compared with simulation [4,5,6] output and analyzed. The material parameters are given in Table 181.1.

Table 181.1 Device parameters of the architectures under study [3, 10, 11]

2 Analytical Model of 2D Halo Doped TFET

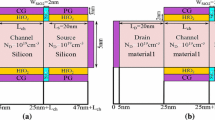
The two dimensional Poisson’s Equation for the device shown in Fig. 181.1a, can be expressed as [7]

Fig. 181.1

a Schematic cross sectional view of p-n-i-n TFET; L_g is the gate length, L_H pocket length = 6 nm, L_ch channel length = 150 nm, t_si is the channel thickness = 30 nm, b band diagram of hetero interface [9], c simulated structure of p-n-i-n TFET

$$ \frac{{\partial^{2} \varphi \left( {x,y} \right)}}{{\partial x^{2} }} + \frac{{\partial^{2} \varphi \left( {x,y} \right)}}{{\partial y^{2} }} = - \frac{qN}{{\varepsilon_{\text{Si}} }} $$

(181.1)

where 0 ≤ x ≤ t_Si and 0 ≤ y ≤ L_g. The 2D potential, $\varphi \left( {x,y} \right)$ can be denoted as φ_H and φ_CH in R_H and R_CH regions. N is the effective doping which is equal to −N_H and ±N_CH respectively. With a parabolic distribution of potential along the x direction, [8]

$$ \varphi_{\text{H}} \left( {x,y} \right) = a_{\text{H}} \left( y \right) + a_{\text{H1}} \left( y \right)x + a_{\text{H2}} \left( y \right)x^{2} $$

(181.2)

$$ \varphi_{\text{CH}} \left( {x,y} \right) = a_{\text{CH}} \left( y \right) + a_{\text{CH1}} \left( y \right)x + a_{\text{CH2}} \left( y \right)x^{2} $$

(181.3)

To ensure the continuity of potential and electric field, boundary conditions [12] are

$$ \varphi_{\text{H}} \left( {0,y} \right) = \varphi_{\text{H}} \left( {t_{\text{Si}} ,y} \right) = \varphi_{\text{SH}} \left( y \right) $$

(181.4)

$$ E_{{x - {\text{H}}}} \left( {0,y} \right) = - \frac{{{\text{d}}\varphi_{\text{H}} \left( {x,y} \right)}}{{{\text{d}}x}}|_{x = 0} = - \frac{{\left( {V_{\text{g}} - V_{\text{fb}} } \right) - \varphi_{\text{SH}} \left( y \right)}}{{\frac{{t_{\text{Si}} }}{\eta }}} $$

(181.5)

$$ \frac{{{\text{d}}\varphi_{\text{H}} \left( {x,y} \right)}}{{{\text{d}}x}}|_{{x = \frac{{t_{\text{Si}} }}{2}}} = 0 $$

(181.6)

$$ \varphi_{\text{CH}} \left( {0,y} \right) = \varphi_{\text{CH}} \left( {t_{\text{Si}} ,y} \right) = \varphi_{\text{SCH}} \left( y \right) $$

(181.7)

$$ E_{{x - {\text{CH}}}} \left( {0,y} \right) = - \frac{{{\text{d}}\varphi_{\text{CH}} \left( {x,y} \right)}}{{{\text{d}}x}}|_{x = 0} = - \frac{{\left( {V_{\text{g}} - V_{\text{fb}} } \right) - \varphi_{\text{SCH}} \left( y \right)}}{{\frac{{t_{\text{Si}} }}{\eta }}} $$

(181.8)

$$ \frac{{{\text{d}}\varphi_{\text{CH}} \left( {x,y} \right)}}{{{\text{d}}x}}|_{{x = \frac{{t_{\text{Si}} }}{2}}} = 0 $$

(181.9)

In the above equations $\varphi_{\text{SH}}$ and $\varphi_{\text{SCH}}$ are the surface potentials in pocket region R_H and channel region R_CH respectively [8]. V_fb denotes the flat band voltage and η is the ratio of gate oxide capacitance and thin film capacitance. Solving for the parameters using the above boundary conditions yields

$$ a_{\text{H/CH}} \left( y \right) = \varphi_{\text{SH/SCH}} \left( y \right) $$

(181.10)

$$ a_{\text{H1/CH1}} \left( y \right) = - \frac{\eta }{{t_{\text{Si}} }}\left( {V_{\text{g}} - V_{\text{fb}} - \varphi_{\text{SH/SCH}} \left( y \right)} \right) $$

(181.11)

$$ a_{\text{H2/CH2}} \left( y \right) = - \frac{\eta }{{t_{\text{Si}}^{2} }}\left( {V_{\text{g}} - V_{\text{fb}} - \varphi_{\text{SH/SCH}} \left( y \right)} \right) $$

(181.12)

$$ \varphi_{\text{H}} \left( {x,L_{\text{H}} } \right) = \varphi_{\text{CH}} \left( {x,L_{\text{H}} } \right) $$

(181.13)

$$ \frac{{{\text{d}}\varphi_{H} \left( {x,y} \right)}}{{{\text{d}}y}}|_{{y = L_{\text{H}} }} = \frac{{{\text{d}}\varphi_{\text{CH}} \left( {x,y} \right)}}{{{\text{d}}y}}|_{{y = L_{\text{H}} }} $$

(181.14)

By substituting $\varphi_{\text{H}}$ in the 2D Poisson’s equation,

$$ \ddot{\varphi }_{\text{SH}} \left( y \right) - \alpha^{2} \varphi_{\text{SH}} \left( y \right) = \beta_{\text{H}} $$

(181.15)

$$ \ddot{\varphi }_{\text{SCH}} \left( y \right) - \alpha^{2} \varphi_{\text{SCH}} \left( y \right) = \beta_{\text{CH}} $$

(181.16)

where, $\alpha = \sqrt {\frac{2\eta }{{t_{\text{Si}}^{2} }}}$, $\beta_{\text{CH}} = - \frac{{2\eta \left( {V_{\text{g}} - V_{\text{fb}} } \right)}}{{t_{\text{Si}}^{2} }} + \frac{{qN_{\text{CH}} }}{{\varepsilon_{\text{Si}} }}$ Solving the above equations gives,

$$ \varphi_{\text{SH}} \left( y \right) = C_{\text{H1}} {\text{e}}^{\alpha y} + C_{\text{H2}} {\text{e}}^{ - \alpha y} - \beta_{\text{H}} /\alpha^{2} $$

(181.17)

$$ \varphi_{\text{SCH}} \left( y \right) = C_{\text{CH1}} {\text{e}}^{\alpha y} + C_{\text{CH2}} {\text{e}}^{ - \alpha y} - \beta_{\text{CH}} /\alpha^{2} $$

(181.18)

Boundary conditions for surface potential at source end, $\varphi_{\text{SH}} \left( 0 \right)$ and drain end, $\varphi_{\text{SCH}} \left( {L_{\text{g}} } \right)$ are

$$ \varphi_{\text{SH}} \left( 0 \right) = \frac{kT}{q}{ \ln }\left( {\frac{{N_{\text{source}} }}{{N_{\text{i}} }}} \right) $$

(181.19)

$$ \varphi_{\text{SCH}} \left( {L_{\text{g}} } \right) = \frac{kT}{q}\ln \left( {\frac{{N_{\text{dr}} }}{{N_{\text{i}} }}} \right) + V_{\text{ds}} $$

(181.20)

$N_{\text{source}}$, $N_{\text{dr}}$ and $N_{\text{i}}$ are the doping concentrations of source, drain and the intrinsic concentration of the channel respectively.

Solving the above equations with given boundary conditions, parameters $C_{\text{H1}} ,C_{\text{H2}} ,C_{\text{CH1}} ,C_{\text{CH2}}$ are evaluated. Further

$$ E_{{x - {\text{H}}}} = a_{\text{H1}} \left( y \right) + 2xa_{\text{H2}} \left( y \right) $$

(181.21)

$$ E_{{y - {\text{H}}}} = C_{\text{H1}} \alpha {\text{e}}^{\alpha y} - C_{\text{H2}} \alpha {\text{e}}^{ - \alpha y} $$

(181.22)

$$ E_{{x - {\text{CH}}}} = a_{\text{CH1}} \left( y \right) + 2xa_{\text{CH2}} \left( y \right) $$

(181.23)

$$ E_{{y - {\text{CH}}}} = C_{\text{CH1}} \alpha {\text{e}}^{\alpha y} - C_{\text{CH2}} \alpha {\text{e}}^{ - \alpha y} $$

(181.24)

would be the electric field expressions in the pocket and channel region respectively.

The effective bandgap for tunnelling can be decreased even further by using heterostructures [2]. Consider (semiconductor 1) p-n (semiconductor 2) junction with two different bandgap materials. Depending upon the difference between their electron affinities, the junction can be classified as in Fig. 181.2.

Fig. 181.2

Surface potential profile from source to drain region for a In_0.7Ga_0.3As homojunction TFET, b moderately staggered GaAs_0.4Sb_0.6/In_0.65Ga_0.35As hetero junction TFET, c high staggered GaAs_0.35Sb_0.65/In_0.7Ga_0.3As

The drive current enhances on replacing an InGaAs homojunction TFET by a heterojunction InGaAs/GaAsSb. Further enhancement can be attained by engineering the effective tunneling barrier height E_beff from 0.58 to 0.25 eV. Moderate-stagger GaAs_0.4Sb_0.6/In_0.65Ga_0.35As and high stagger GaAs_0.35Sb_0.65/In_0.7Ga_0.3As hetero junction TFETs are considered, and their electrical results are compared with the In_0.7Ga_0.3As homojunction TFET (E_beff = 0.58 eV).

Also, boundary conditions for surface potential at source end, $\varphi_{\text{SH}} \left( 0 \right)$ and drain end, $\varphi_{\text{SCH}} \left( {L_{\text{g}} } \right)$ can be evaluated from the band diagram across the hetero junction at the source end as shown in Fig. 181.1b.

$$ \varphi_{\text{SH}} \left( 0 \right) = V_{\text{bi}} = E_{\text{f2}} - E_{\text{f1}} $$

(181.25)

$$ E_{\text{f2}} - E_{\text{c2}} = \frac{kT}{q}{ \ln }\left( {\frac{{N_{\text{d}} }}{{N_{\text{c2}} }}} \right) $$

(181.26)

$$ E_{\text{v1}} - E_{\text{f1}} = \frac{kT}{q}{ \ln }\left( {\frac{{N_{\text{a}} }}{{N_{\text{v1}} }}} \right) $$

(181.27)

$$ \Delta E_{\text{c}} = \chi_{2} - \chi_{1} $$

(181.28)

$$ \Delta E_{\text{c}} + \Delta E_{\text{v}} = \Delta E_{\text{g}} $$

(181.29)

Thus,

$$ \varphi_{\text{SH}} \left( 0 \right) = E_{\text{g1}} - \Delta E_{\text{c}} + \frac{kT}{q}{ \ln }\left( {\frac{{N_{\text{a}} N_{\text{d}} }}{{N_{\text{c2}} N_{\text{v1}} }}} \right) $$

(181.30)

$$ \varphi_{\text{SCH}} \left( {L_{\text{g}} } \right) = \frac{kT}{q}\ln \left( {\frac{{N_{\text{dr}} }}{{n_{\text{i}} }}} \right) + V_{\text{ds}} $$

(181.31)

where $\chi_{2} , \chi_{1}$ are the electron affinity values of the source and the pocket, $N_{\text{a}}$, $N_{\text{d}}$, $N_{\text{c2}}$, $N_{\text{v1}}$ are the doping concentration in source, pocket and intrinsic concentration in source, pocket respectively.$N_{\text{dr}}$ is the doping concentration of the drain, $E_{\text{g1}}$ the band energy of source and $\Delta E_{\text{c}}$ is the conduction band offset. Thus, the parameters are

$$ \begin{aligned} C_{\text{CH2}} & = \frac{1}{{\left( {{\text{e}}^{{\alpha L_{\text{g}} }} - {\text{e}}^{{ - \alpha L_{\text{g}} }} } \right)}}\left[ {\left( {E_{\text{g1}} - \Delta E_{\text{c}} + \frac{kT}{q}\ln \left( {\frac{{N_{\text{a}} N_{\text{d}} }}{{N_{\text{c2}} N_{\text{v1}} }}} \right)} \right){\text{e}}^{{\alpha L_{\text{g}} }} - \frac{kT}{q}\ln \left( {\frac{{N_{\text{dr}} }}{{n_{\text{i}} }}} \right)} \right. \\ & \quad \quad \quad \quad \quad \quad \quad \quad \quad \left. { - V_{\text{ds}} + \left( {k1{\text{e}}^{{\alpha L_{\text{g}} }} - 1} \right)\frac{{\beta_{\text{CH}} }}{{\alpha^{2} }} + \left( {1 - k1} \right){\text{e}}^{{\alpha L_{\text{g}} }} \frac{{\beta_{\text{H}} }}{{\alpha^{2} }}} \right] \\ \end{aligned} $$

$$ \begin{aligned} C_{\text{CH1}} & = \frac{1}{{\left( {{\text{e}}^{{\alpha L_{\text{g}} }} - {\text{e}}^{{ - \alpha L_{\text{g}} }} } \right)}}\left[ {\left( {E_{\text{g1}} - \Delta E_{\text{c}} + \frac{kT}{q}\ln \left( {\frac{{N_{\text{a}} N_{\text{d}} }}{{N_{\text{c2}} N_{\text{v1}} }}} \right)} \right){\text{e}}^{{ - \alpha L_{\text{g}} }} + \frac{kT}{q}\ln \left( {\frac{{N_{\text{dr}} }}{{n_{\text{i}} }}} \right)} \right. \\ & \quad \quad \quad \quad \quad \quad \quad \quad \quad \left. { + V_{\text{ds}} + \left( {1 - k1{\text{e}}^{{ - \alpha L_{\text{g}} }} } \right)\frac{{\beta_{\text{CH}} }}{{\alpha^{2} }} - \left( {1 - k1} \right){\text{e}}^{{ - \alpha L_{\text{g}} }} \frac{{\beta_{\text{H}} }}{{\alpha^{2} }}} \right] \\ \end{aligned} $$

where, $k1 = \frac{{{\text{e}}^{{\alpha L_{\text{H}} }} + {\text{e}}^{{ - \alpha L_{\text{H}} }} }}{2}$

3 Results

A keen assay over the potential plots in Fig. 181.2 at three different V_GS in the pocket region of 0–6 nm the potential increase is essentially identical. The major point of concern is the tunnel region. Pocket purpose was to reduce the tunneling barrier [10], [13]. Further engineering of it is facilitated by hetero junction. However, it is desired that the engineering doesn’t affect other parameters.

As it could be seen, irrespective of the band energies, the electric potential variation is similar. Also is the case for electric field for a value of V_gs and V_ds (Fig. 181.3). This proves to be advantageous for its application as supplant in conventional field.

Fig. 181.3

Electric field profile for a In_0.7Ga_0.3As homojunction TFET, b moderately staggered GaAs_0.4Sb_0.6/In_0.65Ga_0.35As hetero junction TFET, c high staggered GaAs_0.35Sb_0.65/In_0.7Ga_0.3As

Similarly, supporting are the band energy plots in Fig. 181.4. The band bending in pocket region is higher in highly staggered and in homo junction has least. Band bending is observed at the pocket region. The transition from source to pocket and to the intrinsic channel region has a dip in band energy as in the figures above, near to the 0 nm.

Fig. 181.4

Energy band profile for a In_0.7Ga_0.3As homojunction TFET, b moderately staggered GaAs_0.4Sb_0.6/In_0.65Ga_0.35As hetero junction TFET, c high staggered GaAs_0.35Sb_0.65/In_0.7Ga_0.3As

More the band bending, narrower the junction and higher is the possibility of tunneling. High and moderate staggered hetero junction possesses greater steeper transition than that of homo junction. Thus, hetero junction would produce a better on-off current ratio. At commensurate potential hence, a hetero modeled device has promising performance characteristics.

4 Conclusion

Due to the reduction in tunnel barrier height, E_beff, the GaAs_0.35Sb_0.65/In_0.7Ga_0.3As HTFET achieves enhancement in on current over the In_0.7Ga_0.3As homojunction TFET at V_DS = 1 V. Mixed lattice-matched heterojunctions (GaAs_1−xSb_x/In_yGa_1−yAs) provide a wide range of compositionally tunable E_beff. With increasing Sb and In compositions, E_beff can be reduced from 0.5 eV (x = 0.5, y = 0.53) to 0 eV (x = 0.1, y = 1), and hence, the TFET on current can approach the MOSFET level without compromising the steep switching and high on/off current property desirable in a low power logic switch.