Numerical Analysis of Heat Transfer and Entropy Generation for Natural Convection in a Quadrantal Cavity with Non-uniform Heating at the Bottom Wall

Abstract

We analyze the characteristics of thermal transport along with entropy generation in a quadrantal cavity, which is non-uniformly heated along the bottom boundary wall, the upright wall maintained at a constant temperature, while the arched wall being maintained adiabatic. The numerical experimentation is carried out for Rayleigh number (Ra) in the range of 10³–10⁶. The results are depicted through the distribution of streamline contour and isotherm contour within the enclosure, local heat transfer rate (Nu) along the bottom boundary wall and cold upright wall, and also average heat transfer rate. Further, the irreversibility characteristics are also presented in the form of distribution of local entropy generation due to heat transfer attributes and fluid friction attributes within the enclosure and the average Bejan number. The results reveal that Nu at the bottom wall follows a sinusoidal variation and primarily at lesser values of Ra chosen for the study, the means of heat transfer is conduction, while at higher Ra the mechanism is essentially convection. The study also enlightens the fact that at low Ra (=10³), the irreversibility is essentially owing to heat transfer irreversibility (I_HT) while at larger values of Ra (=10⁵ as well 10⁶) fluid friction irreversibility (I_FF) is predominant over I_HT. For an intermediate range of Ra, both I_HT and I_FF are comparable.

23.1 Introduction

Natural convection in an enclosure continues to be a hot topic of research for the last few decades because of its importance in various engineering applications. A host of articles both numerical and experimental are available in the literature pertaining to attributes of fluid flow, thermal transport, and irreversibility analysis in regular geometries. Davis and De [1] were among the first who presented a benchmark explanation and results for natural convection considering air as the working fluid within a square enclosure considering the upright walls being maintained at unequal temperatures. Hamadi et al. [2] executed a laboratory experiment and implemented numerical investigation of free convection of air in a square inclined cavity. From the results presented, they came to conclusions that the laboratory experiment and numerical investigation were in very good compliance. It is important to mention here that the geometry of the enclosure considered in most of the previous studies was regular in nature and accordingly extensive investigations were carried out on natural convection inside enclosures by considering different fluids and choosing distinctive boundary conditions, such as in square enclosures [3,4,5,6] and rectangular enclosures [7, 8]. A comprehensive list of investigation, based on natural convection heating strategy, has also been reported on triangular [9,10,11], parallelogrammic [12,13,14], trapezoidal [15, 16] enclosures in the literature, in the past too.

Generation of irreversibility in an enclosure can be attributed due to transfer of heat and fluid flow with distinct boundary conditions causing a difference of temperature and is an irretrievable process by nature. In order to utilize the energy resources efficiently and hence for a thermodynamically efficient thermal systems, the entropy generation associated with the processes should be minimized. Bejan [39] was the first researcher who popularized the academic fraternity by considering the principle of minimization of entropy generation. Then onward, several authors have investigated the effects of several influencing criteria on the entropy generation characteristics. Many researchers in the past undertook numerical experiments in studying thermal transport and irreversibility for buoyancy-induced convection in enclosures. These studies are well documented in the literature and can be referred here [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]. Abu-Hijileh et al. [17] analyzed the irreversibility associated with buoyancy-induced convection in a horizontal cylinder. The authors came to the conclusion that increasing the radius of cylinder resulted in a decrease of irreversibility. Interested readers working on trapezoidal and triangular enclosures can refer to articles [18, 19]. Analysis of irreversibility has also been carried out in complicated enclosures like wavy wall and Γ-shaped enclosures too and can be referred to articles [21, 22]. Datta et al. [23] theoretically analyzed buoyancy-induced convective thermal transport and irreversibility in a square porous cavity with different block sizes maintained in insulated condition inside the enclosure. The study gave a clear insight into the readers that the presence of insulated blocks affected the transfer of heat inside the enclosure. The authors also pointed out in their study about detailed heatline analysis and multiple regions of heat transfer, like region of heat transfer enhancement, region of heat transfer enhancement together with a decrease in entropy production region, and a third region where heat transfer together with entropy generation abatement was noticed. The authors also highlighted about a critical insulated block size; over and above, this limit resulted in heat transfer abatement. Chakravarty et al. [24] numerically investigated the buoyancy-induced non-equilibrium thermal transport and irreversibility analysis in a porous cylindrical cavity. The numerical study was achieved for a large range of Ra (10⁷–10¹¹) and Darcy number (10⁻⁶–10⁻¹⁰) and clearly disclosed that transfer of heat in the porous zone could be classified into conduction-dominated and convection-dominated regimes. The authors also analyzed the irreversibilities in the system by carrying out an entropy generation analysis too and deduced the fact that entropy generation has a close resemblance to the above-mentioned two porous zone demarcations. In another article, Mani Rathnam et al. [25] did a finite element numerical analysis on irreversibility study inside a right-angled porous triangular cavity considering vertex angles of 15° and 45°. The authors concluded that a triangular enclosure of 15° vertex angle is better for thermal design since it involves higher rate of transfer of heat and lesser irreversibility. Das and Basak [26] carried out several entropy generation comparative analysis studies in square and triangle porous enclosures which were heated along the side boundary walls and concluded that triangular enclosure is better for thermal analysis design since it involves higher rate of transfer of heat and lesser irreversibility. Abu-Nada and Oztop [27] did a finite volume numerical analysis of Al₂O₃water nanofluid natural convection in a wavy-walled complicated geometry and found out that heat transfer enhancements could be attributed to larger Rayleigh number chosen for the study and higher volume fraction of nanofluids considered. The waviness amplitude considered for the study also played a major role in heat transfer. In another study, Oztop and Abu-Nada [28] carried out buoyancy-induced convection in partial rectangular enclosures comprised of nanofluids subjected to flush-mounted heater, heat source. They analyzed different nanofluids and also deduced that the location of heater was primarily responsible for affecting temperature and flow fields.

The literature study reveals the presence of a wide spectrum of practical utilization involving natural convection method in fluid-filled enclosures which are enforced to non-isothermal boundary conditions. Accordingly, a host of articles can be found out in the literature survey. Meshram et al. [29] analyzed natural convection thermal transport along with entropy generation in a porous square cavity, subjected to non-uniform heating at various inclination angles, and came to the conclusion that the angle of inclination affects the heat transfer rate in the enclosure. In another article, Bhardwaj et al. [30] carried out an in-depth numerical investigation in a porous triangular enclosure subjected to non-uniform heating. They came to the conclusions that the undulation parameters in the left upright wall not only resulted in an increase of heat transfer in enclosure, but also produced more entropy inside the enclosure. In another article, Dutta et al. [31] performed a numerical analysis pertaining to heat transfer along with irreversibility subjected to free convection inside rhombic enclosures considering sinusoidal heating appearing in both top and bottom walls, with cold inclined side walls. It was also evaluated and found by the authors that a significant contributor of entropy generation is heat transfer and the positional region of maximum entropy rested with the bearing of phase shift angle of the top wall.

The study of natural convection in irregular geometry, such as quadrantal cavity, is gaining interest from the research community because of the applications of such geometry in the domain of electronics, cooling system, heating coil, etc. Aydin and Yesiloz [32] were the first researchers who carried out a laboratory experiment and numerical investigation within quadrantal enclosure subjected to uniform heating from the bottom boundary, along with upright cold wall, considering Ra in the span of 10³–10⁷. In another article, Yesiloz and Aydin [33] analyzed the thermal transport in an inclined quadrantal cavity by changing the angle of inclination in the span of 0° ≤ ϕ ≤ 360 and varying the Ra from 10⁵ to 10⁷. Sen et al. [34, 35] theoretically analyzed the buoyancy-induced thermal on quadrantal cavity subjected to a constant temperature at bottom wall, along with upright cold wall with adiabatic arched or curved wall and combined heater on bottom and upright walls with arched or curved wall maintained cold. Natural convection in a quadrantal cavity was also analyzed by Dutta and Biswas [36] where they analyzed heat transfer and entropy generation in a porous quadrantal enclosure. They came to the conclusion that the total entropy production was not very high even considering higher Darcy number, and it could be highly recommended in enclosures pertaining to circular design. Recent numerical investigations were also performed by Dutta et al. [37] where the authors investigated the natural convection phenomenon heat transfer along with entropy generation considering quadrantal enclosure, filled with porous media subjected to non-isothermal heating strategy applied to bottom wall.

The objective of the current work is to carry out a numerical investigation on buoyancy-induced convective heat transfer along with entropy generation aspects inside a quadrantal cavity. The boundary conditions adapted for the present study include a heated bottom wall subjected to non-uniform heating strategy. The left upright wall is maintained cold throughout, and also there is a presence of insulated arched wall from the surroundings. The results are depicted through streamline contour, isothermal contour, local heat transfer rate along the heated as well as cold upright wall, average heat transfer rate. The authors have also discussed entropy generation owing to transfer of heat as well as fluid flow friction.

23.2 Problem Description

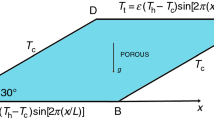
The present investigation is carried out in quadrantal enclosure filled with air and can be found in Fig. 23.1. The bottom wall is heated non-uniformly as per article [37] and can be found out in Eq. (23.1). The left upright wall is kept cold along with right curved wall being maintained in adiabatic condition.

Fig. 23.1

Schematic diagram of the physical model

$$T\left( x \right) = T_{\text{c}} + \frac{{T_{\text{h}} - T_{\text{c}} }}{2}\left( {1 - \text{cos}\left( {\frac{2\pi x}{L}} \right)} \right)$$

(23.1)

Here, T_h is an extreme (max.) temperature corresponding to bottom wall which is non-uniformly heated. T_c is corresponding to cold upright wall temperature. Also, L corresponds to length for the quadrantal model adopted for our study.

23.2.1 Governing Equations and Boundary Conditions

We consider laminar, steady, incompressible flow of Newtonian fluid (air) inside the cavity. All the properties are treated to be constant exempting the density appearing in y-momentum equation in the form of the body force term. The well-known Boussinesq approximation is harnessed to model density variations due to change in temperature. The heat transfer due to radiation is neglected because of very small temperature difference. Viscous dissipation’s presence in the fluid is also ignored.

We first present the resulting dimensionless variables: $X = \frac{x}{L}$, $Y = \frac{y}{L}$, $U = \frac{uL}{\alpha }$, $V = \frac{vL}{\alpha }$, $\theta = \frac{{T - T_{\text{c}} }}{{T_{\text{h}} - T_{\text{c}} }},P = \frac{{pL^{2} }}{{\rho \alpha^{2} }},\,\Pr = \frac{\nu }{\alpha },\,Ra = \frac{{g\beta (T_{\text{h}} - T_{\text{c}} )L^{3} \Pr }}{{\nu^{2} }}.$

The transport equations appropriate to the problem under consideration can be expressed, after due consideration of the dimensionless variables

$$\frac{\partial U}{\partial X} + \frac{\partial V}{\partial Y} = 0$$

(23.2)

$$U\frac{\partial U}{\partial X} + V\frac{\partial U}{\partial Y} = - \frac{\partial P}{\partial X} + Pr\left( {\frac{{\partial^{2} U}}{{\partial X^{2} }} + \frac{{\partial^{2} U}}{{\partial Y^{2} }}} \right)$$

(23.3)

$$U\frac{\partial V}{\partial X} + V\frac{\partial V}{\partial Y} = - \frac{\partial P}{\partial Y} + Pr\left( {\frac{{\partial^{2} V}}{{\partial X^{2} }} + \frac{{\partial^{2} V}}{{\partial Y^{2} }}} \right) + Ra\,Pr\theta$$

(23.4)

$$U\frac{\partial \theta }{\partial X} + V\frac{\partial \theta }{\partial Y} = \frac{{\partial^{2} \theta }}{{\partial X^{2} }} + \frac{{\partial^{2} \theta }}{{\partial Y^{2} }}$$

(23.5)

We now refer to the boundary condition adopted in this chapter.

$$U = V = 0,\theta = 0\;\left( {{\text{along}}\,AC} \right)$$

(23.6a)

$$U = V = 0,\theta = \frac{1}{2}\left( {1 - \cos \left( {2\pi X} \right)} \right)\;\left( {{\text{along}}\,AB} \right)$$

(23.6b)

$$U = V = 0,n \cdot \nabla \theta = 0\;\left( {{\text{along}}\,BC} \right)$$

(23.6c)

The parameter n signifies the perpendicular normal to the corresponding wall.

23.2.2 Nusselt Number

The heat transfer rate (Nu) along any domain of the enclosure is conceivably obtained locally as follows:

$$Nu = - \frac{\partial \theta }{\partial n}$$

(23.7)

The average heat transfer rate ($\overline{{Nu}}$) at the bottom wall is given by:

$$\overline{{Nu_{\text{b}} }} = \frac{{\int\limits_{0}^{1} {Nu_{\text{b}} \text{d}X} }}{{X|_{0}^{1} }} = \int\limits_{0}^{1} {Nu_{\text{b}} } \text{d}X$$

(23.8)

23.2.3 Entropy Generation

While designing an effective thermal enclosed system, care must be taken to minimize the energy losses arising out of irreversibilities inside the enclosure. Any thermal enclosed system having a definite/indefinite temperature gradient will definitely undergo some losses. Some losses will also occur because of inherent fluid flow too. This energy losses primarily attributed due to irreversibilities in the system can be measured in expressions of entropy generation inside the enclosure. Designing an efficient thermal enclosed system means the entropy generation associated with the processes should be kept to a minimum. The mathematical equation relating to entropy distribution and generation for heat and fluid flow for a two-dimensional thermal enclosed system subjected to thermodynamic equilibrium for coupled heat and mass transport in Cartesian coordinates is penned down in definite form as:

$$S_{\theta } = \left( {\frac{\partial \theta }{\partial X}} \right)^{2} + \left( {\frac{\partial \theta }{\partial Y}} \right)^{2}$$

(23.9)

$$S_{\varphi } = \phi \left\{ {2\left( {\left( {\frac{\partial U}{\partial X}} \right)^{2} + \left( {\frac{\partial V}{\partial Y}} \right)^{2} } \right) + \left( {\frac{\partial U}{\partial Y} + \frac{\partial V}{\partial X}} \right)^{2} } \right\}$$

(23.10)

Here, S_θ and S_ψ refer to local entropy produced on account of irreversibility on account of heat transfer (thermal gradient) and fluid friction (fluid flow), respectively. Here, $\varphi$ refers to the irreversibility dissemination ratio and is determined accordingly.

$$\phi = \frac{{\mu T_{0} }}{k}\left( {\frac{\alpha }{L\Delta T}} \right)^{2}$$

(23.11)

The present numerical simulations of this chapter are calculated considering $\phi$ to be $10^{ - 4}$.

The sum total of entropy generation in the presence of transfer of heat ($S_{{\theta ,{\text{total}}}}$) and fluid frictional effects ($S_{{\psi ,{\text{total}}}}$) can be estimated from the dissemination of local entropy generation as follows:

$$S_{{\theta ,{\text{total}}}} = \int_{\Omega } {S_{\theta } {\text{d}}\Omega }$$

(23.12a)

$$S_{{\psi ,{\text{total}}}} = \int_{\Omega } {S_{\psi } {\text{d}}\Omega }$$

(23.12b)

The comprehensive entire total entropy production ($S_{\text{T}}$) in the quadrantal enclosure can be found to be

$$S_{\text{T}} = S_{{\theta ,{\text{total}}}} + S_{{\psi ,{\text{total}}}}$$

(23.13)

Another way of looking into irreversibility distribution parameter is the Bejan number (Be), which is the ratio of rate of entropy generation on account of transfer of heat in the enclosure to the comprehensive entire entropy production rate (refer Bejan [38]).

$$Be = \frac{{S_{\theta } }}{{S_{\theta } + S_{\psi } }}$$

(23.14)

Average Bejan number ($Be_{\text{avg}}$) is referred to quantify the pertinent global influence of entropy generation in relation to transfer of heat in the enclosure and is expressed by:

$$Be_{\text{avg}} = \frac{{S_{{\theta ,{\text{total}}}} }}{{S_{{\theta ,{\text{total}}}} + S_{{\psi ,{\text{total}}}} }}$$

(23.15)

When the Be_avg ≫ 0.5, it signifies the dominance of irreversibility on account of transfer of heat. When Be_avg ≪ 0.5, the limit is just the opposite and it signifies the dominance of irreversibility on account of fluid friction effects.

23.3 Numerical Solution Strategy with Code Validation

The transport equations after converting into non-dimensional form (Eqs. 23.2–23.5) together with the boundary conditions enumerated in (Eqs. 23.6a–23.6c) are solved by a finite element numerical strategy. We employ the well-known Galerkin weighted strategy to remodel the controlling mathematical equations into an arrangement of mathematical integral equations. The exhaustive technique and approach of this method can be found in the book by Zienkiewicz [39]. Further, the Gauss’s quadrature method also referred to the book by Zienkiewicz [39] is utilized to accomplish the numerical integration. The algebraic equations are taken care of by employing the Newton–Raphson iteration method. The solution is assumed to be converged when the relative residual is less than 10⁻⁶.

A grid independency test considering the quadrantal enclosure with the following boundary conditions of uniform heating strategy on bottom wall, cold upright wall, and insulated curved wall had been carried out to establish vividly to prove these results do not depend on the grid used for this numerical simulation. The values of average Nusselt number ($\overline{{Nu}}$) for the bottom wall considering distinctive grid layout are represented in Table 23.1. We use 26,330 elements for numerical simulation, because of the fact that when we increase the number of elements from 26,330 to 35,714, the maximum relative error is 0.5%.

Table 23.1 Comparison of average Nusselt number on the bottom wall with uniform heating for different grid systems with Pr = 0.71

The numerical results obtained in the present study were validated for the published results of Aydin and Yesiloz [32] who had undertaken a numerical study too on quadrantal enclosure considering water to be the working fluid (Pr = 6.62) with the boundary conditions of uniformly heated bottom wall, along with upright wall maintained cold and arched wall being insulated. Figure 23.2 of this chapter demonstrates a correlation of the published results of streamline vortices and isotherms of Aydin and Yesiloz [32] for Ra = $1.7 \times 10^{5}$. The results apparently displayed in Fig. 23.2 are recognized to be in close correlation with the previous results already available in the literature [32].

Fig. 23.2

Streamline and isotherm contours for a quadrantal enclosure filled with a fluid (Pr = 6.62) where bottom wall is heated uniformly, upright side wall is cooled at a constant temperature, while arched wall is insulated at $Ra = 1.7 \times 10^{5}$

23.4 Results and Discussion

The main purpose of the current numerical exploration is to examine the fluid flow and heat transfer along with irreversibility characteristics due to natural convection in a quadrantal cavity. The quadrantal enclosure is heated non-uniformly along the bottom wall, while the perpendicular vertical wall is maintained cold all along. The working fluid for the present investigation is chosen to be air (Pr = 0.71). The resulting flow features are demonstrated through streamline contour, isothermal contour, local and average Nusselt number on hot bottom, cold upright walls, along with illustration of entropy generation. Average Bejan number (Be_avg) has also been discussed in this chapter too.

23.4.1 Streamlines and Isotherms

The streamlines and isotherms in the enclosure are represented in the left and right portion in Fig. 23.3 for four distinctive values of Rayleigh number (Ra = 10³, 10⁴, 10⁵, and 10⁶). It should also be recognized that we allocate positive symbol for ψ, which expresses counterclockwise circulation, while the clockwise circulation is expressed by a negative ψ symbol. It is observed from Fig. 23.3(left) that apart from a primary counterclockwise circulation cell occupying the major portion of the enclosure, there is a formation of secondary cell (clockwise direction) with a lesser vortex strength in the right-hand bottom side of the quadrantal enclosure for the corresponding numerical values of Rayleigh number (Ra) appropriately assigned for this study. It can be observed from Fig. 23.3a that at Ra = 10³, the strength of the vortex of main circulatory cell has a very low value (ψ_max = 1.37) because of high resistance to flow. When Ra is changed from 10³ to 10⁴, the strength of the vortex has changed to an appreciable value ψ_max = 15.5 (counterclockwise circulation) (see Fig. 23.3b). The corresponding clockwise circulation strength changes from a magnitude of 0.49 to 6.65. With further enhancement of Ra subsequently from 10⁴ to 10⁵, we observe a marked increase of circulation strength to ψ_max = 70.8 (counterclockwise) signifying dominance of convective effects in the enclosure. Further increase of Ra from 10⁵ to 10⁶ signifies an even greater effect of buoyancy forces with complete dominant of buoyancy effects. The corresponding value of the strength of the vortex is ψ_max = 183 (anticlockwise circulation) and ψ_max = 55(clockwise circulation) as can be seen in Fig. 23.3d. It can be further observed from streamline contour in Fig. 23.3d that the nature of main circulation strength vortices is no longer smooth and has undergone twist and curving in the centric portion of the enclosure.

Fig. 23.3

Streamlines and isotherms with non-uniform heating for different Rayleigh numbers: a $Ra = 10^{3}$, b $Ra = 10^{4}$, c $Ra = 10^{5}$, d $Ra = 10^{6}$

From the isotherm contour plot as depicted in the right portion in Fig. 23.3, it can be inferred that there is a continuous pattern of isothermal contour in the enclosure as there is an absence of finite discontinuity in this study with the chosen boundary conditions depicted for this study. The isotherm patterns revealed in the quadrantal enclosure for the case Ra = 10³ are found to be profoundly compressed in a zone having a close proximity from the bottom heated wall (0.25 ≤ X ≤ 0.75), considering the non-uniform boundary conditions enforced at this wall (Fig. 23.3a). With a change of Ra from 10³ to10⁴ as depicted in Fig. 23.3b, the isotherms undergo a twist in the region (0.25 ≤ X ≤ 0.75) signifying that convection effects have just set in inside the enclosure. With further increase of Ra = 10⁴ to 10⁵, resistance force due to buoyancy overcomes fluid friction with an increase of distortion of isotherms observed in the region discussed above (Fig. 23.3c), indicating that the prevalent advancement for heat transfer is buoyant convection in the enclosure at Ra = 10⁵. On further increase in Ra from 10⁵ to 10⁶, as observed from Fig. 23.3d, the flow moves away from bottom wall and impinges on the left wall as observed in the pattern of distorted isotherms with strong convection effects.

23.4.2 Nusselt Number

The pattern of local Nusselt number (Nu) on the heated wall is plotted in Fig. 23.4a for distinctive values of Ra. One can see from Fig. 23.4a that the variation of Nu alongside the length of the bottom wall is almost sinusoidal. This is for the non-uniform boundary condition enforced on bottom wall. The values of Nu are positive from X = 0.45 to 0.95 and have negative values in other regions of the enclosure. The negative value of Nu physically connotes that we are transferring the heat from the working fluid, i.e., heated air to the enclosure walls. The maximum value of Nu_max is very close to 15 for Ra = 10⁶.

Fig. 23.4

Variation of local Nusselt number on a heated bottom wall and b cold vertical wall for different values of Rayleigh number

The local Nusselt number (Nu) for vertical cold wall is depicted in Fig. 23.4b and is negative for all sets of Ra at all locations on the wall. The numerical value of Nu escalates with an increase in Ra similar to the case of bottom wall. The position of the maximum value of Nu is dependent on the Ra which can be explained from the isotherm contour. For example, when the Ra is small (10³), Nu initially increases to a small length of the wall, attains its pinnacle, and henceforth decreases. On the contrary, for larger values of Ra, Nu increases almost monotonically except at the corner, where there is a decrease in its value to satisfy the boundary condition.

The numerical values of average Nusselt number ($\overline{{Nu}}$) on heated bottom wall with Ra are presented in Table 23.2. It is self-evident from Table 23.2 that there is a significant enhancement in $\overline{{Nu}}$ for the bottom wall with an increase in Ra. Further, $\overline{{Nu}}$ for cold upright wall is negative and shows a downward trend (negative) with an increase of Ra. We can summarize our discussions, by saying that $\overline{{Nu}}$ is maximum when heat is transmitted from the hot bottom wall in direction of enclosed fluid or from the heated fluid to the adjoined cold wall, whichever the case may be when Ra is maximum pertaining to our study.

Table 23.2 Average Nusselt number for bottom and vertical wall for different values of Rayleigh number

23.4.3 Analysis of Entropy Generation

Noting the points of maximum entropy distribution and generation inside the quadrantal enclosure is of special interest and gives an idea about how to optimize the effects of entropy and irreversibilities. Researchers, working on this area, should also keep in mind that minimum entropy generation with maximum heat transfer holds the key to an efficient design of an enclosure. Figure 23.5 shows the distribution of local entropy generation for three different Ra (=10⁴−10⁶). For Fig. 23.5, it can be visualized that there is a complete absence of entropy generation in the core of enclosure for either fluid friction or heat transfer. This is quite logical to explain from the situation that as the curved wall is adiabatic the entropy bearing is very less there and entropy generation on account of heat transfer is maximum in the close vicinity of hot bottom wall because of imposed temperature profile. It is also realized that, at the conduction dominant occupancy at lesser Ra (≤10⁴), the entropy generation can be attributed to heat transfer irreversibilities, with the maximum value of entropy generation on account of heat transfer (S_{θ max} = 29.5 and corresponding S_{ψ max} = 20). With an increase of Ra to 10⁵, the maximum value of entropy generation as a result of fluid friction is increased manifold to a value of S_{ψ max} = 908.9. On the contrary, although the maximum numerical value of entropy production on account of heat transfer increases, the enhancement is not to that extent (S_θmax = 85.9). Appreciable amount of entropy generates on account of fluid friction. This entropy distribution is also found in close proximity to curved wall. When the Ra is increased further to 10⁶, the value of entropy generation on account of fluid friction throughout the enclosure increases significantly having the maximum value of S_{ψ max} = 23874.7, whereas the corresponding value of entropy generation on account of heat transfer is S_{θ max} = 210. We can summarize our discussions, by saying that both the heat transfer and the frictional irreversibility escalation occur at high Ra for the present nonlinear heating strategy adopted. It is also ascertained that, beyond a critical Rayleigh number, fluid friction irreversibility dictates the total entropy generation inside the quadrantal enclosure.

Fig. 23.5

Local entropy generation due to heat transfer ($S_{\theta }$) and fluid friction ($S_{\psi }$) for a $Ra = 10^{4}$ case, b $Ra = 10^{5}$, and c $Ra = 10^{6}$

23.4.4 Analysis of Bejan Number

As already mentioned, one can predict the global dominance of irreversibility after knowing the average Bejan number (Be_avg). Accordingly, Be_avg is evaluated and reported in Table 23.3. From Table 23.3, it is clear that when Ra is changed from 10³ to 10⁵, the change in the magnitude of S_θmax is almost negligible. However, the magnitude of S_ψmax varies significantly and it records a very less value for Ra = 10³ (S_ψ = 0.1556) and has a very high value for Ra = 10⁵(S_ψ = 908.92) signifying that entropy generation on account of fluid friction escalation occurs with an increase of Ra. The corresponding average Bejan number (Be_avg) noted at Ra = 10³ is 0.989, while at Ra = 10⁵ it is 0.085. When Ra is increased further to 10⁶, the total irreversibility in the presence of heat transfer (S_θ) is increased significantly to S_θ = 210 compared to its value of S_θ = 85.9 at Ra = 10⁵ signifying that irreversibility due to heat transfer increases to a large value with an increase of Ra from 10⁵ to 10⁶. Also, Be_avg values clearly reflect that entropy generation due to heat transfer is the dominating parameter for Ra = 10³ and thereafter at Ra = 10⁴ the effect of irreversibility on account of fluid flow and heat transfer is of equal significance. The average Bejan number (Be_avg) noted at Ra = 10⁴ is 0.596 which clearly proves our discussion in Sect. 2.3. With further increase of Ra to 10⁵ and 10⁶, the irreversibility on account of fluid friction is a commanding factor. The corresponding average Bejan number (Be_avg) noted at Ra = 10⁶ is even lesser which is 0.008. This is attributed to the fact that, for lesser values of Ra, heat transfer is dominated by conduction and accordingly the value of Be_avg is large. However, with an increase in Ra, both the irreversibility on account of heat transfer and the fluid flow increase, although the rate of increase of irreversibility on account of fluid flow friction is more a representative factor than due to heat transfer because of intensified effects of buoyancy force strength above fluid viscous force as already reiterated earlier.

Table 23.3 Total entropy generation rate and average Bejan number for different Rayleigh numbers

23.5 Conclusions

The buoyancy-induced fluid flow, thermal transport, and irreversibility characteristics in a quadrantal cavity have been numerically analyzed. The following boundary conditions are adopted for this chapter. The bottom wall is subjected to non-uniform heating, while the upright left wall is kept cold and at the same time the arched wall is maintained at insulated condition to surroundings. The final conclusions are:

The local Nusselt number at the heated wall follows a sinusoidal variation. At lower values of Ra (=10³,10⁴), the mechanism of thermal transport is conduction, while thermal transport is due to convection at Ra = 10⁶.

At low values of Ra (10³), the entropy generation is essentially generated owing to heat transfer irreversibility (I_HT), while for larger range of Ra (10⁵ and 10⁶) fluid friction irreversibility (I_FF) is predominant over I_HT. For intermediate values of Ra, both I_HT and I_FF are comparable.