Keywords

17.1 Introduction

Earlier, tourbomachinery blades are assumed as twisted beam wherein chordwise bending is found missing particularly in moderate-to-low aspect ratio models and the analysis becomes inaccurate. Thereafter, these blades are modelled as twisted cantilever composite plates. In general, these blades fail due to flutter, which in turn induces high value of repeated stresses. In order to have a safety of operation, these thin plates are very often attached with rib-like structures called stiffeners at suitable orientation to increase the overall stiffness, thereby increasing the fundamental frequency. The high-speed rotation of the turbomachinery blades is very much related to their frequencies and often prone to failure due to the centrifugal force. The deformation of the geometry due to centrifugal force is represented by geometric stiffness called centrifugal stiffening, which is the source of initial stresses. Hence, an intensive study of the stiffened blades considering the effects of different parameters will be extremely useful for design engineers.

Leissa and Ewing [1] presented the free vibration results of turbomachinery blades considering both beam and shallow shell theories and finally reported that beam theory was found inadequate for moderate-to-low aspect ratio blades because chordwise bending was found missing. Kielb et al. [2] carried out the theoretical and numerical analysis of twisted cantilever plates wherein finite elements’ results were obtained considering plate, shell and solid elements. In theoretical method, they considered both shell and beam theory to carry out the investigation. Qatu and Leissa [3] were the first investigators to report the effects of twist angles of the composite plates on the natural frequencies and mode shapes. Liew et al. [4] used Ritz method to study the effects of twist angle on the vibration response and mode shapes of composite conical shells. Kuang and Hsu [5] studied the free vibration results of tapered pretwisted orthotropic composite plate employing differential quadrature method (DQM). Lee et al. [6] investigated the vibration response of composite twisted plates, cylindrical and conical shells with cantilevered boundary conditions employing finite element method (FEM). Sreenivasamurthy and Ramamurti [7] studied the effects of Coriolis component on the natural frequencies of the plates, rotating at different speeds, and reported that its effect is found marginal at low and moderate speed of rotation. Ramamurti and Kielb [8] reported the eigenfrequencies of twisted rotating isotropic plate wherein the effects of rotation were included by using a stress smoothing technique. Karmakar and Sinha [9] worked to investigate the free vibration response of laminated twisted plate at moderate speed neglecting Coriolis effect. They used three-dimensional finite element method to perform the parametric studies. Rao and Gupta [10] presented the fundamental frequencies of twisted and tapered Timoshenko beams rotating at different speeds. Hu et al. [11] computed the free vibration response of cantilevered twisted conical shell subjected to axial and centrifugal force by Rayleigh–Ritz method, while Kee and Kim [12] worked on the free vibration response of rotating twisted thick cylindrical shell structures employing FEM wherein Coriolis acceleration was considered with centrifugal forces. Joseph and Mohanty [13] reported a finite element numerical method to compute the natural frequency of the rotating sandwich plates.

The remarkable researchers [14,15,16,17] investigated the free vibration characteristics of stationary untwisted laminated eccentrically and concentric stiffened plates/shells using FEM based on the kinematics of FSDT. Sadek and Tawafik [18] used higher-order shear deformation theory (HSDT), which eliminates the use of shear correction factor to study the flexural response of the stiffened plates. Qing et al. [19] worked on the free vibration of stiffened plates based on the theory of state-vector equation, wherein the compatibility of stresses and displacement at the interface of stiffener and plate were satisfied. Yuan and Dawe [20] studied the stability and vibration characteristics of sandwich plates stiffened eccentrically employing spline finite strip method, while Guo et al. [21] presented a finite element model based on zigzag theory of the laminated stiffened composite plates, wherein the inter-layer continuity was maintained by employing bilinear in-plane displacement constraints. Li et al. [22] united two theories such as layerwise laminated theory and traditional finite element theory to investigate the static and free vibration response of laminated stiffened cylindrical shells, while Bhar et al. [23] presented a comparative study of laminated stiffened plates employing both the kinematics of FSDT and HSDT. Zaho and Kapania [24] presented an efficient finite element method to investigate the vibration response of laminated composite stiffened panel, wherein curved composite stiffeners were considered. Castro and Donadon [25] developed a semi-analytical model to investigate the buckling and vibration response of laminated composite stiffened panel with inclusion of the debonding problem. Rout et al. [26, 27] presented the free vibration response of rotating stiffened cylindrical shells with preexisting delamination, while Damnjanović et al. [28] used the dynamic stiffness method to investigate the free vibration responses of composite stiffened and cracked plate assemblies based on the HSDT and FSDT theories.

Though plenty of literature is available in the theme of free vibration of stiffened plates, the investigators have not studied the effects of rotational speed on the free vibration characteristics of the initially twisted laminated composite eccentrically stiffened plate. Hence, the present work aims at studying the vibration response of rotating twisted composite stiffened plate employing finite element method, wherein the composite plate is modelled with an eight-noded isoparametric element and the stiffener is with a three-noded isoparametric beam element. The compatibility between the plate element and the stiffener element is established by considering the eccentricity of the stiffener element. The degrees of freedom of the stiffener element at each node are transferred to the corresponding nodes of the plate element. The initial stiffening due to rotation is manifesting itself through geometric stiffness, considering Green–Lagrangian strain components for initial stresses. The effect of fibre orientation angle, twist angles, stiffener depth-to-plate thickness ratio and rotational speeds on the free vibration response of the stiffened plate is furnished. Finally, the influence of twist angles and moderate speed of rotation on the mode shapes of the eccentrically stiffened composite plate is presented.

17.2 Theoretical Formulation

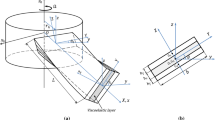
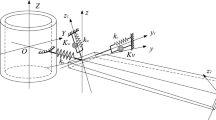
The laminated composite crossed-stiffened plate of uniform thickness h, curvature of twist Rxy, length L is shown in Fig. 17.1 with the global coordinate system. The twist angle of the stiffened plate is expressed as,

Fig. 17.1
figure 1

Typical twisted laminated composite stiffened plate

Full size image
$$ \tan \phi = - \frac{L}{{R_{xy} }} $$
(17.1)

The isoparametric eight-noded plate element consisting of five degrees of freedom including three translations (u, v, w) and two rotations (α, β) per node is considered for discretization of the entire plate. The generalized strain vector of the plate based on the kinematics of FSDT is expressed as,

$$ \begin{aligned} \left[ {\begin{array}{*{20}c} {\varepsilon_{x} } & {\varepsilon_{y} } & {\gamma_{xy} } & {\gamma_{xz} } & {\gamma_{yz} } \\ \end{array} } \right]^{\,T} & = \left[ {\begin{array}{*{20}c} {\varepsilon_{x}^{0} } & {\varepsilon_{y}^{0} } & {\gamma_{xy}^{0} } & {\gamma_{xz}^{0} } & {\gamma_{yz}^{0} } \\ \end{array} } \right]^{\,T} \\ & \quad + z\left[ {\begin{array}{*{20}c} {\kappa_{x} } & {\kappa_{y} } & {\kappa_{xy} } & {\kappa_{xz} } & {\kappa_{yz} } \\ \end{array} } \right]^{T} \\ \end{aligned} $$
(17.2)

where \( \varepsilon_{x}^{0} ,\varepsilon_{y}^{0} ,\gamma_{xy}^{0} ,\gamma_{xz}^{0} ,\gamma_{yz}^{0} \) are the mid-surface strains and \( \kappa_{x} ,\kappa_{y} ,\kappa_{xy} ,\kappa_{xz} ,\kappa_{yz} \) corresponds to the curvatures of the plate.

$$ \left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{0} } \\ {\varepsilon_{y}^{0} } \\ {\gamma_{xy}^{0} } \\ {\gamma_{xz}^{0} } \\ {\gamma_{yz}^{0} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\partial u/\partial x} \\ {\partial v/\partial y} \\ {\partial u/\partial x + \partial v/\partial x + 2w/R_{xy} } \\ {\alpha {\kern 1pt} + \partial w/\partial x} \\ {\beta + \partial w/\partial y} \\ \end{array} } \right\} $$
(17.3)

and

$$ \left\{ {\begin{array}{*{20}c} {\kappa_{x} } \\ {\kappa_{y} } \\ {\kappa_{xy} } \\ {\kappa_{xz} } \\ {\kappa_{yz} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\partial \alpha /\partial x} \\ {\partial \beta /\partial y} \\ {\partial \alpha /\partial y + \partial \beta /\partial x} \\ 0 \\ 0 \\ \end{array} } \right\} $$
(17.4)

The mid-plane strain field and curvatures can be written as,

$$ \left\{ {\overline{\varepsilon } } \right\} = \left[ B \right]\{ d_{e} \} $$
(17.5)

where

$$ \{ d_{e} \} = \left[ {\begin{array}{*{20}c} {u_{1} } & {v_{1} } & {w_{1} } & {\alpha_{1} } & {\beta_{1} } & \cdots & {u_{8} } & {v_{8} } & {w_{8} } & {\alpha_{8} } & {\beta_{8} } \\ \end{array} } \right]^{T} $$
(17.6)
$$ \left[ B \right] = \left[ {\begin{array}{*{20}c} {N_{i,x} } & 0 & 0 & 0 & 0 \\ 0 & {N_{i,y} } & 0 & 0 & 0 \\ {N_{i,y} } & {N_{i,x} } & {2N_{i} /R_{xy} } & 0 & 0 \\ 0 & 0 & 0 & {N_{i,x} } & 0 \\ 0 & 0 & 0 & 0 & {N_{i,y} } \\ 0 & 0 & 0 & {N_{i,y} } & {N_{i,x} } \\ 0 & 0 & {N_{i,x} } & {N_{i} } & 0 \\ 0 & 0 & {N_{i,y} } & 0 & {N_{i} } \\ \end{array} \begin{array}{*{20}c} \cdots \\ \cdots \\ \cdots \\ \cdots \\ \cdots \\ \cdots \\ \cdots \\ \cdots \\ \end{array} } \right]_{i = 1,8} $$
(17.7)

The constitutive relation of the plate can be expressed as,

$$ \left\{ {\begin{array}{*{20}c} N \\ M \\ Q \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {A_{ij} } & {B_{ij} } & 0 \\ {B_{ij} } & {D_{ij} } & 0 \\ 0 & 0 & {S_{ij} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{p} } \\ {\kappa_{b} } \\ {\gamma_{s} } \\ \end{array} } \right\} = \left[ D \right]\left\{ {\overline{\varepsilon } } \right\} $$
(17.8)

where Aij, Bij, Dij and Sij are the stiffness coefficients, while \( \varepsilon_{p} \), \( \kappa_{b} \) and \( \gamma_{s} \) represent the in-plane strains, the curvatures and shear strains in transverse directions, respectively.

Based on the finite element method, the standard formulations used to compute the element stiffness and mass matrices are expressed as,

$$ \left[ {K_{p} } \right] = \int \limits_{ - 1}^{1} {\int \limits_{ - 1}^{1} {[B]^{T} [D][B]\left| J \right| \; {\text{d}}\xi {\text{d}}\eta } } $$
(17.9)
$$ \left[ {M_{p} } \right] = \int \limits_{ - 1}^{1} {\int \limits_{ - 1}^{1} {\left[ N \right]^{T} \left[ m \right]\left[ N \right]} } \left| J \right| \; {\text{d}}\xi {\text{d}}\eta $$
(17.10)

where [B] is the strain–displacement matrix, [D] is the elasticity matrix, [N] is the shape function matrix and [m] is the inertia matrix per unit area of the plate element, respectively.

The stiffener element is considered as a one-dimensional three-noded isoparametric beam element consisting of four degrees of freedom per node, which includes two translations and two rotations. The shape functions considered for the stiffener element are given by,

$$ \begin{aligned} N_{i}^{sx} & = 0.5\xi \xi_{i} (1 + \xi \xi_{i} )\quad {\text{for }}i = 1,3 \\ N_{i}^{sx} & = (1 - \xi^{2} )\quad {\text{for }}i = 2 \\ \end{aligned} $$
(17.11)

The strain–displacement relations of a stiffener, whose axis is parallel to x-axis, is given by,

$$ \left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{sx} } \\ {\gamma_{xy}^{sx} } \\ {\gamma_{xz}^{sx} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{{\partial u^{sx} }}{\partial x} + z\frac{{\partial \alpha^{sx} }}{\partial x}} \\ {z\frac{{\partial \beta^{sx} }}{\partial x}} \\ {\alpha^{sx} + \frac{{\partial w^{sx} }}{\partial x} - y\frac{{\partial \beta^{sx} }}{\partial x}} \\ \end{array} } \right\} $$
(17.12)

The stress resultants developed in the cross section of the x-directional stiffener are computed and arranged as,

$$ \begin{aligned} \left\{ {\begin{array}{*{20}c} {N_{x}^{sx} } \\ {M_{x}^{sx} } \\ {T_{x}^{sx} } \\ {Q_{xz}^{sx} } \\ \end{array} } \right\} & = \left[ {\begin{array}{*{20}c} {A_{11}^{sx} b_{st} } & {B_{11}^{sx} b_{st} } & {B_{16}^{sx} b_{st} } & 0 \\ {B_{11}^{sx} b_{st} } & {D_{11}^{sx} b_{st} } & {D_{16}^{sx} b_{st} } & 0 \\ {B_{16}^{sx} b_{st} } & {D_{16}^{sx} b_{st} } & {\frac{1}{6}\left( {\bar{Q}_{66}^{sx} + \bar{Q}_{44}^{sx} } \right)d_{st} b_{st}^{3} } & 0 \\ 0 & 0 & 0 & {k_{s}^{sx} A_{44}^{sx} b_{st} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\frac{{\partial u^{sx} }}{\partial x}} \\ {\frac{{\partial \alpha^{sx} }}{\partial x}} \\ {\frac{{\partial \beta^{sx} }}{\partial x}} \\ {\alpha^{sx} + \frac{{\partial w^{sx} }}{\partial x}} \\ \end{array} } \right\} \\ & = \left[ {E_{sx} } \right]\left\{ {\varepsilon {}_{sx}} \right\} \\ \end{aligned} $$
(17.13)

The nodes of the plate and the stiffener elements are assumed to be collinear in thickness direction of the global coordinate system. The relation between the nodal displacement vector of the stiffener element and that of the mid-surface of the plate element is expressed as,

$$ \left\{ {\begin{array}{*{20}c} {u^{sx} } \\ {w^{sx} } \\ {\alpha^{sx} } \\ {\beta^{sx} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} 1 & 0 & 0 & e & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} } \right\}\left\{ {\begin{array}{*{20}c} u \\ v \\ w \\ \alpha \\ \beta \\ \end{array} } \right\} = \left[ {T_{ce}^{sx} } \right]\left\{ {\delta^{p} } \right\} $$
(17.14)

In consequence, the elemental nodal degrees of freedom of the x-directional stiffener can be presented in terms of nodal degrees of freedom of the plate element as,

$$ \sum\limits_{i = 1}^{3} {\left\{ {\begin{array}{*{20}c} {u_{i}^{sx} } \\ {w_{i}^{sx} } \\ {\alpha_{i}^{sx} } \\ {\beta_{i}^{sx} } \\ \end{array} } \right\}} = \sum\limits_{i = 1}^{3} {\left[ {T_{ce}^{sx} } \right]} \sum\limits_{j = 1}^{8} {\left[ {\begin{array}{*{20}c} {N_{ij} } & 0 & 0 & 0 & 0 \\ 0 & {N_{ij} } & 0 & 0 & 0 \\ 0 & 0 & {N_{ij} } & 0 & 0 \\ 0 & 0 & 0 & {N_{ij} } & 0 \\ 0 & 0 & 0 & 0 & {N_{ij} } \\ \end{array} } \right]} \;\left\{ {\begin{array}{*{20}c} {u_{j} } \\ {v_{j} } \\ {w_{j} } \\ {\alpha_{j} } \\ {\beta_{j} } \\ \end{array} } \right\} $$
(17.15)

In Eq. (17.15), Nij is defined as the jth quadratic shape function of plate element computed at the ith node of the stiffener element.

Equation (17.15) can be expressed as,

$$ \left\{ {d_{e}^{sx} } \right\} = \left[ {T_{ce}^{sx} } \right]\left[ {T_{sx}^{sh} } \right]\left\{ {d_{e} } \right\} = \left[ {T^{sx} } \right]\left\{ {d_{e} } \right\} $$
(17.16)

where \( \left[ {T_{{}}^{sx} } \right] \) is called as transformation matrix, which is used to transfer the degrees of freedom of the nodes of the stiffener element to the corresponding nodes of the plate element taking eccentricity (e = (h + dst)/2) of the stiffener into account.

The stiffness and mass matrices of the stiffener element are computed as,

$$ \left[ {K_{sxe} } \right] = \int\limits_{ - 1}^{1} {\left[ {T^{sx} } \right]^{T} \left[ {B_{sx} } \right]^{T} \left[ {E_{sx} } \right]\left[ {B_{sx} } \right]\left[ {T^{sx} } \right]} \left| {J^{sx} } \right|\;{\text{d}}\xi $$
(17.17)
$$ \left[ {M_{sxe} } \right] = \int\limits_{ - 1}^{1} {\left[ {T^{sx} } \right]^{T} \left[ {N^{sx} } \right]^{T} \left[ {m^{sx} } \right]\left[ {N^{sx} } \right]\left[ {T^{sx} } \right]\left| {J^{sx} } \right|\;{\text{d}}\xi } $$
(17.18)

where \( \left[ {B_{sx} } \right] \) is the strain–displacement matrix and \( \left[ {m^{sx} } \right] \) is the inertia matrices of the one-dimensional stiffener element. The strain–displacement matrix is expressed as,

$$ \left[ {B_{sx} } \right] = \left[ {\begin{array}{*{20}c} {N_{i,x}^{sx} } & 0 & 0 & 0 \\ 0 & 0 & {N_{i,x}^{sx} } & 0 \\ 0 & 0 & 0 & {N_{i,x}^{sx} } \\ 0 & {N_{i,x}^{sx} } & {N_{i}^{sx} } & 0 \\ \end{array} \begin{array}{*{20}c} \cdots \\ \cdots \\ \cdots \\ \cdots \\ \end{array} } \right]_{i = 1,3} $$
(17.19)

and the inertia matrix of the stiffener is written as,

$$ \left[ {m^{sx} } \right] = \left[ {\begin{array}{*{20}c} {p_{sx} } & 0 & 0 & 0 \\ 0 & {p_{sx} } & 0 & 0 \\ 0 & 0 & {I_{sx} } & 0 \\ 0 & 0 & 0 & {J_{sx} } \\ \end{array} } \right] $$
(17.20)

where \( p_{sx} = \sum \nolimits_{k = 1}^{nl} {b_{st} (z_{k} - z_{k - 1} )\rho_{k} } \), \( J_{sx} = \frac{1}{3}\sum \nolimits_{k = 1}^{nl} {b_{st}^{3} (z_{k} - z_{k - 1} )\rho_{k} } \) and \( I_{sx} = \frac{1}{3}\sum\nolimits_{k - 1}^{nl} {b_{st} (z_{k}^{3} - z_{k - 1}^{3} )\rho_{k} } \).

The same procedure may be adopted to compute the elasticity stiffness matrix and mass matrix of the stiffener placed along y-axis of the plate.

The stiffness matrix and mass matrix of the stiffened plate element can be computed as,

$$ \left[ {K_{e} } \right] = \left[ {K_{p} } \right] + \left[ {K_{sxe} } \right] + \left[ {K_{sye} } \right] $$
(17.21)
$$ \left[ {M_{e} } \right] = \left[ {M_{p} } \right] + \left[ {M_{sxe} } \right] + \left[ {M_{sye} } \right] $$
(17.22)

The generalized dynamic equilibrium equation is derived from Lagrange’s equation of motion. While deriving the dynamic equilibrium equation, it is assumed that the stiffened plate is rotating at moderate speed. For moderate speed of rotation, the Coriolis effect is neglected and the dynamic equilibrium equation in global form is written as [9],

$$ \left[ M \right]\left\{ {\ddot{\delta }} \right\} + \left( {\left[ K \right] + \left[ {K_{\sigma } } \right]} \right)\left\{ \delta \right\} = \left\{ {F(\Omega^{2} )} \right\} $$
(17.23)

In Eq. (17.23), \( [M] \) is the global mass matrix, \( [K] \) is the global elastic stiffness matrix, \( [K_{\sigma } ] \) is the global geometric stiffness matrix, \( \{ \delta \} \) is the global displacement vector and \( \{ F(\Omega ^{2} )\} \) is the global centrifugal force vector [9]. The computation of the geometric stiffness matrix \( [K_{\sigma } ] \) is based on iterative solution [7, 9], because it depends on the values of initial stresses.

$$ \left( {\left[ K \right] + \left[ {K_{\sigma } } \right]} \right)\{ \delta \} = \left\{ {F(\Omega ^{2} )} \right\} $$
(17.24)

In the first phase of solution, the initial stresses are equal to zero and the equation becomes,

$$ [K]\{ \delta \} = \left\{ {F(\Omega^{2} )} \right\} $$
(17.25)

The solution of the above equation gives a stress distribution \( \sigma^{0} \). Taking this stress distribution, the geometric stiffness matrix is derived. The equation becomes,

$$ \left( {\left[ K \right] + \left[ {K_{{\sigma^{0} }} } \right]} \right)\{ \delta \} = \left\{ {F(\Omega ^{2} )} \right\} $$
(17.26)

The solution of Eq. (17.26) gives another new stress distribution \( \sigma^{1} \). Similarly, the procedure can be repeated to get the converged value of the stresses.

The rotational velocity component matrix contributing for angular acceleration is expressed as [7, 9],

$$ \left[ {A_{x} } \right] = \left[ {\begin{array}{*{20}c} {\Omega_{y}^{\prime 2} + \Omega_{z}^{\prime 2} } & { - \Omega_{x}^{\prime } \Omega_{y}^{\prime } } & { - \Omega_{x}^{\prime } \Omega_{z}^{\prime } } \\ { - \Omega_{x}^{\prime } \Omega_{y}^{\prime } } & {\Omega_{x}^{\prime 2} + \Omega_{z}^{\prime 2} } & { - \Omega_{y}^{\prime } \Omega_{y}^{\prime } } \\ { - \Omega_{x}^{\prime } \Omega_{z}^{\prime } } & { - \Omega_{y}^{\prime } \Omega_{z}^{\prime } } & {\Omega_{x}^{\prime 2} + \Omega_{y}^{\prime 2} } \\ \end{array} } \right] $$
(17.27)

The centrifugal force vector of an element can be written as [7, 9],

$$ \left\{ {F_{{\Omega e}} } \right\} = \rho \int\limits_{\text{vol}} {\left[ N \right]^{T} \left[ {A_{x} } \right]\left\{ {\begin{array}{*{20}c} x \\ y \\ z \\ \end{array} } \right\}} \;{\text{d}}({\text{vol}}) $$
(17.28)

In Eq. (17.28), \( \rho \) and \( [N] \) are the density of the composite material and the matrix of shape functions. Considering the Green–Lagrangian nonlinear strain components due to rotation, the geometric stiffness matrix of the stiffened plate element can be computed as [9, 29],

$$ \left\{ {K_{\sigma e} } \right\} = \int\limits_{\text{vol}} {\left[ G \right]^{T} \left[ {M_{\sigma } } \right]\left[ G \right]\;{\text{d}}({\text{vol}})} $$
(17.29)

In the above equation, the matrix \( [G] \) contains the derivatives of shape functions and \( [M_{\sigma } ] \) represents the matrix of initial in-plane stress resultants developed due to rotation. The expressions of [G] and \( [M_{\sigma } ] \) of the stiffened plate are given by,

$$ \left[ G \right] = \left[ {\begin{array}{*{20}c} {N_{i,x} } & 0 & 0 & 0 & 0 \\ {N_{i,y} } & 0 & 0 & 0 & 0 \\ 0 & {N_{i,x} } & 0 & 0 & 0 \\ 0 & {N_{i,y} } & 0 & 0 & 0 \\ 0 & 0 & {N_{i,x} } & 0 & 0 \\ 0 & 0 & {N_{i,y} } & 0 & 0 \\ 0 & 0 & 0 & {N_{i,x} } & 0 \\ 0 & 0 & 0 & {N_{i,y} } & 0 \\ 0 & 0 & 0 & 0 & {N_{i,x} } \\ 0 & 0 & 0 & 0 & {N_{i,y} } \\ 0 & 0 & 0 & {N_{i} } & 0 \\ 0 & 0 & 0 & 0 & {N_{i} } \\ \end{array} \begin{array}{*{20}c} \cdots \\ \cdots \\ \cdots \\ \cdots \\ \cdots \\ \cdots \\ \cdots \\ \cdots \\ \cdots \\ \cdots \\ \cdots \\ \cdots \\ \end{array} } \right]_{i = 1,8} $$
(17.30)
$$ \left[ {M_{\sigma } } \right] = \left[ {\begin{array}{*{20}c} {N_{x} } & {N_{xy} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ {N_{xy} } & {N_{y} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {N_{x} } & {N_{xy} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {N_{xy} } & {N_{y} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {N_{x} } & {N_{xy} } & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {N_{xy} } & {N_{y} } & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & {\frac{{N_{x} h^{2} }}{12}} & {\frac{{N_{xy} h^{2} }}{12}} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & {\frac{{N_{xy} h^{2} }}{12}} & {\frac{{N_{y} h^{2} }}{12}} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\frac{{N_{x} h^{2} }}{12}} & {\frac{{N_{xy} h^{2} }}{12}} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\frac{{N_{xy} h^{2} }}{12}} & {\frac{{N_{y} h^{2} }}{12}} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right] $$
(17.31)

The QR iteration algorithm [30] is used to compute the natural frequencies of stiffened panel. The solution of governing equation of motion is given as,

$$ [A]\{ \delta \} = \lambda \{ \delta \} $$
(17.32)

where \( [A] = \left( {[K] + [K_{\sigma } ]} \right)^{ - 1} [M] \) and \( \lambda = 1/\omega_{n}^{2} \).

17.3 Result and Discussion

For the computational purpose, an in-house computer programme based on the above formulation is developed in MATLAB environment. A mesh convergence study is conducted, and it is found that the mesh size of 8 × 8 gives the converged results. So for the entire analysis of the present study, this mesh size is used to compute the results. The validation of the formulation with respect to stiffened panel is shown in Table 17.1, which shows the agreement of the computed results with that of Nayak and Bandyopadhyay [16] and Das and Chakravorty [31]. The natural frequencies of antisymmetric cross-ply crossed-stiffened laminated composite plates are furnished in Table 17.1. The non-dimensional fundamental frequencies of an isotropic cantilever plate are furnished in Table 17.2 corresponding to different rotational speeds. The computed results corresponding to various rotational speeds show very good agreement with that of Sreenivasamurthy and Ramamurti [7]. The non-dimensional fundamental frequencies of a twisted composite plate are computed and compared with that of Qatu and Leissa [3] corresponding to different fibre orientation angles. These comparisons of results are shown in Table 17.3. The capability of the present MATLAB code in respect of stiffener formulation, rotation of the panel and pretwist angle is well established and acceptable. Therefore, it is obvious that the MATLAB code can effectively compute the natural frequencies of the pretwisted stiffened panel subjected to various rotational speeds.

Table 17.1 Natural frequencies (Hz) of simply supported cross-ply (0°/90°) crossed-stiffened plate, L = b = 254 mm, h = 12.7 mm, bst = 6.35 mm, dst = 25.4 mm, E1 = 144.8 GPa, E2 = 9.67 GPa, G12 = G13 = 4.14 GPa, G23 = 3.45 GPa, ν = 0.3, ρ = 1389.23 kg/m3 and nx = ny = 1
Full size table
Table 17.2 Non-dimensional fundamental frequencies \( \left( {\overline{\omega } = \omega_{n} L^{2} \sqrt {\rho h/D} } \right) \) of an isotropic rotating cantilever plate
Full size table
Table 17.3 Non-dimensional fundamental frequencies \( \left( {\overline{\omega } = \omega_{n} L^{2} \sqrt {\rho /E_{11} h^{2} } } \right) \) of three layer [θ/−θ/θ] graphite–epoxy twisted plates
Full size table

The fundamental frequencies of the composite stiffened plate are presented corresponding to different twist angles and rotational speeds. The geometric and material properties of the composite stiffened plate made of graphite–epoxy are as follows:

$$ \begin{aligned} & L/b = 2,\;L/h = 100,\;b_{st} = h,\;d_{st} = 4h,\;\nu_{12} = 0.30, \, E_{1} = 138.0\;{\text{GPa}}, \\ & G_{12} = G_{13} = 7.1\;{\text{GPa}},E_{2} = 8.96\;{\text{GPa}},G_{23} = 2.84\;{\text{GPa}} \\ \end{aligned} $$

The entire analysis is based on the laminated composite plate with composite stiffeners placed symmetrically along the nodal lines. The stacking sequence of the plate and the stiffener is always same. The boundary condition considered for the stiffened plate is given below:

$$ u = v = w = \alpha = \beta = 0\;{\text{at}}\;x = 0. $$
(17.33)

The effect of fibre orientation angle on the fundamental natural frequency of an eight-layered laminated composite [θ/−θ/θ/−θ]s stiffened plates is presented in Fig. 17.2 for two panels, wherein one panel is attached with a single x-directional stiffener while the second panel is appended with a single y-directional stiffener. At the same time, the stiffened plates of different angles of pretwist are also considered. Form the graph, it may be observed that raise in the value of fibre orientation angle decreases the fundamental frequency irrespective of twist angle. When the fibres of stiffener and plate are orthogonal to the clamped edge (θ = 0°), fundamental frequency is obtained maximum and minimum at θ = 90° irrespective of twist angles. Increase in the value of pretwist angle is found to reduce the value of fundamental frequency because of decrease in structural stiffness, and the results corroborate with the results of Qatu and Leissa [3]. The maximum percentage of reduction in fundamental frequency with increase in twist angle is observed at fibre orientation of 30° while minimum at θ = 90° for x-directional stiffened plate. In case of y-directional stiffened plate, insignificant variation of fundamental frequency is observed corresponding to 15° twist angle. At 30° pretwist angle of y-directional stiffened plate, maximum reduction in fundamental frequency is depicted at θ = 0°. Comparing x- and y-directional stiffened plates, it may be observed that maximum value of fundamental frequency is obtained with x-directional stiffener. Hence, x-directional stiffener is found to be more efficient in rendering maximum stiffness to the plates, thereby increasing the fundamental frequency. This observation is limited to cantilever boundary condition.

Fig. 17.2
figure 2

Variation of fundamental frequency with fibre angle of different twisted stiffened plates

Full size image

The variation of fundamental frequency with increase in number of x-directional stiffener of stationary composite [30°/−30°/30°/−30°]s twisted stiffened plate corresponding to twist angle 0°, 15°, 30° is furnished in Fig. 17.3, because from the previous observation it is clear that x-stiffener is more efficient in terms of increasing fundamental frequency. It reveals that increase in number of stiffeners increases the value of fundamental frequency, as normally expected. However, the rate of increase in fundamental frequency, especially at early stage, gradually decreases with increase in number of stiffeners for all the cases. Excellent performance in terms of improving fundamental frequency is achieved by appending maximum three numbers of stiffeners; thereafter, the increase in fundamental frequency is found marginal as the curves gradually become horizontal.

Fig. 17.3
figure 3

Variation of fundamental frequency with respect to number of stiffeners of various twisted stiffened plates. Stiffeners are symmetrically across the width

Full size image

The variation of first fundamental frequency with stiffener depth-to-plate thickness ratio (dst/h) of both untwisted and twisted laminated composite [30°/−30°/30°/−30°]s stiffened plate is illustrated in Fig. 17.4. A single x-directional composite stiffener placed symmetrically is considered for this particular case. It is evident that increase in (dst/h) increases the fundamental frequency, because it increases the eccentricity of the stiffener, which in turn increases the second moment of area. The rate of increase of fundamental frequency is found slow at early stage while its growth is found rapid after dst/h = 2 in both the cases. This observation will be helpful for the investigators to select the depth of the stiffener.

Fig. 17.4
figure 4

Variation of first fundamental frequency of the stiffened plate with respect to stiffener depth-to-plate thickness ratio

Full size image

Figure 17.5 shows the variation of fundamental frequency of the composite [30°/−30°/30°/−30°]s stiffened plate with non-dimensional rotational speeds (Ω = 0.00, 0.50 and 1.00). Three cases are considered corresponding to twist angles 0°, 15° and 30°, respectively. The present investigation is performed for two different stiffened panels: one is embedded with a single x-stiffener and other with a single y-stiffener. The fundamental frequency is found minimum at twist angle 30° while found maximum in untwisted stiffened plate as normally expected for both the panels. It is evident that increasing the rotational speed raises the value of fundamental frequency because of centrifugal stiffening. The percentage increase in fundamental frequency due to rotational speed is found maximum in the twisted plate (ϕ = 30°) than untwisted plate. This observation is found in x-directional stiffened plate, while in y-directional stiffened plate, no such observation is noticed. Hence, the rotating effect is more pronounced for the twisted plate than the untwisted plate, when attached with x-directional stiffener.

Fig. 17.5
figure 5

Variation of fundamental frequency with rotational speed of composite [30/−30/30/−30]s stiffened plates with different angles of pretwist

Full size image

The mode shapes of the composite stiffened plate for various twist angle and rotational speeds are furnished. First the effect of different twist angles of stiffened plate on its mode shapes is presented in Table 17.4. The continuous and dashed lines denote the upward and downward displacements, respectively. It reveals that the symmetry of mode shapes disappears with increase in twist angles.

Table 17.4 Mode shapes of the cantilevered composite [30°/−30°/30°/−30°]s stiffened plate corresponding to different twist angles
Full size table

The effects of different rotational speeds on the mode shapes of a twisted stiffened plate are shown in Table 17.5. The first five mode shapes of the composite stiffened plate are shown corresponding to non-dimensional rotational speeds 0.0, 0.5 and 1.0, respectively. The first five modes of the non-rotating stiffened plate are, in order, first spanwise bending (1B), first torsional mode (1T), second torsional mode (2T), first chordwise bending mode (1C) and third torsional mode (3T), respectively. The symmetry of mode shapes is not observed due to twist angle and rotational speed. It is observed that the mode-1 is not at all influenced by the rotational speed, while the influence of rotational speed can be seen after mode-2.

Table 17.5 Mode shapes of the cantilevered composite [30°/−30°/30°/−30°]s twisted (30°) stiffened plate corresponding to different rotational speeds
Full size table

17.4 Conclusions

In this investigation, the finite element formulation of the rotating twisted stiffened plate is presented and the accuracy and effectiveness of the formulation are well verified with the results available in the open literature. The major conclusions drawn from the parametric studies are listed below:

  1. 1.

    The fibre orientation of the laminated stiffened plate has large control over the fundamental frequency, wherein maximum and minimum values of fundamental frequency are obtained corresponding to 0° and 90°, respectively.

  2. 2.

    The x-directional stiffener is found to be more efficient in increasing the fundamental frequency of the twisted stiffened plate.

  3. 3.

    The fundamental frequency is noticed to reduce with increase in twist angle of the composite stiffened plate.

  4. 4.

    Increase in stiffener depth-to-plate thickness ratio has also a striking effect on the fundamental frequency.

  5. 5.

    The effect of speed of rotation on the fundamental frequencies is observed to be more prominent in twisted stiffened plates. Increase in the rotational speed of the stiffened plate increases the fundamental frequency due to centrifugal stiffening irrespective of twist angle.