Lamellipodia in Stationary and Fluctuating States

Abstract

We review recent mathematical models describing the diffusive transport, reaction, and turnover of actin and regulators at the leading edge of motile cells. These models are motivated by experimental results using cells with flat, steady lamellipodia studied by Single Molecule Speckle microscopy. The same cells can also be made to exhibit protruding and retracting lamellipodia, which demonstrate how changes in actin polymerization lead to changes in the rate of protrusion. The second part of this chapter provides a description of these fluctuations as an excitable actin system pushing against the cell membrane by polymerization.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Lamellipodia are thin and flat protrusions at the leading edge that allow cells to attach, and move across on flat surfaces. Lamellipodial protrusions have been studied extensively, both due to their importance in cell motility and as model systems of cytoskeletal dynamics [10, 20, 68, 81, 101]. Actin filaments in the lamellipodium form a dynamic network that polymerizes primarily close to the leading edge of the cell, with the filament barbed ends pointing toward the cell membrane. In the dendritic nucleation model, many of these filaments are created as branches off pre-existing filaments [80]. Pushing of the cell front forward is due to the addition of monomers to free barbed ends of the lamellipodial actin network near the cell membrane. The concentration of free barbed ends is regulated by capping proteins. The whole actin network undergoes retrograde flow towards the cell center due to polymerization at the leading edge combined with adhesion and myosin contraction at the rear of the lamellipodium [77, 81, 85, 101]. The difference between the rates of polymerization and retrograde flow results in net lamellipodial protrusion or retraction. The actin subunits in the filament that move towards the back of the network break off from the network due to cofilin-induced severing into oligomers. The disassembled pieces further depolymerize and are recycled close to the leading edge.

Many actin regulatory proteins have been characterized in vitro, but precisely how they control actin polymerization and depolymerization across the lamellipodium has not been completely resolved. The majority of actin polymerization in lamellipodia occurs near the leading edge. As the network moves toward the body of the cell by retrograde flow, F-actin is depolymerized and recycled to be used again.

1.1 Lamellipodium in Homeostasis

Since all lamellipodial components have to be recycled, the transport of disassembled proteins through the cytoplasm back towards the leading edge is an important component of the kinetics in lamellipodia. Some studies suggested that diffusion is fast enough to deliver actin subunits to the leading edge [49, 99] while others have proposed a role for active transport mechanisms such as myosin-based transport [26] or hydrodynamic flow [108]. Previous theoretical work has shown how diffusion may become limiting, depending on both the value of the diffusion coefficient in the cytoplasm and the spatial distribution of sources and sinks of actin subunits in the cytoplasm [72, 92]. One of the difficulties in directly measuring the existence of gradients of diffuse actin experimentally is that the diffuse population is a small fraction of the actin in filaments. Further, the dynamics in photoactivation or photobleaching experiments reflect a combination of reaction and diffusion that can be hard to disentangle [61, 92].

In the first part of this chapter we discuss recent studies that show how mathematical models based on data obtained by single molecule speckle (SiMS) microscopy can be combined with fluorescence recovery after photobleaching (FRAP) or photoactivation (PA) studies to model the dynamics of the diffuse actin pool [92, 92, 99], capping protein, and Arp2/3 complex. In SiMS, cells contain fluorescently labeled proteins at a concentration sufficiently low to resolve single molecules [102]. If a fluorescent protein is diffusing freely in the lamellipodium, it will appear as a diffuse background or localized cloud, depending on its diffusion coefficient and the exposure time of the camera. When the tagged protein binds to the actin network it appears as a speckle undergoing retrograde flow while it remains bound to the network. Speckle disappearance reflects dissociation of the tagged protein to the diffuse pool. By contrast, cells in FRAP or PA experiments typically contain a large fraction of labeled protein that leads to spatially extended intensity fields, the redistribution of which around an area of interest reflects the combined dynamics of reaction, retrograde flow, and diffusion [92].

1.2 Lamellipodia in Fluctuating States of Protrusion and Retraction

In many cells, usually soon after they spread on a surface and before the onset of directed cell motion, the protrusion of the lamellipodium is followed by retraction [88]. This leads to cycles of protrusion and retraction that are periodic and in some cells organize into traveling waves of protrusion along the cell front and sides [4, 8, 22, 29, 55, 58, 59, 84, 87, 88]. This regular behavior involving fluctuations around a steady state can be used to study how the dynamics of actin polymerization are converted into cell motion [88].

Patterns of protrusions and retractions have been observed in XTC cells from Xenopus, which usually adopt a circular shape after introduction to the poly-L-lysine substrate (Figure 4A,B) [88]. The flat lamellipodia within these cells are ideal for quantitative analysis, allowing accurate averaging and calculations of correlations among different components. The retrograde flow rate was approximately constant during protrusion and retraction, suggesting that the changing F-actin localization in these cells stems from variations in the assembly and disassembly of the actin network near the leading edge, as opposed to stemming from changing retrograde flow rates [87].

The observed dynamics are suggestive of excitations driven by noise (i.e., stochastic concentration fluctuations): experimental results of XTC cells from Ryan et al. [87] show cycles of bursts of actin polymerization in a random pattern around the cell, lateral propagation, followed by disassembly. In the second part of this chapter we describe recent models that successfully described these experimental observations.

2 Model of Actin Turnover and FRAP Kinetics in XTC Cells

Numerous experiments provide evidence that actin polymerization and depolymerization occur not just at the leading edge but also throughout the lamellipodium [7, 15, 56, 66, 82, 96, 98, 101]. Most directly, Single Molecule Speckle (SiMS) Microscopy on XTC cells demonstrates single molecules of actin polymerizing throughout the lamellipodium [102] (Figure 1A & D).

Fig. 1

SiMS experimental data and simulated FRAP. (A) Tracking EGFP-actin speckles in experimental SiMS in XTC cells (reproduced with permission from [91]). (B) Model with F-actin and one species of diffuse G-actin. (C) Model for two-species of diffuse actin (G, oligomeric) and F-actin. (D) Appearance profile for EGFP-actin speckles in XTC cells. (E) Lifetime distribution for EGFP-actin speckles in XTC cells. (F) Simulated concentration profiles for F, G, and O actin as a function of distance from the leading edge. (G) Simulated rates of binding for G → F and O → F. (H) Simulated FRAP curves using a model that includes oligomers. (I) Simulated FRAP using a model that includes oligomers. Panels B-H reproduced with permission from [92].

In apparent contradiction to the studies above, which indicate an extended distribution of barbed ends across the lamellipodia, fluorescent recovery after photobleaching (FRAP) experiments show that significant fluorescence recovery occurs fast near or at the leading edge, while recovery away from the leading edge occurs with a delay followed by a more rapid increase [38, 52, 73]. This suggests that actin polymerization occurs only very close to the leading edge and that recovery at the back relies on retrograde flow of unbleached monomers from the very front of the leading edge [52, 53]. However, reassociation of the bleached actin within the bleached area in FRAP experiments may slow down recovery [101] as shown for reaction diffusion models of actin turnover in a spatially homogeneous system without retrograde flow [14, 61, 95].

To address this apparent discrepancy between SiMS and FRAP data, Smith et al. [92] compared models with actin turnover distributed throughout the lamellipodium to FRAP experiments of XTC cells, the same cell type for which SiMS experiments had already been performed. They studied XTC cells that have negligible leading edge protrusion or retraction. While the FRAP recovery in XTC lamellipodia is qualitatively similar to that in other cells [38, 52, 73], these models demonstrated that SiMS and FRAP data do not contradict one another.

Smith et al. developed two models to show that turnover can occur without causing rapid FRAP recovery away from the leading edge. The first model uses diffuse actin that polymerizes and depolymerizes as monomers. FRAP curves simulated with this model are good fits to experiments, but have some different qualitative features. The second model considers two species of diffuse actin that can polymerize and depolymerize throughout the lamellipodium, monomers (G-actin), and oligomers (O-actin). Oligomers are slowly diffusing actin that can anneal to the F-actin network. The presence of a small amount of oligomers further reduces the amount of recovery away from the leading edge in simulated FRAP. The results of this model are in better agreement with both FRAP and SiMS microscopy.

2.1 Model of Actin Profile Based on SiMS Speckle Statistics

In the model by Smith et al. [92], SiMS microscopy data are used to compute the steady-state F-actin concentration profile. This profile is then used to calculate the steady-state G- and O-actin profiles and the corresponding polymerization rates as a function of distance from the leading edge. These reaction rates are then used in a numerical simulation of FRAP.

2.1.1 Calculation of F-Actin Profile

The statistics of single molecules of labeled actin obtained in previous studies of XTC cells (Figure 1A) [91, 102] are an input to the model. The location of speckle appearance events correspond to polymerization and yield an appearance rate, a(x), as a function of distance from leading edge x (Figure 1D) [102]. The units of a(x) in the model are μM/s. To obtain an analytical form for a(x), the appearance curve is approximated with a double exponential:

$$\displaystyle \begin{aligned} a(x)=G_{\infty}K\left[A_1e^{-x/\lambda_1}+A_2e^{-x/\lambda_2}\right]. {} \end{aligned} $$

(1)

The shorter length, λ ₁, corresponds to polymerization at the leading edge while the longer length scale, λ ₂, corresponds to basal polymerization that occurs throughout the lamellipodium. This equation is a phenomenological fit chosen for two reasons: it captures the experimental data, and it yields analytical results in later calculations. The biophysical mechanism that gives rise to the appearance distribution a(x) is not yet fully established. The total rate of appearance is scaled in proportion to the cytoplasmic concentration of labeled actin monomers far from the leading edge, G _∞. For convenience, A ₁ + A ₂ = 1 so K can be used as a parameter that adjusts the total rate of polymerization and the resulting F-actin/G-actin (F/G) ratio. The fit gives A ₁ = 0.84, A ₂ = 0.16, λ ₁ = 0.5 μm, λ ₂ = 4 μm (Figure 1C). While the bin size for appearance data is comparable to λ ₁, the distribution of appearance events within the first 0.5 μm of the leading edge was not crucial for this study. What is more important is the total number of speckles in the first bin.

Measurements of the speckle lifetime distribution in Figure 1E, p(t _l), give the probability distribution of the amount of time t _l that each actin subunit spends as F-actin. The lifetime distribution is approximately constant within the first 3 μm from the leading edge [91, 102]. The lifetime distribution is adequately described by a double exponential:

$$\displaystyle \begin{aligned} p(t_l)/p(0)=C_1e^{-t_l/\tau_1}+C_2e^{-t_l/\tau_2}, {} \end{aligned} $$

(2)

where C ₁ = 0.741, C ₂ = 0.259, τ ₁= 16 s, τ ₂ = 60 s. Exponentials were chosen because they capture the lifetime distribution well. They are also mathematically convenient since they allow use of exponential statistics in simulations and enable obtaining analytical results.

The velocity of retrograde flow v _r provides the remaining parameter necessary to construct an F-actin profile represented by the speckle statistics. Using the appearance rate a(x) as a source of F-actin yields the steady-state concentration profile F(x):

$$\displaystyle \begin{aligned} F(x)=\int\limits_0^{\infty}Y(x,x')a(x')dx'. {} \end{aligned} $$

(3)

The profile Y (x, x′) generated by a point source at x′ is obtained by considering the amount of subunits that have a longer lifetime than the time it took to travel from x′ to x via retrograde flow:

$$\displaystyle \begin{aligned} Y(x,x')=\varTheta (x-x')\frac{1}{v_r}\int\limits_{\frac{x-x'}{v_r}}^{\infty}p(t_l)dt_l, {} \end{aligned} $$

(4)

where the prefactor is found by balancing retrograde flow out of x′ with amount created by the point source and Θ is the step function. Retrograde flow rate can be considered approximately constant within the first 4 μm from the leading edge of XTC cells [87].

2.1.2 Model with Monomers as Only Diffuse Actin Species

The first model considers actin in two states: F-actin that undergoes retrograde flow, and G-actin with diffusion coefficient D = 4 μm²/s [25, 49, 61, 108]. G-actin diffuses freely, polymerizing to become F-actin with rate a(x). A diagram of this model is shown in Figure 1B where F and G are the only two species in the model. At steady state, both retrograde flux of F-actin and diffusive flux of G-actin balance the local exchange between F- and G-actin:

$$\displaystyle \begin{aligned} v_r \frac{\partial F(x)}{\partial x}=-D \frac{\partial^2 G(x)}{\partial x^2}=a(x)-d(x), {} \end{aligned} $$

(5)

where G(x) is the G-actin concentration and d(x) the rate of speckle disappearance. Knowing F(x) from Equation (3), we can solve Equation (5) for the G-actin profile:

$$\displaystyle \begin{aligned} G(x)=G_{\infty}-\frac{v_r}{D}\int\limits_x^{\infty}F(x')dx'. {} \end{aligned} $$

(6)

The value of parameter K determines the F/G ratio since it changes the magnitude (but not the shape) of the F-actin profile. To obtain the steady-state F-actin profile based on SiMs data, we substituted Equations (1) and (2) into (3) and (4). The result of the total amount of F-actin:

$$\displaystyle \begin{aligned} \int\limits_0^{\infty}F(x)dx=G_{\infty}K\sum_{i=1}^2\sum_{j=1}^2A_iC_j\tau_j^2\lambda_i, {} \end{aligned} $$

(7)

demonstrating that the F-actin concentration is directly proportional to parameter K. By substituting Equation (7) into Equation (6) we can calculate the G-actin profile analytically. By increasing K, the G-actin depletion near the leading edge is increased. Increasing the value of the retrograde flow velocity causes a greater depletion of G-actin.

2.1.3 Model with Both Monomers and Oligomers

Actin oligomers could be present in the lamellipodium through cofilin-mediated severing of actin filaments [9, 16, 34, 50] or Arp2/3 complex debranching [12, 60]. The short lifetimes of capping protein speckles in lamellipodia indicate severing of capped filaments [66]. Reassociation of these oligomers to the actin network could be a mechanism for structural reorganization of actin filaments in the lamellipodium [66, 97]. Oligomers with diffusion coefficient D _O ≈ 0.5 μm²/s and a fluorescent subunit would appear as background noise during exposure in SiMS experiments [91]. If they anneal to the network, they would contribute to speckle appearance events in SiMS experiments. When they dissociate from the network (via severing or debranching) they would contribute to speckle disappearances. Since the diffusion coefficient in the cytoplasm decreases with increasing molecular weight of protein complex [75], such D _O values may represent fragments of order ∼10 actin subunits.

In the model shown in Figure 1C, G-actin monomers can associate into F-actin and F-actin subunits depolymerize into O-actin. Subunits of O-actin can become F-actin or disassemble to G-actin with an average lifetime τ _O. The total appearance rate is separated into oligomers, a _O(x), and monomers, a _G(x), with a(x) = a _O(x) + a _G(x). It is then assumed that O-actin accounts for a majority of appearance events away from the leading edge (corresponding to structural reorganization of actin filaments away from the leading edge through severing and reannealing) while G-actin polymerization contributes to most events close to the leading edge (see [92] for other possibilities). At steady state, similar to Equation (5)

$$\displaystyle \begin{aligned} v_r\frac{\partial F(x)}{\partial x}=a_O(x)+a_G(x)-d(x), {} \end{aligned} $$

(8)

$$\displaystyle \begin{aligned} D_G\frac{\partial^2G(x)}{\partial x^2}=a_G(x)-\frac{1}{\tau_O}O(x), {} \end{aligned} $$

(9)

$$\displaystyle \begin{aligned} D_O\frac{\partial^2O(x)}{\partial x^2}=a_O(x)-d(x)+\frac{1}{\tau_O}O(x), {} \end{aligned} $$

(10)

where D _G = 4 μm²/s and D _O are the G- and O-actin diffusion coefficients. The F-actin profile is given by the same expression as in Equation (3), so we can substitute in Equation (8) to solve for d(x), which leads to O(x) through Equation (10) to:

$$\displaystyle \begin{aligned} \begin{array}{rcl} O(x)&\displaystyle =\tau_O \cosh\left(\frac{x}{\sqrt{D_O\tau_O}}\right)\int\limits_0^{\infty}f(x')\exp\left(\frac{-x'}{\sqrt{D_O\tau_O}}\right)dx' \\ &\displaystyle -\tau_O\int\limits_0^x f(x')\sinh \left(\frac{x-x'}{\sqrt{D_O\tau_O}}\right)dx', \end{array} \end{aligned} $$

(11)

where f(x) = a _G(x) − v _r ∂F∕∂x. The G-actin profile can then be solved similar to the model with monomers only, using Equation (9):

$$\displaystyle \begin{aligned} G(x)=G_{\infty}-\frac{D_O}{D_G}O(x)-\frac{v_r}{D_G}\int\limits_x^{\infty}F(x')dx'. {} \end{aligned} $$

(12)

An example of calculated profile is shown in Figure 1F, where D _O = 0.5 μm²/s and τ _O = 20 s. The profile in Figure 1F is consistent with values of the F/G ratio in the range 2–10 [1, 19, 51, 101]. The total amount of O-actin can be quite low compared to the amount of F and G-actin, while still making a contribution to the total speckle appearance rate. O-actin is generated by F-actin disassembly so it peaks close to the leading edge where the F-actin concentration is larger.

2.2 Particle Simulations

To simulate FRAP recovery, Smith et al. [92] assumed the appearance rate is proportional to the local G-actin or O-actin concentration. In the model with just monomers, the rate at which monomers convert to F-actin is:

$$\displaystyle \begin{aligned} r_{G\rightarrow F}(x)=a(x)/G(x). {} \end{aligned} $$

(13)

The O- and G-actin binding rates of the model with oligomers are correspondingly:

$$\displaystyle \begin{aligned} r_{G\rightarrow F}(x) = a_G(x)/G(x),\ \ r_{O \rightarrow F}(x)=a_O(x)/O(x). {} \end{aligned} $$

(14)

Figure 1G shows an example of calculated transition rates for the model with both monomers and oligomers. Estimated values for the concentration of barbed ends are [B] ≈ 1 μM [101]. We expect the transition rate to be proportional to the local concentration of free barbed ends. Using r _G→F = k ⁺[B], the rate constant close to the leading edge is k ⁺ ≈ 0.6 μM⁻¹s⁻¹, consistent with previous estimates [101].

The transition rates in Equations (13) and (14) were used in [92] in an off-lattice 2D Monte Carlo simulation with reaction and diffusion of individual subunits. Each subunit was either diffusing (G-actin, O-actin) or undergoing retrograde flow (F-actin). Every time step, Δt (1 ms or smaller), diffuse particles were moved according to the 2D Gaussian diffusion propagator and checked for association to the F-actin. When a monomer transitions to F-actin, its lifetime is picked from the lifetime distribution p(t _l). After an F-actin subunit is moved, its lifetime is compared to the time elapsed since polymerization to check if it should depolymerize and become G-actin. To simulate images, the particles are treated as diffraction-limited spots that diffuse during camera exposure [91]. Bleached particles are removed from the simulation and do not contribute to intensity.

2.3 FRAP Recovery: Comparison of Model Results to Experiments

A simulated FRAP image is shown in Figure 1I where a region of size 5x20 μm is bleached near the leading edge. Figure 1H shows the recovery of intensity at two strips between 0–0.5 μm and 2.5–3 μm (“Front” and “Back”) from the leading edge using the model with both monomer and oligomers, plotted against experimental data. The simulated recovery curves are very similar to the experiments, with fast recovery at the front and slower recovery at the back. Good fits were obtained for K = 0.4–0.9 s⁻¹, D _O < 1 μm²/s, and τ _O < 60 s The model with oligomers captured two features of the experiment that the monomer-only model does not:

• 1. Recovery at the back (Figure 1I) is slower in the model with oligomers compared to the monomer-only model. In Figure 1I, the FRAP curve at the back does not show significant recovery until retrograde flow carries monomers from the leading edge into the back region. For the chosen parameters, oligomers do not diffuse into the bleached region before retrograde flow transports monomers from the leading edge into the region. Two factors contribute: The time required to travel distance of order 3 μ by free oligomer diffusion is 10 s, but this is slowed down by rebinding of O-actin within the bleached region [95] since $\sqrt {4D_O/r_{O\rightarrow F}} = 3.2~\upmu$m; and generation of a new O-actin subunit, from unbleached monomers that polymerize at the leading edge, requires times of order the average speckle lifetime.

• 2. Unlike in the monomer-only model, the recovery at the front (Figure 1I) does not have a tail at long times. A tail in the front recovery curve occurs in the monomers-only model due to hindered diffusion through the lamellipodium [95]. In the model with oligomers, the region of G-actin polymerization is narrow, and this effect is reduced in magnitude.

The above results support models that include annealing and severing in the lamellipodium [42, 64]. For a more detailed study of the dependence of the FRAP curves on model parameters, we refer the reader to [92]. The above models did not explicitly account for the fact that G-actin monomers can carry different types of nucleotide (ADP or ATP), or that monomers can be bound to profilin, thymosin, or cofilin. It is assumed that the reactions among these different states occur fast enough to be considered quasi-static and also do not modify the diffusion coefficient of bound G-actin [72].

We note that a recent modeling study of lamellipodial actin turnover in keratocyte fragments by Aroush et al. [6] reached different conclusions compared to Smith et al. [92]. These authors concluded that while the actin network disassembles and reassembles throughout the lamellipodium, actin subunits typically diffuse across the entire lamellipodium before reassembling into the network. Aroush et al. also argue that about two-thirds of the lamellipodial actin diffuses in the cytoplasm with nearly uniform density, a much higher fraction of diffuse actin compared to Figure 1F. Future work should address the origin of these discrepancies. A model with the features stated by Aroush et al. (very high concentration of diffuse actin, no local reassembly) would not capture the slow FRAP recovery at the back of the lamellipodium of XTC cells (Figure 1H) or the increase of F-actin intensity starting from the leading edge after photoactivation of actin in the cell middle (Figure 2G below).

Fig. 2

Experiments and Simulations of Actin Photoactivation (reproduced from [99]). (A) Model with three diffuse species of actin: recycled, cytoplasmic, membrane bound as well as F-actin. The rates depend on distance from leading edge, with membrane binding, k(x), occurring close to the leading edge. (B) Simulated steady-state concentration profile using the model in A. (C) Photoactivation in ROI at cell leading edge. (D) Fluorescence decay in ROI of panel C. (E) Simulated photoactivation of 5 by 10 μm box at the leading edge. (F) Simulated fluorescence decay in activation box of panel E. (G) Cell center actin photoactivation. (H) Fluorescence in cell center and close to leading edge after photoactivation of cell center. (I) Simulated photoactivation of cell center. (J) Simulated fluorescence in cell center and close to the leading edge after photoactivation of cell center. Image scale bars, panels C,E,G: 10 μm; panel I: 8 μm.

3 Model of Actin Turnover and Photoactivation Kinetics in Neuronal Cells

Photoactivation (PA) of fluorescently labeled actin is another way to study subcellular actin transport and reaction. In this section we review an extension of the model of [92] of Section 2, developed in [99], to model PA of neuronal CAD (Cath.a differentiated) cells. For these cells, the study in [54] suggested an enhancement of G-actin at the leading edge. To account for this enhancement, which could arise from actin monomers bound to the plasma membrane through a profilin-Tβ4-actin complex [99], a membrane-bound G-actin component close to the leading was added to the model (otherwise the G-actin is depleted rather than enhanced near the leading edge, see Figure 1F). In addition to modeling PA kinetics, another aim of the study in [99] was to examine the effect of G-actin sequestering protein thymosin β4 (Tβ4) in facilitating diffusing actin transport (uninterrupted by polymerization) across the cell.

3.1 Model Description

This model includes 3 pools of diffuse protein instead of 2 (Figure 2A). The three pools are: R, which is a recycling component that represents all actin which has been recently depolymerized (which may include oligomers or actin bound to other protein complexes); G _C, which binds reversibly to Tβ4 in the cytoplasm; and G _M, which represents actin diffusing along the membrane, e.g., as membrane-bound profilin-Tβ4-actin. The G _C pool groups together free and Tβ4-bound actin, assuming they are in rapid equilibrium, given the estimated off rate of 2.5 s⁻¹ for the Tβ4-actin complex [67]. G _C and G _M also group together actin monomers free or in complex with profilin and does not distinguish between ATP- and ADP-actin. All 3 diffuse pools are able to associate with F-actin; however, F-actin only depolymerizes to the recycled actin in this model.

The appearance rate in this model is split between the three actin pools,

$$\displaystyle \begin{aligned} a(x)=a_R(x)+a_C(x)+a_M(x). \end{aligned} $$

(15)

Given the similarities between XTC and neuronal CAD cell lamellipodia, it was assumed that a(x) is given by Equation (1) and the lifetime distribution by Equation (2). The appearances are defined as follows:

$$\displaystyle \begin{aligned} a_C(x)=KG_{\infty}A_Ce^{-x/\lambda_1},\ a_M(x)=KG_{\infty}A_Me^{-x/\lambda_1},\ a_R(x)=KG_{\infty}A_Re^{-x/\lambda_2}.\end{aligned} $$

(16)

Here G _∞ is the concentration of G _C far from the leading edge, K determines the fraction of F to G-actin, and A _C + A _M + A _R = 1.

The concentration of actin at steady state, F(x), can be calculated as in Equation (3). The equations that describe the steady-state concentrations of the diffuse components are as follows:

$$\displaystyle \begin{aligned} D_R\dfrac{d^2R(x)}{dx^2}=a_R(x)+\frac{1}{\tau_R}R(x)-d(x), \end{aligned} $$

(17)

$$\displaystyle \begin{aligned} D_C\dfrac{d^2G_C(x)}{dx^2}=a_C(x)+k(x)G_C(x)-\frac{1}{\tau_{GM}}G_M(x)-\frac{1}{\tau_R}R(x), \end{aligned} $$

(18)

$$\displaystyle \begin{aligned} D_M \dfrac{D^2 G_M(x)}{dx^2}=a_M(x)-k(x)G_C(x)+\frac{1}{\tau_{GM}}G_M(x). \end{aligned} $$

(19)

In these equations D _R, D _C, and D _M are the diffusion coefficients for recycled actin, cytoplasmic actin, and membrane bound actin, respectively. In all these equations, x is the distance from the leading edge. The lifetimes τ _GM and τ _R are the times that G _M and R remain in their respective states until they become G _C. The rate k(x) is a spatially dependent rate that G _C becomes G _M.

The binding rate for the recycled actin, R, to become F-actin is a _R(x)∕R(x) and similarly for G _M and G _C. These rates were then used in a 2D Monte Carlo particle simulation as in Section 2.2. The system is initialized so that the concentrations matched those found after solving Equations (17)–(19). Simulated concentration profiles are shown in Figure 2B and the parameters used to find these profiles are listed in Table 1. To perform photoactivation on a region, all particles outside of that region are deleted and the remaining particles allowed to move and react.

Table 1 Parameter table for simulated photoactivation of PA-GFP actin.

3.2 Comparison to Photoactivation Experiments

An example of experimental photoactivation of PA-GFP actin from [99] is shown in Figure 2C. This photoactivation is over a 5 by 10 μm region at the leading edge showing the retrograde flow of the actin network and the local recycling of the photoactivated actin in nearby regions (clearer in inverted grayscale image in Figure 2C, bottom panel). The decay of fluorescence in the photoactivated region as it moves inwards by retrograde flow is shown in Figure 2D. Simulations of actin photoactivation over the same size and position as that in the experiment capture the behavior seen in experiments (Figure 2E,F) with rebinding near the photoactivated region as well as similar decay in fluorescence.

Simulations were also used to model photoactivation experiments of actin in the cell center (Figure 2G), which demonstrate the transport dynamics of actin across the lamellipodium. Figure 2H shows the normalized fluorescence response within 1 μm of the leading edge as well as at the center. The fast recovery at the leading edge of the cell brings up the question of whether diffusion is sufficiently fast to transport actin from the cell center to the leading edge in this amount of time. Simulations mimicking cell center photoactivation reproduce the observed dynamics (Figure 2I,J), demonstrating that diffusion is likely sufficient for fast delivery of actin from the cell center to the leading edge.

Another photoactivation experiment involved activating PA-GFP actin in the whole lamellipodium [99]. The fluorescence at the leading edge decayed to about 50% of its original value after 120 s. The authors of [99] suggest that this points to a pool of actin that is recycled within the lamellipodium. Simulations of whole lamellipodium activation using the model of this section reproduce the experimental trace [99]; however, the plateau occurs at the level of total amount of actin photoactivated in the simulation box. Further modeling studies that account for the diffusion through the whole 3D cell volume are needed to better interpret these experimental results.

3.3 Simulations of Cells Without Actin Sequestration by Tβ4

Tβ4 binds to actin monomers, not allowing polymerization. Vitriol et al. [99] performed PA experiments after knocking down (KD) Tβ4, using shRNA. In experiments in which the cell center was photoactivated, a lag in recovery at the leading edge was observed compared to the control case. After varying all parameters in the model that would affect this recovery, the authors found that the model matches experiment after: (1) an increase in the binding rate of G _C at the back of the lamellipodium, and (2) reduction of the diffusion coefficient of G _C by 50%, compared to the control case. From this, the model predicted a less sharp sigmoidal recovery at the back of the lamellipodium (2–3 μm away from the leading edge), which agreed with experimental measurements [99].

The results of the PA simulations and experiments suggested actin within the lamellipodium exists within two pools, one which is bound to Tβ4 and allows for fast diffusion through the lamellipodium and another pool which diffuses slowly and is not bound to Tβ4 [99]. Actin bound to Tβ4 is prevented from binding to actin at the back of the lamellipodium and can diffuse fast through the lamellipodium to the leading edge of the cell where it may associate in a complex with profilin and allow the actin to incorporate into the actin network, perhaps through the aid of formins. Tβ4 aids in this diffusion by sequestering the actin monomers and not allowing them to bind promiscuously to other actin binding proteins throughout the lamellipodial network [99]. The actin that is not bound to Tβ4 (recycling actin, likely actin oligomers) is incorporated into the actin network away from the leading edge. This study showed that a large portion of the actin in the lamellipodium is recycled actin and that it plays an important role in the kinetics of turnover of the network.

4 Model of Capping Protein and Arp2/3 Complex Turnover

Capping protein and the Arp2/3 complex are two of the most important regulators of actin dynamics in cells and in in vitro reconstitution experiments [47]. This section summarizes the work in [62] that extends the approach of Smith et al. to capping protein and Arp2/3 complex. For both of these proteins, SiMS and FRAP data have been performed in lamellipodia (albeit by different groups on different cell systems). Similar to the case of diffuse actin, it is possible that both exhibit significant concentration gradients in their diffuse pool. For example, slowly diffusing capping proteins have indeed been observed by SiMS [91], which may reflect capping protein bound to slowly diffusing actin oligomers or to the membrane. The Arp2/3 complex has also been observed to form a slowly diffusing complex with its activators prior to attachment to the actin network [65]. The study by McMillen and Vavylonis [62] addressed these issues.

4.1 Method to Calculate Concentration Profiles

Since proteins in the lamellipodium are frequently associating to larger complexes or binding to the membrane, the simplest model to account for this behavior with two distinct cytoplasmic populations was considered: a fast diffusing cytoplasmic population, C_fast, and a slow diffusing cytoplasmic population, C_slow. Bound protein (B), which is protein bound to filaments in the actin network, can depolymerize into either C_fast with probability s ₁ or C_slow with probability s ₂, where s ₂ = 1 − s ₁. The diffuse protein C_fast can become bound protein with spatially dependent rate $\mathrm {r_{C_{fast}}}(x)$, and C_slow can become bound with spatially dependent rate $\mathrm {r_{C_{slow}}}(x)$, where x is the distance from the leading edge. The diffuse component C_fast can become C_slow with a lifetime of τ _{C fast}, and the component C_slow can become C_fast with a lifetime of $\tau _{C_{\mathrm {slow}}}$.

The appearance profile measured by SiMS was assumed to be the sum of two separate profiles, $a_{\mathrm {{C_{fast}}}}(x)$ and $a_{\mathrm {{C_{slow}}}}(x)$, due to the fast and slow cytoplasmic pools as follows:

$$\displaystyle \begin{aligned} a(x)=a_{\mathrm{C}_{\mathrm{fast}}}(x)+a_{\mathrm{C}_{\mathrm{slow}}}(x). \end{aligned} $$

(20)

How the profile is split into two components is an assumption of the model. Generally, the speckle appearance profile can be fitted by a double exponential with two length-scales λ _short and λ _long. We define C _fast,∞ and C _slow,∞ to be the concentrations of C_fast and C_slow respectively at distances far from the leading edge of the cell. Using C _∞ = C _fast,∞ + C _slow,∞ to normalize concentrations, the constant K defines the magnitude of the association reactions:

$$\displaystyle \begin{aligned} a_{\mathrm{C}_{\mathrm{fast}}}(x)=KC_{\infty}\left(A_1^{\mathrm{C}_{\mathrm{fast}}}e^{-x/\lambda_{\mathrm{short}}}+A_2^{\mathrm{C}_{\mathrm{fast}}}e^{-x/\lambda_{\mathrm{long}}}\right) \end{aligned} $$

(21)

$$\displaystyle \begin{aligned} a_{\mathrm{C}_{\mathrm{slow}}}(x)=KC_{\infty}\left(A_1^{\mathrm{C}_{\mathrm{slow}}}e^{-x/\lambda_{\mathrm{short}}}+A_2^{\mathrm{C}_{\mathrm{slow}}}e^{-x/\lambda_{\mathrm{long}}}\right), \end{aligned} $$

(22)

where the dimensionless coefficients in Equations (21) and (22) satisfy $\mathrm {A}_1^{\mathrm {C}_{\mathrm {fast}}}+ \mathrm {A}_2^{\mathrm {C}_{\mathrm {fast}}}+\mathrm {A}_1^{\mathrm {C}_{\mathrm {slow}}} +\mathrm {A}_2^{\mathrm {C}_{\mathrm {slow}}}=1$.

In the examples we consider in this section, the lifetime distribution for protein speckles p(t) has weak dependence upon distance from the leading edge, within a range of a few μm [66, 91, 102]. It can be fitted with a single exponential as in Equation (2) where C ₂ = 0.

The bound protein profile, B(x) , can be calculated analytically using the function Y (x, x′) of Equation (4) to find the profile of bound protein B ₁(x) and B ₂(x) due to each of the diffuse species, C_fast and C_slow, respectively, such that B(x) = B ₁(x) + B ₂(x), where:

$$\displaystyle \begin{aligned} B_1(x)=\int_0^{\infty}Y(x,x')a_{\mathrm{C}_{\mathrm{fast}}}(x')dx', \ \ \ \ B_2(x)=\int_0^{\infty}Y(x,x')a_{\mathrm{C}_{\mathrm{slow}}}(x')dx'. \end{aligned} $$

(23)

The steady-state reaction diffusion equations that describe the system are as follows:

$$\displaystyle \begin{aligned} v_r \frac{\partial B(x)}{\partial x} =a(x)-d(x), \end{aligned} $$

(24)

$$\displaystyle \begin{aligned} D_{\mathrm{C_{fast}}} \frac{\partial^2 C_{\mathrm{fast}}}{\partial x^2}=a_{\mathrm{C_{fast}}}(x)-s_1 d(x)+\frac{1}{\tau_{\mathrm{C_{fast}}}}C_{\mathrm{fast}} (x)-\frac{1}{\tau_{\mathrm{C_{slow}}}}C_{\mathrm{slow}} (x), \end{aligned} $$

(25)

$$\displaystyle \begin{aligned} D_{\mathrm{C_{slow}}} \frac{\partial^2 C_{\mathrm{slow}}}{\partial x^2}=a_{\mathrm{C_{slow}}}(x)-(1-s_1) d(x)+\frac{1}{\tau_{\mathrm{C_{slow}}}}C_{\mathrm{slow}} (x)-\frac{1}{\tau_{\mathrm{C_{fast}}}}C_{\mathrm{fast}} (x). \end{aligned} $$

(26)

Parameters $D_{C_{\mathrm {fast}}}$ and $D_{C_{\mathrm {slow}}}$ are the diffusion coefficients for C _fast and C _slow respectively and d(x) is the detachment rate of bound proteins to the cytoplasm, which is found by solving Equation (24), given a(x) and B(x) from Equations (20) and (23). The parameter s ₁ is the probability for the bound protein to dissociate into C _fast. The concentrations far from the leading edge obey: $C_{\mathrm {slow},\infty }/C_{\mathrm {fast},\infty }=\tau _{C_{\mathrm {slow}}}/\tau _{C_{\mathrm {fast}}}$. Equations (20)–(26) can be solved numerically to find C _fast(x)/C _fast,∞ and C _slow(x)/C _slow,∞ given v _r, $\tau _{C_{\mathrm {fast}}}$, $\tau _{C_{\mathrm {slow}}}$, $D_{C_{\mathrm {fast}}}$, $D_{C_{\mathrm {slow}}}$, s ₁, and the parameters that define $a_{C_{\mathrm {fast}}}(x)$, $a_{C_{\mathrm {slow}}}(x)$, and p(t). The method used involves adding time dependence to Equations (25) and (26) and allowing them to relax for a sufficiently long time:

$$\displaystyle \begin{aligned} \frac{\partial C_{\mathrm{fast}}}{\partial t}=D_{\mathrm{C_{fast}}} \frac{\partial^2 C_{\mathrm{fast}}}{\partial x^2}-a_{\mathrm{C_{fast}}}(x)+s_1 d(x)-\frac{1}{\tau_{\mathrm{C_{fast}}}}C_{\mathrm{fast}} (x)+\frac{1}{\tau_{\mathrm{C_{slow}}}}C_{\mathrm{slow}} (x), \end{aligned} $$

(27)

$$\displaystyle \begin{aligned} \frac{\partial C_{\mathrm{fast}}}{\partial t}=D_{\mathrm{C_{slow}}} \frac{\partial^2 C_{\mathrm{slow}}}{\partial x^2}-a_{\mathrm{C_{slow}}}(x)+(1-s_1) d(x)-\frac{1}{\tau_{\mathrm{C_{slow}}}}C_{\mathrm{slow}} (x)+\frac{1}{\tau_{\mathrm{C_{fast}}}}C_{\mathrm{fast}} (x). \end{aligned} $$

(28)

A no-flux boundary condition is imposed at the leading edge.

4.2 Calculation of Rate Constants and Simulation

The local rates with which the cytoplasmic protein binds to the network from the fast and slow diffusing states (to be used in Monte Carlo particle simulations) can be found using the appearance profiles and the cytoplasmic protein profiles:

$$\displaystyle \begin{aligned} r_{C_{\mathrm{fast}}}={a_{C_{\mathrm{fast}}}(x)}/{C_{\mathrm{fast}}(x)}, \ \ r_{C_{\mathrm{slow}}}={a_{C_{\mathrm{slow}}}(x)}/{C_{\mathrm{slow}}(x)}. \end{aligned} $$

(29)

These are the reaction rates for C _fast to convert into B ₁ and for C _slow into B ₂. 2D Monte Carlo simulations of independent particles were performed using the method of Smith et al. [92] described previously. The simulation was initialized using the steady-state concentrations evaluated by Equations (27) and (28).

4.3 Application to Capping Protein Dynamics

In [62], the model of Section 4.1 was applied to capping protein, the lamellipodial dynamics of which had been studied in prior studies with both FRAP and SiMS, though in different cell systems. Kapustina et al. [46] analyzed FRAP data of fibroblast cells expressing EGFP-CapZ in a circular region of diameter 5 μm centered at 5 μm from the leading edge of the cell [100]. They fitted the recovery to a model that used Virtual Cell [70] with various components to find values for the diffusion coefficient of capping protein in the cytoplasm, D=5–10 μm²/s, and for its lifetime when bound to the actin network, τ = 10 s. These values are different to those measured with SiMS microscopy of XTC cells [66, 91] where capping protein was found to associate over an extended area of the lamellipodium, to have a slowly diffusing cytoplasmic pool with D ≈ 0.5 μm²/s and to have a shorter bound lifetime, τ ≈ 2s [66, 91]. While both studies show a short lifetime of bound capping protein compared to the lifetime of polymerized actin (Figure 1E), they indicate quantitatively different transport modes in the lamellipodia. One goal in [62] was finding out if the measured SiMS microscopy parameters from Miyoshi et al. can be used to fit the FRAP data from Kapustina et al. and to study the implications for the concentration profile of capping protein across the lamellipodia.

Two previously proposed possibilities for the reasons behind slow capping protein diffusion were considered: one being that capping protein is bound to severed actin oligomers, the other being that capping protein binds to the membrane. Monte Carlo simulations with bleaching of a 5 μm by 5 μm square region centered 5 μm from the leading edge were compared to the data of Kapustina et al. using a circular bleach region (this difference in shape has only a small effect on the recovery curve). In the simulations for capping protein below, the value for retrograde flow used was v _r= 0.03 μm/s [105].

4.3.1 Model Including Oligomers

The model with oligomers shown in Figure 3A,B is a specific case of the general model of Section 4.1. The motivation for this model is the suggested existence of short actin oligomers in the lamellipodium. If severed actin filaments are capped by capping protein, this could explain why 50% of capping protein has been observed in a slowly diffusing state with diffusion coefficient ≈ 0.5 μm²/s [91]. In this model C _fast represents capping protein heterodimers diffusing in the cytoplasm and C _slow represents capping protein heterodimers attached to the barbed end of an actin oligomer diffusing in the cytoplasm. The bound protein can only dissociate into capped oligomers, C _slow, that can either rebind to the network or become uncapped and convert to C _fast.

Fig. 3

Modeling FRAP for Capping Protein and Arp2/3 Complex in lamellipodium (reproduced with permission from [62]). (A) Diagram for model of capping protein including oligomers. (B) Cartoon for model of panel A. (C) Simulated steady-state concentration profiles for capping protein model for model in panel A. (D) Simulated FRAP curve of capping protein after bleaching a 5 μm×5 μm box situated 2.5 μm from the leading edge for model of panel A, compared to experimental data in [46]. (E) Diagram for model of capping protein with membrane binding. (F) Cartoon for model of panel B. (G) Simulated steady-state concentration profiles for capping protein model of panel E. (H) Same as panel D but for model of panel E. (I) Diagram for model of Arp2/3 complex with membrane binding. (J) Cartoon for model of panel I. (K) Simulated steady-state concentration profiles for model of panel I. (L) Simulated FRAP curve of Arp2/3 complex after bleaching a 2 μm× 4 μm box at the leading edge and monitored 0–1 μm and 1–2 μm from the leading edge, compared to experimental data in [52].

Both fast and slow diffusing species were assumed to be able to bind to the network, representing capping of free barbed ends and re-binding of oligomers to the lamellipodial network, respectively (Figure 3A,B,E,F). Since SiMS only measures the total appearance profile, an additional assumption in the model was how a(x) is split into $a_{C_{\mathrm {fast}}}(x)$ and $a_{C_{\mathrm {slow}}}(x)$. Since the total appearance profile of capping protein can be fit to a double exponential [62], the appearance rates were broken up such that $a_{C_{\mathrm {fast}}}(x)$ corresponds to the short length scale and $a_{C_{\mathrm {slow}}}(x)$ to the long length scale:

$$\displaystyle \begin{aligned} a_{C_{\mathrm{fast}}}(x)=KC_{\infty}A_1e^{-x/\lambda_{\mathrm{short}}}, \ \ \ \ a_{C_{\mathrm{slow}}}(x)=KC_{\infty}A_2e^{-x/\lambda_{\mathrm{long}}}, \end{aligned} $$

(30)

with A ₁ = 0.74, A ₂ = 0.26, λ _short = 2.0 μm, and λ _long = 8.65 μm. The function $a_{C_{\mathrm {fast}}}(x)$ accounts for the appearances due to C _fast close to the leading edge, whereas $a_{C_{\mathrm {slow}}}(x)$ accounts for the appearances due to C _slow that are distributed throughout the lamellipodium. Thus, the behavior of capping protein was assumed to follow the behavior of actin oligomer rebinding that contributes to a large fraction of actin speckle appearances at the back of the lamellipodium (Section 2.3).

Parameters in the model were calculated from prior experiments or their range estimated. The lifetime distribution of capping protein bound to the network can be fit with a single exponential with τ = 2.0 s [66]. The lifetime of the capping protein bound to the actin oligomer ($\tau _{C_{\mathrm {slow}}}$) is likely in the range of the lifetime of an actin oligomer, 5–30 s [92]. The diffusion coefficient of the slow component is $D_{C_{\mathrm {slow}}}$ = 0.5 μm²/s [91], and $D_{C_{\mathrm {fast}}}$ =2–5 μm²/s is expected which is comparable to the diffusion coefficient of actin monomers [61, 99]. The value of K that influences the ratio of cytoplasmic to bound protein was calculated to give an estimated ratio of cytoplasmic protein to bound protein 2.3 to 1 [62].

Scanning the model parameters within the range described in the preceding paragraph fits to FRAP data were obtained. The simulated FRAP was applied to a steady state initialized with the concentrations found after relaxing Equations (27) and (28) in time. Figure 3C shows the steady-state concentration profiles using K = 0.5 s⁻¹, $D_{C_{\mathrm {fast}}}$ = 2.0 μm²/s , $D_{C_{\mathrm {slow}}}$ = 0.2 μm²/s, v _r= 0.03 μm/s, τ = 2.0 s, and $\tau _{C_{\mathrm {slow}}}$ = 13.0 s. In order to obtain good fits to the experimental FRAP data for capping protein, the lifetime $\tau _{C_{\mathrm {slow}}}$ needs to be maximized, and the diffusion coefficient $D_{C_{\mathrm {fast}}}$ needs to be minimized, within the range of values described above and the range that gives nonnegative concentration profiles in the model equations. Figure 3D shows the recovery of the intensity in the bleached region along with the recovery in Kapustina et al. The recovery curve for $D_{C_{\mathrm {slow}}}$ = 0.5 μm²/s is an overall good fit to the experimental curve; however, the initial recovery is more rapid compared to experiment. The fit can be improved using $D_{C_{\mathrm {slow}}}$ = 0.2 μm²/s [62].

The above results show that parameters measured with SiMS can be used to model the FRAP data in [46], using a smaller diffusion coefficient $D_{C_{\mathrm {slow}}}$ and faster dissociation time τ compared to [46]. The diffusion of long-lived oligomers out of the bleached region contributes to making the recovery slower initially and a value $\tau _{C_{\mathrm {slow}}} \approx$ 13 s is needed for a good fit. This is in agreement with the fact that slowly diffusing speckles can be tracked for a few seconds and thus the lifetime of the slowly diffusing capping protein is likely in the range of 5–30 s [91]. Even though the dissociation time τ = 2 s is small compared to the measured FRAP half-time, the bound species is a small fraction of the total amount.

4.3.2 Model with Membrane Binding

Another way of accounting for slowly diffusing capping protein is considering that capping protein binds and diffuses along the membrane [91]. Membrane binding can occur through a fast-diffusing state in the cytoplasm or by membrane-induced uncapping of capped barbed ends. The model shown in Figure 3E,F is another possible mechanism of why capping protein dissociates so frequently from the actin network and diffuses slowly. CARMIL is a membrane bound protein complex that also binds capping protein and may account for the very short lifetime of capping protein bound to the actin filament [23, 27, 28]. In this model only fast diffusing cytoplasmic protein is able to become bound (representing capping of barbed ends) so that the appearance rate is:

$$\displaystyle \begin{aligned} a(x)=a_{C_{\mathrm{fast}}}(x)=KC_{\infty}\left(A_1e^{-x/\lambda_{\mathrm{short}}}+A_2e^{-x/\lambda_{\mathrm{long}}}\right), \end{aligned} $$

(31)

with A ₁ = 0.74, A ₂ = 0.26, λ _short = 2.0 μm, and λ _long = 8.65 μm. The bound protein can dissociate into either C _fast or C _slow and the parameter s ₁ is the probability of dissociating into C _fast. The fast diffusing capping protein can convert to slow with lifetime $\tau _{C_{\mathrm {fast}}}$ and slow can become fast with lifetime $\tau _{C_{\mathrm {slow}}}$. The model in Figure 3E, F is another specific case of the general model.

The model with membrane binding (Figure 3E) has more parameters compared to the model with oligomers (Figure 3A).

The new parameters are the lifetimes $\tau _{C_{\mathrm {fast}}}$, $\tau _{C_{\mathrm {slow}}}$, and the dissociation probability s ₁. As mentioned in Section 4.3.1, the lifetime of the slowly diffusing capping protein is likely in the range of 5–30 s. It was assumed that $\tau _{C_{\mathrm {fast}}}$ = $\tau _{C_{\mathrm {slow}}}$ so that C _fast and C _slow each correspond to 50% of the concentration far from the leading edge [91]. Figure 3G shows a concentration profile generated with K = 0.435 s⁻¹, $D_{C_{\mathrm {fast}}}$= 2.0 μm²/s, $D_{C_{\mathrm {slow}}}$= 0.5 μm²/s, v _r = 0.03 μm/s, τ= 2.0 s, $\tau _{C_{\mathrm {fast}}}$ = 5.0 s, $\tau _{C_{\mathrm {slow}}}$ = 5.0 s, s ₁=0.1.

Parameters could be adjusted for the second model to fit the experimental FRAP data. The simulated recovery curves are shown in Figure 3H, along with the experimental data. Both simulated curves with $D_{C_{\mathrm {slow}}}$ = 0.1 μm²/s and $D_{C_{\mathrm {slow}}}$= 0.5 μm²/s fit the data; however, the smaller diffusion coefficient allows for a better fit. Similar to the model with oligomers, $D_{C_{\mathrm {fast}}}$ needs to be on the lower range of the physically plausible values 2–5 μm²/s . Parameter s ₁ needs to be small compared to unity, otherwise the bleached region recovers too quickly and none of the other parameters are able to slow the recovery down enough to capture what occurs in the experiment. Keeping $\tau _{C_{\mathrm {fast}}}$ = $\tau _{C_{\mathrm {slow}}}$, variation of these two parameters together showed that they also need to be in the range of a few seconds [62].

In conclusion, obtaining a good fit drives this model to a similar kinetic scheme as the model with oligomers, with the majority of the bound protein dissociating into slowly diffusing protein.

4.3.3 Comparison of Two Models for Capping Protein Turnover

The pool of slowly diffusing protein is important to fit FRAP recovery with half-time on the order of 10 s, using a bound lifetime of 2 s. Retrograde flow contributes little to FRAP since the distance traveled by retrograde flow during recovery is small compared to the size of the bleached region. Since both models are driven to similar kinetic transition rates, it is hard to distinguish between them using further FRAP data of either the back or front of the lamellipodium. A clearer difference between the two models can be seen in lamellipodium photoactivation simulations with the same parameters as for the FRAP data [62]. Both models demonstrate significant concentration gradients of the two diffuse species across the lamellipodium. This prediction of concentration gradients could be tested in future experiments. The origin of this gradient is mainly the local production of slowly diffusing capping protein close to the leading edge. The inward flux of the slowly diffusing population plus the retrograde flow of the bound species must be balanced by the diffusive flux of the fast species at steady state.

4.4 Application to Arp2/3 Complex Dynamics

Both FRAP and SiMS microscopy experiments have been performed to study the kinetics of Arp2/3 complex in the lamellipodium. In FRAP studies by Lai et al. [52], the bleached region was a 2 μm by 4 μm box positioned at the leading edge of a B16-F1 melanoma cell. Recovery was faster at the leading edge of the cell than it was away from the leading edge. While this has been interpreted to suggest that Arp2/3 complex forms branches within a very narrow region close to the leading edge, SiMS experiments using XTC cells (tagging the p40 and p21 subunits) by Miyoshi et al. [66] show distributed speckle appearances 1 μm away from the leading edge and further, and an exponential distribution of speckle lifetimes with τ = 18 s.

McMillen and Vavylonis [62] used modeling to (i) check if the FRAP recovery observed in Lai et al. [52] is consistent with the distributed appearances in Miyoshi et al. [66], and (ii) explore the implications for the concentration profiles of the diffuse species. FRAP of lamellipodia of B16-F1 melanoma cells [52] has similar qualitative features to FRAP of XTC cells (Figure 1) as well as PA of neuronal cells (Figure 2). The simulations below used a profile with distributed appearances that is narrower compared to the profile measured in XTC cells, which have wider lamellipodia compared to the B16-F1 melanoma cells. This appearance profile was calculated to give an Arp2/3 complex concentration profile that matches the concentration profile of the B16-F1 melanoma cells [62].

Using SiMS microscopy, Millius et al. [65] suggested that some Arp2/3 complexes bind to the WAVE complex on the cell membrane of XTC cells and perform a slow diffusion prior to incorporation of the actin network, while other Arp2/3 complexes are recruited directly from the cytosol. Millius et al. observed slowly diffusing speckles of Arp2/3 complex components within a few μm from the leading edge.

The study in [62] thus considered a model with membrane binding of the Arp2/3 complex (Figure 3I,J). The two diffuse species in this model represent Arp2/3 complex in the cytoplasm, C _fast, and bound to the membrane, C _slow. The bound Arp2/3 complex dissociates into C _fast only, representing debranching and dissociation of the Arp2/3 complex from the pointed end. This occurs with the detachment rate d(x) corresponding to bound lifetime τ. This lifetime may include Arp2/3 complex attachment without branch formation, as observed in single molecule in vitro experiments where bound Arp2/3 complex has bound lifetimes in the range 2–200 s [90].

Binding to the membrane was assumed to occur close to the leading edge with a spatially dependent rate $k (x) = k_m e^{-x/ \lambda _m}$ defined by parameters λ _m and k _m. This was achieved in the simulations by using a spatially dependent $\tau _{C_{fast}}$. Spontaneous unbinding occurs with lifetime $\tau _{C_{\mathrm {slow}}}$. The appearance profile describing association of membrane-bound Arp2/3 complex to the actin network is given by

$$\displaystyle \begin{aligned} a (x) = A_1 e^{-x/\lambda_{\mathrm{short}}} + A_2 e^{-x/\lambda_{\mathrm{long}}} \end{aligned} $$

(32)

with A ₁ = 0.49, A ₂ = 0.51, λ _short = 0.08 μm, and λ _long = 0.43 μm. Using an estimated retrograde flow rate v _r = 0.04 μm/s in [52], $D_{C_{\mathrm {slow}}} = 0.6~\upmu$m/s² (the estimate in Millius et al. [65]) and assuming membrane binding occurs close to the leading edge, λ _m = 0.2 μm, leaves $D_{C_{\mathrm {fast}}}$, K, $\tau _{C_{\mathrm {slow}}}$ and k _m as undetermined parameters. Knowing the larger size of the Arp2/3 complex as compared to actin monomers and capping protein, a diffusion coefficient of 2–6 μm²/s is anticipated.

In the steady-state profile in Figure 3K , D _C = 3 μm²/s , K = 6.0 s⁻¹, $\tau _{C_{\mathrm {slow}}} = 20$ s, and k _m = 40 s⁻¹. With these parameters, the bound protein is sharply peaked close to the leading edge while the fast diffusing protein is small compared to the bound species and slightly depleted at the leading edge.

The model fit the experimental FRAP data by Lai et al. [52], which shows faster recovery at the lamellipodium front as compared to the back. The recovery of simulated FRAP is quantified in Figure 3L where the front recovery curve is taken 0–1 μm from the leading edge, and the back recovery curve is taken 1–2 μm from the leading edge as in Lai et al. [52]. The recovery at the back has a small initial increase due to the diffusion of the cytoplasmic component, followed by a slower recovery. This slower recovery is driven by binding at the back of the lamellipodium and retrograde flow that brings labeled subunits from the cell front. In order to fit the experimental FRAP data the value of K has to be sufficiently high to keep the bound to cytoplasmic ratio sufficiently smaller than unity; otherwise the back of the lamellipodium recovers faster than in experiments. Similarly, decreasing coefficient k _m to a value where the concentration of slowly diffusing species becomes a small fraction of the bound concentration gives a better fit to the FRAP curve at the back. The recovery is also affected by the diffusion coefficient of the fast diffusing species. Values above $D_{C_{\mathrm {fast}}} = 2~\upmu$m²/s give a good fit to the experimental FRAP data.

The results of Figure 3K,L suggest that the diffusing population is a small fraction of the bound. Lewalle et al. [56] also performed FRAP of Arp2/3 complex in lamellipodia and found recovery throughout the lamellipodia pronounced close to the leading edge, consistent with the assumptions in [62]. The fact that the concentration of Arp2/3 complex increases by about 8-fold after stimulation in XTC cells [87] is consistent with the existence of a small fraction of fast-diffusing Arp2/3 complex (presumably the only species present prior to lamellipodia stimulation). Inspection of the movies in Millius et al. [65] indicates however that the number of slowly diffusing speckles is comparable to the bound population. While the slowly diffusing Arp2/3 complex speckles may also represent Arp2/3 complex bound to debranched actin oligomers (not considered here as a separate species), such a pool would also need to be as small for the model to reproduce the FRAP data. This motivates further studies to investigate if the fraction of diffusible Arp2/3 complex varies by a large factor among cell systems and/or during different stages of stimulation of the same cell.

4.5 Discussion

In this section we described how modeling was used to calculate concentration profiles of capping protein (Figure 3C,G) and Arp2/3 complex (Figure 3K) based on prior SiMS and FRAP data. The predicted gradients in the diffuse pool will have implications on the behavior of the lamellipodium when perturbed from steady state, for example during the stimulation of a protrusion by increase of free barbed end concentration close to the leading edge [62]. Diffusion limitations of capping protein or Arp2/3 complex towards the leading edge could become important upon protrusion initiation.

In the results of Figure 3, the capping protein distribution is broader than that of Arp2/3 complex but both are narrower than F-actin (Figure 1). Other studies using fluorescence speckle microscopy however suggest different length scales for each component with capping protein, Arp2/3 complex, and F-actin having increasingly broader concentration profiles [44]. Future work should examine if these differences are cell-type specific.

Hu and Papoian [39, 40] used a stochastic simulation model that includes physical and chemical interactions for actin, Arp2/3 complex, and capping protein in the lamellipodium to model protrusions. They only allow Arp2/3 complex-mediated activation branching very close to the membrane with diffusion coefficient 20 μm²/s for all species, larger than what we used here for the fast and slow diffusing pools. One of the findings in Hu and Papoian is a significant dependence of protrusion dynamics on the concentrations of capping protein and Arp2/3 complex. Since cytoplasmic concentration gradients result for slower values of the diffusion coefficients, this effect would provide an additional influence on protrusion dynamics.

The method presented in this section could be generalized to study the diffusive dynamics of other lamellipodia regulators that have been studied with SiMS, including cofilin and AIP1 [97], which collaborate in actin filament severing, VASP [66], and WAVE [65].

5 Model of Lamellipodium Protrusion and Retraction Driven by Fluctuations in Actin Polymerization

5.1 Motivation from Experiment

We now return to the topic of lamellipodial protrusion and retraction of XTC cells mentioned in Section 1.2. In these cells waves of protrusion were accompanied by waves of LifeAct-labeled F-actin accumulation along the lamellipodium [87] (Figure 4B,C,D). This phenomenon belongs to the general class of cellular actin waves [43] and the regularity of protrusions and retractions during cell spreading indicates a process that can be described by a coarse-grained mathematical model.

Fig. 4

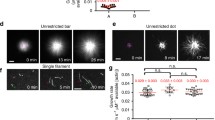
Experimental observations of leading edge protrusion and retraction (reproduced with permission from [87] and panel C from [86]). (A) An XTC cell expressing actin marker LifeAct-mCherry. (B) Kymograph of segment at leading edge of cell in panel A. F-actin polymerized near the leading edge into the cell via retrograde flow, resulting in diagonal striping of kymograph. (C) Distribution of the standard deviation of the radial membrane position at a fixed angular position for three cells. (D) Leading-edge velocity (with respect to fixed substrate) versus angle and time for cell in Figure 1G of [87]. Positive (negative) velocities indicate protrusion (retraction). The retrograde flow speed for this cell was 74 ± 3 nm/s. (E) Average correlation coefficients for leading-edge velocity autocorrelation, LifeAct-mCherry autocorrelation, and LifeAct-mCherry-velocity cross correlation, versus time at a fixed angular position.

The magnitude of protrusions and retractions is shown by the distribution of the standard deviation in Figure 4C. The standard deviation was measured along the radial direction in 1-degree intervals along the entire arc-length of the cell. The protrusion velocity was anti-correlated with the total local F-actin concentration measured by integrating LifeAct intensity over a 5 μm distance into the cell (Figure 4E). The time-dependent cross-correlation function (Figure 4E) showed that, on average, the fastest protrusion (retraction) speeds occurred just 10 s after a minimum (maximum) of integrated F-actin intensity at a given position along the arc-length of the cell.

The constant retrograde flow and fluctuating actin polymerization near the membrane in XTC cell lamellipodia is evident in the kymograph of Figure 4B, in which LifeAct forms diagonal lines of high intensity starting at the cell edge. These indicate an F-actin network that forms near the edge of the cell and processes into the cell as time increases to the right. Alternating high and low intensity over time in Figure 4B points to changing actin polymerization. Net actin polymerization near the membrane, as evidenced by increasing intensity, occurs during protrusion, although the total intensity within the lamellipodium is greatest during retraction, consistent with the anti-correlation of Figure 4E [87]. The notion that fluctuations in actin polymerization can drive such dynamics is further supported by the experimental evidence that other cell types treated with blebbistatin continue to protrude and retract periodically, although the period of oscillations may change [11, 30, 106].

5.2 One-Dimensional Model with Excitable Actin Dynamics

The observed dynamics are suggestive of excitations driven by noise. Excitability typically involves the interaction between an activator and an inhibitor: in an excitation, an activator species self-recruits rapidly; this activator in turn recruits an inhibitor that causes the activator to slowly dissipate [63]. Ryan et al. [87] speculate that the anticorrelation of leading-edge velocity with total actin intensity suggests that F-actin acts as an inhibitor. Likely mechanisms for this inhibition include the formation of actomyosin bundles [5] and adhesions [3] and accumulation of mechanical tension [45, 77]. Many molecules are activator candidates: actin polymerization can be triggered by the Scar/WAVE and WASp proteins that self-recruit on the cell membrane to activate the Arp2/3 complex [36, 76, 79]. Once activated, the Arp2/3 complex generates new barbed ends by nucleating branches off preexisting filaments, thought to lead to autocatalytic dendritic nucleation [71, 93]. Severing of growing filaments could also contribute to diffusive autocatalytic generation of barbed ends [66, 74] through transient association of diffuse cofilin and AIP1 with F-actin [97]. Formin-mediated nucleation of new filaments is another possible activation mechanism [35, 107].

5.2.1 Model that Reproduces Wavelike Propagation

In the one-dimensional model of Ryan et al. [87], the concentrations of a diffusible activator, A(x, t), free barbed ends, B(x, t), and F-actin, F(x, t), are calculated at different positions x along the leading edge over time (Figure 5A). The lamellipodium is modeled in one dimension, each coordinate representing a slice along the arc-length of the leading edge. In this model it is assumed that protrusions and retractions stem from underlying concentration fluctuations in the local actin network and cell membrane displacement is not explicitly considered. Denoting rate constants by k and ρ, the equations governing the concentrations are:

$$\displaystyle \begin{aligned} \frac{\partial A}{\partial t}=(\rho_0+\rho_2A^2)e^{-F/F_S}-k_A^-A+D_A\nabla^2A+\sigma(x,t),\vspace{-3pt} {} \end{aligned} $$

(33)

$$\displaystyle \begin{aligned} \frac{\partial B}{\partial t}=k_B^+A-k_B^-B,\vspace{-3pt} {} \end{aligned} $$

(34)

$$\displaystyle \begin{aligned} \frac{\partial F}{\partial t}=k_F^+B-k_F^-F. {} \end{aligned} $$

(35)

The first term on the right-hand side (rhs) of Equation (33) allows for spontaneous accumulation as well as nonlinear self-recruitment of the activator. A simple quadratic dependence on A is chosen (see Section 5.2.2 below). When F-actin exceeds saturation concentration, F _s, the activator on-rate is reduced. This is the negative feedback in Figure 5B. The second term on the rhs in Equation (33) represents deactivation. Diffusion of the activator (third term on the rhs) along the membrane couples neighboring sites and allows propagation of actin dynamics along the leading edge. The last term in Equation (33) is white noise, $< \sigma (x,t)\sigma (x',t') > = \sigma _0^2 \delta (t-t') \delta (x-x')$ and represents concentration fluctuations [32, 104] that generate excitations by perturbing the system out of its stable state (see Section 5.2.3). Equation (34) describes accumulation of free barbed ends as a result of the activation process. Rate constant $k_B^+$ describes how fast the activator generates new barbed ends. Rate constant $k_B^- \approx 0.4\text{--}8$ s⁻¹ is the rate of free barbed end loss through capping by capping protein [79]. Equation (35) describes change of F-actin as a result of polymerization at free barbed ends and spontaneous disassembly.

Fig. 5

One-dimensional model for an XTC cell leading edge (panels A, B reproduced with permission from [86] and C, D from [87]). (A) The model includes F-actin, F, activator, A, and free barbed ends, B, along the arc-length of the membrane. (B) Reaction network diagram. Assembly of F is promoted by the autocatalytic activator A which generates free barbed ends. Accumulation of F inhibits A. (C) Simulation results, F-actin concentration vs arc-length and time. (D) Correlation coefficients vs time for free barbed end autocorrelation, F-actin autocorrelation, and cross-correlation between B and F-actin at a given arc-length.

Since the capping rate $k_B^-$ is much faster than the frequency of the protrusion and retraction events, generation of barbed ends must be fast enough such that B responds to changes in A quickly. This leads to $B\approx k_B^+ A/k_B^-$ and allows Equation (33) to be rewritten as follows:

$$\displaystyle \begin{aligned} \frac{\partial B}{\partial t}=(r_0+r_2B^2)e^{-F/F_S}-k_A^-B+D_A\nabla^2B+s(x,t). {} \end{aligned} $$

(36)

Here, unknown rate constant $k_B^+$ is absorbed into the new rate constants r ₀ and r ₂ and into the amplitude of the noise that is now s ₀. Equations (35) and (36) form a closed system in terms of B and F. Details on selecting model parameters are given in Section 5.2.4.

Numerical integration of the model produces spikes of free barbed end concentration, followed by spikes in local F-actin concentration. Figure 5C shows that the model captures the wave-like propagation across sections of the membranes arc-length as well as the magnitude and timescale of the actin fluctuations of Figure 4D.

The F-actin autocorrelation function calculated using the model, shown in Figure 5D, matches the experimental result of Figure 4E. A characteristic feature of the cross-correlation function between B and F is that spikes of B precede those of F, demonstrated by the positive shift of the cross-correlation peak to the right of the origin by approximately 25 s. Without the noise term in Equation (36), for the reference parameter values, point excitations propagate laterally along the membrane before returning to a uniform stationary state (Figure 6A,B). Addition of noise to this steady-state system excites actin randomly along the membrane, so that excitations combine into structures similar to those seen in experiment.

Fig. 6

Model response to point excitation and stability analysis predicts characteristics of model solutions (reproduced from [87]). (A) Free barbed end concentration, generated by localizing noise, s(t) = 0.1 μM s ⁻¹, at a single point (at 20 μm) along the membrane for 1.5 s. Simulations were run with the same parameters as Figure 5, except the noise term was zero outside the region described above. Excitations spread from the region at which noise was applied with a speed ∼ 0.17 μm/s. This is similar to the speed of protrusion propagation in Figure 4D. In the presence of multiple sources of noise, excitations combine into transient wave-like patterns. (B) F-Actin concentration corresponding to the free barbed end concentration shown in A. (C) Results of linear stability analysis as function of r ₀ and r ₂ for wave number q = 0. The black star indicates the exact parameters used in Figure 5. Case II (dark gray): unstable oscillatory solutions; Case III (light gray): stable oscillatory solutions. (D) Damping ratio, calculated for regions of parameter space within Case III of panel C (Case II region shown in dark gray). (E) Similar to panel D but displaying period τ for both Case II and Case III solutions.

5.2.2 Choice of Nonlinear Terms

The negative feedback in Equations (33) and (36) uses an exponential cutoff, $e^{-F/F_s}$ that prevents F-actin from accumulating in amounts that far exceeds F _s. Excitations away from steady state are driven by the autocatalytic term ρ(B) = r ₀ + r ₂ B ² in Equation (36). A quadratic was chosen for the following reason. During an excitation, the concentration of actin near the leading edge approximately doubles (see Figure 4 and 5). A change of similar magnitude is anticipated in the concentration of free barbed ends. Now the term $\rho (B) e^{-F/F_s}$ should have approximately the same value at both steady state, B = B ^∗ and F = F ^∗, and at the instant in time when the free barbed end concentration is at a maximum, B ≈ 2B ^∗ and F = αF ^∗. Since B and F are out of phase leads one to estimate 1.1 < α < 1.5. Assuming a power law, ρ(B) ∼ B ⁿ, this would require 2 ≤ n ≤ 5. Ryan et al. [87] chose the smallest integer exponent consistent with this requirement. The constant term r ₀ in ρ(B) prevents unphysical fixed points with very small concentrations of free barbed ends. This term accounts for filaments created by spontaneous nucleation rather than through autocatalytic feedback.

5.2.3 Linear Stability Analysis

Linear stability analysis can be performed on the model described by Equations (35) and (36) without the noise term in Equation (36). Parameters can be chosen such that the system is in a stable steady-state region, close to the boundary of an unstable region. The addition of a noise term then transiently perturbs the stable state of the system, generating spontaneous excitations.

Stability analysis is performed around a homogeneous steady state B = B ^∗ and F = F ^∗. Fixed points B ^∗ and F ^∗ are defined by the nullclines of a homogeneous system (i.e., no dependence on arc-length distance) u(B ^∗, F ^∗) = v(B ^∗, F ^∗) = 0 where

$$\displaystyle \begin{aligned} u(B,F)=(r_0+ r_2B^2 ) e^{-F/F_s}-k_A^- B, {} \end{aligned} $$

(37)

$$\displaystyle \begin{aligned} v(B,F)=k_F^+ B-k_F^- F. {} \end{aligned} $$

(38)

The fixed points can be found numerically. While Equations (37) and (38) can have up to 3 fixed points, for parameter values in [87], there is a single fixed point. Defining b(x, t) = B(x, t) − B ^∗ and f(x, t) = F(x, t) − F ^∗, considering sufficiently small deviations from the fixed point, and Fourier transforming x → q, it is obtained from Equations (35) and (36) (without the noise term):

(39)

The characteristic equation is λ ² −TrJλ + detJ = 0. Solving this for λ one finds two wave-number dependent eigenvalues. These eigenvalues can be used to distinguish between parameter sets based on the type of behaviors they elicit within the model. These behaviors can be separated into three distinct cases (note: the remaining of this subsection below corrects a mislabeling in the Supplementary Material of [87]): (I) both eigenvalues real, (II) both eigenvalues complex with positive real components that give unstable solutions to the linearized equation, and (III) both eigenvalues complex with negative real part that generate stable solutions. Whether eigenvalues are real or complex is determined by the sign of Tr(J)²–4det(J).

Case I. :

Two real eigenvalues occur when Tr(J)² − 4det(J) > 0. Real λ indicate stable or unstable fixed points, depending on the sign of λ.

Case II. :

Complex eigenvalues with positive real components result from parameter sets in which Tr(J)² − 4det(J) < 0 and Tr(J) > 0. In this case the system has an unstable solution fixed point. However, because Equations (35) and (36) give bounded solutions, the solution would evolve into a limit cycle, in which the system exhibits oscillatory behavior. The period of these oscillations, estimated from the linear stability analysis is τ = 2π∕Im(λ).

Case III. :

Complex eigenvalues with negative real components. These solutions fulfill Tr(J)² − 4det(J) < 0 and TrJ < 0. Small q more easily satisfy this condition compared to larger q. If perturbed, such a system will relax back to the stable solution in an oscillatory manner with period τ = 2π∕Im(λ). The relaxation rate is described by the dimensionless damping ratio $\zeta =\mathrm {Tr}J/2\sqrt {\mathrm {det}(J)}$.

5.2.4 Selection of Parameters

In [87], the values of $k_F^+$ and $k_F^-$ were taken from experiment. Five constraints were used to determine the values of r ₂, r ₀, F _S, $k_A^-$, and D _A (Table 2). The first two constraints required fixed points with B ^∗≈ 0.4 μM and F ^∗≈ 1500 μM. The value of B ^∗ was chosen because within a band of width d ∼ 2 μm near the leading edge the concentration of free barbed ends is approximately 1 μM [81]. In this model, which does not distinguish distance from the leading edge, this corresponds to a barbed end concentration 1μM × d∕w = 0.4 μM, where w ∼ 5 μm is the width of the lamellipodium. The third condition required that the system is in a region of parameter space in which relaxation to steady state occurs with underdamped oscillations, such that the q = 0 case of the linear stability analysis lies in a Case III region, but not far from a Case II region. The fourth condition was that the period of oscillation is ∼ 130 s, as observed experimentally. Finally, the diffusion coefficient of the activator was selected to match the width of the spatial correlation function found in experiment.

Table 2 Parameter table for one-dimensional model of lamellipodium protrusion and retraction.

Figure 6C shows linear stability diagrams for q = 0 as a function of two model parameters, r ₀ and r ₂. These two parameters that are important in controlling the response of the system to stimulation of polymerization (last paragraph in this section) need to be adjusted as they are not directly determined from prior experiments. The star indicates the reference parameter set. Figure 6D displays the damping ratio, ζ as a function of the same parameters as in Figure 6C for q = 0. The damping ratio approaches zero close to the region of Case II. Larger values of r ₂ increase the strength of the nonlinear positive feedback and bring the system from a stable (Case III) towards an unstable (Case II) region (Figure 6C). Increase of r ₀ results in increased damping ζ, thus the value of r ₂ must exceed an r ₀-dependent threshold for ζ to become sufficiently low. Figure 6E displays the period τ as a function of the same parameters as in Figure 6C for q = 0, which is less sensitive to changes in r ₂ compared to r ₀.

Selecting the value of the diffusion coefficient of the activator, D _A, required that the damping ratio ζ(q) increases to ∼ 1 at a wavenumber q ≈ 1 μm⁻¹. Activator diffusion coefficient of 0.1 μm²/s fulfills this and reproduces a width for the spatial correlation function similar to experiment (full-width-half maximum approximately 5.2 μm). A decrease to D _A = 0.05 μm²/s results in a full-width-half-maximum of 3.4 μm, while an increase to D _A = 0.4 μm²/s results in a full-width-half-maximum of 8.8 μm.

Short wavelengths are more strongly damped compared to longer wavelengths. For the reference parameters values, the system switches from an underdamped regime (Case III) to an overdamped case (Case I) at a wavenumber q = 0.97 μm⁻¹.

5.2.5 Arp2/3 Complex as Activator and Cell Response to Stimulus

Arp2/3-complex-mediated dendritic growth is autocatalytic: nucleated branches act as nuclei for further branches. Could the Arp2/3 complex be the activator species of the model? Experiments with fluorescently labeled components of the Arp2/3 complex in [87] showed that it accumulates in bursts along the leading edge. These bursts precede maxima of total F-actin amount, indicating a possible role for Arp2/3 complex in the activation process. However, Ryan et al. [87] argued that it is unlikely for it to be the only activator because lateral spreading of Arp2/3 complex-mediated branching would be too slow to cause the observed traveling waves of protrusion: the effective diffusion coefficient calculated by a branching mechanism is 10 times smaller (D = 0.01 μm²/s) than the estimated D value for the activator species. These numbers support the additional involvement of diffuse proteins such as small GTPases, Scar/WAVE and WASp, and PIP3.

A general feature of the model with excitable dynamics is the synchronized response to a sudden global perturbation. In [87], this was tested by exploring the ability of the model to capture response to chemical stimulants. After hours of remaining on slides, protrusions and retractions subside in XTC cells. Introduction of fetal calf serum (FCS) restores the protrusions and retractions similar to the early stages after introduction to the slide. Figure 7A shows the leading edge of a cell expressing p21-EGFP (a protein in the Arp2/3 complex) and LifeAct-mCherry that is stimulated with FCS at 200 s. The increase in p21-EGFP and LifeAct-Cherry intensity after the addition of FCS is quantified in Figure 7B. The model can capture the FCS response through a sudden increase in rate r ₀ and r ₂ (Figure 7C). This change reproduces the experimental behavior, most notably the out-of-phase transient oscillations in Arp2/3 complex and F-actin at late times after stimulation. We note other studies in Dictyostelium response to cAMP have also been interpreted as an indication of excitability [104].

Fig. 7

XTC cell response to FCS and comparison to the model (reproduced with permission from [87]). (A) Montages of leading edge of cell expressing p21-EGFP and LifeAct-mCherry stimulated by FCS at 200 s. The cell had been plated for 4 h. Intensity increases are evident after stimulation. Bar: 5 μm. (B) Intensities of p21-EGFP and LifeAct-mCherry averaged over all angles vs time. (C) Results of model showing concentrations of the free barbed end and F-actin concentrations, averaged over arc-length. Rate constants were functions of time: r _o(t) = 1 μMs⁻¹ + 24 μMs⁻¹ H(t), r ₂(t) = 1 μMs⁻¹ + 624 μMs⁻¹ H(t). Here H(t) = Θ(t − 250s)t ³∕(T ³ + t ³), where T = 220 s and Θ is the step function.

5.3 Two-Dimensional Model of Lamelipodial Protrusions and Retractions

The one-dimensional model of actin accumulation along the arc-length of the cell described above did not address the movement of the cell membrane. In [86] the model was extended into two dimensions. This enabled two-dimensional aspects of XTC lamellipodia to be captured such as the extent and profile of XTC protrusions as well as F-actin concentration versus distance from the leading edge.

As mentioned in Section 2, F-actin assembly is distributed throughout the lamellipodium, and does not occur solely where actin filaments touch the cell membrane. A 2D model of fluctuations in actin polymerization would have to account for the time-variation of appearance rate $a(y)=A_1e^{-y/\lambda _1}+A_2e^{-y/\lambda _2}$ (measuring the rate of new speckle appearance as function of distance from the leading edge), as well as the variations in speckle lifetime (note: unlike Equation (1), y is the direction into the cell). Ryan et al. [86] made a few simplifying approximations. First, they assumed that all the basal speckle appearance events are due to recycling oligomeric actin that break off and reassemble at the back of the lamellipodium [92]. Second, the effective lifetime of F-actin in lamellipodia was approximated by a single exponential with a characteristic time $1/k_F^-$ = 100 s. This lifetime is longer than the speckle lifetime due to several dissociation and local recycling events. In this model, fluctuations in actin polymerization arose from fluctuations in the polymerization rate very close to the membrane of the leading edge (i.e., they represent fluctuations of the amplitude of the λ ₁ term in Equation (1)). This would be consistent with the assumption of a slowly diffusing membrane-bound activator.

5.3.1 The Model

The leading edge is along the x-axis, with the negative y-axis directed into the cell (neglecting the curvature associated with the shape of the whole cell). The displacement of the membrane along the y-axis is h(s, t), where s is arc-length across the membrane, and, approximately, s ≈ x. Periodic boundary conditions are applied along the x-axis after a total width 20 μm. The F-actin network in the lamellipodium is assumed to be a rigid network with sufficiently large modulus to be practically incompressible, consistent with the retrograde flow in the lamellipodium of XTC cells being approximately constant through protrusion and retraction cycles [87]. Computer simulations of the model were implemented on a 40 μm wide and 20 to 40 μm tall system. Concentrations were calculated on a lattice grid with membrane movement allowed on a continuum. Results were obtained after an equilibration period.

Barbed-End and F-Actin Concentrations

Free barbed ends of concentration B(x, t) are generated by an autocatalytic membrane-bound activator with concentration A(x, t). The accumulation of the activator is damped as a result of F-actin polymerization at the lamellipodium near the given arc-length position, similar to the 1D model. Random fluctuations in activator concentration can generate excitations by perturbing the system out of its stable state [32, 63, 87, 104]. Denoting rate constants by symbols k and r, and σ′ as noise obeying Gaussian statistics with zero mean, the equations are:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{\partial A (x,t)}{\partial t}&\displaystyle =&\displaystyle \left[r_0^{\prime}+r_2^{\prime}A(x,t)^2\right]e^{-\int_{-\infty}^{h(x,t)}F(x,y,t)/F_{sat}dy}-k_A^-A(x,t) \\ &\displaystyle &\displaystyle +D_A\frac{\partial^2 A(x,t)}{\partial x^2}+\sigma'(x,t), {} \end{array} \end{aligned} $$

(40)

$$\displaystyle \begin{aligned} \frac{\partial B(x,t)}{\partial t}=k_B^+A(x,t)-k_B^-B(x,t), {} \end{aligned} $$

(41)

$$\displaystyle \begin{aligned} \frac{\partial F(x,y,t)}{\partial t}=\gamma_{pol}(x,t)k_F^+B(x,t)\delta[y-h(x,t)]-k_F^-F(x,y,t)+v_R\frac{\partial F(x,y,t)}{\partial y}.\vspace{6pt} {} \end{aligned} $$

(42)

Equations (40) and (42) are the two-dimensional extension of (33) and (35). The negative feedback in the first term on the rhs of Equation (40) is now the concentration measured by a line integral from the cell membrane towards the cell middle. The first term on the rhs of Equation (42) describes accumulation of F-actin as a result of polymerization at free barbed ends at the membrane. The polymerization rate is reduced compared to the polymerization rate in the absence of load by unitless reduction factor γ _pol(x) with values between 0 and 1 that we describe in more detail below (γ _pol = 1 corresponds to polymerization under no load, while γ _pol = 0 corresponds to stalling of polymerization). The second term in the rhs of Equation (42) is the uniform F-actin disassembly rate. The last term in Equation (42) describes constant retrograde flow (v _R is a positive number). Similar to the one-dimensional model, Equations (40) and (41) can be replaced by:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{\partial B(x,t)}{\partial t}&\displaystyle =&\displaystyle \left[r_0+r_2B(x,t)^2\right]e^{-\int_{-\infty}^{h(x,t)}F(x,y,t)/F_{sat}dy}-k_A^-B(x,t) \\ &\displaystyle &\displaystyle +D_A\frac{\partial ^2 B(x,t)}{\partial x^2}+\sigma(x,t). {} \end{array} \end{aligned} $$

(43)

Here, unknown rate constant $k_B^+$ is absorbed into the new rate constants r ₀ and r ₂ and into the amplitude of the noise that is now σ ₀.

Membrane Motion

The motion of the membrane at the leading edge was assumed to result from the balance of forces due to actin polymerization, f _pol , membrane forces due to membrane tension and conserved cell surface area, f _mem and frictional forces, f _fr, that result from the breaking of links between the cell membrane and the F-actin network [13]. Applying force balance in the y-direction (assuming variation of stresses in the x-direction can be neglected), and using units for f _pol , f _mem and f _fr of force per unit membrane length, one has for a given point on the cell membrane:

$$\displaystyle \begin{aligned} f_{pol}+f_{mem}+f_{fr}=0. {} \end{aligned} $$

(44)

The viscous resistance of the surrounding medium to the movement of the cell membrane is negligible compared to the forces of actin polymerization and membrane load [24] so it is neglected in Equation (44).

Given a local concentration of free barbed ends, B(x, t), that push against the membrane, the actin filament polymerization rate must adjust to satisfy Equation (44). Assuming that a constant fraction of the actin filament elongation is converted into F-actin network expansion along the y direction, which occurs with rate ∂h(x, t)∕∂t + v _R, there exists a force-velocity curve f _pol[B(x, t), ∂h(x, t)∕∂t + v _R]. The frictional force f _fr is also a function of the network expansion rate and the concentration of actin network links with the membrane [13]. The concentration of these links can be assumed to be approximately constant. Alternatively, f _fr could be negligible compared to the membrane force f _mem. In both cases, solving Equation (44) for the membrane extension rate gives

$$\displaystyle \begin{aligned} \frac{\partial h(x,t)}{\partial t}=\gamma_{pol}\left[B(x,t),f_{mem}(x,t)\right]v_0-v_R, {} \end{aligned} $$

(45)

where v ₀ is the network expansion rate at the leading edge in the absence of resisting force, and function γ _pol(B, f _mem), which can be evaluated at any point along the leading edge as a function of time, is the parameter that appeared in Equation (42). Observed maximum protrusion speeds for XTC cells are similar in magnitude to retrograde flow speeds [87] so v ₀ ≈ 2v _R. Forward membrane motion requires a polymerization rate greater than the retrograde flow rate, $\gamma _{pol} > \frac {1}{2}$. When $\gamma _{pol} = \frac {1}{2}$, the system is balanced and the membrane does not move, while $\gamma _{pol} < \frac {1}{2}$ leads to membrane retraction. In the remainder of this subsection we provide expressions for the restorative membrane force, f _mem(x) , which depends on the shape and extension of the leading edge, and consider two possible functional forms of γ _pol(B, f _mem). Equations (42), (43), and (45), together with the following definitions of f _mem(x) and γ _pol(B, f _mem), provide the complete model.

The membrane force includes two components: a global area-conserving force and a component due to membrane curvature, f _mem = f _area + f _curv. Component f _area is directed towards the cell center and is the same for all x at any given time; it depends only on the average extension of the lamellipodium 〈h〉_x measured from a reference extension h _ref:

$$\displaystyle \begin{aligned} f_{area}=-k_{mem}\left( \langle h \rangle _x-h_{ref}\right). {} \end{aligned} $$

(46)

The constant k _mem describes the stiffness associated with uniform increase of the adhered cell radius. The curvature component of the membrane force depends on the membrane curvature κ(x) = ∂ ² h(x, t)∕∂x ² at position x:

$$\displaystyle \begin{aligned} f_{curv}(x)=S \kappa (x), {} \end{aligned} $$

(47)

where S is a constant. As both positive and negative membrane curvatures are possible, this force may point inwards or outwards with respect to the center of the cell. The dependence of f _curv on the second derivative of h represents the effects of membrane tension [31]. More complex dependencies such as 4th order derivatives that represent elastic bending contributions are not included in Equation (47).

For a large enough lamellipodium segment, fluctuations in 〈h〉_x at steady state are very small. Thus f _area settles down to an approximately constant value independent of k _mem and h _ref such that there is no net lamellipodial extension, $\langle \gamma _{pol} \rangle _t\approx \langle \gamma _{pol} \rangle _x\approx \frac {1}{2}$. The values of k _mem and S are related to one another since they both include the effects of membrane tension. However, since only changes in S will have a significant impact in the results, k _mem and S are treated as independent variables for convenience.

Two functional forms of γ _pol were examined, corresponding to exponential (Brownian-ratchet-like) and switch-like force-velocity relationships, respectively. Both models assume that the membrane force is distributed equally among the free barbed ends at the leading edge.

Ratchet Model. In this model each filament end grows with an exponential force-velocity curve as would be expected by a Brownian ratchet mechanism [24, 69, 78],

$$\displaystyle \begin{aligned} \gamma_{pol}^{ratchet}\left[ f_{mem}(x,t),B(x,t)\right]=e^{-\alpha f_{mem}(x,t)/B(x,t)}. {} \end{aligned} $$

(48)

In Equation (48) the polymerization rate decreases exponentially with the force per filament, with a scaling factor α = δ∕k _B T = 0.66 pN⁻¹, where δ = 2.7 nm is the filament elongation length per actin monomer. The ratchet model dictates a gradual change in the actin polymerization rate in response to changes in the ratio of the concentration of free barbed ends and the membrane load. When f _mem is approximately constant, a large change in B is required to transition between maximum protrusion rates (γ _pol = 1) and maximum retraction rates (γ _pol = 0).

Switch-like Model. Interactions among filaments and attachment to the membrane [24] may give rise to nonlinearities in the force-velocity curve leading to concave-down force-velocity curves as observed during gliding motility of keratocytes [33, 48, 83], as well as stick-slip behavior (multiple branches in force-velocity relationship) [17, 21, 103]. Ryan et al. [86] did not consider the more-complex possibility of stick-slip behavior, but investigated a concave dependence given by a Hill function. In a phenomenological description, filament polymerization shifts rapidly from being unencumbered to being stalled upon increasing load:

$$\displaystyle \begin{aligned} \gamma_{pol}^{switch}\left[ f_{mem}(x,t),B(x,t)\right]=1-\frac{\left[\alpha f_{mem}(x,t)/B(x,t) \right]^n }{K_0^n+\left[ \alpha f_{mem}(x,t)/B(x,t)\right]^n}. {} \end{aligned} $$

(49)

The value n = 10 was chosen to produce a steep curve and facilitate rapid switching between protrusion and retraction. The constant K ₀ determines the location of the inflection point of the Hill function, and was chosen to preserve the fixed point of the model from the ratchet polymerization case ($\gamma _{pol} = \frac {1}{2}$ at the same h _ref and f _mem∕B). This step-like change allows a small change in B to influence a transition between near-maximum protrusion rates and near-maximum retraction rates. Similar dependencies were also assumed in models of actin network growth during protrusion of nerve growth cones [18] and keratocytes [2, 8].

5.3.2 Model Reproduces Features of Protrusion and Retraction Observed in Cells

Both the ratchet and switch-like model produce results that are in qualitative agreement with experiments, with the switch-like model exhibiting a sharper behavior (using parameters in Table 3). This model of force dependence of actin polymerization on membrane load, given by Equation (49), coupled with our model of excitable actin dynamics leads to periodic protrusion and retraction of the model membrane, accompanied by periodic increases in the amount of F-actin (Figure 8A,B). The noise term in Equation (43) generates local spikes of free barbed end concentration that spread across the leading edge, causing membrane protrusion. Actin polymerization rates peak during protrusion, leading to increases in F-actin at the membrane during those events. Accumulation of F-actin subsequently causes a reduction of the barbed end concentration, leading to retraction. Retrograde flow of the actin network distributes the F-actin throughout the lamellipodium over time. Combined with the periodic nature of the polymerization rate, this flow causes striping in the kymographs of Figure 8B.

Fig. 8

Results of the 2D lamellipodium (switch-like case). Reproduced with permission from [86] (A) Snapshot for αS = 1 with intensity representing F-actin. (B) Kymographs of the F-actin for the same simulation in A. (C) Average standard deviation of membrane position (average over all positions in simulation at steady state, over 500 s) vs membrane curvature force amplitude αS. (D) Simulation of lamellipodium response to global perturbation of membrane forces. Initial conditions same as panel A. At t = 0 the membrane force is reduced globally and αS reduced to 0.01. Simulations show the membrane expanding upwards, generating large protrusions and retractions after the perturbation. (E) Average position of leading edge over a 5-μm-wide region of panel D. (F) Linear stability analysis results for switch-like model. Top, real components of the eigenvalues vs wavenumber q. Bottom, imaginary components of eigenvalues. Units of vertical axes in 1/s.

Table 3 Parameters for two-dimensional model of lamellipodium protrusion and retraction. Values for $k_F^-$, $k_A^-$, D _A, same as Table 2.

Since the average value of B corresponds to $\gamma _{pol}= \frac {1}{2}$, fluctuations in B cause the system to switch between 0 (stall, resulting in retraction the speed of retrograde flow) and 1 (maximum polymerization rate, which is about twice the retrograde flow rate). The nonlinearity of the switch-like model around $\gamma _{pol}= \frac {1}{2}$ leads to a sharper change from protrusion to retraction as B fluctuates. Due to the weaker dependence of γ _pol on the barbed end concentration B and membrane force f _mem near $\gamma _{pol} =\frac {1}{2}$, the ratchet model produces smaller membrane distortions and membrane speeds compared to the switch-like model.

The standard deviation of membrane position depends on the magnitude of the membrane curvature force (Figure 8C). Membrane extension becomes small at the highest value of αS, indicating the increasing resistance of membrane tension to the formation of protrusions and retractions. The membrane shape and kymograph in Figure 8A,B are very similar to those observed experimentally (Figure 4A,B) with a value αS = 1.

Similar to the one-dimensional model, the two-dimensional model produces short-range traveling waves of F-actin along the arc-length of the cell, which travel along both directions similar to experiment. For both the switch-like and ratchet models of actin polymerization, the cross-correlation of the total actin concentration and the leading edge velocity is similar to that calculated for experimental measurements of LifeAct-mCherry intensity and leading edge velocity in Figure 4E. The model also reproduces the same sequence of peaks in the cross-correlation, velocity autocorrelation, and LifeAct-mCherry intensity autocorrelation as in Figure 4E at around 100 s, which indicates the period of these signals.

5.3.3 Response of Leading Edge to Membrane Force Perturbation

The two-dimensional model generates predictions for the response of lamellipodia to changes in membrane forces. Circularly shaped XTC cells spread on a substrate transition from a state of stable non-oscillating lamellipodia to a transient state of large protrusions and retractions after treatment with blebbistatin [105]. During this response, the adhered cell surface area increases while no change in the retrograde flow rate within the lamellipodium can be detected. Ryan et al. [86] suggested that the transient reduction in membrane tension after blebbistatin [57] arising from the loss of contraction in the medial cell region, contributes to this behavior, in addition to other changes in biochemical reaction rates.

A simulation of a lamellipodium undergoing a perturbation in membrane forces is shown in Figure 8D. Initial conditions were chosen such that the lamellipodium does not exhibit large protrusions and retractions (some fluctuations still remain). When the membrane curvature force and membrane area-conserving force are reduced simultaneously, the leading edge extends by a few μm and large protrusions and retractions develop, similar to the experiment in [105] (Figure 8E).

In conclusion, both the one- and two- dimensional models predict that the lamellipodium can alternate between non-oscillating and oscillating states through perturbations that influence biochemical rates (Figure 7C) or membrane forces (Figure 8D).

5.3.4 Linear Stability Analysis

To interpret the numerical results, linear stability analysis was performed on Equations (42), (43), and (45) without noise, to study the stability of homogeneous sates in parameter space. The addition of noise during simulation then generates spontaneous excitations by perturbing the stable system. Defining $F_{tot}(x,t)=\int _{-\infty }^{h(x,t)}F(x,y,t)dy$, Equation (42) becomes

$$\displaystyle \begin{aligned} \frac{\partial F_{tot}(x,t)}{\partial t}=\gamma_{pol}(x,t)k_F^+B(x,t)-k_F^-F_{tot}(x,t). {} \end{aligned} $$

(50)

Assuming a homogeneous steady state (at which $\gamma _{pol} = \frac {1}{2}$ and using h _ref = 0 μm as the reference point) we find fixed points, B(x, t) = B ^∗, F _tot(x, t) = F ^∗, and h(x, t) = h ^∗. These values can be calculated numerically after setting the time derivatives in Equations (43) (without noise), (45) and (50) equal to zero. Considering sufficiently small perturbations around the fixed points and Fourier transforming x → q, one has:

$$\displaystyle \begin{aligned} \begin{pmatrix} F_{tot}\\ B\\ h \end{pmatrix}= \begin{pmatrix} F^*\\ B^*\\ h^* \end{pmatrix}+J\begin{pmatrix} \delta F\\ \delta B\\ \delta h \end{pmatrix}. {} \end{aligned} $$

(51)

The Jacobian J for the switch-like model is:

$$\displaystyle \begin{aligned} J=\begin{pmatrix} k_F^+\left(n+2 \right)/4&-k_F^-&\frac{nk_F^+(\alpha k_{mem}-\alpha Sq^2)}{4K_0}\\ 2B^*r_2e^{-F^*/F_{sat}}-k_A^-D_Aq^2\ \ \ &\frac{-\left(r_0+r_2B^{*2}\right)}{F_{sat}}e^{-F^*/F_{sat}}&0\\ v_R n/(2 B^*)&0&\frac{v_R n\left(-\alpha k_{mem}-\alpha Sq^2\right)}{2B^*K_0} \end{pmatrix},\vspace{6pt} {} \end{aligned} $$

(52)

where K ₀ = αk _mem h ^∗∕B ^∗ and was chosen to preserve the fixed point between both force-velocity models, so that $\gamma _{pol}^{switch}=\gamma _{pol}^{ratchet}=\frac {1}{2}$ occurs at the same fixed point (B ^∗, F ^∗, h ^∗) in both models. The Jacobian for the ratchet model can be calculated similarly.

Solving for the eigenvalues of J, one finds now three instead of two wave-number dependent eigenvalue. Similar to the one-dimensional model, the signs of their real and imaginary parts result in three Cases: (I) non-oscillatory behavior, (II) unstable oscillatory behavior, and (III) a stable oscillatory behavior. Because the system gives bounded solutions, both cases II and III produce oscillatory behavior with a period given approximately by τ = 2π∕Im[λ(q)]. Similar to the one-dimensional model, this analysis showed that parameters can be chosen that result in the system being close to the boundary between linearly stable and unstable fixed points.

The stability of the homogeneous state depends on the wavenumber. The real and complex components of the eigenvalues as a function of wavenumber for the switch-like model (for the reference model parameter values) are shown in Figure 8F. For small wavenumbers, the eigenvalues correspond to Case III. With increasing wavenumber, the system progresses into Case I.

5.4 Discussion

This section highlighted how the mechanical and biochemical interactions combine nonlinearly to generate fluctuations in actin polymerization that drive lamellipodial protrusions. The near-constancy of retrograde flow in XTC cells allowed focusing on the kinetics of actin polymerization and force balance at the membrane.

Fluctuations in actin polymerization rate was also the basis of a model of waves in keratocytes [8]; however, these authors did not model explicitly the process of local membrane protrusion. The changing density of free barbed ends in the model of [8] is due to VASP which localizes on barbed ends, in the cytosol or in mature adhesions. A cooperative force-velocity curve similar to the switch model was implemented; however, unlike the model discussed in this chapter, a global constraint on membrane tension allowed only one protrusion to occur in the membrane at a time. Another related model where protrusions are driven by nucleation of new filaments is the one-dimensional model in [109, 110]. The actin network in this model consists of a semiflexible region close to the membrane and a gel like region consisting of cross-linked filaments further away.

Membrane protrusions coupled to an excitable biochemical network have also been studied in the context of Dictyostelium morphodynamics [41, 94]. These studies used versions of the phase field method to track movements of cell boundaries. In [94], the positive and negative feedbacks were due to PIP2 phosphorylation and PIP3 dephosphorylation while actin was not explicitly modeled. The model in [41] included a slow excitable system, reflecting the behavior of the signal transduction excitable network and a fast oscillatory system, reflecting the behavior of the cytoskeletal oscillatory network. Future modeling work could investigate in more detail the similarities between Dictyostelium and animal cells, combining the models of signal networks with models of cytoskeletal flows, moving cell boundaries and models of biophysical regulation of actin polymerization [37, 89].