Small World Phenomena

Abstract

In Chap. , we learnt that real-world graphs are no way random since random graphs do not exhibit the require degree distribution and clustering coefficient. This means that to explain the required properties of a real-world graph, a different null model is required. In this chapter, we will look at the Milgram’s experiments, the Columbia small world study and other similar experiments. From these experiments, we will learn the well-known small world phenomenon. We will also look at graph models that generate graphs which exhibit this phenomenon, mainly focusing on the Watts–Strogatz model and Kleinberg model. By describing case studies such as the HP Labs studies Adamic, Adar (Social networks 27 (3): 187–203, 2005, [1]), LiveJournal network Liben-Nowell et al (Proceedings of the national academy of sciences of the United States of America 102 (33): 11623–11628, 2005, [12]) and the human wayfinding study West, Leskovec (Human wayfinding in information networks. In Proceedings of the 21st international conference on World Wide Web, 2012, 619–628. ACM, [18]), we will look at how small-world phenomenon is unwittingly being exhibited in the real world.

We have all had the experience of encountering someone far from home, who turns out to share a mutual acquaintance with us. Then comes the cliché, “My it’s a small world”. Similarly, there exists a speculative idea that the distance between vertices in a very large graph is surprisingly small, i.e, the vertices co-exist in a “small world”. Hence the term small world phenomena.

Is it surprising that such a phenomenon can exist? If each person is connected to 100 people, then at the first step 100 people can be reached, the next step reaches $10^{4}$ people, $10^{6}$ at the third step, $10^{8}$ at the fourth step and $10^{10}$ at the fifth step. Taking into account the fact that there are only 7.6 billion people in the world as of December 2017, the six degrees of separation is not at all surprising. However, many of the 100 people a person is connected to may be connected to one another. Due to the presence of this overlap in connections, the five steps between every inhabitant of the Earth is a longshot.

4.1 Small World Experiment

Stanley Milgram, an American social psychologist aimed at answering the following question: “Given two individuals selected randomly from the population, what is the probability that the minimum number of intermediaries required to link them is $0, 1, 2, \ldots , k$?” [16]. This led to his famous “small-world” experiment [15] which contained two studies. The first study, called the “Kansas study” recruited residents from Wichita, Kansas and the next study, called the “Nebraska study” involved volunteers from Omaha, Nebraska. The targets for these studies were located in Massachusetts. The authors particularly selected the volunteers from these two cities because from a psychological perspective, they are very far away from the target’s location. The target for the Kansas study was the wife of a divinity student living in Cambridge, MA and that for the Nebraska study was a stockbroker who worked in Boston and lived in Sharon, MA.

The volunteers were sent a folder containing a document and a set of tracer cards, with the name and some relevant information concerning their target. The following rules were set: (i) The subjects could only send the folder to individuals they knew on a first-name basis. If the subject did not know the target on this basis, they could send it to only one other person who qualified this condition and was more likely to know the target. (ii) The folder contained a roster on which the subject and all subsequent recipients had to write their name. This roster tells the recipients all the people who were part of this chain and thereby prevents endless loop. (iii) Every participant had to fill out in the tracer card the relationship of the person they are sending it to, and send it back to the authors. This helped the authors keep track of the complete and incomplete links.

Kansas Study

The Kansas study started with 145 participants which shows a certain pattern: 56 of the chains involved a female sending the folder to another female, 58 of them involved a male sending the folder to a male, 18 of them involved a female sending the folder to a male, and 13 of the chains had a male passing the folder to a female. This shows a three times greater tendency for a same-gender passing. 123 of these participants were observed to send the folder to friends and acquaintances while the other 22 sent the folder to relatives. However, the authors indicate that this preference towards friends could be exclusive to the participants and this does not necessarily generalize to the public.

Nebraska Study

The starting population for the Nebraska study was: 296 people were selected, 100 of them were people residing in Boston designated as the “Boston random” group, 100 were blue chip stock holders from Nebraska, and 96 were randomly chosen Nebraska inhabitants called the “Nebraska random” group. Only 64 chains ($29\%$) completed, with $24\%$ by “Nebraska random”, $31\%$ by Nebraska stockholder and $35\%$ by “Boston random”. There were 453 participants who made up the intermediaries solicited by other participants as people likely to extend the chains towards the target. Similar to the Kansas study, $86\%$ of the participants sent the folders to friends or acquaintances, and the rest to relatives. Men were ten times more likely to send the document to other men than to women, while women were equally likely to send the folder to males as to females. These results were probably affected by the fact that the target was male.

Figure 4.1 shows that the average number of intermediaries on the path of the folders was between 4.4 and 5.7, depending on the sample of people chosen. The average number of intermediaries in these chains was 5.2, with considerable difference between the Boston group (4.4) and the rest of the starting population, whereas the difference between the two other sub-populations were not statistically significant. The random group from Nebraska needed 5.7 intermediaries on average. On average, 6.2 steps to make it to the target. Hence the expression “six degrees of separation”. The main conclusion was that the average path length is much smaller than expected, and that geographic location has an impact on the average length whereas other information, such as profession, did not. It was also observed that some chains moved from Nebraska to the target’s neighbourhood but then goes round in circles never making contact to complete the chain. So, social communication is restricted less by physical distance than by social distance. Additionally, a funnelling-like phenomenon was observed because $48\%$ of chains in the last link passed through only 3 of the target’s acquaintances. Thereby, showing that not all individuals in a person’s circle are equally likely to be selected as the next node in a chain.

Fig. 4.1

Frequency distribution of the number of intermediaries required to reach the target

Figure 4.2 depicts the distribution of the incomplete chains. The median of this distributions is found to be 2.6. There are two probable reasons for this: (i) Participants are not motivated enough to participate in this study. (ii) Participants do not know to whom they must send the folder in order to advance the chain towards the target.

Fig. 4.2

Frequency distribution of the intermediate chains

The authors conclude from this study that although each and every individual is embedded in a small-world structure, not all acquaintances are equally important. Some are more important than others in establishing contacts with broader social realms because while some are relatively isolated, others possess a wide circle of acquaintances.

What is of interest is that Milgram measured the average length of the routing path on the social network, which is an upper bound on the average distance (as the participants were not necessarily sending postcards to an acquaintance on the shortest path to the target). These results prove that although the world is small, the actors in this small world are unable to exploit this smallness.

Although the idea of the six degrees of separation gained quick and wide acceptance, there is empirical evidence which suggests that we actually live in a world deeply divided by social barriers such as race and class.

Income Stratification

Reference [3] in a variation of the small world study, probably sent to Milgram for review, not only showed extremely low chain completion rates (below $18\%$) but also suggested that people are actually separated by social class. This study consisted of 151 volunteers from Crestline, Ohio, divided into low-income, middle-income and high-income groups. These volunteers were to try to reach a low-income, middle-income and high-income person in Los Angeles, California. While the chain completion rate was too low to permit statistical comparison of subgroups, no low-income sender was able to complete chains to targets other than the low-income target groups. The middle and high income groups did get messages through to some people in every other income group. These patterns suggest a world divided by social class, with low-income people disconnected.

Acquaintance Networks

Milgram’s study of acquaintance networks [11] between racial groups also reveals not only a low rate of chain completion but also the importance of social barriers. Caucasian volunteers in Los Angeles, solicited through mailing lists, were asked to reach both Caucasian and African-American targets in New York. Of the 270 chains started and directed towards African-American targets, only $13\%$ got through compared to $33\%$ of 270 chains directed towards Caucasian targets.

Social Stratification

Reference [13] investigated a single urbanized area in the Northeast. The research purpose was to examine social stratification, particularly barriers between Caucasians and African-Americans. Of the 596 packets sent to 298 volunteers, 375 packets were forwarded and 112 eventually reached the target—a success rate of $30\%$. The authors concluded that,

Communication flows mainly within racial groups. Crossing the racial boundary is less likely to be attempted and less likely to be effective.

Urban Myth

Reference [10] speculates that the six degrees of separation may be an academic equivalent of an urban myth. In Psychology Today, Milgram recalls that the target in Cambridge received the folder on the fourth day since the start of the study, with two intermediaries between the target and a Kansas wheat farmer. However, an undated paper found in Milgram’s archives, “Results of Communication Project”, reveals that 60 people had been recruited as the starting population from a newspaper advertisement in Wichita. Just 3 of the 60 folders ($5\%$) reached the lady in Cambridge, passing through an average of 8 people (9 degrees of separation). The stark contrast between the anecdote and the paper questions the phenomenon.

Bias in Selection of Starting Population

Milgram’s starting population has several advantages: The starting population had social advantages, they were far from a representative group. The “Nebraska random” group and the stock holders from Nebraska were recruited from a mailing list apt to contain names of high income people, and the “Boston random” group were recruited from a newspaper advertisement. All of these selected would have had an advantage in making social connections to the stockbroker.

The Kansas advertisement was worded in a way to particularly attract sociable people proud of their social skills and confident of their powers to reach someone across class barriers, instead of soliciting a representative group to participate. This could have been done to ensure that the participants by virtue of their inherent social capital could increase the probability of the folder reaching the target with the least amount of intermediaries.

Milgram recruited subjects for Nebraska and Los Angeles studies by buying mailing lists. People with names worth selling (who would commonly occur in mailing lists) are more likely to be high-income people, who are more connected and thus more apt to get the folders through.

Reference [10] questions whether Milgram’s low success rates results from people not bothering to send the folder or does it reveal that the theory is incorrect. Or do some people live in a small, small world where they can easily reach people across boundaries while others do not. Further, the paper suggests that the research on the small world problem may be a familiar pattern:

We live in a world where social capital, the ability to make personal connections, is not widespread and more apt to be a possession of high income, Caucasian people or people with exceptional social intelligence. Certainly some people operate in small worlds such as scientists with worldwide connections or university administrators. But many low-income or minority people do not seem to. What the empirical evidence suggests is that some people are well-connected while others are not. A world not of elegant mathematical patterns where a random connector can zap us together but a more prosaic world, a lot like a bowl of lumpy oatmeal.

Results and Commentaries

People who owned stock had shorter paths (5.4) to stockbrokers than random people (6.7). People from Boston area have even closer paths (4.4). Only 31 out of the 64 chains passed through one of three people as their final step, thus not all vertices and edges are equal. The sources and target were non-random. 64 is not a sufficiently large sample to base a conclusion on. $25\%$ of the approached refused to participate. It was commonly thought that people would find the shortest path to the target but the experiment revealed that they instead used additional information to form a strategy.

When Milgram first published his results, he offered two opposing interpretations of what this six degrees of separation actually meant. On the one hand, he observed that such a distance is considerably smaller than what one would naturally intuit. But at the same time, Milgram noted that this result could also be interpreted to mean that people are on average six worlds apart:

When we speak of five intermediaries, we are talking about an enormous psychological distance between the starting and target points, a distance which seems smaller only because we customarily regard five as a small manageable quantity. We should think of the two points as being not five persons apart, but five circles of acquaintances apart—five structures apart.

Despite all this, the experiment and the resulting phenomena have formed a crucial aspect in our understanding of social networks. The conclusion has been accepted in the broad sense: social networks tend to have very short paths between essentially arbitrary pairs of people. The existence of these short paths has substantial consequences for the potential speed with which information, diseases, and other kinds of contagion can spread through society, as well as for the potential access that the social network provides to opportunities and to people with very different characteristics from one’s own.

This gives us the small world property , networks of size n have diameter O(logn), meaning that between any two nodes there exists a path of size O(logn).

4.2 Columbia Small World Study

All studies concerning large-scale social networks focused either on non-social networks or on crude proxies of social interactions. To buck this trend, Dodds, Muhamad and Watts, sociologists at Columbia University, performed a global, Internet-based social search experiment [4] to investigate the small world phenomenon in 2003. In this experiment, participants registered online and were randomly assigned one of 18 targets of various backgrounds from 13 countries. This was done to remove biases concerning race, gender, nationality, profession, etc. Participants were asked to help relay an email to their allocated target by forwarding it to social acquaintances whom they considered closer than themselves to the target. Of the 98847 individuals who had registered, about $25\%$ had initiated chains. Because subsequent senders were effectively recruited by their own acquaintances, the participation rate after the first step increased to an average of $37\%$. Including the initial and subsequent senders, data were recorded on 61168 individuals from 166 countries, constituting 24163 distinct message chains. The sender had to provide a description of how he or she had come to know the person, alongwith the type and strength of the resulting relationship.

The study observed the following: When passing messages, the senders typically used friendships in preference to business or family ties. Successful chains in comparison with incomplete chains disproportionately involved professional ties (33.9 versus $13.2\%$) rather than friendship and familial relationships (59.8 versus $83.4\%$). Men passed messages more frequently to other men ($57\%$) and women to other women ($61\%$) and this tendency to pass to a same gender contact was strengthened by about $3\%$ if the target was the same gender as the sender and similarly weakened in the opposite case. Senders were also asked why they considered their nominated acquaintance a suitable recipient. Geographical proximity of acquaintance to target and similarity of occupation accounted for atleast half of all choices. Presence of highly connected individuals appear to have limited relevance to any kind of social search involved in this experiment. Participants relatively rarely nominated an acquaintance primarily because he or she had more friends, and individuals in successful chains were far less likely than those in incomplete chains to send messages to hubs (1.6 versus $8.2\%$). There was no observation of message funneling : at most $5\%$ of messages passed through a single acquaintance of any target, and $95\%$ of all chains were completed through individuals who delivered atmost 3 messages. From these observations, the study concluded that social search is an egalitarian exercise, not one whose success depends on a small minority of exceptional individuals.

Although the average participation rate was $37\%$, compounding effects of attrition over multiple links resulted in exponential attenuation of chains as a function of their length and therefore leading to an extremely low chain completion rate. Only a mere 384 of 24163 chains reached their targets. There were three reasons for the termination of chains: (i) randomly, because of an individual’s apathy or disinclination to participate, (ii) chains get lost or are otherwise unable to reach their target, at longer chain lengths, (iii) individuals nearer the target are more likely to continue the chain, especially at shorter chain lengths. However, the random-failure hypothesis gained traction because with the exception of the first step, the attrition rates remain almost constant for all chain lengths at which there is sufficiently large N, and the senders who didn’t forward their messages after a buffer time were asked why they hadn’t participated. Less than $0.3\%$ of those contacted claimed that they couldn’t think of an appropriate recipient, suggesting that lack of interest or incentive, not difficulty, was the main reason for chain termination.

The aggregate of the 384 completed chains across targets (Fig. 4.3) gives us an average length of 4.05 as shown in Fig. 4.4.

Fig. 4.3

Average per-step attrition rates (circles) and $95\%$ confidence interval (triangles)

 

Fig. 4.4

Histogram representing the number of chains that are completed in L steps

However, this number is misleading because it represents an average only over the completed chains, and shorter chains are more likely to be computed. To correct for the $65\%$ dropout per step, the ideal frequency distribution of chain lengths, $n'(L)$, i.e, chain lengths that would be observed in hypothetical limit of zero attrition, may be estimated by accounting for observed attrition as shown in Eq. 4.1.

$$\begin{aligned} n'(L) = \frac{n(L)}{\prod \limits _{i=0}^{L-1}(1-r_{i})} \end{aligned}$$

(4.1)

where n(L) is the observed number of chains completed in L steps and $r_{L}$ is the max-likelihood attrition rate from step L to $L+1$. Figure 4.5 shows the histogram of the corrected number of chains with a poorly specified tail of the distribution, due to the small number of observed chains at large L. This gives us the median, $L_{*} = 7$, the typical ideal chain length for the hypothetical average individual. For chains that started and ended in the same country, $L_{*} = 5$, or in different countries, $L_{*} = 7$.

Fig. 4.5

“Ideal” histogram of chain lengths in Fig. 4.4 by accounting for message attrition in Fig. 4.3

The study finds that successful chains are due to intermediate to weak strength ties. It does not require highly connected hubs to succeed but instead relies on professional relationships. Small variations in chain lengths and participation rates generate large differences in target reachability. Although global social networks are searchable, actual success depends on individual incentives. Since individuals have only limited, local information about global social networks, finding short paths represents a non-trivial search effort.

On the one hand, all the targets may be reachable from random initial seeders in only a few steps, with surprisingly little variation across targets in different countries and professions. On the other hand, small differences in either the participation rates or the underlying chain lengths can have a dramatic impact on the apparent reachability of the different targets. Therefore, the results suggest that if the individuals searching for remote targets do not have sufficient incentives to proceed, the small-world hypothesis will not appear to hold, but that even the slightest increase in incentives can render social searches successful under broad conditions. The authors add that,

Experimental approach adopted here suggests that empirically observed network structures can only be meaningfully interpreted in light of actions, strategies and even perceptions of the individuals embedded in the network: Network structure alone is not everything.

4.3 Small World in Instant Messaging

Reference [5] analyzed a month of anonymized high-level communication activities within the whole of the Microsoft Messenger instant-messaging system. This study was aimed at examining the characteristics and patterns that emerge from the collective dynamics of a large number of people, rather than the actions and characteristics of individuals. The resulting undirected communication graph contained 240 million active user accounts represented as nodes and there is an edge between two users if they engaged in a two-way conversation at any point during the observation period. This graph turned out to have a giant component containing almost all of the nodes, and the distances within this giant component were very small. Indeed, the distances in the Instant Messenger network closely corresponded to the numbers from Milgram’s experiment, with an estimated average distance of 6.6, and an estimated median of 7 (as seen in Fig. 4.6). This study containing more than two million times larger than [15], gives “seven degrees of separation”. There are longer paths with lengths up to 29. A random sample of 1000 users was chosen and breadth-first search was performed from each of these separately. The reason for this sampling is because the graph was so large that performing breadth-first search from each and every one of these users would have taken an astronomical amount of time.

Fig. 4.6

Distribution of shortest path lengths

4.4 Erdös Number

A similar phenomenon is observed in collaborations among researchers. The most popular one is the Erdös number. In the collaboration graph of mathematicians as vertices and an edge between mathematicians if they have co-authored a paper, the Erdös number is the distance between a mathematician and Erdös. Figure 4.7 shows a small hand-drawn piece of the collaboration graph, with paths leading to Paul Erdös. The highlight is that most mathematicians have an Erdös number of atmost 5 and if scientists of other fields were included, it is atmost 6.

Fig. 4.7

A hand-drawn picture of a collaboration graph between various researchers. Most prominent is Erdös

4.5 Bacon Number

The compelling belief that the American actor and musician, Kevin Bacon was at the center of the Hollywood universe, led three college students to adapt the Erdös number into the Bacon number. Here, a collaboration graph has Hollywood performers as nodes and edge between nodes indicates that the performers have appeared in a movie. The Bacon number of a performer gives the number of steps to Kevin Bacon. The average is 2.9 and there is a challenge to find one that is greater than 5. (there is one with Bacon number 8 that involves a 1928 Soviet pirate movie). Only $12\%$ of all performers cannot be linked to Bacon. There is also a computer game called the “Six Degrees of Kevin Bacon”, where players are required to find the shortest path between an arbitrary actor and Kevin Bacon.

4.6 Decentralized Search

Given a graph, s has to send a message to t, passing it along the edges of this graph, so that the least number of steps is taken. s only knows the location of its neighbours as well as the location of the target t, and does not know the neighbours of anyone else except itself. Each vertex has its local information, i.e, a vertex u in a given step has knowledge of:

• 1. The set of local contacts among among all the vertices

• 2. The location of the target t

• 3. The locations and long-range contacts of all the vertices who were part of this message chain

Given this information, u must choose one of its contacts v to pass on the message.

4.7 Searchable

A graph is said to be searchable or navigable if its diameter is $O((log|V|)^{\beta })$, i.e, the expected delivery time of a decentralized algorithm is polylogarithmic. Therefore, a non-searchable or a non-navigable graph is one which has a diameter of $O(|V|^{\alpha })$, i.e, the expected delivery time of a decentralized algorithm is not polylogarithmic.

In other words, a graph is searchable if the vertices are capable of directing messages through other vertices to a specific vertex in only a few hops.

4.8 Other Small World Studies

Small World in an Interviewing Bureau

Reference [7] conducted a small-world study where they analysed 10, 920 shortest path connections and small-world routes between 105 members of an interviewing bureau. They observed that the mean small-world path length (3.23) is $40\%$ longer than the mean of the actual shortest paths (2.30), showing that mistakes are prevalent. A Markov model with a probability of simply guessing an intermediary of 0.52 gives an excellent fit to these observations, thus concluding that people make the wrong small-world choice more than half the time.

Reverse Small World Study

Reference [6] attempted to examine and define the network of a typical individual by discovering how many of her acquaintances could be used as first steps in a small-world procedure, and for what reasons. The starting population were provided background information about each of 1267 targets in the small-world experiment and asked to write down their choice, amongst the people they knew, for the first link in a potential chain from them to each of these targets. The subjects provided information on each choice made and the reason that choice had been made. The reason could be in one or more of four categories: something about the location of the target caused the subject to think of her choice; the occupation of the target was responsible for the choice; the ethnicity of the target; or some other reason.

The study drew the following conclusions. First, a mean of 210 choices per subject. However, only 35 choices are necessary to account for half the world. Of the 210, 95 ($45\%$) were chosen most often for location reasons, 99 ($47\%$) were chosen most often for occupation reasons, and only $7\%$ of the choices were mainly based on ethnicity or other reasons. Second, the choices were mostly friends and acquaintances, and not family. For any given target, about $82\%$ of the time, a male is likely to be chosen, unless both subject and target are female, or if the target has a low-status occupation. Over $64\%$ of the time, this trend appears even when female choices are more likely. Lastly, the order of the reasons given were: location, occupation and ethnicity.

The authors conclude that the strong similarity between predictions from these results and the results of [16] suggests that the experiment is an adequate proxy for behavior.

4.9 Case Studies

4.9.1 HP Labs Email Network

Reference [1] simulates small-world experiments on HP Lab email network, to evaluate how participants in a small world experiment are able to find short paths in a social network using only local information about their immediate contacts.

In the HP Lab network, a social graph is generated where the employees are the vertices and the there is an edge between vertices if there has been atleast 6 emails exchanged between the corresponding employees during the period of the study. Mass emails such as announcements sent to more than 10 individuals at once were removed to minimize likelihood of one-sided communications. With these conditions, Fig. 4.8 shows the graph having 430 vertices with a median of 10 edges and a mean of 12.9. The degree distribution, Fig. 4.9, is highly skewed with an exponential tail. Here, each individual can use knowledge only of their own email contacts, but not their contacts’ contacts, to forward the message. In order to avoid loops, the participants append their names to the message as they receive it.

Fig. 4.8

Email communication between employees of HP Lab

Fig. 4.9

Degree distribution of HP Lab network

The first strategy involved sending the message to an individual who is more likely to know the target by virtue of the fact that he or she knows a lot of people. Reference [2] has shown that this strategy is effective in networks with power law distribution with exponent close to 2. However, as seen in Fig. 4.9, this network does not have a power law, but rather an exponential tail, more like a Poisson distribution. Reference [2] also shows that this strategy performs poorly in the case of Poisson distribution. The simulation confirms this with a median of 16 and an average of 43 steps required between two randomly chosen vertices.

The second strategy consists of passing messages to the contact closest to the target in the organizational hierarchy. In the simulation, the individuals are given full knowledge of organizational hierarchy but they have no information about contacts of individuals except their own. Here, the search is tracked via the hierarchical distance (h-distance) between vertices. The h-distance is computed as follows: individuals have h-distance 1 to their manager and everyone they share a manager with. Then, the distances are recursively assigned, i.e, h-distance of 2 to their first neighbour’s neighbour, 3 to their second neighbour’s neighbour, and so on. This strategy seems to work pretty well as shown in Figs. 4.10 and 4.11. The median number of steps was only 4, close to the median shortest path of 3. The mean was 5 steps, slightly higher than the median because of the presence of a four hard to find individuals who had only a single link. Excluding these 4 individuals as targets resulted in a mean of 4.5 steps. This result indicates that not only are people typically easy to find, but nearly everybody can be found in a reasonable number of steps.

Fig. 4.10

Probability of linking as a function of the hierarchical distance

 

Fig. 4.11

Probability of linking as a function of the size of the smallest organizational unit individuals belong to

The last strategy was based on the target’s physical location. Individuals’ locations are given by their building, the floor of the building, and the nearest building post to their cubicle. Figure 4.12 shows the email correspondence mapped onto the physical layout of the buildings. The general tendency of individuals in close physical proximity to correspond holds: over $87\%$ percent of the 4000 emails are between individuals on the same floor. From Fig. 4.13, we observe that geography could be used to find most individuals, but was slower, taking a median number of 6 steps, and a mean of 12.

Fig. 4.12

Email communication mapped onto approximate physical location. Each block represents a floor in a building. Blue lines represent far away contacts while red ones represent nearby ones

Fig. 4.13

Probability of two individuals corresponding by email as a function of the distance between their cubicles. The inset shows how many people in total sit at a given distance from one another

The study concludes that individuals are able to successfully complete chains in small world experiments using only local information. When individuals belong to groups based on a hierarchy and are more likely to interact with individuals within the same small group, then one can safely adopt a greedy strategy—pass the message onto the individual most like the target, and they will be more likely to know the target or someone closer to them.

4.9.2 LiveJournal Network

Reference [12] performed a study on the LiveJournal online community, a social network comprising of 1.3 million bloggers (as of February 2004). A blog is an online diary, often updated daily, typically containing reports on the user’s personal life, reactions to world events, and commentary on other blogs. In the LiveJournal system, each blogger also explicitly provides a profile, including geographical location among other information, and a list of other bloggers whom he or she considers to be a friend. Of these 1.3 million bloggers, there were about half a million in the continental United States who listed a hometown and state which could be mapped to a latitude and a longitude. Thus, the discussion of routing was from the perspective of reaching the home town or city of the destination individual.

They defined “u is a friend of v” relationship, by the explicit appearance of blogger u in the list of friends in the profile of blogger v. Let d(u, v) denote the geographic distance between u and v. There are about 4 million friendship links in this directed network, an average of about eight friends per user. It was observed that $77.6\%$ of the graph formed a giant component. Figure 4.14 depicts the in-degree and the out-degree distributions for both the full network and the network of the users who could be geographically mapped. The parabolic shape shows that the distribution is more log-normal than a power law.

Fig. 4.14

In-degree and out-degree distributions of the LiveJournal network

They perform a simulated version of the message-forwarding experiment in the LiveJournal, using only geographic information to choose the next message holder in a chain. This was to determine whether individuals using purely geographic information in a simple way can succeed in discovering short paths to a destination city. This approach using a large-scale network of real-world friendships but simulating the forwarding of messages, allowed them to investigate the performance of simple routing schemes without suffering from a reliance on the voluntary participation of the people in the network.

In the simulation, messages are forwarded in the following manner: if a person s currently holds the message and wants to eventually reach a target t, then she considers her set of friends and chooses as the next step in the chain the friend in this set who is geographically closest to t. If s is closer to the target than all of his or her friends, then s gives up, and the chain terminates. When sources and targets are chosen randomly, we find that the chain successfully reaches the city of the target in $\approx {13\%}$ of the trials, with a mean completed-chain length of slightly more than four (as shown in Fig. 4.15).

Fig. 4.15

In each of 500, 000 trials, a source s and target t are chosen randomly; at each step, the message is forwarded from the current message-holder u to the friend v of u geographically closest to t. If $d(v, t) > d(u, t)$, then the chain is considered to have failed. The fraction f(k) of pairs in which the chain reaches t’s city in exactly k steps is shown ($12.78\%$ chains completed; median 4, $\mu = 4.12$, $\sigma = 2.54$ for completed chains). (Inset) For $80.16\%$ completed, median 12, $\mu = 16.74$, $\sigma = 17.84$; if $d(v, t) > d(u, t)$ then u picks a random person in the same city as u to pass the message to, and the chain fails only if there is no such person available.

The authors conclude that, even under restrictive forwarding conditions, geographic information is sufficient to perform global routing in a significant fraction of cases. This simulated experiment may be taken as a lower bound on the presence of short discoverable paths, because only the on-average eight friends explicitly listed in each LiveJournal profile are candidates for forwarding. The routing algorithm was modified: an individual u who has no friend geographically closer to the target instead forwards the message to a person selected at random from u’s city. Under this modification, chains complete $80\%$ of the time, with median length 12 and mean length 16.74 (see Fig. 4.15). The completion rate is not $100\%$ because a chain may still fail by landing at a location in which no inhabitant has a friend closer to the target. This modified experiment may be taken as an upper bound on completion rate, when the simulated individuals doggedly continue forwarding the message as long as any closer friend exists.

To closely examine the relationship between friendship and geographic distance, for each distance $\delta$, $P(\delta )$ denotes the proportion of pairs u, v separated by distance $d(u, v) = \delta$ who are friends. As $\delta$ increases, it is observed that $P(\delta )$ decreases, indicating that geographic proximity indeed increases the probability of friendship (as shown in Fig. 4.16). However, for distances larger than $\approx {1,000}$ km, the $\delta$-versus-$P(\delta )$ curve approximately flattens to a constant probability of friendship between people, regardless of the geographic distance between them. Figure 4.16 shows that $P(\delta )$ flattens to $P(\delta ) \approx {5.0} \times 10^{-6}$ for large distances $\delta$; the background friendship probability $\epsilon$ dominates $f(\delta )$ for large separations $\delta$. It is thus estimated that $\epsilon$ is $5.0 \times 10^{-6}$ . This value can be used to estimate the proportion of friendships in the LiveJournal network that are formed by geographic and non-geographic processes. The probability of a non-geographic friendship between u and v is $\epsilon$, so on average u will have $\approx {2.5}$ non-geographic friends. An average person in the LiveJournal network has eight friends, so $\approx {5.5}$ of an average person’s eight friends ($69\%$ of his or her friends) are formed by geographic processes. This statistic is aggregated across the entire network: no particular friendship can be tagged as geographic or non-geographic by this analysis; friendship between distant people is simply more likely (but not guaranteed) to be generated by the nongeographic process. However, this analysis does estimate that about two-thirds of LiveJournal friendships are geographic in nature. Figure 4.16 shows the plot of geographic distance $\delta$ versus the geographic-friendship probability $f(\delta ) = P(\delta ) - \epsilon$. The plot shows that $f(\delta )$ decreases smoothly as $\delta$ increases. This shows that any model of friendship that is based solely on the distance between people is insufficient to explain the geographic nature of friendships in the LiveJournal network.

Fig. 4.16

a For each distance $\delta$ , the proportion P($\delta$) of friendships among all pairs u, v of LiveJournal users with $d(u, v) = \delta$ is shown. The number of pairs u,v with $d(u, v) = \delta$ is estimated by computing the distance between 10, 000 randomly chosen pairs of people in the network. b The same data are plotted, correcting for the background friendship probability: plot distance $\delta$ versus $P(\delta ) - 5.0 \times 10^{-6}$

Since, geographic distance alone is insufficient as the basis for a geographical model, this model uses rank as the key geographic notion: when examining a friend v of u, the relevant quantity is the number of people who live closer to u than v does. Formally, the rank of v with respect to u is defined as given in Eq. 4.2.

$$\begin{aligned} rank_{u}(v) := |\{w: d(u, w) < d(u, v)\}| \end{aligned}$$

(4.2)

Under the rank-based friendship model, the probability that u and v are geographic friends is modelled as in Eq. 4.3

$$\begin{aligned} Pr[u\rightarrow v] \alpha \frac{1}{rank_{u}(v)} \end{aligned}$$

(4.3)

Under this model, the probability of a link from u to v depends only on the number of people within distance d(u, v) of u and not on the geographic distance itself; thus the non-uniformity of LiveJournal population density fits naturally into this framework.

The relationship between $rank_{v}(u)$ and the probability that u is a friend of v shows an approximately inverse linear fit for ranks up to $\approx {100,000}$ (as shown in Fig. 4.17). An average person in the network lives in a city of population 1, 306. Thus in Fig. 4.17 the same data is shown where the probabilities are averaged over a range of 1, 306 ranks.

Fig. 4.17

The relationship between friendship probability and rank. The probability P(r) of a link from a randomly chosen source u to the rth closest node to u, i.e, the node v such that $rank_{u}(v) = r$, in the LiveJournal network, averaged over 10, 000 independent source samples. A link from u to one of the nodes $S_{\delta } = \{v:d(u, v) = \delta \}$, where the people in $S_{\delta }$ are all tied for rank $r+1, \ldots , r+|S_{\delta }|$, is counted as a ($\frac{1}{|S_{\delta }|}$) fraction of a link for each of these ranks. As before, the value of $\epsilon$ represents the background probability of a friendship independent of geography. a Data for every 20th rank are shown. b The data are averaged into buckets of size 1, 306: for each displayed rank r, the average probability of a friendship over ranks $\{r-652, \ldots , r+653\}$ is shown. c and b The same data are replotted (unaveraged and averaged, respectively), correcting for the background friendship probability: we plot the rank r versus $P(r) - 5.0 \times 10^{-6}$

So, message passing in the real-world begins by making long geography-based hops as the message leaves the source and ends by making hops based on attributes other than geography. Thus there is a transition from geography-based to nongeography-based routing at some point in the process.

4.9.3 Human Wayfinding

Given a network of links between concepts of Wikipedia, [18] studied how more than 30000 trajectories from 9400 people find the shortest path from a given start to a given target concept following hyperlinks. Formally, they studied the game of Wikispeedia in which players (information seekers) are given two random articles with the aim to solve the task of navigating from one to the other by clicking as few hyperlinks as possible. However, the players are given no knowledge of the global structure and must rely solely on the local information they see on each page—the outgoing links connecting current articles to its neighbours—and on expectation about which articles are likely to be interlinked. The players are allowed to use the back button of the browser at any point in the game. This traversal from one webpage to another by information seekers is characterized as human wayfinding.

On first thought, it might obviously occur that each game of Wikispeedia is an instance of decentralized search. Therefore, employing a decentralized search algorithm will solve the problem. However, there is a subtle difference. In a decentralized search problem, each node works with local information and independently forwards the message to the next node, forfeiting control to the successor. While in Wikispeedia, although the information seeker has only local knowledge about the unknown network, she stays in control all the way and can thus form more elaborate strategies than in a multi-person scenario.

Human wayfinding is observed to take two approaches. The first approach is where players attempt to first find a hub. A hub is a high-degree node that is easily reachable from all over the graph and that has connections to many regions of this graph. Then they constantly decrease the conceptual distance to the target thereafter by following content features. While this strategy is sort of “playing it safe” and thus commonly preferred by most of the players, it is observed that this is not the most efficient. The other approach is to find the shortest paths between the articles while running the risk of repeatedly getting lost. This technique is a precarious one but is efficient, successful and thus particularly used by the top players.

This study identified aggregate strategies people use when navigating information spaces and derived insights which could be used in the development of automatically designing information spaces that humans find intuitive to navigate and identify individual links that could make the Wikipedia network easier to navigate.

Based on this study, we understand that although global information was unavailable, humans tend to be good at finding short paths. This could be because they possess vast amounts of background knowledge about the world, which they leverage to make good guesses about possible solutions. Does this mean that human-like high-level reasoning skills are really necessary for finding short paths?

In an attempt to answer this question, [17] designed a number of navigation agents that did not possess these skills, instead took decisions based solely on numerical features.

The agents were constrained by several rules to make them behave the same way humans would, thereby levelling the playing field. The agents could only use local node features independent of global information about the network. Only nodes visited so far, immediate neighbours, and the target may play a role in picking the next node. The user can only follow links from the current page or return to its immediate predecessor by clicking the back button. Jumping between two unconnected pages was not possible, even if they were both visited separately before.

The agent used the navigation algorithm given in Algorithm 6. Here, s is the start node, t is the target node and V is the evaluation function. V is used to score each neighbour $u'$ of the current node u and is a function of u, $u'$ and t only. Thus, $V(u'|u,t)$ captures the likelihood of u’s neighbour, $u'$ being closer to t than u is.

The following are the candidates for the evaluation V:

• Degree-based navigation (DBN): $V(u'|u,t) = out-degree(u')$

• Similarity-based navigation (SBN): $V(u'|u,t) = tf-idf(u',t)$

• Expected value navigation (EVN): $V(u'|u,t) = 1 - (1 - q_{u't})^{out-degree(u')}$

• Supervised learning to learn $V_{i}$ for every iteration i

• Reinforcement learning learns V i for every iteration i

The supervised and reinforcement learning were found to obtain the best results. With the exception of DBN, even the fairly simple agents were found to do well.

The study observed that agents find shorter paths than humans on average and therefore, no sophisticated background knowledge or high-level reasoning is required for navigating networks. However, humans are less likely to get totally lost during search because they typically form robust high-level plans with backup options, something automatic agents cannot do. Instead, agents compensate for this lack of smartness with increased thoroughness: since they cannot know what to expect, they always have to inspect all options available, thereby missing out on fewer immediate opportunities than humans, who focused on executing a premeditated plan, may overlook shortcuts. In other words, humans have a common sense expectation about what links may exist and strategize on the route to take before even making the first move. Following through on this premeditated plan, they might often just skim pages for links they already expect to exist, thereby not taking notice of shortcuts hidden in the abundant textual article contents. These deeper understanding of the world is the reason why their searches fail completely less often: instead of exact, narrow plans, they sketch out rough, high-level strategies with backup options that are robust to contingencies.

4.10 Small World Models

We have observed that random graphs have a low clustering and a low diameter, a regular graph has a high clustering and a high diameter. But, a real-world graph has a clustering value comparable with that of a regular graph but a diameter of the order of that of a random graph. This means that neither the random graph models nor a regular graph generator is the best model that can produce a graph with clustering and diameter comparable with those of real-world graphs. In this section, we will look at models that are capable of generating graphs that exhibit the small world property.

4.10.1 Watts–Strogatz Model

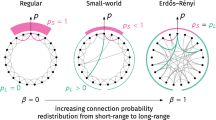
In the Watts–Strogatz model, a generated graph has two kinds of edges, local and long-range. Start with a set V of n points spaced uniformly on a circle, and joins each point by an edge to each of its k nearest neighbours, for a small constant k. These form the local edges which ensure the desired high value of clustering. But this still has a higher than desired diameter. In order to reduce the diameter, we introduce the long-range edges. First, add and remove edges to create shortcuts between remote parts of the graph. Next, for each edge with probability p, move the other end to a random vertex. This gives the small world property for the graph which is pictorially depicted in Fig. 4.18.

Fig. 4.18

Depiction of a regular network proceeding first to a small world network and next to a random network as the randomness, p increases

This Watts–Strogatz model provides insight on the interplay between clustering and small world. It helps capture the structure of many realistic networks and accounts for the high clustering of real-world networks. However, this model fails to provide the correct degree distribution.

The Watts–Stogatz model having $O(|V|^{\frac{2}{3}})$ is a non-searchable graph.

4.10.2 Kleinberg Model

In this model, [8] begins with a set of nodes that are identified with a set of lattice points in a $n\times n$ square, $\{(i,j): i\ \epsilon \ \{1,2,\ldots ,n\}, j\ \epsilon \ \{1,2,\ldots ,n\}\}$ and the lattice distance between two nodes (i,j) and (k,l) is the number of lattice steps between them $d((i,j),(k,l)) = |k-i| + |l-j|$. For a universal constant $p\ge 1$, node u has a directed edge to every other node within lattice distance p. These are node u’s local contacts. For universal constants $q\ge 0$ and $r\ge 0$, we construct directed edges from u to q other nodes using independent random trials; the $i^{th}$ directed edge from u has endpoint v with probability proportional to $[d(u,v)]^{-r}$. These are node u’s long-range contacts. When r is very small, the long range edges are too random to facilitate decentralized search (as observed in Sect. 4.10.1), when r is too large, the long range edges are not random enough to provide the jumps necessary to allow small world phenomenon to be exhibited.

This model can be interpreted as follows: An individual lives in a grid and knows her neighbours in all directions for a certain number of steps, and the number of her acquaintances progressively decrease as we go further away from her.

The model gives the bounds for a decentralized algorithm in Theorems 6, 7 and 8.

Theorem 6

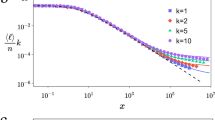
There is a constant $\alpha _{0}$, depending on p and q but independent of n, such that when $r = 0$, the expected delivery time of any decentralized algorithm is atleast $\alpha _{0}n^{\frac{2}{3}}$

As n increases, decentralized algorithm performs best at q closer and closer to 2 (Fig. 4.19). One way to look at why this value of 2 leads to best performance is that at this value, the long range edges are being formed in a way that is spread uniformly over all different scales of resolution. This allows people fowarding the message to consistently find ways of reducing their distance to the target, no matter the distance from it.

Fig. 4.19

Log of decentralized search time as a function of the exponent

Theorem 7

There is a decentralized algorithm $\mathcal {A}$ and a constant $\alpha _{2}$, independent of n, so that when $r = 2$ and $p = q = 1$, the expected delivery time of $\mathcal {A}$ is atmost $\alpha _{2}(logn)^{2}$.

When the long-range contacts are formed independent of the geometry of the grid (as is the case in Sect. 4.10.1), short chains will exist but the nodes will be unable to find them. When long-range contacts are formed by a process related to the geometry of the grid in a specific way, however, then the short chains will still form and the nodes operating with local knowledge will be able to construct them.

Theorem 8

• 1. Let $0 \le r < 2$. There is a constant $\alpha _{r}$, depending on p, q, r but independent of n, so that the expected delivery time of the decentralized algorithm is atleast $\alpha _{r}n^{\frac{2-r}{3}}$.

• 2. Let $r > 2$. There is a constant $\alpha _{r}$, depending on p, q, r but independent of n, so that the expected delivery time of any decentralized algorithm is atleast $\alpha _{r}n^{\frac{r-2}{r-1}}$.

Kleinberg’s model is a searchable graph because its diameter is $O((log|V|)^{2})$.

4.10.2.1 Hierarchical Model

Consider a hierarchy using b-ary tree T for a constant b. Let V denote the set of leaves of T and n denote the size of V. For two leaves v and w, h(v, w) denotes the height of the least common ancestor of v and w in T and $f(\cdot )$ determines the link probability. For each node $v\in V$, a random link to w is created with probability proportional to f(h(v, w)), i.e, the probability of choosing w is $f(h(v, w))/\sum \limits _{x\ne v}f(h(v, x))$. k links out of each node v is created in this way, choosing endpoint w each time independently and with repetitions allowed. This results in a graph G on the set V. Here the out-degree is $k = clog^{2}n$ for constant c. This process of producing G is the hierarchical model with exponent $\alpha$ if f(h) grows asymptotically like $b^{-\alpha h}$.

$$\begin{aligned} \lim _{h\rightarrow \infty } \frac{f(h)}{b^{-\alpha ' h}} = 0\ \forall \ \alpha ' < \alpha \ and\ \lim _{h\rightarrow \infty } \frac{b^{-\alpha '' h}}{f(h)} = 0\ \forall \ \alpha '' > \alpha \end{aligned}$$

A decentralized algorithm has knowledge of the tree T, and knows the location of a target leaf that it must reach; however, it only learns the structure of G as it visits nodes. The exponent $\alpha$ determines how the structures of G and T are related.

Theorem 9

• 1. There is a hierarchical model with exponent $\alpha = 1$ and polylogarithmic out-degree in which decentralized algorithm can achieve search time of O(logn).

• 2. For every $\alpha \ne 1$, there is no hierarchical model with exponent $\alpha$ and polylogarithm out-degree in which a decentralized algorithm can achieve polylogarithm search time.

4.10.2.2 Group-Induced Model

A group structure consists of an underlying set of nodes and a collection of subsets of V. The collection of groups must include V itself, and must satisfy the following two properties, for constants $\lambda < 1$ and $\beta > 1$.

• 1. If R is a group of size $q \ge 2$ containing a node v, then there is a group $R' \subseteq R$ containing v that is strictly smaller than R, but has size atleast $\lambda q$.

• 2. If $R_{1}, R_{2}, \ldots$ are groups that all have sizes atmost q and all contain a common node v, then their union has size almost $\beta q$.

Given a group structure (V,{$R_{i}$}), and a monotone non-increasing function $f(\cdot )$, we generate a graph on V in the following manner. For two nodes v and w, q(v, w) denotes the minimum size of the group containing both v and w. For each node $v\ \epsilon \ V$, we create a random link to w with probability proportional to f(q(v, w)). Repeating this k times independently yields k links out of v. This is referred to as group-induced model with exponent $\alpha$ if f(q) grows asymptotically like $q^{-\alpha }$.

$$\begin{aligned} \lim _{h\rightarrow \infty } \frac{f(q)}{q^{-\alpha }} = 0\ \forall \ \alpha ' < \alpha \ and\ \lim _{h\rightarrow \infty } \frac{q^{-\alpha ''}}{f(q)} = 0\ \forall \ \alpha '' > \alpha \end{aligned}$$

A decentralized search algorithm in this network is given knowledge of the full group structure, and must follow links of G to the designated target t.

Theorem 10

• 1. For every group structure, there is a group-induced model with exponent $\alpha = 1$ and polylogarithm out-degree in which a decentralized algorithm can achieve search time of O(logn).

• 2. For every $\alpha < 1$, there is no group-induced model with exponent $\alpha$ and polylogarithm out-degree in which a decentralized algorithm can achieve polylogarithm search time.

4.10.2.3 Hierarchical Models with a Constant Out-Degree

To start with a hierarchical model and construct graphs with constant out-degree k, the value of k must be sufficiently large in terms of other parameters of this model. To obviate the problem that t itself may have no incoming links, the search problem is relaxed to finding a cluster of nodes containing t. Given a complete b-ary tree T, where b is a constant, let L denote the set of leaves of T and m denote the size of L. r nodes are placed at each leaf of T, forming a set V of $n = mr$ nodes total. A graph G on V is defined for a non-increasing function $f(\cdot )$, we create k links out of each node $v\in V$, choosing w as an endpoint with probability proportional to f(h(v, w)). Each set of r nodes at a common leaf of T is referred to as a cluster and the resolution of the hierarchical model is defined to be r.

A decentralized algorithm is given the knowledge of T, and a target node t. It must reach any node in the cluster containing t.

Theorem 11

• 1. There is a hierarchical model with exponent $\alpha = 1$, constant out-degree and polylogarithmic resolution in which a decentralized algorithm can achieve polylogarithmic search time.

• 2. For every $\alpha \ne 1$, there is no hierarchical model with exponent $\alpha$, constant out-degree and polylogarithmic resolution in which a decentralized algorithm can achieve polylogarithmic search time.

The proofs for Theorems 9, 10 and 11 can be found in [9].

4.10.3 Destination Sampling Model

Reference [14] describes an evolutionary model which by successively updating shortcut edges of a small-world graph generates configurations which exhibit the small world property.

The model defines V as a set of vertices in a regular lattice and E as the set of long-range (shortcut) edges between vertices in V. This gives a digraph G(V, E). Let $G'$ be G augmented with edges going both ways between each pair of adjacent vertices in lattice.

The configurations are generated in the following manner: Let $G_{s} = (V, E_{s})$ be a digraph of shortcuts at time s and $0< p < 1$. Then $G_{s+1}$ is defined as:

• 1. Choose $y_{s+1}$ and $z_{s+1}$ uniformly from V.

• 2. If $y_{s+1} \ne z_{s+1}$ do a greedy walk in $G_{s}'$ from $y_{s}$ to $z_{s}$. Let $x_{0} = y_{s+1}, x_{1}, \ldots , x_{t} = z_{s+1}$ denote the points of this walk.

• 2. For each $x_{0}, x_{1}, \ldots , x_{t-1}$ with atleast one shortcut, independently with probability p replace a randomly chosen shortcut with one to $z_{s+1}$.

Updating shortcuts using this algorithm eventually results in a shortcut graph with greedy path-lengths of $O(log^{2}n)$. p serves to dissociate shortcut from a vertex with its neighbours. For this purpose, the lower the value of $p > 0$ the better, but very small values of p will lead to slower sampling.

Each application of this algorithm defines a transition of Markov chain on a set of shortcut configurations. Thus for any n, the Markov chain is defined on a finite state space. Since this chain is irreducible and aperiodic, the chain converges to a unique stationary distribution.

Problems

Download the General Relativity and Quantum Cosmology collaboration network available at https://snap.stanford.edu/data/ca-GrQc.txt.gz.

For the graph corresponding to this dataset (which will be referred to as real world graph), generate a small world graph and compute the following network parameters:

33

Degree distribution

34

Short path length distribution

35

Clustering coefficient distribution

36

WCC size distribution

37

For each of these distributions, state whether or not the small world model has the same property as the real world graph

38

Is the small world graph generator capable of generating graphs that are representative of real world graphs?